
10.9 Trasmissione del calore
Il primo principio della termodinamica riguarda gli scambi energetici che avvengono durante una trasformazione termodinamica.
Lo scambio di lavoro concerne il lavoro meccanico macroscopico legato allo spostamento di qualche oggetto, ad esempio la parete mobile di un recipiente pieno di gas.
Lo scambio di calore presuppone invece un meccanismo microscopico, cui accenneremo in seguito, e avviene quando due corpi sono a contatto, direttamente o attraverso altri corpi.
Lo scambio e anche il trasporto di calore entro un sistema possono avvenire tramite tre meccanismi distinti, che nel loro complesso sono indicati come trasmissione del calore: conduzione, convezione e irraggiamento termici. I tre meccanismi operano sempre in presenza di una differenza di temperatura tra sistema e ambiente o all’interno dello stesso sistema.
Conduzione di calore
Consideriamo un corpo esteso in cui la temperatura non sia uniforme e tracciamo le superficie isoterme, cioè il luogo dei punti in cui la funzione T (x, y, z) assume un valore costante, per esempio T1 sulla superficie isoterma S1, T2 su S2 , ecc.
La legge fenomenologica che regola la conduzione del calore è la legge di Fourier, formulata nel 1815. Se dS è un elemento di una superficie isoterma, dT / dn il modulo del gradiente di temperatura, ortogonale a dS e diretto nel verso delle temperature crescenti, il calore che passa attraverso dS nel tempo dt è dato da
Legge di Fourier

Conducibilità termica
la grandezza k, detta conducibilità o conduttività termica, è tipica del materiale ed è in generale funzione della temperatura (le unità di misura sono J/m s K).
Il segno negativo in (10.19) indica che il flusso di calore avviene nel senso in cui la temperatura diminuisce, cioè nel verso opposto al gradiente di temperatura, dalla regione a temperatura maggiore a quella a temperatura minore.
L’esistenza di un gradiente di temperatura in un corpo, ovvero la mancanza di equilibrio termico, indica che c’è una trasmissione di calore attraverso il corpo, regolata dalla legge di Fourier.
La conducibilità termica varia da sostanza a sostanza anche di diversi ordini di grandezza, come appare nella tabella 10.8 dove sono riportate anche le temperature a cui si riferisce il valore di k.

I metalli sono buoni conduttori termici, i gas e i dielettrici, eccetto il diamante, sono invece cattivi conduttori termici; i liquidi sono in una situazione intermedia.
La conducibilità termica ha una diversa dipendenza dalla temperatura per le varie sostanze. Nei gas semplici k cresce debolmente con la temperatura, in proporzione alla radice quadrata della stessa. Anche nei liquidi e nei dielettrici non vi è una notevole variazione con la temperatura. Nei metalli puri la conducibilità presenta sempre un massimo a bassa temperatura, che è due o tre ordini di grandezza maggiore del valore a temperatura ambiente. Il rame, per esempio, ha un massimo nella conducibilità termica a circa 20 K, con un valore di 2 · 104 J/ m s K da confrontare con 3.9 · 102 J/m s K a temperatura ambiente; a 2 K il valore è di 4 · 103 J/m s K.

Figura 10.11
Come vedremo nel secondo volume, esiste un legame tra conduttività termica e conduttività elettrica.
Per illustrare l’uso di (10.19) consideriamo un problema particolare, quello della parete piana indefinita, posta tra due ambienti alle temperature costanti T1 e T2 , con T1 > T2 . Lo spessore della parete è s (vedi figura 10.11), k la conduttività termica, assunta costante. L’elemento di parete indicato in figura ha superficie dS (ortogonale all’asse x), spessore dx, volume dS dx e contiene la massa dm = ρ dV = ρ dS dx ; ρ è la densità costante del materiale.
Attraverso l’elemento di superficie dS (con coordinata x) viene ceduto a dm il calore dQ1 , mentre dm cede dQ2 attraverso un elemento di superficie dS (con coordinata x + dx):

nel passaggio dal primo al secondo membro di dQ2 abbiamo utilizzato lo sviluppo
in serie di Taylor di arrestandoci al primo termine.
Complessivamente l’elemento di massa dm riceve da sinistra il calore dQ1 e cede a destra il calore dQ2 , per cui assorbe
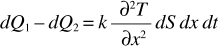
e si ha in corrispondenza un aumento di temperatura, secondo (10.9):
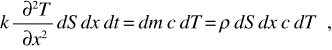
essendo c il calore specifico del materiale. Pertanto

L’equazione (10.20) regola la variazione di temperatura in funzione del tempo e della posizione all’interno della parete, con le condizioni al contorno T = T1 per x = 0 e T = T2 per x = s in qualsiasi istante.
A regime, quando la temperatura in ciascun punto ha raggiunto un valore stazionario, costante nel tempo, si ha
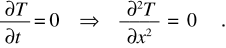
Di conseguenza in regime stazionario la soluzione di (10.20) deve avere la forma T = a x + b, cioè la temperatura deve essere una funzione lineare di x. Imponendo per x = 0 T1 = b e per x = s T 2 = a s + b si ottiene
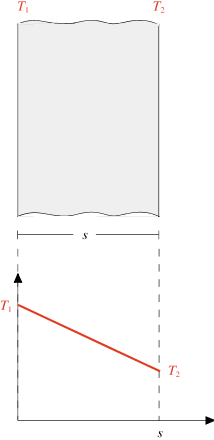
Figura 10.12

La temperatura decresce nella parete dal valore T1 al valore T2 , con gradiente costante ovvero linearmente.
Attraverso una superficie finita S nel tempo t passa dall’ambiente posto a sinistra della parete a quello a destra il calore

Ad esempio attraverso 1 m2 di una parete di mattoni, spessa 10 cm e sottoposta a una differenza di temperatura ΔT = 20°C, passa in un’ora il calore Q = 4.2 · 106 J.
Assumendo T2 come temperatura dell’ambiente esterno e T1 come temperatura di una stanza si può avere, in base al calcolo precedente, un’idea del calore che deve essere fornito da un impianto di riscaldamento per mantenere una data temperatura interna. Un calcolo realistico dovrà tener conto anche della diversa conducibilità termica e delle diverse caratteristiche delle varie aperture nella stanza, tipo porte e finestre.
Notiamo come in regime stazionario il calore che entra nella parete dal lato ad alta temperatura sia eguale al calore che esce dal lato a bassa temperatura: c’è solo flusso di energia, ma non cessione di calore alla parete. Notiamo inoltre che, per unità di tempo e per unità di superficie, passa tanto più calore quanto più grandi sono il gradiente di temperatura e la conducibilità termica. Viceversa arriviamo a capire, almeno qualitativamente, da quali parametri dipende il tempo necessario per raggiungere l’equilibrio termico quando due corpi sono posti a contatto termico tramite una parete.
Convezione del calore
La conduzione termica è importante nei solidi metallici; essa avviene anche nei fluidi, però le conducibilità termiche sono piuttosto piccole, come è evidente dai dati in tabella 10.8. Inoltre la conduzione nei fluidi è difficile da osservare perché in essi si manifesta un altro fenomeno di trasmissione del calore, la convezione, che descriviamo qualitativamente.
Se si riscalda una massa fluida, quella parte più vicina alla sorgente di calore assume una temperatura maggiore e diminuisce di densità, dilatandosi. Viene alterato l’equilibrio statico nel fluido, poiché gli elementi di fluido più caldi risentono, dalle parti di fluido circostante più fredde, di una spinta di Archimede maggiore del loro peso. Si originano correnti ascensionali (dette di convezione), che permettono ad elementi con temperatura minore di avvicinarsi a loro volta alla sorgente di calore. La trasmissione di calore avviene con spostamenti di materia, tramite correnti convettive.
La convezione è responsabile del movimento delle masse d’aria nell’atmosfera o delle correnti marine, con effetti sulle condizioni climatiche e metereologiche.
Irraggiamento
Un corpo a temperatura T emette energia sotto forma di onde elettromagnetiche, che si propagano nello spazio circostante, anche se vuoto. Il potere emissivo del corpo ε, che ha il significato di energia emessa per unità di tempo e per unità di superficie, è dato dalla legge di Stefan-Boltzmann:
Legge di Stefan-Boltzmann

dove σ è una costante universale, pari a 5.67 · 10–8 J/m2 s K4 , ed e una grandezza, detta emissività, che può variare tra 0 e 1, dipendendo dalle proprietà della superficie. Se e = 1 la superficie è detta superficie nera e presenta, a parità di temperatura, il massimo potere emissivo.
Contemporaneamente il corpo assorbe una parte dell’energia elettromagnetica emessa da altri corpi e che lo colpisce; in particolare una superficie nera assorbe tutta l’energia che incide su di essa.
Tramite questi fenomeni la temperatura di un corpo aumenta o diminuisce a seconda del bilancio tra energia irradiata ed assorbita; se il bilancio è in parità la temperatura resta costante, il corpo è in equilibrio con l’ambiente circostante. Naturalmente l’equilibrio può essere mantenuto anche fornendo o sottraendo energia con altri mezzi, per compensare l’irraggiamento.
È attraverso il meccanismo dell’irraggiamento che il sole trasmette energia alla superficie terrestre, nella misura di 1.53 · 103 J/m2 s.
Malgrado gli effetti termici descritti siano equivalenti a quelli dovuti a scambi di calore, in realtà è improprio parlare di trasmissione del calore per irraggiamento, se per calore intendiamo un particolare modo di trasmissione di energia legato a fenomeni meccanici microscopici, ma non all’emissione e all’assorbimento di onde elettromagnetiche.
Parete adiabatica. Vaso Dewar
Vediamo in base ai vari effetti studiati come è possibile realizzare una parete adiabatica. Se lo scopo è quello di limitare lo scambio di calore in presenza di piccole differenze di temperatura è sufficiente una opportuna combinazione di materiali isolanti, cioè materiali a bassa conducibilità termica; questa tecnica è usata, per esempio, nelle pareti dei comuni frigoriferi.

Figura 10.13
Se invece si vuole ridurre al massimo lo scambio di calore, come è necessario per conservare a lungo in un contenitore un liquido criogenico (ad esempio azoto a 70K o idrogeno a 20K) oppure per studiare i fenomeni chimico-fisici che avvengono a bassissime temperature, bisogna innanzitutto impedire conduzione e convezione. Si utilizza allo scopo un contenitore detto vaso Dewar dal nome del suo inventore, costituito da due pareti isolanti, per esempio di vetro, internamente argentate, tra le quali è fatto il vuoto: in questo modo si minimizza la trasmissione di calore per conduzione e convenzione nell’intercapedine. Resta la possibilità di trasmissione di energia per irraggiamento, anche se piccola a basse temperature, secondo (10.21): per questa ragione l’interno dell’intercapedine è argentato, per ridurre il potere emissivo (che è nullo per un parete perfettamente riflettente).
Passaggio di calore da un solido a un fluido
La trasmissione di calore da un solido ad un fluido è molto comune nella pratica; avviene per esempio nel riscaldamento di un locale tramite i termosifoni.
Consideriamo un solido alla temperatura T, con una superficie pari a S, mentre il fluido si trova, nei punti non prossimi al solido, alla temperatura T0 < T. Il fenomeno è complesso perché avvengono sia convezione che conduzione e irraggiamento. Tuttavia, in prima approssimazione, se ΔT = T – T0 non è molto grande, il fenomeno può essere descritto con una legge molto semplice, scoperta da Newton: il modulo del calore scambiato nel tempo t, ceduto dal solido e assorbito dal fluido, è dato da
Legge di Newton

La costante h è detta conducibilità termica esterna; per un filo caldo (perché percorso da corrente elettrica) immerso in aria h = 10 J/m2 s K.

Figura 10.14