Gas ideali e reali11
11.1 Leggi dei gas. Equazione di stato dei gas ideali
Ricordiamo quanto abbiamo visto nei capitoli 7 e 8; un gas è un fluido con le seguenti caratteristiche:
a) non ha forma né volume proprio, occupa pertanto tutto il volume a disposizione, per esempio quello del recipiente che lo contiene;
b) è comprimibile facilmente, con conseguenti variazioni notevoli di volume, densità e pressione.
Considerata una certa quantità di gas, le variabili termodinamiche più appropriate per descrivere lo stato termodinamico del gas e le eventuali trasformazioni sono la pressione p, il volume V e la temperatura T.
Nel capitolo 8, studiando le proprietà statiche e dinamiche dei fluidi, abbiamo discusso il comportamento del fluido ideale, incompressibile e privo di viscosità, e sottolineato che, nel moto in un condotto, un gas si avvicina molto alla condizione di moto di un fluido ideale. In questo capitolo invece non ci occupiamo della dinamica di un gas: consideriamo il gas racchiuso dentro un contenitore di volume V, con un valore della pressione eguale in tutti i punti, se V non è molto grande.
Quando il volume del contenitore cambia, come può avvenire se una parte dello stesso è mobile, si realizza uno scambio di lavoro con l’ambiente esterno; inoltre, a seconda del tipo di pareti del contenitore, diatermiche o adiabatiche, è possibile o viene impedito lo scambio di calore con l’ambiente. Il gas può dunque compiere trasformazioni in cui scambia soltanto lavoro o calore con l’ambiente, oppure entrambi; in ogni caso il bilancio energetico è regolato dal primo principio della termodinamica.
Ci occuperemo più avanti degli aspetti energetici delle trasformazioni di un sistema gassoso; adesso stabiliamo alcune semplici relazioni tra le coordinate termodinamiche di un gas, che sono tanto meglio verificate quanto più un gas si avvicina a condizioni di pressione sufficientemente bassa e di temperatura alta rispetto a quella per cui si avrebbe condensazione (alla data pressione). Si parla in tal caso di comportamento ideale, con un significato diverso del termine ideale, già usato nel moto di un fluido. Vedremo più chiaramente nel paragrafo 11.10 le condizioni fisiche che individuano un gas ideale.
Legge isoterma di Boyle
Si abbia un gas in equilibrio termodinamico ad una certa pressione entro un dato volume e a temperatura T: se si fanno variare i valori della pressione e del volume, mantenendo costante la temperatura, si trova che in tutti i possibili stati di equilibrio isotermi il prodotto della pressione per il volume ha sempre lo stesso valore. Vale cioè la legge di Boyle
Legge di Boyle
a temperatura costante la pressione è inversamente proporzionale al volume.
Una trasformazione isoterma tra due stati di equilibrio di un gas si può realizzare, ad esempio, se il contenitore, a pareti diatermiche, è mantenuto in contatto termico con una sorgente di calore alla temperatura T e la parete mobile si muove a seguito di una differenza infinitesima di pressione tra gas e ambiente esterno. Si hanno condizioni di equilibrio meccanico e termico e possiamo assumere che durante la trasformazione la temperatura sia costante e la pressione del gas sempre eguale a quella esterna.
Comunque il gas passi da uno stato di equilibrio a pressione p1 e volume V1 ad un altro con pressione p2 e volume V2 , ma con la stessa temperatura, sia cioè compiendo la trasformazione sopra descritta che una qualsiasi altra in cui la temperatura vari (crescendo e diminuendo o viceversa), la legge di Boyle (11.1) stabilisce che si ha sempre
Isoterme del gas ideale
In un sistema di coordinate cartesiane ortogonali nel piano, con il volume sull’asse delle ascisse e la pressione sull’asse delle ordinate, il luogo dei punti che rappresentano gli stati di equilibrio di un gas a una data temperatura è costituito da un ramo di iperbole: infatti la (11.1) è l’equazione di una iperbole equilatera nelle coordinate p,V. Per ogni temperatura si ha una diversa iperbole e le curve così ottenute si chiamano le isoterme del gas ideale. Nella figura 11.1 sono mostrate alcune isoterme; poiché la costante di (11.1) è proporzionale alla temperatura, come vedremo tra breve, si ha T3 > T2 > T1 .
Il piano (p,V) utilizzato per la rappresentazione degli stati di equilibrio del gas viene detto piano di Clapeyron.
Figura 11.1
Legge isobara di Volta-Gay Lussac
Se la pressione di un gas durante una trasformazione resta costante, si parla di trasformazione isobara; si verifica che in condizioni isobare il volume varia linearmente con la temperatura:
Nella (11.2) la temperatura è espressa in gradi Celsius, V0 è il volume occupato dal gas per t = 0 e α è una costante che varia poco al variare del tipo di gas, detta coefficiente di dilatazione termica; in effetti da (11.2) si può ricavare una relazione analoga a (10.24).
Per provare la validità della legge isobara di Volta-Gay Lussac (11.2) si può mettere il gas in equilibrio termico con diverse sorgenti di calore, mantenendo sempre l’equilibrio meccanico con l’ambiente (pressione interna eguale alla pressione esterna costante) e ogni volta misurare il volume del contenitore, che ha una parete mobile come nel caso precedente.
La trasformazione isobara, nel piano (p,V) già considerato, è rappresentata da un segmento di retta parallelo all’asse dei volumi (figura 11.2).
Legge isocora di Volta-Gay Lussac
Se invece si mantiene costante il volume di un gas la pressione risulta funzione lineare della temperatura:
Figura 11.2
Anche ora la temperatura è espressa in gradi Celsius; p0 è la pressione del gas per t = 0 e β una costante, praticamente indipendente dal tipo di gas.
Una trasformazione a volume costante si dice isocora; nel piano (p,V) essa è rappresentata da un segmento di retta parallelo all’asse delle pressioni (figura 11.2).
La verifica della legge isocora di Volta-Gay Lussac (11.3) si può eseguire utilizzando il solito contenitore, mantenendo bloccata la parete mobile e misurando la pressione in diversi stati di equilibrio, con il gas in contatto termico con diverse sorgenti di calore.
Ricordiamo quanto detto all’inizio e cioè che il comportamento dei diversi gas è in accordo con le leggi (11.1), (11.2), (11.3) quanto più ci si avvicina alle condizioni di gas ideale (bassa pressione e alta temperatura). Così facendo si osserva anche che le costanti α e β assumono lo stesso valore per tutti i gas:
Le due leggi (11.2) e (11.3) si possono pertanto scrivere
dove con è indicata la temperatura misurata in kelvin (vedi α paragrafo 10.3). Abbiamo così ritrovato la relazione tra i valori della temperatura espressi in gradi Celsius e in kelvin, dandone una giustificazione.
Legge di Avogadro
La quarta legge dei gas è la legge di Avogadro, di carattere completamente diverso dalle precedenti leggi elementari, in quanto direttamente collegata alla struttura microscopica di un gas. Essa stabilisce che volumi eguali di gas diversi, alla stessa temperatura e pressione, contengono lo stesso numero di molecole.
Avogadro dedusse la legge che porta il suo nome osservando che quando due gas, alla stessa temperatura e pressione, si combinano in una reazione chimica dando luogo a un composto (2H2 + O2 → 2H2O, H2 + Cl2 → 2HCl, S2 + 2O2 → 2SO2), i valori dei volumi delle quantità di gas che partecipano alla reazione stanno in rapporti semplici tra loro (2:1, 1:1, 1:2 negli esempi visti) e questi rapporti sono immutabili.
Notiamo che anche la legge di Avogadro si riferisce a gas che abbiano un comportamento ideale e quindi obbediscano alle leggi precedentemente enunciate. Per esempio due volumi di gas, eguali a una data temperatura e pressione, restano eguali ad un’altra temperatura se i due gas si comportano esattamente alla stessa maniera al variare della temperatura; ovvero eguali numeri di molecole di due gas diversi occupano sempre lo stesso volume, nelle stesse condizioni di pressione e temperatura, solo se i gas sono ideali.
Detta M la massa totale del gas e m la massa di ciascuna delle molecole che lo compongono, il numero di molecole è N = M / m. La massa m è il prodotto della massa molecolare A per l’unità di massa atomica mu, cioè
Chilomole
Considerando una massa M numericamente eguale ad A, ovvero A chilogrammi di gas, quantità che si chiama chilomole (kmol), risulta
Numero di Avogadro
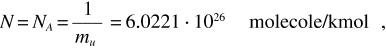
Mole
numero detto di Avogadro. Se invece si considera una massa M eguale ad A grammi di gas, quantità che si chiama mole (mol), il numero di Avogadro vale
Numero di Avogadro
Dalla legge di Avogadro discende la definizione della settima unità fondamentale, quella della quantità di materia (vedi appendice B). Si chiama mole una quantità di materia che contiene tante entità elementari quanti sono gli atomi contenuti in 0.012 kg dell’isotopo 12C del carbonio, ovvero NA = 6.0221 · 1023 entità elementari. Una chilomole corrisponde a 103 moli e contiene 6.0221 · 1026 entità elementari.
È importante sottolineare che con la mole non viene introdotta una diversa unità di massa. Infatti una mole di idrogeno gassoso (A = 2) corrisponde ad una massa di 2 · 10–3 kg, una di ossigeno gassoso (A = 32) a 32 · 10–3 kg, una di acqua (A = 18) a 18 · 10–3 kg: quindi ad una quantità di materia data da un certo numero di moli corrispondono masse diverse a seconda della sostanza considerata, però queste masse contengono tutte lo stesso numero di molecole.
Come conseguenza della legge di Avogadro una mole di qualsiasi gas, a una data temperatura e pressione, occupa sempre lo stesso volume. Si trova che se la pressione è quella atmosferica (p0 = 101325 Pa) e la temperatura è T0 = 273.15 K = 0 °C, tale volume vale
Volume molare
Vm viene indicato col nome di volume molare. Pertanto n moli occupano un volume pari a nVm e in particolare una chilomole occupa 22.414 m3 , nelle dette condizioni di pressione e temperatura.
Equazione di stato del gas ideale
Se consideriamo n moli di un gas alla pressione atmosferica p0 e alla temperatura T0 = 273.15 K, esse occupano, come abbiamo appena detto, il volume V0 = nVm . Mantenendo costante il volume e portando la temperatura al valore T, la pressione in base alla (11.5) assume il valore
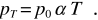
Moltiplicando per V0 si ha
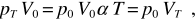
dove la seconda eguaglianza è in accordo con (11.4). V0 e pT sono le coordinate termodinamiche in un particolare stato di equilibrio alla temperatura T, come lo sono p0 e VT per un altro stato, sempre alla temperatura T. In base alla (11.1)
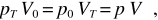
essendo p e V le coordinate in un generico stato di equilibrio, purché a temperatura T. Otteniamo dunque
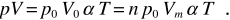
Il prodotto p0 Vm α è una costante universale, che ha lo stesso valore per tutti i gas, e quindi
Equazione di stato del gas ideale
con
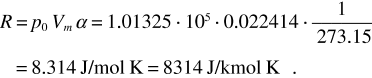
Costante del gas ideale
Definiamo, sulla base delle tre leggi elementari e della legge di Avogadro, come gas ideale un sistema le cui coordinate termodinamiche in uno stato di equilibrio obbediscono alla (11.6), detta equazione di stato di un gas ideale. Pertanto in un gas ideale il prodotto della pressione per il volume è proporzionale al numero di moli e alla temperatura attraverso la costante universale R, detta costante dei gas ideali. Osserviamo che nella relazione tra p, V e T espressa da (11.6) la quantità significativa è il numero di moli, cioè il numero di molecole del gas, e non la sua massa.
Gas ideale
La (11.6) mostra che in un gas ideale in equilibrio sono indipendenti solo due variabili, in quanto la terza si ricava appunto tramite l’equazione di stato. Vediamo allora che, per un dato numero di moli, un punto nel piano (p,V) rappresenta completamente uno stato di equilibrio del gas, potendosi ricavare subito la temperatura da (11.6).
L’equazione di stato contiene (11.1), (11.4), (11.5): infatti basta mantenere costante T, p o V in (11.6) e si ottengono le tre leggi isoterma, isobara o isocora. Anche la legge di Avogadro è contenuta in (11.6), se R è una costante universale.
È possibile scrivere l’equazione di stato in forme diverse da (11.6). Ricordando che n = N / NA , con N numero di molecole del gas, abbiamo
la costante universale
Costante di Boltzmann
è detta costante di Boltzmann.
Se al posto del volume si utilizza la densità ρ= M / V e al posto della massa M del gas si mette An, con A massa molecolare, la (11.6) diventa
Ricordiamo ancora una volta che l’equazione di stato dei gas ideali esprime un comportamento limite, al quale si avvicinano i gas reali quanto più lontana è la loro temperatura da T = 0 e quanto più bassa è la loro pressione ovvero la loro densità, cioè quanto più sono caldi e rarefatti. In queste condizioni le differenze di comportamento dei diversi gas praticamente scompaiono e tutti seguono approssimativamente (11.6).
Esempio 11.1
Un gas ideale è contenuto in un volume V = 10–3 m3 alla pressione p = 105 Pa e alla temperatura T = 300 K. Calcolare il numero di molecole contenute nel volume. Se la pressione scende a p' = 10–9 Pa, di quanto varia la risposta?
Soluzione
Dall’equazione di stato n = pV/RT = 4 · 10–2 moli; il numero di molecole nel volume V, che è pari ad un litro, è
Se la pressione scende a 10–9 Pa (alto vuoto), cioè diminuisce di un fattore 1014, di altrettanto diminuisce N, a parità degli altri fattori, e risulta
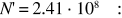sono rimasti 241 milioni di molecole nel volume V.Visualizza Soluzione
Esempio 11.2
Una massa m = 5 · 10–3 kg di idrogeno è contenuta in un volume V = 100 litri alla temperatura T = 20°C. Calcolare quanto vale la pressione. Quale massa di ossigeno produce lo stesso risultato?
Soluzione
Una mole di idrogeno ha una massa pari a 2 · 10–3 kg e quindi nel volume V ci sono 2.5 moli. La pressione è
Se il gas è ossigeno, 2.5 moli equivalgono ad una massa m = 2.5 · 32 · 10–3 = 80 · 10–3 kg (16 volte maggiore della massa di idrogeno, nel rapporto cioè delle masse molecolari).Visualizza Soluzione