11.3 Trasformazioni di un gas. Lavoro
Consideriamo due stati di equilibrio A e B di un sistema formato da n moli di gas ideale. Noti i valori della pressione e del volume, dall’equazione di stato (11.6) si ricavano i valori della temperatura:
Figura 11.5
Una trasformazione che porti il gas dallo stato A allo stato B può svolgersi attraverso stati di equilibrio termodinamico ed è rappresentabile nel piano (p,V) di Clapeyron da una curva continua (figura 11.5a). Se invece la trasformazione ha luogo attraverso stati di non equilibrio si usa una rappresentazione simbolica a tratto per indicare che si ignorano i valori delle coordinate durante il processo (figura 11.5b).
La trasformazione attraverso stati di non equilibrio può realizzarsi in conseguenza di un processo di espansione o compressione rapida, per cui non sussiste né equilibrio meccanico né termico, o per effetto di una espansione o compressione lenta con una differenza di pressione finita così che, pur potendoci essere equilibrio termico, non c’è equilibrio meccanico, oppure a seguito di contatto termico con differenza finita di temperatura (possibile equilibrio meccanico, ma non equilibrio termico).
Figura 11.6
Quando un gas si espande o viene compresso avviene uno scambio di lavoro che in termini infinitesimi si può scrivere in generale dW = p dV, come si è visto nel paragrafo 8.1 per un fluido sottoposto a forze di pressione. In una trasformazione finita dallo stato A allo stato B si avrebbe
però bisogna fare attenzione perché questa espressione esplicita del lavoro è utile soltanto quando si conosce la funzione p(V), circostanza verificata sostanzialmente in due sole situazioni:
a) la trasformazione è reversibile e pertanto si può calcolare l’integrale, dato che la pressione è determinata in ogni stato intermedio, p = pgas = p amb ;
b) è nota la pressione esterna che, per esempio, è costante, caso tipico di quando il processo avviene sotto la pressione atmosferica; allora, anche se la trasformazione non è reversibile, il lavoro è calcolabile ed è dato da
In tutti gli altri casi in cui la pressione non è nota non si può applicare la (11.11).
Ad ogni modo, se la trasformazione è isocora (V = costante, ΔV = 0), il lavoro è sempre nullo; se il gas si espande il volume finale VB è maggiore del volume iniziale VA e il gas compie un lavoro sull’ambiente che secondo la convenzione adottata è positivo; se il gas viene compresso, VB < VA e il gas subisce un lavoro (negativo), compiuto dall’ambiente.
Figura 11.7
Il lavoro, se si può utilizzare (11.11), ha un semplice significato geometrico nel piano di Clapeyron. Nel caso di una trasformazione che passa attraverso stati di equilibrio ed è quindi rappresentabile con una curva continua, la curva p = p(V) nel piano (p,V), il lavoro, in accordo con il significato geometrico dell’operazione di integrazione, è pari all’area compresa tra la curva e l’asse dei volumi (figura 11.6a). Nelle figure 11.6b e 11.6c sono mostrati i casi dell’espansione (W > 0) e della compressione (W < 0), entrambe reversibili. Infine nella figura 11.6d è rappresentata una trasformazione ciclica reversibile e il lavoro è dato dall’area racchiusa dal ciclo: esso è positivo se il ciclo è percorso in senso orario, negativo in caso contrario.
Dalle considerazioni appena esposte si comprende l’importanza della rappresentazione di una trasformazione nel piano (p,V) rispetto alle possibili alternative (p,T) e (V,T), almeno per quel che riguarda il lavoro. Ad esempio, dall’osservazione delle trasformazioni reversibili disegnate in figura 11.7, si verifica che, a parità di stato iniziale e finale, il lavoro dipende dalla trasformazione, W1 ≠ W2 ≠ W3 . Si noti però che tale conclusione è valida anche per le trasformazioni non reversibili, che non possono essere rappresentate nel piano (p,V).
Figura 11.8 (Esempio 11.4)
Esempio 11.4
Si calcoli il lavoro per le varie trasformazioni reversibili rappresentate in figura 11.8, che collegano gli stati di equilibrio termodinamico A (pA , VA) e B (pB , VB).
Soluzione
Lungo la prima trasformazione AA'B
Nella trasformazione 2, lungo il segmento congiungente A con B ,
in quanto l’area sotto la curva è un trapezio. Infine lungo AB'B
Risulta pertanto W1 > W2 > W3 .Visualizza Soluzione
Figura 11.9 (Esempio 11.5)
Esempio 11.5
Si determini il lavoro per le varie trasformazioni cicliche reversibili rappresentate in figura 11.9.
Soluzione
Il lavoro nel ciclo a) è dato da
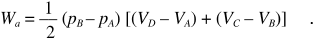
Nel secondo caso il lavoro, calcolato sempre dall’area racchiusa dal ciclo, è
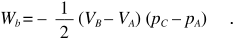
Il segno negativo è dovuto al fatto che il ciclo viene percorso in senso antiorario. Fisicamente, in questo ciclo il gas subisce un lavoro. Per il ciclo c) il lavoro è dato da
Infine nel ciclo d), percorso in senso antiorario, il gas subisce complessivamente il lavoro
Visualizza Soluzione
Concludiamo l’argomento lavoro riprendendo l’osservazione fatta alla fine del paragrafo 10.6 e verificandola nel caso di un sistema gassoso. Se un gas compie una trasformazione reversibile dallo stato A allo stato B, quando questa viene percorsa in senso opposto, da B ad A, il lavoro cambia soltanto di segno, come è evidente da (11.11): WBA = – WAB . Per definizione la proprietà è valida in ogni caso per la variazione di energia interna e dal primo principio segue che QBA = – QAB . Niente di simile si può invece affermare se la trasformazione è irreversibile.