12.5 Teorema di Clausius

La relazione (12.4), conseguenza del teorema di Carnot per le macchine reversibili che lavorano tra due sorgenti, può essere estesa e generalizzata a macchine termiche operanti con più sorgenti di calore. Sussiste infatti il teorema di Clausius: data una macchina M qualsiasi che scambia calore con n sorgenti, è valida la relazione

Figura 12.10

dove Q₁ , Q₂ , … , Q_n sono i calori scambiati con le sorgenti a temperatura T₁ , T₂ , …, T_n . La situazione è schematizzata nella figura 12.10, in cui non sono indicati i versi degli scambi energetici, che possono essere qualsiasi purché sia soddisfatta (12.10).

Per dimostrare (12.10), immaginiamo di aggiungere n macchine reversibili funzionanti tra le sorgenti già considerate alle temperature T₁ , T₂ , … , T_n e una sorgente a temperatura T₀ : ciascuna di queste macchine R_i scambia con la sorgente a T_i il calore – Q_i, opposto a quello scambiato con la stessa sorgente dalla macchina M, e con la sorgente a T₀ il calore Q_0i. L’insieme è mostrato in figura 12.11.

Figura 12.11

Applichiamo (12.4) a ciascuna macchina reversibile:

e sommando su tutte le macchine

Alla fine di un ciclo della macchina M e delle macchine reversibili R₁ , … , R_n le sorgenti a T₁ , … , T_n sono rimaste invariate in quanto ciascuna ha scambiato calori eguali ed opposti con le macchine. Pertanto la macchina complessiva costituita da M e dalle n macchine ausiliarie compie una trasformazione ciclica monoterma perché scambia calore solo con la sorgente a temperatura T₀ . Come abbiamo visto nel paragrafo 12.1, il calore totale scambiato durante un ciclo monotermo non può essere positivo e quindi

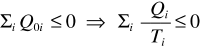
poiché T₀ > 0. Abbiamo così dimostrato (12.10).

Se lo scambio di calore di M avviene con una serie infinita di sorgenti, detto dQ il calore scambiato con la sorgente a temperatura T, la (12.10) diventa

dove il simbolo ∮ che l’integrale è esteso a tutto il ciclo descritto dalla macchina M.

Le (12.10) e (12.11) esprimono il teorema di Clausius per una macchina generica. Se la macchina M è reversibile invertiamo tutti i cicli: tutti gli scambi di calore cambiano di segno e deve essere Σ (– Q_0i) ≤ 0. Ne segue che le diseguaglianze di (12.10) e (12.11) vanno invertite e si ha compatibilità tra i due casi solo se

Macchine reversibili

Queste relazioni esprimono il teorema di Clausius per le macchine reversibili; la prima in particolare appare come generalizzazione di (12.4).

Quando il processo ciclico è irreversibile, a rigore vale il segno di minore o eguale; però, sulla base delle considerazioni sui processi irreversibili sviluppate nel paragrafo 12.3, possiamo assumere che in generale si verifica la diseguaglianza e scrivere il teorema di Clausius per le macchine irreversibili come

Macchine irreversibili

Si tenga presente che la temperatura T nelle (12.12) e (12.13) è quella della sorgente con cui avviene lo scambio di calore: essa coincide con la temperatura del sistema che compie il ciclo solo se il processo è reversibile. Inoltre i calori sono quelli visti dal sistema, positivi se il sistema li assorbe, negativi se li cede.

Osserviamo infine che mentre la somma dei calori scambiati è sempre diversa da zero per un ciclo che scambia lavoro, in accordo con il primo principio, quando il calore scambiato viene diviso per il valore della temperatura della sorgente con cui avviene lo scambio e si somma su tutto il ciclo, il risultato è nullo se il ciclo è reversibile e negativo negli altri casi.