12.8 Calcoli di variazioni di entropia

In questo paragrafo trattiamo alcuni processi tipici, in cui sistemi costituiti da corpi solidi o liquidi scambiano calore tra loro o con sorgenti, e calcoliamo le corrispondenti variazioni di entropia. L’argomento è completato nel paragrafo 12.9, dove ci occupiamo di sistemi costituiti da gas ideali.

Trasformazioni adiabatiche

Un sistema che compie una trasformazione adiabatica costituisce un caso particolare di universo termodinamico, in cui si assume che il sistema sia isolato termicamente dall’ambiente: l’ambiente non scambia calore col sistema, ma soltanto lavoro; pertanto ΔS_amb = 0 e

Se la trasformazione è reversibile ΔS_sist = 0, la trasformazione cioè è isoentropi-ca. Come già detto nel paragrafo 12.6, il risultato si ottiene anche direttamente dalla definizione (12.14).

Per una trasformazione adiabatica irreversibile invece ΔS_sist > 0, l’entropia aumenta. In effetti questa volta dQ = 0 non implica dS = 0: il calore scambiato lungo la trasformazione è nullo, però ΔS_sist non è calcolabile lungo questa trasformazione, bensì lungo un’altra con gli stessi estremi, ma reversibile, che non può essere adiabatica a sua volta. Questo perché due stati collegati con una adiabatica irreversibile hanno necessariamente entropia diversa e non possono quindi essere collegati anche con una adiabatica reversibile, che è isoentropica (e viceversa, due stati diversi per i quali è ΔS = 0 non possono essere collegati con un’adiabatica irreversibile).

Scambi di calore con sorgenti

Consideriamo prima il caso della cessione di calore Q da una sorgente a temperatura T₂ a una sorgente a temperatura T₁ < T₂ .

La sorgente che assorbe il calore Q ha una variazione di entropia

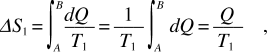
mentre per la sorgente a T₂ che cede il calore – Q si ha

L’universo è costituito dalle due sorgenti e

si verifica che la variazione è positiva, dato che T₁ < T₂ . L’entropia della sorgente fredda è aumentata, quella della sorgente calda è diminuita, però | ΔS₂ | < ΔS₁ . Il processo contrario è proibito perché comporterebbe una diminuzione di entropia dell’universo.

Il fenomeno descritto è irreversibile; esso si può realizzare ponendo a contatto termico le sorgenti per il tempo necessario a scambiare il calore Q. Comunque sia, per definizione il processo di scambio di calore da parte di una sorgente è isotermo; per tale ragione abbiamo utilizzato (12.17) nel calcolo ΔS₁ e ΔS₂ , immaginando di compiere, per ciascuna sorgente, una trasformazione isoterma reversibile tra gli stessi stati iniziale e finale.

Esempio 12.3

Due sorgenti, una alla temperatura T₂ = 380 K e l’altra alla temperatura T₁ = 280 K, vengono messe in contatto termico tramite una lastra di alluminio, di area S = 100 cm² e spessore d = 2.5 cm. Calcolare, a regime, quanto calore passa in un secondo da una sorgente all’altra e la variazione di entropia dell’universo in un minuto.

Soluzione

Ricorriamo alla formula di Fourier per la trasmissione del calore per conduzione (paragrafo 10.9):

In un minuto passa il calore Q' = 4.824 · 10⁵ J e la variazione di entropia richiesta vale

L’entropia della lastra non varia, in quanto il calore assorbito è eguale, in modulo, al calore ceduto e la distribuzione di temperatura è costante nel tempo.

Visualizza Soluzione

Un passaggio di calore tra due sorgenti avviene anche quando tra di esse lavora una macchina, secondo la figura 12.16. La variazione di entropia del sistema macchina è nulla in un ciclo; l’ambiente è costituito dalle due sorgenti e la variazione complessiva di entropia è

Figura 12.16

Il segno meno è dovuto al fatto che con Q₁ e Q₂ intendiamo i calori scambiati dal sistema, mentre ora stiamo calcolando la variazione di entropia dell’ambiente, per il quale i calori hanno segno opposto. Dal teorema di Clausius (12.10) vediamo che il termine tra parentesi è non positivo e quindi ΔS_u ≥ 0, come deve. Se la macchina è reversibile vale (12.12) e ΔS_u = 0, altrimenti ΔS_u > 0.

Il ragionamento resta valido se la macchina della figura 12.16 è frigorifera.

Esempio 12.4

Tra due sorgenti alle temperature T₂ = 330 K e T₁ = 280 K lavora una macchina termica: il lavoro W = 100 J prodotto in un ciclo viene utilizzato integralmente per fare compiere un ciclo tra le stesse temperature ad un frigorifero reversibile. In un ciclo completo delle due macchine la variazione di entropia dell’universo è ΔS_u = 0.28 J/K. Calcolare il rendimento della macchina termica e i calori scambiati complessivamente con le sorgenti.

Soluzione

L’entropia dell’universo può cambiare solo durante il ciclo della prima macchina, poiché la seconda è reversibile. Chiamiamo Q₂ e Q₁ i calori scambiati dalla prima macchina e utilizziamo (12.24) e il primo principio:

da cui ricaviamo

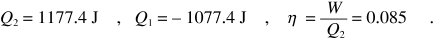
Invece il rendimento di una macchina reversibile che lavora tra le stesse sorgenti è

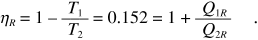
Se questa macchina produce il lavoro W = 100 J, pari a Q_1R + Q_2R , si ha

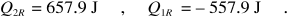
Cambiati di segno, questi sono gli scambi energetici del frigorifero reversibile: assorbe – Q_1R = 557.9 J a T₁ , assorbe –W = – 100 J e cede – Q_2R = – 657.9 J a T₂. Facendo il bilancio complessivo:

Il risultato finale è il passaggio di 519.5 J dalla sorgente a 330 K a quella a 280 K. Se calcoliamo ΔS_u per questo processo diretto con la formula – Q/T₂ + Q/T₁ troviamo ovviamente 0.28 J/K.

Visualizza Soluzione

Consideriamo adesso lo scambio di calore tra un corpo di massa m, calore specifico c costante, temperatura T₁ e una sorgente a temperatura T₂ , con cui il corpo viene messo a contatto termico.

Il processo è irreversibile (non c’è equilibrio termico); per il calcolo della variazione di entropia del corpo immaginiamo un processo reversibile con scambio di calore tra il corpo e infinite sorgenti a temperatura crescente T₁ + dT, T₁ + 2 dT, … , T₂ – dT, T₂ . Con ciascuna sorgente viene scambiato il calore dQ = mcdT e, da (12.14),

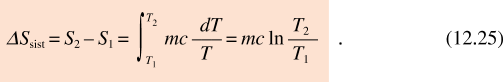
Se T₁ < T₂ il corpo assorbe calore dalla sorgente e la sua entropia aumenta; se T₁ > T₂ il corpo invece cede calore alla sorgente e la sua entropia diminuisce.

Il calore scambiato dal corpo è

e quindi il calore scambiato dalla sorgente è – Q. La variazione di entropia della sorgente è

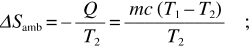
essa è di segno opposto rispetto aΔS_sist ed è diversa in modulo. La variazione di entropia dell’universo è data da

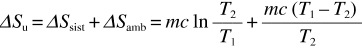
ed è facile verificare che essa è sempre positiva, sia per T₂ > T₁ che per T₂ < T₁ . Per esempio, nel caso T₂ > T₁ ,

essendo sempre T < T₂ durante il processo, dS_sist > | dS_amb | e la diseguaglianza si mantiene a integrazione effettuata:

Quando T₁ > T₂ , cambiano i segni delle variazioni di entropia ed è sempre T > T₂ , per cui dS_amb > | dS_sist | e si ottiene di nuovo ΔS_u > 0.

Con un ragionamento quasi identico si verifica, per il corpo, (12.21): infatti

mentre nel processo reale irreversibile la temperatura a cui avviene lo scambio di calore è la temperatura T₂ della sorgente per cui

Quando T₂ > T₁ , dT è positivo, T è minore di T₂ , dT/T è maggiore di dT/T₂ ; quando T₂ < T₁ , dT è negativo, T è maggiore di T₂ e di nuovo dT/T è maggiore di dT/T₂ (in modulo è minore, ma si tratta di numeri negativi).

Scambi di calore tra due corpi

Un corpo di massa m₁ , calore specifico costante c₁ e temperatura T₁ , viene messo a contatto, in un recipiente isolato termicamente, con un altro corpo di massa m₂ , calore specifico c₂ e temperatura T₂ > T₁ . Avviene uno scambio di calore irreversibile, considerata la differenza iniziale di temperatura tra i due corpi (irreversibilità termica), e i due corpi raggiungono l’equilibrio termico alla temperatura T_e data da

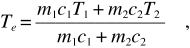
come si ricava eguagliando i moduli dei calori scambiati (vedi paragrafo 10.7). Per le variazioni di entropia dei due corpi utilizziamo (12.25):

L’intero processo è adiabatico (irreversibile) per cui ΔS_u = ΔS₁ + ΔS₂ e si ha sempre $\Delta S_u>0$.

Esempio 12.5

Due masse d’acqua, m₂ = 100 kg e m₁ = 240 kg, si trovano alle temperature T₂ = 90°C e T₁ = 10°C. I recipienti che le contengono vengono posti in contatto termico tra loro e isolati dall’ambiente esterno. Calcolare la variazione di entropia. Ripartendo dalle stesse condizioni iniziali si fa lavorare tra le due masse una macchina termica reversibile finché viene raggiunto l’equilibrio termico. Calcolare la temperatura di equilibrio.

Soluzione

Nel primo caso m₁c (T_e – T₁) = – m₂c (T_e – T₂) da cui risulta

La variazione di entropia vale

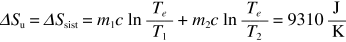
ricordando che c = 4186.8 J/kg K (e che le temperature devono essere espresse in kelvin).

Nel secondo caso il processo è reversibile e quindi la variazione di entropia dell’universo è nulla:

È interessante notare come sia l’espressione matematica del secondo principio a fornire l’equazione risolutiva. È anche importante rendersi conto che in questo caso la macchina non lavora tra due sorgenti, ma tra due corpi con capacità termica finita la cui temperatura varia durante il processo. Il calore assorbito dalla macchina è $Q_A=m_{2}c\left(T_2-T_e^{\text{'}}\right)$ quello ceduto è $Q_c=m_{1}c\left(T_1-T_e^{\text{'}}\right)$ , il lavoro prodotto è W = Q_A + Q_C , il rendimento η = W/Q_A .

Visualizza Soluzione

Cambiamenti di fase

I cambiamenti di fase sono processi isotermi: mettendo insieme (12.17) e (10.18), la variazione di entropia di m chilogrammi di una sostanza che cambia fase alla temperatura T è

Esempio 12.6

Un blocco di ghiaccio alla temperatura T₁ = 0°C viene posto a contatto, in un ambiente termicamente isolato, con un blocco di rame alla temperatura T₂ = 100°C; ad equilibrio raggiunto si è sciolta una quantità m_x di ghiaccio. La capacità termica del blocco di rame è C = 6 · 10³ J/K e il calore latente di fusione del ghiaccio è λ = 3.34 · 10⁵ J/kg. Calcolare il valore di m_x e la variazione di entropia dell’universo.

Soluzione

Dal testo si deduce che la temperatura di equilibrio è T₁ , in quanto non fonde tutto il ghiaccio. La massa che fonde si ricava da

La variazione di entropia del ghiaccio che cambia fase è, da (12.26),

mentre quella del blocco di rame si ricava da (12.25):

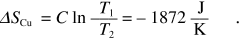
Per l’universo ΔS_u = ΔS_g + ΔS_Cu = 325 J/K .

Visualizza Soluzione

Esempio 12.7

Una macchina termica lavora tra una massa d’acqua m₂ = 10⁶ kg alla temperatura T₂ = 10°C e una massa di ghiaccio m₁ = 0.2 · 10⁶ kg alla temperatura T₁ = 0°C. Calcolare il massimo lavoro ottenibile.

Soluzione

Il massimo lavoro si ha impiegando una macchina reversibile che assorbe calore dall’acqua e cede calore al ghiaccio facendolo fondere; nel processo la temperatura dell’acqua diminuisce e alla fine diventa T₁ . Infatti il calore che il ghiaccio può assorbire dall’acqua è

inferiore al calore che sarebbe necessario per fondere tutto il ghiaccio

Essendo la macchina reversibile ΔS_u = 0, ovvero, essendo ΔS_sist = 0,

dove Q₀ è il calore assorbito dal ghiaccio, che risulta pari a 4.11 · 10¹⁰ J. La macchina pertanto assorbe Q, cede – Q₀ e compie il lavoro

con rendimento η = W/Q = 0.019. Se la temperatura dell’acqua restasse costante durante il processo, il rendimento sarebbe

Visualizza Soluzione

Riscaldamento per attrito

Riprendiamo dal paragrafo 10.6 l’esempio del corpo il cui moto viene frenato da una forza di attrito. Il lavoro dissipativo W è eguale all’opposto della variazione di energia interna del corpo e del sistema che esercita la forza di attrito, secondo (10.2): W = U_A – U_B e, siccome il lavoro è negativo, l’energia interna aumenta (U_B > U_A) e aumenta la temperatura da T_amb a T. Successivamente viene ceduto calore all’ambiente, Q = U_A – U_B = W e la temperatura dei corpi che hanno partecipato al fenomeno ritorna al valore iniziale T_amb , così come U ritorna da U_B a U_A .

In definitiva i corpi hanno subito una trasformazione ciclica: la loro entropia è aumentata durante il riscaldamento ed è calcolabile con formule tipo (12.25), immaginando una cessione di calore reversibile al posto del processo reale adiabatico irreversibile; però durante la cessione di calore all’ambiente l’entropia dei corpi diminuisce e alla fine l’unica variazione di entropia diversa da zero è quella dell’ambiente, che riceve il calore – Q (si ricordi che Q è negativo, in quanto è il calore ceduto dal corpo):

Quello descritto è solo un caso particolare; è possibile mantenere costante la velocità del corpo con la fornitura di lavoro motore che bilanci il lavoro resistente (equilibrio dinamico nel moto uniforme reale) e ciò comporta una cessione continua di calore all’ambiente. Oppure si può considerare il caso dell’innalzamento stabile di temperatura di un corpo in quiete in cui si raggiunge un equilibrio energetico nel senso che il calore ceduto dal corpo all’ambiente è compensato dall’energia fornita al corpo attraverso fenomeni di attrito. In ogni situazione si verifica sempre ΔS_u > 0, segnale dell’irreversibilità di questi processi.