13.6 Sistemi aperti. Potenziale chimico. Regola delle fasi

In tutte le situazioni esaminate finora, il sistema in esame scambiava soltanto energia con l’ambiente, ma la sua massa era ritenuta costante. Pur conservando questa proprietà di costanza della massa totale, sono molto comuni i casi in cui un sistema è suddiviso in più parti, tra le quali può esserci anche scambio di massa: ciò avviene, per esempio, nel cambiamento di fase di una sostanza, nella dissoluzione di una sostanza in un’altra, nei processi di diffusione; anche una reazione chimica provoca una situazione di questo tipo, in cui alcune sostanze presenti nello stato iniziale possono scomparire del tutto o in parte per dare luogo ad altre sostanze.

Un sistema chiuso può quindi essere composto da sottoinsiemi aperti, e si può pensare di essere sempre in tali condizioni anche in presenza di un unico sistema aperto se si include l’ambiente. Limitandoci ai sistemi pVT vediamo che per la descrizione di un sistema aperto non sono più sufficienti due sole variabili termodinamiche scelte nella terna p, V, T, ma ne è necessaria un’altra per esprimere la quantità di materia contenuta nel sistema (o la massa).

La (13.28) deve allora essere scritta in forma più generale,

Potenziale chimico

dove l’ultimo termine esprime il contributo alla variazione di energia interna del sistema dovuto al cambiamento dn del numero di moli; assumiamo dn > 0 se la materia entra nel sistema. In conseguenza di (13.55) la variazione di entalpia si scrive

e analogamente

La grandezza intensiva μ così definita si chiama potenziale chimico. Se con-frontiamo le relazioni appena scritte con l’espressione del differenziale totale di una funzione troviamo che

Il potenziale chimico del sistema esprime così la variazione di una delle grandezze U, H, F, G rispetto alla variazione del numero di moli, calcolata mantenendo costanti le relative variabili naturali.

Considerando in particolare l’energia libera e l’entalpia libera, la loro natura di grandezze estensive permette di scrivere F = nf e G = ng per cui, da (13.59),

In un processo a temperatura e volume costanti il potenziale chimico coincide con l’energia libera molare, mentre in un processo a temperatura e pressione costanti esso coincide con l’entalpia libera molare.

Prendiamo in esame un sistema chiuso formato da due sottosistemi, costituiti dalla stessa sostanza e messi a contatto, cosicché possano scambiare materia (contatto chimico o diffusivo): essi sono posti in un recipiente a pareti rigide, di volume totale V, e sono separati da una parete porosa permeabile alla sostanza; inoltre essi sono alla stessa temperatura T, che è mantenuta costante tramite il contatto termico con un serbatoio. Sappiamo dal paragrafo 13.1 che lo stato di equilibrio, a T e V costanti, è quello in cui l’energia libera del sistema è minima, fatto che si esprime con la condizione dF = 0.

L’energia libera varia durante il processo per effetto del cambiamento del numero di moli n₁ e n₂ delle due parti, cambiamento però soggetto alla condizione n₁ + n₂ = costante. Pertanto, all’equilibrio abbiamo

Questa relazione è compatibile con dn₁ + dn₂ = 0 solo se

ovvero, da (13.59), solo se

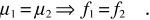
Nello stato di equilibrio del processo considerato i potenziali chimici delle due parti, ovvero le energie libere molari, devono essere uguali.

Il flusso spontaneo di materia, in assenza di forze esterne, avviene dalla zona a potenziale chimico maggiore a quella a potenziale chimico minore. Infatti in una fase intermedia del processo deve essere dF < 0, cioè

Da dn₁ + dn₂ = 0 si ha dn₂ = – dn₁ e quindi

Il flusso di materia dalla parte 1 alla parte 2, che comporta dn₁ < 0, si ha solo se μ₁ > μ₂ ; esso termina quando il potenziale chimico, ovvero l’energia libera molare, sono uniformi in tutto il sistema. In questi processi il potenziale chimico rispetto al flusso di materia gioca lo stesso ruolo della temperatura rispetto al flusso di calore.

Esempio 13.18

Un gas ideale è contenuto in un recipiente a pareti rigide di volume V, suddiviso in due parti separate da una parete rigida permeabile al gas; nella parte 1, di volume V₁ , ci sono n_{1, 0} moli di gas alla pressione p₁ , nella parte 2, di volume V₂ , n_{2, 0} moli di gas alla pressione p₂ . La temperatura del sistema è mantenuta costante al valore T. Determinare, nello stato finale di equilibrio, la distribuzione del numero di moli.

Soluzione

In equilibrio deve essere μ₁ = μ₂ , cioè f₁ = f₂ , ovvero

Siccome il gas è lo stesso e la temperatura è la stessa ovunque, l’energia interna molare, che dipende solo dalla temperatura, deve essere la stessa dalle due parti, u₁ = u₂ ; ciò comporta s₁ = s₂ . L’entropia molare dipende da due variabili, per esempio temperatura e pressione: ne segue che la pressione nelle due parti deve essere la stessa e quindi

Nello stato di equilibrio il numero di moli di una parte è proporzionale al volume di quella parte, cioè la densità è costante in tutto il sistema.

Il flusso avviene dalla parte a pressione maggiore a quella a pressione minore: infatti, sappiamo che durante il processo dF < 0, cioè ( f₁ – f₂) dn₁ < 0, ovvero f₁ > f₂ se il flusso è dalla parte 1 alla parte 2. Poiché è sempre u₁ = u₂ abbiamo

Per l’espressione dell’entropia ricorriamo a (12.27):

Notiamo che, per tutto il sistema, la condizione dF = dU – TdS < 0 corrisponde a dS > 0 essendo dU = 0: ciò è in accordo col fatto che il processo è irreversibile e avviene senza scambio di calore (oltre a dU = 0 è anche dW = 0). Bisogna dire che i risultati si potevano ottenere direttamente dalla definizione di equilibrio termodinamico (che deve essere anche meccanico); però così abbiamo verificato, in un caso semplice, l’applicazione di un metodo generale.

Visualizza Soluzione

Quando un processo si svolge a temperatura e pressione costanti lo stato di equilibrio è quello in cui è minima l’entalpia libera (dG = 0). In un sistema formato

da due parti come quelli analizzati negli esempi relativi all’energia libera ciò comporta μ₁ = μ₂ ovvero g₁ = g₂: l’entalpia libera molare è eguale nelle due parti. Abbiamo già trovato tale risultato in un tipico processo a T e p costanti, come l’evaporazione di una sostanza pura (paragrafo 13.1). Le applicazioni più comuni si hanno nelle reazioni chimiche, che di norma avvengono a temperatura e pressione costanti.

Regola delle fasi

Una conseguenza molto importante della formulazione delle condizioni di equilibrio tramite il potenziale chimico è la cosiddetta regola delle fasi.

Premettiamo la definizione di fase di un sistema: si chiama così una qualsiasi parte di un sistema che sia omogenea e che abbia limiti geometrici ben definiti; essa può essere composta anche da più specie chimiche diverse. Per esempio, una miscela di gas è un’unica fase gassosa, una soluzione liquida un’unica fase liquida, un liquido in equilibrio col suo vapore è un sistema a due fasi (ma con un solo componente). Per ciascuna fase in equilibrio meccanico e termico è possibile definire il volume, la pressione, la temperatura e la composizione, dando il numero di moli delle varie specie chimiche.

Osserviamo che questa definizione di fase contiene in sé quella più restrittiva usata in precedenza, riferita soltanto a una sostanza pura (p.e. acqua in fase solida, liquida o gassosa).

Supponiamo ora di avere un sistema formato da f fasi che contengono in totale c componenti, in equilibrio meccanico (p uniforme), termico (T uniforme) e chimico. Ciascun componente può essere distribuito nelle varie fasi, però deve esserci equilibrio e di conseguenza il potenziale chimico, ovvero l’entalpia libera molare, di ciascun componente devono essere gli stessi ovunque (accenniamo soltanto al fatto che in questa trattazione si suppongono trascurabili eventuali energie associate alle superficie di contatto tra le diverse fasi). Pertanto devono valere le eguaglianze

Ciascuna riga è composta da f – 1 equazioni che affermano appunto l’eguaglianza del potenziale chimico di un dato componente nelle f fasi; le righe sono c e in totale il numero di equazioni è c(f – 1).

I potenziali chimici sono funzioni di p, T e delle frazioni molari r_i = n_i /n (n_i è il numero di moli dell’i-esimo componente); le frazioni molari sono c, ma devono soddisfare alla condizione Σ_i r_i = 1, per cui quelle indipendenti sono c – 1; il ragionamento va esteso a tutte le fasi e quindi in totale abbiamo (c – 1) f variabili indipendenti più pressione e volume, cioè (c – 1)f + 2.

La differenza tra il numero di variabili indipendenti e il numero di equazioni è detta varianza del sistema (o numero di gradi di libertà del sistema): essa dà il numero di variabili che possono essere fissate arbitrariamente in uno stato di equilibrio del sistema. Dalla differenza di (c – 1)f + 2 e c(f – 1) risulta

Regola delle fasi

La (13.63), dovuta a Gibbs, si dice regola delle fasi. Vediamo alcuni esempi per chiarirne il significato.

1) Sistema omogeneo chimicamente definito: c’è un solo componente ed una sola fase, quindi v = 2, si possono fissare arbitrariamente le variabili p e T.

2) Sistema omogeneo miscela di due sostanze pure: c = 2, f = 1, v = 3; si possono fissare arbitrariamente p, T e il rapporto n₁ /n₂ . Se le sostanze sono m, f = 1, v = m + 1 in corrispondenza a p, T e m – 1 frazioni molari.

3) Sostanza pura solida o liquida in equilibrio col suo vapore: c = 1, f = 2, v = 1; se è data la temperatura la pressione è fissata e corrisponde alla tensione di vapore a quella temperatura secondo una formula tipo (11.29).

4) Sostanza pura in tre fasi diverse (solida, liquida, gassosa) in equilibrio: c = 1, f = 3, v = 0. Non c’è alcun grado di libertà, l’equilibrio si ha solo per una particolare coppia valori di temperatura e pressione (punto triplo).

Punto eutettico
Composizione eutettica

5) Sistema costituito da due sostanze solubili allo stato liquido, ma insolubili allo stato solido: ci sono due componenti e quattro fasi (solido a, solido b, soluzione liquida, vapore) per cui v = 0. Esiste un solo insieme di valori p, T, n_a/n_b per cui le quattro fasi possono coesistere in equilibrio. Tali valori determinano il cosiddetto punto eutettico e il rapporto n_a/n_b di equilibrio si dice composizione eutettica.

L’insieme degli argomenti trattati fa capire l’importanza del concetto di potenziale chimico nella ricerca degli stati di equilibrio di un sistema pVT, soprattutto a temperatura e pressione costanti.

Come abbiamo già avuto modo di rilevare in altri casi simili, le leggi trovate sono poi di utilità pratica se abbiamo a disposizione espressioni analitiche dei potenziali chimici in funzione di coordinate termodinamiche misurabili. A questo proposito, se si tratta di miscele di gas ideali, tornano utili le espressioni ricavate nel paragrafo 13.5; negli altri casi occorrono opportuni modelli, derivati da ipotesi teoriche o da misure sperimentali. Ricordiamo quanto detto alla fine del paragrafo 10.1: la trattazione termodinamica, per la sua grande generalità, può essere applicata a qualsiasi sistema, però, proprio per questo, non può dare risultati che tengono conto di particolari strutture atomiche o molecolari.