What_is_this_thing_called

The Bayesian approach

Many of us had sufficient confidence in the prediction of the most recent return of Halley’s comet that we booked weekends in the country, far from city lights and well in advance, in order to observe it. Our confidence proved not to be misplaced. Scientists have enough confidence in the reliability of their theories to send manned spacecraft into space. When things went amiss in one of them, we were impressed, but perhaps not surprised, when the scientists, aided by computers, were able to rapidly calculate how the remaining rocket fuel could be utilised to fire the rocket motor in just the right way to put the craft into an orbit that would return it to earth. These stories suggest that perhaps the extent to which theories are fallible, stressed by the philosophers in our story so far, from Popper to Feyerabend, are misplaced or exaggerated. Can the Popperian claim that the probability of all scientific theories is zero be reconciled with them? It is worth stressing, in this connection, that the theory used by the scientists in both of my stories was Newtonian theory, a theory falsified in a number of ways at the beginning of the twentieth century according to the Popperian account (and most others). Surely something has gone seriously wrong.

One group of philosophers who do think that something has gone radically wrong, and whose attempts to put it right have become popular in the last few decades, are the Bayesians, so called because they base their views on a theorem in probability theory proved by the eighteenth-century mathematician Thomas Bayes. The Bayesians regard it as inappropriate to ascribe zero probability to a well-confirmed theory, and they seek some kind of inductive inference that will yield non-zero probabilities for them in a way that avoids the difficulties of the kind described in chapter 4. For example, they would like to be able to show how and why a high probability can be attributed to Newtonian theory when used to calculate the orbit of Halley’s comet or a spacecraft. An outline and critical appraisal of their viewpoint is given in this chapter.

Bayes’ theorem

Bayes’ theorem is about conditional probabilities, probabilities for propositions that depend on (and hence are conditional on) the evidence bearing on those propositions. For instance, the probabilities ascribed by a punter to each horse in a race will be conditional on the knowledge the punter has of the past form of each of the horses. What is more, those probabilities will be subject to change by the punter in the light of new evidence, when, for example, he finds on arrival at the racetrack that one of the horses is sweating badly and looking decidedly sick. Bayes’ theorem is a theorem prescribing how probabilities are to be changed in the light of new evidence.

In the context of science the issue is how to ascribe probabilities to theories or hypotheses in the light of evidence. Let P(h/e) denote the probability of a hypothesis h in the light of evidence e, P(e/h) denote the probability to be ascribed to the evidence e on the assumption that the hypothesis h is correct, P(h) the probability ascribed to h in the absence of knowledge of e, and P(e) the probability ascribed to e in the absence of any assumption about the truth of h. Then Bayes’ theorem can be written:

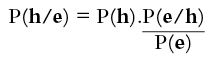
P(h) is referred to as the prior probability, since it is the probability ascribed to the hypothesis prior to consideration of the evidence, e, and P(h/e) is referred to as the posterior probability, the probability after the evidence, e, is taken into account. So the formula tells us how to change the probability of a hypothesis to some new, revised probability in the light of some specified evidence.

The formula indicates that the prior probability, P(h), is to be changed by a scaling factor P(e/h)/P(e) in the light of evidence e. It can readily be seen how this is in keeping with common intuitions. The factor P(e/h) is a measure of how likely e is given h. It will take a maximum value of 1 if e follows from h and a minimum value of zero if the negation of e follows from h. (Probabilities always take values in between 1, representing certainty, and zero, representing impossibility.) The extent to which some evidence supports a hypothesis is proportional to the degree to which the hypothesis predicts the evidence, which seems reasonable enough. The term in the divisor of the scaling factor, P(e), is a measure of how likely the evidence is considered to be when the truth of the hypothesis, h, is not assumed. So, if some piece of evidence is considered extremely likely whether we assume a hypothesis or not, the hypothesis is not supported significantly when that evidence is confirmed, whereas if that evidence is considered very unlikely unless the hypothesis is assumed, then the hypothesis will be highly confirmed if the evidence is confirmed. For instance, if some new theory of gravitation were to predict that heavy objects fall to the ground, it would not be significantly confirmed by the observation of the fall of a stone, since the stone would be expected to fall anyway. On the other hand, if that new theory were to predict some small variation of gravity with temperature, then the theory would be highly confirmed by the discovery of that effect, since it would be considered most unlikely in the absence of the new theory.

An important aspect of the Bayesian theory of science is that the calculations of prior and posterior probabilities always take place against a background of assumptions that are taken for granted, that is, assuming what Popper called background knowledge. So, for example, when it was suggested in the previous paragraph that P(e/h) takes the value 1 when e follows from h, it was taken for granted that h was to be taken in conjunction with the available background knowledge. We have seen in earlier chapters that theories need to be augmented by suitable auxiliary assumptions before they yield testable predictions. The Bayesians take these considerations on board. Throughout this discussion it is assumed that probabilities are calculated against a background of assumed knowledge.

It is important to clarify in what sense Bayes’ theorem is indeed a theorem. Although we will not consider the details here, we note that there are some minimal assumptions about the nature of probability which taken together constitute the so-called probability calculus. These assumptions are accepted by Bayesians and non-Bayesians alike. It can be shown that denying them has a range of undesirable consequences. It can be shown, for example, that a gambling system that violates the probability calculus is ‘irrational’ in the sense that it makes it possible for wagers to be placed on all possible outcomes of a game, race or whatever in such a way that the participants on one or other side of the betting transaction will win whatever the outcome. (Systems of betting odds that allow this possibility are called Dutch Books. They violate the probability calculus.) Bayes’ theorem can be derived from the premises that constitute the probability calculus. In that sense, the theorem in itself is uncontentious.

So far, we have introduced Bayes’ theorem, and have tried to indicate that the way in which it prescribes that the probability of a hypothesis be changed in the light of evidence captures some straightforward intuitions about the bearing of evidence on theories. Now we must press the question of the interpretation of the probabilities involved more strongly.

Subjective Bayesianism

The Bayesians disagree among themselves on a fundamental question concerning the nature of the probabilities involved. On one side of the division we have the ‘objective’ Bayesians. According to them, the probabilities represent probabilities that rational agents ought to subscribe to in the light of the objective situation. Let me try to indicate the gist of their position with an example from horse racing. Suppose we are confronted by a list of the runners in a horse race and we are given no information about the horses at all. Then it might be argued that on the basis of some ‘principle of indifference’ the only rational way of ascribing probabilities to the likelihood of each horse winning is to distribute the probabilities equally among the runners. Once we have these ‘objective’ prior probabilities to start with, then Bayes’ theorem dictates how the probabilities are to be modified in the light of any evidence, and so the posterior probabilities that result are also those that a rational agent ought to accept. A major, and notorious, problem with this approach, at least in the domain of science, concerns how to ascribe objective prior probabilities to hypotheses. What seems to be necessary is that we list all the possible hypotheses in some domain and distribute probabilities among them, perhaps ascribing the same probability to each employing the principle of indifference. But where is such a list to come from? It might well be thought that the number of possible hypotheses in any domain is infinite, which would yield zero for the probability of each and the Bayesian game cannot get started. All theories have zero probability and Popper wins the day. How is some finite list of hypotheses enabling some objective distribution of non-zero prior probabilities to be arrived at? My own view is that this problem is insuperable, and I also get the impression from the current literature that most Bayesians are themselves coming around to this point of view. So let us turn to ‘subjective’ Bayesianism.

For the subjective Bayesian the probabilities to be handled by Bayes’ theorem represent subjective degrees of belief. They argue that a consistent interpretation of probability theory can be developed on this basis, and, moreover, that it is an interpretation that can do full justice to science. Part of their rationale can be grasped by reference to the examples I invoked in the opening paragraph of this chapter. Whatever the strength of the arguments for attributing zero probability to all hypotheses and theories, it is simply not the case, argue the subjective Bayesians, that people in general and scientists in particular ascribe zero probabilities to well-confirmed theories. The fact that I pre-booked my trip to the mountains to observe Halley’s comet suggests that they are right in my case at least. In their work, scientists take many laws for granted. The unquestioning use of the law of refraction of light by astronomers and Newton’s laws by those involved in the space program demonstrates that they ascribe to those laws a probability close, if not equal, to unity. The subjective Bayesians simply take the degrees of belief in hypotheses that scientists as a matter of fact happen to have as the basis for the prior probabilities in their Bayesian calculations. In this way they escape Popper’s strictures to the effect that the probability of all universal hypotheses must be zero.

Bayesianism makes a great deal of sense in the context of gambling. We have noted that adherence to the probability calculus, within which Bayes’ theorem can be proved, is a sufficient condition to avoid Dutch Books. Bayesian approaches to science capitalise on this by drawing a close analogy between science and gambling systems. The degree of belief held by a scientist in a hypothesis is analogous to the odds on a particular horse winning a race that he or she considers to be fair. Here there is a possible source of ambiguity that needs to be addressed. If we stick to our analogy with horse racing, then the odds considered to be fair by punters can be taken as referring either to their private subjective degrees of belief or to their beliefs as expressed in practice in their betting behaviour. These are not necessarily the same thing. Punters can depart from the dictates of the odds they believe in by becoming flustered at the race-track or by losing their nerve when the system of odds they believe in warrants a particularly large bet. Not all Bayesians make the same choice between these alternatives when applying the Bayesian calculus to science. For example, Jon Dorling (1979) takes the probabilities to measure what is reflected in scientific practice and Howson and Urbach (1993) take them to measure subjective degrees of belief. A difficulty with the former stand is knowing what it is within scientific practice that is meant to correspond to betting behaviour. Identifying the probabilities with subjective degrees of belief, as Howson and Urbach do, at least has the advantage of making it clear what the probabilities refer to.

Attempting to understand science and scientific reasoning in terms of the subjective beliefs of scientists would seem to be a disappointing departure for those who seek an objective account of science. Howson and Urbach have an answer to that charge. They insist that the Bayesian theory constitutes an objective theory of scientific inference. That is, given a set of prior probabilities and some new evidence, Bayes’ theorem dictates in an objective way what the new, posterior, probabilities must be in the light of that evidence. There is no difference in this respect between Bayesianism and deductive logic, because logic has nothing to say about the source of the propositions that constitute the premises of a deduction either. It simply dictates what follows from those propositions once they are given. The Bayesian defence can be taken a stage further. It can be argued that the beliefs of individual scientists, however much they might differ at the outset, can be made to converge given the appropriate input of evidence. It is easy to see in an informal way how this can come about. Suppose two scientists start out by disagreeing greatly about the probable truth of hypothesis h which predicts otherwise unexpected experimental outcome e. The one who attributes a high probability to h will regards e as less unlikely than the one who attributes a low probability to h. So P(e) will be high for the former and low for the latter. Suppose now that e is experimentally confirmed. Each scientist will have to adjust the probabilities for h by the factor P(e/h)/P(e). However, since we are assuming that e follows from h, P(e/h) is 1 and the scaling factor is 1/P(e). Consequently, the scientist who started with a low probability for h will scale up that probability by a larger factor than the scientist who started with a high probability for h. As more positive evidence comes in, the original doubter is forced to scale up the probability in such a way that it eventually approaches that of the already convinced scientist. In this kind of way, argue the Bayesians, widely differing subjective opinions can be brought into conformity in response to evidence in an objective way.

Applications of the Bayesian formula

The preceding paragraph has given a strong foretaste of the kind of ways in which the Bayesians wish to capture and sanction typical modes of reasoning in science. In this section we will sample some more examples of Bayesianism in action.

In earlier chapters it was pointed out that there is a law of diminishing returns at work when testing a theory against experiment. Once a theory has been confirmed by an experiment once, repeating that same experiment under the same circumstances will not be taken by scientists as confirming the theory to as high a degree as the first experiment did. This is readily accounted for by the Bayesian. If the theory T predicts the experimental result E then the probability P(E/T) is 1, so that the factor by which the probability of T is to be increased in the light of a positive result E is 1/P(E). Each time the experiment is successfully performed, the more likely the scientist will be to expect it to be performed successfully again the subsequent time. That is, P(E) will increase. Consequently, the probability of the theory being correct will increase by a smaller amount on each repetition.

Other points in favour of the Bayesian approach can be made in the light of historical examples. Indeed, I suggest that it is the engagement by the Bayesians with historical cases in science that has been a key reason for the rising fortunes of their approach in recent years, a trend begun by Jon Dorling (1979). In our discussion of Lakatos’s methodology we noted that according to that methodology it is the confirmations of a program that are important rather than the apparent falsifications, which can be blamed on the assumptions in the protective belt rather than on the hard core. The Bayesians claim to be able to capture the rationale for this strategy. Let us see how they do it, by looking at a historical example utilised by Howson and Urbach (1993, pp. 136–42).

The example concerns a hypothesis put forward by William Prout in 1815. Prout, impressed by the fact that atomic weights of the chemical elements relative to the atomic weight of hydrogen are in general close to whole numbers, conjectured that atoms of the elements are made up of whole numbers of hydrogen atoms. That is, Prout saw hydrogen atoms as playing the role of elementary building blocks. The question at issue is what the rational response was for Prout and his followers to the finding that the atomic weight of chlorine relative to hydrogen (as measured in 1815) was 35.83, that is, not a whole number. The Bayesian strategy is to assign probabilities that reflect the prior probabilities that Prout and his followers might well have assigned to their theory together with relevant aspects of background knowledge, and then use Bayes’ theorem to calculate how these probabilities change in light of the discovery of the problematic evidence, namely, the non-integral value of the atomic weight of chlorine. Howson and Urbach attempt to show that when this is done the result is that the probability of Prout’s hypothesis falls just a little, whereas the probability of the relevant measurements being accurate falls dramatically. In light of this it seems quite reasonable for Prout to have retained his hypothesis (the hard core) and to have put the blame on some aspect of the measuring process (the protective belt). It would seem that a clear rationale has been given for what in Lakatos’s methodology appeared as ‘methodological decisions’ that were not given any grounding. What is more, it would seem that Howson and Urbach, who are following the lead of Dorling here, have given a general solution to the so-called Duhem-Quine problem. Confronted with the problem of which part of a web of assumptions to blame for an apparent falsification, the Bayesian answer is to feed in the appropriate prior probabilities and calculate the posterior probabilities. These will show which assumptions slump to a low probability, and consequently which assumptions should be dropped to maximise the chances of future success.

I will not go through the details of the calculations in the Prout case, or any of the other examples that Bayesians have given, but I will say enough to at least give the flavour of the way in which they proceed. Prout’s hypothesis, h, and the effect of the evidence, e, the non-integral atomic weight of chlorine, on the probability to be assigned to it is to be judged in the context of the available background knowledge, a. The most relevant aspect of the background knowledge is the confidence to be placed in the available techniques for measuring atomic weights and the degree of purity of the chemicals involved. Estimates need to be made about the prior probabilities of h, a and e. Howson and Urbach suggest a value of 0.9 for P(h), basing their estimate on historical evidence to the effect that the Proutians were very convinced of the truth of their hypothesis. They place P(a) somewhat lower at 0.6, on the grounds that chemists were aware of the problem of impurities, and that there were variations in the results of different measurements of the atomic weight of particular elements. The probability P(e) is assessed on the assumption that the alternative to h is a random distribution of atomic weights, so, for instance, P(e/not h & a) is ascribed a probability 0.01 on the grounds that, if the atomic weight of chlorine is randomly distributed over a unit interval it would have a one in a hundred chance of being 35.83, rather than 35.82, 35.61 or any of the hundred possibilities between 35.00 and 36.00. These probability estimates, and a few others like them, are fed into Bayes’ theorem to yield posterior probabilities, P(h/e) and P(a/e), for h and a. The result is 0.878 for the former and 0.073 for the latter. Note that the probability for h, Prout’s hypothesis, has fallen only a small amount from the original 0.9, whereas the probability of a, the assumption that the measurements are reliable, has fallen dramatically from 0.6 to 0.073. A reasonable response for the Proutians, conclude Howson and Urbach, was to retain their hypothesis and doubt the measurements. They point out that nothing much hinges on the absolute value of the numbers that are fed into the calculation so long as they are of the right kind of order to reflect the attitudes of the Proutians as reflected in the historical literature.

The Bayesian approach can be used to mount a criticism of some of the standard accounts of the undesirability of ad hoc hypotheses and related issues. Earlier in this book I proposed the idea, following Popper, that ad hoc hypotheses are undesirable because they are not testable independently of the evidence that led to their formulation. A related idea is that evidence that is used to construct a theory cannot be used again as evidence for that theory. From the Bayesian point of view, although these notions sometimes yield appropriate answers concerning how well theories are confirmed by evidence, they also go astray, and, what is more, the rationale underlying them is misconceived. The Bayesians attempt to do better in the following kinds of ways.

Bayesians agree with the widely held view that a theory is better confirmed by a variety of kinds of evidence than by evidence of a particular kind. There is a straightforward Bayesian rationale that explains why this should be so. The point is that there are diminishing returns from efforts to confirm a theory by a single kind of evidence. This follows from the fact that each time the theory is confirmed by that kind of evidence, then the probability expressing the degree of belief that it will do so in the future gradually increases. By contrast, the prior probability of a theory being confirmed by some new kind of evidence may be quite low. In such cases, feeding the results of such a confirmation, once it occurs, into the Bayesian formula leads to a significant increase in the probability ascribed to the theory. So the significance of independent evidence is not in dispute. Nevertheless, Howson and Urbach urge that, from the Bayesian point of view, if hypotheses are to be dismissed as ad hoc, the absence of independent testability is not the right reason for doing so. What is more, they deny that data used in the construction of a theory cannot be used to confirm it.

A major difficulty with the attempt to rule out ad hoc hypotheses by the demand for independent testability is that it is too weak, and admits hypotheses in a way that at least clashes with our intuitions. For instance, let us consider the attempt by Galileo’s rival to retain his assumption that the moon is spherical in the face of Galileo’s sightings of its moons and craters by proposing the existence of a transparent, crystalline substance enclosing the observable moon. This adjustment cannot be ruled out by the independent testability criterion because it was independently testable, as evidenced by the fact that it has been refuted by the lack of interference from any such crystalline spheres experienced during the various moon landings. Greg Bamford (1993) has raised this, and a range of other difficulties with a wide range of attempts to define the notion of ad hocness by philosophers in the Popperian tradition, and suggest that they are attempting to define a technical notion for what is in effect nothing more than a commonsense idea. Although Bamford’s critique is not from a Bayesian point of view, the response of Howson and Urbach is similar, insofar as their view is that ad hoc hypotheses are rejected simply because they are considered implausible, and are credited with a low probability because of this. Suppose a theory t has run into trouble with some problematic evidence and is modified by adding assumption a, so that the new theory, t, is (t & a). Then it is a straightforward result of probability theory that P(t & a) cannot be greater than P(a). From a Bayesian point of view, then, the modified theory will be given a low probability simply on the grounds that P(a) is unlikely. The theory of Galileo’s rival could be rejected to the extent that his suggestion was implausible. There is nothing more to it, and nothing else needed.

Let us now turn to the case of the use of data to construct a theory, and the denial that that data can be considered to support it. Howson and Urbach (1993, pp. 154–7) suggest counter examples. Consider an urn containing counters, and imagine that we begin with the assumption that all of the counters are white and none of them coloured. Suppose we now draw counters 1,000 times, replacing the counter and shaking the urn after each draw, and that the result is that 495 of the counters are white. We now adjust our hypothesis to be that the urn contains white and coloured counters in equal numbers. Is this adjusted hypothesis supported by the evidence used to arrive at the revised, equal numbers, hypothesis? Howson and Urbach suggest, reasonably, that it is, and show why this is so on Bayesian grounds. The crucial factor that leads to the probability of the equal numbers hypothesis increasing as a result of the experiment that drew 495 white counters is the probability of drawing that number if the equal numbers hypothesis is false. Once it is agreed that that probability is small, the result that the experiment confirms the equal numbers hypothesis follows straightforwardly from the Bayesian calculus, even though the data were used in the construction of the hypothesis.

There is a standard criticism often levelled at the Bayesian approach that does strike at some versions of it, but I think the version defended by Howson and Urbach can counter it. To utilise Bayes’ theorem it is necessary to be able to evaluate P(e), the prior probability of some evidence that is being considered. In a context where hypothesis h is being considered, it is convenient to write P(e) as P(e/h).P(h) + P(e/not h).P(not h), a straightforward identity in probability theory. The Bayesian needs to be able to estimate the probability of the evidence assuming the hypothesis is true, which may well be unity if the evidence follows from the hypothesis, but also the probability of the evidence should the hypothesis be false. It is this latter factor that is the problematic one. It would appear that it is necessary to estimate the likelihood of the evidence in the light of all hypotheses other than h. This is seen as a major obstacle, because no particular scientist can be in a position to know all possible alternatives to h, especially if, as some have suggested, this must include all hypotheses not yet invented. The response open to Howson and Urbach is to insist that the probabilities in their Bayesian calculus represent personal probabilities, that is, the probabilities that individuals, as a matter of fact, attribute to various propositions. The value of the probability of some evidence being true in the light of alternatives to h will be decided on by a scientist in the light of what that scientist happens to know (which will certainly exclude hypotheses not yet invented). So, for instance, when dealing with the Prout case, Howson and Urbach take the only alternative to Prout’s hypothesis to be the hypothesis that atomic weights are randomly distributed on the basis of historical evidence to the effect that that is what the Proutians believed to be the alternative. It is the thoroughgoing nature of their move to subjective probabilities that makes it possible for Howson and Urbach to avoid the particular problem raised here.

In my portrayal of the elements of the Bayesian analysis of science, I have concentrated mainly on the position outlined by Howson and Urbach because it seems to me to be the one most free of inconsistencies. Because of the way in which probabilities are interpreted in terms of degrees of the beliefs actually held by scientists, their system enables non-zero probabilities to be attributed to theories and hypotheses, it gives a precise account of how the probabilities are to be modified in the light of evidence, and it is able to give a rationale for what many take to be key features of scientific method. Howson and Urbach embellish their system with historical case studies.

Critique of subjective Bayesianism

As we have seen, subjective Bayesianism, the view that consistently understands probabilities as the degrees of belief actually held by scientists, has the advantage that it is able to avoid many of the problems that beset alternative Bayesian accounts that seek for objective probabilities of some kind. For many, to embrace subjective probabilities is to pay too high a price for the luxury of being able to attribute probabilities to theories. Once we take probabilities as subjective degrees of belief to the extent that Howson and Urbach, for example, urge that we do, then a range of unfortunate consequences follow.

The Bayesian calculus is portrayed as an objective mode of inference that serves to transform prior probabilities into posterior probabilities in the light of given evidence. Once we see things in this way, it follows that any disagreements in science, between proponents of rival research programs, paradigms or whatever, reflected in the (posterior) beliefs of scientists, must have their source in the prior probabilities held by the scientists, since the evidence is taken as given and the inference considered to be objective. But the prior probabilities are themselves totally subjective and not subject to a critical analysis. They simply reflect the various degrees of belief each individual scientist happens to have. Consequently, those of us who raise questions about the relative merits of competing theories and about the sense in which science can be said to progress will not have our questions answered by the subjective Bayesian, unless we are satisfied with an answer that refers to the beliefs that individual scientists just happen to have started out with.

If subjective Bayesianism is the key to understanding science and its history, then one of the most important sources of information that we need to have access to in order to acquire that understanding is the degrees of belief that scientists actually do or did hold. (The other source of information is the evidence, which is discussed below.) So, for instance, an understanding of the superiority of the wave theory over the particle theory of light will require some knowledge of the degrees of belief that Fresnel and Poisson, for instance, brought to the debate in the early 1830s. There are two problems here. One is the problem of gaining access to a knowledge of these private degrees of belief. (Recall that Howson and Urbach distinguish between private beliefs and actions and insist that it is the former with which their theory deals, so we cannot infer beliefs of scientists from what they do, or even write.) The second problem is the implausibility of the idea that we need to gain access to these private beliefs in order to grasp the sense in which, say, the wave theory of light was an improvement on its predecessor. The problem is intensified when we focus on the degree of complexity of modern science, and the extent to which it involves collaborative work. (Recall my comparison with workers constructing a cathedral in chapter 8.) An extreme, and telling, example is provided by Peter Galison’s (1997) account of the nature of the work in current fundamental particle physics, where very abstruse mathematical theories are brought to bear on the world via experimental work that involves elaborate computer techniques and instrumentation and requires state-of-the-art engineering for its operation. In situations like this there is no single person who grasps all aspects of this complex work. The theoretical physicist, the computer programmer, the mechanical engineer and the experimental physicist all have their separate skills, which are brought to bear on a collaborative enterprise. If the progressiveness of this enterprise is to be understood as focusing on degrees of belief, then whose degree of belief do we choose and why?

The extent to which degrees of belief are dependent on prior probabilities in Howson and Urbach’s analysis is the source of another problem. It would seem that, provided a scientist believes strongly enough in his or her theory to begin with (and there is nothing in subjective Bayesianism to prevent degrees of belief as strong as one might wish), then this belief cannot be shaken by any evidence to the contrary, however strong or extensive it might be. This point is in fact illustrated by the Prout study, the very study that Howson and Urbach use to support their position. Recall that in that study we assume that the Proutians began with a prior probability of 0.9 for their theory that atomic weights are equal multiples of the atomic weight of hydrogen and a prior probability of 0.6 for the assumption that atomic weight measurements are reasonably accurate reflections of actual atomic weights. The posterior probabilities, calculated in the light of the 35.83 value obtained for chlorine, were 0.878 for Prout’s theory and 0.073 for the assumption that the experiments are reliable. So the Proutians were right to stick to their theory and reject the evidence. I point out here that the original incentive behind Prout’s hypothesis was the near integral values of a range of atomic weights other than chlorine, measured by the very techniques that the Proutians have come to regard as so unreliable that they warrant a probability as low as 0.073! Does this not show that if scientists are dogmatic enough to begin with they can offset any adverse evidence? Insofar as it does, there is no way that the subjective Bayesian can identify such activity as bad scientific practice. The prior probabilities cannot be judged. They must be taken as simply given. As Howson and Urbach (1993, p. 418) observe, ‘how prior distributions are determined is simply not something that comes within the scope of [their] theory’.

Bayesians seem to have a counter to the Popperian claim that the probability of all theories must be zero, insofar as they identify probabilities with the degrees of belief that scientists happen, as a matter of fact, to possess. However, the Bayesian position is not that simple. For it is necessary for the Bayesians to ascribe probabilities that are counterfactual, and so cannot be simply identified with degrees of belief actually held. Let us take the problem of how past evidence is to count for a theory as an example. How can the observations of Mercury’s orbit be taken as confirmation of Einstein’s theory of general relativity, given that the observations preceded the theory by a number of decades? To calculate the probability of Einstein’s theory in the light of this evidence, the subjective Bayesian is required, among other things, to provide a measure for the probability an Einstein supporter would have given to the probability of Mercury’s orbit precessing in the way that it does without a knowledge of Einstein’s theory. That probability is not a measure of the degree of belief that a scientist actually has but a measure of a degree of belief they would have had if they did not know what they in fact do know. The status of these degrees of belief, and the problem of how one is to evaluate them, pose serious problems, to put it mildly.

Let us now turn to the nature of ‘evidence’ as it figures in subjective Bayesianism. We have treated the evidence as a given, something that is fed into Bayes’ theorem to convert prior probabilities to posterior probabilities. However, as the discussion of the early chapters of this book should have made clear, evidence in science is far from being straightforwardly given. The stand taken by Howson and Urbach (1993, pp. 406–7) is explicit and totally in keeping with their overall approach.

The Bayesian theory we are proposing is a theory of inference from data; we say nothing about whether it is correct to accept the data or even whether your commitment to the data is absolute. It may not be, and you may be foolish to repose in it the confidence you actually do. The Bayesian theory of support is a theory of how the acceptance as true of some evidential statement affects your belief in some hypothesis. How you come to accept the truth of the evidence and whether you are correct in accepting it as true are matters which, from the point of view of the theory, are simply irrelevant.

Surely this is a totally unacceptable position for those who purport to be writing a book on scientific reasoning. For is it not the case that we seek an account of what counts as appropriate evidence in science? Certainly a scientist will respond to some evidential claim, not by asking the scientist making the claim how strongly he or she believes it, but by seeking information on the nature of the experiment that yielded the evidence, what precautions were taken, how errors were estimated and so on. A good theory of scientific method will surely be required to give an account of the circumstances under which evidence can be regarded as adequate, and be in a position to pinpoint standards that empirical work in science should live up to. Certainly experimental scientists have plenty of ways of rejecting shoddy work, and not by appealing to subjective degrees of belief.

Especially when they are responding to criticism, Howson and Urbach stress the extent to which both the prior probabilities and the evidence which need to be fed into Bayes’ theorem are subjective degrees of belief about which the subjective Bayesian has nothing to say. But to what extent can what remains of their position be called a theory of scientific method? All that remains is a theorem of the probability calculus. Suppose we concede to Howson and Urbach that this theorem, as interpreted by them, is indeed a theorem with a status akin to deductive logic. Then this generous concession serves to bring out the limitation of their position. Their theory of scientific method tells us as much about science as the observation that science adheres to the dictates of deductive logic. The vast majority, at least, of philosophers of science would have no problem accepting that science takes deductive logic for granted, but would wish to be told much more.