Chapter 25

Trends and Patterns

“LATER” AND “LAST” PASSAGES: THE QUESTIONS HOLD THE ANSWERS

In this chapter, we will look at some more difficult Science passages and some of the ways that the answer choices can teach us what we need to know about challenging passages. Our Basic Approach remains the same:

1.  Work the Figures
Look for variables and trends.

2.  Work the Questions
Work from easy to hard, from short to long.

3.  Work the Answers
Use POE.

Believe it or not, as the passages become more complex, it is equally important to remember: Don’t try to understand the science. In this chapter, we will particularly focus on effective ways to use POE and to let the questions teach us about the passage.

Passage VII is a bit of a monster, but if we use the questions, we can find everything we need to know and select answer choices confidently.

Passage VII

Engineers studied the trajectories of a cannonball launched from a cannon under various conditions.

Study 1

On a level surface during a mild day, engineers launched a cannonball from a cannon as shown in Figure 1.

Figure 1

A camera was fixed atop the cannon so that it would point in the direction of the cannonball’s launch. A receiver was also fixed to the cannon to record the cannonball’s position as recorded by the camera.

As the cannonball traveled through the air, angle θ, which is defined in Figure 1, consistently changed. The change in θ was captured by the camera every 0.25 seconds after launch until the cannonball landed. For each recorded image, θ was measured (Figure 2).

Figure 2

Furthermore, every 0.25 sec after launch, the receiver sent out a radar pulse, part of which was reflected by the cannonball to the receiver. The roundtrip travel time of each pulse was recorded to determine the distance, d, between the receiver and the ball at any given time (see Figure 3).

Figure 3

Using d and θ, the engineers determined the ball’s height, h, and distance, r, at the end of each 0.25 sec interval. A curve plotting h vs. r was constructed.

This procedure was followed using cannonball launch starting speeds of 135 ft/sec, 150 ft/sec, and 180 ft/sec. For each launch speed, the ball was launched at θ = 30°. The curves representing h and r for each of the launch speeds were connected by lines for time, t = 2 sec, 3 sec, 4 sec, and 5 sec after launch (see Figure 4).

Figure 4

Study 2

Using an algorithm, the engineers calculated h and r at 0.25 sec intervals for the same cannonball launched in a vacuum in otherwise similar conditions to those in Study 1. The results are plotted in Figure 5.

Figure 5

There is a lot of content in this passage, which already makes it a bit more difficult than the others we have seen. But let’s use our Basic Approach to see if we can simplify it as much as we did the others.

There are five figures in this passage, but Figures 1−3 don’t have any obvious trends. If we remember our basic mantra—Don’t try to understand the science—we should feel okay ignoring Figures 1−3 until a question tells us that we need them.

Figure 4

The variables are r (ft), h (ft), t (sec), and some unspecified values in (ft/sec).

There are a few basic relationships in this figure as well:

• As r increases, h increases then decreases.

• As r increases, t increases.

• As r increases, the (ft/sec) values increase.

Figure 5

All of the variables and relationships are the same as those in Figure 4. A question might ask us to differentiate between the two figures, but let’s not waste our time trying to understand the difference until we have to.

That’s it! Let’s move on to the questions.

35.  Suppose the cannonball were launched at 30° in a vacuum from a height of 5 ft. Based on Figure 5, the cannonball would land approximately how many feet farther from the cannon if it were launched at 150 ft/sec than if it were launched at 135 ft/sec?

  A.    50 ft

  B.  150 ft

  C.  500 ft

  D.  650 ft

36.  While the cannonball was in flight, how often did the camera record the position of the ball?

  F.   Once per second

  G.  Twice per second

  H.  Three times per second

  J.   Four times per second

37.  The cannon was an instrumental weapon used during the Ottoman invasion of the city of Constantinople in 1453. Assume that cannonballs identical to those used in Study 1 were launched on a windless day with a starting height of 5 ft above the ground and an angle of θ = 30°. If the launch speed of each cannonball were 180 ft/sec, how close would the cannon have needed to be to the 40-ft-tall wall surrounding Constantinople in order to travel over it?

  A.  425 ft

  B.  575 ft

  C.  700 ft

  D.  850 ft

38.  Based on Figure 4, as the initial speed of the launched cannonball was increased, how did the values of h and r change at t = 4 sec?

                     h                           r

  F.   decreased            decreased

  G.  decreased            increased

  H.   increased            decreased

  J.    increased            increased

39.  Based on Figure 5, if the ball were launched in a vacuum from a height of 5 ft at 135 ft/sec and θ = 30°, how long would the cannonball most likely be in flight from launch to landing?

  A.  Between 4 sec and 5 sec

  B.  Between 5 sec and 6 sec

  C.  Between 6 sec and 7 sec

  D.  Between 7 sec and 8 sec

40.  Based on Figure 3, if c represents the speed of light, which of the following represents the time taken by each radar pulse to make the roundtrip between the receiver and the ball?

  F.   2c/d

  G.  2d/c

  H.  c/r

  J.   r/c

As in the previous chapter, a large part of Working the Questions consists of answering the questions in a good order. Look for numbers, number words, and relationships.

Question 38 seems like a good place to start because the question is relatively short, and the answers are entirely composed of number words.

38.  Based on Figure 4, as the initial speed of the launched cannonball was increased, how did the values of h and r change at t = 4 sec?

                     h                           r

  F.   decreased            decreased

  G.  decreased            increased

  H.   increased            decreased

  J.    increased            increased

Here’s How to Crack It

Recall the initial relationships we determined. There was one, in ft/sec, that we didn’t have a name for. This question has given it to us: “initial speed.”

The question asks us to synthesize information about four different variables. Start with the most specific: t = 4 sec. This value represents the diagonal line toward the right edge of the graph. Then, move to the next specific piece of information, “as the initial speed of the launched cannonball was increased.” Each of the curves represents a different speed, and it seems that as the speeds go from 135 to 150 to 180, they move further along the x-axis, or their r values increase. Already, we can eliminate choices (F) and (H), which both say that the r value decreases.

Finally, let’s simply pull the rest of the information from the graph. At t = 4, the curve for the 135 ft/sec initial speed has an h value of approximately 30 ft. At t = 4, the curve for the 150 ft/sec initial speed has an h value of approximately 80 ft. The h value is increasing, so only choice (J) can work as the correct answer.

This is a difficult first question, but notice how much assistance it provided us in clarifying how all these variables relate to one another. We now know what all the variables are called, and we can see some of the basic ways that those variables interact.

The remaining questions are all either long or unfamiliar, so let’s do them in order. We’ll start with question #35.

35.  Suppose the cannonball were launched at 30° in a vacuum from a height of 5 ft. Based on Figure 5, the cannonball would land approximately how many feet farther from the cannon if it were launched at 150 ft/sec than if it were launched at 135 ft/sec?

  A.    50 ft

  B.  150 ft

  C.  500 ft

  D.  650 ft

Here’s How to Crack It

Start with the information you know. Figure 5 shows 135 ft/sec and 150 ft/sec, and we can see the arcs that each of those initial speeds create. The 150 ft/sec seems to go a bit farther along both axes, but we need to figure out which one we’re dealing with.

We can use the units in the answer choices as a guide: “ft” will likely go with either h or r. We’ll need to figure out which one it is, so now we’ll use the weird figures we ignored before. Think of how much more intelligible Figure 3 becomes when you approach it with a specific question! We now see that there’s a cannon that creates a right triangle: h is its vertical height from the ground, and r is the horizontal distance from the cannon itself. The cannonball, then, must be launched more or less on this path from various initial speeds. In this case, as in many others, the question has elucidated a new part of the passage.

This question asks “how many feet farther from the cannon” will a cannonball launched from one initial speed be from a cannonball launched at another initial speed. Distance from the cannon, we’ve just learned, is r. In Figure 5, the cannonball with an initial speed of 135 ft/sec maxes out around 500 ft/sec, and the cannonball with an initial speed of 150 ft/sec maxes out around 650 ft/sec. The faster ball, therefore, goes about 150 feet further, as choice (B) indicates.

36.  While the cannonball was in flight, how often did the camera record the position of the ball?

  F.   Once per second

  G.  Twice per second

  H.  Three times per second

  J.   Four times per second

Here’s How to Crack It

The only t values we have seen are in increments of one second, but the curves seem to be more precise than that. Let’s use the introduction but read it selectively. We’re looking for the lead words “camera,” “record,” “position,” or anything relating to time.

The relevant piece of information shows up above Figure 3: …every 0.25 sec after launch, the receiver sent out a radar pulse, part of which was reflected by the cannonball to the receiver. It’s not quite “camera,” but this would seem to be what we’re looking for, and if the pulse is captured every 0.25 seconds, that makes 4 times per second, choice (J).

37.  The cannon was an instrumental weapon used during the Ottoman invasion of the city of Constantinople in 1453. Assume that cannonballs were launched on a windless day with a starting height of 5 ft above the ground and an angle of θ = 30°. If the launched speed of each cannonball were 180 ft/sec, how close would the cannon have needed to be to the 40-ft-tall wall surrounding Constantinople in order to travel over it?

  A.  425 ft

  B.  575 ft

  C.  700 ft

  D.  850 ft

Here’s How to Crack It

As riveting as all the military history in this question is, let’s ignore it and go straight to the data. We’ve got a few data points: a starting height of 5 ft, an angle of θ = 30°, an initial speed of 180 ft/sec, and a 40-ft-tall wall, or a value of h = 40 ft.

Since we already know what to do with initial speeds and h values, let’s figure out what’s going on with these other two figures, which also showed up in question 35, but in that case we knew to go to Figure 5, so we ignored them. We have no such guidance here, though, so let’s go digging.

Figure 1 shows a height of 5 ft, which seems to be the starting height of the cannonball. Then, Study 1 mentions an angle of θ = 30°. Typically, if certain values that don’t show up anywhere on the graphs or tables are mentioned frequently, those values are the constants for the entire experiment. Remember the basic Scientific Method: change what you are measuring and keep everything else constant. Any experiment will contain a number of variables that are held constant, and for this experiment, the starting height and the angle are fixed values.

Next, we need to figure out whether to draw information from Figure 4 or Figure 5. What’s the difference? It seems that Figure 4 represents the actual trials of the experiment, and Figure 5 is done using an algorithm for a cannonball launched in a vacuum. In other words, Figure 4 shows how the cannon works when it is actually fired, while Figure 5 shows how the cannon should work under ideal mathematical conditions.

This question is asking about a historical moment, i.e., one not taking place in a laboratory or a series of equations, so we will need to draw on Figure 4. Let’s recall the two bits of information we haven’t used yet: 180 ft/sec initial speed, and h = 40 ft. We see the 180 ft/sec curve on the graph, and it seems to intersect h = 40 ft at two different points, once around r = 60 ft and once around r = 425 ft. We won’t have to choose, fortunately, because the only one that appears in our answer choices is 425, choice (A).

We should now have more than enough information to answer the remainder of the questions.

39.  Based on Figure 5, if the ball were launched in a vacuum from a height of 5 ft at 135 ft/sec and θ = 30°, how long would the cannonball most likely be in flight from launch to landing?

  A.  Between 4 sec and 5 sec

  B.  Between 5 sec and 6 sec

  C.  Between 6 sec and 7 sec

  D.  Between 7 sec and 8 sec

Here’s How to Crack It

We’ve already seen that we can ignore the 5 ft and θ = 30° values, and we know that vacuum refers to Figure 5 (note that the question tells us this as well). Let’s go to the curve for 135 ft/sec.

This cannonball travels approximately 500 feet, and it reaches its endpoint between t = 4 sec and t = 5 sec. Only choice (A) works. Alternatively, once we understood how this question worked, we could have immediately eliminated choices (B), (C), and (D) because those values don’t show up anywhere on the table.

40.  Based on Figure 3, if c represents the speed of light, which of the following represents the time taken by each radar pulse to make the roundtrip between the receiver and the ball?

  F.   2c/d

  G.  2d/c

  H.  c/r

  J.   r/c

Here’s How to Crack It

This question asks us to draw upon some very basic outside knowledge: distance = rate × time. The question is asking about time, and it tells us that the “rate” will be represented as c. In other words, d = ct. Rearrange this equation to solve for time, t = d/c. We know that c has to be in the denominator, which eliminates choices (F) and (H). Finally, the question asks about a “roundtrip,” which means whichever distance we are dealing with will need to be doubled, so only choice (G), which contains a 2, can be the correct answer.

Let’s try another passage bearing what we’ve learned in mind.

Passage VI

The term “evolution” is often used in the context of biological changes in organism populations over time, but it can also be applied to the change in the chemical composition of the Earth’s atmosphere. The hypotheses of two studies claim that this chemical evolution has altered the types of chemicals found in the atmosphere between the early stages of Earth’s existence and the present day.

Study 1

Based on the hypothesis that volcanic eruptions were the source of gases in the early Earth’s atmosphere, scientists recreated four model volcanic eruptions in closed chambers, each containing different percentages of the same volcanic particulate matter. They then observed the gases in the air above this model over time. The percent composition of this air after 1 day, when the air achieved a steady state of constant gas concentrations, is represented in Table 1.

Since the experiment provided only a suggestion of the gas levels in the early Earth’s atmosphere, the scientists then analyzed the amount of trapped gases in sediment layers, which indicate the changing atmospheric levels of gases over billions of years. The data collected on O₂ and H₂O vapor are presented in Figure 1.

Study 2

A separate study used the same volcanic models as in Study 1, but hypothesized that the scientists in Study 1 underestimated the amount of H₂ in the early Earth atmosphere. They proposed a different composition of gases, highlighting an increased H₂ level in the atmosphere, also represented in Table 1. Based on these new data, the scientists proposed an alternative graph for the changing atmospheric levels of O₂ and H₂O vapor, also shown in Figure 1.

Figure 1

When we Work the Figures in this passage, we come up with almost nothing. Table 1 has no consistent trends, and Figure 1 has two contrary trends. The one thing we can see from Figure 1 is that the H₂O levels go down as the O₂ levels go up. Since there’s not much we can do with the figures, let’s see if the questions can help to elucidate the passage.

Question #29 is clearly the place to start because it is short and has number words in the answer choices.

29.  According to the results of Study 2, between 4 and 3 billion years before the present day, the percent composition of O₂ in the atmosphere:

  A.  increased only.

  B.  increased, then decreased.

  C.  decreased only.

  D.  decreased, then increased.

Here’s How to Crack It

This question is about as easy as they come. Let’s go back to Figure 1 and look between 4 and 3 billion years before the present day. The question asks about O₂ level, which increases during this period. The best answer in choice (A).

Let’s move on to question #30, which deals with the same figure and is similarly short.

30.  According to the results of Study 1, the percent composition of H₂O vapor in the atmosphere decreased most rapidly over what period of time?

  F.   Between 2.5 and 2 billion years ago

  G.  Between 2 and 1.5 billion years ago

  H.  Between 1.5 and 1 billion years ago

  J.   Between 1 and 0.5 billion years ago

Here’s How to Crack It

Again, let’s use Figure 1, though this time we will look at H₂O rather than O₂. Because it’s hard to know exactly which range showed the most rapid decrease, let’s use the answer choices and POE.

Between 2.5 and 2 billion years ago, the percent composition decreased by about 10. Between 2 and 1.5 billion years ago, it decreased by about 15. Between 1.5 and 1 billion years ago, it decreased by about 20. Between 1 and 0.5 billion years ago, it decreased very little. The greatest decrease occurred between 1.5 and 1 billion years ago, as choice (H) suggests.

Question #31 asks about Table 1, which we have not yet used because we found no consistent trends. This question will help us to see how the table works.

31.  Suppose that the actual early Earth atmosphere had a high H₂ composition of 42%. Based on Study 2, is it likely that the corresponding H₂S and N₂ compositions of this atmosphere were each 3%?

                3% H₂S          3% N₂

  A.  Yes                 Yes

  B.  Yes                  No

  C.  No                   Yes

  D.  No                   No

Here’s How to Crack It

This question asks us to determine a relationship where we could not find one before. Let’s look back at the chart now that we know what we’re looking for: an H₂ composition of 42%.

In Study 2 on Table 1, H₂ values decrease from left to right. The other relevant values for this question, H₂S and N₂, increase as H₂ values decrease. With this pattern in place, we can begin to make some predictions. An H₂ composition of 42% would fall between volcanic eruption models 1 and 2. As a result, the H₂S and N₂ will need to be between the model 1 and 2 values as well. That puts H₂S between 2% and 5% and N₂ between 0.5% and 1%. With these ranges, we can answer the question: H₂S could be 3%, but N₂ could not, as choice (B) indicates.

Question #32 asks a very similar question, one that begins with the word “Suppose.”

32.  Suppose that in a new trial in Study 2, the percent composition of H₂ in the atmosphere was set at 33% and the percent composition of N₂ was found to be 2%. The percent composition of H₂O vapor in this trial would most likely be:

  F.   greater than 40%.

  G.  greater than 35% and less than 40%.

  H.  exactly 35%.

  J.   greater than 30% and less than 35%.

Here’s How to Crack It

We saw in the last question that there are more relationships in Table 1 than initially meets the eye. H₂, for example, decreases, making predictions about H₂ levels possible.

If the H₂ level in this question is 33%, that would put the value right between volcanic eruption models 3 and 4. Further, the N₂ value in both models 3 and 4 is 2%, which matches what is given in our question. Finally, we look at H₂O vapor, which is 35% in both trials, at H₂ compositions of both 30% and 35%. We have no good reason to think that the H₂O vapor levels will change, so we can infer that the value will be exactly 35%, as it was in the other two models. Choice (H) is the only answer that can work.

Question #33 is much wordier than the others we’ve seen, but hopefully by this point you’re able to see all the POE opportunities in the answer choices before you’ve even read the question.

33.  Consider an early Earth environment that featured microorganisms. Based on the results of Study 2, is it more likely that aerobic organisms (those that require O₂ to survive) or anaerobic organisms (those that do not require O₂ to survive) would have existed on Earth 4 billion years ago?

  A.  Aerobic organisms, because of the high H₂O level 4 billion years ago

  B.  Aerobic organisms, because of the low O₂ level 4 billion years ago

  C.  Anaerobic organisms, because of the high H₂O level 4 billion years ago

  D.  Anaerobic organisms, because of the low O₂ level 4 billion years ago

Here’s How to Crack It

Right off the bat, we can eliminate choices (A) and (C), which address the H₂O levels in a question that is exclusively concerned with O₂ levels. Then, because all that remains are options that refer to “the low O₂ level 4 billion years ago,” the organisms must be anaerobic, given that anaerobic organisms “do not require O₂ to survive.” Only choice (D) can work, and we didn’t need the figures at all! All you need is POE.

Question #34 seems to ask for a synthesis of all the information in the passage, but let’s see.

34.  According to Study 2, how long did it take the H₂O vapor level to decrease to 75% of its composition 4 billion years before the present day?

  F.   500 million years

  G.  1 billion years

  H.  1.5 billion years

  J.   2 billion years

Here’s How to Crack It

We’re back to the graph. Don’t overthink this one! In Study 2, 4 billion years ago, the H₂O vapor level was 40%. 75% of that would be an H₂O vapor level of 30%. In Study 2, the H₂O vapor level is 30% approximately 2.5 billion years ago. From 4 billion to 2.5 billion is 1.5 billion, or choice (H).

In conclusion, we entrusted our knowledge of this passage to the questions, and as we’ve now seen, we need to know very little about the passage itself beyond the figures. The questions helped us to see the relationships in the figure that we would not have otherwise seen, and they guided us through a series of figures we had an almost impossible time trying to “work” in the first step.

CONFUSING FIGURES AND THE QUESTIONS WHO LOVE THEM

In this exercise, you will be given a confusing figure and a question associated with it. Note how the question tells you what you need to know about the figure. Answers and explanations will be at the end of the exercise.

  1.  Suppose, in Study 1, the scientists had found another seabed layer with fossilized shells that were radiocarbon dated and found to be 86,000 years old. Based on the results of Study 1, the scute pattern percents for the group of shells would most likely have been closest to which of the following?

            

  A.  

  B.  

  C.  

  D.  

  2.  Considering only the gases listed in Table 1, which gas is more abundant in the atmosphere of Jupiter than in the atmosphere of either Neptune or Saturn?

  F.   H

  G.  CH₃

  H.  NH₃

  J.   He

Figure 1

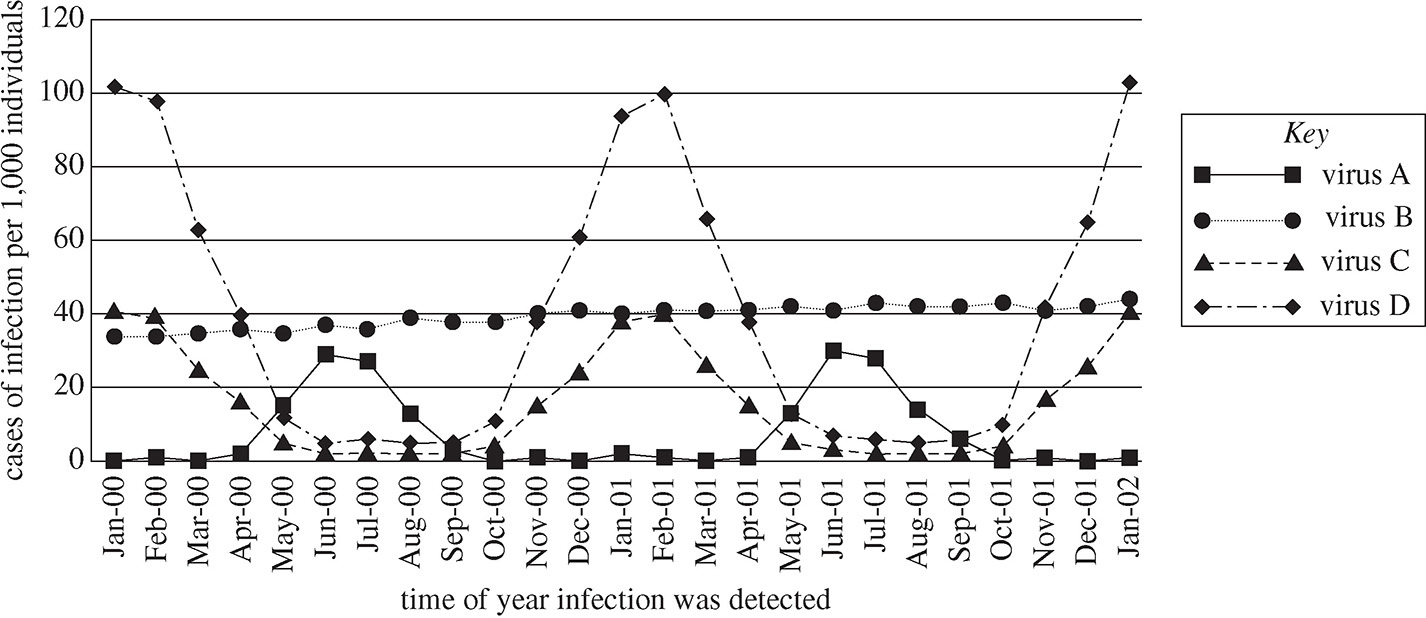
  3.  According to Figure 1, the incidence of at least 3 of the viruses is most alike during which of the following months?

  A.  April 2000

  B.  September 2000

  C.  November 2001

  D.  January 2002

Figure 2

  4.  Based on the information in Figure 2, a ball being dropped from 1 meter height with an elasticity of 0.2 Pa and a weight of 0.5 kg would have a maximum post-impact velocity of:

  F.   less than 0.50 m/s.

  G.  0.75 m/s.

  H.  1.0 m/s.

  J.   greater than 1.25 m/s.

Figure 1

  5.  Figure 1 shows that a lunar orbiter at point P would be able to view which of the following?

  A.  The moon only

  B.  The Sun only

  C.  The moon and the Earth only

  D.  The moon, the Sun, and the Earth

CONFUSING FIGURES DRILL ANSWERS AND EXPLANATIONS

  1.  D  There are no obvious trends in the table other than the fact that “Age of shells” decreases from the top of the table to the bottom. This allows us to situate 86,000 years between two values on the table: 87,0000 and 85,000. Because the new value is between the two known values, we can assume that the other values will be as well. Choice (D) gives three values that fit between the others in the table.

  2.  H  While we may not know what any of the terms mean or how they relate to the three planets listed, we can pull this information directly from the chart. The answer must be choice (F), because NH₃ has a relative abundance of 0.0045% on Jupiter but of 0% on Neptune and 0.0035% on Saturn. POE got us there!

  3.  B  Find three overlapping dots. Choices (A), (B), and (D) all refer to months in which the dots are fairly spread out. Only choice (B) gives a month, September 2000, in which three of the dots are very close to one another.

  4.  F  Work with the specific information given in the question. 0.2 Pa leads to the third graph in Figure 2, and the weight of 0.5 kg will lead to the second hump within that graph, which shows 3 kg, 2 kg, and 1 kg. Because those three curves seem to go in increasing order, we can infer that 0.5 kg will be somewhere below 1 kg. 1 kg maxes out at a velocity of 0.50 m/s, so a weight of 0.5 kg will max out at a velocity less than that, as choice (F) indicates.

  5.  C  Find Point P on the figure (which, by the way, looks like a big eyeball). Point P, it seems, is between the eyeball (the moon) and the Earth, so someone standing at Point P would be able to see both. This eliminates choices (A) and (B), which don’t contain both elements. As for the Sun, it looks like the eyeball is blocking Point P from a good view of it, so choice (D) can be eliminated as well. Choice (C) contains the correct elements.