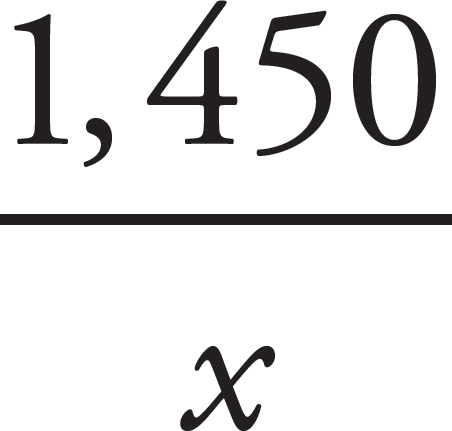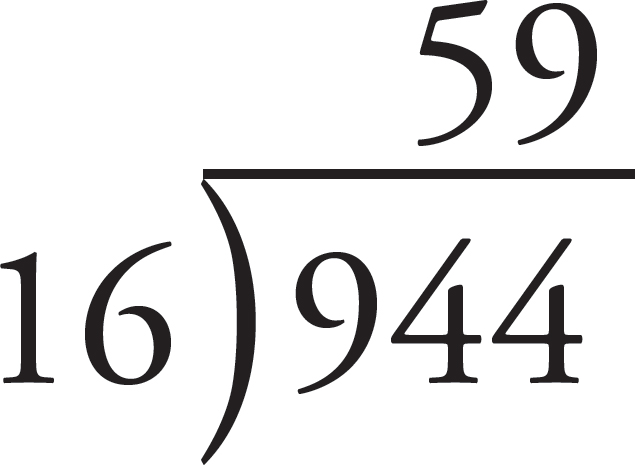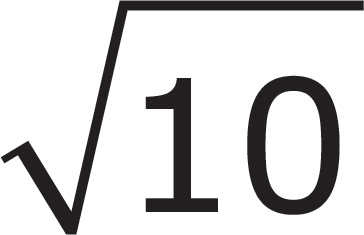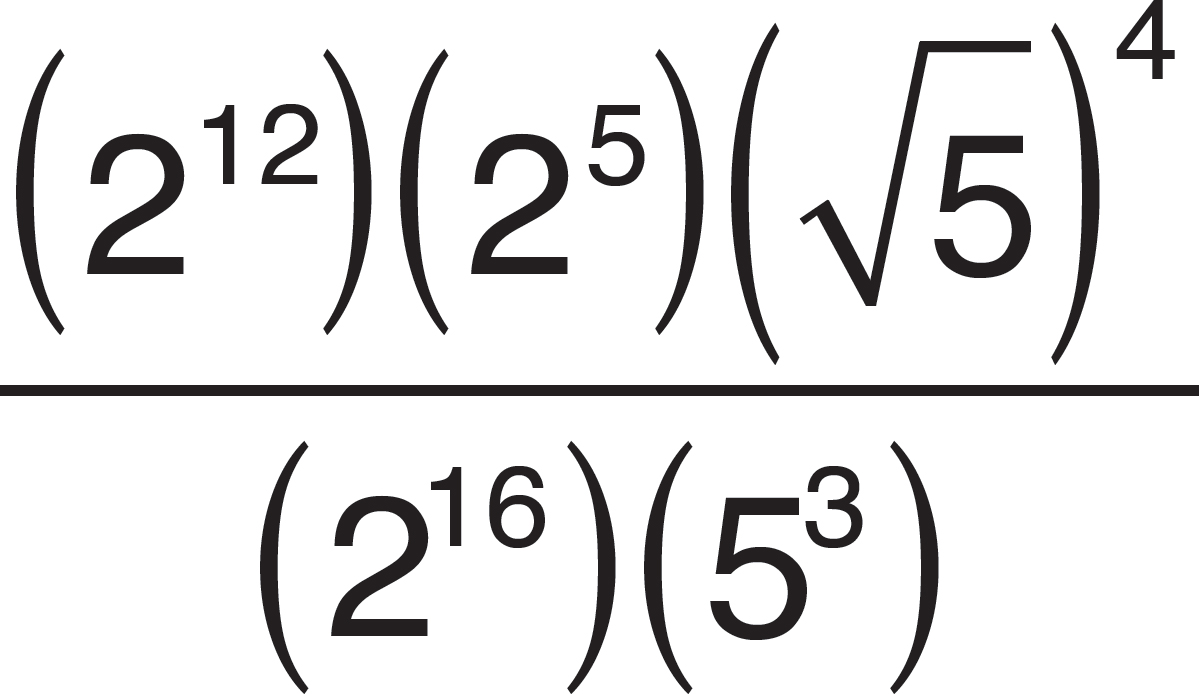Chapter 14
Applied Arithmetic
In this chapter, we go over more arithmetic problems involving setup problems, averages, ratios and proportions, rate problems, charts and graphs, exponents, radicals, scientific notation, probability, and counting.
Now we’re going to show you some additional arithmetic concepts that build on the ideas you’ve already learned in the last chapter. As in that chapter, we’ll introduce a concept first and then give you some sample GED® questions followed by a short drill. At the end of the chapter, you’ll find a big drill that mixes and matches all the different concepts. These are the subjects we’ll cover.
SETUP PROBLEMS
Wouldn’t it be interesting if a test question asked you to do the entire setup of a problem, but didn’t want you to actually solve it? In fact, if you go on to college, you will find that this is often exactly what college math tests are like. College professors are much more interested in seeing how you think than how careful you are with your addition and subtraction.
Here’s an example:

1. Jim started a business selling mattresses. He sold 12 standard mattresses and 7 deluxe mattresses last week. Which expression below represents how many dollars he took in last week if the standard mattress costs $100 and the deluxe costs $160?
A. 12(100) + 7(100)
B. 12(160) + 7(100)
C. 12(100) + 7(160)
D. 12(160) + 7(160)
Here’s How to Crack It
To find out the total price, you have to multiply the number of standard mattresses by the price of a standard mattress, and the number of deluxe mattresses by the price of a deluxe mattress. There were 12 standards at $100 each, so that’s 12(100). There were seven deluxes at $160 each, so that’s 7(160). Altogether that’s 12(100) + 7(160). The correct answer is (C).

Take Your Time…
Try not to be in too much of a rush on setup problems. The answer choices are all close variations of one another, and it’s easy to pick the wrong one if you’re in a hurry. In addition, sometimes the GED® test writers may not have written their equation in quite the same way that you did. For example, in this problem, you might have written your equation starting with the expensive mattresses—7(160) + 12(100)—in which case, if you looked through the answer choices quickly, you might have thought your answer wasn’t there. So be prepared to be flexible as you look at the answer choices on a setup problem. You may have to add the numbers in a different order or convert a fraction to a decimal.
…But Not Too Much Time
Some test takers actually solve setup problems; they find the correct answer (even though the problem does not require it) and then find the answer choice that adds up to the same number they calculated. We think this generally takes a little too much time. However, if there’s one problem that you’re really not sure of, you can check the equation you wrote by solving the problem and then making sure that the answer you chose agrees with the number you calculated.
Here’s another setup problem, this time about percentages:

2. Mr. James goes into an investment with two partners. Together the three of them put a total of $30,000 into an investment that pays annual interest of 12%. At the end of the year, the three people share the interest evenly. How much did Mr. James receive in interest?
A. 
B. 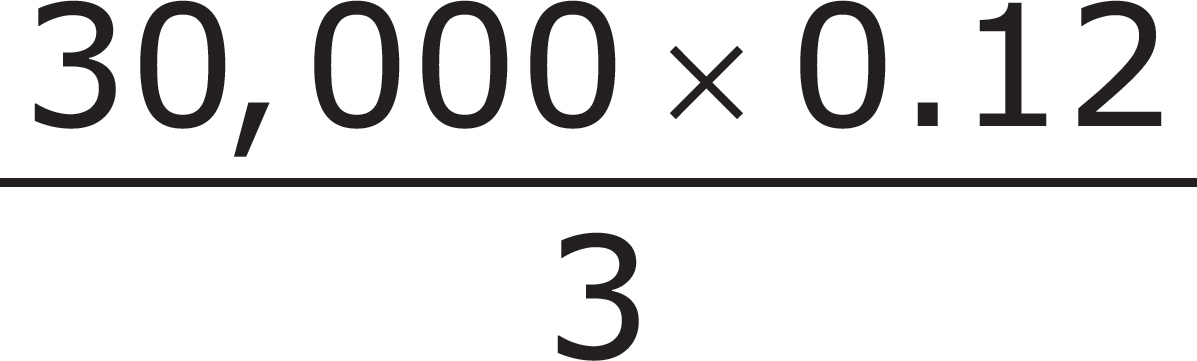
C. 
D. 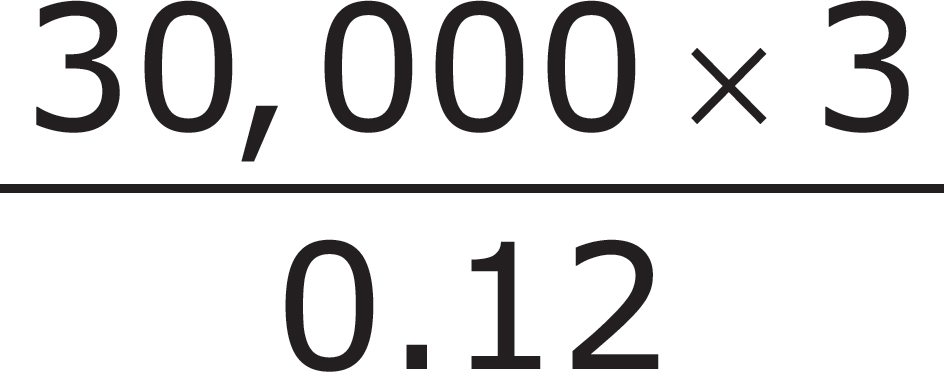
Here’s How to Crack It
Mr. James and his two partners share the interest evenly. If this were a normal problem, first you would find 12% of $30,000, and then you would figure out Mr. James’s share. If you want to, you can do the problem this way—actually solve it and then figure out the numeric value of each of the answer choices, one by one, until you find the one that matches your solution. Unfortunately, as we said, this can take some time.
Rather than solving this problem, it may be better to set it up as if you were going to solve it using a traditional equation. When we first discussed percents in Chapter 13, we said that the word of always means multiply. If we want to find 12% of $30,000, we could write that in two ways:
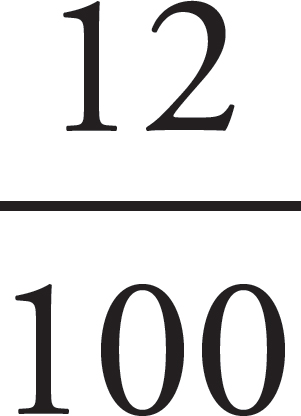 × 30,000 or 0.12 × 30,000
× 30,000 or 0.12 × 30,000
They both mean the same thing.
Whatever this number is—and remember, in this problem, you don’t need to know what it is—it represents the entire amount of interest. The problem is asking for only Mr. James’s share. Because all three investors share the interest evenly, you have to divide the entire amount by 3.
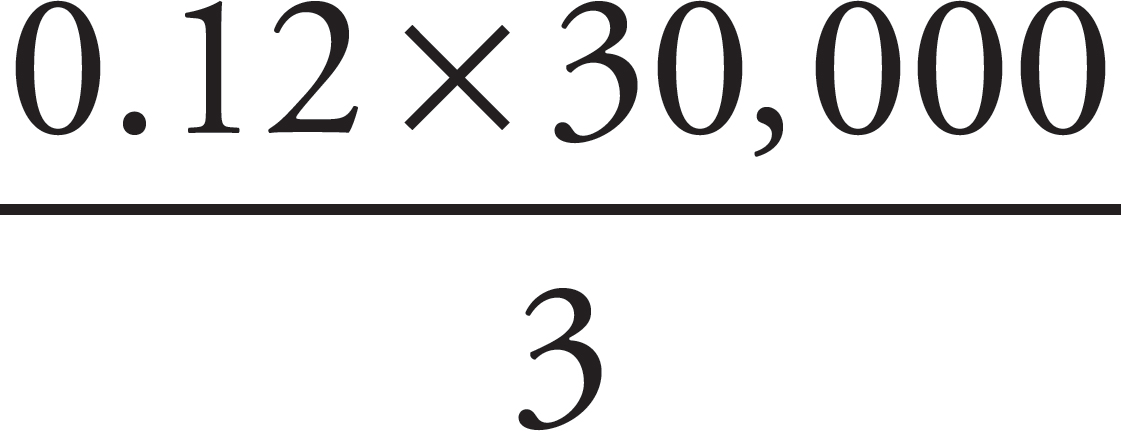
The correct answer is (B).


Setup Quiz
Q: Which two setups below are identical?
(A) 40($1.25) + 25($0.90)
(B) 25($0.90) + 40($1.25)
(C) (40 + 25)($1.25 + $0.90)
Turn to this page for the answer.
Setup Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.Sam works 8 hours per day, 6 days a week, delivering flowers. If he earns $5.50 per hour, how much does he make in 4 weeks?
A. 8 × 6 × 4 × 5.50
B. 8 × 6 × 5.50
C. [4(8) + 4(6)] 5.50
D. 5.50 × 8 + 5.50 × 4
2.This year, the price of a particular model of car went up 4% from last year’s price of $12,000. Which of the following represents the new price?
A. 0.04($12,000)
B. 0.04($12,000) + $12,000
C. 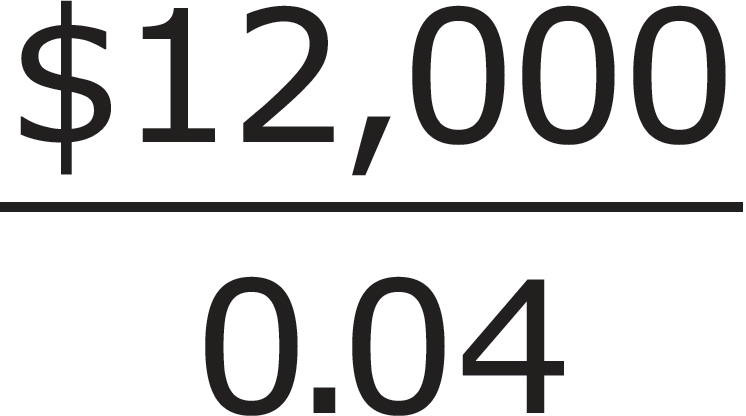 + $12,000
+ $12,000
D. 0.96($12,000) + $12,000
Mean, Median, Mode, Range, and Weighted Mean
The mean, or average, is a single number that represents the central value of a set of numbers. In spite of its name, a mean problem is almost always pretty gentle and easy. To find the mean of several different numbers, first add them up, and then divide the sum of the numbers by the actual number of items that you added. For example, to find the average of 5, 10, and 15, first add the three numbers:
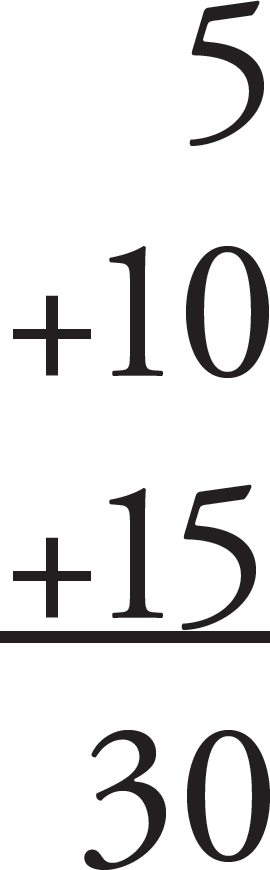
Then, because there are three items being added, divide the sum of the numbers by three:
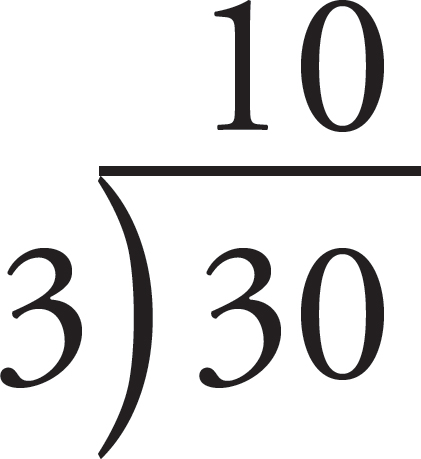
That’s it. The mean (average) of 5, 10, and 15 is 10. Let’s try a problem like some you’ll see on the GED® test.

1.A realtor hires a plumber to make x repairs. The plumber bills the realtor $1,450 in total. Which expression determines the average cost of each repair?
A. 1,450x
B. 1,450 + x
C. 
D. 
Here’s How to Crack It
This problem is different from the above example in two ways. First, there is no actual number of repairs. Instead, that number is represented by a variable, x; second, in this problem you don’t have to add up the individual elements (i.e., the cost of each of the individual repairs) because it has already been done for you.
In spite of these differences, this is still an average problem and we can solve it using the average formula:
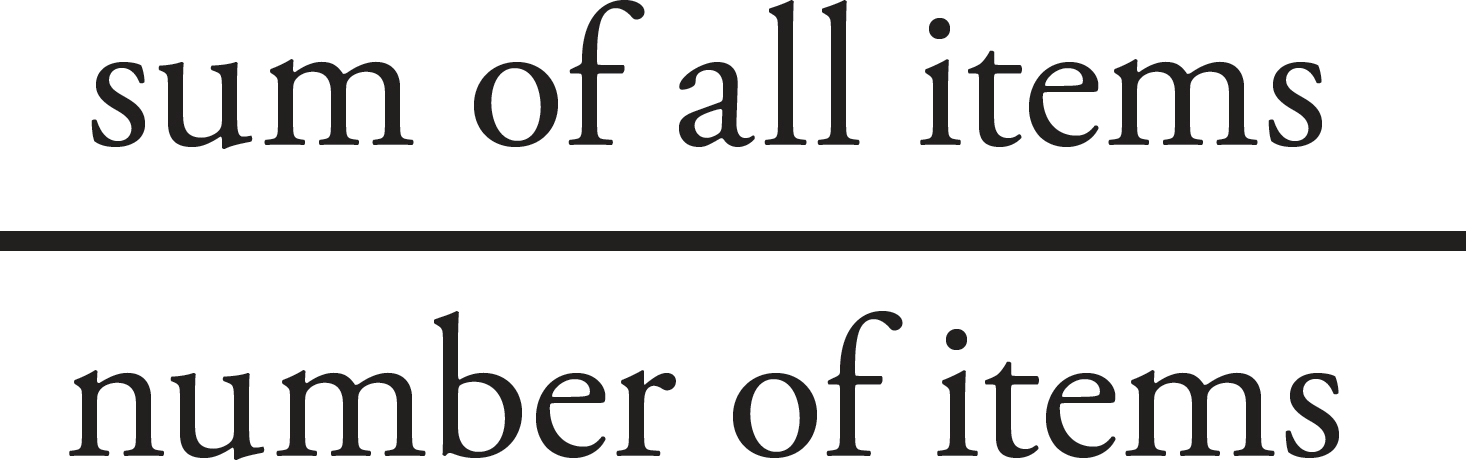 = average
= average
Okay, let’s start by adding the elements to get the sum of all the elements—oh, wait, the elements have already been added. The total cost of all the repairs is $1,450. All that’s left to do is divide the total cost ($1,450) by the number of repair jobs—oh, wait, there is no precise number. Well, you do at least have a variable representing this number, so divide by the variable:
The correct answer is (C).

Setup Quiz
A: (A) 40($1.25) + 25($0.90) is the same as (B) 25($0.90) + 40($1.25).
The median of a set of ordered numbers is the number right in the middle. For example, the median of 3, 16, and 17 is 16. The median of 139, 234, 326, 327, and 328 is 326.
The median is usually different from the mean.
Let’s take the numbers 2, 3, and 10. The mean of these numbers is 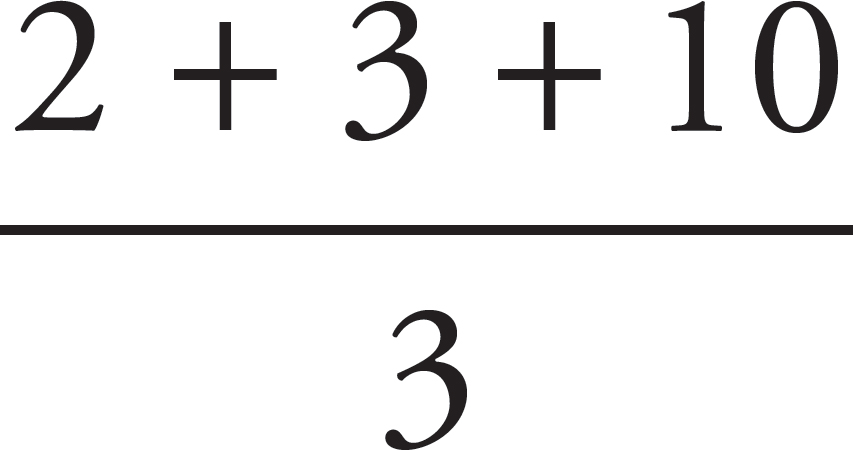 , or
5, but the median is simply the middle number, or 3.
, or
5, but the median is simply the middle number, or 3.
If you are asked to find the median of a set of numbers that is not in ascending order, first put the numbers in ascending order, and then take the middle number. For example, the median of 3, 7, and 6 would be 6.
What if there is no middle number? Take the following list of numbers:
4, 8, 10, 20
This time, two numbers are sharing the middle. In cases like this (where there is an even number of items), take the mean of the two middle numbers. This time, the median is 9.
How do median problems look on the Mathematical Reasoning test?
Ballparking Averages
The average of a string of numbers has to be less than the biggest number and more than the smallest number.

2. Missy played 4 Starmaster games at a video arcade. Her scores were 125, 135, 120, and 140.
Click on the numbers you want to select and drag them into the boxes.
What was her mean (average) score? 
What was her median score? 

Here’s How to Crack It
As soon as you see the words mean and average, you know just what to do: Add the four numbers together, and divide by four.

The correct answer to the first question is 130.
To find the median, you must first order the numbers from least to greatest: 120, 125, 135, 140. What number is in the middle? There are two numbers in the middle, 125 and 135, which means you must take the mean of those two. Find the sum, 125 + 135 = 260, and then divide by two, 260 ÷ 2 = 130.
The correct answer to the second question is also 130!

The mode of a set of numbers is the number that appears the most often. For example, the mode of 1, 4, 4, 5, 5, 5, 8 is 5. The number 4 occurs twice, but the number 5 occurs three times, so 5 occurs the most in this list.
Sometimes there is more than one mode. Let’s look at another example set: 2, 5, 9, 2, 4, 1, 8, and 5. First you should order the numbers from least to greatest: 1, 2, 2, 4, 5, 5, 8, 9. Now it is much easier to see which numbers repeat. Both 2 and 5 occur twice, and no number occurs more than twice. So, both 2 and 5 are the modes.
Try it out on this problem:

3. If there were 24 traffic summonses issued in September, 45 in October, 24 in November, and 39 in December, what was the mode number of summonses issued over the three months?

Here’s How to Crack It
First, put the numbers in ascending order: 24, 24, 39, 45. Now, do any numbers appear more than once? That’s right—the correct answer is 24.

The range of a set of numbers is the distance between the smallest value and the largest value. For example, look at the following set: 2, 5, 6, 8, 99. The largest value is 99 and the smallest value is 2, so the range is 99 – 2 = 97. As with the mean, median, and mode, be sure your numbers are in ascending order before subtracting!
See if you can solve the following GED® range question.

Jill’s Work Week
|
Number of Hours Worked |
Hourly Pay |
|
| Monday |
6 |
$15.00 |
| Tuesday |
5 |
$15.00 |
| Wednesday |
8 |
$12.50 |
| Thursday |
7 |
$12.50 |
| Friday |
4 |
$15.00 |
4. Jill gets paid different rates for working on different projects. She worked on one project Monday, Tuesday, and Friday of last week, and worked on the second project on Wednesday and Thursday of last week. Her hours spent working and pay rates are shown in the table above. What was the range of Jill’s daily earnings last week?
A. $2.50
B. $20.00
C. $37.50
D. $40.00
Here’s How to Crack It
This question asks about Jill’s daily earnings. Do you know how much she earned each day? No, but you can find out. Multiply the number of hours worked each day by the hourly rate for that day to find Jill’s daily earnings.
On Monday, Jill earned 6 × $15.00 = $90.00.
On Tuesday, Jill earned 5 × $15.00 = $75.00.
On Wednesday, Jill earned 8 × $12.50 = $100.00.
On Thursday, Jill earned 7 × $15.00 = $87.50.
On Friday, Jill earned 4 × $15.00 = $60.00.
Therefore, the greatest daily earnings was $100.00 on Wednesday and the least was $60.00 on Friday.
To calculate the range, we need to find the distance, or difference, between those two values. So we subtract $100.00 – $60.00 = $40.00. The correct answer must be (D).

The weighted mean is used when the numbers in a set are not all equally important. Those with more importance are given more weight when calculating the mean, or average. Here’s how.
Let’s say there are 4 tests in total for a certain class: Exam A, the Midterm Exam, Exam B, and the Final Exam. Exams A and B may be worth only 20% each of your final grade, while the Midterm and Final Exams may each be worth 30% of your final grade. You happen to score the following on each:
Exam A—95
Midterm Exam—90
Exam B—92
Final Exam—87
To calculate your final grade for the class, you can’t just take the mean (average), since the Midterm and Final exams have more weight than Exams A and B. So you must find the weighted mean. Start by writing the weights next to each corresponding item.
| Exam A—95 | 20% |
| Midterm Exam—90 | 30% |
| Exam B—92 | 20% |
| Final Exam—87 | 30% |
Now multiply each score by its weight and write that new value off to the right.
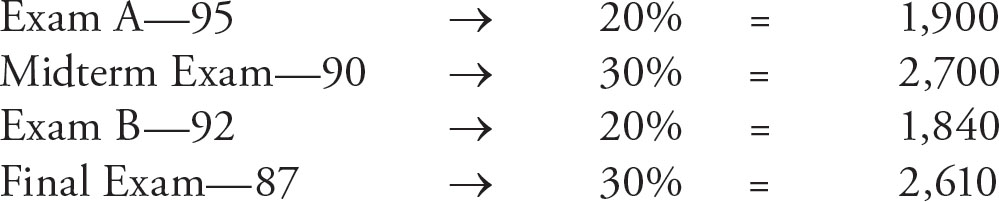
Add up both the final column and the weights column.

Now divide the total value by the total of the weights to get the weighted average:
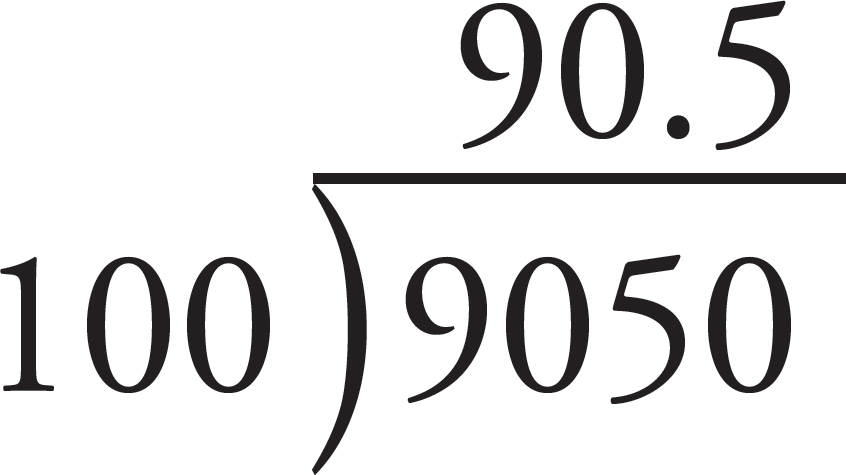
Your final grade in the class would be 90.5.
In summary, you can calculate the weighted mean by following these steps:
1. Multiply your values by their respective weights.
2. Add all your weights together and all your new values together.
3. Divide the total new value by the total weight.
Try another weighted mean problem.

5. Bryce is the best player on his basketball team. During the first 8 weeks of the season, he scored on 65% of his attempts. For the following 4 weeks, Bryce scored on only 32% of his attempts. During the final 4 weeks of playoffs, Bryce practiced more and scored on 74% of his attempts. If Bryce made the same number of attempts each game, then what percent of his attempts during the entire season did he score?
A. 57%
B. 59%
C. 63%
D. 67%
Here’s How to Crack It
This may not seem like a weighted mean problem at first, but look closer. The percentages given throughout the season represent Bryce’s average scoring over those periods. So in order to find his percentage for the entire season, you must combine the 65 percent, 32 percent, and 74 percent. Notice that if you calculate just the mean (average) of 65, 32, and 74, you get (A), 57 percent. This is a trap!
Each percentage represents a portion of the season—65 percent for 8 weeks, 32 percent for 4 weeks, and 74 percent for 4 weeks. First multiply these percentages by the length of time over which they occurred.
65 × 8 = 520
32 × 4 = 128
74 × 4 = 296
Since the question asks about the entire season, find the total number of weeks and the total of the new weighted values.
8 + 4 + 4 = 16
520 + 128 + 296 = 944
Now divide the total weighted value by the total number of weeks.
The correct answer is (B).

Mean, Median, Mode, Range, and Weighted Mean Drill
You can check your answers in Part VIII: Answer Key to Drills.
Do these problems on your own. Then, on another piece of paper, do them again using your calculator.
1.A consumer group buys identical radios at 14 different stores. If the mean (average) price per radio is $23.40, how much did the consumer group spend for all the radios?
$
2.The data below represents the scores students achieved on a test.
92, 85, 86, 92, 86, 89
Complete the line plot to display the data. Click on the red X and drag it onto the graph as many times as necessary.

3.What is the range of weekly business expenses of a sewing supply shop over a three-week period if $65.00, $73.23, and $35.77 were the weekly expense totals for the three weeks?
A. $8.23
B. $29.23
C. $37.46
D. $58.00

4.What is the mean (average) number of ice cream cones sold at the store “Cone Central” during the period shown in the graph above?
A. 95
B. 105
C. 110
D. 119
5.What is the median number of ice cream cones sold at the store “Cone Central” during the period shown in the graph above?
A. 95
B. 105
C. 110
D. 119
6.Olivia is calculating her grade in math class. Her scores for the class are recorded in the table below.

The five in-class tests account for 50% of her final grade, while the midterm and final exams account for the other 50%. What is Olivia’s grade in math class, rounded to the nearest percent?
A. 84%
B. 87%
C. 88%
D. 89%
RATIOS AND PROPORTIONS
As we said earlier, a fraction can be expressed in many
different forms. For example,  =
=  =
=  ….A ratio or proportion problem merely asks you to
express a particular fraction in a slightly different form. Here’s an example:
….A ratio or proportion problem merely asks you to
express a particular fraction in a slightly different form. Here’s an example:

1. A map uses a scale in which 1 inch = 200 miles. If the distance between two cities measures 5 inches on the map, how many miles separate the two cities?
A. 1,000
B. 800
C. 600
D. 400
Here’s How to Crack It
Let’s talk about this problem in terms of inches per mile, which can be expressed as follows:
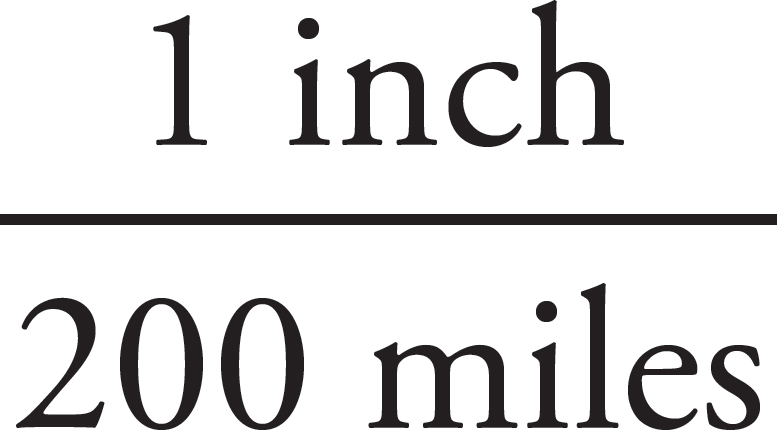
This is actually a ratio, which is a way of writing a part-to-part comparison. A ratio is very similar to a fraction, and has many of the same properties that a fraction does. Like a fraction, a ratio can be expressed in an infinite number of different equivalent ratios. For example, it could equal a ratio with a numerator of 5:

You have just set up a proportion, which is two equivalent ratios. One inch represents 200 miles, so five inches represents…you don’t know yet. Instead of “?” put an x in its place, to represent the number you don’t know yet. To find out how many miles are represented by five inches, cross multiply the denominator of the left-hand ratio with the numerator of the right, and then the denominator of the right-hand ratio with the numerator of the left:

And x = 1,000 miles. To check this, you can stick this number into the proportion you just wrote:
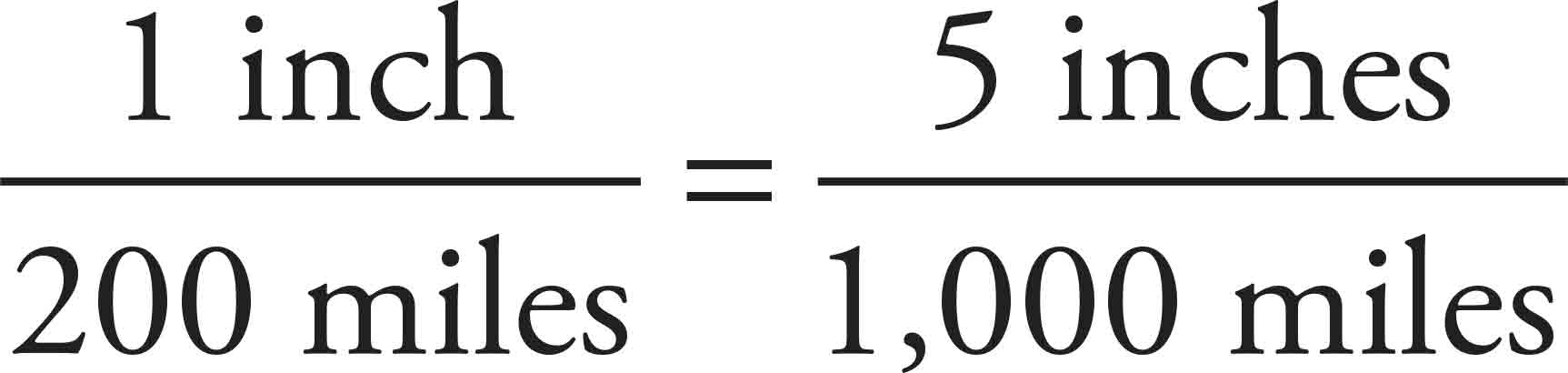
Does 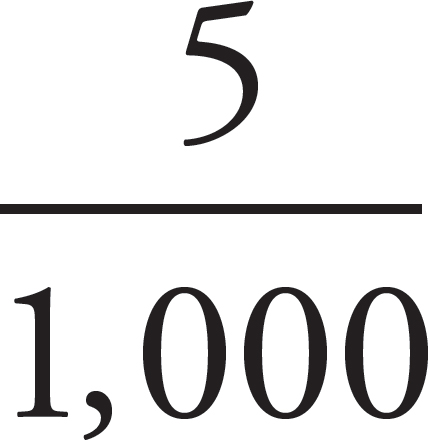 reduce to
reduce to 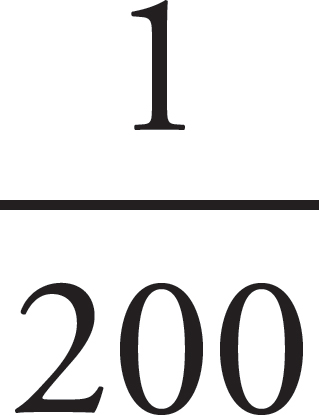 ? You bet. The correct answer is (A).
? You bet. The correct answer is (A).

Let’s do another:

2. If Jane can finish her work assignment in half an hour, what part of it can she finish in 20 minutes?
A. 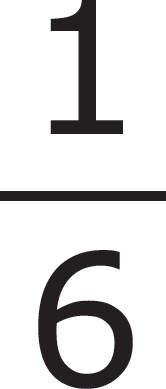
B. 
C. 
D. 
Here’s How to Crack It
First of all, did you notice that this is the same type of problem we just did above? Jane can do one job in 30 minutes, so how much can she do in 20 minutes? To solve this, set up a proportion.
To make our job easier, we should use the same time measurement throughout the problem, so instead of talking about half an hour, permanently convert that to 30 minutes. Now, on to the proportion.

As you did before, cross multiply.
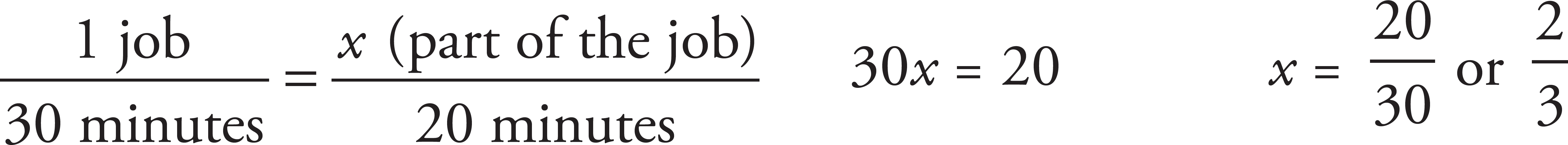
The correct answer is (C).

Could you have done some Ballparking here? Of
course! If the whole job takes 30 minutes, obviously 20 minutes is time to do more
than half the job. Both (A) and (B) are less than half and can be eliminated right
away. In fact, you might even have noticed that 20 minutes out of 30 minutes was without even setting up the proportion. But it’s always a good idea to do the work,
just to make sure.
without even setting up the proportion. But it’s always a good idea to do the work,
just to make sure.
Ratios and Proportions Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.If a shrub 5 feet tall casts a 2-foot shadow, how tall is a tree standing next to the shrub that casts a 10-foot shadow at the same moment?
A. 50 feet
B. 25 feet
C. 20 feet
D. 13 feet
2.Two songwriting collaborators decide that they will share profits in a song in a ratio of 3 parts for the lyric writer to 2 parts for the music writer. If the music writer gets $2,500, how much does the lyric writer receive?
A. $2,500
B. $3,750
C. $5,000
D. $7,500
3.A particular lawn requires 6 bags of fertilizer. A lawn next door requires 4 bags of fertilizer. How big is the lawn next door?
A. 10 square feet
B. 24 square feet
C. 50 square feet
D. Not enough information is given.
RATE PROBLEMS
It’s easy to spot rate problems: They almost always use the word “per” in the question.
You may not think so, but you already know the formula to solve every rate problem. Don’t believe us? Let’s say you drive in a car for 2 hours at 50 miles per hour. How far have you traveled? That’s right: 100 miles. Fifty miles per hour is the rate at which you traveled, 2 hours is the time it took you to travel, and 100 miles is the distance you traveled.
The formula looks like this:
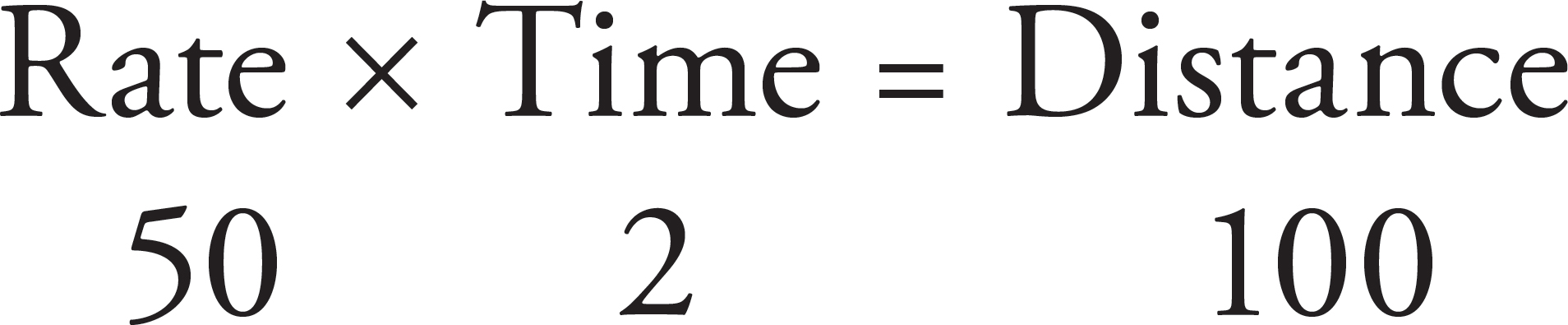
Or like this:
Rate = 
Both equations are the same, as you will see in Chapter 15, Algebra. Memorizing this formula can save you a headache later on when you aren’t sure whether to divide or multiply. Let’s try two problems.

1. A train traveled at a speed of 120
kilometers per hour for 2 hours. How many kilometers did the train
travel?
hours. How many kilometers did the train
travel?
A. 300
B. 280
C. 240
D. 200
Here’s How to Crack It
As soon as you see the words “kilometers per hour” and “hours,” you should immediately be writing down R × T = D on your scratch paper, even before you finish reading the problem. Now all you’ll have to do is plug in the numbers they gave you:
R × T = D
120 × 2 = ?
= ?
Multiplying 120 × 2 , you
get 300, which is (A).
, you
get 300, which is (A).

Could you have ballparked this question? Sure. If the train is traveling at 120 kilometers per hour, then in one hour it must have traveled 120 kilometers. Since your train has been traveling for more than two hours, it must have traveled more than 240 kilometers. Eliminate (C) and (D).
Here’s another example:

2. Flying at 400 miles per hour, approximately how long will it take for a plane to travel between two cities that are 2,600 miles apart?
A. between 4 and 5 hours
B. between 5 and 6 hours
C. between 6 and 7 hours
D. between 7 and 8 hours
Here’s How to Crack It
Again, after reading the first line, you should have been reaching for your scratch paper to write down R × T = D. Plug in the numbers the problem gives you.
R × T = D
400 × ? = 2,600
Ballpark a little first, before you solve this. The answer choices give you some clues as to what this missing number T should be. Start with (A). If T were 4 hours, given that the rate is 400, what would the distance be? 4 × 400 = 1,600. You need a larger T if you want the distance to be 2,600. Now if T were 5 hours, 5 × 400 = 2,000. That’s still not large enough. Let’s try 6 hours: 6 × 400 = 2,400. Well, you’re getting closer. How about 7 hours? 7 × 400 = 2,800. Now this is too big. The correct time must be between 6 and 7 hours.
How do you calculate this problem the
traditional way? Solve for the missing T. If R × T = D, then T=  =
=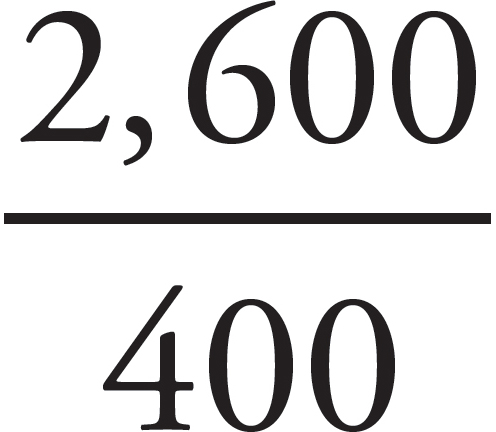 = 6.5 hours. The correct answer is (C).
= 6.5 hours. The correct answer is (C).

Rate Problem Quiz
A: It will use the word “per” in the question.
Rate Problems Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.If a man runs 12 miles in 3 hours, what is his rate in miles per hour?

2.A glacier is moving at a rate of 4 feet per year. At this rate, how long will it take the glacier to travel one mile? (1 mile = 5,280 feet)
A. 920 years
B. 1,100 years
C. 1,320 years
D. 1,540 years
3.Marie drives from her home to the supermarket 10 miles away and then drives back home after shopping. If it takes her two hours for the entire trip, including one hour spent shopping in the supermarket, what was her average speed driving to and from the supermarket?
A. 5 mph
B. 10 mph
C. 15 mph
D. 20 mph
SCALE AND UNIT CONVERSION
Sometimes you will be asked to find the scale on which something is drawn. The easiest way to find the scale is to set up a proportion, which you already know how to do! Let’s see how this might be introduced to a problem.

1. Amy builds a toothpick model of a bridge for a school project. The real bridge is 1,650 feet long and 134 feet high. Amy’s model bridge is only 8 inches high. Find the scale that Amy uses for her model bridge. Then determine the approximate length of her model bridge shown in the drawing below.
Click on the numbers you want to select and drag them into the boxes.

Here’s How to Crack It
Set up a proportion for the measurements of the heights versus the lengths:
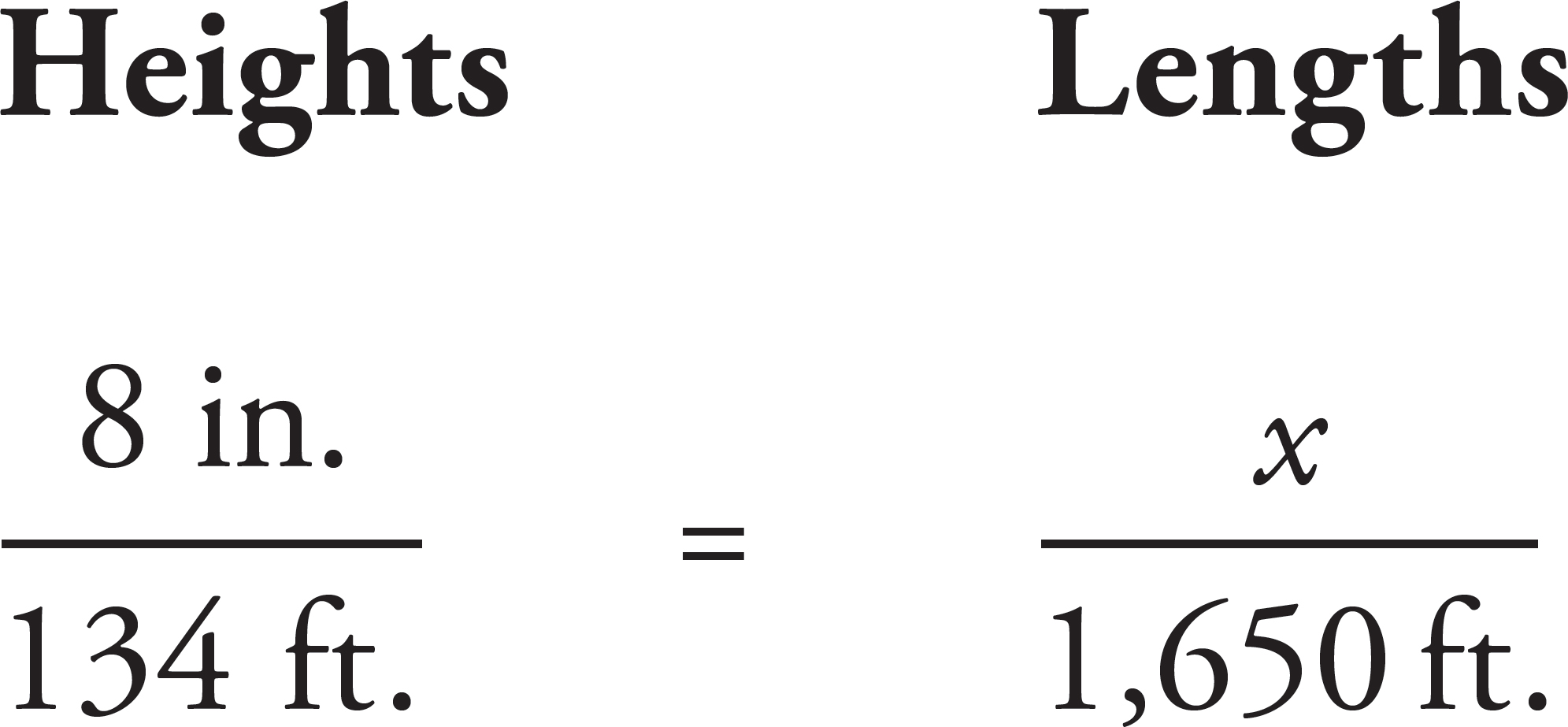
Now cross multiply to get
1,650 × 8 = 134x?
The length of the model bridge must be
approximately 98.5, or 98 inches.
inches.
Now, to determine the scale, set up a similar proportion as before, but to determine the number of feet represented by 1 in:
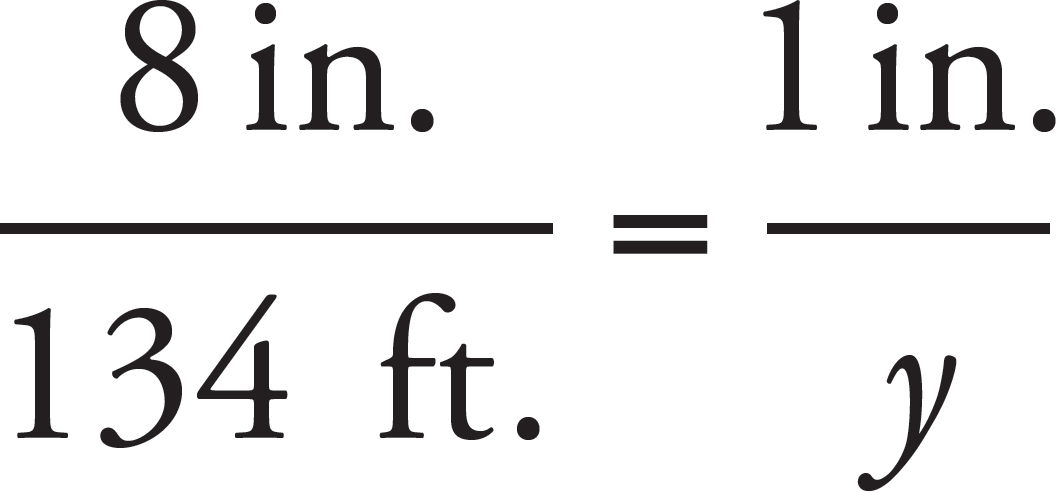
Now cross multiply to get
134 × 1 = 8y
The scale must be 16.75, or 16 .
.

Similarly, if a question requires that you convert between units, you can use (you guessed it!) a proportion.
Take a look:

2. A football coach makes his players run two laps around the football field to warm up before practice. If the field is 120 yards long and 160 feet wide, how many miles do the players run to warm up? (Hint: There are 3 feet in a yard and 5,280 feet in a mile.)
A. 0.1 miles
B. 0.2 miles
C. 0.4 miles
D. 0.5 miles
Here’s How to Crack It
This problem uses three different units of measurement—feet, yards, and miles. Yikes! Before you do any major calculations, try to get all of the numbers in the same unit. You start with 120 yards and 160 feet. Which one will be easier to work with? Feet. So convert 120 yards:

120 × 3 = 1x
360 = x
Now you know that the football field is 360 feet long, and the width is already in feet. How far is one lap around the field? The 360 feet and 160 feet are only one length and one width, but a lap consists of running two lengths and two widths. You could add all four measurements: 360 + 160 + 360 + 160 = 1,040. Or you can add the single length and single width, and then multiply by two:
360 + 160 = 520
520 × 2 = 1,040
Either way will result in the same answer. You know how far one lap around the field is, but the question asks for two laps. Double the answer: 1,040 × 2 = 2,080. You’re not done yet! All of the answer choices are in miles. Convert 2,080 feet to miles:
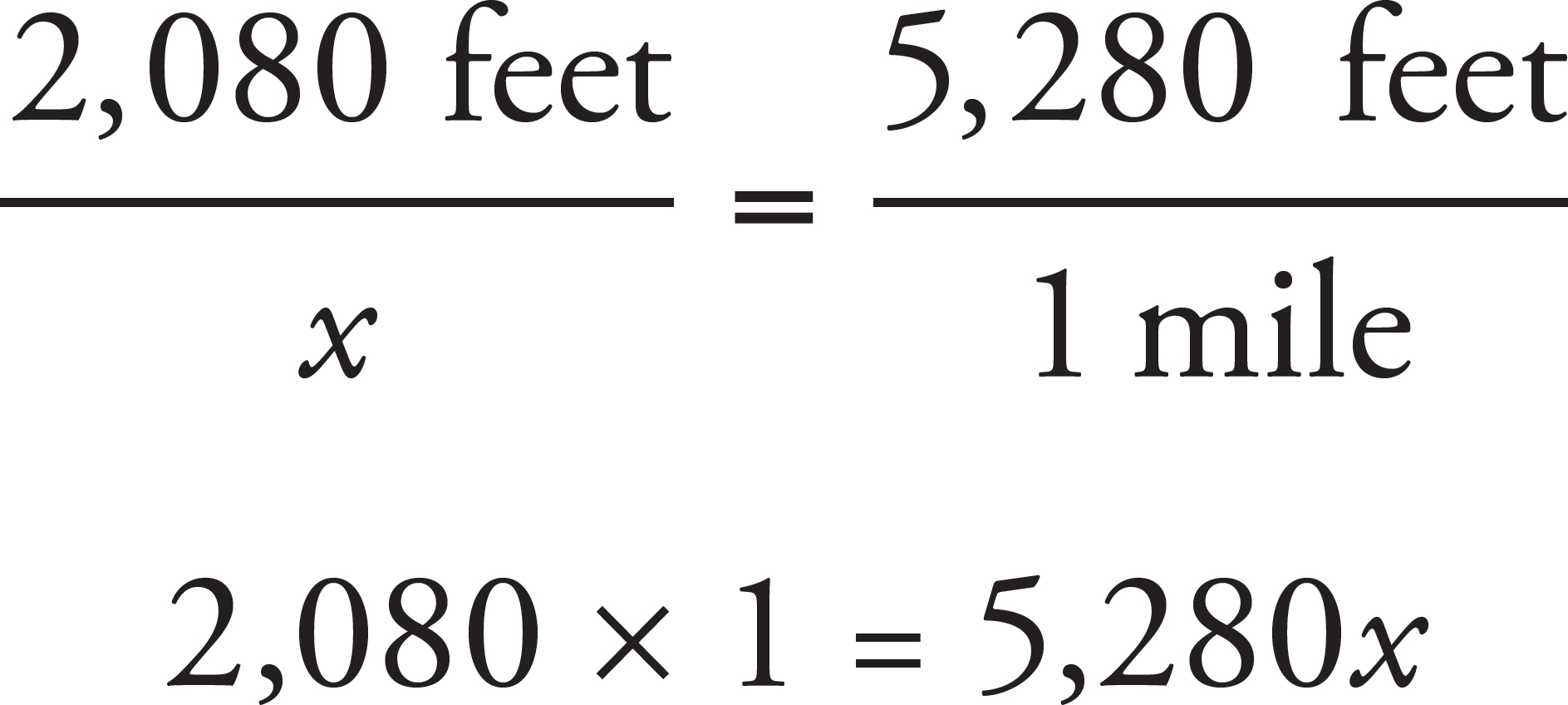
Then divide 2,080 by 5,280 to find the answer in miles: 2,080 ÷ 5,280 = 0.4 miles, or (C).
You can also use common sense to help in converting units. You have 120 yards and want to convert to feet. There are 3 feet in a yard. Since you are converting to a smaller unit, multiply 120 by 3 to find the answer.
Let’s look at converting 2,080 feet to miles. There are 5,280 feet in a mile. Are miles a bigger or smaller unit than feet? They are bigger, so you will divide 2,080 by 5,280.

Scale and Unit Conversion Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.A man who weighs 200 pounds goes on a diet and loses 16% of his body weight. How much weight, in ounces, did he lose? (Hint: 1 pound = 16 ounces.)
A. 2
B. 32
C. 200
D. 512
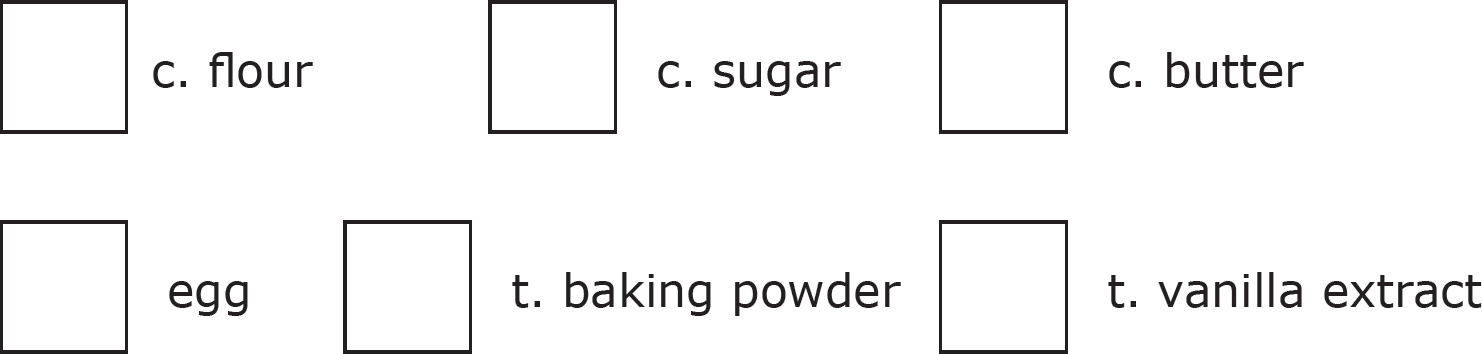
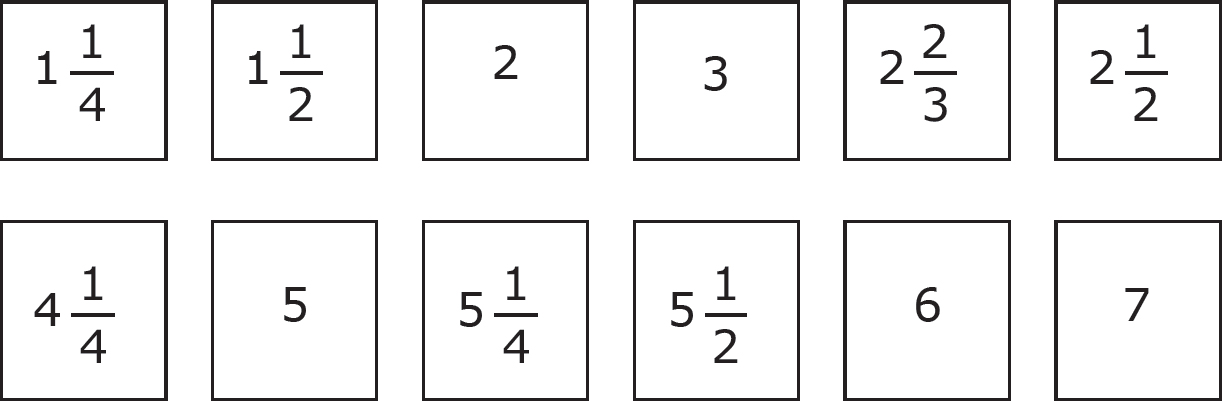
2.A cookie recipe that makes 24 cookies calls for the following ingredients:
2 c. flour
c. flour
1 c. sugar
c. sugar
 c. butter
c. butter
1 egg
3 t. baking powder
t. baking powder
1 t. vanilla extract
t. vanilla extract
Amy is hosting a party and will have a total of 16 people in attendance, including herself. She wants to make one large batch of cookies to accommodate everyone. If each person will eat three cookies, what are the new amounts that Amy must measure for each ingredient?
Click on the numbers you want to select and drag them into the boxes.
CHARTS AND GRAPHS
Some test takers are scared by charts and graphs. If you count yourself among them, we recommend that you review our “Understanding Graphics” supplement, which you can download online once you register your book. Roughly one-third to one-half of the Mathematical Reasoning test questions include a graphic of some sort. This can be a figure, a chart, a graph, or a table. One great thing about the graphics is that they are roughly drawn to scale, so you can always ballpark. Math test graphics review all the concepts included in this book, from the number line and percentages to the slope and equation of a line. Look at the following problems:

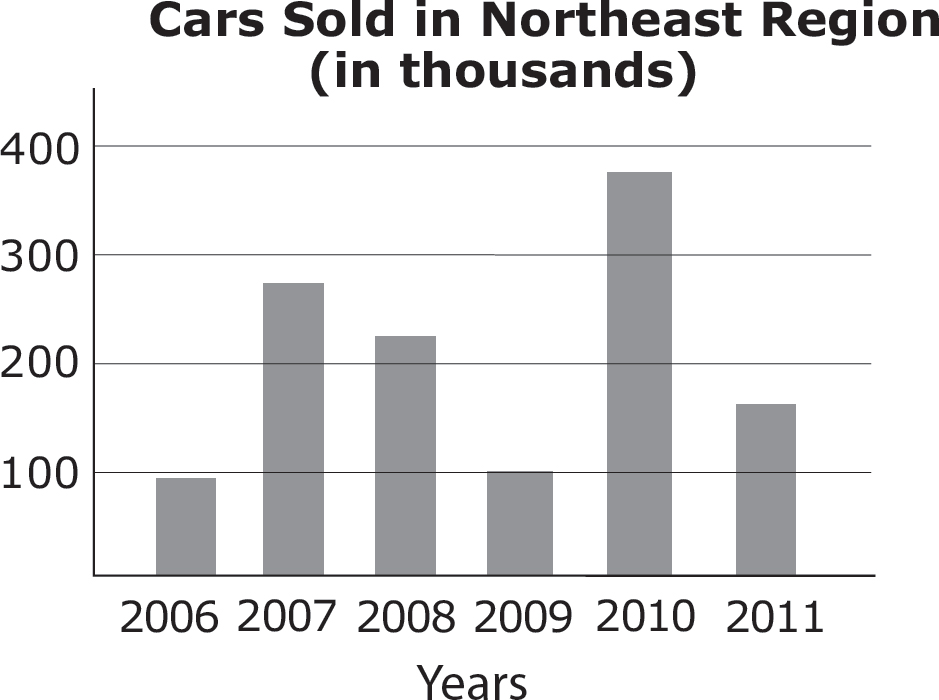
1. In the figure above, by approximately how much did sales of cars increase from 2009 to 2010?
A. 100,000
B. 200,000
C. 260,000
D. 360,000
Here’s How to Crack It
If you’ve read the “Understanding Graphics” supplement, you know that you should always take a moment to read the title of the graph and study the two variables. You are looking at the number of cars sold in a particular region, broken down by year. The number of cars is expressed in thousands.
In 2009, according to the graph, 100,000 cars were sold. In 2010, more than 300,000 were sold. How many more? It’s difficult to say exactly because the scale on the left is marked only every 100,000 cars, but it looks to be a little more than half the distance between the markings, or about 70,000 more. So the total 2010 figure is about 370,000. The question wants to know the increase from 2009 to 2010. How do you get that? Subtract. Roughly 370,000 minus 100,000 is roughly 270,000. Is this close to any of the answers? Yes. The correct answer is (C).
In effect, this was officially sanctioned Ballparking. There was no way to get the precise answer mathematically. The GED® test writers expected you to use your eyes and estimate in order to get the right answer.

Let’s try another.

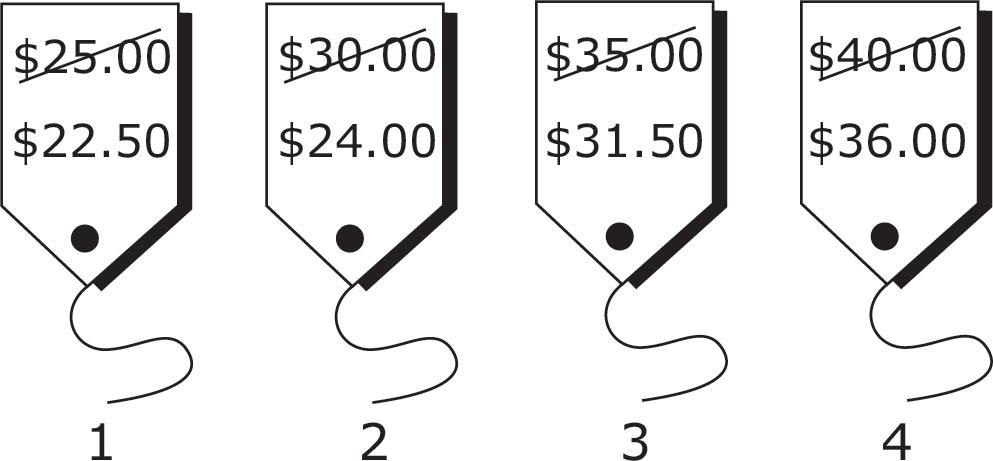
2. A man is searching through a bin of shirts that are on sale, some for 10% off and some for 20% off. Which sales tag above has been reduced by 20%?
A. 1
B. 2
C. 3
D. 4
Here’s How to Crack It
In spite of the fact that there is a graphic that goes with it, this is just a percent problem. The question asks you to identify the tag that has been reduced by 20 percent. Begin with the first tag. It started at $25.00, and has been reduced to $22.50. Take away 20 percent from 25 and see if you get 22.50. If you do, it’s the answer. If you don’t, you can throw it back in the bin and try another. Twenty percent of $25.00 is $5.00, so the reduced price ought to be $20.00 if this were the correct answer. It isn’t, so you can eliminate (A). Go to the next tag: It started at $30.00 and has been reduced to $24.00. What is 20 percent of 30? That’s right: 6. If you take away the $6, you are left with $24.00. Bingo! The answer is (B).

Charts and Graphs Drill
You can check your answers in Part VIII: Answer Key to Drills.

1.In the figure above, the number of regular telephones in use is how many times the number of cellular phones?
A. 2.5 times
B. 3 times
C. 4 times
D. 7.5 times
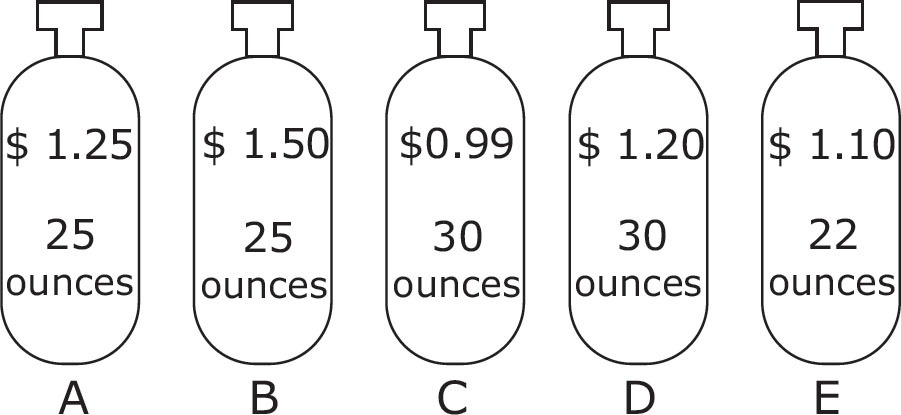
2.Each of the bottles in the figure above contains different amounts of cola at different prices. Which bottle represents the cheapest price per ounce?

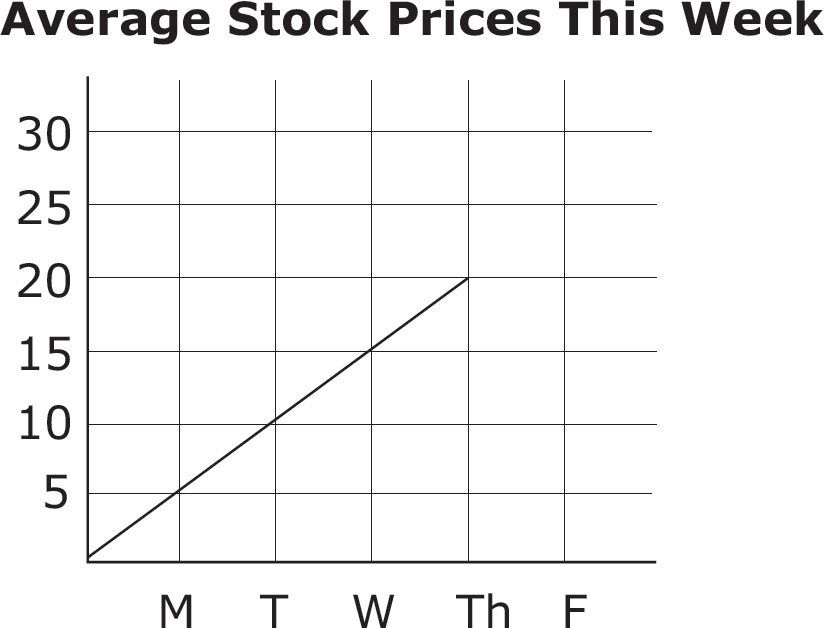
3.The price of a particular stock has been increasing at the same rate each day for the first four days of the week, as shown in the graph above. If the increase continues at its present rate, what should the price be on Friday?
A. 20
B. 25
C. 30
D. Not enough information is given.
EXPONENTS
An exponent is shorthand for multiplication. The expression 4 × 4 × 4 × 4 × 4 can also be written as 45, because the 4 is being multiplied 5 times. This is expressed as “4 to the fifth power.” The large number (4) is called the base, and the little number (5) is called the exponent.
Although there aren’t very many exponent questions on the GED® test, there are a few rules that you should remember.
Multiplying Numbers with the Same Base
When you multiply numbers that have the same base, you simply add the exponents.
62 × 63 = 6(2 + 3) = 65
Why is this true? Let’s write this out in long form:
62 = 6 × 6 63 = 6 × 6 × 6
so, 62 × 63 = 6 × 6 × 6 × 6 × 6 or 65
Dividing Numbers with the Same Base
When you divide numbers that have the same base, you simply subtract the bottom exponent from the top exponent.
= 6
Why is this true? Let’s write it out in long form:
=
=
= 6
Raising a Number with an Exponent to Another Exponent
When you raise a number with an exponent to another exponent, multiply the exponents.
(62)3 = 62 × 3 = 66
Why is this true? Let’s write this out in long form:
(62)3 = 62 × 62× 62 = (6 × 6) × (6 × 6) × (6 × 6) = 66
Exponent Facts
50 = 1
51 = 5
52 = 25
If x2 = 25, then x = 5
or –5.
The Zero Power
It may seem strange, but any number to the zero power is 1.
40 = 1 x0 = 1
The First Power
Anything to the first power equals that number.
41 = 4
–31 = –3
But Watch Out For…
There are several operations that seem like they ought to work with exponents but don’t.
Does x2+ x3= x5? NO!!
Does x4– x2= x2? NO!!!
Does
=z4? NO!!!!
In fact, none of these three expressions can be reduced.
You would expect that raising a number to a power would increase that number, and usually it does, but there are exceptions.
-
If you raise a positive fraction of less than 1 to a power, the fraction gets smaller.

-
If you raise a negative number to an odd power, the number gets smaller.
(–3)3 = (–3)(–3)(–3) = –27
(Remember –27 is smaller than –3.)
-
If you raise a negative number to an even power, the number becomes positive.
(–3)2 = (–3)(–3) = 9
Exponent problems on the GED® test tend to be pretty basic.

1. 33 equals which of the following values?
A. 9 × 9
B. 3 × 3
C. 3 × 9
D. 127
Here’s How to Crack It
The expression 33 equals 27. All you have to do is find the answer choice that also equals 27. You got it. The correct answer is (C).

RADICALS
The square root of a positive number x is the number that, when squared, equals x.

To find the square root of a number on your TI-30XS, first press the “2nd” key, then the “x2” key, enter the number, and then press the right arrow key.
For example:
-
The square root of 16 equals 4 because 4 × 4 = 16.
-
The square root of 9 equals 3 because 3 × 3 = 9.
-
The square root of 4 equals 2 because 2 × 2 = 4.
The symbol for a positive square root is 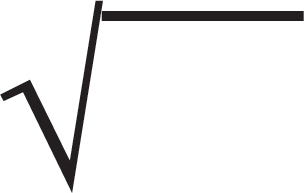 ,
also called a radical.
,
also called a radical.
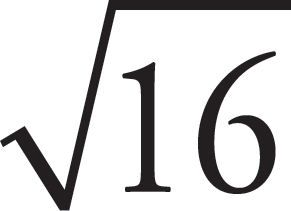 = 4
= 4
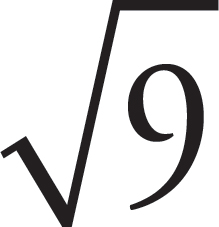 = 3
= 3
Many numbers do not have a whole number square
root. For example, there is no whole number whose value is 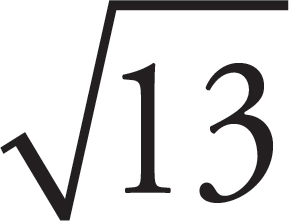 .
But we can say that
.
But we can say that 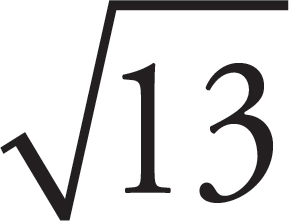 is between 3 and 4. Here’s an example:
is between 3 and 4. Here’s an example:
Radical Facts
 = 2
= 2
 = 2
= 2
If x = 4, then
 = positive 2.
= positive 2.

1. The square root of 7 is between which of the following pairs of numbers?
A. 2 and 3
B. 3 and 4
C. 4.5 and 5.5
D. 9 and 10
Here’s How to Crack It
There is no whole number square root of 7, so see what
numbers it is between that do have a square root. The expression 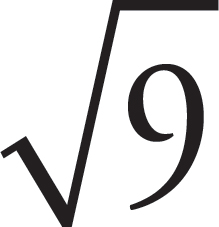 is
the next biggest number that comes out evenly:
is
the next biggest number that comes out evenly: 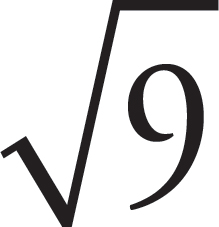 =
3. The expression
=
3. The expression  is the next smallest number that comes out evenly:
is the next smallest number that comes out evenly: =
2. Thus, the square root of 7 is between 2 and 3. The correct answer is (A).
=
2. Thus, the square root of 7 is between 2 and 3. The correct answer is (A).

Sometimes a question will ask for the square root of a
fraction. To do this, take the square root of the numerator and denominator
separately. For example, to determine 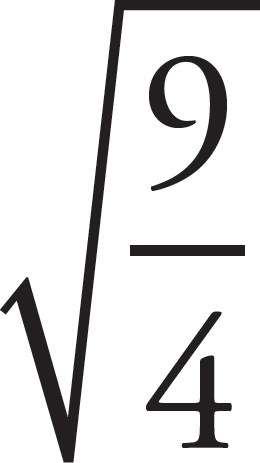 ,
start with the fact that
,
start with the fact that 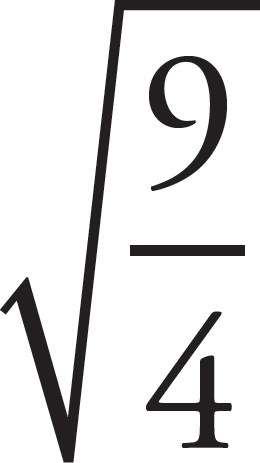 =
= 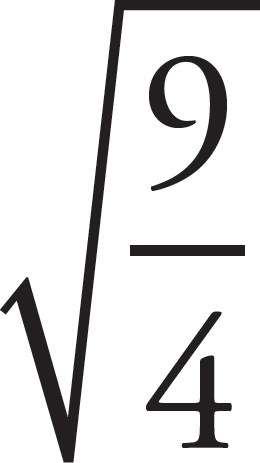 . Since
. Since 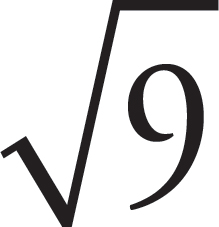 = 3
and
= 3
and  =
2,
=
2, 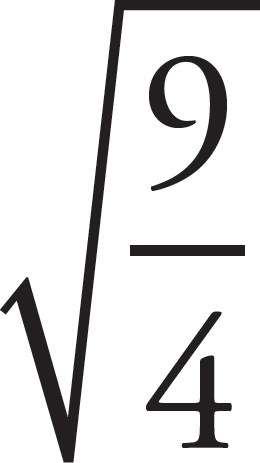 =
=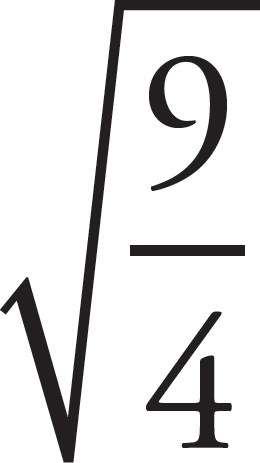 =
= .
Let’s look at another example.
.
Let’s look at another example.

2. What is  ?
?
A. 0.005
B. 0.05
C. 0.5
D. 5
Take 0.25 and convert it to a fraction: 0.25 =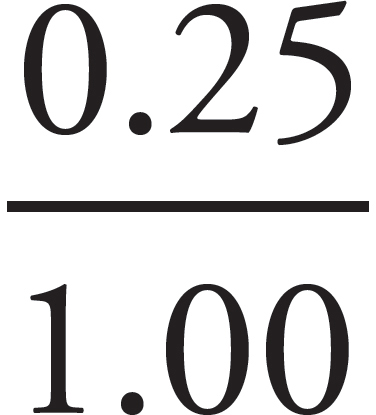 =
=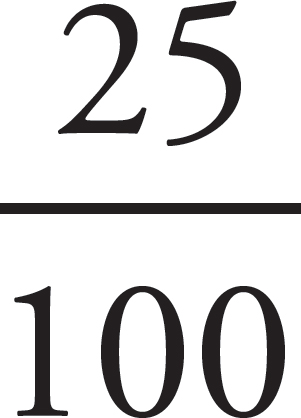 =
= .
Since 0.25 =
.
Since 0.25 =  ,
, 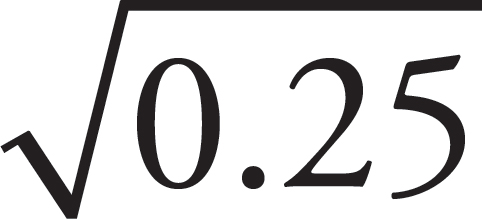 =
= 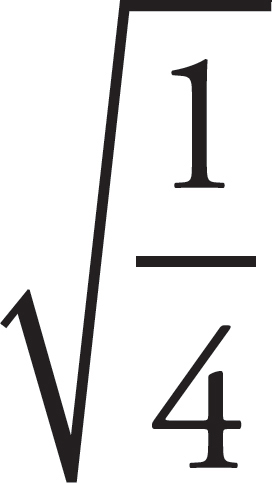 =
= 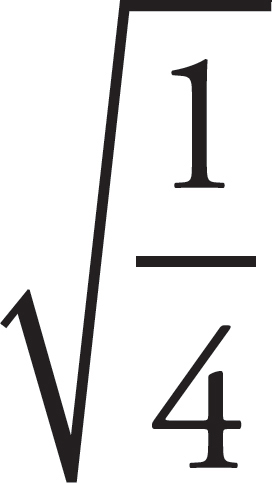 =
=  . Since the answer choices are decimals, convert
. Since the answer choices are decimals, convert  into
a decimal:
into
a decimal: 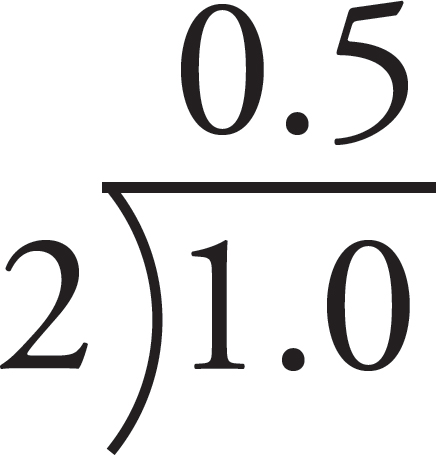 . The correct answer is (C).
. The correct answer is (C).

Exponents and roots are two related concepts. In
fact, a root can be expressed as an exponent. For example, how can 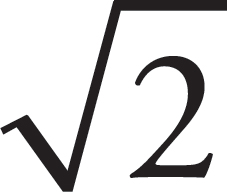 be
expressed as a number with an exponent? Note that
be
expressed as a number with an exponent? Note that  = 2,
since the square root and the square are inverses. Remember also that this equation
can be rewritten as
= 2,
since the square root and the square are inverses. Remember also that this equation
can be rewritten as = 21. If we rewrite
= 21. If we rewrite 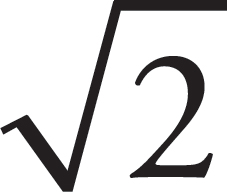 as
2x, we get (2x)2 =
21. Multiply the exponents on the left side of the equation to get
22x = 21. Therefore 2x = 1 and x =
as
2x, we get (2x)2 =
21. Multiply the exponents on the left side of the equation to get
22x = 21. Therefore 2x = 1 and x =  , so
, so 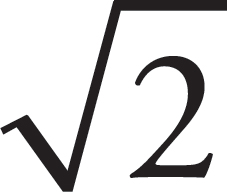 =
2
=
2 .
Let’s look at an example.
.
Let’s look at an example.

3. What is the value of 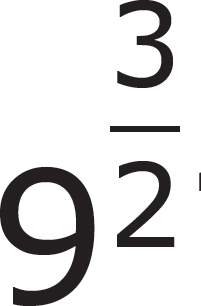 ?
?
A. 3
B. 9
C. 27
D. 81
Here’s How to Crack It
Rewrite the exponent  as
as × 3
to get
× 3
to get  .
Multiplication within the exponent is equivalent to raising to an exponent, so
.
Multiplication within the exponent is equivalent to raising to an exponent, so  =
=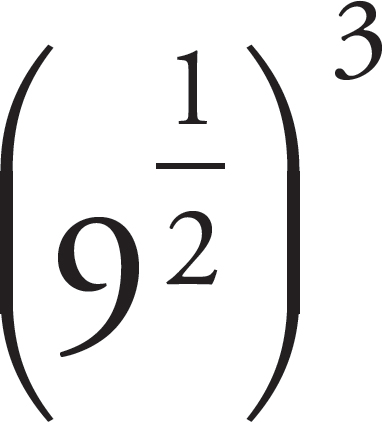 .
Since,
.
Since,  =
=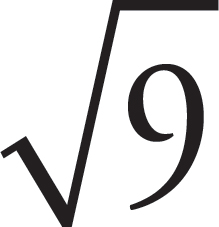 =
3,
=
3, 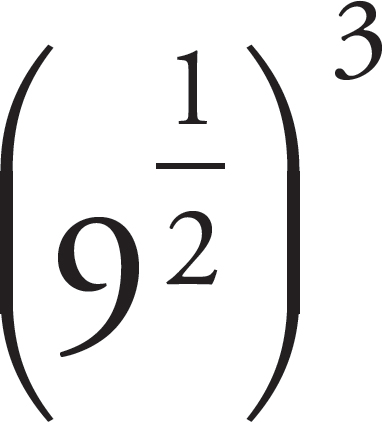 =
33 = 27. The correct answer is (C).
=
33 = 27. The correct answer is (C).

Exponents and Radicals Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.Which of the following values is equal to 23?
A. (2 + 2)2
B. 22 + 2
C. 42
D. 2(22)
2.33 + 22 = ?

3.What is the value of  –
–  ?
?
A. 22
B. 
C. 162 + 42
D. 
SCIENTIFIC NOTATION
Scientific notation combines your knowledge of decimals and your knowledge of exponents to allow you to express very large numbers without endless strings of zeros. Take the number 3,200,000,000. Numbers like this can be difficult to read and even more difficult to add or subtract. Here is the same number in scientific notation:
3.2 × 109
How do you expand this out to its full size? Let’s start with an easier example.
3.2 × 102
All you have to do to simplify this expression is move the decimal point over to the right by the same number as the power of ten. In this case, two places.
3.2 × 102 = 320
3.2 × 103 = 3,200
3.2 × 104 = 32,000
How do you contract a big number into scientific notation? Just perform the same process in reverse. Let’s take 4,750,000. If you wanted to express this as 4.75 to the nth power of ten, what would the nth power be? On the large number, put your pencil point where you want the decimal to be (in this case, between the digit 4 and the digit 7), and now count the number of places you have to move the pencil to the right to get to the end of the number. Did you move your pencil 6 places? You are now a certified scientific notationalist.
4,750,000 = 4.75 × 106
Let’s try a problem.

1. Which of the following expresses the number 5.6 × 104?
A. 0.00056
B. 5,600
C. 56,000
D. 560,000
Here’s How to Crack It
On a piece of scratch paper, write down 5.6 with some space to the right of it. Now, take your pencil, and move the tip of the pencil over four times, like this:

Fill in the 0s. The correct answer is (C).

PROBABILITY
If you flip a coin, what are the odds that it’s going to come
out tails? If you said anything but “ ,” “1
out of 2,” or “fifty-fifty,” then there’s a poker game we’d like to invite you to
next Thursday.
,” “1
out of 2,” or “fifty-fifty,” then there’s a poker game we’d like to invite you to
next Thursday.
To figure out the probability that something is
going to happen, you take the number of chances that the thing could happen and
compare that to the total number of possible outcomes of all kinds.
For example, let’s take that coin we just mentioned. If you toss the coin once, how
many chances are there on this one toss that it will be heads? One chance.
And how many total possible outcomes are there? There are two possible
outcomes—heads or tails. Therefore, you have a 1 out of 2,  , or
fifty-fifty chance of seeing tails.
, or
fifty-fifty chance of seeing tails.
On the GED® test, probabilities are generally expressed as fractions. The number of possibilities that one thing could happen is the numerator. The number of total possibilities is the denominator.

Probability Quiz
Q: If there is one probability question on your 46-question Mathematical Reasoning test, what’s the probability that the first question on the test will be a probability question?
Turn to this page for the answer.
Let’s try a problem.

1. 9 workers decide to draw straws to see who will be the one to stay late and clean up. If there are 9 straws, 8 long and 1 short, what is the probability that Jim, who goes first, will draw the short straw?
A. 
B. 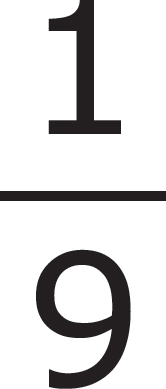
C. 
D. 
Here’s How to Crack It
To solve any GED® probability problem, you have to find the number of chances that a particular thing could happen (in this case, there is only one short straw, so Jim has only one chance of picking a short straw). This is your numerator. Then you have to find the total number of outcomes of any kind (in this case, the total number of straws is 9). This is your denominator. The correct answer to this question is (B).

Let’s try another.

2. If a box of chocolates contains 3 caramels, 3 nut clusters, and 5 raspberry creams, which of the following fractions represents the chance of picking a caramel on the first try?
A. 
B. 
C. 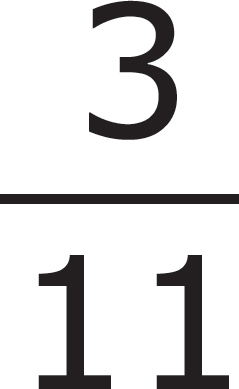
D. 
Here’s How to Crack It
As before, figure out the number of possible ways to pick a caramel. There are three caramels, so there are three possibilities for picking one. That becomes your numerator.
Now, you need the total number of possibilities of
any kind. There are a total of 11 chocolates, so that becomes your denominator. The
correct answer is  or (C).
or (C).

Probability Quiz
A: 1 out of 46
Scientific Notation and Probability Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.A painting has three lights illuminating it, each with an output of 2,550 lumens. What is the total amount of light illuminating the painting, in lumens, expressed in scientific notation?
A. 51.0 × 104
B. 76.5 × 103
C. 7.65 × 103
D. 5.1 × 103
2.Erica’s closet has no light. Erica owns 2 blue dresses, 1 green dress, 1 purple dress, and 2 green dresses. What is the probability that she will pick a blue dress?
A. 
B. 
C. 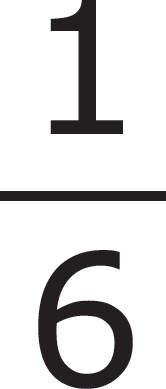
D. 
3.Which of the following is equivalent to (3.4 × 103) + (4.1 × 104)?
A. 75,000
B. 750,000
C. 444,000
D. 44,400
COMBINATIONS AND PERMUTATIONS
On some GED® questions, you will have to determine the number of possible choices that you can make in a given situation. If you’re choosing what to have for lunch and are offered either a sandwich, soup, or a salad, how many choices would you have? That’s right: 3. However, the GED® test is not likely to ask questions like this. The GED® test is more likely to ask questions that require you to determine the total number of options when making multiple choices. Let’s look at an example below.

1. The manager of a department store has to hire a new cashier, a new salesperson, and a new shift supervisor. If there are 3 applicants for cashier, 8 applicants for salesperson, and 5 applicants for shift supervisor, and no applicant applies for more than one position, how many different ways can the manager hire one person for each of the three positions?
A. 17
B. 20
C. 60
D. 120
Here’s How to Crack It
The manager needs to hire people to fill three positions. The question tells you that no applicant applies for more than one position. This means that there is a completely different pool of applicants for each position. When there is a different source for each choice, treat each choice independently. Draw a slot for each position as below.

Now, for each position, fill in the number of possible applicants as below.
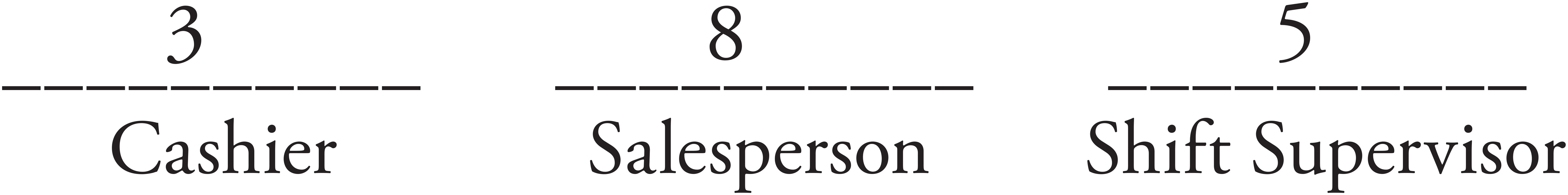
Now, multiply each of the three numbers to get 3 × 8 × 5 = 120. The correct answer is (D).

Sometimes, however, you’ll be working with the same source of items for each choice that you’re making. In some of these examples, the order will matter but not in others. If the order doesn’t matter, mathematicians call it a combination; if order does matter, it’s called a permutation. The method you use to solve questions in which there is one source and order matters is actually very similar to that for questions in which there are multiple sources. This is common in questions that ask about arrangements or filling different positions. Let’s look at one below.
2. A DJ has enough time to play four more songs at a school dance. If she has seven different songs available to choose from, how many different orderings of songs can she choose?
A. 22
B. 35
C. 840
D. 2,401
Here’s How to Crack It
The DJ needs to choose four songs. Just as before, draw a slot for each position as below.

Now, for each song, fill in the number of possible choices. For the first song, there are seven choices. For the second song, there are six choices remaining (since you already used one song as the first selection). For the third song, there are five choices remaining (since you already used two songs). For the fourth song, there are four choices remaining (since you already used three songs). Fill this in as below.

Now, multiply each of the three numbers to get 7 × 6 × 5 × 4 = 840. The correct answer is (C).

In other cases, though, the order will not matter. This means there will be fewer possibilities than cases in which order does matter. In these cases, you will follow the same method as when order matters but with an extra step to reduce the number of possibilities. This is common when questions ask about teams or committees. Look at an example below.

1. A DJ is choosing four new records to add to his collection. If he is in a store that has seven different records available to choose from, how many different groups of records can he choose?
A. 22
B. 35
C. 840
D. 2,401
Here’s How to Crack It
This looks similar to the previous question, and it is but with a key difference. The DJ needs to choose four records. Just as before, draw a slot for each position as below.

Now, for each record, fill in the number of possible choices. For the first song, there are seven choices. For the second song, there are six choices remaining (since you already used one song as the first selection). For the third song, there are five choices remaining (since you already used two songs). For the fourth song, there are four choices remaining (since you already used three songs). Fill this in as below.

So far, it is the same as the previous question. The difference is that since each record will simply either be purchased or not purchased, the order doesn’t matter. When this is the case, you want to divide by the number of possible ordering of each set of 4. This is 4 × 3 × 2 × 1. Divide this by the numbers above to get the following:
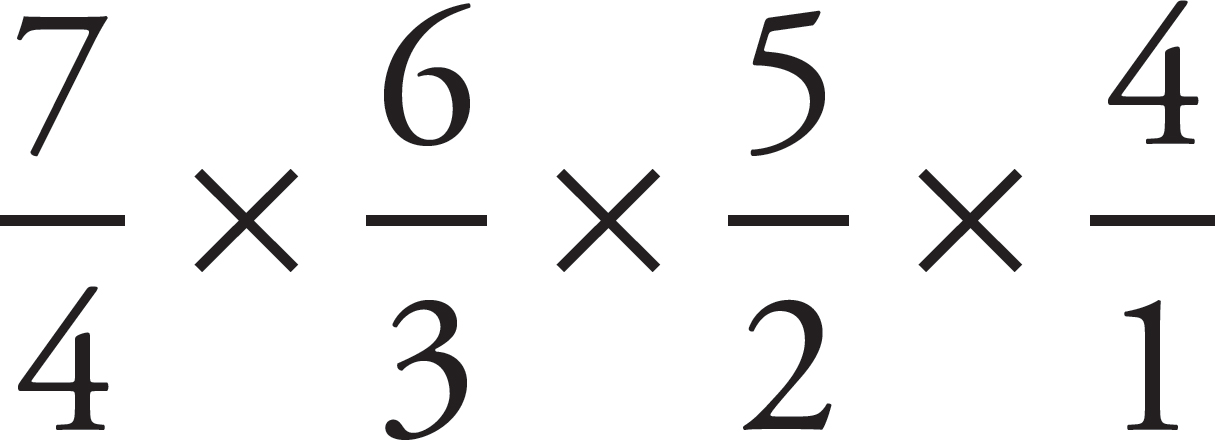
Reduce these fractions before you multiply them. The 6 in the numerator can cancel with the 3 and 2 in the denominator and the 4 in the numerator can cancel with the 4 in denominator to get the following:
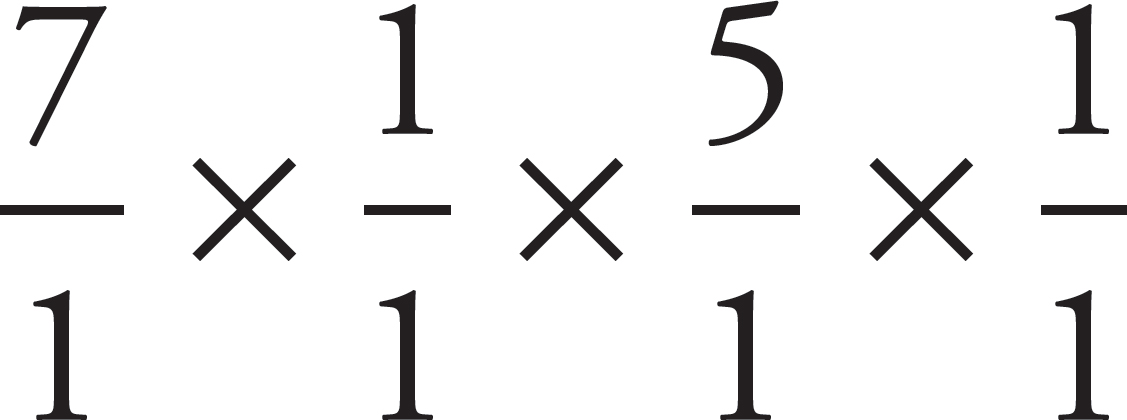
Now, multiply what remains to get 7 × 5 = 35. The correct answer is (B).
Combinations and Permutations Drill
You can check your answers in Part VIII: Answer Key to Drills.
1.A deli offers a made-to-order sandwich to its customers. Customers can choose one type of bread, one type of meat, one type of cheese, and one type of lettuce. If the deli has four types of bread, five types of meat, eight types of cheeses, and three types of lettuce, how many different types of sandwiches can a customer order?
A. 20
B. 120
C. 240
D. 480
2.A school president is choosing three cabinet members to appoint: a vice president, a secretary, and a treasurer. If she has eight candidates to choose from, each of whom can serve any cabinet position, how many possible cabinets can the president appoint?
A. 21
B. 56
C. 336
D. 512
3.A teacher is selecting students for a trivia bowl. If there are nine interested students and a trivia bowl team consists of three players, how many different teams can the teacher select?
A. 24
B. 84
C. 252
D. 504
PUTTING IT ALL TOGETHER
Now that you’ve seen the basics of applied arithmetic one topic at a time, we’re going to give you a drill that mixes up all the different applied arithmetic concepts we’ve discussed in this chapter. This drill will help to reveal whether you’re having trouble recognizing individual types of problems, as we discussed in the last chapter. Some people are fine once they know that a question is about probabilities or percents, for example, but they have trouble spotting the key words that should tell them what type of problem they’re dealing with. As you do this drill, make it a point to identify each question before you start calculating:
“This is an average question.”
“That is a rate problem.”
“This one is an exponent question.”
Applied Arithmetic Drill
You can check your answers in Part VIII: Answer Key to Drills.
Click here to download a PDF of Practice Test 1
1.Darryl puts $5,000 into an insured bank account that pays simple interest of 8%. How much interest will he earn in 2 years?
A. 2[0.08(5,000)]
B. 
C. 2[0.92(5,000)]
D. 2[1.08(5,000)]
2.If Laverne walks steadily at a rate of 5 kilometers per hour, how long will it take her to walk 17.5 kilometers?
A. 1 hours
hours
B. 3 hours
hours
C. 52 hours
D. 87 hours
hours
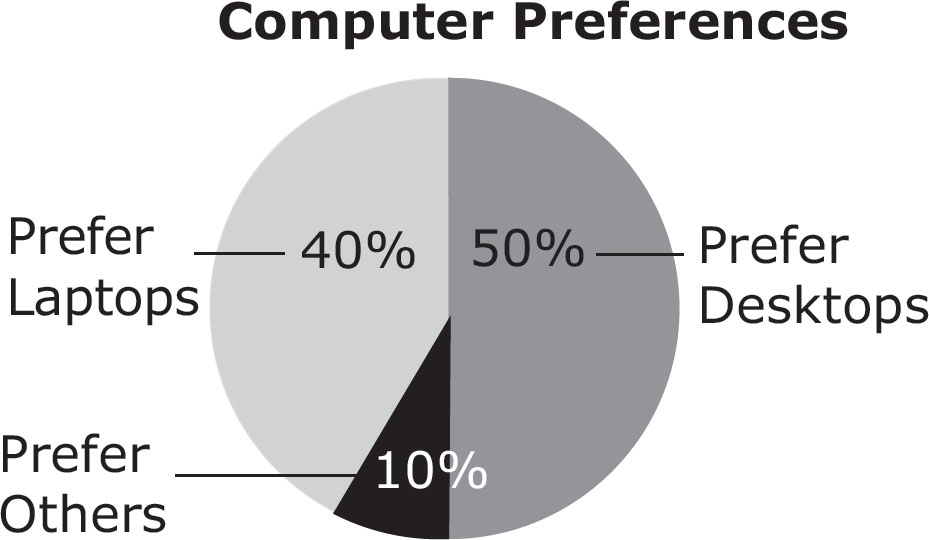
3.The figure above shows the results of a survey of a group of 200 professionals who were asked what type of computer they preferred. How many more people prefer desktop computers than prefer laptop computers?
A. 5
B. 10
C. 15
D. 20
4.There are a total of four tests in Sara’s history class. She earned 94, 88, and 85 on the first three. What score does Sara need on the fourth test to pass the class with an average of 90 (the equivalent of an A)?
A. 89
B. 90
C. 91
D. 93
7.Michael calls a taxi to pick him up at his house. He knows that the taxi company has 1 limousine, 2 sedans, 3 vans, and 1 compact. What is the probability that he will ride in a sedan?

8.A set contains the following five numbers: 12, 4, 8, 16, 23. What is the median of the set?

9.Sheila works in a factory for $14.50 per hour for any hours up to 40. After 40 hours, she is paid an overtime rate that is one and a half times her regular pay. If Sheila worked 43 hours last week, which expression below shows how much she earned?
A. 40(14.50) + 3(1.5)
B. 40(14.50) + 3(1.5)(14.50)
C. 43(1.5)(14.50)
D. 43(14.50)
10.If one cell is 2.3 × 104 microns wide and another cell is 3.2 × 104 microns wide, then one cell is how much bigger than the other in microns?
A. 0.9
B. 11.0
C. 110.0
D. 9,000.0
11.Marie has five television shows recorded on her DVR. She has enough time to watch three of them today, and must decide in what order she will watch them. How many different orderings of the three shows she watches today can Marie choose?
A. 10
B. 30
C. 60
D. 120