Qu’est-ce qu’un poème,
et qu’en pense la philosophie ?
La critique radicale de la poésie, dans le livre X de la République, manifeste-t-elle les limites singulières de la philosophie platonicienne de l’Idée ? Ou est-elle, au contraire, un geste constitutif de la philosophie elle-même, de la philosophie « telle quelle », qui manifesterait ainsi originellement son incompatibilité avec le poème ?
Pour ne pas affadir la discussion, il importe de saisir que le geste platonicien au regard du poème n’est pas, aux yeux de Platon, secondaire ou polémique. Il est réellement crucial. Platon n’hésite pas à déclarer ceci : « La cité dont nous venons de fixer le principe est la meilleure, avant tout en raison des mesures prises à l’encontre de la poésie. »
Il faut absolument conserver intact le tranchant de cet énoncé extraordinaire. Il nous dit sans détour que ce qui sert de mesure au principe politique est proprement l’exclusion du poème. Ou du moins de ce que Platon nomme la « dimension imitative » du poétique. Le destin de la politique vraie se joue sur la fermeté de l’attitude à l’égard du poème.
Or, qu’est-ce que la politique vraie, la politéia bien fondée ? C’est la philosophie elle-même, pour autant qu’elle assure la prise de la pensée sur l’existence collective, sur le multiple rassemblé des hommes. Disons que la politéia est le collectif venu à sa vérité immanente. Ou encore, le collectif commensurable à la pensée.
Il faut donc, si l’on suit Platon, poser ceci : la cité, qui est le nom de l’humanité dans son rassemblement, n’est pensable que pour autant qu’on en tient le concept à l’abri du poème. Abriter la subjectivité collective du charme puissant du poème est nécessaire pour que la cité s’expose à la pensée. Ou encore : tant qu’elle est « poétisée », la subjectivité collective est aussi soustraite à la pensée, elle lui demeure hétérogène.
L’interprétation usuelle – largement autorisée par le texte de Platon – est que le poème, situé qu’il est à une distance double de l’Idée (imitation seconde de cette imitation première qu’est le sensible), interdit tout accès au principe suprême dont dépend que la vérité du collectif advienne à sa propre transparence. Le protocole de bannissement des poètes dépendrait de la nature imitative de la poésie. Une seule et même chose serait d’interdire le poème et de critiquer la mimésis.
Or, il ne me paraît pas que cette interprétation soit à la mesure de la violence du texte platonicien. Violence dont Platon ne dissimule pas qu’elle est aussi dirigée contre lui-même, contre l’incoercible puissance du poème sur sa propre âme. La raisonnable critique de l’imitation ne légitime pas entièrement qu’il faille arracher de soi les effets d’une telle puissance.
Posons que la mimésis n’est pas le fond du problème. Qu’il soit nécessaire, pour penser la cité, d’interrompre le dire poétique, requiert, comme en amont de la mimésis, un malentendu fondateur.
Il semble qu’il y ait, entre la pensée telle que la philosophie la pense, et le poème, un discord bien plus radical, bien plus ancien, que celui qui concerne les images et l’imitation.
C’est à ce discord ancien et profond que Platon fait, je crois, allusion, quand il écrit :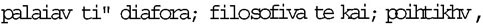 
, « ancien est le discord de la philosophie et du poétique ».
Cette antiquité du discord porte évidemment sur la pensée, sur l’identification de la pensée.
À quoi, dans la pensée, la poésie s’oppose-t-elle ? Elle ne s’oppose pas directement à l’intellect, au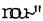 
, à l’intuition des idées. Elle ne s’oppose pas à la dialectique, comme forme suprême de l’intelligible. Platon est très clair sur ce point : ce que la poésie interdit, c’est la pensée discursive, la dianoia. Le poème, dit Platon, est « ruine de la discursivité de ceux qui l’écoutent ». La dianoia, c’est la pensée qui va à travers, la pensée qui enchaîne et déduit. Le poème, lui, est affirmation et délectation, il ne va pas à travers, il se tient sur le seuil. Le poème n’est pas franchissement réglé, mais offrande, proposition sans loi.
Aussi bien Platon dira que le véritable recours contre le poème, c’est « la mesure, le nombre et le poids ». Et que la partie antipoétique de l’âme, c’est « le labeur du logos calculant »,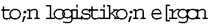 
. Il dira aussi que, dans le poème théâtral, ce qui triomphe est le principe du plaisir et de la douleur, contre la loi et le logos.
La dianoia, la pensée qui enchaîne et traverse, la pensée qui est un logos soumis à une loi, possède un paradigme : c’est la mathématique. On peut donc soutenir que ce à quoi, dans la pensée, le poème s’oppose, c’est proprement à la juridiction sur la pensée elle-même de la rupture mathématique, de la puissance intelligible du mathème.
L’opposition fondatrice est bien finalement celle-ci : la philosophie ne peut commencer, et ne peut se saisir du réel politique, que si elle substitue l’autorité du mathème à celle du poème.
Le motif profond de cette opposition entre mathème et poème est double.
D’une part, c’est le plus évident, le poème reste asservi à l’image, à l’immédiate singularité de l’expérience. Alors que le mathème prend son départ dans l’idée pure, et ne fait ensuite confiance qu’à la déduction. En sorte que le poème entretient avec l’expérience sensible un lien impur, qui expose la langue aux limites de la sensation. De ce point de vue, il est toujours douteux qu’il y ait réellement une pensée du poème, ou que le poème pense.
Mais qu’est-ce pour Platon qu’une pensée douteuse, une pensée indiscernable de la non-pensée ? C’est une sophistique. Il se pourrait que le poème soit en réalité le complice capital de la sophistique.
C’est bien ce qui est suggéré dans le dialogue Protagoras. Car Protagoras s’abrite derrière l’autorité du poète Simonide, et c’est lui qui déclare que, « pour un homme, la partie cruciale de l’éducation est d’être compétent en matière de poésie ».
On pourrait donc poser que ce que la poésie est au sophiste, la mathématique l’est au philosophe. L’opposition du mathème et du poème soutiendrait, dans les disciplines qui conditionnent la philosophie, l’incessant travail de la philosophie pour se disjoindre de son double discursif, de ce qui lui ressemble et, par cette ressemblance, corrompt son acte de pensée : la sophistique. Le poème serait, comme le sophiste, une non-pensée qui se présente dans la puissance langagière d’une pensée possible. Interrompre cette puissance serait l’office du mathème.
Mais, d’autre part, et plus profondément, à supposer même qu’il y ait une pensée du poème, ou que le poème soit une pensée, cette pensée est inséparable du sensible, elle est une pensée qu’on ne peut discerner ou séparer comme pensée. Disons que le poème est une pensée impensable. Alors que la mathématique est une pensée qui s’écrit immédiatement comme pensée, une pensée qui précisément n’existe qu’autant qu’elle est pensable.
On pourrait donc aussi bien poser que pour la philosophie la poésie est une pensée qui n’est pas pensée, ni même pensable. Mais que, précisément, la philosophie n’a pas d’autre enjeu que de penser la pensée, d’identifier la pensée comme pensée de la pensée. Et qu’elle doit donc exclure de son champ toute pensée immédiate, s’appuyant pour ce faire sur les médiations discursives du mathème.
« Que nul n’entre ici s’il n’est géomètre » : Platon fait entrer la mathématique par la grande porte, en tant que procédure explicite de la pensée, ou pensée qui ne peut s’exposer que comme pensée. Dès lors, il faut que la poésie, elle, sorte par l’escalier dérobé. Cette poésie encore omniprésente dans la déclaration de Parménide comme dans les sentences d’Héraclite, mais qui oblitère la fonction philosophique, parce que la pensée s’y accorde le droit de l’inexplicite, de ce qui prend puissance dans la langue d’ailleurs que de la pensée qui s’expose comme telle.
Cependant, cette opposition dans la langue de la transparence du mathème à l’obscurité métaphorique du poème nous pose, à nous modernes, de redoutables problèmes.
Déjà Platon ne peut tenir jusqu’au bout cette maxime, qui promeut le mathème et bannit le poème. Il ne le peut, parce que lui-même explore les limites de la dianoia, de la pensée discursive. Quand il s’agit du principe suprême, de l’Un, ou du Bien, Platon doit convenir que nous sommes là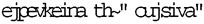 
, « au-delà de la substance », et par conséquent hors de tout ce qui s’expose dans la découpe de l’Idée. Il doit avouer que la donation en pensée de ce principe suprême, qui est la donation en pensée de l’être au-delà de l’étant, ne se laisse traverser par aucune dianoia. Il doit lui-même avoir recours aux images, comme celle du soleil, aux métaphores, comme celles du « prestige » et de la « puissance », au mythe, comme celui d’Er le Pamphylien, qui revient du royaume des morts. Bref : là où ce qui est en jeu est l’ouverture de la pensée au principe du pensable, quand la pensée doit s’absorber dans la saisie de ce qui l’institue comme pensée, voici que Platon lui-même soumet la langue à la puissance du dire poétique.
Mais nous, modernes, endurons de tout autre façon qu’un Grec l’intervalle langagier du poème et du mathème.
D’abord parce que nous avons pris entière mesure, non seulement de tout ce que le poème doit au Nombre, mais de sa vocation proprement intelligible.
Mallarmé est ici exemplaire : l’enjeu du coup de dés poétique est bien que surgisse, « issu stellaire », ce qu’il appelle « l’unique nombre qui ne peut pas être un autre ». Le poème est au régime idéal de la nécessité, il ordonne le désir sensible à l’avènement aléatoire de l’Idée. Le poème est un devoir de la pensée :
Tout en moi s’exaltait de voir
La famille des iridées
Surgir à ce nouveau devoir.
Mais en outre, le poème moderne s’identifie lui-même comme pensée. Il n’est pas seulement l’effectivité d’une pensée livrée dans la chair de la langue, il est l’ensemble des opérations par lesquelles cette pensée se pense. Les grandes figures poétiques, qu’il s’agisse pour Mallarmé de la Constellation, du Tombeau ou du Cygne, ou pour Rimbaud du Christ, de l’Ouvrier ou de l’Époux infernal, ne sont pas des métaphores aveugles. Elles organisent un dispositif consistant, où le poème vient machiner la présentation sensible d’un régime de la pensée : soustraction et isolement pour Mallarmé, présence et interruption pour Rimbaud.
Symétriquement, nous modernes savons que la mathématique, qui pense directement les configurations de l’être-multiple, est traversée d’un principe d’errance et d’excès dont elle ne peut elle-même donner la mesure. Les grands théorèmes de Cantor, de Gödel, de Cohen marquent, dans le siècle, les apories du mathème. Le discord entre l’axiomatique ensembliste et la description catégorielle établit l’ontologie mathématique dans la contrainte d’options de pensée dont aucune prescription purement mathématique ne peut normer le choix.
En même temps que le poème advient à la pensée poétique de la pensée qu’il est, le mathème s’organise autour d’un point de fuite où son réel est en impasse de toute reprise formalisante.
Disons qu’en apparence la modernité idéalise le poème et sophistique le mathème. Par quoi elle renverse le jugement platonicien plus sûrement que Nietzsche ne le désirait du biais de la « transvaluation de toutes les valeurs ».
Il en résulte un déplacement crucial du rapport de la philosophie au poème.
Car ce n’est pas de l’opposition du sensible et de l’intelligible, ou du beau et du bien, ou de l’image et de l’Idée, qu’un tel rapport peut désormais se soutenir. Le poème moderne est d’autant moins la forme sensible de l’Idée que, bien plutôt, c’est le sensible qui se présente comme nostalgie subsistante, et impuissante, de l’idée poétique.
Dans L’Après-midi d’un faune, de Mallarmé, le « personnage » qui monologue se demande s’il existe dans la nature, dans le paysage sensible, une trace possible de son rêve sensuel. Est-ce que l’eau ne porte pas témoignage de la froideur d’une des femmes désirées ? Est-ce que le vent ne se souvient pas des soupirs voluptueux de l’autre ? S’il faut écarter cette hypothèse, c’est que l’eau et le vent ne sont rien au regard de la puissance de suscitation par l’art de l’idée de l’eau, de l’idée du vent :
le matin frais s’il lutte,
Ne murmure point d’eau que ne verse ma flûte
Au bosquet arrosé d’accords ; et le seul vent
Hors des deux tuyaux prompt à s’exhaler avant
Qu’il disperse le son dans une pluie aride,
C’est, à l’horizon pas remué d’une ride,
Le visible et serein souffle artificiel
De l’inspiration, qui regagne le ciel.
Par la visibilité de l’artifice, qui est aussi la pensée de la pensée poétique, le poème surpasse en puissance ce dont le sensible est capable. Le poème moderne est le contraire d’une mimésis. Il exhibe par son opération une Idée dont l’objet et l’objectivité ne sont que de pâles copies.
La philosophie ne peut donc saisir le couple du poème et du mathème dans l’opposition simple de l’image délectable et de l’idée pure. Où donc fait-elle passer la disjonction de ces deux régimes de la pensée dans la langue ? Je dirai que c’est au point où l’une et l’autre de ces pensées trouvent leur innommable.
Posons, en diagonale du bannissement platonicien des poètes, cette équivalence : poème et mathème sont, examinés du point de la philosophie, l’un comme l’autre inscrits dans la forme générale d’une procédure de vérité.
La mathématique fait vérité du multiple pur comme inconsistance primordiale de l’être en tant qu’être.
La poésie fait vérité du multiple comme présence venue aux limites de la langue. Soit le chant de la langue comme aptitude à présentifier la notion pure du « il y a », dans l’effacement même de son objectivité empirique.
Quand Rimbaud énonce poétiquement que l’éternité est « la mer allée/ avec le soleil », ou quand Mallarmé résume toute la transposition dialectique du sensible en Idée par les trois mots « nuit, désespoir et pierrerie », ou « solitude, récif, étoile », ils fondent au creuset de la nomination le référent qui colle aux vocables pour faire exister intemporellement la disparition temporelle du sensible.
En quoi il est toujours vrai qu’un poème est une « alchimie du verbe ». Mais cette alchimie, à la différence de l’autre, est une pensée, la pensée de ce qu’il y a, en tant que « là » désormais suspendu aux puissances d’évidement et de suscitation de la langue.
Du multiple imprésenté et insensible dont la mathématique fait vérité, l’emblème est le vide, l’ensemble vide.
Du multiple donné ou éclos, retenu aux lisières de sa disparition, dont le poème fait vérité, l’emblème est la Terre, cette Terre affirmative et universelle dont Mallarmé déclare :
Oui, je sais qu’au lointain de cette nuit, la Terre
Jette d’un grand éclat l’insolite mystère.
Or toute vérité, qu’elle soit enchaînée au calcul ou extraite du chant de la langue naturelle, est d’abord une puissance. Elle a puissance sur son propre devenir infini. Elle peut en anticiper fragmentairement l’univers inachevable. Elle peut forcer la supposition de ce que serait l’univers si les effets complets d’une vérité en cours s’y déployaient sans limite.
C’est ainsi que, d’un théorème nouveau et puissant, on suppute les conséquences, qui réorientent la pensée, et l’ordonnent à de tout nouveaux exercices.
Mais c’est ainsi que, d’une poétique fondatrice, se tirent de nouvelles méthodes de la pensée poétique, une nouvelle prospection des ressources de la langue, et non pas seulement la délectation d’un éclat de présence.
Ce n’est pas pour rien que Rimbaud s’exclame : « Nous t’affirmons, méthode ! » ou qu’il se déclare « pressé de trouver le lieu et la formule ». Ou que Mallarmé se propose d’installer le poème comme une science :
Car j’installe, par la science,
L’hymne des cœurs spirituels
En l’œuvre de ma patience
Atlas, herbiers et rituels.
En même temps qu’il est, comme pensée de la présence sur fond de disparition, une action immédiate, le poème, comme toute figure locale d’une vérité, est aussi un programme de pensée, une anticipation puissante, un forçage de la langue par avènement d’une « autre » langue à la fois immanente et créée.
Mais en même temps qu’elle est une puissance, toute vérité est une impuissance. Car ce sur quoi elle a juridiction ne saurait être une totalité.
Que vérité et totalité soient incompatibles est sans doute l’enseignement décisif – ou posthégélien – de la modernité.
Jacques Lacan l’exprime par son aphorisme fameux : la vérité ne peut se dire « toute », elle ne peut que se mi-dire. Mais déjà Mallarmé critiquait les Parnassiens, lesquels, disait-il, « prennent la chose entièrement et la montrent ». Par là, ajoutait-il, « ils manquent le mystère ».
De quoi que ce soit qu’une vérité soit vérité, on ne saurait prétendre qu’elle l’investit « entièrement », ou en soit la monstration intégrale. La puissance de révélation du poème s’enroule autour d’une énigme, en sorte que le pointage de cette énigme fasse tout le réel d’impuissance de la puissance du vrai. En ce sens, le « mystère dans les lettres » est un véritable impératif. Quand Mallarmé soutient qu’« il doit y avoir toujours énigme en poésie », il fonde une éthique du mystère qui est le respect, par la puissance d’une vérité, de son point d’impuissance.
Le mystère est proprement que toute vérité poétique laisse en son centre ce qu’elle n’a pas le pouvoir de faire venir à la présence.
Plus généralement, une vérité rencontre toujours, en un point de ce qu’elle investit, la limite où se prouve qu’elle est cette vérité singulière, et non la conscience de soi du Tout.
Que toute vérité, quoiqu’elle procède à l’infini, soit également toujours une procédure singulière, s’atteste dans le réel par un point au moins d’impuissance, ou, comme dit Mallarmé, « un roc, faux manoir tout de suite évaporé en brumes qui imposa une borne à l’infini ».
Une vérité bute sur le roc de sa propre singularité, et c’est là seulement que s’énonce, comme impuissance, qu’une vérité existe.
Appelons cette butée l’innommable. L’innommable est ce dont une vérité ne peut forcer la nomination. Ce dont elle ne peut anticiper la mise en vérité.
Tout régime de la vérité se fonde en réel sur son innommable propre.
Si nous revenons alors sur l’opposition platonicienne du poème et du mathème, demandons-nous ceci : qu’est-ce qui différencie « en réel », et donc quant à leur innommable propre, les vérités mathématiques et les vérités poétiques ?
Ce qui caractérise la langue mathématique est la fidélité déductive. Entendons par là la capacité à enchaîner des énoncés de telle sorte que cet enchaînement soit contraint, et que l’ensemble des énoncés obtenus soutienne victorieusement l’épreuve de la consistance. L’effet de contrainte relève du codage logique sous-jacent à l’ontologie mathématique. L’effet de consistance est central. Qu’est-ce en effet qu’une théorie consistante ? C’est une théorie telle qu’il existe des énoncés qui sont impossibles dans la théorie. Une théorie est consistante s’il existe au moins un énoncé « correct » du langage de cette théorie qui est ininscriptible dans la théorie, ou que la théorie n’admet pas comme véridique.
De ce point de vue, la consistance atteste la théorie comme pensée singulière. Car si n’importe quel énoncé était admissible dans la théorie, cela voudrait dire qu’il n’y a aucune différence entre « énoncé grammaticalement correct » et « énoncé théoriquement véridique ». La théorie ne serait alors qu’une grammaire, et ne penserait rien.
Le principe de consistance est ce qui assigne la mathématique à une situation d’être de la pensée, ce qui fait qu’elle n’est pas un simple ensemble de règles.
Mais nous savons, depuis Gödel, que la consistance est précisément le point d’innommable de la mathématique. Il n’est pas possible, pour une théorie mathématique, d’établir comme véridique l’énoncé de sa propre consistance.
Si nous nous tournons maintenant vers la poésie, nous voyons que ce qui en caractérise l’effet est la monstration des puissances de la langue elle-même. Tout poème fait venir dans la langue un pouvoir, le pouvoir de fixer éternellement la disparition de ce qui se présente. Ou de produire la présence elle-même comme Idée par la retenue poétique de son disparaître.
Cependant, ce pouvoir de la langue est précisément ce que le poème ne peut nommer. Il l’effectue, en puisant dans le chant latent de la langue, dans l’infini de sa ressource, dans la nouveauté de son assemblage. Mais, précisément parce que c’est à l’infini de la langue que le poème s’adresse pour en orienter le pouvoir vers la retenue d’une disparition, il ne peut fixer cet infini même.
Disons que la langue comme puissance infinie ordonnée à la présence est précisément l’innommable de la poésie.
L’infini langagier est l’impuissance immanente à l’effet de puissance du poème.
Ce point d’impuissance, ou d’innommable, est représenté par Mallarmé de deux façons au moins.
Tout d’abord, par ceci que l’effet du poème suppose une garantie qu’il ne constitue pas, ni ne peut valider poétiquement. Cette garantie est la langue saisie comme ordre, ou syntaxe : « Quel pivot, j’entends, dans ces contrastes, à l’intelligibilité ? Il faut une garantie – La syntaxe. » La syntaxe est, dans le poème, le pouvoir latent où le contraste de la présence et de la disparition (l’être comme néant) peut se présenter à l’intelligible. Mais la syntaxe n’est pas poétisable, si loin que je pousse sa distorsion. Elle opère sans se présenter.
Ensuite, Mallarmé indique clairement qu’il ne saurait y avoir de poème du poème, de métapoème. C’est tout le sens du fameux « ptyx », ce nom qui ne nomme rien, qui est « aboli bibelot d’inanité sonore ». Sans doute le ptyx serait-il le nom de ce dont le poème est capable : faire surgir de la langue une venue en présence antérieurement impossible. Sauf que, justement, ce nom n’est pas un nom, ce nom ne nomme pas. En sorte que le poète (le Maître de la langue) emporte avec lui ce faux nom dans la mort :
Car le Maître est allé puiser des pleurs au Styx
Avec ce seul objet dont le Néant s’honore.
Le poème lui-même, en tant qu’il effectue localement l’infini de la langue, reste, pour le poème, innommable. La puissance de la langue, le poème, qui n’a pas d’autre office que de la manifester, est impuissant à la nommer véridiquement.
C’est aussi bien ce que Rimbaud veut dire quand il taxe son entreprise poétique de « folie ». Certes, le poème « note l’inexprimable », ou « fixe des vertiges ». Mais la folie est de croire qu’il peut aussi ressaisir et nommer la ressource profonde et générale de ces notations, de ces fixations. Pensée active qui ne peut nommer sa propre puissance, le poème reste pour toujours infondé. Ce qui, aux yeux de Rimbaud, l’apparente au sophisme : « J’expliquai mes sophismes magiques avec l’hallucination des mots. »
Dès le début de son œuvre, Rimbaud remarquait du reste qu’il y a dans le poème, conçu subjectivement, une irresponsabilité. Le poème est comme un pouvoir qui traverse la langue involontairement : « tant pis pour le bois qui se trouve violon », ou « si le cuivre s’éveille clairon, il n’y a rien de sa faute ».
Au fond, pour Rimbaud, la pensée poétique a pour innommable cette pensée elle-même dans son éclosion, dans sa venue. Ce qui est bien aussi la venue de l’infini de la langue comme chant, ou symphonie qui ensorcelle la présence : « j’assiste à l’éclosion de ma pensée : je la regarde, je l’écoute ; je lance un coup d’archet : la symphonie fait son remuement dans les profondeurs, ou vient d’un bond sur la scène ».
Disons que l’innommable propre du mathème est la consistance de la langue, cependant que l’innommable propre du poème est sa puissance.
Aussi bien, la philosophie va se placer sous la double condition du poème et du mathème, tant du côté de leur puissance de véridicité que du côté de leur impuissance, de leur innommable.
La philosophie est théorie générale de l’être et de l’événement, tels que noués par la vérité. Car une vérité est le travail auprès de l’être d’un événement évanoui dont il ne reste que le nom.
La philosophie reconnaîtra que toute nomination d’un événement, convoquant la retenue de ce qui disparaît, toute nomination de la présence événementielle, est d’essence poétique.
Elle reconnaîtra aussi que toute fidélité à l’événement, tout travail auprès de l’être guidé par une prescription que rien ne fonde, doit avoir une rigueur dont le paradigme est mathématique, se soumettre à la discipline d’une contrainte continue.
Mais elle retiendra, de ce que la consistance est l’innommable du mathème, l’impossibilité d’une fondation réflexive intégrale, et que tout système comporte un point d’entame, une soustraction aux pouvoirs du vrai. Un point proprement inforçable par la puissance d’une vérité, quelle qu’elle soit.
Et de ce que la puissance infinie de la langue est l’innommable du poème, elle retiendra que, si forte puisse être une interprétation, le sens qu’elle atteint ne rend jamais raison de la capacité au sens. Ou encore, que jamais une vérité ne peut délivrer le sens du sens.
Platon bannissait le poème parce qu’il soupçonnait que la pensée poétique ne peut être pensée de la pensée. Nous accueillerons quant à nous le poème, parce qu’il nous évite de supposer qu’on puisse remplacer la singularité d’une pensée par la pensée de cette pensée.
Entre la consistance du mathème et la puissance du poème, ces deux innommables, la philosophie renonce à établir les noms qui obturent ce qui se soustrait. Elle est en ce sens, après le poème, après le mathème, et sous leur condition pensante, la pensée toujours lacunaire du multiple des pensées.
Elle ne l’est toutefois qu’en se gardant de juger le poème et, singulièrement, de vouloir, fût-ce par des exemples empruntés à tel ou tel poète, lui administrer des leçons politiques. Ce qui veut le plus souvent dire, et c’est bien en ce sens que Platon comprenait la leçon philosophique donnée au poème : exiger la dissipation de son mystère, fixer d’avance des limites à la puissance de la langue. Ce qui revient à forcer l’innommable, à « platoniser » contre le poème moderne. Et il arrive même à de grands poètes de platoniser en ce sens. Je vais en donner un exemple.