3
Structural Attributes of Turbulent Flow over a Complex Topography
ABSTRACT
The structural attributes of turbulent flow over a complex roughness topography are explored with stereo particle-image velocimetry (PIV) measurements in a streamwise–spanwise plane deep within the roughness sublayer (within approximately five characteristic roughness heights of the surface) and in a wall-normal–spanwise measurement plane. The roughness under consideration was replicated from a turbine blade damaged by deposition of foreign materials and contains a broad range of topographical scales arranged in a highly irregular manner. This roughness was reproduced over a long streamwise fetch in a boundary layer wind tunnel and the measurements were performed at a momentum thickness Reynolds number ∼14 000. Instantaneous velocity fields in each measurement plane revealed structural attributes qualitatively consistent with smooth-wall flow structure, particularly patterns consistent with the existence of large-scale motions termed hairpin vortex packets. However, single-point turbulence statistics revealed significant statistical heterogeneity in the form of well-defined low-and high-momentum flow pathways marked by enhanced Reynolds stresses and turbulent kinetic energy. The low-momentum flow pathways were also marked by intense vortical activity along their spanwise boundaries, indicating that these pathways could represent preferential ‘channelling’ of large-scale motions due to the roughness below or the generation of ‘trains’ of vortical structures shed from the roughness that advect along a common path downstream. In addition, some of these flow pathways were found to extend well into the outer layer of the flow. The occurrence of such statistical heterogeneities due to roughness could have a profound effect on how one models these complex flows, as any turbulence model must capture such effects in order to properly predict both the bulk and local flow behaviour.
3.1 Introduction
The spatial characteristics of large-scale motions in wall turbulence have been the subject of intense study, particularly with recent evidence suggesting that these scales modulate the smaller-scale motions in the near-wall region (Mathis et al., 2009). The streamwise–wall-normal (x–y) plane two-dimensional particle-image velocimetry (PIV) measurements of Adrian et al. (2000b) provided a direct visualization of the coherent ordering of hairpin-like structures into larger scale structural entities termed hairpin vortex packets. In particular, the streamwise alignment of individual hairpin-like structures into larger scale packets observed by Adrian et al. (2000b) across the boundary layer in a hierarchy of scales is marked by an inclined interface formed by the spanwise-oriented heads of each structure beneath which a region of streamwise momentum deficit is apparent due to the collectively induced ejection events generated by each of the vortices in a packet. Thus, these large-scale packets induce low-momentum regions (LMRs) previously identified in streamwise–spanwise (x–z) plane PIV measurements that are bounded by wall-normal vortex cores likely associated with the legs/necks of the individual vortices of hairpin packets (Ganapathisubramani et al., 2003; Tomkins and Adrian, 2003; Wu and Christensen, 2010) and within which intense ejections of low-speed fluid are generated (Ganapathisubramani et al., 2003; Wu and Christensen, 2010). Instantaneous PIV fields in the x–z plane within the log layer also reveal the existence of high-momentum regions (HMRs) adjacent to LMRs within which strong sweep events are observed. This spanwise-alternating behaviour of LMRs and HMRs is consistent with the spanwise-alternating sign of the two-point correlation of streamwise velocity in the x–z plane (Ganapathisubramani et al., 2005; Wu and Christensen, 2010). More recently, hot-wire measurements indicate that the LMRs observed in δ-scale PIV studies (where δ is the boundary-layer thickness) can actually extend several δ in the streamwise direction (Hutchins and Marusic, 2007a). These ‘superstructures’ can meander significantly in the spanwise direction (Hutchins and Marusic, 2007a) and can embody a significant fraction of the turbulent kinetic energy and Reynolds shear stress (Kim and Adrian, 1999). It is these motions that appear to amplitude modulate the smaller scales in the near-wall region of the flow (Mathis et al., 2009). Leveraging these amplitude-modulation observations, Marusic et al. (2010) and Mathis et al. (2011) proposed a predictive inner−outer model for the streamwise turbulence statistics in smooth-wall turbulence at high Reynolds numbers (Re).
While providing significant information about the structural characteristics of the flow, measurements at fixed wall-normal locations (i.e. fixed x–z PIV planes) unfortunately do not provide details as to the wall-normal dependence of the dominant spanwise scales of motion. Measurements in the wall-normal–spanwise (y–z) plane overcome such limitations; however, PIV measurements in this cross-stream plane are extremely challenging, as the bulk flow direction is normal to the laser sheet. Nevertheless, a few studies have successfully employed PIV to study wall turbulence in the cross-stream plane (Carlier and Stanislas, 2005; Ganapathisubramani et al., 2005; Hutchins et al., 2005). In particular, Hutchins et al. (2005) and Ganapathisubramani et al. (2005) used stereo PIV in cross-stream planes inclined at 45o and 135o to the streamwise direction in a replication of the original flow-visualization imaging planes of Head and Bandyopadhyay (1981). These measurements revealed inclined vortical structures bounding LMRs that are consistent with the hairpin vortex packet model of wall turbulence. Spanwise-adjacent HMRs were also observed in the instantaneous fields, with both LMR and HMR events extending well into the outer layer of the flow. Analysis of spatial correlations of velocity in these inclined cross-stream planes also uncovered imprints consistent with hairpin vortex packets. Hutchins and Marusic (2007b) used channel-flow DNS fields to compute the conditionally averaged velocity field associated with an LMR in the wall-normal–spanwise plane at low Re. This field was characterized by an LMR bounded on either spanwise side by an HMR, between which streamwise vortices resided. Similar conditional average results for the large scales were reported by Chung and McKeon (2010) from large-eddy simulations (LES) of turbulent channel flow at friction Re of 2,000 and 200,000.
The impact of roughness on this structural skeleton of smooth-wall flow is not yet fully understood. While some efforts indicate that roughness alters the structural and/or statistical attributes of the flow throughout the entire boundary layer (Krogstad and Antonia, 1994; Tachie et al., 2000, 2003; Keirsbulck et al., 2002), other studies (Ligrani and Moffat, 1986; Raupach et al., 1991; Volino et al., 2007; Wu and Christensen, 2007, 2010; Mejia-Alvarez and Christensen, 2010) indicate that the effect of roughness is confined within the immediate vicinity of the roughness – the so-called roughness sublayer (∼3–5k, where k is a measure of the characteristic roughness height). This latter notion is consistent with Townsend's wall similarity hypothesis (Townsend, 1976), extended to rough-wall turbulence by Raupach et al. (1991), which states that at high Re, surface conditions set the wall shear stress and the boundary-layer thickness, δ, while the turbulence outside the roughness sublayer adjusts itself to these conditions in an universal manner. A necessary condition for this similarity to exist is a broad-scale separation between k and the outer length scale of the flow (typically taken as δ). Previous efforts indicate δ/k must exceed 40–50 for this similarity to exist (Jimenez, 2004; Flack et al., 2005). The geometrical details of the roughness can also play a critical role as to the existence of outer-layer similarity, with flow over three-dimensional (3D) roughness topographies often displaying such similarity in contrast to flow over two-dimensional (2D) topographies wherein the large spanwise extent of the roughness generates large-scale flow structures that grow well into the outer layer (Krogstad and Antonia, 1999; Lee and Sung, 2007; Volino et al., 2009).
From a structural viewpoint, the PIV measurements of Nakagawa and Hanratty (2001) in the streamwise–wall-normal (x–y) plane of turbulent channel flow with a wavy bottom wall revealed the spatial coherence of this flow to be quite similar to that of smooth-wall flow in the outer region. This observation is interesting given that the wavy wall under consideration was 2-D in nature. Volino et al. (2007) observed the spatial signatures of hairpin vortex packets in instantaneous PIV velocity fields in x–y and x–z measurement planes for a turbulent boundary layer (TBL) over woven wire mesh (3-D roughness). Two-point correlations indicated a slight reduction in the streamwise spatial coherence close to the wall, compared to smooth-wall flow, that quickly diminished with increasing wall-normal position. Finally, Wu and Christensen (2007) reported outer-layer similarity for flow over highly irregular roughness replicated from a turbine blade damaged by deposition of foreign materials based on PIV measurements in the x–y plane. In a follow-up effort, Wu and Christensen (2010) reported that this irregular roughness altered the characteristic streamwise and, to a lesser extent, the spanwise length scales of the flow based on stereo PIV measurements in a streamwise–spanwise plane near the outer edge of the roughness sublayer (y ≈ 0.2δ relative to the mean elevation of the roughness). Nevertheless, the rough-wall flow was still found to embody many of the structural attributes of hairpin vortex packets, including elongated LMRs bounded by wall-normal vortex cores interpreted as slices through the legs/necks of hairpin vortices.
The intent of the present contribution is to further explore the structural attributes of a TBL in the presence of the highly irregular roughness topography employed in our previous efforts (Wu and Christensen, 2007, 2010; Mejia-Alvarez and Christensen, 2010). However, in contrast to these initial PIV measurements in the streamwise–wall-normal plane and a streamwise–spanwise plane at the outer edge of the roughness sublayer, the stereo PIV measurements reported herein were conducted deep within the roughness sublayer of a TBL (y ≈ 0.1δ, relative to the mean elevation of the roughness) to interrogate the ‘local’ impact of the topography on the flow, particularly its structural attributes and spatial coherence. In addition, stereo PIV experiments were conducted in the wall-normal–spanwise plane to provide a simultaneous assessment of the spanwise spatial characteristics of the flow, as well as their coherence in the wall-normal direction.
3.2 Experiments
The TBL experiments were conducted in an open-circuit Eiffel-type, boundary-layer wind tunnel. The test section of the tunnel is 6 m long, 45.7 cm tall and 91.4 cm wide, and all boundary layers were formed on a smooth boundary-layer plate suspended above the bottom wall of the tunnel. This plate consists of two 3 m long and 91.4 cm wide smooth-wall sections smoothly joined at the streamwise centre. Zero pressure gradient conditions were achieved via an adjustable ceiling in the test section. Measurements were performed for both smooth and rough surface conditions. Table 3.1 summarizes the relevant experimental parameters for these measurements. For reference, the boundary-layer thickness δ was taken as the wall-normal location where the mean streamwise velocity U was 99% of the free-stream velocity Ue.
Table 3.1 Relevant experimental parameters.
The rough surface used was the same as that originally fabricated and studied by Wu and Christensen (2007, 2010). This surface is a scaled version of a profilometric surface scan of a turbine blade damaged by deposition of foreign materials, which was first reported by Bons et al. (2001). Figure 3.1a presents a topographical map of the rough surface, which is marked by a broad range of topographical scales arranged in an irregular manner. The average peak-to-valley roughness height of this surface is k = 4.25 mm while the root-mean square (RMS) roughness height krms is 1.0 mm. As described in Wu and Christensen (2010), a 3 m long replica of this topography was achieved by mirroring it in both the streamwise and spanwise directions and fabricated with a powder-deposition printer. This roughness was mounted on cast aluminium plates and placed along the downstream half of the boundary-layer plate by adjusting its height above the bottom wall of the tunnel such that the mean elevation of the roughness was coincident with the upstream smooth-wall conditions. Thus, the boundary layers under study were allowed to develop initially over the first 3 m of the smooth boundary-layer plate followed by an additional 3 m of development over the roughness. In all cases the flow was tripped with a cylindrical rod near the upstream end of the boundary-layer plate and all measurements were conducted approximately 2.3 m downstream of the leading edge of the roughness. Wu and Christensen (2007) previously reported this rough-wall flow to have achieved self-similar conditions at this measurement location. Figure 3.1c presents a zoomed-in photograph of a portion of the roughness replica in the wind tunnel. This highlights the complex, multiscale nature of the topography that, despite being replicated from a damaged turbine blade, is qualitatively reminiscent of landscape encountered in nature, including, for example, gravel river beds (Hardy et al., 2009) as well as dune (Endo et al., 2004) and drumlin fields (Shaw, 1994). As in the present experiments, the features of these natural topographies typically protrude into the outer (logarithmic) region of the flow but are an order of magnitude smaller than the characteristic flow depth (δ).
Figure 3.1 (a) Topographical map of roughness. Bounding box demarcates field of view of the streamwise-spanwise plane stereo PIV measurements at y = 0.1δ. Dashed line demarcates the streamwise location of the wall-normal–spanwise stereo PIV measurement plane. (b) Illustration highlighting views from the two PIV measurement planes relative to the flow direction and roughness. (c) Photo of the replicated roughness in the wind tunnel from a view that the oncoming flow would encounter.
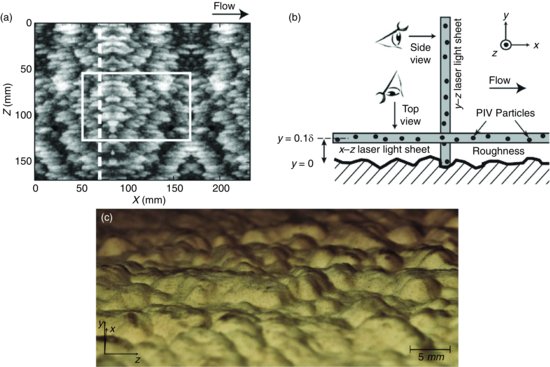
Stereo PIV was used to measure all three velocity components in a streamwise–spanwise (x–z; wall-parallel) plane of the flow followed by similar measurements in the wall-normal–spanwise (y–z; cross-stream) plane. The bounding box in Figure 3.1a highlights the field of view for the wall-parallel measurements while the dashed line demarcates the streamwise position of the cross-stream measurements. The wall-parallel plane measurements were conducted at y = 0.1δ where the wall-normal origin is taken as the mean elevation of the roughness. The PIV system employed in both cases consisted of two 4000 × 2750 pixel, 12-bit, frame-straddle CCD cameras (TSI 11MP) and a 190 mJ/pulse dual-cavity pulsed Nd:YAG laser (Quantel). A 1.0 mm thick laser lightsheet was formed by three cylindrical lenses and directed into the wind-tunnel test section via a glass side wall in the x–z and y–z planes for the wall-parallel and cross-stream measurements, respectively. Figure 3.2 presents a schematic of the stereo PIV arrangement for each measurement plane. The cameras viewed the x–z-oriented lightsheet at angles of ±13o from the wall-normal (y) direction through a transparent section in the wind-tunnel ceiling and the y–z oriented lightsheet from upstream through optical-grade glass side-walls of the wind tunnel at angles of ±45o from the streamwise (x) direction. In both measurement planes the angle between each lens and camera CCD array was adjusted to satisfy the Scheimpflug condition which ensured uniform focus across the field of view. The flow was seeded with 1 μm olive-oil droplets generated by a Laskin nozzle. Timing of the cameras, lasers and image acquisition was controlled with a timing unit with 1 ns resolution.
Figure 3.2 Schematics of experimental arrangements in the (a) streamwise–spanwise (x–z) measurement plane at y = 0.1δ and the (b) wall-normal–spanwise (y–z) measurement plane.
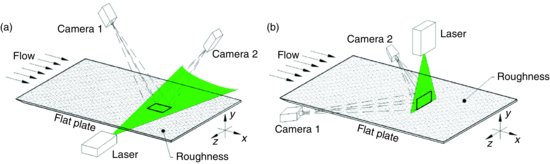
Accurate stereo PIV measurements required careful calibration of the imaging system to map properly the image coordinate system to the object plane defined by the laser lightsheet. In the case of the wall-parallel measurements, a dual-plane (1 mm separation) target containing white dots spaced at in-plane intervals of 10 mm over a 20 cm × 20 cm area was employed. The use of this dual-plane target alleviated the need to physically translate the target in the depth direction through the lightsheet thickness. Instead, the target was carefully aligned in the field of view so that its mid-plane coincided with the laser lightsheet. A single-plane target consisting of dots spaced at 2 mm in both the horizontal and vertical directions was utilized in the cross-stream experiments because the physical dimensions of the dual-plane target were insufficient to cover the entire field of view. The front face of this target was carefully aligned with the centre of the lightsheet. Images of this target were acquired by both cameras at this position as well as with the target translated ±500 μm upstream and downstream of lightsheet centre. The resulting calibration images for each measurement plane were used to generate calibration mapping functions to map the two, 2-D image planes to the 3-D space defined by the laser lightsheet using the least-squares method of Soloff et al. (1997). Thus, the out-of-plane fluid motion was discerned from the distinct views of the tracer-particle motion within the laser lightsheet as imaged by the two cameras for each of the stereo PIV experiments.
Two-thousand five-hundred statistically-independent planar, three-component velocity fields were acquired in the wall-parallel and cross-stream measurement planes (note that the two measurements were not conducted in a simultaneous manner). As mentioned above, each three-component velocity field was derived from two, 2-D displacement fields generated from the time-delayed pairs of images acquired by each camera. These pairs of time-delayed images were interrogated using a recursive, two-frame cross-correlation methodology. The first-pass interrogation was performed with a bulk window offset to minimize loss of particle pairs, while the final-pass interrogation was performed with square interrogation spots of size 162 pixels with 50% overlap to satisfy the Nyquist sampling criterion, and the second window was locally offset by an integer pixel displacement determined during the first-pass interrogation. Statistical validation tools were employed between passes to identify and replace erroneous vectors as well as after the final interrogation pass was completed, including Rohaly et al. (2002) replacement with displacements assessed from alternate correlation peaks identified during the interrogation process. All fields were then low-pass filtered with a narrow Gaussian filter to remove high-frequency noise. Each pair of 2-D displacement fields was then recombined using the aforementioned mapping function to reconcile all three instantaneous velocity components on the measurement plane defined by the laser lightsheet.
3.3 Results
3.3.1 Instantaneous velocity fields
Figure 3.3a presents a representative instantaneous fluctuating velocity field in the wall-parallel (x–z) plane at y = 0.1δ for flow over the roughness presented in Figure 3.1a. The in-plane streamwise (u′) and spanwise (w′) velocity fluctuations are shown as vectors while the out-of-plane wall-normal (v′) velocity fluctuations are presented as background contours with the streamwise mean flow from left to right. In addition, it should be noted that the spanwise origin, z = 0, is taken at centre span of the wind tunnel while, as mentioned previously, the wall-normal origin, y = 0, represents the mean elevation of the roughness for all results presented herein (regardless of measurement plane). This instantaneous velocity field is marked by regions of low and high streamwise momentum (LMRs and HMRs, respectively) that are elongated in the streamwise direction and alternate in the spanwise direction. These large-scale motions are consistent with δ-scale LMRs and HMRs previously identified in wall-parallel PIV measurements of smooth-wall turbulence (Ganapathisubramani et al., 2003; Tomkins and Adrian, 2003) and more recently linked to superstructures that can extend several δ in the streamwise direction and meander in the span (Hutchins and Marusic, 2007a). Within these large-scale regions of streamwise momentum deficit (u′ < 0; LMRs) and surplus (u′ > 0; HMRs) exist the most intense v′ events (typically v′ > 0 in LMRs and v′ < 0 in HMRs). As such, these large-scale motions embody a significant fraction of the intense Reynolds-shear-stress (RSS)producing events (u′v′). Inspection of the spanwise boundaries of the LMRs reveals that the upper boundary is often populated by clockwise-rotating vortex cores (ωy < 0, where ωy is the wall-normal component of vorticity) while the lower boundary is populated by counter clockwise-rotating vortex cores (ωy > 0). Taken together, these spatial characteristics are reminiscent of the overall structural characteristics of hairpin vortex packets that populate smooth-wall turbulence. In particular, the streamwise–elongated LMR is consistent with the momentum deficit generated by the collective induction of hairpin-like vortices in such packets. Further, the counter-rotating wall-normal vortex cores residing along the spanwise boundaries of the LMR are consistent with slices through the legs/necks of the individual, streamwise–aligned hairpin-like vortices in the packet. Therefore, despite the presence of a rough boundary, the overall structure in this log-layer, wall-parallel measurement plane is quite consistent with the overall structural attributes of smooth-wall turbulence (Ganipathisubramani et al., 2003; Tomkins and Adrian, 2003, Wu and Christensen, 2010).
Figure 3.3 Representative instantaneous fluctuating velocity fields in the (a) streamwise–spanwise (x–z) plane at y = 0.1δ and the (b) wall-normal–spanwise (y–z) plane for flow over the roughness. Background contours in (a) and (b) represent fluctuating components of wall-normal (v′) and streamwise (u′) velocity, respectively. Note that these fields were not acquired simultaneously, so they are entirely uncorrelated.
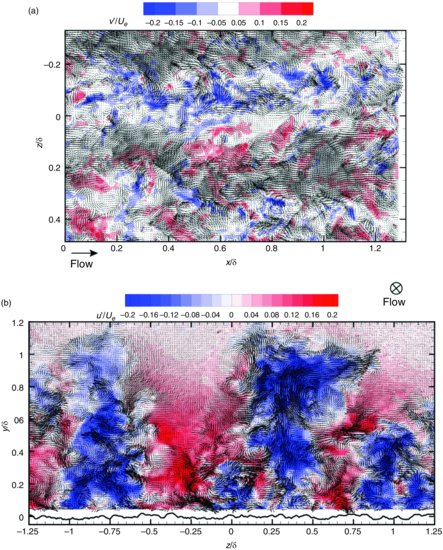
Figure 3.3b presents a representative fluctuating velocity field in the cross-stream (y–z) measurement plane with the in-plane wall-normal (v′) and spanwise (w′) velocity fluctuations shown as vectors and the out-of-plane streamwise velocity fluctuations (u′) presented as background contours. Note that the positive streamwise (x) direction, and hence the mean streamwise flow, is into Figure 3.3b. Furthermore, this realization is entirely uncorrelated with the x–z field shown in Figure 3.3a. The streamwise velocity fluctuations are marked by large-scale (δ-scale) regions of low and high streamwise momentum that appear to alternate in the spanwise direction with a spacing of ∼0.5δ. These patterns are interpreted as the cross-plane signatures of the LMRs and HMRs evident in the wall-parallel measurement plane in Figure 3.3a and can often extent to the edge of the boundary layer. Focusing upon the large-scale LMR near z = 0.25δ in Figure 3.3b, its left boundary is populated by counter-clockwise-rotating vortex cores (ωx<0, where ωx is the streamwise component of vorticity) while its right boundary is populated by vortex cores with clockwise rotation (ωx > 0). Furthermore, as with the instantaneous LMR identified in the wall-parallel PIV result in Figure 3.3a, rather intense, positive wall-normal velocity fluctuations (v′) are observed within this LMR, resulting in a large-scale region of low-speed fluid ejected away from the wall, which contributes heavily to the mean RSS. This LMR is flanked on its spanwise boundaries by HMRs within which intense, negative v′ create a large-scale sweep of high-speed fluid towards the wall, which also contributes heavily to the mean RSS. Apart from these δ-scale events, smaller LMRs and HMRs are visualized in the near-wall region that are often bounded by streamwise vortex cores. These smaller scale regions appear to coexist beneath the larger scale LMRs and HMRs, supporting the contention that such structures occur in a hierarchy of scales across the flow. As proposed by Adrian et al. (2000b) for smooth-wall turbulence, packets of varying size would be expected throughout the wall-normal extent of the flow, with smaller, younger, slower packets residing closer to the wall where they are likely formed and successively larger, older packets populating the outer region of the flow while maintaining a near-wall footprint. Thus, despite the presence of a rough boundary, the overall structural attributes of the flow are quite consistent, at least qualitatively, with those of smooth-wall turbulence. This observation is in accordance with Townsend's wall similarity hypothesis (Townsend, 1976) whereby the wall sets the wall shear stress and the boundary-layer thickness and the turbulence in the outer region simply adjusts itself to these constraints in a universal manner.
3.3.2 Single-point statistics
Figure 3.4 presents ensemble-averaged, single-point statistics in the x–z measurement plane at y = 0.1δ. These statistics were computed by averaging over the ensemble of 2500 statistically independent velocity realizations acquired in this measurement plane. No spatial averaging was performed in order to retain the streamwise and spanwise dependence of these statistics. The mean, outer scaled streamwise velocity (U/Ue; Figure 3.4a) shows strong heterogeneity in the form of a spanwise-localized low-momentum pathway (LMP; demarcated by a horizontal dashed line) near z = 0.15δ bounded in the spanwise direction by high-momentum pathways (HMP). These heterogeneities are quite distinct from the character of smooth-wall turbulence, which reflects the expected uniform (homogeneous) U in this plane at fixed wall-normal position (not shown for brevity). This result suggests that the roughness under consideration induces a ‘channelling’ effect in the flow or the possible existence of persistent wakes generated by dominant roughness features in the case of the LMP. These low-and high-momentum pathways are distinct from the LMRs and HMRs identified in the instantaneous realizations of Figure 3.3 (and in the studies of smooth-wall turbulence mentioned above) because they appear in the ensemble-averaged field of the streamwise velocity. In particular, the LMPs and HMPs can be interpreted as preferential pathways for these low-and high-momentum motions in contrast to the instantaneous LMRs and HMRs that, in the case of smooth-wall flow, occur randomly in space and have clear spatial coherence. Thus, the roughness under consideration appears to generate large-scale heterogeneity in the mean streamwise velocity in the form of preferred spatial pathways for low-and high-momentum events. While preferential flow paths have been observed, and are likely expected, in the near-wall region of flow over periodic surface features (Hong et al., 2011, for example), this flow channelling phenomenon persists despite the complex nature of the present surface topography (Figure 3.1c).
Figure 3.4 Ensemble-averaged, single-point statistics in the streamwise–spanwise (x−z) plane at y = 0.1δ. (a) Mean streamwise velocity, U/Ue; (b) Reynolds shear stress, –〈u′v′〉/Ue2; (c) Turbulent kinetic energy, TKE/Ue2; (d) Ensemble-averaged signed swirling strength,〈
ci〉(δ/Ue). Solid and dashed lines in (d) represent positive and negative contour levels, respectively. ‘LMP’ and dashed horizontal line denotes the spanwise position of the persistent low-momentum pathway identified in (a).
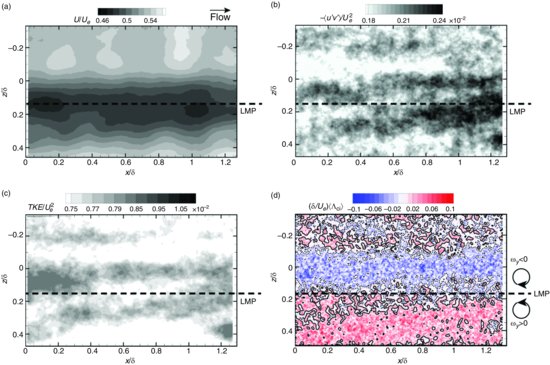
Figures 3.4b and 3.4c present contour plots of outer scaled mean RSS (–〈u′v′〉/Ue2) and turbulent kinetic energy (TKE; 1/2(u′2+v′2+w′2)/Ue2) in the x–z plane at y = 0.1δ. Both of these single-point turbulence statistics display significant heterogeneity in the form of streamwise–elongated regions of enhanced RSS and TKE that are coincident with the spanwise boundaries of the LMP identified in the mean streamwise velocity (Figure 3.4a). Similar elongated regions of enhanced behaviour are also notable in the other RSS components (〈u′w′〉 and〈v′w′〉 which are quite weak in smooth-wall flow; not shown for brevity) spatially coincident with the spanwise boundaries of the identified LMP. Since the Reynolds shear stresses play a defining role in the production of TKE from the mean flow, these results suggest that the roughness under consideration may promote generation of TKE in preferential regions within the roughness sublayer.
Finally, Figure 3.4d presents contours of outer-scaled, ensemble-averaged signed swirling strength, 〈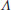ci〉(δ/Ue). Here, 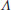ci ≡ λciωy/|ωy| where λci is the imaginary portion of the complex-conjugate eigenvalue pair of the local velocity gradient tensor, which has previously been shown to be an effective vortex marker (Adrian et al., 2000a). In particular, λci is frame independent and does not incorrectly identify regions of local shear as vortices (as vorticity can in wall-bounded flows). Thus, λci ≠ 0 indicates the presence of local vortical motion and is marked with the sign of the in-plane wall-normal vorticity (ωy) to retain the sense of the rotation within 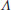ci. Interestingly, 〈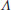ci〉 in Figure 3.4d is quite heterogeneous in space, with a streamwise–elongated region of 〈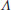ci〉< 0 spatially coincident with the upper spanwise boundary of the LMP identified in Figure 3.4a and a streamwise–elongated region of 〈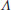ci〉> 0 spatially coincident with the lower spanwise boundary of this LMP. A region of 〈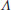ci〉 ≈ 0 is noted within the LMP. This pattern is consistent with a preferential alignment of clockwise-and counter-clockwise-rotating wall-normal vortex cores along the upper and lower boundaries of the LMP, respectively. As sketched in Figure 3.4d, the combined effect of such vortical alignments would induce flow against that of the streamwise mean and thus is consistent with the existence of a region of low streamwise momentum between these vortex paths. It should be noted that the spatial signature of hairpin vortex packets in streamwise–spanwise measurement planes yields qualitatively similar characteristics, particularly the existence of spanwise-separated counter-rotating wall-normal vortex cores (slices of the hairpin vortex legs/necks) between which a region of streamwise momentum deficit exists. Therefore, these patterns in 〈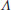ci〉 may be indicative of a preferential alignment of such structures due to the roughness upstream and/or below the measurement plane or the generation of such structures directly by the roughness. Alternatively, this pattern could also be interpreted as a train of structures that are the result of unsteady shedding from dominant roughness elements either upstream or below the measurement plane. However, under this scenario it is not clear whether such ‘trains’ of vortices exhibit the same large-scale streamwise coherence as vortex packets. Regardless of the origin, this evidence suggests that vortical structures are likely responsible for the streamwise–elongated LMP identified in the mean streamwise velocity (Figure 3.4a) as well as the RSS (Figure 3.4b) and TKE (Figure 3.4c) deep within the roughness sublayer.
Figure 3.5 presents similar single-point statistics in the y–z measurement plane generated by ensemble-averaging through the 2500 statistically-independent velocity realization acquired in this plane. The outer-scaled mean streamwise velocity (U/Ue; Figure 3.5a) U displays significant heterogeneity in the spanwise direction, with low-and high-momentum pathways evident across the field of view that are akin to those identified in the x–z plane results (Figure 3.4a). In particular, a large-scale LMP is noted near z ≈ 0.15δ (whose spanwise position is highlighted in Figure 3.5 with a vertical dashed line) that extends well into the outer region of the flow. Recalling that the spanwise origin of the plots in both Figures 3.4 and 3.5 are both referenced to the centre of the wind tunnel span, this LMP occurs at the same spanwise position as that noted in Figure 3.4a. Thus, this persistent region of mean streamwise momentum deficit is not only elongated in the streamwise direction noted in Figure 3.4a but also extends far from the wall to near the edge of the boundary layer as reflected in Figure 3.5a. The HMPs observed to bound this LMP in Figure 3.4a are also clearly evident in U within the y–z plane (Figure 3.5a).
Figure 3.5 Ensemble-averaged, single-point statistics in the wall-normal–spanwise (y–z) plane. (a) Mean streamwise velocity, U/Ue; (b) Reynolds shear stress, –〈u′v′〉/Ue2; (c) Turbulent kinetic energy, TKE/Ue2; (d) Ensemble-averaged signed swirling strength,〈ci〉(δ/Ue). Solid and dashed lines in (d) represent positive and negative contour levels, respectively. ‘LMP’ and dashed horizontal line denotes the spanwise position of the persistent low-momentum pathway identified in (a).
Consistent with the results in Figure 3.4, enhanced regions of RSS (Figure 3.5b) and TKE (Figure 3.5c) reside along the spanwise boundaries of the identified LMP. In addition, the unique view afforded by the y–z measurement plane reveals that these regions of enhanced RSS and TKE are not confined to the near-wall region but in fact extend quite far from the wall (y ≈ 0.6δ). Furthermore, the ensemble-averaged signed swirling strength in the y–z plane (Figure 3.5d),〈ci〉 ≡ 〈λciωx/|ωx|〉 reveals the identified LMP to be bounded by counter-rotating streamwise vortex core activity along its spanwise boundaries. The overall rotational sense of this counter-rotating vortical activity is shown schematically in Figure 3.5d and is consistent with the ejection of low-speed fluid from the near-wall region into the outer region of the boundary layer. Thus, while the instantaneous structural attributes of the rough-wall flow (Figure 3.3) were found to be qualitatively consistent with smooth-wall flow, and therefore indicate a relative insensitivity of the outer layer to roughness effects, these single-point statistics reveal a well-defined imprint of roughness that can extend well into the outer layer of the flow.
3.3.3 Two-point velocity correlations
While well-defined regions of low-and high-momentum pathways were identified in the x–z and y–z single-point statistics, it is not known whether these pathways represent spatially correlated turbulent events or a concatenation of uncorrelated turbulent events that simply advect along the same streamwise path. To assess the spatial coherence of these motions, two-point inhomogeneous velocity correlation coefficients were computed with the reference location taken at the centre of the LMP identified in the measurement planes. These correlations are computed as
(3.1)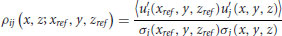 
in a fixed x–z plane at fixed y where (xref, zref) defines the spatial location of the reference point, σi is the root-mean-square velocity of the ith velocity component and 〈•〉 represents an ensemble average. Similarly, these correlations are computed as
(3.2)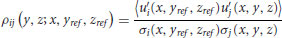 
in the y–z plane at fixed x where (yref, zref) defines the spatial location of the reference point in this measurement plane.
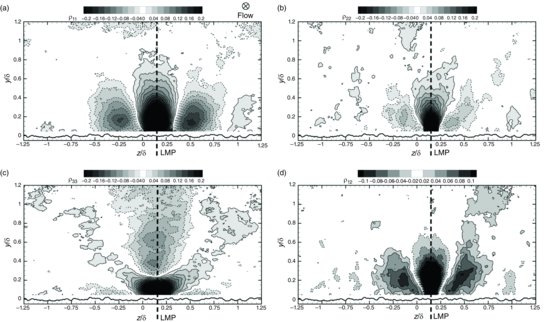
Figure 3.6 presents two-point velocity correlation coefficients in the x–z plane at y = 0.1δ for a reference point situated at (xref, zref) = (0.66δ, 0.15δ), which is centred in the streamwise field of view and sits at the spanwise centre of the LMP identified in Figure 3.4a (demarcated with an ‘X’ in Figure 3.6). The two-point correlation of streamwise velocity (ρ11; Figure 3.6a) is quite elongated in the streamwise direction and is bounded in the spanwise direction by local correlation minima. This latter characteristic is consistent with the alternating nature of low-and high-momentum events previously observed in smooth-wall turbulence (Tomkins and Adrian, 2003; Ganapathisubramani et al., 2005) and identified here for rough-wall flow (Figure 3.3) while the δ-scale streamwise elongation of ρ11 indicates that the streamwise velocity fluctuations are strongly correlated along the streamwise extent of the LMP. Similar streamwise elongation is notable in the two-point cross-correlation of streamwise and wall-normal velocities (ρ12; Figure 3.6d). This correlation indicates a δ-scale streamwise coherence consistent with the collective induction of RSS-producing events along the LMP. On the other hand, the two-point correlation of wall-normal velocity (ρ22; Figure 3.6b) also exhibits streamwise elongation, albeit shorter than ρ11 and ρ12. This streamwise elongation of ρ22, coupled with the local streamwise momentum deficit along the LMP, indicates patterns of streamwise–coherent v′ fluctuations that would be consistent with streamwise–aligned trains of events (possibly vortices) collectively inducing ejections of low-momentum fluid away from the wall. Thus, the streamwise coherence noted in ρ12 is likely linked directly to the streamwise coherence of the v′ fluctuations themselves. Such patterns are reminiscent of the overall spatial characteristics of hairpin vortex packets, for example. Finally, the two-point correlation of spanwise velocity (ρ33; Figure 3.6c) displays a broader spatial coherence than ρ22 in both the spanwise and streamwise directions. In particular, it is of equivalent spatial coherence to ρ11 and ρ12 in the spanwise direction but narrower than both in the streamwise direction. Taken together, these correlations in the x–z plane at y = 0.1δ highlight the significant streamwise coherence of the turbulent velocity fluctuations along the streamwise path of the identified LMP. This coherence therefore indicates that the motions travelling along this LMP are probably not statistically independent smaller scale events simply advecting along a common streamwise path but more likely motions that are statistically related to form the larger scale LMP observed in Figure 3.4a.
Figure 3.6 Two-point velocity correlation coefficients in the streamwise–spanwise (x–z) plane at y = 0.1δ for a reference point positioned within the LMP identified in Figure 3.4 at (xref, zref) = (0.66δ, 0.15δ). (a) Autocorrelation of streamwise velocity, ρ11; (b) Autocorrelation of wall-normal velocity, ρ22; Autocorrelation of spanwise velocity, (c) ρ33; (d) Cross-correlation of streamwise and wall-normal velocities, ρ12.
Figure 3.7 presents two-point velocity correlation coefficients in the y−z measurement plane for a reference point situated at (yref, zref) = (0.1δ, 0.15δ). The wall-normal position of this reference point is consistent with the location of the x–z measurement plane position and its spanwise position is coincident with that of the LMP identified in Figures 3.4a and 3.5a. Analogous to the two-point correlations in the x−z plane (Figure 3.6), ρ11 (Figure 3.7a) is marked by a primary peak at (yref, zref) = (0.1δ, 0.15δ) that is bounded in the spanwise direction by correlation minima. The correlation maximum at the reference location indicates that the motions that travel along the identified LMP have significant wall-normal coherence (δ-scale) in addition to the elongated streamwise coherence noted in Figure 3.6a. The alternating positive/negative nature of ρ11 in this y–z plane is again consistent with the occurrence of spanwise-alternating LMRs and HMRs in instantaneous velocity fields (Figure 3.3) and indicates the LMP identified in Figure 3.5 is often bounded in the spanwise direction by high-speed pathways. In contrast, ρ22 (Figure 3.7b) is smaller in spanwise scale, although it is still characterized by a primary correlation peak at (yref, zref) = (0.1δ, 0.15δ) that is bounded by correlation minima in the spanwise direction. Similar behaviour is noted in ρ12 (Figure 3.7d). Taken together with the correlations in the x−z plane (Figure 3.6), the characteristics of ρ11, ρ22 and ρ12 in the y–z plane are consistent with the imprint of streamwise–oriented vortices, or a larger scale collection of such structures, which pump low-speed fluid away from the wall and draw high-speed fluid towards the wall. Such motions result in the generation of intense RSS-producing events. Finally, ρ33 (Figure 3.7c) displays a V-shaped region of positive correlation above which a wall-normally elongated region of strong negative correlation resides. The symmetry of this correlation with respect to the location of the LMP suggests consistency with spanwise pairs of counter-rotating streamwise vortex cores. In other words, the configuration of ρ33, particularly its persistence into the outer region of the boundary layer, is consistent with the combined action of the legs of hairpin-like, or similarly oriented, vortical structures.
Figure 3.7 Two-point velocity correlation coefficients in the wall-normal–spanwise (y–z) plane for a reference point positioned within the LMP identified in Figure 3.5 at (yref, zref) = (0.1δ, 0.15δ). (a) Autocorrelation of streamwise velocity, ρ11; (b) Autocorrelation of wall-normal velocity, ρ22; Autocorrelation of spanwise velocity, (c) ρ33; (d) Cross-correlation of streamwise and wall-normal velocities, ρ12.
Thus, the spatial coherence, observed in the rough-wall boundary layer through the two-point correlations of velocity fluctuations in the x−z and y−z planes centred along the spatial position of the LMP identified in Figures 3.4 and 3.5, indicates a high degree of spatial coherence along this preferential flow path. As such, these observations do not support the hypothesis that the identified LMP is simply a concatenation of uncorrelated turbulent events advecting along the same streamwise path. In contrast, the spatial characteristics exhibited by the mean flow, particularly the identified LMP, appear to be associated with larger scale spatial coherence traveling along this preferred flow path. This observation is consistent with at least two structural scenarios: (i) ‘trains’ of statistically-correlated vortices that are shed from dominant roughness features that travel along the common flow path demarcated by the LMP or, (ii) a ‘channelling’ of existing large-scale motions (perhaps existing hairpin vortex packets, for example) along preferred paths over the roughness. It should be noted that two-point correlations computed in regions devoid of LMPs and HMPs more closely resemble those of smooth-wall flow. Acquiring time-resolved velocity data in x−z and y−z measurement planes might provide additional insight as to the exact origin of these structures.
3.4 Discussion
Turbulent boundary layers in the presence of roughness have been the subject of significant research attention due both to their complexity and their ubiquitous occurrence in technological and environmental flow applications. Despite this extensive effort, important open questions remain, particularly regarding the impact of highly irregular roughness, reminiscent of the surface roughness encountered in practice, on the underlying spatial structure of TBLs. To this end, zero-pressure-gradient TBLs over a spatially complex rough surface replicated from a damaged turbine blade were studied via stereo PIV measurements in the wall-normal–spanwise (y–z; cross-stream) and streamwise–spanwise (x–z; wall-parallel) planes. For the latter case, the measurement plane was intentionally situated deep within the roughness sublayer (y = 0.1δ) to study the ‘local’ impact of the roughness on the spatial organization of the flow. Interestingly, these measurements revealed a wealth of information regarding roughness-induced effects. While the instantaneous characteristics of the rough-wall flow were found to be qualitatively consistent with that previously observed in canonical smooth-wall turbulence, the roughness studied here generated significant spatial heterogeneity in the single-point mean and turbulence statistics. In particular, the ensemble-averaged streamwise velocity embodied regions of persistent low-and high-momentum flow pathways. Though large-scale regions of low and high streamwise momentum are often observed in instantaneous realizations of both smooth- and rough-wall turbulence, they typically occur randomly in space such that they leave no inhomogeneous imprint within the flow statistics. The present roughness, however, appears to induce a ‘channelling’ effect along these preferred heterogeneous pathways identified in the mean streamwise velocity. Such preferential flow paths have been observed, and are probably expected, in the near-wall region of flow overlying periodic surface structures (Hong et al., 2011, for example). Remarkably, however, this flow channelling phenomenon persists despite the complex nature of the present surface topography. Enhanced regions of TKE and RSS were found to occur spatially coincident with the low-momentum pathways, indicating the possibility of local regions of enhanced turbulence production/dissipation due to roughness. Finally, vortical activity was identified along the spanwise boundaries of the LMP, indicating that these statistical heterogeneities are associated with the turbulent motions induced by coherent vortical structures.
Two-point correlations of velocity were computed spatially coincident with the LMP identified in the mean streamwise velocity and significant streamwise and wall-normal spatial coherence was noted. These observations suggest that these persistent low-momentum pathways are much more than simply a preferred path along which seemingly uncorrelated turbulent events happen to advect. Instead, the spatial coherence identified along the LMP suggests the possibility of ‘channelling’ of existing large-scale motions (hairpin vortex packets, for example) along this particular streamwise path owing to the roughness. Alternatively, it is also possible that vortical structures generated from specific roughness features (persistent wakes, for example) could be responsible for the identified LMP, though the extensive streamwise and wall-normal spatial coherence identified herein would require these vortical motions to be strongly correlated with one-another. Regardless of their origin, these patterns of heterogeneity in the near-wall region of rough-wall flow highlight the significant flow complexity introduced by roughness. In particular, these heterogeneities must be accounted for in numerical simulations of such flows, particularly the regions of enhanced TKE and RSS observed to occur along the boundaries of the identified LMP.
3.5 Conclusions
While the present measurements shed significant light on the structural features of flow in the immediate vicinity of complex roughness, much still remains to be understood. For example, time-resolved measurements would provide information regarding the shedding processes from the larger-scale roughness protrusions. Such data could also clarify the exact degree of correlation between these structures in both space and time (See animation of recent high-speed stereo PIV measurements over this same roughness on the Wiley web site www.wiley.com/go/venditti/coherentflowstructures). Furthermore, data within the valleys of the roughness and between larger scale protrusions is necessary to full characterize the mechanisms of friction generation as well as for validation of computations that may not use full representations of complex roughness but instead employ simplified topographical characterizations.
With regard to modifications of the smooth-wall structural paradigm, while it appears that the overall outer-layer structure of smooth-wall turbulence remains intact in flow overlying the present complex roughness topography, the small-scale structures generated at the roughness must play a role in the overall structural development of the flow. Temporally and spatially resolved near-wall data will help clarify the role of this new population of structures. In addition, the lack of outer-layer modifications indicates that the rough-wall flow is not entirely driven by near-wall processes as is proposed in the so-called ‘bottom-up’ model of low-Re, smooth-wall flow. More recent smooth-wall turbulence measurements at much higher Re have found the outer layer flow to amplitude-modulate the near-wall flow, providing evidence of significant ‘top-down’ interactions that appear to strengthen with increasing Re (Mathis et al., 2009; Marusic et al., 2010; Mathis et al., 2011). The impact of roughness on these outer−inner interactions has yet to be explored (and must be characterized for proper modelling of rough-wall turbulence). However, the present observations wherein the normal near-wall production cycle of smooth-wall flow was disrupted by surface topography yet the outer-flow structure remained remarkably similar to smooth-wall flow hints at fundamental processes driven by the outer-layer flow. Characterizing the full details of this physics will undoubtedly improve our ability to simulate, model and predict such flows with greater fidelity.
Finally, while the observations presented here were derived from studying a topography replicated from a practical engineering application (a damaged turbine blade), they nevertheless will likely extend, to some degree, to flows of geophysical interest. As mentioned previously, the present topography is qualitatively reminiscent of a variety of landscapes encountered in nature, including, for example, gravel river beds (Hardy et al., 2009) as well as dune (Endo et al., 2004) and drumlin fields (Shaw, 1994). All of these natural topographies are marked by complex, multi-scale features that are wholly distinct from those employed in nearly all of the idealized roughness (ordered arrays of single-scale elements, wire mesh, sand grain, etc.) studies reported in the literature. Despite these topographical consistencies between the present roughness and that encountered in nature, the ratio of the characteristic roughness height (k) to the flow depth (δ) must be of similar magnitude in order to extend these observations, even in a qualitative manner, to those that might occur in natural environments. In the case of dune and drumlin fields, for example, their height can extend to 5–10% of the atmospheric boundary-layer thickness. Thus, these surface protrusions will extend into the outer (logarithmic) layer of the flow but remain small compared to the overall flow depth, consistent with the present roughness experiments. Thus, it is expected that the present results can provide, at least qualitatively, some guidance as to the complex processes that mark flow over similarly complex topography in nature.
3.6 Acknowledgements
This work was supported by the Air Force Office of Scientific Research under Grant Nos. FA9550-07-1-0129 and FA9550-10-1-0372 (Dr John Schmisseur, Program Manager). The roughness sample under consideration was graciously loaned to us by Professor J. Bons of Ohio State University.
References
Adrian, R.J., Christensen, K.T. and Liu, Z.-C. (2000a) Analysis and interpretation of instantaneous turbulent velocity fields. Experiments in Fluids 29, 275–290.
Adrian, R.J., Meinhart, C.D. and Tomkins, C.D. (2000b) Vortex organization in the outer region of the turbulent boundary layer. Journal of Fluid Mechanics 422, 1–54.
Bons, J.P., Taylor, R.P., McClain, S.T. and Rivir, R.B. (2001) The many faces of turbine surface roughness. Journal of Turbomachinery 123, 739–748.
Carlier, J. and Stanislas, M. (2005) Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. Journal of Fluid Mechanics 535, 143–188.
Chung, D. and McKeon, B. J. (2010) Large-eddy simulation of large-scale structures in long channel flow. Journal of Fluid Mechanics 661, 341–364.
Endo, N., Taniguchi, K. and Katsuki, A. (2004) Observation of the whole process of interaction between barchans by flume experiments. Geophysical Research Letters 31, L12503. DOI: 10.1029/2004GL020168.
Flack, K.A., Schultz, M.P. and Shapiro, T.A. (2005) Experimental support for Townsend's Reynolds number similarity hypothesis on rough walls. Physics of Fluids 17, 035102. DOI: 10.1063/1.1843135
Ganapathisubramani, B., Hutchins, N., Hambleton, W.T., Longmire, E.K. and Marusic, I. (2005) Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. Journal of Fluid Mechanics 524, 57–80.
Ganapathisubramani, B., Longmire, E.K., and Marusic, I. (2003) Characteristics of vortex packets in turbulent boundary layers. Journal of Fluid Mechanics 478, 35–46.
Hardy, R.J., Best, J.L., Lane, S.N. and Carbonneau, P.E. (2009) Coherent flow structures in a depth-limited flow over a gravel surface: the role of near-bed turbulence and influence of Reynolds number. Journal of Geophysical Research 114, F01003. DOI: 10.1029/2007JF000970.
Hutchins, N., Hambleton, W. T. and Marusic, I. (2005) Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. Journal of Fluid Mechanics 541, 21–54.
Hutchins, N. and Marusic, I. (2007a) Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. Journal of Fluid Mechanics 579, 1–28.
Hutchins, N. and Marusic, I. (2007b) Large-scale influences in near-wall turbulence. Philosophical Transactions of the Royal Society A1852, 647–664.
Head, M. R. and Bandyopadhyay, P. (1981) New aspects of turbulent boundary-layer structure. Journal of Fluid Mechanics 107, 297–338.
Hong, J., Katz, J. and Schultz, M.P. (2011) Near-wall turbulence statistics and flow structures over 3D roughness in a turbulent channel flow Journal of Fluid Mechanics 667, 1–37.
Jimenez, J. (2004) Turbulent flow over rough walls. Annual Review of Fluid Mechanics 36, 173–196.
Keirsbulck, L., Labraga, L., Mazouz, A. and Tournier, C. (2002) Surface roughness effects on turbulent boundary layer structures. Journal of Fluids Engineering 124, 127–135.
Kim, K.C. and Adrian, R.J. (1999) Very large-scale motions in the outer layer. Physics of Fluids 11, 417–422.
Krogstad, P.A. and Antonia, R.A. (1994) Structure of turbulent boundary layers on smooth and rough walls. Journal of Fluid Mechanics 277, 1–21.
Krogstad, P.A. and Antonia, R.A. (1999) Surface roughness effects in turbulent boundary layers. Experiments in Fluids 27, 450–460.
Lee, S.H. and Sung, H.J. (2007) Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. Journal of Fluid Mechanics 584, 125–146.
Ligrani, P.M. and Moffat, R.J. (1986) Structure of transitionally rough and fully rough turbulent boundary layers. Journal of Fluid Mechanics 162, 69–98.
Marusic, I., Mathis, R, and Hutchins, N. (2010) Predictive model for wall-bounded turbulent flow. Science 329, 193–196.
Mathis, R, Hutchins, N. and Marusic, I. (2009) Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. Journal of Fluid Mechanics 628, 311–337.
Mathis, R, Hutchins, N. and Marusic, I. (2011) A predictive inner-outer model for streamwise turbulence statistics in wall-bounded flows. Journal of Fluid Mechanics 681,537–566.
Mejia-Alvarez, R. and Christensen, K. T. (2010) Low-order representations of irregular surface roughness and their impact on a turbulent boundary layer. Physics of Fluids 22, 015106.
Nakagawa, S. and Hanratty, T.J. (2001) Particle image velocimetry measurements of flow over a wavy wall. Physics of Fluids 13, 3504–3507.
Raupach, M.R., Antonia, R.A. and Rajagopalan, S. (1991) Rough-wall turbulent boundary layers. Applied Mechanics Reviews 44, 1–25.
Rohaly, J., Frigerio, F., and Hart, D. (2002) Reverse hierarchical PIV processing. Measurement Science and Technology 13, 984–996.
Shaw, J. (1994) Hairpin erosional marks, horseshoe vortices and subglacier erosion. Sedimentary Geology 91, 269–283.
Soloff, S.M., Adrian, R.J., and Liu, Z.-C. (1997) Distortion compensation for generalized stereoscopic particle image velocimetry. Measurement Science and Technology 8, 1441–1454.
Tachie, M.F., Bergstrom, D.J. and Balachandar, R. (2000) Rough wall turbulent boundary layers in shallow open channel flow. Journal of Fluids Engineering 122, 533–541.
Tachie, M.F., Bergstrom, D.J. and Balachandar, R. (2003) Roughness effects in low-Reh open channel turbulent boundary layers. Experiments in Fluids 35, 338–346.
Tomkins, C.D. and Adrian, R.J. (2003) Spanwise structure and scale growth in turbulent boundary layers. Journal of Fluid Mechanics 490, 37–74.
Townsend, A.A. (1976) The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press, Cambridge.
Volino, R.J., Schultz, M.P. and Flack, K.A. (2007) Turbulence structure in rough-and smooth-wall boundary layers. Journal of Fluid Mechanics 592, 263–293.
Volino, R.J., Schultz, M.P. and Flack, K.A. (2009) Turbulence structure in a boundary layer with two-dimensional roughness. Journal of Fluid Mechanics 635, 75–101.
Wu, Y. and Christensen, K.T. (2007) Outer-layer similarity in the presence of a practical rough-wall topography. Physics of Fluids 19, 085108, 15pp.
Wu, Y. and Christensen, K.T. (2010) Spatial structure of a turbulent boundary layer with irregular surface roughness. Journal of Fluid Mechanics 455, 380–418.