8
Critical Reflections on the Coherent Flow Structures Paradigm in Aeolian Geomorphology
ABSTRACT
Equilibrium concepts are widespread in aeolian geomorphology, especially those incorporating time-averaged parameterizations of fluid flow and sediment transport. The main objective of this chapter is to reflect critically on whether a new paradigm based on coherent flow structures (CFS) is emerging as a viable alternative to the traditional steady-state perspective on aeolian processes. A survey of recent research addressing the existence and nature of CFS in aeolian systems indicates that: (i) there is as yet no convincing evidence in support of the classic bursting process or of any discrete flow structure with a characteristic topology (e.g. hairpin vortex) for the case of near-surface boundary layer flow over flat sandy surfaces (with or without saltation); (ii) there are instances in which near-surface vortices of varying geometry are found in association with small obstacles (e.g. logs, pebbles, vegetation clumps) on sandy surfaces, but it is not always apparent what the pattern of erosion or deposition in the vicinity of the obstacle will be, given that there are additional controls that involve surface hardness and sediment delivery from upwind; (iii) flow over aeolian dunes is generally well understood and very similar to flow over fluvial dunes with characteristic zonation, including flow acceleration and streamline compression on the stoss slope and a recirculation eddy and wake region in the lee; and (iv) the importance of these dune-related flow zones to sediment transport response is more reliably understood through examination of a range of turbulence parameters (e.g. Reynolds stress, turbulent kinetic energy) in addition to the time-averaged flow quantities alone. In order to advance our understanding of CFS in aeolian geomorphology, it will be essential to develop better technologies for high-frequency monitoring of wind and sediment flux, to focus attention on sediment transport events with specific topologies (e.g. streamers) rather than attempt to capture flow events and hope that there is an accompanying transport signal, to move beyond simple quadrant analysis and adopt analytical methods that elucidate the time-history of event signatures, and to reformulate existing time-averaged parameterizations of sediment flux to incorporate event-based information.
8.1 Introduction
For much of the twentieth century, the field of aeolian geomorphology has operated within a conceptual paradigm that privileged equilibrium parameterizations of process-form interactions. The use and meaning of ‘equilibrium’ differ among authors and this has led to periodic reflection, reinterpretation and redefinition of the concept (e.g. Howard, 1988; Mayer, 1992; Phillips, 1992; 1999; 2011; Thorn and Welford, 1994). Howard (1988, pp.49–50) described several key characteristics of equilibrium and suggested that ‘the value of the output at a given time is related by a single-valued, temporally invariant functional relationship to the value(s) of the input(s) at the same time, within a consensual degree of accuracy.’ It is in the context of this paradigmatic, single-valued functional relation between inputs and outputs, specifically the power-law relation between time-averaged wind strength and sediment flux (with accommodation for confounding state parameters such as moisture content, grain texture, vegetation cover, surface roughness, crusting, etc.), that most aeolian geomorphologists have worked since the seminal contributions of R.A. Bagnold (1941).
At the scale of sand grains, aeolian sediment transport has been modelled as an equilibrium relation among the many forces acting upon individual grains within a flow field (e.g. drag, lift, gravity, spin, added mass) in concert with those arising subsequently from grain-grain interactions (e.g. friction, collision, rebounding, cratering). The equilibrium is sustained by negative feedback between saltating grains in their ballistic trajectories and the near-surface boundary layer flow, which is continuously adjusted to the presence of the grains due to momentum extraction or infusion on the rising and falling limbs of the trajectory, respectively (e.g. see comprehensive reviews by Andreotti, 2004, and Durán et al., 2011). The equilibrium condition requires that the number of grains leaving the surface is equal to the number returning to the surface, which has been referred to as the ‘saturated saltation flux’ (Durán and Herrmann, 2006). Advanced models of aeolian transport dynamics (e.g. Spies et al., 2000) allow for short-term disequilibria to occur as the saltation system adjusts to imposed wind unsteadiness (Spies and McEwan, 2000), but the system attains a new saturated state after a short relaxation interval (of order 10–40 seconds).
At landform scales, the evolution, maintenance, and migration of desert dunes, such as the barchanoid forms studied by Bagnold (1941) and many others (e.g. Wipperman and Gross, 1986; Haynes Jr., 1989; Lancaster et al., 1996; Hesp and Hastings; 1998; Hermann and Sauermann, 2000; Tsoar and Blumberg, 2002; Schwämmle and Herrmann, 2005; Weaver and Wiggs, 2011; Baddock et al., 2011; Wiggs and Weaver, 2012), have been investigated by relating patterns of erosion and deposition across the dune to the (rarely measured) spatial gradient in sediment transport intensity (i.e. the divergence of mass flux,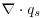 
, where qs is sediment mass transport per unit width), which is assumed to be functionally related to the shear stress field imparted by the near-surface wind (e.g. Cooke and Warren, 1973; Howard et al., 1978; McKenna Neuman et al., 2000; Sauermann, 2001; Walker and Nickling, 2002; Livingstone et al., 2007). Feedbacks between the flow field, the evolving topographic form, and the resultant transport flux lead to spatially explicit patterns of erosion and deposition that ultimately produce characteristic forms and process suites that are diagnostic of preferred system states (i.e. the classic barchan, parabolic, seif, and star dunes appearing in textbook diagrams). Simulation models of the evolution of transverse and coastal dune fields have been proposed recently that further take into account the growth and influence of dune vegetation (Nield and Baas, 2008; Luna et al., 2009; 2011; Barchyn and Hugenholtz, 2012), and these suggest similarly that equilibrium states are achieved after sufficiently long periods.
It is sobering, nevertheless, to realize that our capacity to predict sediment mass flux in field situations using existing transport models – all of which are based on single-valued functional relations between average wind strength and average sediment flux – is quite limited and imprecise (e.g. Sherman and Li., 2011 and references contained therein), although there are exceptions (cf., Rasmussen and Sørenson, 1999; Ould Ahmedou et al., 2007). This reality figures prominently on our ability to understand and model the evolution of aeolian forms at meso and macro scales (van Boxel et al., 1999; McKenna Neuman et al., 2000; Livingstone et al., 2007) despite recent numerical simulations that reproduce natural-looking dunes on the basis of the saturated flux condition (e.g. Herrmann and Sauermann, 2000; Andreotti et al., 2009; Parteli et al., 2011). It is in the context of this inadequacy of predictive models of aeolian flux that the importance of coherent flow structures (CFS) to sediment transport mechanics and to the maintenance of classic equilibrium dune forms holds considerable promise. Indeed, CFS are of interest because they may provide a semi-deterministic foundation upon which to analyse and understand flow signatures across a hierarchy of temporal and spatial scales. If this is the case, the need to rely on time-averaged (steady state) or stochastic treatments of micro-scale fluid and sediment interactions is avoided. Coherent flow structures may also provide a firmer foundation upon which to interpret theories of self-organization and complex behaviour (Werner, 1995; Baas, 2002; Kocurek and Ewing, 2005), which deploy simple macro-scale rule structures that are able to reproduce and emulate many aspects of dune geometry in both arid and coastal environments. Thus, the promise of CFS is immense for advancing the field of aeolian geomorphology beyond a simplistic equilibrium paradigm while still maintaining focus on the physics of fluid-sediment interactions and their fundamental importance to understanding landform evolution.
The objectives of this chapter are: (i) to summarize some of the recent research that was motivated by, and addresses the existence and nature of, coherent flow structures in aeolian geomorphology; (ii) to indicate where some level of consensus is emerging and where challenges have arisen in adopting a CFS-based approach, and thereby point to possible research agendas that might resolve some of the uncertainty; and (iii) to reflect critically on whether the CFS paradigm is fulfilling the promise of lending a new perspective on aeolian geomorphology that has predictive power. Discussion is restricted to aeolian systems dominated by large grain sizes (in the sand range) and by saltation as the dominant mode of transport, in full recognition that there is a growing and sophisticated literature dealing with dust transport for which suspension is critically important. This reflects the authors' limitations more than any bias regarding relevance or importance.
8.2 Coherent flow structure end-member reference states
Robinson (1991, p. 602) defined ‘coherent motion’ in a flow field as
a three-dimensional region of the flow over which at least one fundamental flow variable (velocity component, density, temperature, etc.) exhibits significant correlation with itself or with another variable over a range of space and/or time that is significantly larger than the smallest local scales of the flow.
He used the term ‘coherent motion’ interchangeably with ‘turbulent structure’ and noted that the Reynolds shear stress (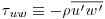
, comprising the fluid density (ρ) and the fluctuating components (u′, w′) of the streamwise (u) and wall-normal (w) velocities, where overbar refers to a mean quantity) would be zero on average if the turbulent motions were purely random. A nonzero value for Reynolds shear stress implies, therefore, that the fluctuating velocities are correlated, at least weakly and, thus, there exists some form of structure(s) within the flow field. Indeed, positive Reynolds shear stress values are a standard feature of near-surface flows across beaches, deserts, agricultural fields, and sandy areas, regardless of whether the surface is flat and homogeneous or occupied by dunes and other topographical features or roughness elements. The question of whether such nonzero correlation values can be explained by the presence of coherent flow structures with distinct topologies and lifespans that are time varying (but are manifested as a steady shearing signal through the time-averaging process) has yet to be explored in detail by aeolian geomorphologists interested in sediment transport processes and dune maintenance.
For our purposes, two end-member reference states can be identified for which the origin and scale of the flow structures are distinctly different: (i) topographically unconstrained; and (ii) topographically forced. Although a spectrum of possibility exists between these end-member states, it is convenient (and consistent with practice) to consider topographically forced structures as occurring largely at meso to macro scales whereas CFS that are topographically unconstrained are typically associated with micro-scale processes. Both situations have implications for aeolian transport (intensity, directionality, intermittency, scaling), and they are not mutually exclusive.
8.2.1 Topographically unconstrained
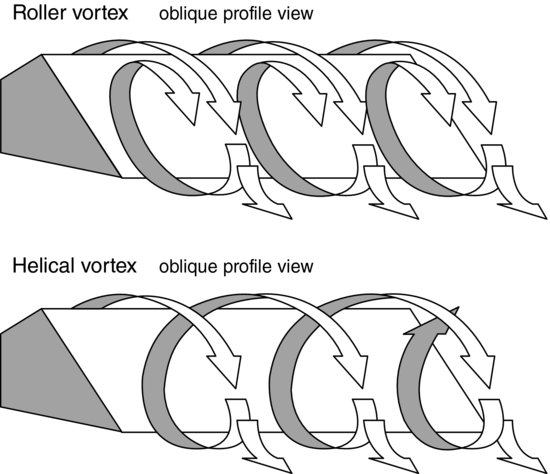
When flow is physically unbounded and not constrained to any significant degree by topographical elements (excepting the presence of a bottom boundary and the small-scale roughness elements that populate its surface) it can be thought of as being ‘topographically unconstrained.’ In such situations, usually requiring laterally extensive, homogenous surfaces relative to the scales of the flow, the embedded structures exist (if at all) as features that evolve spontaneously from within the flow close to the boundary. The classic bursting process in the near-wall region of low Reynolds-number flows over smooth surfaces is the canonical example (e.g. Theodorsen, 1952; Kline et al., 1967; Blackwelder and Eckelmann, 1979). An idealized conceptualization of the sequence of events leading to the violent ejection of low-streamwise-momentum fluid outward involves the development of low-speed streaks evolving into, or interacting with, vortex tubes and thence into hairpin-like (horseshoe) vortices that are stretched and deformed to create tilted three-dimensional structures that become unstable before erupting from the surface (Figure 8.1). Mass and momentum conservation require that the evacuated fluid (the ‘ejection’ phase) be replaced by an inrush of high-streamwise-momentum fluid from above (the ‘sweep’ phase), and collectively these processes have been referred to as the bursting phenomenon (Blackwelder and Eckelmann, 1979). The bursting process is highly intermittent and Reynolds-number dependent, and scales with inner-layer parameters such as fluid (dynamic) viscosity, μ, and shear velocity, u*.
Figure 8.1 Schematic of the inner layer bursting process showing the topology of the evolving roller vortex and the probable velocity profile down the centre line. Reprinted from Hinze, 1975, with permission from McGraw-Hill.
Topographically unconstrained CFS may also exist at meso and macro scales. For example, shear waves and internal waves are often found in stratified flow situations far away from solid boundaries, and these are thought to be subject to Kelvin–Helmholtz and Holmboe modes of unstable growth leading to vortical motion (Tedford et al., 2009). Dust devils, tornadoes, and hurricanes are also topographically unconstrained in the sense that their origins are not dependent on flow-form interaction (although buoyancy effects are critical in these examples). An outstanding issue in meteorology and also aeolian geomorphology is the degree to which top-down versus bottom-up conceptualizations of CFS are relevant as drivers of sediment transport (Bauer et al., 1998; Sterk et al., 1998; Baas, 2008). In the former, the characteristic unsteadiness of near-surface wind is forced from above as a consequence of larger structures (e.g. ‘splats’) that are advected downward and along the surface within the mean flow (e.g. Hunt and Morrison, 2000), whereas in the latter the unsteadiness is driven from below due to the amalgamation and evolution of inner-layer structures into larger, stacked structures (vortex trains or packets) that grow outward and dominate the dynamics of the buffer region (e.g. Adrian et al., 2000).
8.2.2 Topographically forced
When a turbulent wind flows across a relatively flat surface and encounters a significant obstacle (i.e. hill, dune, bluff, or scarp), the flow field adjusts to the presence of the topographical impediment in grossly predictable ways according to principles of mass, momentum, and energy conservation. Among the possible flow modifications are topographic steering (laterally and vertically), flow acceleration (speed-up) or deceleration (stagnation), and flow divergence or separation in the lee (Figure 8.2). The precise response depends on the size and geometry of the obstacle, the roughness properties of the surface, and the nature of the approaching wind (e.g. speed, direction, turbulence intensity). We assume, for simplicity and for the balance of this chapter, that the lower atmosphere is neutrally buoyant and well mixed (appreciating fully that atmospheric stability is critical to understanding the nature of turbulence in desert and polar regions and under a broad range of meteorological conditions). As a consequence of this topographical encounter, alterations to the mean flow quantities occur with an accompanying redistribution of internal stress, which affects the turbulent quantities as well as the turbulent structures embedded within the mean flow. The structural attributes of the flow are created or altered either directly through flow-form interaction or because the turbulence signatures of embedded structures in the incident flow are modified substantially in ways that depend critically on topographical form (i.e. stoss/lee slope steepness, hill height, hill half length, crest/brink angle, dune spacing, surface roughness).
Figure 8.2 Generalized dune lee-side vortices for crest-perpendicular (upper) and oblique (lower) wind approach angles. Reproduced from Walker and Nickling, 2002, with permission from Sage Publications.
8.3 Flow structures over flat sandy surfaces
8.3.1 Wind unsteadiness and quadrant signatures in aeolian transport
Interest in the effects of turbulent fluctuations in aeolian boundary layers stemmed from the pragmatic realization that wind unsteadiness – whatever its origin – might be a critical element in saltation mechanics because of the nonlinear relation between sediment flux and wind (shear) velocity. Specifically, if qs = f(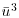
), where 
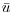is the mean value of a general flow parameter (u) that is time varying (i.e. unsteady), then it becomes critical to appreciate that 
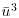is not equal to 
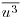. Thus, there is an incommensurability between how sediment transport is parameterized in predictive equations (based on the cube of a mean quantity, 
) and the physics of the problem, which dictate that the sand grains respond in a nonlinear fashion to the instantaneous forces that arise from variations in the wind field (u3) rather than the long-term mean of the nonlinear quantity 
.
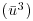Lee (1987) was one of the earliest to undertake a field study in which high-speed instrumentation (hot-wire anemometry and a load-cell trap) was deployed to investigate the relation between sediment flux and wind gustiness. The study was hampered by technical limitations (e.g. slow data transfer rates yielded frequent gaps in the time series) but it implemented novel analytical methods to quantify the magnitude and duration of gusts. Lee (1987) concluded that incorporating gust statistics in a multiple linear regression contributed little additional explanatory power beyond what was already contained in the raw wind-speed time series. His approach was purely statistical and little attention was given to the detailed mechanics of sediment transport. Nevertheless, the study was innovative in that it treated the time series as comprising a sequence of events (gusts) rather than an assemblage of random turbulent motions that could be simply time averaged without loss of critical detail.
Butterfield (1991, 1993) conducted detailed wind-tunnel experiments on aeolian saltation and wind unsteadiness to provide insight into the physics of saltation under tightly controlled conditions and with advanced instrumentation. These wind-tunnel tests confirmed what the numerical models had suggested (e.g. Anderson and Haff, 1988; McEwan and Willetts, 1993), specifically that there is a lag of approximately 1–2 s between a stepwise increase in wind speed and the response of the sediment transport system. More importantly, the models and wind-tunnel experiments show that there is a longer term adjustment (order of 10–40 s) during which the system relaxes to a new equilibrium between mass flux, shear velocity, and effective roughness. One manifestation of these complex, sediment-laden boundary layer adjustments is an ‘overshoot’ phenomenon (Shao and Raupach, 1992) that involves a rapid ramp-up of shear velocity and sediment transport at the upwind end of wind tunnels followed by a gradual decrease in the downwind direction. The implication of these studies is that aeolian saltation systems are likely to be in a state of perpetual disequilibrium or continuous adjustment given the ubiquity of wind unsteadiness and spatial surface heterogeneity in nature.
Field studies by Bauer et al. (1998) and Sterk et al. (1998) assessed the relation between sediment transport and unsteady winds in the specific context of turbulence, as characterized by quadrant signatures. Bauer et al. (1998) used a hot-wire anemometer (0.53 m above bed; 20 Hz sampling rate) and load-cell sand traps (1 Hz sampling rate) to collect high-frequency data on wind velocity and sand transport across a beach. Simple quadrant splitting after sensor rotation showed that ejection-like events (i.e. Q2: u′ < 0; w′ > 0) and sweep-like events (i.e. Q4: u′ > 0; w′ < 0) contributed 39.5% and 50.6%, respectively, of total kinematic Reynolds-shear stress (calculated as the sum of the absolute value of stress in all four quadrants). Thus, the combined contribution was 90.1% of the stress during only 73% of the total time. Accordingly, the quadrant ellipses were heavily skewed toward the Q2 and Q4 quadrants, with much greater u′ excursions in the positive direction than in the negative direction. These results are similar to those reported by Sterk et al. (1998) who used a Gill-type UVW propeller anemometer deployed approximately 3 m above the surface of an agricultural field in conjunction with acoustic sediment sensing instruments (saltiphones) and a 1 Hz sampling rate. They reported stress percentages as the magnitude of the Reynolds shear stress in each quadrant (positive or negative) divided by the mean Reynolds shear stress of the entire time series, which is typically positive in a boundary layer because of the mean surface-directed momentum flux. Thus, the percentages do not sum to 100% and are dependent on overall stress magnitude (i.e. ellipsoid shape and skew). The contribution of the Q2 and Q4 quadrants was 39.7% and 61.5 %, respectively, for one data set and 36.9% and 45.1%, respectively, for another data set. In both the Bauer et al. (1998) and Sterk et al. (1998) studies, the contributions from the Q1 (u′ > 0; w′ > 0) and Q3 (u′ < 0; w′ < 0) quadrants were significantly smaller than the Q2 and Q4 contributions (typically less than 15% each with Q3 generally being smaller than Q1).
Sterk et al. (1998) further related sediment flux to the kinematic Reynolds shear stress time series, but found very small levels of statistical explanation (correlation coefficients smaller than 0.14). The instantaneous sediment transport values were partitioned and sorted according to velocity quadrant signatures (using a hole size equal to one standard deviation of the kinematic shear stress time series; e.g. Lu and Willmarth, 1973), which demonstrated that the largest mean saltation fluxes occurred during stress excursions that were located in the Q1 and Q4 quadrants. In contrast, excursions located in the Q2 and Q3 quadrants were unable to sustain appreciable saltation activity. Sterk et al. (1998) concluded that the horizontal velocity fluctuations (u′) were much more important for aeolian sediment transport than the vertical velocity fluctuations (w′) or the kinematic shear stress (u′w′). Subsequent studies by Schönfeldt and von Löwis (2003) and Leenders et al. (2005) using more sophisticated instrumentation (e.g. sonic anemometry) have confirmed these general conclusions. Leenders et al., (2005) demonstrated that the degree of correlation between various flow parameters such as horizontal and vertical velocity and kinematic stress is spatially dependent, indicating that the scales of the structures that produce the flow signatures are of limited spatial extent. The flow signatures were most coherent with respect to horizontal velocity and least coherent with respect to vertical velocity (and therefore stress). Since vertical fluctuations are inherently constrained by distance from the bottom boundary, as well as the overall scale of the structure itself, the near-surface fluctuations were not well correlated to vertical fluid motions higher in the profile. This explains why measurements of Reynolds shear stress taken at a distance of 1 m or more from the bottom are typically poorly correlated to sediment flux.
Bauer et al. (1998) also found that sediment transport fluxes were not readily predicted by the kinematic shear stress time series nor were they closely associated with shear velocity (derived from a vertical array of cup anemometers). A variable-interval time-averaging (VITA) approach was used, which identifies statistically significant excursions (or ‘events’) in velocity time series using the local variance within a moving time window. Variable-interval time-averaging events were not consistently associated with pronounced shear stress excursions (e.g. extreme Q2 or Q4 signatures) nor did they accurately predict transport events (with many false positives and false negatives). In order to predict sediment transport events (and flux magnitude) accurately, Bauer et al. (1998) suggested that it might become necessary to incorporate a range of flow parameters, including the overall mean speed, some descriptor of the magnitude of fluctuations (e.g. standard deviation), as well as a stress-type term that accounts for significant flow accelerations. Sediment entrainment (or flux enhancement) occurs during time increments when the mean speed is at or above the threshold of motion and when a significant gust of large magnitude with strong acceleration is superimposed on the mean flow. The analytical challenge is to identify such critical conditions in a time series, which can be particularly problematic given that various combinations of mean wind speed and flow acceleration may produce different sediment responses depending on whether sediments are already in saltation.
8.3.2 Aeolian streamers as manifestations of coherent flow structures
Much of the geomorphic research on coherent flow structures in aeolian, fluvial, and marine environments has adopted a perspective that is fluid focused. It begins with the proposition that fluid stresses drive sediment transport, while acknowledging that there can be important flow-form-transport feedbacks. Coherent flow structures embedded within fluid flow fields are considered to govern the magnitude, form and scaling of sediment transport events. Experiments are then designed to quantify the flow field while simultaneously collecting data on sediment flux with the primary objective to associate certain types of turbulence signatures with major sediment flux excursions that are loosely defined as ‘events’, as described in the sub-section immediately above. This approach has yielded a growing number of studies that report bulk summary statistics on quadrant signatures in relation to total sediment flux for each of the quadrants (e.g. Sterk et al., 1998; Leenders et al., 2005; Wiggs and Weaver, 2012; Chapman et al., 2012). An event-based paradigm is asserted implicitly through the use of such terms as ‘ejections’ and ‘sweeps’ that originate in the fluid mechanics literature dealing with true flow events known to occur in the sublayer of turbulent boundary layers (i.e. the bursting process). Whether these fluid excursions identified through quadrant analysis are manifestations of distinct structural events with discrete topologies and characteristic scales is rarely addressed (cf., Best, 2005).
An alternative approach is to focus on sediment transport events (as tracers of plausibly coherent flow structures), and then design experiments that attempt to reveal their dynamical flow attributes. In rivers, for example, ‘kolks’ or ‘boils’ have been identified as discrete transport events, and a significant amount of effort has been devoted to characterizing them and relating them to the flow signatures characterizing dune-related macroturbulence (e.g. Best, 2005, and references therein). Baas and Sherman (2005) adopted a similar approach for aeolian sediment transport by designing a series of experiments to quantify the nature of streamers (also called ‘sand snakes’), which are quasi-linear, undulating concentrations of wind-blown sediment (or snow; Dery and Taylor, 1996) that extend and propagate in the streamwise direction. Large numbers of high-frequency sensors were deployed in tightly spaced arrays with both horizontal and vertical coverage in order to collect a data base that would enable statistical correlations between flow and sediment flux parameters across a range of spatial and temporal scales. Considerable attention was paid to eliminating the possibility of surface controls (moisture, texture, bedforms) on the initiation and evolution of streamers (Baas, 2008).
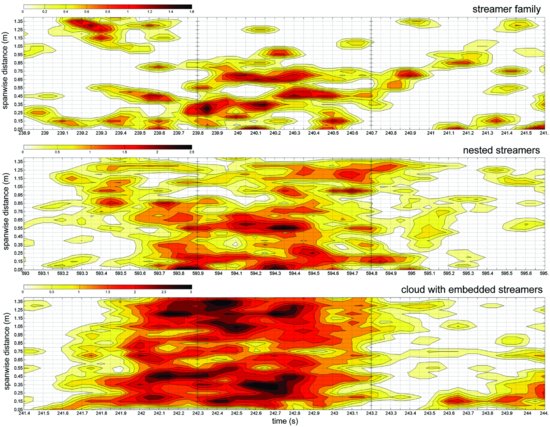
Figure 8.3 shows examples of spatio-temporal maps of normalized sediment transport intensity during periods when streamers were visually present at the site. Horizontal axes show the time history of sediment transport measured by the array of impact sensors (4 cm height above the surface) with scaling adjustments, via Taylor's frozen turbulence hypothesis, to represent the true length scales of the streamers (relative to the horizontal spanwise spacing of the array). When the mean wind speed was slightly above the threshold of motion, sediment transport was highly intermittent and streamers occurred as semi-distinct features within ‘streamer families.’ The spanwise correlation between sensor pairs decreased with horizontal distance, and some sensors did not measure any transport while others experienced intense pulses of transport as the streamers undulated through the array. Increases in wind speed coincided with increases in mean transport intensity, and streamers became embedded within saltation clouds of large spatial extent. The clouds were aperiodic, perhaps forced by roller-type vortices or splats that were of much larger size than the instrument array was able to resolve. Nevertheless, these saltation clouds contained elongated features of more intense transport, which Baas and Sherman (2005) refer to as ‘embedded streamers.’ Streamer propagation speeds in their study were of the order of 3.6 m s−1, which is faster than the particle velocities (of order 2-3 m s−1). The implication is that streamer structures are a complex manifestation of the weak coupling between the wind field and the transport process rather than a direct reflection of the fluid structures, as one might expect if suspended particles were advected with the fluid motion. Coherent flow structures embedded within the boundary layer flow seem to ‘drag’ the sediment streamers along, but not at the same speed as the propagating fluid structures because of limitations imposed by the inherent response times of saltation.
Figure 8.3 Contour plots of normalized transport intensity showing the typical spatio-temporal patterns of aeolian streamers (sand snakes). As transport intensity increases, the patterns evolve from isolated streamers that typically appear in ‘families’ (upper), to streamers nested within larger groups of streamers (middle), and streamers embedded within a much larger saltation cloud (lower) that still retains a distinct identity as an event. Reprinted from Baas and Sherman, 2005. Copyright © 2005 American Geophysical Union, with permission from John Wiley & Sons.
An analysis of the scales of the streamers using correlation techniques yielded a characteristic width of approximately 0.2 m and a lateral spacing of about 1 m. These scales remained fairly constant despite changes in incident wind conditions. Analysis of the anemometer data showed that there was poor spatial coherence in the flow field, suggesting that the fluid motions were essentially random and without discernible structure. In addition, since the dry sand surface was raked flat and free of obstructions, there were no ‘anchoring’ effects that might have preferentially spawned streamers or coherent flow structures, as is often the situation with fluvial ‘kolks’. Baas and Sherman (2005) performed VITA analysis on the wind speed data and found that VITA events were generally poorly correlated to transport events and that sweep-like motions with strongly positive u′ signals were dominant over ejection-like motions. This is consistent with the findings of Bauer et al. (1998) which also showed that ejection-like and sweep-like events were not consistently sequenced as might be expected if they were part of a classic near-wall bursting phenomenon.
Figure 8.4 shows simultaneous contour maps of transport intensity, horizontal wind speed, and VITA variance in association with the passage of a streamer family. The VITA event – signalled by large, localized variance in the time series – precedes the arrival of the streamers by about 1 second and has length scales that appear to encapsulate the entire streamer family. Baas and Sherman (2005) interpreted these patterns as having a probable origin in large eddy-like structures originating in the outer layer advecting downward and dragging across the sand surface while also breaking into long, narrow vortices that spawn the sediment streamers. Hunt and Morrison (2000) provide a detailed description of the mechanism by which these top-down structures might evolve, but much work remains to determine how such fluid structures manifest themselves as sediment transport events with characteristic dimensions and spacing.
Figure 8.4 Spatio-temporal representation of a streamer family (upper) in relation to wind speed (middle) and the variable-interval time averaging (VITA) variance of the wind speed record (lower). The VITA peak occurs in advance of the maxima in wind speed and transport intensity, which indicates a period of accelerating flow prior to sediment entrainment. Reprinted from Baas and Sherman, 2005. Copyright © 2005 American Geophysical Union, with permission from John Wiley & Sons.
Figure 8.4 also indicates how challenging it is to relate sediment transport flux to a single flow parameter such as wind speed or kinematic shear stress using simple correlation analysis in the time domain alone. There are spatial elements in the transport field that manifest themselves in the time series of sediment flux in somewhat unpredictable ways. For example, the simple meandering of a streamer past a single sensor will create a time-varying flux signal, even if the downstream propagation speed of the streamer is constant, because the streamer has a ‘snakelike’ topology. Thus the unsteadiness in the transport record is unlikely to correlate neatly to the steady wind speed record. Moreover, there are well-known lags in the response time of the sand surface to imposed wind stress (Spies et al., 2000), and this is quite evident in Figure 8.4 in relation to the initiation of sediment motion at the beginning of the event. During the waning portions of the event, the correlation between wind speed and sediment flux is very poor since the structure of the streamer family simply breaks down diffusively rather than concluding abruptly.
Spies and McEwan (2000) and Spies et al. (2000) showed that the response dynamics of saltation vary in time and space, depending critically on the overall mean wind speed as well as the magnitude, duration, and shape of the gusts that are superimposed on the mean flow. Response times on the acceleration phases of gusts tend to be faster than those on the deceleration phase, which means there is inherent hysteresis to saltation response curves. Moreover, this hysteresis is event dependent in the sense that the time-scales of adjustment are not only asymmetric on the acceleration and deceleration phases, but they depend on the magnitude of speed increase and decrease (e.g. Baas, 2007). Therefore, a regression analysis comparing sediment flux and wind speed will always show scatter even if the global data set is adjusted according to a single lag time that yields an optimal R2 between the speed and flux time series. This effect will be most pronounced at smaller mean wind speed (Davidson-Arnott and Bauer, 2009; Carneiro et al., 2011), and it suggests that simple correlation methods are inappropriate tools for investigating these highly nonlinear signals.
8.3.3 Flow structures around small obstructions
The fluid mechanics literature is replete with studies on turbulent flow around bluff bodies (e.g. Taylor et al., 2011 and references therein) that deal with vortex formation and shear layer evolution in the vicinity of an obstruction, whereas studies examining the pattern of erosion or deposition around flow obstacles (e.g. Iverson et al., 1991) are few in number. Figure 8.5 shows two instances in which small obstructions commonly found in aeolian environments have modified the flow field, and hence, the sedimentation pattern in the vicinity of the object. Figure 8.5a shows a piece of driftwood on a beach that is aligned obliquely to the dominant wind direction. Sand accumulation in front of the log usually begins with the formation of an echo micro-dune that grows to build a sand ramp, as seen in the photo. Scour hollows were excavated on the margins and in the lee of the log. To the rear right of the log, a linear accumulation of sand trails away from the zone of flow disturbance, demonstrating the complex nature of erosion-deposition patterns that can accompany such irregularly shaped obstructions. Oddly shaped obstacles will affect the flow patterns differently and lead to the formation of various types of lee features (e.g. Howard, 1985; Iverson et al., 1991).
Figure 8.5 Photos of sediment erosion and deposition in the vicinity of obstacles that force the creation of coherent flow structures during wind events. (a). A log on a beach with erosion in the lee and deposition in the stagnation zone in front of the obstacle and in the form of a trailing arm (photo by B. Bauer). (b). Shadow-dune like features in the lee of large ventifacts on a glacio-fluvial sediment surface. These moss and lichen covered features are created by erosion of the surrounding surface, leaving a remnant of the old surface in the protected wake region in the lee of large boulders (photo by C. McKenna Neuman).
Figure 8.5b shows the existence of elongated, vegetated ‘shadow’ features in the lee of large ventifact boulders in an Arctic setting. While similar-looking shadow dunes (Hesp, 1981) are widespread in some coastal and desert environments and usually evolve through accretion in the lee of vegetation clumps, the features in Figure 8.5b arise through differential erosion of a glaciofluvial deposit. Saltating particles are physically obstructed by the presence of the large boulders, thereby sheltering the lee area from progressive erosion and allowing moss and lichens to colonize and thrive. The contrasting context of these two situations suggests that simply knowing the nature of coherent flow structures (and stress distributions) that develop in the vicinity of obstructions may not necessarily provide insight into whether the lee will be predominantly depositional or erosional.
Figure 8.6 shows a sequence of images of flow and sediment transport around a fixed cube in a series of carefully controlled wind-tunnel experiments. All images use the same cube positioned in the same location in the wind tunnel, with flow from right to left. Figure 8.6a is an ink-flow image that provides insight into the stress exerted on the surface in response to coherent flow structures developed in the vicinity of the block. Most prominent among these are the flow stagnation zone in front of the obstacle and the flow separation zones at the sides of the block that spawn the paired counter-rotating vortices in the lee. These are likely parts of a larger horseshoe vortex, as is commonly thought to occur in turbulent flow around bluff bodies (Brighton, 1978). Figure 8.6b shows the pattern of sand strip erosion on either side of the block where flow acceleration leads to enhanced shear stress and vorticity. The image is a collage of 20 separate runs during which a single sand strip was emplaced at a different position independently of the others so as to isolate the effects of entrainment by fluid drag in excess of the threshold condition and to avoid contamination from saltating particles introduced from upwind. In addition, the horizontal surface retains a planar form because no topographical adjustments are allowed via scour or sediment accumulation. Under these conditions, the black sand-free regions on either side of the block closely match the flow perturbation zones in the ink-flow image, and presumably reflect the scales of the coherent flow structures en masse.
Figure 8.6 Photo collages showing patterns of ink flow (a) and erosion/deposition (b–f) in the vicinity of a cube placed in a wind tunnel. See text for explanation (photos courtesy of C. McKenna Neuman).
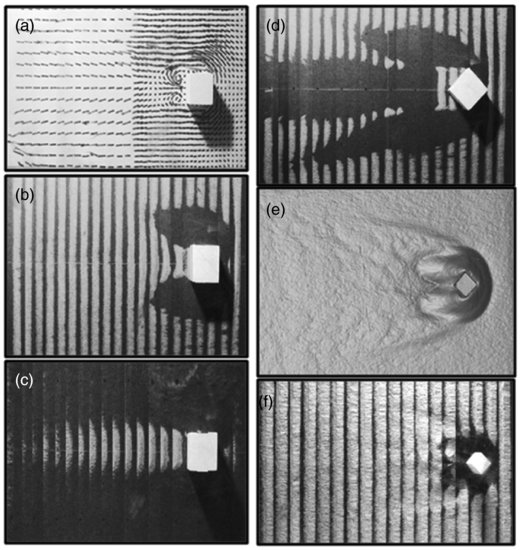
In contrast, Figure 8.6c shows the pattern of sand-strip evolution when a small amount of sediment feed from upwind was introduced into the system, which was otherwise identical in every other respect. A small amount of sediment remains in front of the cube as an ‘echo dune-like’ deposit, and significant sand is retained in the lee of the cube for a considerable distance downwind. Everywhere else on the planar surface, the sand strips were eroded. Although the lee feature bears some similarity to a shadow dune, it clearly arises through erosion of the sand strips outside the wake zone rather than through deposition in the immediate lee of the obstacle. In this regard, Figure 8.6c closely emulates the conditions that likely were responsible for the features in Figure 8.5b. In both instances, the imprint of vorticity on the margins of the obstacle is obscured, leading to a false impression of the importance of the lee-side wake as a benign fluid environment where deposition is favoured.
Figure 8.6d is identical to Figure 8.6b except for the 45° rotation of the cube relative to the incident wind. The black streamwise strip to the lee of the cube aligns with counter-rotating, corkscrew vortices that extend beyond the point of flow reattachment, as described by Sutton and McKenna Neuman (2008) and evident as weak structures in the ink flow image in Figure 8.6a. When the cube is rotated ‘edge-on’ to the flow, these vortices are stretched and increase in angular velocity.
The simulations shown in Figure 8.6a-d do not strictly reflect what happens on a deformable sand surface like that shown in Figure 8.5a. Experiments were re-run with a layer of sand covering the wind tunnel floor, and Figure 8.6e shows a digital elevation model (DEM) of the scour hollow that evolved. This topographically adjusted surface was then ‘fixed’ using black lacquer, and the sand strip experiment, with no sediment feed, was repeated. Figure 6f shows a very different pattern from Figure 8.6d, the only alteration being the initial presence of an ‘equilibrium’ bed surface rather than a planar topography. The scour topography leads to vortex annihilation, and as a consequence, surface disturbance is restricted to a ring very close to the obstruction. The absence of particles in this ring area has more to do with particles rolling down the steep slope (and out the back of the well behind the obstacle) than with vorticity. These experiments therefore suggest that the potential role of coherent flow structures in the vicinity of small obstructions is a very dynamic one. There are the obvious dependencies on the geometry and size of the obstruction relative to the magnitude and direction of the wind as well as the height of the saltation cloud. In addition, the vortices that initially form will be altered progressively by the evolving surface topography (which may or may not be easily eroded) as well as the nature of the upwind sediment source, which may be sediment starved (fetch-limited environment such as a foreshore) or sediment rich (the middle of an extensive dunefield).
In the case of isolated or discrete roughness elements such as clumps of vegetation, the flow patterns can be similar to those described above, but differ due to the porous nature of the elements. As the flow approaches a plant, there is a degree of ‘bleed flow’ through the plant depending on the porosity of the plant. According to Dong et al. (2008), bleed flow dominates below a critical plant density, and for extremely low plant densities, flow separation occurs around each individual plant stem (Bouma et al., 2007). In contrast, dune grasses such as Ammophila tend to be very dense at the base, so there is little flow penetration near the surface. With increasing height above the plant, the bleed flow becomes more pronounced. Therefore, plant form (height, width, density, stem stiffness) affects the flow structure. Total shear stress at the surface increases as the roughness increases (Finnigan, 2000; Brown et al., 2008), and flow acceleration around the plant increases as plant size increases (Vandenbruwaene et al., 2011). Sand deposition will commonly take place within vegetation patches where, according to Poggi et al. (2004), von Kármán vortex streets dominate the flow. As a consequence, a nebkha (Cooke et al., 1993) may be formed, and a horseshoe vortex is often found in the lee due to flow separation around the obstruction. Deposition between the two arms of the horseshoe leads to the development of a pyramidal shadow dune (Figure 8.7). Shadow dune height and width are strongly dependent on plant morphology and width (Hesp, 1981). As nebkhas become larger due to enhanced sand entrapment within increasingly dense stands of vegetation, there is a greater probability that the upwind flow will separate around the incipient dune. Corkscrew vortices and a scour zone will develop in front of and around the sides of the nebkha. This pattern of flow is somewhat similar to that shown in Figure 8.6e, except that due to the typical semi-circular form of a nebkha, the vortex shedding is not as pronounced and therefore the flaring of the erosion zone is not as well developed.
Figure 8.7 Shadow dunes (nebkhas) formed in the lee of vegetation clumps (photo by P. Hesp).
8.4 Flow structures over dunes
8.4.1 Macro-scale structures
Much of the research on turbulent flow over aeolian dunes follows the conceptual and methodological templates established by fluvial researchers (e.g. Bennett and Best, 1995; Ashworth et al., 1996; Best, 2005; Venditti, 2007, 2013). Frank and Kocurek (1994, 1996a, 1996b) synthesized the state of knowledge of wind flow on the stoss and lee slopes of desert dunes, while recent updates appear in Walker and Nickling (2002), Dong et al. (2007), Livingstone et al. (2007), Baddock et al. (2011), and Walker and Hesp (2013). It is well known, for example, that when flow encounters a large hill or transverse dune with idealized geometry, a series of boundary layer adjustments will occur in consequence of mass and momentum conservation (e.g. Taylor and Gent, 1974), which include streamline compression and deflection, progressive flow acceleration toward the crest, and associated modifications in shear stress and turbulent kinetic energy. Consequently, the near-surface velocity profile is altered in ways that deviate from the classic ‘law of the wall’ (Jackson and Hunt, 1975; Mulligan, 1988; Wiggs et al., 1996; van Boxel et al., 1999; Walker and Nickling, 2002). The effects are most pronounced in the inner layer where such streamline compression and flow acceleration produce near-surface velocity profiles that have a speed bulge or zone of ‘speed-up’. Such distorted velocity profiles are particularly evident in the crest region of coastal dunes and cliffs (Jarmalavičuis et al., 2012) where there can be jetlike flows (e.g. Hesp et al., 2009). The near-surface velocity gradient below the speed bulge (in the lower 0.5 m on large dunes) becomes over-steepened, leading to local enhancement of mean shear stress.
Because the flow field must adjust to the presence of the dune, streamline curvature in the region of the dune toe is concave (upward) whereas farther up the stoss slope it shifts to a convex (upward) geometry. Streamline curvature alters the structure of turbulence (Ramaprian and Shivaprasad, 1978), whereby concave curvature facilitates the diffusion of enhanced turbulent energy toward the wall and shifts the spectral distribution of Reynolds shear stresses toward smaller wave numbers (i.e. larger length scales). Wiggs et al. (1996) speculated that this ‘destabilizing’ effect of concave curvature on turbulence has implications for sustaining sediment transport across the toe region, where the stagnation in mean velocity would otherwise lead to deposition (Qian et al., 2011).
While a great deal of field research continues to focus on the dynamics of flow across the stoss slope of desert and coastal dunes (e.g. Lancaster et al., 1996; Hesp, 2002; Livingstone et al., 2007; Hesp et al., 2009; Walker et al., 2009a,b; Weaver and Wiggs, 2011; Chapman et al., 2012), increasing attention is shifting to the lee side of dunes because the flow dynamics in the lee are proving to be equally important to understanding dune maintenance and morphodynamics (Nickling et al., 2002). Walker and Nickling (2002), for example, built on earlier ideas related to fluvial dunes (e.g. McLean and Smith, 1986; McLean et al., 1996) and proposed a detailed conceptual model (Figure 8.8) of lee-side flow zonation for isolated and closely-spaced transverse dunes under crest-normal flow. This aeolian dune model is widely accepted despite the general absence of high-quality data to verify much more than the gross features attributable to the mean flow (cf., Delgado-Fernandez et al., 2011).
Figure 8.8 Conceptual model of flow zonation in the lee of large dunes. Reproduced from Walker and Nickling, 2002, with permission from Sage Publications.
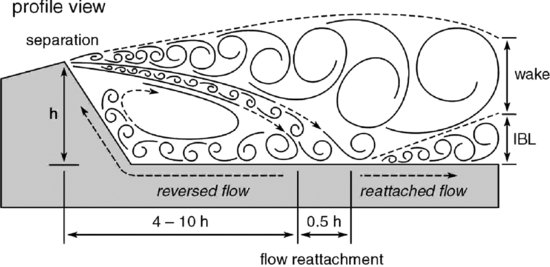
Field studies and wind-tunnel experiments on two-dimensional transverse dunes indicate that the streamwise extent of the recirculation eddy is approximately 4–15 h (where h is dune height) measured in the downwind direction from the point of flow detachment. Flow separation usually occurs near the brink, where the lee-side slip face (avalanche slope) rises to meet the upper, concave portion of the dune. On crest-brink-coincident (CBC) dunes, the brink aligns with the crest (defined as the highest point on the dune profile), whereas on longer crest-brink-separated (CBS) dunes the brink is some distance downwind of the crest. The region between the crest and brink has a negative (concave downward) slope leading toward the slip face. Schatz and Herrmann (2006) used numerical simulations to characterize turbulent flow over a range of CBC and CBS dune geometries and found that the shape and length of the recirculation zone (which varied from 4 to 9h) scaled with brink height and brink angle. This result agrees well with the wind-tunnel measurements of Walker and Nickling (2002), although earlier simulations by Parsons et al., (2004) suggested that the separation length was of order 15 h. Jackson et al. (2011) suggested that such discrepancies may arise from differences among the numerical codes, specifically how turbulence closure is handled, rather than from simple differences in dune geometry alone. Delgado-Fernandez et al. (2011) concluded that separation length is approximately 4h for their field study, and they noted that this scaling was independent of incident flow speed and Reynolds number, which is consistent with results for subaqueous dunes (e.g. Paarlberg et al., 2007).
Nevertheless, a large number of uncertainties remain to be explored before any of these results can be accepted as indicative of the existence of any universal scaling relation. Dune size (height) appears to be a critical factor in determining separation length (e.g. Parsons et al., 2004; Schatz and Herrmann, 2006) because surface roughness (due to sand texture, ripples and vegetation) will not scale up proportionally as dune size increases. Therefore the flow dynamics on the stoss slope and crest-brink region may be altered, which affects the character of lee-side recirculation (von Boxel et al., 1999). A number of field studies on aeolian dunes indicate that dune size and shape are indeed important parameters for understanding lee-side flow dynamics (e.g. Arens et al., 1995; Frank and Kocurek, 1996a; Parsons et al. 2004; Lynch et al., 2010; Jackson et al., 2011). The difference between crest-brink-coincident (CBC) dunes and crest-brink-separated (CBS) dunes is just beginning to be addressed (Baddock et al., 2011), as is the effect of dune spacing and three-dimensionality on separation lengths and the development of internal boundary layers downwind (e.g. Walker and Nickling, 2002, 2003; Baddock et al., 2007). Liu et al. (2011) modelled flow over two- and three-dimensional dunes and demonstrated that there were significant differences in the flow patterns, especially in the lee, because pyramid dunes induce lateral (as well as vertical) flow separation and recirculation. Very little is known about three-dimensional coherent flow structures (e.g. corkscrew vortices), which are clearly relevant to the evolution and maintenance of parabolic and barchan dunes. The presence of vegetation cover may also affect boundary roughness (Hesp et al., 2005; Peterson et al., 2011), and since tall grasses such as Ammophila have very flexible stems, a dynamically rough surface introduces new sources of complexity to the problem.
The nature of lee-side flow on aeolian dunes is controlled further by wind approach angle as it interacts with varying dune shape (Lynch et al., 2008; 2010; Liu et al., 2011). A conceptual model proposed by Sweet and Kocurek (1990; Figure 12, p.1033) identifies three lee-face flow classes: (i) separated flow; (ii) attached and deflected flow; and (iii) attached and undeflected flow. When wind incidence angles are highly oblique, flow remains attached and is typically deflected (steered) especially when the lee-side slope angle is greater than 20°. With wind incidence angles that are perpendicular to the crest line, flow will remain attached when the lee-side slope angle is less than 20° but will separate when the lee-side slope angle is greater than 20°, particularly when the aspect ratio exceeds 0.2 (i.e. h > 1/5L).
Lynch et al. (2008, 2009, 2010) and Jackson et al. (2011; 2013) measured and modelled leeside airflow patterns seaward of a large foredune system (i.e. on the beach) during offshore winds, and confirmed the general findings of Sweet and Kocurek (1990). In this foredune system, the recirculation cell (and near-surface reversed flow) is the dominant mechanism by which the foredune is maintained. When the offshore wind blows-perpendicular to the dune crest line, a recirculation cell develops in the lee of this tall (11+ m) sharp-crested dune. Flow separation was not evident over smaller, more rounded dunes for the same incident wind. Lynch et al. (2010) concluded that foredunes with lee-side aspect ratios greater than 0.6 experience separated flow at the crest whereas more rounded (or complex) dunes with aspect ratios less than 0.6 typically exhibit attached and deflected flows. Small dunes (order 3 m or less) with gradual lee slope angles and aspect ratios less than 0.1 resulted in attached and undeflected flow. A critical incidence angle of about 20° or greater relative to crest-normal seems to coincide with a transition from flow separation to flow deflection with attachment, although this also depends on wind speed.
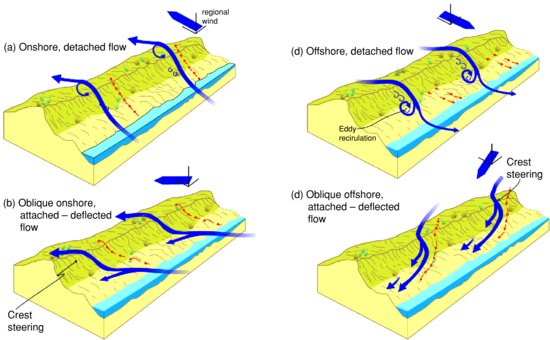
Bauer et al. (2012) reaffirmed these general tendencies for oblique flow across coastal foredunes and proposed a generalized conceptual model (Figure 8.9) covering four cases: (a) onshore, detached; (b) oblique onshore, attached-deflected; (c) offshore, detached; and (d) oblique offshore, attached-deflected. There is a transition from separated flow in the lee of the dune to attached-deflected flow when the incidence angle is about 15°–20° from crest normal. Of potentially greater relevance to sediment transport pathways and dune maintenance are two observations on flow steering in front of the dune. The first is that the incident wind at the base of the dune (on the beach, in the case of obliquely onshore wind) is turned toward a more alongshore direction, thereby driving sediment along the beach rather than into the dune. The second is that the obliquely incident wind flowing up the stoss slope is accelerated and steered to a more shore-perpendicular direction immediately in front of the crest before it dips over into the lee and is strongly steered alongshore again as attached-deflected flow. Thus, there can be flow divergence on the windward side of the dune under oblique winds, which effectively decouples the transport processes on the beach from those higher up the stoss slope of the dune.
Figure 8.9 Conceptual model of flow patterns in the vicinity of coastal foredunes during onshore (a), obliquely onshore (b), offshore (c), and obliquely offshore (d) regional winds. Near-surface flow patterns are strongly influenced by flow-form interaction. Probable sediment transport pathways are indicated by red arrows. Reproduced from Bauer, et al., 2012, with permission from John Wiley & Sons.
8.4.2 Signatures of turbulence in flow over dunes
The generalized model of flow zonation over aeolian dunes introduced in the previous section is based on time-averaged flow parameters. Aeolian geomorphologists have been slow to verify the model using detailed measurements of turbulence, but the introduction of ultrasonic anemometry and other sophisticated technologies has facilitated novel field and wind-tunnel experiments that are providing new insights into flow-form interaction across aeolian dunes (e.g. van Boxel et al., 2004; Walker, 2005; Livingstone et al., 2007; Delgado-Fernandez et al., 2011; Jackson et al., 2011; Chapman et al., 2012). Nevertheless, there are surprisingly few papers that provide comprehensive data on such basic turbulence parameters as Reynolds shear stresses (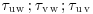
), the streamline-parallel Reynolds normal stress (
), turbulence intensity (
, where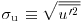 
is the standard deviation of u, and U is the Reynolds-averaged mean of u), or the mean turbulent kinetic energy 
.
Dong et al. (2009) used PIV techniques in a wind tunnel to analyse the structure of turbulence in the lee of two-dimensional triangular dunes of fixed height with varying stoss slope angles (ranging from 3° to 25°) and a fixed lee slope angle of 30°. The results indicate that there are well-established regions of enhanced shear (vorticity) emanating from the brink and diffusing downstream, as well as zones of intense turbulent kinetic energy occupying elongated zones in the dune lee. The precise nature of these zones changed according to incident wind speed (8–14 m s−1) and with dune geometry. Low-angle dunes with stoss slopes less than about 10° displayed one pattern of flow structure, which was quite distinct from high-angle dunes with slopes greater than about 10°. The most strongly developed recirculation cell occurred when the stoss slope had an angle of about 15°. The utility of such a detailed wind-tunnel data set is that it provides a firm basis upon which field experiments can be organized for the purpose of testing the laboratory results and providing new insight into dune morphodynamics. Significant progress has been made in the fluvial literature following a similar methodology (e.g. Bennett and Best, 1995, 1996; Venditti and Bennett, 2000; Venditti and Bauer, 2005).
Baddock et al. (2011) measured near-surface turbulence across two, isolated barchan dunes and found that the magnitude of the Reynolds shear and normal stresses were at their maximum in the recirculation cell close to the point of flow reattachment and decreased in the downwind direction for distances of about 20 h. Velocity recovery in the internal boundary layer downwind of the dune occurred at about 10–17 h, similar to recovery lengths of 10–15 h reported by Lancaster (1995). Recovery of turbulent parameters (relative to upwind values in front of the dune) occurred over slightly longer distances (of order 25 h), which is consistent with the stress recovery distances of about 15–30 h reported by Walker and Nickling (2002). These separation lengths and recovery lengths differ between isolated dunes versus sequences of dunes in dune fields, and therefore dune spacing and its influence on lee-side flow dynamics and sediment transport delivery is a critical yet underexplored factor (Walker and Nickling, 2003; Baddock et al., 2007).
Baddock et al. (2011) also documented the anticipated decrease in mean velocity upwind of the dune close to the dune toe. A local velocity minimum occurred slightly past the dune toe on the lower stoss slope. In contrast, the Reynolds shear stress,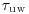 
, increased toward the toe and then followed an irregular pattern up the stoss slope eventually achieving a maximum some distance upwind of the crest where the mean speed also peaked. Such Reynolds stress maxima upwind of the crest are typical for low-amplitude hills and low-angle dunes, although the pattern differs from what is found for shear velocity (based on the gradient of the mean velocity profile), which typically shows shear stress maxima at the crest where flow acceleration is most pronounced. Baddock et al. (2011) found that both mean wind speed and average Reynolds shear stress decreased from the crest to the brink, suggesting that this is a zone of negative sediment flux divergence and potential deposition.
Similar trends in mean flow parameters were found by Weaver and Wiggs (2011). In addition, they showed that the horizontal Reynolds normal stress,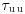 
, remained essentially constant in front of the dune and part-way up the stoss, whilst the vertical Reynolds normal stress, 
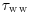, increased toward the dune toe and lower stoss. These trends are consistent with the observation that concave curvature has a greater effect on w′ than on u′ (Ramaprian and Shivaprasad, 1978). In contrast, the Reynolds shear stress, 
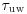, increased toward the toe and lower stoss, after which there was a general decrease toward the brink region. Notably, the precise nature of the spatial gradients in all turbulence parameters depended on the elevation above the surface at which the measurements were taken. In this regard, it is conceivable that much of the important fluid dynamics affecting the sand surface, and therefore sediment transport, occurs at a level that cannot be accessed using standard sonic anemometry (i.e. less than about 0.2 m).
8.4.3 Flow-sediment interactions across aeolian dunes
Flow acceleration on the stoss slopes of hills and dunes creates a spatial gradient in mean surface shear stress, which yields a progressive increase in sediment transport potential from the foot of the dune to the crest. Empirical support for these general trends comes from field and wind-tunnel studies (Hesp et al., 1989; Wiggs et al., 1996; Walker and Nickling, 2002, 2003; Livingstone et al., 2007) as well as from numerical models (e.g. Wipperman and Gross, 1986; van Boxel et al., 1999; Herrmann and Sauermann, 2000; Sauermann, 2001; Parsons et al., 2004; Parteli et al., 2011). The evidence has encouraged a belief that aeolian dunes display (or trend toward) equilibrium behaviour with long-term maintenance of dune size and shape (e.g. Cooke and Warren, 1973; Hesp and Hastings, 1998; Andreotti et al., 2009). Nevertheless, there are a range of uncertainties regarding how sediment transport is sustained across the dune toe given the tendency toward flow stagnation upwind of a bluff body (Wiggs et al., 1996) and how sediment deposition or erosion in the crest region is controlled by such factors as transport intermittency (e.g. McKenna Neuman et al., 2000) and crest-brink geometry (e.g. Schatz and Herrmann, 2006; Baddock et al., 2011). As a consequence, increasing effort has been devoted to understanding the signatures of turbulence across the near-surface profiles of dunes as well as to the nature of flow-form interaction across multiple dunes in sequence, as is generally the situation in dune fields or ergs (e.g. Baddock et al., 2011; Weaver and Wiggs, 2011; Wiggs and Weaver, 2012).
Measurements of turbulence across the stoss slope of dunes in the field and in wind tunnels (e.g. Walker and Nickling, 2003; Baddock et al., 2011; Weaver and Wiggs, 2011; Chapman et al., 2012), demonstrate that the magnitude of the Reynolds stresses and turbulent kinetic energy typically increase at the toe region relative to upwind locations, and that this may compensate for the reduction in mean horizontal wind speed as it affects sediment transport potential across the stagnation zone (Wiggs et al., 1996). Wiggs and Weaver (2012) further showed that there was an increase in Q2 and Q4 quadrant activity toward the dune toe with a concomitant decrease in Q1 and Q3 quadrant activity. As the flow field was deflected up the stoss slope of the dune, the relative importance of Q1 and Q4 activity increased toward the crest, mostly at the expense of Q2 activity. As a consequence, Reynolds shear stress initially increased toward the toe (where Q2 and Q4 dominate) and then decreased toward the crest (where Q1 counterbalances the positive stress contributions from Q4 so as to yield an overall reduction in the total Reynolds shear stress).
Recent studies have begun to relate the quadrant signatures of turbulent flows over dunes to sediment transport probabilities (e.g. Chapman et al., 2012; Wiggs and Weaver, 2012), and some common trends are being discovered. On the upwind margin of dunes, the typical elliptical shear pattern evident in quadrant plots (with Q2–Q4 skew) is prevalent and these quadrant signatures persist up the stoss slope. Toward the crest, the Q1 and Q4 quadrants begin to dominate, whereas in the immediate lee of the crest the quadrant plots are circular. Sediment transport pulses are dominantly associated with Q2–Q4 skew at the dune toe because of the contributions that these quadrants make to the Reynolds shear stress, which tends to increase toward the dune toe. At the dune crest, sediment transport is associated with the Q1 and Q4 quadrants due to the dominance of +u′ fluctuations arising from accelerated flow and streamline compression. This latter observation confounds the well-established relation between transport flux and shear stress that underpins most models of sediment transport across dunes because the Q1 excursions transfer streamwise momentum away from the surface and thereby provide a negative contribution to the mean Reynolds shear stress. As a consequence, there can be significant reductions in Reynolds shear stress (as distinct from estimates of shear stress derived from velocity profiles) at the crest of a dune even though sediment transport can be sustained by the combination of Q4 and Q1 quadrant activity. Fluid excursions into the Q2 quadrant are proportionately less important at the crest relative to the dune toe, whereas Q3 activity appears to contribute little to the overall stress field and is of minimal relevance to aeolian transport. These findings suggest a primary role of the +u′ fluctuations associated with sweep-like (Q4) activity in sustaining sediment transport in saltation–dominated systems, as found by Bauer et al. (1998), Sterk et al. (1998), and Leenders et al. (2005) over relatively flat surfaces.
8.5 Discussion
A primary motivation for this chapter is to assess critically the relative importance of the coherent flow structures paradigm in aeolian geomorphology. Evidence in support of the existence and relative importance of the classic bursting process (Theodorson, 1952) in aeolian saltation over flat sand surfaces is circumstantial at best. Experiments in the field and in wind tunnels have failed to provide data that capture the ejection-sweep sequence in its entirety, which is a fundamental aspect of the bursting phenomenon as a structural event with a specific topology. The small number of studies that have attempted to quantify this phenomenon (e.g. Bauer et al., 1998; Sterk et al., 1998; Schönfeldt and von Löwis, 2003; Leenders et al., 2005; Baas and Sherman, 2005; Ellis, 2006) using quadrant analysis, VITA analysis, or wavelet analysis, conclude that ejection-like fluid signatures are not typically associated with sweep-like fluid signatures in sequential fashion. Nevertheless, these studies are hardly definitive, and much more research needs to be undertaken to reach a firm conclusion regarding the existence and properties of coherent flow structures during aeolian saltation.
Relatively little is known about the characteristic scales of event-like motions in aeolian saltation systems because researchers have been constrained by the limited technologies available to sense the three-dimensional near-surface flow field at ultra-high frequencies alongside the sediment motions. This remains a major challenge for aeolian geomorphologists because: (i) fluid and particle velocities are an order of magnitude greater in air than in water, which implies the need for faster and more precise instrumentation deployed in tighter arrays across greater distances; (ii) the propagation speed of sound is about four times slower in air than in water, which makes acoustic Doppler approaches technically challenging in air; and (iii) the specific (submerged) density of sand particles in air is more than three orders of magnitude greater than in water, which means that sediment suspension is relatively unimportant in aeolian sand systems. This latter point is critical because rather than sediment being advected by the fluid and passively mirroring the topologies of coherent flow structures, as is thought to happen in fluvial boils and kolks (e.g. Best, 2005), the particles in aeolian transport systems move predominantly via saltation. Particles follow ballistic trajectories, and the mean particle speeds are initially much smaller than the mean fluid velocity, thereby extracting momentum from the flow (e.g. McKenna Neuman and Nickling, 1994; Rasmussen and Sørenson, 2008). In so doing, the velocity profile is altered (see Bauer et al., 2004 and Li et al., 2004, and references therein) and the structure of turbulence in the saltation layer is modified, which likely has implications for the spawning and evolution of coherent structures in the near-surface layer. Not only is the inner layer velocity profile changed because a portion of the total stress in the saltation layer is borne by the moving grains, but the entire saltation layer serves to enhance the overall effective roughness of the surface (Owen, 1964), The experiments by Baas and Sherman (2005) on sand streamers remain the only attempt at characterizing the typical scales of flow structures and transport events in aeolian systems, and these data suggest that the scales of the fluid and sediment structures do not coincide. Much work remains to assess the origin of wind unsteadiness in the near-surface in relation to the time-varying character of flow in the outer boundary layer. Whether this unsteadiness is organized and related to coherent flow structures may, in the end, prove to be moot because there is a growing body of research that shows the importance of the larger, long-period velocity fluctuations to sediment transport (e.g. Spies et al., 2000; Spies and McEwan, 2000), and these are unlikely to be forced by inner-layer dynamics (Baas, 2008).
Studies dedicated to quantifying the three-dimensional flow field in relation to aeolian transport flux at high frequencies are likely to become commonplace in the near future, and there will be a tendency to replicate the methodologies and analytical approaches used previously to assess the nature of turbulence in the flow field. In this regard, it is worthwhile noting that a simple quadrant analysis is not an ideal event-detection technique although it is commonly adopted for this purpose. Quadrant analysis provides a great deal of information on the nature of turbulent kinetic energy and Reynolds shear stress production and distribution at a point. Nevertheless, the quadrant plot does not provide information on the time history of fluid signatures that characterize a structural event in the flow field. Thus, despite the common tendency to associate specific quadrant signatures (e.g. Q2 and Q4) with event-like nomenclature (i.e. ejections and sweeps), this is a deceptively misleading practice that implies the presence of coherent structure (events) in the flow field when none may exist. Furthermore, since the terms ‘ejection’ and ‘sweep’ were originally proposed as part of the bursting phenomenon, the additional implication is that significant fluid excursions within the Q2 and Q4 quadrants are due to the passage of a coherent structure such as a hairpin vortex or a vortex packet (Adrian et al., 2000). No evidence in support of the existence of a specific type of structural topology that is topographically unconstrained has yet been published in reference to aeolian systems. The work of Sukhodolov and Rhoads (2001) related to the identification of helical structures near river confluences deals with some of the analytical challenges faced in making inferences about the three-dimensional topologies of flow structures as they propagate past fixed instrument arrays. The questions of appropriate sampling frequencies, time series durations, and averaging intervals for quadrant analysis also loom large.
The case for the importance of coherent flow structures in relation to topographically forced states is much more compelling. Obstructions such as logs, boulders, and clumps of vegetation clearly have an influence on the near-surface flow field. The consequent vortex dynamics are critical to interpreting the patterns of erosion and deposition near such obstructions. However, the initial flow-form interactions that spawned the sediment deposit will be systematically altered as the form evolves. Thus, the potential importance of coherent flow structures in mobilizing and transporting sediments at a particular stage in the evolution of the dune form may ultimately be subsumed by the broader geomorphic conditions that govern sediment supply and vegetation growth over the long term. Logs and other coastal flotsam may provide only temporary controls on aeolian saltation across beaches, eventually being removed by storm waves or buried by progressive deposition. Thus, they may only provide local ‘noise’ within a stronger suite of long-term signals that ultimately control beach-dune interaction (Short and Hesp, 1982; Sherman and Bauer, 1993; Bauer and Sherman, 1999; Houser and Hamilton, 2009), although there are compelling examples where the role of large woody debris on beach evolution is fundamentally important (e.g. Walker and Barrie, 2006; Eamer and Walker, 2010).
The existence of coherent macrostructures in flow over large coastal foredunes and desert dunes is undeniable. There is ample evidence, for example, in support of the existence of a recirculation zone in the lee of sharp-crested dunes, and there seem to be consistent similarities to flow fields over fluvial dunes. Nevertheless, there remain significant outstanding issues, such as the effect of dune slope, crest-brink geometry, and vegetation cover on flow acceleration/deceleration across the dune profile and flow separation in the lee (including the size of the recirculation eddy). Relatively little is known about how dune size and spacing influences these macrostructures or how these modified flow zones then feed back into dune field evolution via altered sediment transport pathways. With the advent of high resolution LIDAR surveys giving extremely detailed three-dimensional dune surface topography, information is now available to support the use of complex airflow simulations across aeolian dunes and dune fields (Jackson et al., 2011; Jerolmack et al., 2012). Recent modelling efforts using computational fluid dynamics (CFD) will be of great utility in assessing these issues, especially in relation to complex, irregular dune geometries (e.g. Lynch et al., 2008; Smyth et al., 2011). Robust data sets from carefully planned field experiments, guided by wind-tunnel results, will become increasingly important in constraining, calibrating, and verifying these numerical simulations. More effort will need to be dedicated to quantifying the signatures of turbulence in critical flow zones such as the near-surface boundary layer on the stoss slope and the wake region in the lee of dunes so that appropriate turbulence closure schemes are adopted in the simulation procedure and related algorithms.
Even if we continue to evolve greater skill in simulating complex flow dynamics over dunes, this may not lead to better understanding of how dunes evolve or how an equilibrium dune form could be maintained. For example, there seems to be growing consensus that a majority of sediment transport is associated with sweep-like excursions in the Q4 quadrant, with Q1 activity also playing a significant role, indicating that the positive u′ motions are critically important (e.g. Delgado-Fernadez et al., 2011; Chapman et al., 2012; Wiggs and Weaver, 2012). Ejection-like (Q2) excursions appear to play a secondary role, whereas Q3 activity is only weakly correlated to transport events. It is difficult to know how to embed this information in any sort of predictive model of aeolian transport and, in this context, we remain trapped in an equilibrium (steady state) paradigm that fundamentally ignores the role of wind unsteadiness as well as the importance of specific stress-generating events distributed across the full stress tensor (incorporating normal and tangential Reynolds stresses).
It has proven equally difficult to decipher the most important controls on the pattern of sediment erosion and deposition across simple dune profiles and, therefore, there is little consensus on how (and when) dunes grow and what ultimately limits their size and shape, despite significant advances in numerical modelling since the early 2000s. Controlling mechanisms have been proposed, including streamline curvature and enhanced turbulence (Wiggs et al., 1996), flow acceleration and Reynolds normal stresses (Walker and Nickling, 2002, 2003; Wiggs and Weaver, 2012), and transport intermittency as driven by the regional mean wind speed (e.g. McKenna Neuman et al., 2000). In coastal settings, foredunes evolve through a series of punctuated steps involving wave erosion of the dune toe to produce dune scarps and to rip up vegetation, (re)construction of sand ramps by aeolian processes that heal the scarps, and extreme seasonal events that have the capacity to mobilize sediment on the vegetated stoss slope and transport it over the dune crest (Carter et al., 1990; Christiansen, 2003; Christiansen and Davidson-Arnott, 2004; Hesp et al., 2005, 2009; Delgado-Fernandez and Davidson-Arnott, 2011; Ollerhead et al., 2013). Moreover, the near-surface velocity and transport vectors vary widely in aeolian dune systems due to micro-scale flow-form modulation of the regional wind (Bauer et al., 2012). This has significant ramifications for understanding how coherent flow structures that are topographically forced at the scale of the dune might impact sediment transport processes at specific locations on the dune toe, stoss slope, and crest.
8.6 Summary and conclusions
Aeolian sediment transport predictions were founded on equilibrium concepts and steady flow assumptions that rely on mean parameterizations averaged over time intervals that are much longer than the inherent unsteadiness of naturally turbulent wind fields. Recognition of the existence of coherent flow structures (CFS) embedded within otherwise steady flows has stimulated new research that promised deeper understanding of aeolian saltation as a process involving sequences of transport events driven by distinct stress excursions rather than semi-random fluctuations superposed on a mean flow. This chapter has assessed the degree to which the promise has been fulfilled to date and whether the CFS paradigm has provided new insights into aeolian geomorphology more generally.
For convenience, two end-member reference states were identified. Topographically unconstrained states are those characterized by spatially extensive, homogeneous surfaces (e.g. flat deserts or beaches) for which the flow structures are generated within the inner layer (as with the classic bursting process) or imposed from above via the outer layer (e.g. Hunt and Morrison, 2000). Topographically forced states refers to systems for which CFS originate from or are modified through the interaction with large topographic elements (e.g. dunes, scarps).
Over flat sand surfaces, there is relatively little empirical evidence to date that suggests that CFS are critically important to understanding the mechanics of aeolian saltation. Early efforts at correlating quadrant signatures with sediment transport pulses (e.g. Bauer et al., 1998; Sterk et al., 1998) were unconvincing and unable to link transport intensity to the bursting process. These and subsequent studies have shown the importance of fluid motions characterized by strong +u′ excursions found in the Q1 and Q4 quadrants for sediment transport across flat surfaces and over dunes (e.g. Leenders et al., 2005; Chapman et al., 2012; Wiggs and Weaver, 2012). Investigations targeted at recognizable transport features such as aeolian streamers (‘sand snakes’) may hold the best prospect for providing convincing evidence in favour of CFS and their importance to aeolian saltation (Baas, 2008). However, the challenges are significant. In aqueous systems, the density difference between the fluid and sediment is of order one, and therefore the angular momentum contained in a vortical structure, such as a kolk, can be effectively transferred to suspended sediment. Since the sediment is advected passively within the structure, the topology of the kolk is unaltered by the sediment (to first degree) and assessment of the fluid structure provides insight into the sediment event. In contrast, the density difference between air and sand is of order 1000, which implies much less efficient momentum transfer from the fluid to the sediment. Once sediment is mobilized in air, saltating grains will rapidly modify the character of the near-surface boundary layer, which implies that the turbulence is altered and that the fluid signatures of CFS are unlikely to remain coherent for very long. Thus, it seems highly unlikely that the inner layer bursting process is a viable mechanism by which CFS might be spawned in aeolian systems. The top-down origin of CFS (Hunt and Morrison, 2000) by which flow structures in the upper regions of the boundary layer are advected downward and subsequently modified via dynamic interaction with the surface still holds considerable promise and is worthy of future investigation.
The research on macro-scale CFS in topographically constrained systems is, in contrast, proving more fruitful. Field and wind-tunnel studies on turbulent flow over aeolian dunes demonstrate that there are strong similarities to flow over fluvial dunes, which is reassuring but perhaps unsurprising given that flow compression, separation, and reattachment are the primary controls on the overall flow dynamics. The nature of turbulent signatures in the lee of aeolian dunes has yet to be explored in a systematic and comprehensive fashion, and there are very few data sets from the field that provide information on the shear layer, wake region, and recirculation zone. It is an open question as to whether wind-tunnel dunes provide reliable analogues to field dunes (similar debates appear in the fluvial literature with respect to flumes, e.g. Best and Kostaschuk, 2002), and it is well known that the physical constraints imposed by wind tunnels on momentum and energy conservation often lead to simulation results that must be interpreted with great care (e.g. White, 1979; 1996; Farrell and Sherman, 2004). In the absence of reliable field data, the laboratory simulations and numerical codes are not well constrained, so sustained effort in all three areas is needed. In order to advance our understanding of CFS in aeolian geomorphology, it will be essential to develop better technologies for high-frequency monitoring of wind and sediment flux, to focus attention on sediment transport events with specific topologies (e.g. streamers) rather than attempt to capture flow events and hope that there is an accompanying transport signal, to move beyond simple quadrant analysis and adopt analytical methods that elucidate the time-history of event signatures, and to reformulate existing time-averaged parameterizations of sediment flux to incorporate event-based information.
References
Adrian, R.J., Meinhart, C.D. and Tomkins, C.D. (2000) Vortex organization in the outer region of the turbulent boundary layer. Journal of Fluid Mechanics 422, 1–54.
Anderson, R.S. and Haff, P.K. (1988) Simulation of aeolian saltation. Science 241, 820–823.
Andreotti, B. (2004) A two-species model of aeolian sand transport. Journal of Fluid Mechanics 510, 47–70.
Andreotti, B., Fourrière, A., Ould-Kaddour, F. et al. (2009) Giant aeolian dune size determined by the average depth of the atmospheric boundary layer. Nature 457, 1120–1123.
Arens, S.M., van Kaam-Peters, H.M.E. and van Boxel, J.H. (1995) Air flow over foredunes and implications for sand transport. Earth Surface Processes and Landforms 20, 315–332.
Ashworth, P.J., Bennett, S.J., Best, J.L. and McLelland, S.J. (1996) Coherent Flow Structures in Open Channels, John Wiley & Sons, Inc., New York.
Baas, A.C.W. (2002) Chaos, fractals and self-organization in coastal geomorphology: simulating dune landscapes in vegetated environments. Geomorphology 48, 309–328. DOI: 10.1016/S0169-555X(02)00187-3
Baas, A.C.W. (2007) Complex systems in aeolian geomorphology. Geomorphology 91, 311–331.
Baas, A.C.W. (2008) Challenges in aeolian geomorphology: investigating aeolian streamers. Geomorphology 93, 3–16.
Baas, A.C.W and Sherman, D.J. (2005) Formation and behavior of aeolian streamers. Journal of Geophysical Research 110, F03011. DOI: 10.1029/2004JF000270.
Baddock, M.C., Livingstone, I. and Wiggs, G.F.S. (2007) The geomorphological significance of airflow patterns in transverse dune interdunes. Geomorphology 87, 322–336.
Baddock, M.C., Wiggs, G.F.S. and Livingstone, I. (2011) A field study of mean and turbulent flow characteristics upwind, over and downwind of barchan dunes. Earth Surface Processes and Landforms 36, 1435–1448.
Bagnold, R.A. (1941) The Physics of Blown Sand and Desert Dunes, Methuen, London.
Barchyn, T.E. and Hugenholtz, C.H. (2012) Aeolian dune field geomorphology modulates the stabilization rate imposed by climate. Journal of Geophysical Research 117, F02035. DOI: 10.1029/201 1JF002274.
Bauer, B.O. and Sherman, D.J. (1999) Coastal dune dynamics: problems and prospects. In Aeolian Environments, Sediments and Landforms (eds A.S. Goudie, I. Livingstone and S. Stokes). John Wiley & Sons, Ltd, Chichester, pp. 71–104.
Bauer, B.O., Houser, C.A. and Nickling, W.G. (2004) Analysis of velocity profiles from wind tunnel experiments with saltation. Geomorphology 59, 81–98.
Bauer, B.O., Yi, J., Namikas, S.L. and Sherman, D.J. (1998) Event detection and conditional averaging in unsteady aeolian systems. Journal of Arid Environments 39, 345–375.
Bauer, B.O., Davidson-Arnott, R.G.D., Walker, I.J. et al. (2012) Wind direction and complex sediment transport response across a beach-dune system. Earth Surface Processes and Landforms 37, 1661–1667. DOI: 10.1002.esp3306.
Bennett, S.J. and Best, J.L. (1995) Mean flow and turbulence structure over fixed, two-dimensional dunes: implications for sediment transport and dune stability. Sedimentology 42, 491–513.
Bennett, S.J. and Best, J.L. (1996) Mean flow and turbulence structure over fixed ripples and the ripple-dune transition. In Coherent Flow Structures in Open Channels (eds P.J. Ashworth, J.L. Best, S.J. Bennett and S.J. McLelland). John Wiley & Sons, Inc., New York, pp. 281–304.
Best, J. (2005) Kinematics, topology and significance of dune-related macroturbulence: some observations from the laboratory and field. In Fluvial Sedimentology, Vol. 2 (eds M.D. Blum, S.B. Marriott and S.L. LeClair). Blackwell, Oxford, pp. 41–60.
Best, J. and Kostaschuk, R. (2002) An experimental study of turbulent flow over a low-angle dune. Journal of Geophysical Research 107, 3135, DOI: 10.1029/2000JC000294.
Blackwelder, R.F. and Eckelmann (1979) Streamwise vortices associated with the bursting phenomenon. Journal of Fluid Mechanics 94, 577–594.
Bouma, T.J., van Duren, L.A., Temmerman, S. et al. (2007) Spatial flow and sedimentation patterns within patches of epibenthic structures: Combining field, flume and modeling experiments. Continental Shelf Research 27, 1020–1045.
Brighton, P.W.M. (1978) Strongly stratified flow past three-dimensional obstacles. Quarterly Journal of the Royal Meteorological Society 104, 289–307.
Brown, S., Nickling, W.G. and Gillies, J.A. (2008) A wind tunnel examination of shear stress partitioning for an assortment of surface roughness distributions. Journal of Geophysical Research 113, F02S06. DOI: 10.1029/2007JF000790.
Butterfield, G.R. (1991) Grain transport in steady and unsteady turbulent airflows. Acta Mechanica Supplementum 1, 97–122.
Butterfield, G.R. (1993) Sand transport response to fluctuating wind velocity. In Turbulence: Perspectives on Flow and Sediment Transport (eds N.J. Clifford, J.R. French and J. Hardisty). John Wiley & Sons, Inc., pp. 305–336.
Carneiro, M.V., Pähtz, T. and Herrmann, H.J. (2011) Jump at the onset of saltation. Physical Review Letters 107, 098001.
Carter, R.W.G., Hesp, P.A. and Nordstrom, K.F. (1990) Geomorphology of erosional dune landscapes. In Coastal Dunes: Processes and Morphology (eds K. Nordstrom, N. Psuty and R.W.G. Carter). John Wiley & Sons, Ltd, Chichester, pp. 217–250.
Chapman, C.A., Walker, I.J., Hesp, P.A. et al. (2012) Turbulent Reynolds stress and quadrant event activity in wind flow over a coastal foredune. Geomorphology 151–152, 1–12. DOI: 10.1016/j.geomorph.2011.11.015
Christiansen, M.B. (2003) Effects of dune ramps on sediment supply to coastal foredunes: Skallingen, SW Denmark. Proceedings of the International Conference on Coastal Sediments 2003. CD-ROM. World Scientific Publishing Corp. and East Meets West Productions, Corpus Christi, TX.
Christiansen, M.B. and Davidson-Arnott, R. (2004) Rates of landward sand transport over the foredune at Skallingen, Denmark and the role of dune ramps. Geografisk Tidsskrift (Danish Journal of Geography) 104, 31–43.
Cooke, R.U. and Warren, A. (1973) Geomorphology in Deserts, University of California Press, Berkeley, CA.
Cooke, R.U., Warren, A. and Goudie, A.S. (1993) Desert Geomorphology, UCL Press, London.
Davidson-Arnott, R.D.G. and Bauer, B.O. (2009) Aeolian sediment transport on a beach: thresholds, intermittency, and high frequency variability. Geomorphology 105, 117–126.
Delgado-Fernandez, I., Jackson, D.W.T., Cooper, J.A.G. et al. (2011) Re-attachment zone characterization under offshore winds blowing over complex foredune topography. Journal of Coastal Research SI64, 273–277.
Dery, S.J. and Taylor, P.A. (1996) Some aspects of the interaction of blowing snow with the atmospheric boundary layer. Hydrological Processes 10, 1345–1358.
Dong, Z., Luo, W., Qian, G. and Lu, P. (2008) Wind tunnel simulation of the three-dimensional airflow patterns around shrubs. Journal of Geophysical Research 113, FO2016. DOI: 10.1029/2007JF000880.
Dong, Z., Qian, G., Luo, W. and Wang, H. (2007) A wind tunnel simulation of the effects of stoss slope on the lee airflow pattern over a two-dimensional transverse dune. Journal of Geophysical Research 112, F03019. DOI: 10.1029/2006JF000686.
Dong, Z., Qian, G., Lu, P., Luo, W. and Wang, H. (2009) Turbulence fields in the lee of two-dimensional transverse dunes simulated in a wind tunnel. Earth Surface Processes and Landforms 34, 204–216.
Durán, O. and Herrmann, H. (2006) Modelling of saturated sand flux. Journal of Statistical Mechanics: Theory and Experiment 07, P07011.
Durán, O., Claudin, P. and Andreotti, B. (2011) On aeolian transport: Grain-scale interactions, dynamical mechanisms and scaling laws. Aeolian Research 3, 242–270.
Eamer, J.B.R. and Walker, I.J. (2010) Quantifying sand storage capacity of large woody debris on beaches using LiDAR. Geomorphology 118, 33–47.
Ellis, J.T. (2006) Coherent Structures and Aeolian Saltation. Ph.D. dissertation, Texas A&M University.
Farrell, E.J. and Sherman, D.J. (2004) Process-scaling issues for aeolian transport modeling in field and wind tunnel experiments: roughness length and mass flux distributions. Journal of Coastal Research SI39, 384–389.
Finnigan, J. (2000) Turbulence in plant canopies. Annual Review of Fluid Mechanics 32, 519–571.
Frank, A.J. and Kocurek, G. (1994) Effects of atmospheric conditions on wind profiles and aeolian sand transport with an example from White Sands National Monument. Earth Surface Processes and Landforms 19, 735–745.
Frank, A.J. and Kocurek, G. (1996a) Airflow up the stoss slope of sand dunes: limitations of current understanding. Geomorphology 17, 47–54.
Frank, A.J. and Kocurek, G. (1996b) Toward a model of airflow on the lee side of aeolian dunes. Sedimentology 43, 451–458.
Haynes Jr., C.V. (1989) Bagnold's barchan: a 57-yr record of dune movement in the eastern Sahara and implications for dune origin and paleoclimate since Neolithic times. Quaternary Research 32, 153–167.
Herrmann, H.J. and Sauermann, G. (2000) The shape of dunes. Physica A 283, 24–30.
Hesp, P.A. (1981) The formation of shadow dunes. Journal of Sedimentary Petrology 51, 101–112.
Hesp, P.A. (2002) Foredunes and blowouts: initiation, geomorphology, and dynamics. Geomorphology 48, 245–268.
Hesp, P.A. (2005) Flow reversal and dynamics of foredunes and climbing dunes on a leeward east coast, New Zealand. Coasts Under Stress II 141, 123–134.
Hesp, P.A., Davidson-Arnott, R.G.D., Walker, I.J. and Ollerhead, J. (2005) Flow dynamics over a foredune at Prince Edward Island, Canada. Geomorphology 65, 71–84.
Hesp, P.A. and Hastings, K. (1998) Width, height and slope relationships and aerodynamic maintenance of barchans. Geomorphology 22, 193–204.
Hesp, P.A., Illenberger, W., Rust, I. et al. (1989) Some aspects of transgressive dunefield and transverse dune geomorphology and dynamics, south coast, South Africa. Zeitschrift fur Geomorpologie Supplement-Band 73, 111–123.
Hesp, P.A., Walker, I.J., Namikas, S.L. et al. (2009) Storm wind flow over a foredune, Prince Edward Island, Canada. Journal of Coastal Research SI56, 312–316.
Hinze, J.O. (1975) Turbulence, 2nd edn, McGraw-Hill, New York.
Houser, C. and Hamilton, S. (2009) Sensitivity of post-hurricane beach and dune recovery to event frequency. Earth Surface Processes and Landforms 34, 613–628.
Howard, A.D. (1985) Interaction of sand transport with topography and local winds in the northern Peruvian coastal desert. In Proceedings International Workshop on the Physics of Blown Sand. Aarhus, May 28–31, (eds O.E. Barndorff-Nielsen, J.T. Moller, K. Rasmussen and B.B. Willetts) Department of Theoretical Statistics, Institute of Mathematics, University of Aarhus.
Howard, A.D. (1988) Equilibrium models in geomorphology. In Modelling Geomorphological Systems (ed. M.G. Anderson). John Wiley & Sons, Ltd, Chichester, pp. 49–70.
Howard, A.D., Morton, J.B., Gad-El-Hak, M. and Pierce, D.B. (1978) Sand transport model of barchan dune equilibrium. Sedimentology 25, 307–338.
Hunt, J.C.R. and Morrison, J.F. (2000) Eddy structure in turbulent boundary layers. European Journal of Mechanics B- Fluids 19, 673–694.
Iversen, J.D., Wang, W.P., Rasmussen, K.R. et al. (1991) Roughness element effect on local and universal saltation transport. Acta Mechanica Supplementum 2, 65–75.
Jackson, D.W.T., Beyers, M., Delgado-Fernandez, I., Baas, A.C.W., Cooper, A.J., and Lynch, K. (2013) Airflow reversal and alternating corkscrew vortices in foredune wake zones during perpendicular and oblique offshore winds. Geomorphology 187, 86–93.
Jackson, D.W.T., Beyers, J.H.M., Lynch, K. et al. (2011) Investigation of three-dimensional wind flow behavior over coastal dune morphology under offshore winds using computational fluid dynamics (CFD) and ultrasonic anemometry. Earth Surface Processes and Landforms 36, 1113–1134.
Jackson, P.S. and Hunt, J.C.R. (1975) Turbulent wind flow over a low hill. Quarterly Journal of the Meteorological Society 101, 929–955.
Jerolmack, D.J., Ewing, R.C., Falcini, R. et al. (2012) Internal boundary layer model for the evolution of desert dune fields. Nature Geoscience 5, 206–209.
Jarmalavičuis, D., Satkūnas, J., Žilinskas, G. and Pupienis, D. (2012) The influence of coastal morphology on wind dynamics. Estonian Journal of Earth Sciences 61, 120–130.
Kline, S.J., Reynolds, W.C., Schraub, F.A. and Rundstadler, P.W. (1967) The structure of turbulent boundary layers. Journal of Fluid Mechanics 30, 741–773.
Kocurek, G. and Ewing, R.C. (2005) Aeolian dune field self-organization – implications for the formation of simple versus complex dune-field patterns. Geomorphology 72, 94–105.
Lancaster, N. (1995) Geomorphology of Desert Dunes, Routledge, London.
Lancaster, N., Nickling, W.G., McKenna Neuman, C. and Wyatt, V.E. (1996) Sediment flux and airflow on the stoss slope of a barchan dune. Geomorphology 17, 55–62.
Lee, J.A. (1987) A field experiment on the role of small scale wind gustiness in aeolian sand transport. Earth Surface Processes and Landforms 12, 331–335.
Leenders, J.K., van Boxel, J.H. and Sterk, G. (2005) Wind forces and related saltation transport. Geomorphology 71, 357–372.
Li, Z, Ni, J.R. and Mendoza, C. (2004) An analytic expression for wind velocity profile within the saltation layer. Geomorphology 60, 359–369.
Liu, B., Qu, J., Zhang, W. and Qian, G. (2011) Numerical simulation of wind flow over transverse and pyramid dunes. Journal of Wind Engineering and Industrial Aerodynamics 99, 879–888.
Livingstone, I., Wiggs, G.F.S. and Weaver, C.M. (2007) Geomorphology of desert sand dunes: a review of recent progress. Earth-Science Reviews 80, 239–257.
Lu, S.S. and Willmarth, W.W. (1973) Measurements of the structure of the Reynolds stress in a turbulent boundary layer. Journal of Fluid Mechanics 60, 481–511.
Luna, M.D. de M., Parteli, E.J.R., Durán, O. and Herrmann, H.J. (2009) Modeling transverse dunes with vegetation. Physica A 388, 4205–4217.
Luna, M.D. de M., Parteli, E.J.R., Durán, O. and Herrmann, H.J. (2011) Model for the genesis of coastal dune fields with vegetation. Geomorphology 129, 215–224.
Lynch, K., Jackson, D.W.T. and Cooper, J.A.G. (2008) Aeolian fetch distance and secondary airflow effects: the influence of micro-scale variables on meso-scale foredune development. Earth Surface Processes and Landforms 33, 991–1005.
Lynch, K., Jackson, D.W.T. and Cooper, J.A.G. (2009) Foredune accretion under offshore winds. Geomorphology 105, 139–146.
Lynch, K., Jackson, D.W.T. and Cooper, J.A.G. (2010) Coastal foredune topography as a control on secondary airflow regimes under offshore winds. Earth Surface Processes and Landforms 35, 344–353.
Mayer, L. (1992) Some comments on equilibrium concepts and geomorphic systems. Geomorphology 5, 277–295.
McEwan, I.K. and Willetts, B.B. (1993) Adaptation of the near-surface wind to the development of sand transport. Journal of Fluid Mechanics 252, 99–115.
McKenna Neuman, C., Lancaster, N. and Nickling, W.G. (2000) The effect of unsteady winds on sediment transport on the stoss slope of a transverse dune, Silver Peak, NV, USA. Sedimentology 47, 211–226.
McKenna Neuman, C. and Nickling, W.G. (1994) Momentum extraction with saltation: implications for experimental evaluation of wind profile parameters. Boundary-Layer Meteorology 68, 35–50.
McLean, S.R. and Smith, J.D. (1986) A model for flow over two-dimensional bed forms. Journal of Hydraulic Engineering 112, 300–317.
McLean, S.R., Nelson, J.M. and Shreve, R.L. (1996) Flow-sediment interactions in separating flows over bedforms. In Coherent Flow Structures in Open Channels (eds P. Ashworth, S.J. Bennett, J.L. Best and S.J. McLelland). John Wiley & Sons, Inc., New York, pp. 203–226.
Mulligan, K.R. (1988) Velocity profiles measured on the windward slope of a transverse dune. Earth Surface Processes and Landforms 13, 573–582.
Nickling, W.G., McKenna Neuman, C. and Lancaster, N. (2002) Grainfall processes in the lee of transverse dunes, Silber Peak, Nevada. Sedimentology 49, 191–209.
Nield, J.M. and Baas, A.C.W. (2008) Investigating parabolic and nebkha dune formation using a cellular automaton modelling approach. Earth Surface Processes and Landforms 33, 724–740. DOI: 10.1002/esp.1571.
Ollerhead, J., Davidson-Arnott, R.G.D., Walker, I.J. and Mathew, S. (2013) Annual to decadal morphodynamics of the beach-foredune system at Greenwich Dunes, Prince Edward Island, Canada. Earth Surface Processes and Landforms 38, 294–298.
Ould Ahmedou, D., Ould Mahfoudh, A., Dupont, P. et al. (2007) Barchan dune mobility in Mauritania related to dune and interdune sand fluxes. Journal of Geophysical Research 112, F02016. DOI: 10.1029/2006JF000500.
Owen, P.R. (1964) Saltation of uniform grains in air. Journal of Fluid Mechanics 20, 225–242.
Paarlberg, A.J., Dohmen-Janssen, C.M., Hulsher, S.J.M.H. and Termes, P. (2007) A parameterization of flow separation over subaqueous dunes. Water Resources Research 43, W12147. DOI: 10.1029/2006WR005425.
Parsons, D.R., Walker, I.J. and Wiggs, G.F.S. (2004) Numerical modelling of flow structures over idealized transverse aeolian dunes of varying geometry. Geomorphology 59, 149–164.
Parteli, E.J.R., Andrade, J.S. and Herrmann, H.J. (2011) Transverse instability of dunes. Physical Review Letters 107, 188001 (1–5).
Peterson, P.S., Hilton, M.J. and Wakes, S.J. (2011) Evidence of aeolian sediment transport across an Ammophila arenaria-dominated foredune, Mason Bay, Stewart Island. New Zealand Geographer 67, 174–189.
Phillips, J.D. (1992) The end of equilibrium? Geomorphology 5, 195–201.
Phillips, J.D. (1999) Divergence, convergence, and self-organization in landscapes. Annals of the Association of American Geographers 89, 466–488.
Phillips, J.D. (2011) Emergence and pseudo-equilibrium in geomorphology. Geomorphology 132, 319–326.
Poggi, D., Porporato, A., Ridolfi, L. et al. (2004) The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorology 111, 565–587.
Qian. G., Dong, Z., Luo, W. and Lu, J. (2011) Mean airflow patterns upwind of topographic obstacles and their implications for the formation of echo dunes: a wind tunnel simulation of the effects of windward slope. Journal of Geophysical Research 116, F04026, DOI: 10.1029/2011JF002020.
Ramaprian, B.R. and Shivaprasad, B.G. (1978) The structure of turbulent boundary layers along mildly curved surfaces. Journal of Fluid Mechanics 85, 273–303.
Rasmussen, K.R. and Sørensen, M. (1999) Aeolian mass transport near the saltation threshold. Earth Surface Processes and Landforms 24, 413–422.
Rasmussen, K.R. and Sorensen, M. (2008) Vertical variation of particle speed and flux density in aeolian saltation. Journal of Geophysical Research 113, F02S12. DOI: 10.1029/2007JF000774.
Robinson, S.K. (1991) Coherent motions in the turbulent boundary layer. Annual Review of Fluid Mechanics 23, 601–639.
Sauermann, G. (2001) Modeling of Wind Blown Sand and Desert Dunes, Logos Verlag, Berlin.
Schatz, V. and Herrmann, H.J. (2006) Flow separation in the lee side of transverse dunes: A numerical investigation. Geomorphology 81, 207–216.
Schwämmle, V. and Herrmann, H.J. (2005) A model of barchan dunes including lateral shear stress. European Physics Journal E. 16, 57–65.
Schönfeldt, H.J. and von Löwis, S. (2003) Turbulence-driven saltation in the atmospheric boundary layer. Meteorologische Zeitschrift 12, 257–268.
Shao, Y. and Raupach, M.R. (1992) The overshoot and equilibration of saltation. Journal of Geophysical Research 97, 20559–20564.
Sherman, D.J. and Bauer, B.O. (1993) Dynamics of beach-dune systems. Progress in Physical Geography 17, 413–447.
Sherman, D.J and Li, B. (2011) Predicting aeolian sand transport rates: A reevaluation of models. Aeolian Research 3, 371–378. DOI: 10.1016/j.aeolia.2011.06.002.
Short, A.D. and Hesp, P.A. (1982) Wave, beach and dune interactions in South Eastern Australia. Marine Geology 48, 259–284.
Smyth, T.A.G., Jackson, D.W.T. and Cooper, J.A.G. (2011) Computational fluid dynamic modeling of three-dimensional airflow over dune blowouts. Journal of Coastal Research SI64, 314–318.
Spies, P.-J. and McEwan, I.K. (2000) Equilibration of saltation. Earth Surface Processes and Landforms 25, 437–453.
Spies, P.-J., McEwan, I.K. and Butterfield, G.R. (2000) One-dimensional transitional behaviour in saltation. Earth Surface Processes and Landforms 25, 505–518.
Sterk, G., Jacobs, A.F.G. and van Boxel, J.H. (1998) The effect of turbulent flow structures on saltation sand transport in the atmospheric boundary layer. Earth Surface Processes and Landforms 23, 877–887.
Sukhodolov, A.N. and Rhoads, B.L. (2001) Field investigation of three-dimensional flow structure at stream confluences: 2. Turbulence. Water Resources Research 37, 2411–2424.
Sutton, S.L.F. and McKenna Neuman, C. (2008) Variation in bed level shear stress on surfaces sheltered by nonerodible roughness elements. Journal of Geophysical Research 113, F03016. DOI: 10.1029/2007JF000967.
Sweet, M.L. and Kocurek, G. (1990) An empirical model of aeolian dune lee-face airflow. Sedimentology 37, 1023–1038.
Taylor, P.A. and Gent, P.R. (1974) A model of atmospheric boundary-layer flow above an isolated two-dimensional ‘hill’: an example of flow above ‘gentle topography.’ Boundary Layer Meteorology 7, 349–362.
Taylor, Z.J., Palombi, E., Gurka, R. and Kopp, G.A. (2011) Features of the turbulent flow around symmetrical elongated bluff bodies. Journal of Fluids and Structures 27, 250–265.
Tedford, E.W., Pieters, R. and Lawrence, G.A. (2009) Symmetric Holmboe instabilities in a laboratory exchange flow. Journal of Fluid Mechanics 636, 137–153.
Theodorsen, T. (1952) Mechanism of turbulence. In Proceedings of 2nd Midwestern Conference on Fluid Mechanics, 452. The Ohio State University, Columbus, Ohio, 1–19.
Thorn, C.E. and Welford, M.R. (1994) The equilibrium concept in geomorphology. Annals of the Association of American Geographers 84, 666–696.
Tsoar, H. and Blumberg, D.G. (2002) Formation of parabolic dunes from barchan and transverse dunes along Israel's Mediterranean coast. Earth Surface Processes and Landforms 27, 1147–1161.
van Boxel, J.H., Arens, S.M. and van Dijk, P.M. (1999) Aeolian processes across transverse dunes 1: Modelling the air flow. Earth Surface Processes and Landforms 24, 255–270.
van Boxel, J.H., Sterk, G. and Arens, S.M. (2004) Sonic anemometers in aeolian sediment transport research. Geomorphology 59, 131–147.
Vandenbruwaene, W., Temmerman, S., Bouma, T.J. et al. (2011) Flow interaction with dynamic vegetation patches: Implications for biogeomorphic evolution of a tidal landscape. Journal of Geophysical Research 116, F01008, DOI: 10.1029/2010JF001788.
Venditti, J.G. (2007) Turbulent flow and drag over fixed two- and three-dimensional dunes. Journal of Geophysical Research, 112, F04008, DOI: 10.1029/2006JF000650.
Venditti, J.G. (2013) Bedforms in sand-bedded rivers. In Treatise on Geomorphology (ed. J. Shroder, Jr.). Academic Press, San Diego, CA.
Venditti, J.G. and Bauer, B.O. (2005) Turbulent flow over a dune: Green River, Colorado. Earth Surface Processes and Landforms 30, 289–304.
Venditti, J.G. and Bennett, S.J. (2000) Spectral analysis of turbulent flow and suspended sediment transport over fixed dunes. Journal of Geophysical Research 105, 22035–22047.
Walker, I.J. (2005) Physical and logistical considerations of using ultrasonic anemometers in aeolian sediment transport research. Geomorphology 68, 57–76.
Walker, I.J. and Barrie, J.V. (2006) Geomorphology and sea-level rise on one of Canada's most ‘sensitive’ coasts: Northeast Graham Island, British Columbia. Journal of Coastal Research SI39, 220–226.
Walker, I.J., Davidson-Arnott, R.G.D., Hesp, P.A. et al. (2009a) Mean flow and turbulence response in airflow over foredunes: new insights from recent research. Journal of Coastal Research SI56, 366–370.
Walker, I.J. and Hesp, P.A. (2013) Fundamentals of aeolian sediment transport: airflow over dunes. In Treatise on Geomorphology, Vol 11, Chpt 11.7: 109–133. (ed. J. Shroder, Jr.). Elsevier Academic Press, San Diego, CA.
Walker, I.J., Hesp, P.A., Davidson-Arnott, R.G.D. et al. (2009b) Responses of three-dimensional flow to variations in the angle of incident wind and profile form of dunes: Greenwich Dunes, Prince Edward Island, Canada. Geomorphology 105, 127–138, DOI: 10.1016/j.geomorph.2007.12.019.
Walker, I.J. and Nickling, W.G. (2002) Dynamics of secondary airflow and sediment transport over and in the lee of transverse dunes. Progress in Physical Geography 26, 47–75.
Walker, I.J. and Nickling, W.G. (2003) Simulation and measurement of surface shear stress over isolated and closely spaced transverse dunes in a wind tunnel. Earth Surface Processes and Landforms 28, 1111–1124. DOI: 10.1002/esp.520
Weaver C.M. and Wiggs, G.F.S. (2011) Field measurement of mean and turbulent airflow over a barchan sand dune. Geomorphology 128, 32–41.
Werner, B. (1995) Eolian dunes: computer simulations and attractor interpretation. Geology 23, 1107–1110.
White, B.R. (1979) Soil transport by winds on Mars. Journal of Geophysical Research 84, 4643–4651.
White, B.R. (1996) Laboratory simulation of aeolian sand transport and physical modeling of flow around dunes. Annals of Arid Zones 35, 187–213.
Wiggs, G.F.S., Livingstone, I. and Warren, A. (1996) The role of streamline curvature in sand dune dynamics: Evidence from field and wind tunnel measurements. Geomorphology 17, 29–46.
Wiggs, G.F.S. and Weaver, C.M. (2012) Turbulent flow structures and aeolian sediment transport over a barchans sand dune. Geophysical Research Letters 39, L05404. DOI: 10.1029/2012GL050847.
Wipperman, F.K. and Gross, G. (1986) The wind-induced shaping and migration of an isolated dune: a numerical experiment. Boundary-Layer Meteorology 36, 319–334.