21
Effect of Migrating Bed Topography on Flow Turbulence: Implications for Modelling Sediment Transport
ABSTRACT
Understanding and quantifying the co-evolution of migrating bed topography and flow turbulence is crucial for characterizing sediment transport in alluvial rivers. The self-organized bed forms at the bottom of these rivers exhibit a complex multi-scale structure that affects and is affected by the dynamics of near-bed turbulence and particle transport. Here we review and integrate some recent results related to the space-time characterization of gravel bed elevation, near-bed 3D turbulence, and sediment transport fluctuations, using simultaneous data obtained in a large-scale laboratory experiment in a 84 m long, 2.75 m wide flume for a range of discharges. We show that migrating bed topography imprints a distinct signature on the power spectral density of near-bed velocity fluctuations, presenting the possibility of inferring bed form characteristics from long time series of turbulence measurements above the bed. A quadrant analysis of velocity fluctuations depicts the sweep-ejection nature of flow turbulence and its relation to particle transport patterns. We report that the probability density functions (PDFs) of the bed elevation increments and the instantaneous Reynolds stress exhibit heavy-tailed statistics and a strong asymmetry, revealing two-way feedbacks between bed form dynamics and near-bed turbulence and having implications for particle movement contribution to large fluctuations in sediment transport. Deviation of these PDFs from Gaussian form calls for looking beyond the distribution of the energy across scales (spectrum) and we present a higher order moments analysis using the standard multifractal formalism of turbulence. We show that both the roughness parameter and the intermittency parameter of the bed elevation fluctuations increase with increasing discharge. Finally, we propose a simple relation to quantify sediment transport rates from bedform averaged instantaneous Reynolds stress.
21.1 Introduction
Migrating bed forms exhibit highly complex dynamics and have been shown to vary with flow strength, grain-size distribution, and local hydraulic, hydrologic and geomorphologic properties (Nordin, 1971; Dinehart, 1989; 1992; Paola and Borgman, 1991; Jerolmack and Mohrig, 2005a, 2005b; van der Mark et al. 2008; McElroy and Mohrig, 2009; Singh et. al., 2009a, 2009b, 2011). Quantifying this bed form variability and complexity is important for understanding its interaction with flow turbulence and particle-scale dynamics (Nelson et al. 1993, 1995; American Society of Civil Engineers Task Force, 2002; Best, 2005; Venditti et al., 2005; Jerolmack and Mohrig, 2005c; Venditti, 2007), for subsurface permeability characterization (Weber, 1980; Best, 2005), stratigraphic record interpretation (Leclair, 2002; Bridge, 2003), aquatic habitat restoration (Yarnell, 2000), and for developing predictive models of sediment transport (Simons et al. 1965; Engel and Lau, 1980; McElroy and Mohrig, 2009). Bed forms have also been shown to influence hyporheic exchange (Packman et al., 2000a, 2000b, 2004) with implications for modeling water cycle and nutrient dynamics in streams.
Many studies have focused on characterizing bed topography both in sand and gravel bed environments and relating it to flow attributes. For example, on the basis of flume experiments, empirical relationships were first developed relating the steady state bed form features (i.e. height, length and migration speed) to physical parameters such as flow intensity, flow depth and sediment size (see, among others Allen, 1962; Van Rijn, 1984; Julien and Klaassen, 1995; Coleman et al., 2006). More recently, increasingly refined numerical models have been developed to investigate the morphodynamic evolution of these bed forms, starting from a plane bed configuration and evolving towards an equilibrium state with bed forms of different scales continuously merging and splitting (Gabel, 1993; Federici and Seminara, 2003; Giri and Shimizu, 2006).
Statistical approaches (e.g. spectral analysis, structure function analysis) have also received significant attention, though, mainly in sand bed environments (see, for e.g. Nordin and Algert, 1966; Hino, 1968; Jain and Kennedy, 1974; Nakagawa and Tsujimoto, 1984; Nikora et al., 1997; Nikora and Goring, 2001; Aberle et al., 2010; Singh et al., 2011), acknowledging the fact that variability is present over many scales, i.e. smaller bed forms riding on larger bed forms. The presence of a broad scaling regime (log-log linear spectrum or second-order structure functions) in the statistical structure of sand bed elevations both in space and time, along with a scale-dependent celerity of migrating sand dunes (e.g. Raudkivi and Witte, 1990; Coleman and Melville, 1994; Nikora et al., 1997; Best, 2005; Jerolmack and Mohrig, 2005b), has been established. In gravel bed rivers, the statistical properties of bed topography have only recently been analysed and mostly on plane beds (Nikora et al., 1998; Marion et al., 2003; Nikora and Walsh, 2004; Aberle and Nikora, 2006), apart from a few studies on gravel bed forms (Dinehart, 1992; Singh et al., 2009a, 2010, 2011).
A parallel body of work has been devoted to understanding the influence of bed forms on flow turbulence (McLean and Smith, 1979; Best, 1993; Venditti and Bennett, 2000; Best, 2005; Jerolmack and Mohrig, 2005c; Venditti, 2007). These bedforms exert a significant influence on the generation of turbulent flow structures (also known as coherent flow structures) that are related to the wakes of bedforms as well as to the jetting of higher velocity between bedforms, and also show attributes of boundary layer flows (Hardy et al., 2009; Keylock et al., 2013). It has been argued that the flow structures generated over these bed forms have many important implications for flow resistance, bed shear stress, and nutrient and sediment transport (e.g. Best, 2005; Nelson et al., 2005). However, most of these studies focused on either fixed bed forms or slow moving bed forms, and mainly in sand bed environments. To the best of our knowledge, the multiscale statistical structure of migrating gravel bed forms and its influence on flow turbulence has not been investigated before, apart from the studies of Dinehart (1999) and Schvidchenko and Pender (2001) and more recently Singh et al. (2010, 2012a).
Bed-form dynamics certainly influence sediment transport rates. It has been argued that, in the presence of bed forms, which create spatially variable bed shear stress fields (Brownlie, 1981; Paola et al., 1999), the total transport rate is significantly different, in fact higher, compared to a channel with spatially uniform bed shear stress (Wilcock and Kenworthy, 2002). Therefore, to account for the effect of bed forms on sediment transport, a surrogate predictor other than average bed shear stress is required. For such a purpose, understanding and classifying flow turbulence above a moving bed may provide a better insight for further physical understanding of turbulence – bed form –sediment interactions leading to more accurate sediment transport models and parameterizations (McLean et al., 1994; Nelson et al., 1995; Best, 2005; Singh et al., 2010).
This chapter presents and integrates some recent results in understanding and quantifying the interaction of multiscale migrating gravel bed form topography with flow turbulence and the implications for modelling sediment transport. We use long time series of simultaneously collected velocity fluctuations, bed elevations and sediment transport rates to characterize the multiscale variability in both flow and bed structures and relate this variability to sediment transport rates. Some of the results discussed herein have been presented in Singh et al. (2010, 2011, and 2012a).
The chapter is structured as follows. In Section 21.2 a brief review of the experimental setup and data collected is given. Section 21.3 presents physical characteristics along with multiscale statistics of gravel bed topography. Section 21.4 focuses on the statistical characterization of flow turbulence, whereas interaction of flow turbulence with bed topography is presented in Section 21.5. Section 21.6 presents quantification of sediment transport from instantaneous Reynolds stress. Finally, concluding remarks are presented in Section 21.7.
21.1.1 Experimental setup and data collected
In order to investigate the interaction of bed topography with flow turbulence and the implications of this interaction for sediment transport, we embarked a few years ago on a large-scale controlled experiment in the main channel facility at the St Anthony Falls Laboratory of University of Minnesota (see Singh et al., 2013), for the scope of this experiment, termed StreamLab). The main channel used in this study is 84 m long, 2.75 m wide and 1.8 m deep (only the 55 m long upstream section of the flume was used as the test section) with a maximum discharge capacity of 8000 L s−1. It is a partial-recirculating flume, in that it has the ability to recirculate gravel while the water flows through the flume without recirculation. Water for the channel is drawn directly from the Mississippi River. The channel bed was composed of a mixture of sand and gravel with a broad particle size distribution characterized by d50 = 7.7 mm, d16 = 2.2 mm and d84 = 21.2 mm. The mean specific density of sediment of all size fractions was ∼ 2.65. The thickness of the bed at the start of the each run was approximately 0.45 m.
Prior to data collection, a constant water discharge, Q, was fed into the channel to achieve dynamic equilibrium in transport and slope adjustment for both water surface and bed. The assessment of this dynamic equilibrium state was evaluated by checking the stability of the 60 min average total sediment flux at the downstream end of the test section. In other words, when the average of the previous 60 min of instantaneous sediment flux values computed from the weigh pan data stabilized, we determined the channel to be in dynamic equilibrium and proceeded with formal data collection and sampling. After attaining equilibrium, experiments were run for approximately 20 h. Details about the experimental setup and the dynamic equilibrium conditions can be found in Singh et al. (2009a, 2010).
High resolution velocity fluctuations, temporal bed elevation at several locations, and sediment transport rates were measured at the downstream end of the test section. The velocity fluctuations were measured using an acoustic Doppler velocitimeter (ADV) at an approximate distance Dp of 10 cm above the mean bed level with a sampling frequency of 200 Hz. Although the distance, Dp, changed as a function of discharge we kept the ratio k (where k = Dp/σb, σb = std. dev. of bed elevation) constant and ∼5 (Table 21.1). For the bed elevation fluctuations submersible sonar transducers of 2.5 cm diameter were deployed 0.3 m (on an average) below the water surface. The sampling interval of bed elevation measurements was 5 s with a vertical precision of 1 mm. Sediment transport rates were measured using bedload traps located at the downstream end of the test section, consisting of five weighing pans of equal size that spanned the width of the channel. Any bedload sediment transported to the end of the test-section of the channel would fall into the weigh pans, which automatically recorded the mass they contained every 1.1 s. Figure 21.1a shows the schematic diagram of the setup of ADV, sonars and bedload traps (pans) located at the downstream end of the test section. Measurements were taken over a range of discharges corresponding to different bed shear stresses for approximately 20 h. Here we report the analysis of the data collected at discharges of 1500 L s−1 and 2800 L s−1 corresponding to Shields stress of about 0.049 and 0.099 respectively.
Table 21.1 Hydraulic conditions and bed elevation characteristics.
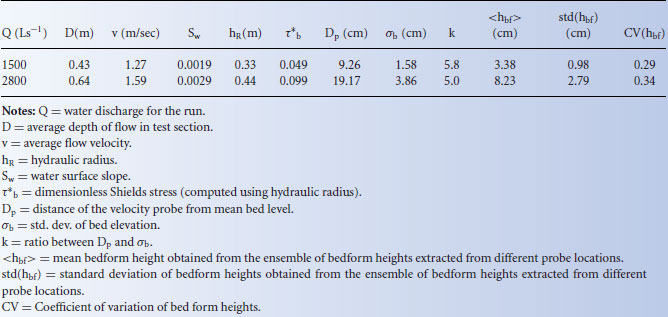
Figure 21.1 (a) Schematic of the main channel showing the location of ADV, sonars and sediment pans. Velocity fluctuations were measured by ADV, bed elevations by sonars and sediment flux by pans for the discharges of 1500 Ls−1 and 2800 Ls−1. Note that the shaded parts (solid dots and box) along the centerline (dashed line) as we move from upstream to downstream represent the locations of velocity, temporal bed elevation and sediment transport rates, respectively, used in this study. (b) Bed forms formed in the main channel at a discharge of 2800 Ls−1. The direction of the flow is from top to the bottom of the Figure 21.1(b).

21.2 Characterization of bed topography
21.2.1 Physical characteristics of bed topography
Figure 21.1b shows the bed forms formed in the main channel at the discharge of 2800 L s−1. At the low discharge (1500 L s−1) the bed forms were mainly two-dimensional bedload sheets and were changing to three-dimensional dunes at higher discharges (2800 L s−1). The temporal variability of bed elevation as recorded by a sonar transducer (sonar 3) at a resolution of 5 s is shown in Figure 21.2a whereas Figure 21.2b shows the simultaneously sampled (5 min averaged) sediment transport rates for the discharge of 2800 L s−1. Bed form characteristics were extracted from the time series of bed elevation using methodologies described in (Singh et al., 2011, 2012a). and their statistics (mean and standard deviation of bed form height) are shown in Table 21.1 for both discharges of 1500 L s−1 and 2800 L s−1. From Table 21.1 it can be seen that the mean bed form height increases with increasing discharge (3.38 cm and 8.23 cm, respectively for 1500 L s−1 and 2800 L s−1) and so does their standard deviation (0.98 cm and 2.79 cm, respectively), keeping however the coefficient of variation approximately constant and equal to 0.3.
Figure 21.2 Time series of the bed elevation (a), sediment transport rates (b), velocity fluctuations in the longitudinal direction (c) and velocity fluctuations in the vertical direction (d) for the discharge of 2800 Ls−1.
21.2.2 Multiscale statistics of bed topography
Bed elevation and its evolution are found to exhibit variability across a range of scales from the grain-size scale to the bed-form scale. A common way to characterize this variability is via computing the power spectral density (hereafter PSD) or wavelet spectrum. Both spectra measure the distribution of energy (variance) as a function of scale. In the absence of significant nonstationarities calling for localized analysis via wavelets, these spectra are comparable although the wavelet spectrum is smoother (as it integrates over frequency bands, see the detailed discussion and comparison in Singh et al. 2011).
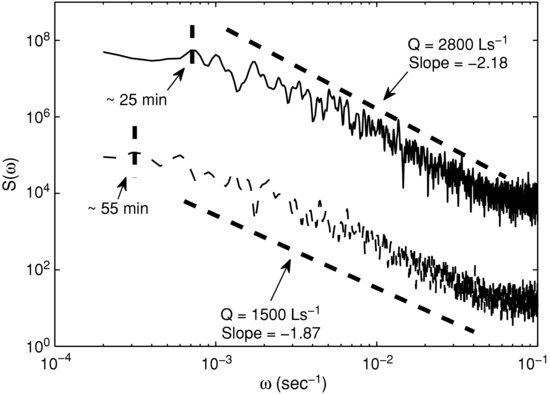
Figure 21.3 shows the PSD of the bed elevation series for the discharges of 1500 L s−1 (bottom spectrum) and 2800 L s−1 (top spectrum). From Figure 21.3 it can be seen that the PSD follows a power law-decay with a slope of ∼1.87 and ∼2.18 for 1500 L s−1 and 2800 L s−1, respectively, suggesting the presence of statistical scaling in the bed elevation series. At the same time, as the slope increases with increasing discharge, the time-scale corresponding to the largest bed form decreases, indicating, as expected, faster bedform movement at higher discharge. For example, the time-scale of the largest bed form at 1500 L s−1 is 55 min whereas at 2800 L s−1 it is 25 min.
Figure 21.3 Power spectral density of temporal bed elevation for the discharge of 1500 Ls−1 (bottom spectrum: broken line) and 2800 Ls−1 (top spectrum: solid line). Note that the time scale of the largest bed form is higher for the lower discharge. Also note that the spectrum at higher discharge (2800 Ls−1) is displaced by two orders of magnitude vertically.
The PSD of a signal, and therefore the variance of its increments as a function of scale, characterizes how the second order moment changes with scale/frequency and as such it fully characterizes only a Gaussian PDF of increments over scales. Figure 21.4a, shows the PDFs of the bed elevation increments (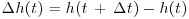 , where
, where 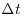 is the resolution of the measurement, i.e. 5 s) at 1500 L s−1 and 2800 L s−1. The positive increments of the bed elevation series (
is the resolution of the measurement, i.e. 5 s) at 1500 L s−1 and 2800 L s−1. The positive increments of the bed elevation series (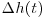 > 0) correspond to depositional events (i.e. to an increase of elevation at the point of measurement during an interval
> 0) correspond to depositional events (i.e. to an increase of elevation at the point of measurement during an interval 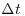 ) and negative values (
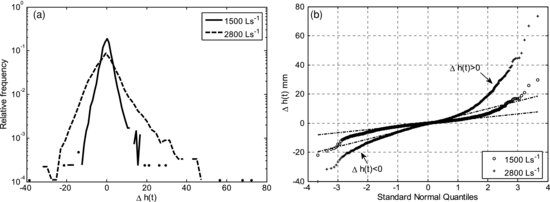
) and negative values (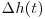 < 0) to erosional events. As can be seen from Figure 24.4a the PDFs of bed elevation increments show significant deviation from the Gaussian distribution and also a pronounced asymmetry. A formal way to quantify this asymmetry is by computing the asymmetry index
< 0) to erosional events. As can be seen from Figure 24.4a the PDFs of bed elevation increments show significant deviation from the Gaussian distribution and also a pronounced asymmetry. A formal way to quantify this asymmetry is by computing the asymmetry index 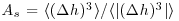 . For 1500 L s−1 discharge As was found to be 0.25 and for 2800 L s−1 0.54, suggesting that the asymmetry in the PDF of bed elevation increments increases with increasing discharge. Another way of characterizing this asymmetry is via higher order distributional plots reported in Singh et al., (2012a).
. For 1500 L s−1 discharge As was found to be 0.25 and for 2800 L s−1 0.54, suggesting that the asymmetry in the PDF of bed elevation increments increases with increasing discharge. Another way of characterizing this asymmetry is via higher order distributional plots reported in Singh et al., (2012a).
Figure 21.4 Comparison of the pdfs (left) and q–q plots (right) of bed elevation increments for the discharges of 1500 Ls−1 and 2800 Ls−1. The dash lines in the q–q plots represent the Gaussian pdfs.
Along with asymmetry, the PDF of the bed elevation increments shows a concave up shape for the positive tails, depicting a heavy-tailed behaviour. This heavy-tailed behaviour, along with the deviation from Gaussian distribution, can be strongly appreciated from quantile-quantile plots (Figure 21.4b), where the dotted lines represent the Gaussian distribution. A formal parameterization of these heavy-tailed distributions can be found in Singh et al., (2012a).
Deviation from a Gaussian distribution calls for the examination of higher order statistical moments of bed elevation increments. For this, a higher order structure function analysis, which quantifies the manner in which higher order statistical moments of the local fluctuations in the bed elevation series change with scale, was performed. In particular, a statistical analysis was performed on the differences (or increments) of the bed elevation time series h(t) at different scales a, denoted by 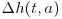 , and defined as
, and defined as
(21.1) 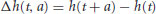
where t is the time and a is the scale. The qth order statistical moment estimates of the absolute values of the increments at scale a, M(q, a), are defined as
(21.2) 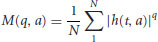
where N is the number of data points of the series at scale a. As an extension to second order (spectral) scaling, higher order statistical scaling or scale-invariance requires M(q, a) to be a power law function of the scale a, that is
(21.3) 
where τ(q) is called the scaling exponent function. A linear dependence of τ(q) on the order of the moment q is the signature of simple scaling and the proportionality coefficient H is the so-called Hurst exponent. H relates to the spectral slope 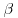 as
as 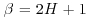 (Singh et al., 2011), implying that a single exponent H completely characterizes how all the statistical moments (and therefore the whole PDF) change with scale.
(Singh et al., 2011), implying that a single exponent H completely characterizes how all the statistical moments (and therefore the whole PDF) change with scale.
In most natural phenomena (e.g. atmospheric turbulence, precipitation series, streamflows, cloud structures, soil hydraulic conductivity, etc.) the nature of scaling is more complex and more than one parameter is needed to characterize the nonlinear dependence of τ(q) on q. The standard multifractal formalism of turbulence (Parisi and Frisch, 1985) asserts that two parameters c1 and c2, under the assumption of a quadratic approximation of 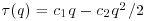 , deriving from a log-normal cascade phenomenology, characterize the change of the non-Gaussian PDF over scales and thus the dependence of higher order structure functions on scale. The parameter c1 is a measure of the average “roughness” ' of the series whereas the parameter c2, the intermittency parameter, gives a measure of the inhomogeneous arrangement of the local abrupt fluctuations in the series. The reader is referred to Venugopal et al. (2006) and Singh et al. (2011) for more details on the theoretical foundations, interpretations and the details of this analysis.
, deriving from a log-normal cascade phenomenology, characterize the change of the non-Gaussian PDF over scales and thus the dependence of higher order structure functions on scale. The parameter c1 is a measure of the average “roughness” ' of the series whereas the parameter c2, the intermittency parameter, gives a measure of the inhomogeneous arrangement of the local abrupt fluctuations in the series. The reader is referred to Venugopal et al. (2006) and Singh et al. (2011) for more details on the theoretical foundations, interpretations and the details of this analysis.
Figures 21.5a and 21.5b show the computed τ(q) curves from the slopes of the log-log plots of the moments M(q, a) (not shown here for brevity) within the scaling range for the bed elevations at 1500 L s−1 and 2800 L s−1 discharge, respectively. (Note that the scaling range, i.e. the range of scales where the structure functions show log-log linearity, is of the order of 0.5–8 min at 1500 L s−1 and 0.5–7 min at 2800 L s−1; see Singh et al. (2012a) for details about structure functions scaling range.) It can be seen from Figures 25.5a and 25.5b that the τ(q) has a nonlinear dependence on q, which is an indication of the presence of multifractality. A summary of the computed multifractal parameters c1 and c2 along with the scaling ranges for both studied discharges is presented in Table 21.2. It is interesting to note that both the roughness coefficient c1 and the intermittency coefficient c2 increase with increasing discharge.
Table 21.2 Multiscale statistics of temporal bed elevations.

Figure 21.5 Scaling exponents τ(q) estimated from the log–log linear regressions within the scaling regions of statistical moments of order q for discharges of 1500 Ls−1 (a) and 2800 Ls−1 (b). Notice the deviation of τ(q) from the straight line, establishing the presence of multifractality.
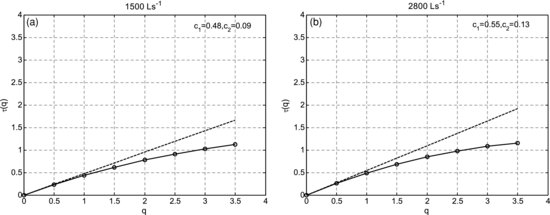
Several observations can be made from the multifractal properties of the bed elevation series shown in Table 21.2. First, the increase of c1 (roughness parameter) with increasing discharge suggests that bed elevation fluctuations are smoother overall at higher discharge than at lower discharge. Second, the increase of c2 with increasing discharge suggests a faster rate of change of the PDF shape across a range of scales and a more inhomogeneous arrangement of the various strength singularities, or abrupt bed elevation fluctuations, over time at higher discharge than at lower discharge. In the case of a mono-fractal (c2 = 0) the shape of the PDF of the increments does not change with scale. However, the above analysis does not explicitly incorporate the asymmetric nature of the PDFs in scaling parameterization and this topic needs further study.
21.3 Flow velocities above migrating bed forms
21.3.1 Streamwise and vertical velocity spectra: implications for grain sorting
Velocity fluctuations over homogeneous surfaces or plane bed topography have been analysed previously in terms of their PSD, scaling properties, intermittency and characteristic shape of their PDF at different scales (Kolmogorov, 1961; Perry et al. 1986; Nezu and Nakagawa, 1993; Katul et al. 1995; Malecot et al. 2000; Porté-Agel et al. 2000). In the PSD of velocity fluctuations, three different ranges of scale have been identified. The first scaling range is observed at the low frequencies also known as the ‘production range’ and is found at scales larger than approximately 2πz (where z is the distance to the surface) and smaller than the integral scale of the turbulence (on the order of the depth of flow in a channel). This range is characterized by a −1 spectral slope (Kader and Yaglom, 1991; Katul et al., 1995). The second scaling range is observed at the intermediate frequencies and is often referred to as the ‘inertial subrange’. This range is characterized by a −5/3 spectral slope (Kolmogorov, 1961) and is associated with eddy scales smaller than approximately 2πz. The third scaling subrange is the viscous subrange observed at smaller scales than the surface roughness size where spectra decay much faster than in the inertial subrange (Nezu and Nakagawa, 1993; Nikora and Goring, 2000). In addition to the power-law scaling ranges in the PSD of velocity fluctuations, the PDFs of velocity fluctuations have been shown to roughly evolve from a stretched exponential shape near the Kolmogorov scale to a Gaussian shape near the integral scale (e.g. Malecot et al. 2000).
In the case of an inhomogeneous surface such as, for example, flow velocities above a bedform dominated bed, the statistics of the velocity field are affected by these roughness elements and their spatial distribution along the channel reach (Robert et al., 1992; Robert et al., 1993; Roy et al., 2004; Lamarre and Roy, 2005). This effect can be seen in Figures 21.6a and 21.6b, where the PSD of the streamwise velocity fluctuations for the discharges of 1500 L s−1 and 2800 L s−1 are shown. From these figures, two clear power-law scaling ranges can be observed, separated by a spectral gap. For relatively small scales (high frequencies), for example, in the case of 1500 L s−1, in the range of 0.1 s to 1.5 s, the slope of the PSD is –5/3, which corresponds to the Kolmogorov spectrum of turbulence. It is associated with turbulent eddy motions of sizes smaller than the distance from the velocity sensor to the gravel bed. A second scaling range, which we refer to here as the ‘dynamic scaling range’, is observed for scales between 50 s and 65 min, for which the slope of the PSD is ∼−1.05 (Figure 21.6a). The range of the observed spectral gap is from 8 s to 50 s (see Figure 21.6a). The scales from the high-frequency end of the spectral gap, which also coincides with the integral scale of the turbulence, to the low-frequency end of the inertial subrange shows a spectral slope of ∼−1.
Figure 21.6 Power spectral densities of velocity fluctuations in the streamwise direction for the discharge of 1500 Ls−1 (a) and 2800 Ls−1 (b). In the velocity spectra, scaling at small scales is due to turbulence (slope = –5/3) and at larger scales is affected by the migrating bed topography (slope ≈ – 1.05 for 1500 Ls−1 and slope ≈ – 1.15 for 2800 Ls−1).
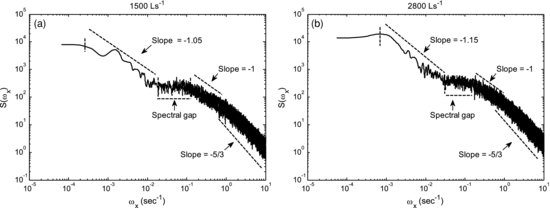
At 2800 L s−1, the dynamic scaling range in the PSD of velocity fluctuations is shifted towards higher frequencies and is from 35 s to 28 min with a spectral slope ∼–1.15 (Figure 21.6b). This shift of the dynamic scaling range towards higher frequencies at increased discharge suggests, as expected, that the bed forms at higher flow (2800 L s−1) are moving faster than the bed forms at the lower flow (1500 L s−1). The spectral gap in the case of 2800 L s−1 is from 6 s to 35 s. It is interesting to note that at the 2800 L s−1, the dynamic scaling range is much smoother than the dynamic scaling range at 1500 L s−1. We hypothesize that this is due to the presence of smaller bed forms riding on the longer wavelength (smaller relief) bed load sheets present at the lower discharge. Also note that the largest time-scale present in the PSD of velocity fluctuations (65 min and 28 min for 1500 L s−1 and 2800 L s−1, respectively) is similar to the largest time scale present in the PSD of bed elevation fluctuations (55 min and 25 min, respectively), suggesting that bed elevation imprints a distinct signature onto the velocity fluctuations. From the above results, it can be concluded that some of the characteristics of bed forms can be inferred from flow structures sampled close to the bed, although the field application of this method would require a long time series of river flow velocities. More detailed discussion of the different scaling regimes of the PSD of velocity fluctuations in the streamwise direction can be found in Singh et al. (2010).
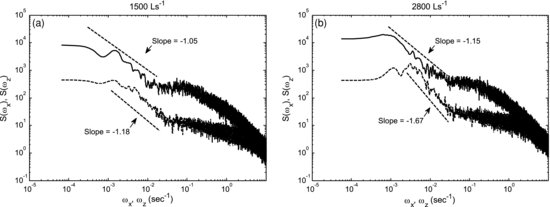
In comparison with the PSD of the streamwise velocity fluctuations, the PSD of vertical velocity fluctuations show that the evolving bed forms imprint a distinct signature on vertical velocities although with different characteristics than those of the streamwise component. Figures 21.7a and 21.7b compare the spectra of streamwise and vertical velocity components at 1500 L s−1 and 2800 L s−1, respectively. The following observations are made. First, the dynamic scaling range is much smaller in the vertical than in the streamwise components (50 sec to 15 min and 25 sec to 40 min at 1500 L s−1 and 2800 L s−1 discharges, respectively; see Table 21.3 for summary). Second, the spectral slopes in these regimes are significantly higher compared to their streamwise velocity counterparts (–1.18 and –1.67, respectively for 1500 L s−1 and 2800 L s−1). This indicates that transfer of energy across scales in the vertical direction is much faster compared to the streamwise direction. Third, the anisotropy (streamwise versus vertical component statistics) increases as discharge increases. This is evidenced by the relative change of spectral slopes in Figure 21.7. It is partially explained by the increasing heterogeneity in the bed topography at higher discharges (see Tables 21.1 and 21.2), suggesting a strong feedback between the complex bed topography and anisotropic flow above. (Note that in the case of isotropic turbulence the slope of the PSD of the velocity fluctuations remains the same regardless of the direction of measurement).
Table 21.3 Statistics of velocity fluctuations.

Figure 21.7 Comparison of power spectral density of velocity fluctuations in the streamwise direction ( : solid line/top PSD) and in the vertical direction (
: solid line/top PSD) and in the vertical direction ( : broken line/bottom PSD) for the discharge of 1500 Ls−1 (a) and 2800 Ls−1 (b). Note the significant difference between the slope of
: broken line/bottom PSD) for the discharge of 1500 Ls−1 (a) and 2800 Ls−1 (b). Note the significant difference between the slope of 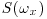 and
and 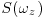 , and its increase with increasing discharge indicating higher anisotropy at higher discharge.
, and its increase with increasing discharge indicating higher anisotropy at higher discharge.
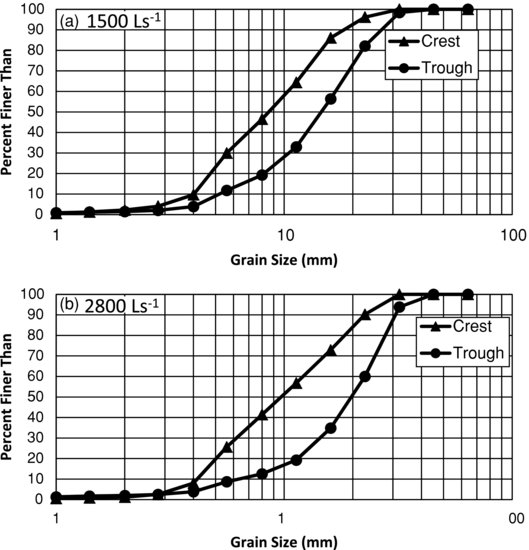
The anisotropic flow, influenced by bed forms, leads to grain sorting within the bed form (Schvidchenko and Pender, 2001; Best, 2005). This effect can be seen in Figures 21.8a and 21.8b which show that the grain size distribution (hereafter GSD) obtained from surface sampling of the bed is much coarser in the bed form trough than the GSD obtained from bed form crest. In fact, the difference between crest and trough GSD increases with higher discharge. For example, d50 for the crest of the bed forms at 1500 L s−1 and at 2800 Ls−1 are 8.65 mm and 9.9 mm, whereas d50 for the trough of the bed forms are 14.76 mm and 19.88 mm. These GSDs are obtained from the ensemble average of two surface samples for both crest and trough using an approach similar to that of Klingeman (see Singh et al. 2012c for details about surface GSD sampling).
Figure 21.8 Grain size distribution (GSD) obtained from the surface patches (30 cm X 30 cm in size) on the crest and the trough of the bed form for the discharges of 1500 Ls−1 (a) and 2800 Ls−1 (b). Note that these GSDs are the ensemble average of two random samples for both crest and trough.
21.3.2 Instantaneous Reynolds stress
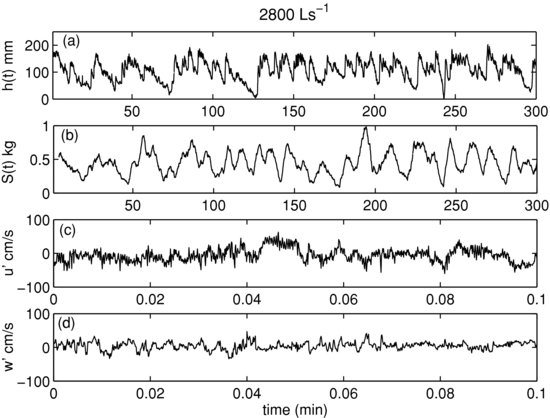
Having studied the multiscale structure of streamwise and vertical velocity components, we turn our attention to the instantaneous Reynolds stress, which is more relevant for particle entrainment and characterizing variability in sediment transport rates. These instantaneous Reynolds stresses, ρwu′w′, were computed as the product of mean-removed velocity fluctuations in the longitudinal (u′: Figure 21.2) and vertical (w′: Figure 21.2d) directions. Here, ρw is the density of the water, assumed to be 1000 kg m−3. Figure 21.9 shows the PDFs of the normalized instantaneous Reynolds stress for 1500 L s−1 and 2800 L s−1 discharge. The normalization was performed by dividing by (ρs − ρw)gd50, where ρs is the specific density of sediment (2650 kg m−3), g is the acceleration due to gravity and d50 is the median particle size diameter. We use the term ‘instantaneous Reynolds stress’ for the product of ρu′w′, not to be confused with ‘local Reynolds stress’ or ‘Reynolds stress’, which is the average of instantaneous Reynolds stress ρu′w′, denoted by < ρu′w′ >.
Figure 21.9 Semilog pdfs of normalized instantaneous Reynolds stress for the discharges of 1500 Ls−1 and 2800 Ls−1.
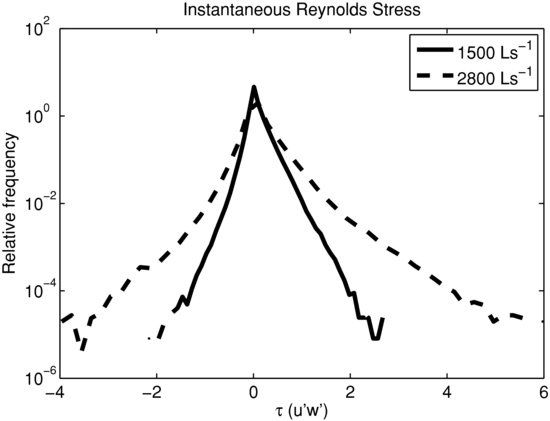
From Figure 21.9, it is observed that as the discharge increases the magnitude of the instantaneous Reynolds stress values increases with a strong asymmetry towards larger positive values, i.e. as Q increases u′w′ > 0 increases faster than u′w′ < 0. To examine this further, it is instructive to look at the joint PDF of u′ and w′ by plotting these velocity fluctuation components in the so-called quadrant plot, as done in the next section.
21.4 Turbulence patterns modulated by bed forms
The highly asymmetric PDFs of the instantaneous Reynolds stress indicate the presence of very large amplitude positive fluctuations in instantaneous Reynolds stress. These high fluctuations could arise due to very large fluctuations in u′ and/or w′. The contribution of each velocity component (u and w) to the turbulent flow field can be quantified by plotting the joint probability distribution of the longitudinal u′ and vertical w′ velocity fluctuations. These plots are referred to as quadrant plots (Lu and Willmarth, 1973; Bennett and Best, 1995; Nelson et al., 1995; Buffin-Belanger et al., 2000; Best, 2005; Hardy et al., 2009, 2010).
Four regions of distinct fluid motion characteristics with respect to the mean flow are differentiated in quadrant plots. Quadrant 1 (Q1) represents outward interaction, where u′ > 0 and w′ > 0; Quadrant II (Q2) represents ejection, where u′ < 0 and w′ > 0; Quadrant III (Q3) represents inward interaction, where u′ < 0 and w′ < 0; and Quadrant IV (Q4) represents sweep motion, where u′ > 0 and w′ < 0 (Nelson et al. 1995; Buffin-Bélanger et al., 2000; Best, 2005; Hardy et al., 2009, 2010; Singh et al., 2012a). Ejection and sweeps contribute positively to the instantaneous Reynolds stress whereas outward interaction and inward interaction contribute negatively. Positive values in the vertical direction (w′ > 0) indicate flow which is upward and away from the bed. Also, in Q2, large-scale vorticities arise both along the shear layer and at the flow reattachment (Bennett and Best, 1995; Best, 2005).
Nelson et al. (1995) suggested that quadrant analysis can be used to partition the total Reynolds stress (ρu′w′) between different components and assess the importance of each of these for sediment transport. In particular, Nelson et al. (1995) argued that sweeps are extremely common, contribute positively to the instantaneous Reynolds stress, and collectively move the majority of sediment. However, they also mentioned that outward interactions are relatively rare, contribute negatively to instantaneous Reynolds stress, and individually move as much sediment as sweeps and much more than ejections and inward interactions.
Figures 21.10a and 21.10b show the joint probability distribution of u′ with w′ for 1500 L s−1 and 2800 L s−1 discharge, respectively. It can be seen from these figures that, although the mass of the distribution is more concentrated in Q4, the scatter of the joint distribution of velocity fluctuations is higher in Q2 and increases with increasing discharge. To characterize the observed scatter in the quadrant plots, ellipses were fit (using least squares) to the scatter plots. These ellipses show the asymmetric growth of the quadrants as a function of discharge (Figure 21.10c). It is interesting that the scatter of the joint distribution of velocity fluctuations in Q2 increases with increasing discharge, leading to anisotropic growth of the ellipse as a function of discharge. (The relative contribution of the instantaneous Reynolds stress to each quadrant can be seen in Figures 21.10a and 21.10b for 1500 L s−1 and 2800 L s−1, respectively.) The higher scatter in the velocity fluctuations in Q2 is due to the presence of prominent topography (taller bed forms), which increases as the bed form height increases as these taller bed forms create more space for ejection events.
Figure 21.10 Scatter plot of u′ (streamwise velocity fluctuations) with w′ (vertical velocity fluctuations) for the discharges of 1500 Ls−1 (a), 2800 Ls−1 (b) and the asymmetric growth of the quadrants captured by the best fitted ellipse as a function of discharge (c). Notice that, although the mass is more concentrated in quadrant 4, the scatter of the joint distribution of velocity fluctuations in quadrant 2 becomes more prominent as the discharge increases leading to anisotropic growth of the ellipse as a function of discharge.
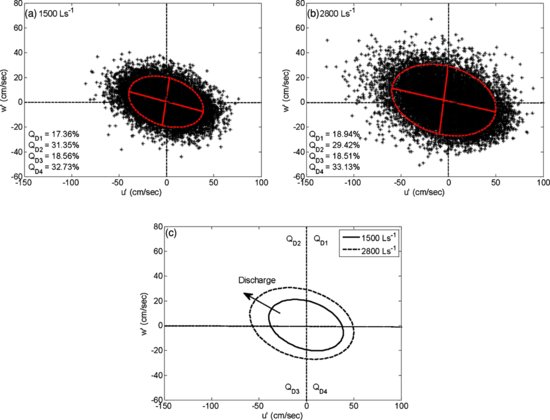
21.5 Sediment transport modelling
Sediment transport prediction over bed forms is highly complex and depends on estimation of the shear stress over the bed (Smith and McLean, 1977; McLean et al. 1999; Best, 2005). Experimental and field studies have suggested that the existing methods are inappropriate for modelling sediment transport over bed form fields (Nelson et al., 1993; McLean et al., 1994; Nelson et al., 1995; Best, 2005) since most of these formulas were obtained over a flat or plane bed (see Wong and Parker, 2006 and references therein). In recent years, it has been argued that the turbulent flow field over bed forms is critical in determining instantaneous bed shear stress (Nelson et al. 1993; McLean et al.1994; Nelson et al. 1995; Best, 2005). However, characterizing sediment transport from observations at a single point is challenging due to the spatial/temporal heterogeneities on the bed topography (Boyer et al., 2006). In the case of steady uniform flow (e.g. plane bed), turbulence can be fully characterized by the local bed shear stress (Nelson et al., 1995; Schmeeckle and Nelson, 2003). However, in the case of nonuniform flow (e.g. bed with bedforms) the total shear stress is divided into skin friction and form drag (see Wiberg and Nelson, 1992; Best, 2005). In such flows, modelling sediment transport generally requires more information than just the local bed shear stress (Nelson et al., 1995; Sumer et al., 2003).
Figure 21.11 shows the dimensionless transport rate 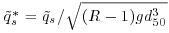 versus dimensionless shear stress,
versus dimensionless shear stress, 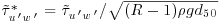 . Here,
. Here, 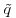 and
and 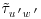 are the total transport rate and instantaneous Reynolds stress averaged over the bed form time scales, R is sediment-specific gravity, and g is the acceleration due to gravity. These bedform averaged quantities were obtained by performing a filtering of the sediment transport rate series (Figure 21.2b) and the instantaneous Reynolds stress series via a moving average window of size equal to the average bed form time scale (more details about the bed form averaging can be found in Singh et al., 2012a). It is noticed from Figure 21.11 that the variability, one standard deviation above and below the mean, for both the sediment transport rates and the averaged instantaneous Reynolds stress increases with increasing discharge.
are the total transport rate and instantaneous Reynolds stress averaged over the bed form time scales, R is sediment-specific gravity, and g is the acceleration due to gravity. These bedform averaged quantities were obtained by performing a filtering of the sediment transport rate series (Figure 21.2b) and the instantaneous Reynolds stress series via a moving average window of size equal to the average bed form time scale (more details about the bed form averaging can be found in Singh et al., 2012a). It is noticed from Figure 21.11 that the variability, one standard deviation above and below the mean, for both the sediment transport rates and the averaged instantaneous Reynolds stress increases with increasing discharge.
Figure 21.11 Sediment transport rate as a function of instantaneous Reynolds stress, averaged over bed form time-scales. Error bars indicate the standard deviation about the bed form averaged quantities. The dashed line represents the modified Meyer-Peter and Müller transport relation using τc* = 0.03.
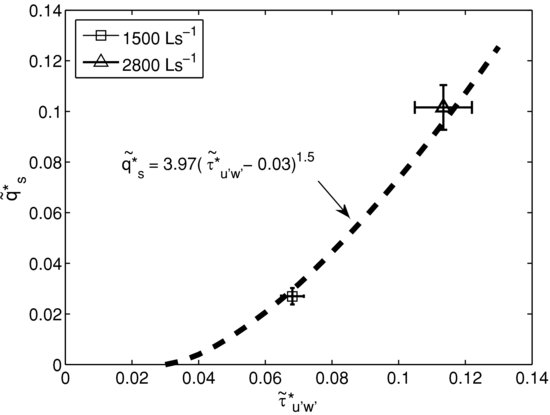
From Figure 21.11 it can be seen that the trend closely matches that of the Meyer-Peter and Müller (1948) relation as modified by Wong and Parker (2006), suggesting that the bedform averaged instantaneous Reynolds stress provides an effective form-drag correction. However, to match the transport function to the observations, it is necessary to use a critical Shields number τc* = 0.03, i.e. adapting the relation 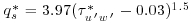 (see dotted line in Figure 21.11), which is considerably smaller than the value of 0.047 found by Meyer-Peter and Müller to match the plane-bed transport of well-sorted gravels. A value of the order of τc* = 0.03 was also found by Wilcock, (1998) for the total transport of widely sorted sandy gravel mixtures, although general guidelines for the appropriate value of τc* for the total transport rates of sandy gravel mixtures are not available. A more detailed description of the relation between instantaneous Reynolds stress and the sediment transport rate with one more experimental data set is given in Singh et al. (2012a).
(see dotted line in Figure 21.11), which is considerably smaller than the value of 0.047 found by Meyer-Peter and Müller to match the plane-bed transport of well-sorted gravels. A value of the order of τc* = 0.03 was also found by Wilcock, (1998) for the total transport of widely sorted sandy gravel mixtures, although general guidelines for the appropriate value of τc* for the total transport rates of sandy gravel mixtures are not available. A more detailed description of the relation between instantaneous Reynolds stress and the sediment transport rate with one more experimental data set is given in Singh et al. (2012a).
21.6 Summary and concluding remarks
In this chapter, we used simultaneously sampled high-resolution temporal data of gravel bed elevation, velocity fluctuations and sediment transport rates to understand and quantify the interaction of flow and bed forms above the sediment-water interface. The experiments were conducted in a large experimental channel at the St Anthony Falls Laboratory, University of Minnesota. The main results of this study can be stated as follows.
- A deviation from Gaussian distribution (presence of thick tails or large probability of extreme values) and a strong asymmetry in the PDFs of the bed elevation increments and instantaneous Reynolds stresses was observed.
- The higher order statistical moments analysis of bed elevations increments demonstrates the presence of a nonlinear relation between the scaling exponent and the order of moment (multifractal scaling). which we parameterized here with two parameters: the roughness and the intermittency parameters. Both the roughness parameter and the intermittency parameter were found to increase with increasing discharge.
- The signature of bedform evolution on the near-bed velocity fluctuations was confirmed via the presence of two distinct power-law scaling regimes separated by a spectral gap in the PSD (power spectral density) of streamwise velocity fluctuations. It is suggested that the bed structures can be inferred from flow structures sampled close to the bed, although the field application of this method would require a long time series of river flow velocities.
- From the PSD of velocity fluctuations in the longitudinal and vertical direction, it was demonstrated that with an increase in the multiscale variability of the bed topography, the anisotropy in the flow field increases, suggesting complex interaction between the bed topography and near-bed turbulence.
- The influence of evolving bed topography (i.e. at higher discharges taller bed forms) can be seen on the joint probability distribution of streamwise and vertical velocity fluctuations (quadrant plots). Namely, as discharge increases the elongation of the shape of the PDF towards larger magnitude of u′w′ < 0 (i.e. positive instantaneous Reynolds stresses) increases due to the increased variability of bed form sizes and the faster transfer of energy from larger to smaller scale bed structures (as seen by the larger spectral slope of bed elevation fluctuations for larger discharges).
- A simple relation to quantify sediment transport rates using bedform averaged instantaneous Reynolds stress is proposed. It is suggested that the bedform averaged instantaneous Reynolds stress can serve as a form-drag surrogate parameter, which results in a Meyer-Peter-Müller type of sediment transport equation although with an ‘adjusted’ critical Shields number significantly lower than the commonly used value in plane-bed transport. Further data would be needed to validate the applicability and generality of such a sediment transport equation over bed forms.
21.7 Acknowledgements
This research was supported by the National Center for Earth-surface Dynamics (NCED), a Science and Technology Center funded by NSF under agreement EAR-0120914 as well as by NSF grants EAR-0824084 and EAR-0835789. The experiments performed for this study are the follow up of previous experiments (known as StreamLab06) conducted at the St Anthony Falls Laboratory as part of an NCED program to examine physical-biological aspects of sediment transport (http://www.nced.umn.edu). The authors are grateful to Jeff Marr, Craig Hill and Sara Johnson for providing help in running the experiments. We thank Peter Wilcock, Fernando Porté-Agel and Stefano Lanzoni for many fruitful discussions and collaborations. We also thank Mike Church and Sean Bennett whose suggestions and constructive comments substantially improved our presentation and refined our interpretations. Computer resources were provided by the Minnesota Supercomputing Institute, Digital Technology Center at the University of Minnesota.
References
Aberle, J. and Nikora, V. (2006) Statistical properties of armored gravel bed surfaces. Water Resources Research 42,W11414, DOI: 10.1029/2005WR004674.
Aberle, J., Nikora, V., Henning, M. et al. (2010) Statistical characterization of bed roughness due to bed forms: a field study in the Elbe River at Aken, Germany. Water Resources Research 46, W03521, DOI: 10.1029/2008WR007406.
Allen, J.R.L. (1962) Asymmetrical ripple marks and the origin of cross-stratification. Nature 194, 167–169.
American Society of Civil Engineers, Task Force. (2002) Flow and transport over dunes. Journal of Hydraulic Engineering 128, 726–728.
Bennett, S.J. and Best, J.L. (1995) Mean flow and turbulence structure over fixed, two-dimensional dunes: implications for sediment transport and dune stability. Sedimentology 42, 491–513.
Best, J. (1993) On the interactions between turbulent flow structure, sediment transport and bedform development: some considerations from recent experimental research. In Turbulence: Perspectives on Flow and Sediment Transport (ed. N.J. Clifford, J.R. French and J. Hardisty), John Wiley & Sons, Ltd, Chichester, pp. 61–92.
Best, J. (2005) The fluid dynamics of river dunes: a review and some future research directions. Journal of Geophysical Research 110, F04S02. DOI: 10.1029/2004JF000218.
Boyer, C., Roy, A.G. and Best, J.L. (2006) Dynamics of a river channel confluence with discordant beds: flow turbulence, bed load sediment transport, and bed morphology. Journal of Geophysical Research 111, F04007. DOI: 10.1029/2005JF000458.
Bridge, J.S. (2003) Rivers and Floodplains: Forms, Processes and Sedimentary Record, Blackwell, Malden, MA.
Brownlie, W.R. (1981) Prediction of Flow Depth and Sediment Discharge in Open Channels. W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, Report KH-R-43A.
Buffin-Bélanger, T.A., Roy, A.G. and Kirkbride, A.D. (2000) On large-scale flow structures in a gravel-bed river. Geomorphology 32, 417–435.
Coleman, S.E. and Melville, B.W. (1994) Bed-form development. Journal of Hydraulic Engineering 120, 544–560.
Coleman, S.E., Nikora, V.I., McLean, S.R., Clunie, T.M., Schlicke, T. and Melville B.W. (2006) Equilibrium hydrodynamics concept for developing dunes. Physics of Fluids 18, 105104. DOI: 10.1063/1.2358332.
Dinehart, R.L. (1989) Dune migration in a steep, coarse-bedded stream. Water Resources Research 25, 911–923.
Dinehart, R.L. (1992) Evolution of coarse gravel bedforms: field measurements at flood stage. Water Resources Research 28, 2667–2689.
Dinehart, R. L. (1999) Correlative velocity fluctuations over a gravel river bed, Water Resources Research 35, 569–582.
Engel, P. and Lau, Y.L. (1980) Computation of bed load using bathymetric data. Journal of the Hydraulics Division, ASCE 106, 380–639.
Federici, B. and Seminara, G. (2003) On the convective nature of bar instability. Journal of Fluid Mechanics 487, 125–145.
Gabel, S.L. (1993) Geometry and kinematics of dunes during steady and unsteady flows in the Calamus River, Nebraska, USA. Sedimentology 40, 237–269.
Giri, S. and Shimizu, Y. (2006) Numerical computation of sand dune migration with free surface flow. Water Resources Research 42, W10422. DOI: 10.1029/2005WR004588.
Hardy, R.J., Best, J.L., Lane, S.N. and Carbonneau P.E. (2009) Coherent flow structures in a depth-limited flow over a gravel surface: The role of near-bed turbulence and influence of Reynolds number. Journal of Geophysical Research 114, F01003. DOI: 10.1029/2007JF000970.
Hardy, R.J., Best, J.L., Lane, S.N. and Carbonneau P.E. (2010) Coherent flow structures in a depth-limited flow over a gravel surface: The influence of surface roughness. Journal of Geophysical Research 115, F03006. DOI: 10.1029/2009JF001416.
Hino, M. (1968) Equilibrium-range spectra of sand waves formed by flowing water. Journal of Fluid Mechanics 34, 565–573.
Jain, S.C. and Kennedy, J.F. (1974) The spectral evolution of sedimentary bedforms. Journal of Fluid Mechanics 63, 301–314.
Jerolmack, D.J. and Mohrig, D. (2005a) Frozen dynamics of migrating bedforms. Geology 33, 57–60.
Jerolmack, D.J. and Mohrig, D. (2005b) A unified model for subaqueous bed form dynamics. Water Resources Research 41, W12421. DOI: 10.1029/2005WR004329.
Jerolmack, D.J. and Mohrig, D. (2005c) Interactions between bed forms: topography, turbulence and transport. Journal of Geophysical Research 110, F02014. DOI: 10.1029/2004JF000126.
Julien, P.Y. and Klaassen, G.J. (1995) Sand-dune geometry of large rivers during floods. Journal of Hydraulic Engineering 121, 657–663.
Kader, B.A. and Yaglom, A.M. (1991) Spectra and correlation functions of surface layer atmospheric turbulence in unstable thermal stratification. In Turbulence and Coherent Structures (eds O. Métais and M. Lesieur). Kluwer, Dordrecht, pp. 387–412.
Katul, G.G., Chu, C.R., Parlange, M.B. et al. (1995) Low wavenumber spectral characteristics of velocity and temperature in the atmospheric boundary layer. Journal of Geophysical Research 100, 14 243–14 255.
Keylock, C., Singh, A., Foufoula-Georgiou, E. (2013) The influence of migrating bedforms on the velocity-intermittency structure of turbulent flow over a gravel bed. Geophysical Research Letters DOI: 10.1002/grl.50337
Kolmogorov, A. (1961) Dissipation of energy in the locally isotropic turbulence. In Turbulence: Classic Papers on Statistical Theory (eds S.K. Friedlander and L. Topper), Wiley-Interscience, Hoboken, NJ, pp. 151–155.
Lamarre, H. and Roy, A.G. (2005) Reach scale variability of turbulent flow characteristics in a gravel-bed river. Geomorpholgy 60, 95–113.
Leclair, S.F. (2002) Preservation of cross-strata due to migration of subaqueous dunes: an experimental investigation. Sedimentology 49, 1157–1180.
Lu, S.S. and Willmarth, W.W. (1973) Measurements of structure of Reynolds stress in a turbulent boundary layer. Journal of Fluid Mechanics 60, 481–511.
Malecot, Y., Auriault, C., Kahalerras, H. et al. (2000) A statistical estimator of turbulence intermittency in physical and numerical experiments. European Physical Journal B16, 549–561.
Marion, A., Tait, S.J. and McEwan, I.K. (2003) Analysis of small-scale gravel bed topography during armoring. Water Resources Research 39, 1334. DOI: 10.1029/2003WR002367.
McElroy, B. and Mohrig, D. (2009) Nature of deformation of sandy bed forms. Journal of Geophysical Research 114, F00A04. DOI: 10.1029/2008JF001220.
McLean, S.R. and Smith, J.D. (1979) Turbulence measurements in the boundary layer over a sand wave field. Journal of Geophysical Research 84, 7791–7808. DOI: 10.1029/JC084iC12p07791.
McLean, S.R., Wolfe, S.R. and Nelson, J.M. (1999) Predicting boundary shear stress and sediment transport over bedforms. Journal of Hydraulic Engineering 125, 725–736.
McLean, S.R., Nelson, J.M. and Wolfe, S.R. (1994) Turbulence structure over two-dimensional bed forms: implications for sediment transport. Journal of Geophysical Research 99, 12 729–12 747.
Meyer-Peter, E. and Müller, R. (1948) Formulas for bed-load transport. Proceedings of the Second Meeting of the International Association for Hydraulic Research, Stockholm, Sweden, pp. 39–64.
Nakagawa, H. and Tsujimoto, T. (1984) Spectral analysis of sand bed instability. Journal of Hydraulic Engineering 110, 467–483.
Nelson, J., Burman, A.R., Shimizu, Y. et al. (2005) Computing flow and sediment transport over bedforms. In Fourth International Conference on River, Coastal. and Estuarine Morphodynamics (RCEM), Proceedings (G. Parker and M.H. Garcia), Taylor & Francis, London, pp. 861–868.
Nelson, J.M., McLean, S.R. and Wolfe, S.R. (1993) Meanflow and turbulence fields over two-dimensional bedforms. Water Resources Research 29, 3935–3953.
Nelson, J.M., Shreve, R.L., McLean, S.R. and Drake T.G. (1995) Role of near-bed turbulence structure in bed load transport and bed form mechanics. Water Resources Research 31, 2071–2086. DOI: 10.1029/95WR00976.
Nezu, I. and Nakagawa, H. (1993) Turbulence in Open-Channel Flows, A.A. Balkema, Rotterdam.
Nikora, V.I., Goring, D.G. and Biggs, B.J.F. (1998) On gravel-bed roughness characterization. Water Resources Research 34, 517–527.
Nikora, V.I. and Goring, D.G. (2000) Flow turbulence over fixed and weakly mobile gravel beds. Journal of Hydraulic Engineering 126, 679–690.
Nikora, V.I. and Goring, D.G. (2001) Extended self-similarity in geophysical and geological applications. Mathematical Geology 33, 251–271. DOI: 10.1023/A:1007630021716.
Nikora, V.I., Sukhodolov, A.N. and Rowinski, P.M. (1997) Statistical sand wave dynamics in one-directional water flows. Journal of Fluid Mechanics 351, 17–39.
Nikora, V.I. and Walsh, J. (2004) Water-worked gravel surfaces: High-order structure functions at the particle scale. Water Resources Research 40, W12601. DOI: 10.1029/2004WR003346.
Nordin, C.F., Jr. (1971) Statistical Properties of Dune Profiles, United States Geological Survey, Washington, DC.
Nordin, C.F., and Algert, J.H. (1966) Spectral analysis of sand waves. Journal of the Hydraulics Division, ASCE 92(HY5), 95–114.
Packman, A.I., Brooks, N.H. and Morgan J.J. (2000a) A physicochemical model for colloid exchange between a stream and a sand streambed with bed forms. Water Resources Research 36, 2351–2361.
Packman, A.I., Brooks, N.H. and Morgan, J.J. (2000b) Kaolinite exchange between a stream and streambed: Laboratory experiment and validation of a colloid transport model. Water Resources Research, 36, 2363–2372.
Packman, A.I., Salehin, M. and Zaramella, M. (2004) Hyporheic exchange with gravel beds: basic hydrodynamic interactions and bedform-induced advective flows. Journal of Hydraulic Engineering 130, 647–656.
Paola, C. and Borgman, L. (1991) Reconstructing random topography from preserved stratification. Sedimentology 38, 553–565. DOI: 10.1111/j.1365-3091.1991.tb01008.x.
Paola, C., Parker, G., Mohrig, D.C. and Whipple, K.X. (1999) The influence of transport fluctuations on spatially averaged topography on a sandy, braided fluvial plane. Numerical Experiments in Stratigraphy (special paper) 62, 211–218.
Parisi, G. and Frisch, U. (1985) On the singularity structure of fully developed turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics, vol. 88 (ed. M. Ghil). North-Holland, Amsterdam, pp. 84–87.
Perry, A.E., Henbest, S. and Chong, M.S. (1986) A theoretical and experimental study of wall turbulence. Journal of Fluid Mechanics 165, 163–199.
Porté-Agel, F., Meneveau, C. and Parlange, M.B. (2000) A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. Journal of Fluid Mechanics 415, 216–284.
Raudkivi, A.J. and Witte, H.H. (1990) Development of bed features. Journal of Hydraulic Engineering 116, 1063–1079.
Robert, A., Roy, A.G. and de Serres, B. (1992) Changes in velocity profiles at roughness transitions in coarse-grained channels. Sedimentology 39, 725–735.
Robert, A., Roy, A.G. and de Serres, B. (1993) Space–time correlations of velocity measurements at a roughness transition in a gravel-bed river. In Turbulence: perspectives on flow and sediments transport (eds N.J. Clifford, J.R. French and J. Hardisty). John Wiley & Sons, Ltd, Chichester, pp. 167–183.
Roy, A.G., Buffin-Bélanger, T., Lamarre H. and Kirkbride, A.D. (2004) Size, shape and dynamics of large-scale turbulent flow structures in a gravel-bed river. Journal of Fluid Mechanics 500, 1–27.
Schmeeckle, M.W. and Nelson, J.M. (2003) Direct simulation of bedload transport using a local, dynamic boundary condition. Sedimentology 50, 279–301.
Shvidchenko, A.B. and Pender, G. (2001) Macroturbulent structure of open-channel flow over gravel beds. Water Resources Research 37, 709–719.
Simons, D.B., Richardson, E.V. and Nordin, Jr., C.F. (1965) Bedload Equation for Ripples and Dunes, United States Geological Survey, Washington D.C., pp. 1–9.
Singh, A., Czuba, J., Marr, J.D.G. et al. (2013) StreamLab Collaboratory: Experiments, Data sets and Research Synthesis. Water Resources Research 49. DOI: 10.1002/wrcr.20142.
Singh, A., Fienberg, K., Jerolmack, D.J. et al. (2009a) Experimental evidence for statistical scaling and intermittency in sediment transport rates. Journal of Geophysical Research 114, F01025. DOI:10.1029/2007f000963.
Singh, A., Foufoula-Georgiou, E, Porté-Agel, F. and Wilcock, P.R. (2012a) Coupled dynamics of the co-evolution of bed topography, flow turbulence and sediment transport in an experimental flume. Journal of Geophysical Research 117, F04016. DOI:10.1029/2011JF002323.
Singh, A., Guala, M., Lanzoni, S. and Foufoula-Georgiou E. (2012b) Bedform effect on the reorganization of surface and subsurface grain size distribution in gravel bedded channel, Acta Geophysica 60, 1607-1638. DOI: 10.2478/s11600-012-0075-z.
Singh, A., Lanzoni, S. and Foufoula-Georgiou, E. (2009b) Nonlinearity and complexity in gravel-bed dynamics. Stochastic Environmental Research and Risk Assessment 23, 967–975. DOI: 10.1007/S00477-008-0269-8.
Singh, A., Lanzoni, S., Wilcock, P.R. and Foufoula-Georgiou, E. (2011) Multi-scale statistical characterization of migrating bedforms in gravel and sand bed rivers. Water Resources Research 47, W12526. DOI: 10.1029/2010WR010122.
Singh, A., Porte-Agel, F. and Foufoula-Georgiou, E. (2010) On the influence of gravel bed dynamics on velocity power spectra. Water Resources Research 46,W04509. DOI: 10.1029/2009WR008190.
Smith, J.D. and McLean, S.R. (1977) Spatially-averaged flow over a wavy surface. Journal of Geophysical Research 82, 1735–1746.
Sumer, B.M., Chua, L.H.C., Cheng, N.-S and Fredsoe J. (2003) Influence of turbulence on bed load sediment transport. Journal of Hydraulic Engineering 129, 585–596.
van der Mark, C.F., Blom, A. and Hulscher, S.J.M.H. (2008) Quantification of variability in bedform geometry. Journal of Geophysical Research 113, F03020. DOI: 10.1029/2007JF000940.
van Rijn, L.C. (1984) Sediment transport, part III: Bed forms and alluvial roughness. Journal of Hydraulic Engineering 110, 1733–1754.
Venditti, J.G. and Bennett, S.J. (2000) Spectral analysis of turbulent flow and suspended sediment transport over fixed dunes. Journal of Geophysical Research 105, 22035–22047.
Venditti, J.G., Church, M.A. and Bennett, S.J. (2005) Morphodynamics of small-scale superimposed sandwaves over migrating dune bedforms. Water Resources Research 41, W10423. DOI: 10.1029/2004WR003461.
Venditti, J.G. (2007) Turbulent flow and drag over fixed two- and three-dimensional dunes. Journal of Geophysical Research 112, F04008. DOI: 10.1029/2006JF000650.
Venugopal, V., Roux, S.G., Foufoula-Georgiou, E. and Arneodo, A. (2006) Revisiting multifractality of high-resolution temporal rainfall using a wavelet-based formalism. Water Resources Research 42, W06D14. DOI: 10.1029/2005WR004489.
Weber, K. J. (1980) Influence on fluid flow of common sedimentary structures in sand bodies. Society of Petroleum Engineers, Tulsa OK, Paper SPE 9247.
Wiberg, P.L. and Nelson, J.M. (1992) Unidirectional flow over asymmetric and symmetric ripples. Journal of Geophysical Research 97, 12 745–12 761. DOI: 10.1029/92JC01228.
Wilcock, P.R. (1998) Two-fraction model of initial sediment motion in gravel-bed rivers. Science 280, 410–412.
Wilcock, P.R. and Kenworthy, S.T. (2002) A two-fraction model for the transport of sand/gravel mixtures. Water Resources Research 38, 1194. DOI: 10.1029/2001WR000684.
Wong, M. and Parker, G. (2006) Reanalysis and correction of bed-load relation of Meyer-Peter and Müller using their own database, Journal of Hydraulic Engineering 132, 1159–1168.
Yarnell, S.M. (2000) The Influence of Sediment Supply and Transport Capacity on Foothill Yellow-Legged Frog Habitat, South Yuba River, California. MS thesis, University of California, Davis, CA.