when a ≡ 0, when 
is solvable, and when a ≡ x2 is not solvable modulo p, respectively. Show thatExercise: For an odd prime p let when a ≡ 0, when is solvable, and when a ≡ x2 is not solvable modulo p, respectively. Show that
a)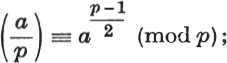 
b) If 
(mod p), then 
where μ(a) denotes the number of solutions of the congruence ax ≡ —y (p) satisfying 
c)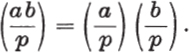 
(Hint: Compute the transfer from the multiplicative group 
of the prime residue classes modulo p to the subgroup 
of ± 1 (mod p) in a) according to (19) and in b) by taking 
(mod p) as representative system.)