2

                   

THE MEASURE OF ALL THINGS

An Introduction to Scaling

Before turning to the many issues and questions raised in the opening chapter I want to devote this chapter to a broad introduction to some of the basic concepts used throughout the rest of the book. Although some readers may well be familiar with some of this material, I want to make sure we’re all on the same page.

The overview is primarily from a historical perspective, beginning with Galileo explaining why there can’t be giant insects and ending with Lord Rayleigh explaining why the sky is blue. In between, I will touch upon Superman, LSD and drug dosages, body mass indices, ship disasters and the origin of modeling theory, and how all of these are related to the origins and nature of innovation and limits to growth. Above all, I want to use these examples to convey the conceptual power of thinking quantitatively in terms of scale.

1. FROM GODZILLA TO GALILEO

From time to time, like many scientists I receive requests from journalists asking for an interview, usually about some question or problem related to cities, urbanization, the environment, sustainability, complexity, the Santa Fe Institute, or occasionally even about the Higgs particle. Imagine my surprise, then, when I was contacted by a journalist from the magazine Popular Mechanics informing me that Hollywood was going to release a new blockbuster version of the classic Japanese film Godzilla and that she was interested in getting my views on it. You may recall that Godzilla is an enormous monster that mostly roams around cities (Tokyo, in the original 1954 version) causing destruction and havoc while terrorizing the populace.

The journalist had heard that I knew something about scaling and wanted to know “in a fun, goofy, nerdy sort of way, about the biology of Godzilla (to tie in with the release of the new movie) . . . how fast such a large animal would walk . . . how much energy his metabolism would generate, how much he would weigh, etc.” Naturally, this new twenty-first-century all-American Godzilla was the biggest incarnation of the character yet, reaching a lofty height of 350 feet (106 meters), more than twice the height of the original Japanese version, which was “only” 164 feet (50 meters). I immediately responded by telling the journalist that almost any scientist she contacted would tell her that no such beast as Godzilla could actually exist because, if it were made of pretty much the same basic stuff as we are (meaning all of life), it could not function because it would collapse under its own weight.

The scientific argument upon which this is based was articulated more than four hundred years ago by Galileo at the dawn of modern science. It is in its very essence an elegant scaling argument: Galileo asked what happens if you try to indefinitely scale up an animal, a tree, or a building, and with his response discovered that there are limits to growth. His argument set the basic template for all subsequent scaling arguments right up to the present day.

For good reason, Galileo is often referred to as the “Father of Modern Science” for his many seminal contributions to physics, mathematics, astronomy, and philosophy. He is perhaps best known for his mythical experiments dropping objects of different sizes and compositions from the top of the Leaning Tower of Pisa to show that they all reached the ground at the same time. This nonintuitive observation contradicted the accepted Aristotelian dogma that heavy objects fall faster than lighter ones in direct proportion to their weight, a fundamental misconception that was universally believed for almost two thousand years before Galileo actually tested it. It is amazing in retrospect that until Galileo’s investigations no one seems to have thought of, let alone bothered, testing this apparently “self-evident fact.”

Galileo at ages thirty-five and sixty-nine; he died less than ten years later. Aging and impending mortality, vividly exhibited in these portraits, will be discussed in some detail in chapter 4.

Galileo’s experiment revolutionized our fundamental understanding of motion and dynamics and paved the way for Newton to propose his famous laws of motion. These laws led to a precise quantitative mathematical, predictive framework for understanding all motion whether here on Earth or across the universe, thereby uniting the heavens and Earth under the same natural laws. This not only redefined man’s place in the universe, but provided the gold standard for all subsequent science, including setting the stage for the coming of the age of enlightenment and the technological revolution of the past two hundred years.

Galileo is also famous for perfecting the telescope and discovering the moons of Jupiter, which convinced him of the Copernican view of the solar system. By continuing to insist on a heliocentric view derived from his observations, Galileo was to end up paying a heavy price. At the age of sixty-nine and in poor health, he was brought before the Inquisition and found guilty of heresy. He was forced to recant and after a brief imprisonment spent the rest of his life under house arrest (nine more years during which he went blind). His books were banned and put on the Vatican’s infamous Index Librorum Prohibitorum. It wasn’t until 1835, more than two hundred years later, that his works were finally dropped from the Index, and until 1992—almost four hundred years later—and for Pope John Paul II to publicly express regret for how Galileo had been treated. It is sobering to realize that words written long ago in Hebrew, Greek, and Latin, based on opinion, intuition, and prejudice, can so overwhelmingly outweigh scientific observational evidence and the logic and language of mathematics. Sad to say, we are hardly free from such misguided thinking today.

Despite the terrible tragedy that befell Galileo, humanity reaped a wonderful benefit from his incarceration. It may very well have happened anyway, but it was while he was under house arrest that he wrote what is perhaps his finest work, one of the truly great books in the scientific literature, titled Discourses and Mathematical Demonstrations Relating to Two New Sciences.¹ The book is basically his legacy from the preceding forty years during which he grappled with how to systematically address the challenge of understanding the natural world around us in a logical, rational framework. As such, it laid the groundwork for the equally monumental contribution of Isaac Newton and pretty much for all of the science that followed. Indeed, in praising the book, Einstein was not exaggerating when he called Galileo “the Father of Modern Science.”²

It’s a great book. Despite its forbidding title and somewhat archaic language and style, it’s surprisingly readable and a lot of fun. It is written in the style of a “discourse” between three men (Simplicio, Sagredo, and Salviati) who meet over four days to discuss and debate the various questions, big and small, that Galileo is seeking to answer. Simplicio represents the “ordinary” layperson who is curious about the world and asks a series of apparently naive questions. Salviati is the smart fellow (Galileo!) with all of the answers, which are presented in a compelling but patient manner, while Sagredo is the middleman who alternates between challenging Salviati and encouraging Simplicio.

On the second day of their discourse they turn their attention to what appears to be a somewhat arcane discussion on the strength of ropes and beams, and just as you are wondering where this somewhat tedious, detailed discussion is going, the fog clears, the lights flash, and Salviati makes the following pronouncement:

From what has already been demonstrated, you can plainly see the impossibility of increasing the size of structures to vast dimensions either in art or in nature; likewise the impossibility of building ships, palaces, or temples of enormous size in such a way that their oars, yards, beams, iron-bolts, and, in short, all their other parts will hold together; nor can nature produce trees of extraordinary size because the branches would break down under their own weight; so also it would be impossible to build up the bony structures of men, horses, or other animals so as to hold together and perform their normal functions if these animals were to be increased enormously in height . . . for if his height be increased inordinately he will fall and be crushed under his own weight.

There it is: our paranoid fantasies of giant ants, beetles, spiders, or for that matter, Godzillas, so graphically displayed by the comic and film industries, had already been conjectured nearly four hundred years ago by Galileo, who then brilliantly demonstrates that they are a physical impossibility. Or, more precisely, that there are fundamental constraints as to how large they can actually get. So many such science-fiction images are indeed just that: fiction.

Galileo’s argument is elegant and simple, yet it has profound implications. Furthermore, it provides an excellent introduction to many of the concepts we’ll be investigating in the following chapters. It consists of two parts: a geometrical argument showing how areas and volumes associated with any object scale as its size increases (Figure 5) and a structural argument showing that the strength of pillars holding up buildings, limbs supporting animals, or trunks supporting trees is proportional to their cross-sectional areas (Figure 6).

In the accompanying box, I present a nontechnical version of the first of these, showing that if the shape of an object is kept fixed, then when it is scaled up, all of its areas increase as the square of its lengths while all of its volumes increase as the cube.

GALILEO’S ARGUMENT ON HOW AREAS AND VOLUMES SCALE

To begin, consider one of the simplest possible geometrical objects, namely, a floor tile in the shape of a square, and imagine scaling it up to a larger size; see Figure 5. To be specific let’s take the length of its sides to be 1 ft. so that its area, obtained by multiplying the length of two adjacent sides together, is 1 ft. × 1 ft. = 1 sq. ft. Now, suppose we double the length of all of its sides from 1 to 2 ft., then its area increases to 2 ft. × 2 ft. = 4 sq. ft. Similarly, if we were to triple the lengths to 3 ft., then its area would increase to 9 sq. ft., and so on. The generalization is clear: the area increases with the square of the lengths.

This relationship remains valid for any two-dimensional geometric shape, and not just for squares, provided that the shape is kept fixed when all of its linear dimensions are increased by the same factor. A simple example is a circle: if its radius is doubled, for instance, then its area increases by a factor of 2 × 2 = 4. A more general example is that of doubling the dimensions of every length in your house while keeping its shape and structural layout the same, in which case the area of all of its surfaces, such as its walls and floors, would increase by a factor of four.

(5) Illustration of how areas and volumes scale for the simple case of squares and cubes. (6) The strength of a beam or limb is proportional to its cross-sectional area.

This argument can be straightforwardly extended from areas to volumes. Consider first a simple cube: if the lengths of its sides are increased by a factor of two from, say, 1 ft. to 2 ft., then its volume increases from 1 cubic foot to 2 × 2 × 2 = 8 cubic. Similarly, if the lengths are increased by a factor of three, the volume increases by a factor of 3 × 3 × 3 = 27. As with areas, this can straightforwardly be generalized to any object, regardless of its shape, provided we keep it fixed, to conclude that if we scale it up, its volume increases with the cube of its linear dimensions.

Thus, when an object is scaled up in size, its volumes increase at a much faster rate than its areas. Let me give a simple example: if you double the dimensions of every length in your house keeping its shape the same, then its volume increases by a factor of 23 = 8 while its floor area increases by only a factor of 22 = 4. To take a much more extreme case, suppose all of its linear dimensions were increased by a factor of 10, then all surface areas such as floors, walls, and ceilings would increase by a factor of 10 × 10 = 100 (that is, a hundredfold), whereas the volumes of its rooms would increase by the much larger factor of 10 × 10 × 10 = 1,000 (a thousandfold).

This has huge implications for the design and functionality of much of the world around us, whether it’s the buildings we live and work in or the structure of the animals and plants of the natural world. For instance, most heating, cooling, and lighting is proportional to the corresponding surface areas of the heaters, air conditioners, and windows. Their effectiveness therefore increases much more slowly than the volume of living space needed to be heated, cooled, or lit, so these need to be disproportionately increased in size when a building is scaled up. Similarly, for large animals, the need to dissipate heat generated by their metabolism and physical activity can become problematic because the surface area through which it is dissipated is proportionately much smaller relative to their volume than for smaller ones. Elephants, for example, have solved this challenge by evolving disproportionately large ears to significantly increase their surface area so as to dissipate more heat.

This essential difference in the way areas and volumes scale was very likely appreciated by many people before Galileo. His additional new insight was to combine this geometric realization with his realization that the strength of pillars, beams, and limbs is determined by the size of their cross-sectional areas and not by how long they are. Thus a post whose rectangular cross-section is 2 inches by 4 inches (= 8 sq. in.) can support four times the weight of a similar post of the same material whose cross-sectional dimensions are only half as big, namely 1 inch by 2 inches (= 2 sq. in.), regardless of the length of either post. The first could be 4 feet long and the second 7 feet, it doesn’t matter. That’s why builders, architects, and engineers involved in construction classify wood by its cross-sectional dimensions, and why lumber yards at Home Depot and Lowe’s display them as “two-by-twos, two-by-fours, four-by-fours,” and so on.

Now, as we scale up a building or an animal, their weights increase in direct proportion to their volumes provided, of course, that the materials they’re made of don’t change so that their densities remain the same: so doubling the volume doubles the weight. Thus, the weight being supported by a pillar or a limb increases much faster than the corresponding increase in strength, because weight (like volume) scales as the cube of the linear dimensions whereas strength increases only as the square. To emphasize this point, consider increasing the height of a building or tree by a factor of 10 keeping its shape the same; then the weight needed to be supported increases a thousandfold (103) whereas the strength of the pillar or trunk holding it up increases by only a hundredfold (102). Thus, the ability to safely support the additional weight is only a tenth of what it had previously been. Consequently, if the size of the structure, whatever it is, is arbitrarily increased it will eventually collapse under its own weight. There are limits to size and growth.

To put it slightly differently: relative strength becomes progressively weaker as size increases. Or, as Galileo so graphically put it: “the smaller the body the greater its relative strength. Thus a small dog could probably carry on his back two or three dogs of his own size; but I believe that a horse could not carry even one of his own size.”

2. MISLEADING CONCLUSIONS AND MISCONCEPTIONS OF SCALE: SUPERMAN

Superman made his earthly debut in 1938 and still remains one of the great icons of the sci-fi/fantasy world. I have reproduced the first page of the original Superman comic from 1938 in which his origins are explained.³ He had arrived as a baby from the planet Krypton “whose inhabitants’ physical structure was millions of years advanced of our own. Upon reaching maturity the people of his race became gifted with titanic strength.” Indeed, upon maturity Superman “could easily leap ⅛th of a mile; hurdle a twenty-story building . . . raise tremendous weights . . . run faster than an express train . . .” all triumphantly summed up in the famous introduction to the radio serials and subsequent TV series and films: “Faster than a speeding bullet. More powerful than a locomotive. Able to leap tall buildings in a single bound. . . . It’s Superman.”

All of which may well be true. However, in the last frame of that first page there is another bold pronouncement, so important that it warranted being put in capital letters: A SCIENTIFIC EXPLANATION OF CLARK KENT’S AMAZING STRENGTH . . . incredible? No! For even today on our world exist creatures with super-strength!” To support this, two examples are given: “The lowly ant can support weights hundreds of times its own” and “the grasshopper leaps what to man would be the space of several city blocks.”

As persuasive as these examples might appear to be, they represent a classic case of misconceived and misleading conclusions drawn from correct facts. Ants appear to be, at least superficially, much stronger than human beings. However, as we have learned from Galileo, relative strength systematically increases as size decreases. Consequently, scaling down from a dog to an ant following the simple rules of how strength scales with size will show that if “a small dog could probably carry on his back two or three dogs of his own size,” then an ant can carry on his back a hundred ants of his size. Furthermore, because we are about 10 million times heavier than an average ant, the same argument shows that we are capable of carrying only about one other person on ours. Thus, ants have, in fact, the correct strength appropriate for a creature of their size, just as we do, so there’s nothing extraordinary or surprising about their lifting one hundred times their own weight.

The origin myth of Superman and an explanation for his superstrength; from the opening page of the first Superman comic book in 1938.

The misconception arises because of the natural propensity to think linearly, as encapsulated in the implicit presumption that doubling the size of an animal leads to a doubling of its strength. If this were so, then we would be 10 million times stronger than ants and be able to lift about a ton, corresponding to our being able to lift more than ten other people, just like Superman.

3. ORDERS OF MAGNITUDE, LOGARITHMS, EARTHQUAKES, AND THE RICHTER SCALE

We just saw that if the lengths of an object are increased by a factor of 10 without changing its shape or composition, then its areas (and therefore strengths) increase by a factor of 100, and its volumes (and therefore weights) by a factor of 1,000. Successive powers of ten, such as these, are called orders of magnitude and are typically expressed in a convenient shorthand notation as 101, 102, 103, et cetera, with the exponent—the little superscript on the ten—denoting the number of zeros following the one. Thus, 106 is shorthand for a million, or 6 orders of magnitude, because it is 1 followed by 6 zeros: 1,000,000.

In this language Galileo’s result can be expressed as saying that for every order of magnitude increase in length, areas and strengths increase by two orders of magnitude, whereas volumes and weights increase by three orders of magnitude. From which it follows that for a single order of magnitude increase in area, volumes increase by 3/2 (that is, one and a half) orders of magnitude. A similar relationship therefore holds between strength and weight: for every order of magnitude increase in strength, the weight that can be supported increases by one and a half orders of magnitude. Conversely, if the weight is increased by a single order of magnitude, then the strength only increases by ⅔ of an order of magnitude. This is the essential manifestation of a nonlinear relationship. A linear relationship would have meant that for every order of magnitude increase in area, the volume would have also increased by one order of magnitude.

Even though many of us may not be aware of it, we have all been exposed to the concept of orders of magnitude, including fractions of orders of magnitude, through the reporting of earthquakes in the media. Not infrequently we hear news announcements along the lines that “there was a moderate-size earthquake today in Los Angeles that measured 5.7 on the Richter scale which shook many buildings but caused only minor damage.” And occasionally we hear of earthquakes such as the one in the Northridge region of Los Angeles in 1994, which was only a single unit larger on the Richter scale but caused enormous amounts of damage. The Northridge earthquake, whose magnitude was 6.7, caused more than $20 billion worth of damage including sixty fatalities, making it one of the costliest natural disasters in U.S. history, whereas a 5.7 earthquake caused only negligible damage. The reason for this vast difference in impact despite an apparently small increase in magnitude is that the Richter scale expresses size in terms of orders of magnitude.

So an increase of one unit actually means an increase of one order of magnitude, so that a 6.7 earthquake is actually 10 times the size of a 5.7 earthquake. Likewise, a 7.7 earthquake, such as the Sumatra one of 2010, is 10 times bigger than the Northridge quake and 100 times bigger than a 5.7 earthquake. The Sumatra earthquake was in a relatively unpopulated area but still caused widespread destruction via a tsunami that displaced more than twenty thousand people and killed almost five hundred. Sadly, five years earlier, Sumatra had suffered an even more destructive earthquake whose magnitude was 8.7 and therefore yet another 10 times larger. Obviously, in addition to its size, the destruction wreaked by an earthquake depends a great deal on the local conditions such as population size and density, the robustness of buildings and infrastructure, and so on. The 1994 Northridge earthquake and the more recent 2011 Fukushima one, both of which caused huge amounts of damage, were “only” 6.7 and 6.6, respectively.

The Richter scale actually measures the “shaking” amplitude of the earthquake recorded on a seismometer. The corresponding amount of energy released scales nonlinearly with this amplitude in such a way that for every order of magnitude increase in the measured amplitude the energy released increases by one and a half (that is 3⁄2) orders of magnitude. This means that a difference of two orders of magnitude in the amplitude, that is a change of 2.0 on the Richter scale, is equivalent to a factor of three orders of magnitude (1,000) in the energy released, while a change of just 1.0 is equivalent to a factor of the square root of 1,000 = 31.6.⁴

Just to give some idea of the enormous amounts of energy involved in earthquakes, here are some numbers to peruse: the energy released by the detonation of a pound (or half a kilogram) of TNT corresponds roughly to a magnitude of 1 on the Richter scale; a magnitude of 3 corresponds to about 1,000 pounds (or about 500 kg) of TNT, which was roughly the size of the 1995 Oklahoma City bombing; 5.7 corresponds to about 5,000 tons, 6.7 to about 170,000 tons (the Northridge and Fukushima earthquakes), 7.7 to about 5.4 million tons (the 2010 Sumatra earthquake), and 8.7 to about 170 million tons (the 2005 Sumatra earthquake). The most powerful earthquake ever recorded was the Great Chilean Earthquake of 1960 in Valdivia, which registered 9.5, corresponding to 2,700 million tons of TNT, almost a thousand times larger than Northridge or Fukushima.

For comparison, the atomic bomb (“Little Boy”) that was dropped on Hiroshima in 1945 released the energy equivalent of about 15,000 tons of TNT. A typical hydrogen bomb releases well over 1,000 times more, corresponding to a major earthquake of magnitude 8. These are enormous amounts of energy when you realize that 170 million tons of TNT, the size of the 2005 Sumatra earthquake, can fuel a city of 15 million people, equivalent to the entire New York City metropolitan area, for an entire year.

This kind of scale where instead of increasing linearly as in 1, 2, 3, 4, 5 . . . we increase by factors of 10 as in the Richter scale: 101, 102, 103, 104, 105 . . . is called logarithmic. Notice that it’s actually linear in terms of the numbers of orders of magnitude, as indicated by the exponents (the superscripts) on the tens. Among its many attributes, a logarithmic scale allows one to plot quantities that differ by huge factors on the same axis, such as those between the magnitudes of the Valdivia earthquake, the Northridge earthquake, and a stick of dynamite, which overall cover a range of more than a billion (109). This would be impossible if a linear plot was used because almost all of the events would pile up at the lower end of the graph. To include all earthquakes, which range over five or six orders of magnitude, on a linear plot would require a piece of paper several miles long—hence the invention of the Richter scale.

Because it conveniently allows quantities that vary over a vast range to be represented on a line on a single page of paper such as this, the logarithmic technique is ubiquitously used across all areas of science. The brightness of stars, the acidity of chemical solutions (their pH), physiological characteristics of animals, and the GDPs of countries are all examples where this technique is commonly utilized to cover the entire spectrum of the variation of the quantity being investigated. The graphs shown in Figures 1–4 in the opening chapter are plotted this way.

4. PUMPING IRON AND TESTING GALILEO

An essential component of science that often distinguishes it from other intellectual pursuits is its insistence that hypothesized claims be verified by experiment and observation. This is highly nontrivial, as evidenced by the fact that it took more than two thousand years before Aristotle’s pronouncement that objects falling under gravity do so at a rate proportional to their weight to actually be tested—and when carried out, to be found wanting. Sadly, many of our present-day dogmas and beliefs, especially in the nonscientific realm, remain untested yet rigidly adhered to without any serious attempt to verify them—sometimes with unfortunate or even devastating consequences.

So following our detour into powers of ten, I want to use what we’ve learned about orders of magnitude and logarithms to address the issue of checking Galileo’s predictions about how strength should scale with weight. Can we show that in the “real world” strength really does increase with weight according to the rule that it should do so in the ratio of two to three when expressed in terms of orders of magnitude?

In 1956, the chemist M. H. Lietzke devised a simple and elegant confirmation of Galileo’s prediction. He realized that competitive weight lifting across different weight classes provides us with a data set of how maximal strength scales with body size, at least among human beings. All champion weight lifters try to maximize how big a load they can lift, and to accomplish this they have all trained with pretty much the same intensity and to the same degree, so if we compare their strengths we do so under approximately similar conditions. Furthermore, championships are decided by three different kinds of lifts—the press, the snatch, and the clean and jerk—so taking the total of these effectively averages over individual variation of specific talents. These totals are therefore a good measure of maximal strength.

Using the totals of these three lifts from the weight lifting competition in the 1956 Olympic Games, Lietzke brilliantly confirmed the ⅔ prediction for how strength should scale with body weight. The totals for the individual gold medal winners were plotted logarithmically versus their body weight, where each axis represented increases by factors of ten. If strength, which is plotted along the vertical axis, increases by two orders of magnitude for every three orders of magnitude increase in body weight, which is plotted along the horizontal axis, then the data should exhibit a straight line whose slope is ⅔. The measured value found by Lietzke was 0.675, very close to the prediction of ⅔ = 0.667. His graph is reproduced in Figure 7.⁵

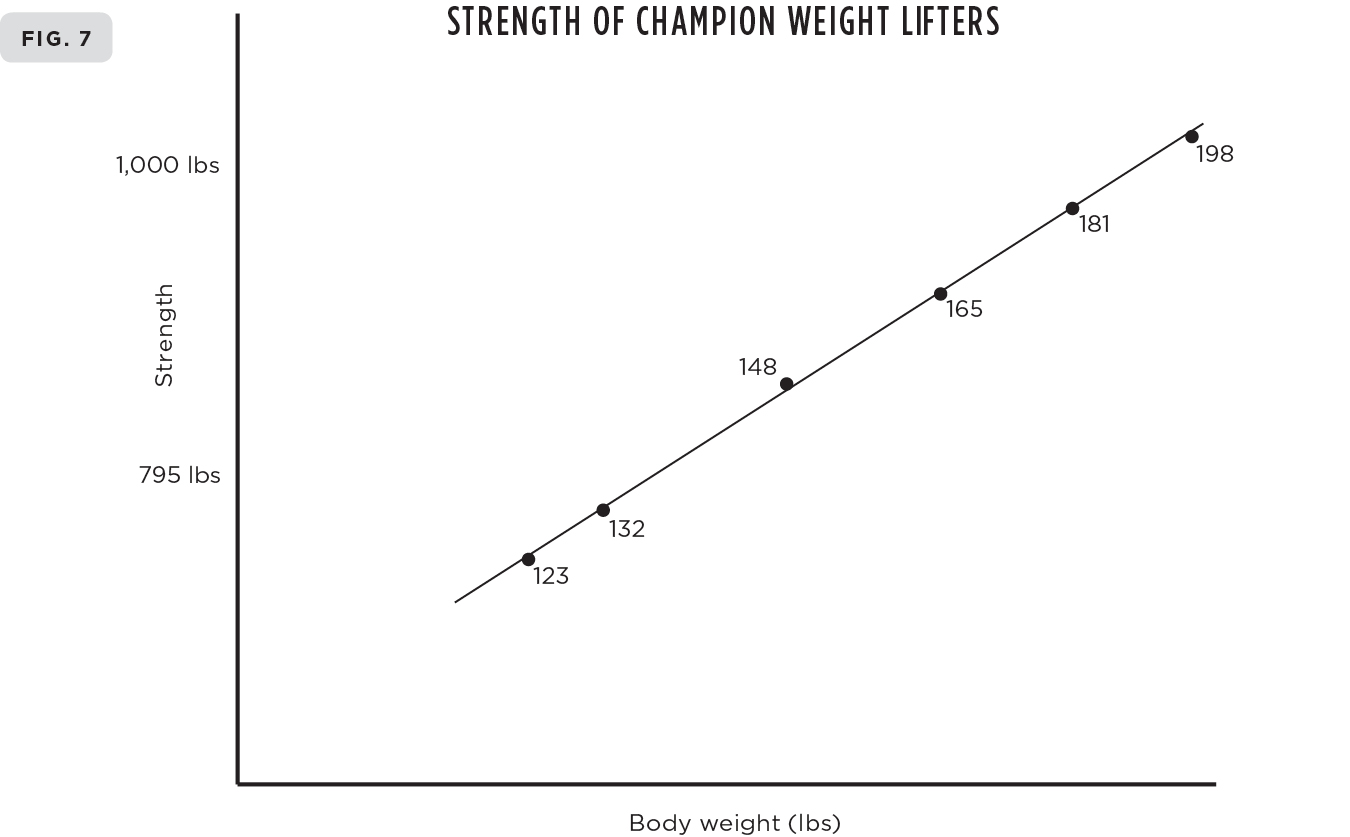
Total weights lifted by champion weight lifters in the 1956 Olympic Games plotted logarithmically versus their body weights, confirming the ⅔ prediction for the slope. Who was the strongest and who was the weakest?

5. INDIVIDUAL PERFORMANCE AND DEVIATIONS FROM SCALING: THE STRONGEST MAN IN THE WORLD

The regularity exhibited by the weight lifting data and its close agreement with the ⅔ prediction for the scaling of strength might seem surprising given the simplicity of the scaling argument. After all, each of us has a slightly different shape, different body characteristics, different history, slightly different genetics, and so on, none of which is accounted for in the derivation of the ⅔ prediction. Using the total sum of the weights lifted by champions who have trained to approximately the same degree helps to average over some of these individual differences. On the other hand, all of us are to a good approximation made of pretty much the same stuff with very similar physiologies. We function very similarly and, as manifested in Figure 7, approximate scaled versions of one another at least as far as strength is concerned. Indeed, by the end of the book, I hope to convince you that this broad similarity extends to almost every aspect of your physiology and life history. So much so in fact that when I talk about “we” being approximately scaled versions of one another, I will mean not just all human beings, but all mammals and, to varying degrees, all of life.

Another way of viewing these scaling laws is that they provide an idealized baseline that captures the dominant, essential features that unite us not only as human beings but also as variations on being an organism and an expression of life. Each individual, each species, and even each taxonomic group deviates to varying degrees from the idealized norms manifested by the scaling laws, with deviations reflecting the specific characteristics that represent individuality.

Let me illustrate this using the weight lifting example. If you look carefully at the graph of Figure 7 you can clearly see that four of the points lie almost exactly on the line, indicating that these weight lifters are lifting almost precisely what they should for their body weights. However, notice that the remaining two, the heavyweight and the middleweight, both lie just a little off the line, one below and one above. Thus, the heavyweight, even though he has lifted more than anyone else, is actually underperforming relative to what he should be lifting given his weight, whereas the middleweight is overperforming relative to his weight. In other words, from the egalitarian level playing field perspective of a physicist, the strongest man in the world in 1956 was actually the middleweight champion because he was overperforming relative to his weight. Ironically, the weakest of all of the champions from this scientific scaling perspective is the heavyweight, despite the fact that he lifted more than anyone else.

6. MORE MISLEADING CONCLUSIONS AND MISCONCEPTIONS OF SCALE: DRUG DOSAGES FROM LSD AND ELEPHANTS TO TYLENOL AND BABIES

The role of size and scale pervades medicine and health even though the ideas and conceptual framework inherent in scaling laws are not explicitly integrated into the biomedical professions. For example, we are all very familiar with the idea that there are standard charts showing how height, growth rate, food intake, and even the circumference of our waists should correlate with our weight, or how these metrics should change during our early development. These charts are none other than representations of scaling laws that have been deemed applicable to the “average healthy human being.” Indeed, doctors are trained to recognize how such variables should on average be correlated with the weight and age of their patients.

Also well known is the related concept of an invariant quantity, such as our pulse rate or body temperature, which does not change systematically with the weight or height of the average healthy individual. Indeed, substantial deviations from these invariant averages are routinely used in the diagnosis of disease or ill health. Having a body temperature of 101°F or a blood pressure of 275/154 is a signal that something’s wrong. These days, a standard physical examination results in a plethora of such metrics that your doctor uses to assess the state of your health. A major challenge of the medical and health industry is to ascertain the quantifiable baseline scale of life, and consequently the extended suite of metrics for the average, healthy human being, including how large a variation or deviation from them can be tolerated.

Not surprisingly, then, many critical problems in medicine can be addressed in terms of scaling. In later chapters several important health issues that concern us all, ranging from aging and mortality to sleep and cancer, will be addressed using this framework. Here, however, I first want to whet the appetite by considering some equally important medical issues that involve ideas stemming from Galileo’s insight into the tension between the way in which areas and volumes scale. These will reveal how easy it is to form misconceptions that lead to seriously misleading conclusions arising from unconsciously using linear extrapolation.

In the development of new drugs and in the investigation of many diseases, much of the research is conducted on so-called model animals, typically standard cohorts of mice that have been bred and refined precisely for research purposes. Of fundamental importance to medical and pharmaceutical research is how results from such studies should be scaled up to human beings in order to prescribe safe and effective dosages or draw conclusions regarding diagnoses and therapeutic procedures. A comprehensive theory of how this can be accomplished has not yet been developed, although the pharmaceutical industry devotes enormous resources to addressing it when developing new drugs.

A classic example of some of the challenges and pitfalls is an early study investigating the potentially therapeutic effects of LSD on humans. Although the term “psychedelic” was already coined by 1957, the drug was almost unknown outside of a specialized psychiatric community in 1962, when the psychiatrist Louis West (no relation), together with Chester Pierce at the University of Oklahoma and Warren Thomas, a zoologist at the Oklahoma City zoo, proposed investigating its effects on elephants.

Elephants? Yes, elephants and, in particular, Asiatic elephants. Although it may sound somewhat eccentric to use elephants rather than mice as the “model” for studying the effects of LSD, there were some not entirely implausible reasons for doing so. It so happens that Asiatic elephants periodically undergo an unpredictable transition from their normal placid obedient state to one in which they become highly aggressive and even dangerous for periods of up to two weeks. West and his collaborators speculated that this bizarre and often destructive behavior, known as musth, was triggered by the autoproduction of LSD in elephants’ brains. So the idea was to see if LSD would induce this curious condition and, if so, thereby gain insight into LSD’s effects on humans from studying how they react. Pretty weird, but maybe not entirely unreasonable.

However, this immediately raises an intriguing question: how much LSD should you give an elephant?

At that time little was known about safe dosages of LSD. Although it had not yet entered the popular culture it was known that even dosages of less than a quarter milligram would induce a typical “acid trip” for a human being and that a safe dose for cats was about one tenth of a milligram per kilogram of body weight. The investigators chose to use this latter number to estimate how much LSD they should give to Tusko the elephant, their unsuspecting subject that resided at the Lincoln Park Zoo in Oklahoma City.

Tusko weighed about 3,000 kilograms, so using the number known to be safe for cats, they estimated that a safe and appropriate dose for Tusko would be about 0.1 milligram per kilogram multiplied by 3,000 kilograms, which comes out to 300 milligrams of LSD. The amount they actually injected was 297 milligrams. Recall that a good hit of LSD for you and me is less than a quarter milligram. The results on Tusko were dramatic and catastrophic. To quote directly from their paper: “Five minutes after the injection he [the elephant] trumpeted, collapsed, fell heavily onto his right side, defecated, and went into status epilepticus.” Poor old Tusko died an hour and forty minutes later. Perhaps almost as disturbing as this awful outcome was that the investigators concluded that elephants are “proportionally very sensitive to LSD.”

The problem, of course, is something we’ve already stressed several times, namely the seductive trap of linear thinking. The calculation of how big a dosage should be used on Tusko was based on the implicit assumption that effective and safe dosages scale linearly with body weight so that the dosage per kilogram of body weight was presumed to be the same for all mammals. The 0.1 milligram per kilogram of body weight obtained from cats was therefore naively multiplied by Tusko’s weight, resulting in the outlandish estimate of 297 milligrams, with disastrous consequences.

Exactly how doses should be scaled from one animal to another is still an open question that depends, to varying degrees, on the detailed properties of the drug and the medical condition being addressed. However, regardless of details, an understanding of the underlying mechanism by which drugs are transported and absorbed into specific organs and tissues needs to be considered in order to obtain a credible estimate. Among the many factors involved, metabolic rate plays an important role. Drugs, like metabolites and oxygen, are typically transported across surface membranes, sometimes via diffusion and sometimes through network systems. As a result, the dose-determining factor is to a significant degree constrained by the scaling of surface areas rather than the total volume or weight of an organism, and these scale nonlinearly with weight. A simple calculation using the ⅔ scaling rule for areas as a function of weight shows that a more appropriate dose for elephants should be closer to a few milligrams of LSD rather than the several hundred that were actually administered. Had this been done, Tusko would no doubt have lived and a vastly different conclusion about the effects of LSD would have been drawn.

The lesson is clear: the scaling of drug dosages is nontrivial, and a naive approach can lead to unfortunate results and mistaken conclusions if not done correctly with due attention being paid to the underlying mechanism of drug transport and absorption. It is clearly an issue of enormous importance, sometimes even a matter of life and death. This is one of the main reasons it takes so long for new drugs to obtain approval for their general use.

Lest you think this was some fringe piece of research, the paper on elephants and LSD was published in one of the world’s most highly regarded and prestigious journals, namely Science.⁶

Many of us are very familiar with the problem of how drug doses should be scaled with body weight from having dealt with children with fevers, colds, earaches, and other such vagaries of parenting. I recall many years ago being quite surprised when trying to console a screaming infant struggling in the middle of the night with a high fever to discover that the recommended dose of baby Tylenol, printed on the label of the bottle, scaled linearly with body weight. Being familiar with the tragic story of Tusko I felt a certain degree of concern. The label had a small chart on it showing how big a dose should be given to a baby of a given age and weight. For example, for a 6-pound baby, the recommended dose was ¼ teaspoon (40 mg) whereas for a baby of 36 pounds (six times heavier) the dose was 1½ teaspoons (240 mg), exactly six times larger. However, if the nonlinear ⅔ power scaling law is followed, the dosage should only have been increased by a factor of 6⅔ ≈ 3.3, corresponding to 132 milligrams, which is just over half of the recommended dose! So if the ¼ teaspoon recommended for the 6-pound baby is correct, then the dose of 1½ teaspoons recommended for the 36-pound baby was almost twice too large.

Hopefully this has not been putting children at risk, but I have noticed in more recent years that such a chart no longer appears on the bottle or on the pharmaceutical company Web site. However, the Web site still shows such a chart indicating linear scaling for the recommended dosages for infants from 36 to 72 pounds, although they now wisely recommend that a physician be consulted for babies less than 36 pounds (less than two years old). Nevertheless, other reputable Web sites still recommend linear scaling for babies younger than this.⁷

7. BMI, QUETELET, THE AVERAGE MAN, AND SOCIAL PHYSICS

Another important medical issue related to scale is the use of the body-mass index (BMI) as a proxy for body fat content and, by extrapolation, as an important metric of health. This has become very topical in recent years because of its ubiquitous use in the diagnosis of obesity and its association with many deleterious health issues including hypertension, diabetes, and heart disease. Although introduced more than 150 years ago by the Belgian mathematician Adolphe Quetelet as a simple means of classifying sedentary individuals, BMI has taken on a powerful authority among physicians and the general public despite its somewhat murky theoretical underpinnings.

Until the 1970s and the rise of its popularity, the BMI was actually known as the Quetelet index. Although trained as a mathematician, Quetelet was a classic polymath who contributed to a wide range of scientific disciplines including meteorology, astronomy, mathematics, statistics, demography, sociology, and criminology. His major legacy is the BMI, but this was just a very small part of his passion for bringing serious statistical analysis and quantitative thinking to problems of societal interest.

Quetelet’s goal was to understand the statistical laws underlying social phenomena such as crime, marriage, and suicide rates and to explore their interrelationships. His most influential book, published in 1835, was On Man and the Development of His Faculties, or Essays on Social Physics. The title was shortened for the English translation to the much more grandiose-sounding Treatise on Man. In the book, he introduces the term social physics and describes his concept of the “average man” (l’homme moyen). This concept is very much in the spirit of our earlier discussion concerning Galileo’s argument on how the strength of the mythical “average person” scales with his or her weight and height, or the idea that there are meaningful average baseline values for physiological characteristics such as our body temperature and blood pressure.

The “average man” (and woman!) is characterized by the values of the various measurable physiological and social metrics averaged over a sufficiently large population sample. These include everything from heights and life spans to the numbers of marriages, the amount of alcohol consumed, and the rates of disease. However, Quetelet brought something new and important to these analyses, namely the statistical variation of these quantities around their mean values, including estimates of their associated probability distributions. He found, though sometimes he merely assumed, that these variances mostly followed a so-called normal, or Gaussian, distribution, popularly known as the bell curve. Thus, in addition to measuring average values of these various quantities, he analyzed the distribution of how much they varied around that mean. So health, for example, would be defined not just as having specific values of these metrics (such as having a body temperature of 98.6°F) but that these should fall within well-defined bounds determined by the variation from the mean value for healthy individuals in the entire population.

Quetelet’s ideas, and his use of the term social physics, were somewhat controversial at the time because they were interpreted as implying a deterministic framework for social phenomena and therefore contradicted the concepts of free will and freedom of choice. In retrospect this is surprising given that Quetelet was obsessed with statistical variation, which we now might view as providing a quantitative measure of how much “freedom of choice” we have to deviate from the norm. This tension between the role of underlying “laws” that constrain the structure and evolution of a system, whether social or biological, and the extent to which they can be “violated” is a recurring theme that will be returned to later. How much freedom do we have in shaping our destiny, whether collectively or individually? At a detailed, high-resolution level, we may have great freedom in determining events into the near future, but at a coarse-grained, bigger-picture level where we deal with very long timescales life may be more deterministic than we think.

Although the term social physics faded from the scientific landscape it has been resurrected more recently by scientists from various backgrounds who have started to address social science questions from a more quantitative analytic viewpoint typically associated with the paradigmatic framework of traditional physics. Much of the work that my colleagues and I have been involved in and which will be elucidated in some detail in later chapters could be described as social physics, although it is not a term any of us uses with ease. Ironically, it has been picked up primarily by computer scientists, who are neither social scientists nor physicists, to describe their analysis of huge data sets on social interactions. As they characterize it: “Social Physics is a new way of understanding human behavior based on analysis of Big Data.”⁸ While this body of research is very interesting, it is probably safe to say that few physicists would recognize it as “physics,” primarily because it does not focus on underlying principles, general laws, mathematical analyses, and mechanistic explanations.

Quetelet’s body-mass index is defined as your body weight divided by the square of your height and is therefore expressed in terms of pounds per square inch or kilograms per square meter. The idea behind it is that weights of healthy individuals, and in particular those with a “normal” body shape and proportion of body fat, are presumed to scale with the square of their heights. So dividing the weight by the square of the height should lead to a quantity that is approximately the same for all healthy individuals, with values falling within a relatively narrow range (between 18.5 and 25.0 kg/sq. m). Values outside of this range are interpreted as an indication of a potential health problem associated with being either over- or underweight relative to height.⁹

The BMI is therefore presumed to be approximately invariant across idealized healthy individuals, meaning that it has roughly the same value regardless of body weight and height. However, this implies that body weight should increase as the square of height, which seems to be seriously at odds with our earlier discussion of Galileo’s work where we concluded that body weight should increase much faster as the cube of height. If this is so, then BMI, as defined, would not be an invariant quantity but would instead increase linearly with height, thereby consistently overdiagnosing taller people as overweight while underdiagnosing shorter ones. Indeed, there is evidence that tall people have uncharacteristically high values compared with their actual body fat content.

So how in fact does weight scale with height for human beings? Various statistical analyses of data have led to varying conclusions, ranging from confirmation of the cubic law to more recent analyses suggesting exponents of 2.7 and values that are even smaller and closer to two.¹⁰ To understand why this might be so, we have to remind ourselves of a major assumption that was made in deriving the cubic law, namely that the shape of the system, our bodies in this case, should remain the same when its size increases. However, shapes change with age, from the extreme case of a baby, with its large head and chunky limbs, to a mature “well-proportioned” adult, and finally to the sagging bodies of people my age. In addition, shapes also depend on gender, culture, and other socioeconomic factors that may or may not be correlated with health and obesity.

Many years ago I analyzed a data set on the heights of men and women as a function of their weights and found excellent agreement with the classic cubic law. Serendipitously, the data I had analyzed came from a relatively narrow cohort of U.S. males aged fifty to fifty-nine and U.S. females aged forty to forty-nine. Because these were analyzed separately by gender and within a similar, rather narrow age group, these cohorts represented meaningful “average” healthy men and women having similar characteristics. Ironically, this is in contrast to much more serious and comprehensive studies in which the averaging was performed over all age groups with diverse characteristics, making the interpretation much less clear. It is therefore not surprising that they resulted in exponents that differ from the idealized value of three. This suggests that a more reasonable approach would be to deconstruct the entire data set into cohorts with similar characteristics, such as age, and develop metrics for the resulting subgroups.

Unlike the cubic scaling law, the conventional definition of the BMI has no theoretical or conceptual underpinning and is therefore of dubious statistical significance. In contrast, the cubic law does have a conceptual basis and if we control for the characteristics of the cohort is supported by data. It is not surprising, therefore, that an alternative definition of the BMI has been suggested in which the BMI is defined as body weight divided by the cube of the height; it is known as the Ponderal index. Although it does somewhat better than the Quetelet definition in being meaningfully correlated with body fat content, it nevertheless suffers from similar problems because it has not been deconstructed into cohorts having similar characteristics.

Of course, good physicians use a range of BMI values to assess health, thereby mitigating gross misinterpretations with the exception perhaps of individuals with BMIs near the boundaries. In any case, it is clear that the classic BMI as presently used should not be taken too seriously without further investigation and the development of more subtle detailed indices that recognize, for example, age and cultural differences, especially for those who might appear to be at risk.

I have used these examples to illustrate how the conceptual framework of scaling underlies the use of critical metrics in our health care repertoire and in so doing have revealed potential pitfalls and misconceptions. As with drug doses, this is a complex and very important component of medical practice whose underlying theoretical framework has not yet been fully developed or realized.¹¹

8. INNOVATION AND LIMITS TO GROWTH

Galileo’s deceptively simple argument for why there are limits to the heights of trees, animals, and buildings has profound consequences for design and innovation. Earlier, when explaining his argument I concluded with the remark: Clearly, the structure, whatever it is, will eventually collapse under its own weight if its size is arbitrarily increased. There are limits to size and growth. To which should have been added the critical phrase “unless something changes.” Change and, by implication, innovation, must occur in order to continue growing and avoid collapse. Growth and the continual need to be adapting to the challenges of new or changing environments, often in the form of “improvement” or increasing efficiency, are major drivers of innovation.

Galileo, like most physicists, did not concern himself with adaptive processes. We had to wait for Darwin to learn how important these are in shaping the world around us. As such, adaptive processes are primarily the domain of biology, economics, and the social sciences. However, in the mechanical examples he considered, Galileo introduced the fundamental concept of scale and by implication growth, both of which play an integral role in complex adaptive systems. Because of the conflicting scaling laws that constrain different attributes of a system—for example, the strengths of structures supporting a system scale differently from the way the weights being supported scale—growth, as manifested by an open-ended increase in size, cannot be sustained forever.

Unless, of course, an innovation occurs. A crucial assumption in the derivation of these scaling laws was that the system maintains the same physical characteristics, such as shape, density, and chemical composition, as it changes size. Consequently, in order to build larger structures or evolve larger organisms beyond the limits set by the scaling laws, innovations must occur that either change the material composition of the system or its structural design, or both.

A simple example of the first kind of innovation is to use a stronger material such as steel in place of wood for bridges or buildings, while a simple example of the second kind is to use arches, vaults, or domes in their construction rather than just horizontal beams and vertical pillars. The evolution of bridges is, in fact, an excellent example of how innovations in both materials and design were stimulated by the desire, or perceived requirement, to meet new challenges: in this case, to traverse wider and wider rivers, canyons, and valleys in a safe, resilient manner.

The most primitive kind of bridge is simply a log that has fallen across a stream or has been purposely placed there by humans—already an act of innovation. Perhaps the first significant act of engineering innovation in constructing bridges was to use purposely cut wooden logs or planks. Driven by the challenges of safety, stability, resilience, convenience, and the desire to span wider rivers, this was extended to incorporate stone structures as simple support systems on each bank, forming what is known as a beam bridge. Given the limited tensile strength of wood there is clearly a limit as to how long a span can be traversed in this way. This was solved by the simple design innovation of introducing stone support piers in the middle of the river that effectively extended the bridge to be a succession of individual beam bridges.

An alternative strategy was the much more sophisticated innovation of constructing bridges entirely of stone and using the physical principles of the arch, thereby changing both the materials and design. Such bridges had the great advantage of being able to withstand conditions that would damage or destroy earlier designs. Remarkably, arched stone bridges go back more than three thousand years to the Greek Bronze Age (thirteenth century BC), with some still in use today. The greatest stone arch bridge builders of antiquity were the Romans, who built vast numbers of beautiful bridges and aqueducts throughout their empire, many of which still stand.

To cross ever wider and deeper chasms such as the Avon Gorge in England or the entrance to San Francisco Bay in the United States required new technology, new materials, and new design. In addition, increases of traffic density and the need to support larger loads, especially with the coming of the railway, led to the development of arched cast iron bridges, truss systems of wrought iron, and eventually to the use of steel and the development of the modern suspension bridge. There are many variants of these designs, such as cantilevered bridges, tied arch bridges (Sydney Harbor being the most famous), and movable bridges like Tower Bridge in London. In addition, modern bridges are now constructed from a plethora of different materials, including combinations of concrete, steel, and fiber-reinforced polymers. All of these represent innovative responses to a combination of generic engineering challenges, including the constraints of scaling laws that transcend the individuality of each bridge, and the multiple local challenges of geography, geology, traffic, and economics that define the uniqueness and individuality of each bridge.

All of these innovative variations, driven by the perceived need to traverse wider and ever more challenging chasms, eventually hit a limit. Innovation in this context can then be viewed as the response to the challenge of continually scaling up the width of space to be crossed, beginning with a tiny stream and ending up with the widest expanses of water and the deepest and broadest canyons and valleys. You cannot cross San Francisco Bay with a long plank of wood. To bridge it you need to embark on a long evolutionary journey across many levels of innovation to the discovery of iron and the invention of steel and their integration with the design concept of a suspension bridge.

This way of thinking about innovation, which relates it to the drive or need to grow bigger, to expand horizons and compete in ever-larger markets with its inevitable confrontation with potential limitations imposed by physical constraints, will form the paradigm later in the book for addressing similar kinds of innovation in the larger context of biological and socioeconomic adaptive systems.

In the following sections, this will be extended to show how the idea of modeling a system arose. Modeling is now so commonplace and so taken for granted that we don’t usually recognize that it is a relatively modern development. We can hardly countenance a time when it was not an essential and inseparable feature of industrial processes or scientific activity. Models of various kinds have been built for centuries, especially in architecture, but these were primarily to illustrate the aesthetic characteristics of the real thing rather than as scale models to test, investigate, or demonstrate the dynamical or physical principles of the system being constructed. And most important, they were almost always “made to scale,” meaning that each detailed part was in some fixed proportion to the full size—1:10, for example—just like a map. Each part of the model was a linearly scaled representation of the actual-size ship, cathedral, or city being “modeled.” Fine for aesthetics and toys but not much good for learning how the real system works.

Nowadays, every conceivable process or physical object, from automobiles, buildings, airplanes, and ships to traffic congestion, epidemics, economies, and the weather, is simulated on computers as “models” of the real thing. I discussed earlier how specially bred mice are used in biomedical research as scaled-down “models” of human beings. In all of these cases, the big question is how do you realistically and reliably scale up the results and observations of the model system to the real thing? This entire way of thinking has its origins in a sad failure in ship design in the middle of the nineteenth century and the marvelous insights of a modest gentleman engineer into how to avoid it in the future.

9. THE GREAT EASTERN, WIDE-GAUGE RAILWAYS, AND THE REMARKABLE ISAMBARD KINGDOM BRUNEL

Failure and catastrophe can provide a huge impetus and opportunity in stimulating innovation, new ideas, and inventions whether in science, engineering, finance, politics, or one’s personal life. Such was the case in the history of shipbuilding and the origins of modeling theory and the role played by an extraordinary man with an extraordinary name: Isambard Kingdom Brunel.

In 2002 the BBC conducted a nationwide poll to select the “100 Greatest Britons.” Perhaps predictably, Winston Churchill came in first with Princess Diana third (she had only been dead for five years at that time), followed by Charles Darwin, William Shakespeare, and Isaac Newton, a pretty impressive triumvirate. But who was second? None other than the remarkable Isambard Kingdom Brunel!

On occasions when I mention Brunel’s name in lectures outside of the United Kingdom I usually ask the audience if they’ve ever heard of him. At best, there is a small smattering of hands, usually by people from Britain. I then inform them that according to a BBC poll, Brunel is the second-greatest Briton of all time ahead of Darwin, Shakespeare, Newton, and even John Lennon and David Beckham. It gets a good laugh but more important provides a natural segue into some provocative issues related to science, engineering, innovation, and scaling.

So who was Isambard Kingdom Brunel, and why is he famous? Many consider him the greatest engineer of the nineteenth century, a man whose vision and innovations, particularly concerning transport, helped make Britain the most powerful and richest nation in the world. He was a true engineering polymath who strongly resisted the trend toward specialization. He typically worked on all aspects of his projects beginning with the big-picture concept through to the detailed preparation of the drawings, carrying out surveys in the field and paying attention to the minutiae of design and manufacture. His accomplishments are numerous and he left an extraordinary legacy of remarkable structures ranging from ships, railways, and railway stations to spectacular bridges and tunnels.

Brunel was born in Portsmouth in the south of England in 1806 and died relatively young in 1859. His father, Sir Marc Brunel, was born in Normandy, France, and was also a highly accomplished engineer. They worked together when Isambard was only nineteen years old building the first ever tunnel under a navigable river, the Thames Tunnel at Rotherhithe in East London. It was a pedestrian tunnel that became a major tourist attraction with almost two million visitors a year paying a penny apiece to traverse it. Like many such underground walkways it sadly became the haunt of the homeless, muggers, and prostitutes and in 1869 was eventually transformed into a railway tunnel, becoming part of the London Underground system still in use to this day.

In 1830 at age twenty-four Brunel won a very stiff competition to build a suspension bridge over the River Avon Gorge in Bristol. It was an ambitious design and, upon its eventual completion in 1864, five years after his death, it had the longest span of any bridge in the world (702 feet, and 249 feet above the river). Brunel’s father did not believe that a single span of such a length was physically possible and recommended that Isambard include a central support for the bridge, which he duly ignored.

Brunel subsequently became the chief engineer and designer for what was considered the finest railway of its time, the Great Western Railway, running from London to Bristol and beyond. In this role he designed many spectacular bridges, viaducts, and tunnels—the Box Tunnel, near Bath, was the longest railway tunnel in the world at the time—and even stations. Familiar to many, for example, is London’s Paddington Station with its marvelous wrought-iron work.

One of his most fascinating innovations was the unique introduction of a broad gauge of 7 feet ¼ inch for the width between tracks. The standard gauge of 4 feet 8½ inches, which was used in all other British railways at that time, was adopted worldwide and is used on almost all railways today. Brunel pointed out that the standard gauge was an arbitrary carryover from the mine railways built before the invention of the world’s first passenger trains in 1830. It had simply been determined by the width needed to fit a cart horse between the shafts that pulled carriages in the mines. Brunel rightly thought that serious consideration should be given to determining what the optimum gauge should be and tried to bring some rationality to the issue. He claimed that his calculations, confirmed by a series of trials and experiments, showed that his broader gauge was the optimum size for providing higher speeds, greater stability, and a more comfortable ride to passengers. Consequently, the Great Western Railway was unique in having a gauge that was almost twice as wide as every other railway line. Unfortunately, in 1892, following the evolution of a national railway system, the British Parliament forced the Great Western Railway to conform to the standard gauge, despite its acknowledged inferiority.

A rakish-looking Isambard Kingdom Brunel posing in front of the chains he designed for the launching of the Great Eastern in 1858. Also shown is the giant ship under construction and the Clifton suspension bridge over the River Avon, which he designed in 1830 when only twenty-four years old.

The parallels with similar issues we are facing today regarding the inevitable tension and trade-offs between innovative optimization and the uniformity and fixing of standards determined by historical precedence, especially in our fast-developing high-tech industry, are clear. The battle over railway track gauges provides an informative case study of how innovative change may not always lead to the optimum solution.

Though Brunel’s projects were not always completely successful, they typically contained inspired innovative solutions to long-standing engineering problems. Perhaps his grandest achievements—and failures—were in shipbuilding. As global trade was developing and competitive empires were being established, the need to develop rapid, efficient ocean transport over long distances was becoming increasingly pressing. Brunel formulated a grand vision of a seamless transition between the Great Western Railway and his newly formed Great Western Steamship Company so that a passenger could buy a ticket at Paddington Station in London and get off in New York City, powered the entire way by steam. He whimsically called this the Ocean Railway. However, it was widely believed that a ship powered purely by steam would not be able to carry enough fuel for the trip and still have room for sufficient commercial cargo to be economically viable.

Brunel thought otherwise. His conclusions were based on a simple scaling argument. He realized that the volume of cargo a ship could carry increases as the cube of its dimensions (like its weight), whereas the strength of the drag forces it experiences as it travels through water increases as the cross-sectional area of its hull and therefore only as the square of its dimensions. This is just like Galileo’s conclusions for how the strength of beams and limbs scale with body weight. In both cases the strength increases more slowly than the corresponding weight following a ⅔ power scaling law. Thus the strength of the hydrodynamic drag forces on a ship relative to the weight of the cargo it can carry decreases in direct proportion to the length of the ship. Or to put it the other way around: the weight of its cargo relative to the drag forces its engines need to overcome systematically increases the bigger the ship. In other words, a larger ship requires proportionately less fuel to transport each ton of cargo than a smaller ship. Bigger ships are therefore more energy efficient and cost effective than smaller ones—another great example of an economy of scale and one that had enormous consequences for the development of world trade and commerce.¹²

Although these conclusions were nonintuitive and not generally believed, Brunel and the Great Western Steamship Company were convinced. Brunel boldly proceeded to design the company’s first ship, the Great Western, which was the first steamship purposely built for crossing the Atlantic. She was a paddle-wheel ship constructed of wood (with four sails as backup, just in case) and, when completed in 1837, was the largest and fastest ship in the world.

Following the success of the Great Western and confirmation of the scaling argument that bigger ships were more efficient than smaller ones, Brunel moved to build an even larger one, brazenly combining new technologies and materials never before incorporated into a single design. The Great Britain, launched in 1843, was built of iron rather than wood and driven by a screw propeller in the rear rather than paddle wheels on the sides. In so doing, the Great Britain became the prototype for all modern ships. She was longer than any previous ship and was the first iron-hulled, propeller-driven ship to cross the Atlantic. You can still see her today fully renovated and preserved in the dry dock built in Bristol by Brunel for her original construction.

Having conquered the Atlantic, Brunel turned his attention to the biggest challenge of all, namely, connecting the far-flung reaches of the burgeoning British Empire to consolidate its position as the dominant global force. He wanted to design a ship that could sail nonstop from London to Sydney and back without refueling using only a single load of coal (and this was before the opening of the Suez Canal). This meant that the ship would have to be more than twice the length of the Great Britain at almost 700 feet and have a displacement (effectively its weight) almost ten times bigger. It was named the Great Eastern and launched in 1858. It took almost fifty years and into the twentieth century before another ship approached its size. Just to give a sense of scale, the huge oil supertankers plying the world’s oceans today more than 150 years later are still only a little more than twice as long as the Great Eastern.

Sadly, however, the Great Eastern was not a success. Though an extraordinary engineering accomplishment that raised the bar to a level not again reached until well into the twentieth century, it suffered like many of Brunel’s achievements from construction delays and budget overruns. But more pointedly, the Great Eastern was not a technical success either. She was ponderous and ungainly, rolled too much even in moderately heavy waves, and, most pertinent, could barely move her gargantuan mass at even moderate speeds. Nor, surprisingly, was she very efficient and as a result was never used for her original grandiose purpose of serving the Empire by shipping large loads of cargo and large numbers of passengers to and from India and Australia. She made a small number of transatlantic crossings before being ignominiously transformed into a ship for laying cables. The first resilient transatlantic telegraph cable was laid by the Great Eastern in 1866, enabling reliable telecommunication between Europe and North America, thereby revolutionizing global communication.

The Great Eastern ended up as a floating music hall and advertising billboard in Liverpool before being broken up in 1889. Such was the sad ending to a glorious vision. A bizarre footnote to this tale that is probably of interest only to ardent soccer fans is that in 1891 when the famous British football club Liverpool was being founded, they searched for a flagpole for their new stadium and purchased the top mast of the Great Eastern for that purpose. It still proudly stands there today.

How did all of this happen? How could such a marvelous vision overseen by one of the most brilliant and innovative practitioners of all time end in such a shambles? The Great Eastern was hardly the first ship to be poorly designed, but its sheer size, its innovative vision, and its huge cost relative to its serious underperformance made it a spectacular failure.

10. WILLIAM FROUDE AND THE ORIGINS OF MODELING THEORY

When systems fail or designs don’t meet their expectations there are usually a plethora of reasons that could be the problem. These include poor planning and execution, faulty workmanship or materials, poor management, and even a lack of conceptual understanding. However, there are key examples like that of the Great Eastern where the major reason for failure was that they were designed without a deep understanding of the underlying science and of the basic principles of scale. Indeed, until the last half of the nineteenth century, neither science nor scale played any significant role in the manufacture of most artifacts, let alone ships.

There were some significant exceptions to this, the most salient being in the development of steam engines where understanding the relationship between pressure, temperature, and volume of steam helped advance the design of very large, efficient boilers, the kind that allowed engineers to contemplate building great ships the size of the Great Eastern that could sail across the globe. More significant, investigations into understanding the fundamental principles and characteristics of efficient engines and the nature of different forms of energy, whether heat, chemical, or kinetic, led to the development of the fundamental science of thermodynamics. And of even greater significance, the laws of thermodynamics and the concepts of energy and entropy extend far beyond the narrow confines of steam engines and are universally applicable to any system where energy is being exchanged, whether for a ship, an airplane, a city, an economy, your body, or the entire universe itself.

Even at the time of the Great Eastern, there was very little, if any, such “real” science in shipbuilding. Success in designing and building ships had been achieved by the gradual accumulation of knowledge and technique via a process of trial and error, resulting in well-established rules of thumb passed on, to a large extent, by the mechanisms of apprenticeship and learning on the job. Typically, each new ship was a minor variant on a previous one, with small changes here and there as demanded by the projected needs and uses of the vessel. Small errors resulting from simple extrapolation from what had worked before to the new situation usually had a relatively small impact. So increasing the length of a ship by 5 percent, for example, might produce a vessel that didn’t quite meet design expectations or one that didn’t behave quite as expected, but these “errors” could be readily corrected and even improved upon by an appropriate adjustment or inspired innovation in future versions. Thus, to a large extent, shipbuilding, like almost all other developments in artifactual manufacturing, evolved almost organically, mimicking a process akin to natural selection.

Superimposed on this incremental and essentially linear process was an occasional inspired innovative nonlinear leap that changed something significant in the design or in the materials used, such as the introduction of sails, propellers, or the use of steam and iron. Although such innovative leaps still built on previous designs, they required a rethinking and oftentimes major readjustments before a new successful prototype emerged.

The tried and tested process of simply extrapolating from previous design worked well when designing and building new ships, provided the changes were incremental. There was no need for a deep scientific understanding of why something worked the way it did because the long succession of previous successful vessels effectively ensured that most of the problems to be addressed had already been solved. This paradigm is succinctly summarized in a comment about the shipwrights who built a much earlier catastrophic failure, the Swedish warship Vasa: “The trouble at that time was that the science of ship design wasn’t fully understood. There was no such thing as construction drawings and ships were designed by ‘rule of thumb’; largely based on previous experience.”¹³ Shipwrights were given the overall dimensions and used their own experience to produce a ship with good sailing qualities.

Sounds pretty straightforward, and it might well have been had the Vasa been just a minor extension of previous ships built by the Stockholm shipyard. However, King Gustav Adolf had demanded a ship that was 30 percent longer than previous ships with an extra deck carrying much heavier artillery than usual. With such radical demands, no longer would a small mistake in design lead to a small error in performance. A ship of this size is a complicated structure and its dynamics, especially regarding its stability, are inherently nonlinear. A small error in design could, and did, result in macroscopic errors in performance, resulting in catastrophic consequences. Unfortunately, the shipwrights did not have the scientific knowledge to know how to correctly scale up a ship by such a large amount. In fact, they didn’t have the scientific knowledge to know how to correctly scale up a ship by a small amount either, but this hardly mattered. Consequently, the ship ended up being too narrow and too top-heavy so that even a light breeze was sufficient to capsize her—and it did, even before she left the harbor in Stockholm on her maiden voyage, resulting in the loss of many lives.¹⁴

The same may be said of the Great Eastern where the increase in size was even greater, with the length being doubled and the weight increased by almost a factor of ten. Brunel and his colleagues simply didn’t have the scientific knowledge to correctly scale up a ship by such a large factor. Fortunately, in this case, there were no human catastrophes, only economic ones. In such a fiercely competitive economic market, underperformance is the kiss of death.

It was only in the decade prior to the building of the Great Eastern that the underlying science governing the motion of ships was developed. The field of hydrodynamics was first formalized independently by the French engineer Claude-Louis Navier and the great Irish mathematical physicist George Stokes. The fundamental equation, which is universally known as the Navier-Stokes equation, arises from applying Newton’s laws to the motion of fluids, and by extension to the dynamics of physical objects moving through fluids, such as ships through water or airplanes through air.

This may sound pretty arcane, and it is very likely that you’ve never heard of the Navier-Stokes equation, but it has played, and continues to play, a major role in almost all aspects of your life. Among many other things, it underlies the design of airplanes, automobiles, hydroelectric power stations, and artificial hearts, the understanding of blood flow in your circulatory system, and the hydrology of rivers and water supply systems. It is fundamental to understanding and predicting the weather, ocean currents, and the analysis of pollution and is consequently a key ingredient in the science of climate change and the predictions of global warming.

I do not know if Brunel was familiar with the discovery of these equations that governed the motion of the ships he was designing, but he did have the insight and intuition to engage someone who probably was. That man was William Froude, who had studied mathematics at Oxford and had worked as a young engineer on the Great Western Railway some years earlier.

During the building of the Great Eastern, Brunel had asked Froude to investigate the problem of the rolling and stability of ships. This eventually led him to answer the critical question as to what the optimum shape of a hull should be that would minimize the viscous drag forces of water. The economic implications for shipping and global trade resulting from his work were huge. Thus was born the modern science of ship design. However, of even greater impact and longer-term importance was his introduction of the revolutionary concept of modeling a system in order to determine how the real system worked.

Although the Navier-Stokes equation describes fluid motion under essentially any conditions it is extremely difficult, and in almost all cases impossible, to solve exactly because it is inherently nonlinear. Roughly speaking, the nonlinearity arises from feedback mechanisms in which water interacts with itself. This is manifested in all kinds of fascinating behaviors and patterns such as those we see in the eddies and whirlpools of rivers and streams, or the wakes left by ships as they move through water, or the awesome specter of hurricanes and tornadoes and the beauty and infinite variation of ocean waves. All of these are manifestations of turbulence and are encapsulated in the hidden richness of the Navier-Stokes equation.

Indeed, studying turbulence gave us the first important mathematical insights into the concept of complexity and its relationship to nonlinearity. Complex systems often manifest chaotic behavior in which a small change or perturbation in one part of the system produces an exponentially enhanced response in some other part. As we discussed earlier, in traditional linear thinking a small perturbation produces a commensurately small response. The highly nonintuitive enhancement in nonlinear systems is popularly expressed as “the butterfly effect,” in which the mythical flapping of a butterfly’s wings in Brazil produces a hurricane in Florida. Despite 150 years of intense theoretical and experimental study, a general understanding of turbulence remains an unsolved problem in physics even though we have learned an enormous amount about it. Indeed the famous physicist Richard Feynman described turbulence as “the most important unsolved problem of classical physics.”¹⁵

Froude may not have fully recognized just how big a challenge he was facing but he did perceive that for applications to shipbuilding a new strategy was needed. It was in this context that he invented the new methodology of modeling and, by extension, the concept of scaling theory for determining how quantitative results from small-scale investigations could be used to help predict how full-size ships would behave. In the spirit of Galileo, Froude realized that almost all scaling is nonlinear, so traditional models based on a faithful 1:1 representation were not useful for determining how the actual system works. His seminal contribution was to suggest a quantitative mathematical strategy for figuring out how to scale from the small-size model to the full-size object.

Like many new ideas that threaten to change the way we think about an old problem, Froude’s endeavors were at first dismissed as irrelevant by the cognoscenti of the time. John Russell, who founded the Institution for Naval Architects in England in 1860 in order to encourage the formal education of ship designers, ridiculed Froude: “You will have on the small scale a series of beautiful, interesting little experiments which, I am sure, will afford Mr. Froude infinite pleasure in the making of them . . . and will afford you infinite pleasure in the hearing of them; but which are quite remote from any practical results upon the large scale.”

Many of us recognize this kind of rhetoric, often aimed at scholarly or academic research with the implication that it is out of touch with the “real world.” Well, no doubt, much of it is. But much of it isn’t and, more to the point, it is very often difficult to perceive in the moment the potential impact of some piece of seemingly arcane research. Much of our entire technologically driven society and extraordinary quality of life that many of us are privileged to enjoy is the result of such research. There is a continuing tension in society between supporting what is perceived as pie-in-the-sky basic research with no obvious immediate benefit versus highly directed research focused on “useful, real world” problems.

In 1874 after Froude had revolutionized ship design, Russell to his credit relented and enthusiastically embraced Froude’s methodology and ideas, lamely claiming, however, that he himself had already thought of all of this and done the experiments years earlier. Russell had, in fact, been Brunel’s main partner in building the Great Eastern and it is true that he had actually tinkered with models, but he had unfortunately not appreciated either their significance or the underlying conceptual framework.

Froude made small models of ships, three to twelve feet long, that he dragged through water contained in long tanks and measured their resistance to flow as well as their stability characteristics. With his mathematical background he possessed the technical machinery for knowing how to scale up his findings to large ships.

He realized that the primary quantity that determined the character of their relative motion was something that later became known as the Froude number. It is defined as the square of the ship’s velocity divided by its length multiplied by the acceleration due to gravity. This is a bit of a mouthful and may sound a little intimidating, but it’s actually quite simple because “the acceleration due to gravity” that occurs in this expression is the same for all objects, regardless of their size, shape, or composition. This is just a restatement of Galileo’s observations that falling objects of different weights reach the ground in the same time. So in terms of the quantities that actually vary, Froude’s number is simply proportional to the velocity squared divided by the length. This ratio plays a central role in all problems involving motion, ranging from speeding bullets and running dinosaurs to flying airplanes and sailing ships.

The crucial point recognized by Froude was that because the underlying physics remains the same, objects of different sizes moving at different speeds behave in the same way if their Froude numbers have the same value. Thus, by making the length and speed of the model ship have the same Froude number as that of the full-size version, one can determine the dynamical behavior of the full-size ship before building it.

Let me give a simple illustration of this by asking how fast a 10-foot-long model ship would have to move to mimic the motion of the 700-foot-long Great Eastern moving at 20 knots (a little over 20 mph). If they are to have the same Froude number (that is, the same value of the square of their velocity divided by their length), then the velocity must scale as the square root of their lengths. Now, the ratio of the square root of their lengths is √(700 ft./10 ft.), which is √70 = 8.4. So, for the 10-foot model to mimic the Great Eastern it must move with a speed of approximately 20/8.4 = 2.5 knots, which is just about walking speed. In other words, the dynamics of a 10-foot-long model ship moving at just 2.5 knots simulates that of the 700-foot-long Great Eastern moving at 20 knots.

I have oversimplified his methodology in that there are typically other numbers analogous to Froude’s number that can enter the problem and which explicitly include other dynamical effects such as, for example, the viscosity of water. Nevertheless, the example illustrates the essence of Froude’s method and provides the generic template for modeling and scaling theory. It represents the transition from a primitive trial-and-error, rule-of-thumb approach that served us well for thousands of years toward a more analytic, principled scientific strategy for solving problems and designing modern artifacts ranging from computers and ships to airplanes, buildings, and even companies. Froude’s water tank design is still used today to study ships, and its extension to wind tunnels, which strongly influenced the Wright brothers, plays an analogous role for airplanes and automobiles. Sophisticated computer analyses are now central in the design process, thereby simulating the principles of scaling theory in order to optimize performance. The phrase “computer model” is an integral part of our vocabulary. Effectively, we are now able to “solve,” or simulate solutions to, the Navier-Stokes equations, or their equivalent, leading to greater accuracy in predicting performance.

One of the curious unintended consequences of these advances is that almost all automobiles, for example, now look alike because all manufacturers are solving the same equations to optimize similar performance parameters. Fifty years ago, before we had access to such high-powered computation and therefore less accuracy in predicting outcomes, and before we became so concerned about fuel performance and exhaust pollution, the diversity of car design was much more varied and consequently much more interesting. Compare a 1957 Studebaker Hawk or a 1927 Rolls-Royce to a relatively boring-looking 2006 Honda Civic or a 2014 Tesla, even though these latter vehicles are far superior machines.

11. SIMILARITY AND SIMILITUDE: DIMENSIONLESS AND SCALE-INVARIANT NUMBERS

The scaling methodology introduced by Froude has now evolved to become a powerful and sophisticated component of the tool kit of science and engineering and has been applied with great effect to a very broad and diverse range of problems. It was not formalized as a general technique until the beginning of the twentieth century, when the eminent mathematical physicist Lord Rayleigh wrote a provocative and highly influential paper in the journal Nature titled “The Principle of Similitude.”¹⁶ This was his term for what we have been calling scaling theory. His major emphasis was on the primary role played in any physical system by special quantities that have the property of being dimensionless. These are combinations of variables, like the Froude number, whose value is the same regardless of the system of units used to measure them. Let me elaborate.

Typical quantities that you are accustomed to measuring in your daily life such as lengths, times, and pressures depend upon the units used to measure them, such as feet, seconds, pounds per square inch, and so on. The same quantity can, however, be measured using different units: for instance, the distance from New York to Los Angeles is 3,210 miles, but it could just as well be expressed as 5,871 kilometers. Even though these are different numbers they represent the same thing. Similarly, the distance between London and Manchester can be expressed as either 278 miles or 456 kilometers. However, the ratio of the distance from New York to Los Angeles to that of London to Manchester (either 3,210 miles ÷ 278 miles, or 5,871 kilometers ÷ 456 kilometers) is the same (14.89) regardless of what units are used.

This is the simplest example of a dimensionless quantity: it is a “pure” number that does not change when a different system of units is used to measure it. This scale invariance expresses something absolute about the quantities they represent in that the dependence on the arbitrariness of the human choice of units and measurement has been removed. Specific units are convenient inventions of human beings for communicating measures in a standardized language, especially regarding construction, commerce, and the exchange of goods and services. Indeed, the introduction of standardized measures marked a critical stage in the evolution of civilization and the rise of cities, as they were crucial in developing a trustworthy political fabric subject to the rule of law.

Perhaps the most famous dimensionless number is pi (π), the ratio of the circumference of a circle to its diameter. This has no units, because it is the ratio of two lengths, and has the same value for all circles everywhere, at all times, no matter how small or how large they are. π therefore embodies the universal quality of “circleness.”

This concept of “universality” is the reason why the acceleration due to gravity was included in the definition of the Froude number, even though it played no explicit role in how to scale from model ships to the real thing. It turns out that the ratio of the square of the velocity to the length is not dimensionless and so depends on the units used, whereas dividing by gravity renders it dimensionless and therefore scale invariant.

But why was gravity chosen and not some other acceleration? Because gravity ubiquitously constrains all motion on Earth. This is pretty evident in our own walking and running where we have to continually fight gravity to raise our legs with each step forward, especially when going uphill. Not quite so obvious is how it enters into the motion of ships, because the buoyancy of water balances gravity (remember Archimedes’ principle). However, as a ship moves through water it continually creates wakes and surface waves whose behavior is constrained by the pull of gravity—in fact, the waves you are familiar with on oceans and lakes are technically called gravity waves. So indirectly gravity plays an important role in the motion of ships. Consequently, Froude’s number embodies a “universal” quality associated with all motion on Earth transcending the specific details of the object that is moving. Its value is therefore a major determinant not only in the motion of ships, but also for cars, airplanes, and ourselves. Furthermore, it also tells us how these motions on another planet with a different gravitational strength would differ from the same motion on Earth.

Because the essence of any measurable quantity cannot depend on an arbitrary choice of units made by human beings, neither can the laws of physics. Consequently, all of these and indeed all of the laws of science must be expressible as relationships between scale-invariant dimensionless quantities, even though conventionally they are not typically written that way. This was the underlying message of Rayleigh’s seminal paper.

His paper elegantly illustrates the technique with many well-chosen examples, including one that provides the scientific explanation for one of the great mysteries of life that all of us have pondered at some time, namely, why is the sky blue? Using an elegant argument based solely on relating purely dimensionless quantities, he shows that the intensity of light waves scattered by small particles must decrease with the fourth power of their wavelength. Thus, when sunlight, which is a combination of all of the colors of the rainbow, scatters from microscopic particles suspended in the atmosphere, the shortest wavelengths, corresponding to blue light, dominate.

Actually, Rayleigh had derived this stunning result much earlier in a tour de force based on a masterful mathematical analysis of the problem that provided a detailed mechanistic explanation for the origin of the shift toward the blue end of the spectrum. His point in presenting the simple derivation in his similitude paper was to show that the same result could have been derived “after a few minutes’ consideration,” as he put it, using a scaling argument in the guise of the “great principle of similitude” without the detailed sophisticated mathematics. His scaling argument showed that the shift to shorter wavelengths is an inevitable outcome of any analysis once you know what the important variables are. What is missing from such a derivation is a deeper understanding of the mechanism by which the result comes about. This is characteristic of many scaling arguments: general results can be derived, but details of their mechanistic origins sometimes remain hidden.

Rayleigh’s mathematical analysis of the scattering of waves formed the basis of what became known as “scattering theory.” Its application to many problems, from water waves to electromagnetic waves and especially radar, and more recently IT communication, has been incredibly important, not least its role in the development of quantum mechanics. It provided the basis for the formalism developed for extracting discoveries from “scattering experiments” performed at large particle accelerators such as CERN in Geneva, where the famous Higgs particle was recently discovered.

If you look up his original paper, published in 1870 when he was only twenty-eight years old, you will find that the author’s name isn’t Lord Rayleigh but rather the more earthy John Strutt, sounding more like a Thomas Hardy character than a distinguished professor of physics at Cambridge. This was Rayleigh’s name before he inherited his aristocratic title from his father in 1873, after which he identified himself as Lord Rayleigh. The name Strutt is best known to the public via his younger brother Edward, who founded a famous real estate and property management firm, Strutt & Parker, which today is one of the largest property partnerships in the United Kingdom. Look for their signs on upscale properties in central London next time you’re there.

Rayleigh was a great polymath. Among his many other great accomplishments, he developed the mathematical theory of sound and discovered argon gas, for which he received one of the very first Nobel Prizes in 1904 (the fourth ever awarded).