8
CONSEQUENCES AND PREDICTIONS
From Mobility and the Pace of Life to Social Connectivity, Diversity, Metabolism, and Growth
In this chapter I am going to explore some of the consequences of our big-picture theory of cities developed in the previous chapter. Even though the theory remains a work in progress, I will show from a few examples that much of what we experience in cities, and more generally in our daily participation in socioeconomic activity, is embodied in this quantitative framework. In this respect it should be viewed as complementary to traditional social science and economic theories whose character is typically more qualitative, more localized, more based on narrative, less analytic, and less mechanistic. Critical from the physics perspective is to make quantitative predictions that are subsequently confronted with data, and in some cases big data.
The theory already passes its first test, namely, to provide a natural explanation for the origin of the many scaling laws reviewed earlier. It also explains their universal character across diverse metrics and urban systems, as well as the self-similar and fractal nature of cities. Furthermore, the analysis condenses and explains an enormous amount of data implicitly encapsulated in the many scaling laws that cover much of what we can measure about the structure and organization of cities, including the socioeconomic life of their citizens.
Although this represents a significant accomplishment, it is just a beginning. It provides a point of departure for extending the theory to a broad range of problems pertinent not just to cities and urbanization but also to economies and fundamental questions of growth, innovation, and sustainability. An important component of this is to test and confirm the theory by confronting new predictions with data, such as for metrics quantifying the social connectivity between people, their movement within cities, and the attractiveness of specific locations. For example, how many people visit a given place in a city? How often do they go there and from how far away? What is the diversity distribution of occupations and businesses? How many eye doctors, criminal lawyers, shop assistants, computer programmers, or beauticians can we expect to find in a city? Which of these grow and which contract? What is the origin of the accelerating pace of life and open-ended growth? And finally the key question addressed in chapter 10, can any of this be sustainable?
1. THE INCREASING PACE OF LIFE
I showed in the previous chapter that increasing a city’s size generates more social interactions per capita while at the same time, and to the same degree, costing less. This dynamic is manifested in the extraordinary enhancement in innovation, creativity, and open-ended growth as city size increases. At the same time, it also leads to another profound feature of modern life, namely that its pace seems to be continually speeding up.
As was discussed earlier, if we think of social networks as layered hierarchies beginning with individuals as the “invariant terminal units” and progressing systematically up through modular groupings of increasing size from families, close friends, and colleagues to acquaintances, working clusters, and organizations, then the corresponding strengths of interaction and amounts of information exchanged at each level systematically decrease, resulting in superlinear scaling. A typical person is considerably more connected and spends much more time exchanging significantly more information with other individuals, whether they’re family, close friends, or colleagues, than with much larger, more anonymous collectives such as the administrations of their city or workplace.
The opposite hierarchy pertains to infrastructural networks. Sizes and flows systematically increase from terminal units (houses and buildings) up through the network, leading to sublinear scaling and economies of scale I showed in chapter 3 when considering circulatory and respiratory systems of organisms that a further consequence of this kind of network architecture is the systematic slowing down of the pace of life as the size of organisms increases. Bigger animals live longer, have slower heart and respiratory rates, take longer to grow, mature, and produce offspring, and generally live life at a slower pace. Biological time systematically and predictably expands as size increases following the quarter-power scaling laws. A scurrying mouse is in many respects just a revved-up, scaled-down, ponderous elephant.
Knowing the inverse linkage between these two different kinds of networks, it should come as no great surprise that precisely the opposite behavior arises in social networks. Rather than the pace of life systematically decreasing with size, the superlinear dynamics of social networks leads to a systematic increase in the pace of life: diseases spread faster, businesses are born and die more often, commerce is transacted more rapidly, and people even walk faster, all following the 15 percent rule. This is the underlying scientific reason why we all sense that life is faster in a New York City than in a Santa Fe and that it has ubiquitously accelerated during our lifetimes as cities and their economies grew.
This effective speeding up of time is an emergent phenomenon generated by the continuous positive feedback mechanisms inherent in social networks in which social interactions beget ever more interactions, ideas stimulate yet more ideas, and wealth creates more wealth as size increases. It is a reflection of the incessant churning that is the very essence of city dynamics and leads to the multiplicative enhancement in social connectivity between people that is manifested as superlinear scaling and the systematic speeding up of socioeconomic time. Just as biological time systematically and predictably expands as size increases following quarter-power scaling laws, so socioeconomic time contracts following the 15 percent scaling laws, both following mathematical rules determined by underlying network geometry and dynamics.
2. LIFE ON AN ACCELERATING TREADMILL: THE CITY AS THE INCREDIBLE SHRINKING TIME MACHINE
Even if you are very young you probably don’t need much convincing that almost all aspects of life have been speeding up during your lifetime. It’s certainly true for me. Even though I am now in my mid-seventies with many of the big hurdles and challenges of life behind me, I still find myself struggling to keep up with the ever-present treadmill that seems to be getting progressively faster and faster. My inbox is always full no matter how many messages I delete and how many I answer, I am dangerously behind with completing not just this year’s but last year’s taxes, there are continuous seminars, meetings, and events that I would love and am supposed to attend, I struggle to remember the semi-infinite number of passwords that allow me to access myself through my various accounts and affiliations, and on and on. You surely have your own version of this, a similar litany of time pressures that never seem to abate no matter how hard you try to defeat them. And this is even worse if you live in a large city, have small children, or run a business.
This speeding up of socioeconomic time is integral to modern life in the Urbanocene. Nevertheless, like many of us, I harbor a romantic image that not so long ago life was less hectic, less pressured, and more relaxed and that there was actually time to think and contemplate. But read what the great German poet, writer, scientist, and statesman Johann Wolfgang von Goethe said on the subject almost two hundred years ago in 1825, soon after the beginning of the Industrial Revolution1:
Everything nowadays is ultra, everything is being transcended continually in thought as well as in action. No one knows himself any longer; no one can grasp the element in which he lives and works or the materials that he handles. Pure simplicity is out of the question; of simplifiers we have enough. Young people are stirred up much too early in life and then carried away in the whirl of the times. Wealth and rapidity are what the world admires. . . . Railways, quick mails, steamships, and every possible kind of rapid communication are what the educated world seeks but it only over-educates itself and thereby persists in its mediocrity. It is, moreover, the result of universalization that a mediocre culture [then] becomes [the] common [culture]. . . .
Although it’s a curious mixture of comments on the accelerating pace of life and the resulting erosion of culture and values, expressed in a slightly archaic language, it sounds hauntingly familiar.
So it’s hardly news that the pace of life has been accelerating, but what is surprising is that it has a universal character that can be quantified and verified by analyzing data. Furthermore, it can be understood scientifically using the mathematics of social networks by relating it to the positive feedback mechanisms that enhance creativity and innovation, and which are the source of the many benefits and costs of social interaction and urbanization. In this sense cities are time accelerator machines.
The contraction of socioeconomic time is one of the most remarkable and far-reaching features of modern existence. Despite pervading all of our lives, it has hardly received the attention it deserves. I’d like to give a personal anecdote that exemplifies the speeding up of time and the concomitant changes that accompany it.
I first came to the United States in September 1961 to attend graduate school in physics at Stanford University in California. I took a steam train from King’s Cross Station in London up to Liverpool, where I boarded the Canadian steamship the Empress of England and sailed for almost ten days across the Atlantic, down the St. Lawrence River, eventually disembarking in Montreal. I stayed overnight before taking a Greyhound bus that deposited me in California four days later, having spent one night at the YMCA in Chicago, where I changed buses. The entire journey was an extraordinary experience that transported me across many dimensions, not least of which was an amazing introduction to the variety, diversity, and eccentricity of American life, including an appreciation of its immense geographical size. Fifty-five years later I am still trying to process everything I experienced on that road trip as I continue to grapple with the meaning and enigma of America and all that it stands for.
Although I came from a rather modest background, such a journey would have been typical of most students at that time. Overall, it took me well over two weeks to get from London to Los Angeles, where I stayed with a friend before being driven up to Palo Alto. Today, even the poorest student would complete the journey from London to L.A. in less than twenty-four hours, and the vast majority would do it in many hours less. A direct flight nowadays takes about eleven hours, and even by the late 1950s one could comfortably fly from London to Los Angeles in less than fifteen hours if one could afford it. However, had I undertaken this same journey a hundred or so years earlier it could have taken me many months.
This is just one graphic example of how the time required for travel has dramatically shrunk over the last couple of hundred years. It is often expressed with the platitude that the world has shrunk. Obviously it hasn’t shrunk—the distance between London and Los Angeles is still 5,470 miles—what has shrunk is time, and this has had profound consequences for every aspect of life from the personal to the geopolitical. In 1914 the famous Scottish mapmaker John Bartholomew, cartographer royal to King George V, published An Atlas of Economic Geography, a wonderful collection of data and factoids about economic activity, resources, health and climatic conditions, and goodness knows what else concerning all known places across the globe.2 One of his unique illustrations was a world map showing how long it took to get to any general area on the planet. It’s quite illuminating. For instance, the boundaries of Europe were about five days’ journey apart, whereas today they have shrunk to a mere few hours. Similarly, the boundaries of the British Empire extended over several weeks in 1914, but today its ghostly remains can be traversed in less than a day. Most of central Africa, South America, and Australia required in excess of forty days’ travel, and even Sydney was over a month away.
But travel time is just one manifestation of the extraordinary acceleration of the pace of life that has been enabled by the dizzying proliferation of time-shrinking innovations. Just in my lifetime alone we have experienced transitions to jet airplanes and bullet trains in travel; personal computers, cell phones, and the Internet in communication; home shopping and fast-food drive-through restaurants in food and material supplies; microwaves, washing machines, and dishwashers in home aids; gas chambers, carpet bombing, and nuclear weapons in warfare; and so on. And before any of these came along, think of the revolutionary changes wrought by the steam engine, the telephone, photography, film, television, and radio.
One of the great ironies in all of these marvelous inventions (with the possible exception of the gruesome weapons of destruction) is that they all promised to make life easier and more manageable and therefore give us more time. Indeed, when I was a young man, pundits and futurists were speaking of the glorious future anticipated from such time-saving inventions, and a topic that was much discussed was what we would do with all free time that would now be at our disposal. With cheap energy available from nuclear sources and these fantastic machines doing all our manual and mental labor, the workweek would be short and we would have large swaths of time to really enjoy the good life with our families and friends, a little like the boring privileged lives of aristocratic ladies and gentlemen of previous centuries. In 1930 the great economist John Maynard Keynes wrote:
For the first time since his creation man will be faced with his real, his permanent problem—how to use his freedom from pressing economic cares, how to occupy the leisure, which science and compound interest will have won for him, to live wisely and agreeably and well.
And in 1956, Sir Charles Darwin, grandson of the Charles Darwin, wrote an essay on the forthcoming Age of Leisure in the magazine New Scientist in which he argued:
Take it that there are fifty hours a week of possible working time. The technologists, working for fifty hours a week, will be making inventions so the rest of the world need only work twenty-five hours a week. The more leisured members of the community will have to play games for the other twenty-five hours so they may be kept out of mischief. . . . Is the majority of mankind really able to face the choice of leisure enjoyments, or will it not be necessary to provide adults with something like the compulsory games of the schoolboy?
They could not have been more wrong. The main challenge they foresaw was how to keep people occupied so that they wouldn’t become bored to death. Instead of giving us more time, “science and compound interest” driven by “technologists working for fifty hours a week” have, in fact, given us less time. The multiplicative compounding of socioeconomic interactivity engendered by urbanization has inevitably led to the contraction of time. Rather than being bored to death, our actual challenge is to avoid anxiety attacks, psychotic breakdowns, heart attacks, and strokes resulting from being accelerated to death.
I suppose that in a rather different sense one could argue that unwittingly Sir Charles did in fact get part of it right. After all, one could argue that the greatest impact that television and the IT revolution have had on society has been to “provide adults with something like the compulsory games of the schoolboy.” What else are Facebook, Twitter, Instagram, selfies, texts, and all of the other entertainment media that dominate our lives and fill up our time? Well, they do serve other purposes and can certainly increase the quality of life, but their addictive temptations have been hard to resist. It’s tempting to perceive them as having evolved into “compulsory games” or as having replaced religion as the twenty-first-century version of Marx’s “opiate of the people.” In any case, these are prime examples of recent innovations that have contributed to the acceleration of social time.
Below, I will introduce a theory of growth inspired by the network scaling theory and show that innovations and paradigm shifts need to be made at a faster and faster pace in order to maintain continuous open-ended growth, thereby contributing even further to the acceleration of time. Before discussing this, however, I want to present some explicit examples, some using big data, to substantiate and test various quantitative predictions of the theory including the increasing pace of life.
3. COMMUTING TIME AND THE SIZE OF CITIES
In the 1970s an Israeli transportation engineer, Yacov Zahavi, wrote a series of fascinating reports on transportation in cities for the U.S. Department of Transportation and later for the World Bank to help address specific concerns about traffic and mobility as cities continued to grow and gridlock was becoming the norm. As expected, these reports were data rich, quite detailed, and aimed at providing solutions to specific urban transport problems. However, in addition to presenting standard analyses from a classic consulting engineer’s perspective, Zahavi unexpectedly cast his results in a coarse-grained big-picture framework much as a theoretical physicist might have done. His model, which he grandiosely dubbed the “Unified Mechanism of Travel Model,” takes no account of either the physical or social structure of cities, nor of the fractal nature of road networks, but is based almost entirely on optimizing the economic costs of travel for an average individual relative to his or her income (roughly speaking, travelers use the fastest travel mode they can afford). Although his model doesn’t seem to have generated universal acclaim and wasn’t published in academic journals, one of its many intriguing conclusions has entered into urban folklore and provides an interesting twist on the question of the increasing pace of life.
Using data from cities across several countries, including the United States, England, Germany, and some developing nations, Zahavi discovered the surprising result that the total amount of time an average individual spends on travel each day is approximately the same regardless of the city size or the mode of transportation. Apparently, we tend to spend about an hour each day traveling, whoever and wherever we are. Roughly speaking, the average commute time from home to work is about half an hour each way independent of the city or means of transportation.
Thus even though some people travel faster, some by car or train, some by bus or subway, and some much slower by bicycling or walking, on average all of us spend up to an hour or so traveling to and from work. So the increase in transportation speed resulting from the marvelous innovations of the past couple of hundred years has not been used to reduce commuting time but instead has been used to increase commuting distances. People have taken advantage of these advancements to live farther away and simply travel longer distances to work. The conclusion is clear: the size of cities has to some degree been determined by the efficiency of their transportation systems for delivering people to their workplaces in not much more than half an hour’s time.
Zahavi’s fascinating observations made a powerful impression on the Italian physicist Cesare Marchetti, who was a senior scientist at the International Institute for Applied Systems Analysis (IIASA) in Vienna. IIASA has been a major player in questions of global climate change, environmental impact, and economic sustainability, and this is where Marchetti’s interests and contributions have mostly been. He became intrigued by Zahavi’s work and in 1994 published an extensive paper elaborating on the approximate invariance of daily commute times and promoted the idea that the true invariant is actually overall daily travel time, which he called exposure time.3 So even if an individual’s daily commute time is less than an hour, then he or she instinctively makes up for it by other activities such as a daily constitutional walk or jog. In support of this Marchetti wryly remarked, “Even people in prison for a life sentence, having nothing to do and nowhere to go, walk around for one hour a day, in the open.”
Because walking speed is about 5 kilometers an hour, the typical extent of a “walking city” is about 5 kilometers across (about 3 miles), corresponding to an area of about 20 square kilometers (about 7 square miles). According to Marchetti, “There are no city walls of large, ancient cities (up to 1800), be it Rome or Persepolis, which have a diameter greater than 5km or a 2.5km radius. Even Venice today, still a pedestrian city, has exactly 5km as the maximum dimension of the connected center.” With the introduction of horse tramways and buses, electric and steam trains, and ultimately automobiles, the size of cities could grow but, according to Marchetti, constrained by the one-hour rule. With cars able to travel at 40 kilometers an hour (25 mph), cities, and more generally metropolitan areas, could expand to as much as 40 kilometers or 25 miles across, which is typical of the catchment area for most large cities. This corresponds to an area of about 12 hectares or 450 square miles, more than fifty times the area of a walking city.
This surprising observation of the approximately one-hour invariant that communal human beings have spent traveling each day, whether they lived in ancient Rome, a medieval town, a Greek village, or twentieth-century New York, has become known as Marchetti’s constant, even though it was originally discovered by Zahavi. As a rough guide it clearly has important implications for the design and structure of cities. As planners begin to design green carless communities and as more cities ban automobiles from their centers, understanding and implementing the implied constraints of Marchetti’s constant becomes an important consideration for maintaining the functionality of the city.
4. THE INCREASING PACE OF WALKING
Zahavi and Marchetti presumed that for a given mode of transportation, such as walking or driving, travel speed did not change with city size. As we saw above, Marchetti estimated the approximate size of a city whose dominant form of mobility is walking by assuming that the average walking speed is 5 kilometers per hour (3.1 mph). But in large cities with diverse modes of transportation, walking occurs in busy areas where individuals effectively become part of a crowd and social network dynamics come into play. We are subliminally influenced by the presence of other individuals and infected by the increasing pace of life, unconsciously finding ourselves in a hurry to get to a store, the theater, or to meet a friend. In small towns and cities, pedestrian streets are rarely crowded and the general pace of life is much more leisurely. Consequently, one might expect walking speed to increase with city size, and it’s tempting to speculate that it obeys the 15 percent rule because the mechanism underlying the increase is partially driven by social interaction.
Amusingly, data confirm that walking speeds do indeed increase with city size following an approximate power law, though its exponent is somewhat less than the canonical 0.15, being closer to 0.10 (see Figure 42). This is hardly surprising given the simplicity of the model and that social interactions are only partially responsible for this whimsical effect. It’s interesting to note that, according to the data, average walking speeds increase by almost a factor of two from small towns with just a few thousand inhabitants to cities with populations of over a million, where the average walking speed is a brisk 6.5 kilometers per hour (4 mph). It’s very likely that this saturates, and walking speeds don’t appreciably increase in much larger cities because there are obvious biophysical limitations to how fast people can comfortably walk.
An unexpected expression of this hidden dynamic is the recent introduction of fast lanes for walking in the British city of Liverpool. Apparently, people were getting so frustrated at fellow pedestrians not walking fast enough that the city introduced a special fast lane for walkers (see Figure 43). The caption on the photograph is an amazing expression of the increasing pace of life: half of all people surveyed said they were inhibited from shopping downtown because of the slow pace of walking set by other pedestrians. This has spurred a burgeoning interest from cities around the world to follow Liverpool’s lead, so I suspect we’ll be seeing more of this curious phenomenon on streets in downtown areas of major cities.


(42) The average walking speed plotted logarithmically against population size showing how it systematically increases across various European cities. (43) Fast lanes for pedestrians in Liverpool, England.
5. YOU ARE NOT ALONE: MOBILE TELEPHONES AS DETECTORS OF HUMAN BEHAVIOR
One of the most revolutionary manifestations of our highly connected twenty-first-century world is the extraordinary ubiquity of mobile (or cell) phones. The easy access to cheap, sophisticated smart phones coupled to the Internet has been a major contributor to ramping up the pace of life and shrinking time. Instantly transmitted sound bites in the form of tweets, text messages, and e-mails have swamped traditional telephone communication, not to speak of the carefully composed letters of yesteryear or, god forbid, intimate face-to-face conversation. I’ll return to discuss some of the implications and unintended consequences of this amazing innovation later, but here I want to focus on a mostly unappreciated aspect of cell phones that has begun to revolutionize a small corner of science.
You probably know that your provider keeps track of every phone call or text message you make, when you made it, how long it lasted, to whom you were talking or texting, where you were and where they were. . . and very likely, in some cases, what was being said. This is an enormous amount of data and in principle provides unprecedented and highly detailed information on social interaction and mobility, especially because nowadays almost everyone uses such devices. There are now more cell phones in use than people on the planet. In the United States alone there are more than a trillion phone calls made each year, and on average a typical person spends more than three hours a day fixated by his or her cell phone. Almost twice as many people have access to cell phones in the world as they do to toilets—an interesting comment on our priorities.
This has been a huge boon to even the poorest countries, as they have been able to leapfrog traditional technology and jump immediately into twenty-first-century communication infrastructure at a fraction of the huge cost of installing and maintaining landlines, which most were unable to afford at the scale of coverage that mobile technology provides. It is no surprise that proportionally the greatest percentage of mobile phone usage occurs in developing countries.
So analyzing massive data sets of cell phone calls can potentially provide us with new and testable quantitative insight into the structure and dynamics of social networks and the spatial relationships between place and people and, by extension, into the structure and dynamics of cities. This unforeseen consequence of mobile phones and other IT devices has ushered in the era of big data and smart cities with the somewhat hyperbolic promise that these will provide the tools for solving all of our problems. And not just the infrastructural challenges in cities: the promise extends to all aspects of life from health and pollution to crime and entertainment. This is just one manifestation of the rapid emergence of “smart” industries based on the availability of enormous amounts of data that we ourselves unwittingly generate, whether through our mobile devices, our mobility, or our health records. This developing paradigm certainly provides us with new and powerful tools that, used sensibly, can undoubtedly have beneficial consequences in addition to providing new ways for companies and entrepreneurial individuals to create yet more wealth. Later, however, I will sound some strong words of caution aimed primarily at the naïveté and even danger inherent in this approach.4
Here I want to concentrate on how cell phone data can be used scientifically to test predictions and consequences of our emerging theoretical framework for understanding cities. Apart from the fact that cities, and social systems more generally, are complex adaptive systems, one of the traditional obstacles to developing quantitative testable theories in the social sciences has been the obvious difficulty of obtaining large amounts of credible data and performing controlled experiments. A major reason that the physical and biological sciences have made the tremendous progress they have is that the systems under study can be manipulated or contrived to test specific well-defined predictions and consequences derived from proposed hypotheses, theories, and models.
Giant particle accelerators, such as the Large Hadron Collider in Geneva, Switzerland, where the Higgs particle was recently discovered, are a quintessential example of such artificially controlled experimentation. By combining results from the analysis of many experiments involving ultrahigh energy collisions between particles with the development of a sophisticated mathematical theory, physicists have over many years discovered and determined the properties of the fundamental subatomic constituents of matter as well as the forces of interaction between them. This has led to one of the great achievements of twentieth-century science, the development of the standard model of the elementary particles. This incorporates, integrates, and explains a breathtaking spectrum of the world around us including electricity, magnetism, Newton’s laws of motion, Einstein’s theory of relativity, quantum mechanics, electrons, photons, quarks, gluons, protons, neutrons, Higgs particles, and much more, all in a unifying mathematical framework whose detailed predictions have been spectacularly verified by continuous and ongoing experimental tests.
Equally spectacular is that the energies and distances being probed in such experiments shed light on phenomena that determined the evolution of the universe after the Big Bang. In these experiments we are artificially re-creating events that literally last took place at the beginning of the universe. The resulting theoretical framework has given us a credible quantitative understanding of how galaxies formed and why the heavens look the way they do. Obviously we can’t do experiments on the heavens themselves or on the universe—they are what they are and represent a singular unique event that, unlike experiments in the laboratory, cannot be repeated. We can only observe. Like geology and for that matter the social sciences, astronomy is a historical science in that we can test our theories only by making postdictions for what should have happened according to the equations and narratives of our theories, and then searching in the appropriate place for their verification. This is none other than Newton’s strategy when he derived Kepler’s laws of planetary motion from his fundamental laws of motion and the law of gravity, which had been developed to explain the mundane motion of objects moving in the immediate world around him. He couldn’t do experiments directly on the planets themselves, but could compare his predictions for their motion with Kepler’s observations and measurements and so verify that they were correct. Over the past hundred years this strategy has proven to be remarkably successful in both astrophysics and geology. Consequently, we are confident that we understand how both the universe and the Earth got to be the way they are. So in the case of these historical sciences success has been achieved by a shrewd integration of sophisticated observation coupled with appropriate traditional experimentation on proxy situations in the here and now.
Despite the obvious difficulties when it comes to social systems, social scientists have been very imaginative in devising analogous quantitative experiments to inspire and test hypotheses, and these have proven to give insight into social structure and dynamics. Many involve surveys and responses to various questionnaires and are subject to limitations that depend on the role of the experimental teams who have to interact with the subjects. Consequently it is very difficult to obtain large amounts of data for more than a relatively small sampling across a broad enough range of people and social situations, and this can lead to questions of credibility and generality of results and conclusions.
The beauty of mobile phone data, or data from social media such as Facebook or Twitter, for investigating social behavior is that these sorts of problems can be significantly mitigated. Not that using such data doesn’t bring its own tricky issues. How representative of the entire population are cell phone users, and how representative of social interactions are cell phone calls? These are debatable questions, but what is clear is that this form of communication is now a dominant feature of social behavior, providing a quantitative window onto how, where, and when we interact.
6. TESTING AND VERIFYING THE THEORY: SOCIAL CONNECTIVITY IN CITIES
Carlo Ratti is an Italian architect/designer in the architecture department at MIT, where he runs an outfit with the catchy title Senseable City Lab. I first met Carlo when we were on the same program at the annual DLD conference in Munich. This aspires to be a sort of TED-like affair, though it’s narrower in scope with more emphasis on art and design. Like TED and the Davos meeting of the World Economic Forum, it’s basically a several-day networking cocktail party with a dense program of talks in an ambience of “this is where it’s at,” trying to project an image of futuristic culture, high-tech commerce, and “innovation.” An eclectic mix of interesting and even influential people are in attendance, and there are occasional glimpses of substance and brilliant insight in the presentations, though these are modulated with a heavy dose of flaky, somewhat superficial bullshit wrapped up in superb PowerPoint presentations. This is the way of the world, and there are now many such high-profile events just like these. Despite their shortcomings they do serve an important purpose of creating cross-currents and exposing businesspeople, entrepreneurs, technologists, artists, writers, the media, politicians, and an occasional scientist to new and innovative, if occasionally crazy and provocative, ideas and, of course, to other such people—a little bit like a city does, though greatly compressed in space and time. By the way, like TED, you would be hard pressed to find anyone who any longer remembers what the acronym DLD stands for; I vaguely recall that the D in both of them stands for “design.” Acronyms are also the way of the world and represent yet another subtle manifestation of the accelerating pace of life. 2M2H. LOL.
Although not a scientist, Carlo became enthusiastic about bringing a scientific perspective to understanding cities and tried to convince me that cell phone data was a great way of testing the theory and of investigating other aspects of urban dynamics. I was skeptical, mostly because I didn’t think cell phone usage was sufficiently broad, diverse, and representative that it could be justified as a credible proxy for measuring social interaction and mobility. However, Carlo is not a man easily deterred. Slowly I began to pay attention to statistics on the extraordinary growth of cell phone usage, especially in developing nations where they were now being used by up to 90 percent of the population, and slowly I began to appreciate that Carlo and others like him were right. Many researchers were beginning to take advantage of this new source of data, mostly to investigate network structure and dynamics and provide insight into processes like the spread of disease and ideas.
Inspired by our scaling work, Carlo had hired several smart young physicist/engineers to pursue the use of cell phone data, and together with Luis Bettencourt and me in Santa Fe we started a collaboration to test one of the fundamental predictions of the theory. One of the most intriguing aspects of the scaling of cities is its universal character. As we’ve seen, seemingly unrelated socioeconomic quantities ranging from income and patent production to the incidence of crime and disease scale superlinearly with city size with a similar exponent of about 1.15. In the previous chapter I argued that this surprising commonality across different cities, urban systems, and metrics reflects the degree of interaction between people and has its origins in the universal structure of social networks. People across the globe behave in pretty much the same way regardless of history, culture, and geography. Thus without having to resort to any fancy mathematical theory, this idea predicts that the number of interactions between people in cities should scale with city size in the same way that all of the diverse socioeconomic quantities scale, namely, as a superlinear power law with an exponent of around 1.15 regardless of the urban system. In other words, the systematic 15 percent increase in socioeconomic activity with every doubling of city size, whether in wages and patent production or crime and disease, should track a predicted 15 percent increase in the interaction between people.
So how do you measure the number of interactions between people? Traditional methods have relied on written surveys, which are time consuming, labor intensive, and subject to sampling biases because they are necessarily limited in scope. Even if some of these challenges could be overcome, carrying out such surveys across an entire urban system consisting of hundreds of cities is daunting and probably not feasible. On the other hand, the recent availability of large-scale data sets automatically collected from mobile phone networks covering a large representative percentage of the population across the globe opens up unprecedented possibilities for systematically studying social dynamics and organization in all cities. Fortunately, our MIT colleagues had access to such large data sets consisting of billions of anonymized call records (meaning that we didn’t know the names or numbers of the callers). Obviously, some of these were just one-off calls, so only those where there was a reciprocal call between two callers within a set period of time were counted. From this, the total number of interactions between callers, the total volume of calls, and the total time spent calling within each city was extracted.5
Our analysis was based on two independent data sets: mobile phone data from Portugal and landline data from the United Kingdom. The results are shown in Figures 44–46, where the total number of contacts between people in a city over an extended period of time is plotted logarithmically versus the population size of the city. As you can see, a classic straight line is revealed for both sets of data, indicating power law scaling with the exponent in both cases having the same value very close to the predicted 1.15, in spectacular agreement with the hypothesis. To illustrate this visually, I have placed this graph next to a composite plot derived from Figures 34–38 in chapter 7 showing the universality of socioeconomic urban scaling: a subset of these disparate indicators—GDP, income, patent production, and crime—has been plotted on the same graph to show how they all scale together when appropriately rescaled.
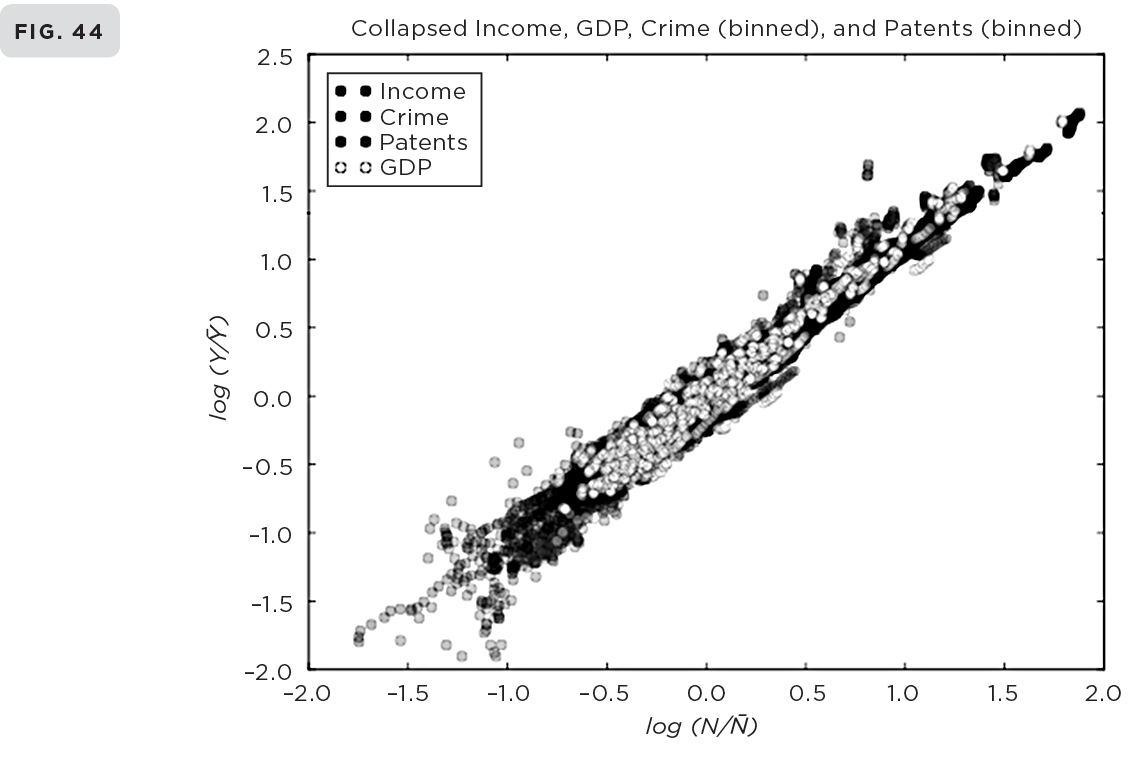


Here: (44) The scaling of four disparate urban metrics—income, GDP, crime, and patents—rescaled from Figures 34–38 to show how they all scale with a similar exponent of about 1.15. (45) The scaling of the connectivity between people as measured by the number of reciprocal phone calls between individuals across cities in Portugal and the United Kingdom showing a similar exponent confirming the prediction of the theory. (46) The size of modular groups of friends of individuals is approximately the same regardless of the size of the city.
This result is a very satisfying confirmation of the hypothesis that social interactions do indeed underlie the universal scaling of urban characteristics. Further confirmation is provided by the observation that both the total time people spent on phone call interactions and the total volume of all of their calls systematically increase with city size in a similar fashion. These results also verify that the accelerating pace of life originates in the increasing connectivity and positive feedback enhancement in social networks as city size increases. For instance, over the fifteen-month period in which the Portuguese data were collected, an average resident of Lisbon, with a population of 560,000, spent about twice as much time on about twice as many reciprocated calls as an average resident of Lixa, a small rural town whose population is only about 4,200. In addition, if the one-off nonreciprocal calls are included in the analysis, then the scaling exponent systematically increases, suggesting that the number of individual solicitations, such as commercial advertisements and political canvassing, is proportionately higher in larger cities. Life in the big city is faster and more intense in every way, including being increasingly bombarded by even more mindless nonsense than in a small town.
Actually, not quite in every way. When we investigated how many of an individual’s contacts—his or her “friends”—are friends of one another, the answer was quite unexpected. In general, an individual’s entire social network spans a highly diverse group of people ranging from close family, friends, and colleagues to relatively distant casual relationships, such as their car mechanic or handyman. Many of these know and interact with one another, but most do not. For example, your dear old mum may never talk to or barely even know your closest colleague at work, despite your having a close relationship with both of them. So how many members of your entire social network—the sum total of all your contacts—talk to one another? This subset defines your “extended family” and the size of your social module. Because there is significantly greater access to larger numbers of people in bigger cities, you might expect that your extended family would likewise be concomitantly bigger and that it would scale superlinearly in much the same way that other socioeconomic quantities do. I certainly did. But to our great surprise, the data revealed that quite to the contrary, it doesn’t scale at all. The size of an average individual’s modular cluster of acquaintances who interact with one another is an approximate invariant—it doesn’t change with city size. For example, the size of the “extended family” of an average individual living in Lisbon, which has more than 500,000 inhabitants, is no larger than that of an average individual living in the small town of Lixa with less than 5,000 inhabitants. So even in large cities we live in groups that are as tightly knit as those in small towns or villages. This is a bit like the invariance of the Dunbar numbers I talked about in the previous chapter and, like those, probably reflects something fundamental about how our neurological structure has evolved to cope with processing social information in large groups.
There is, however, an important qualitative difference in the nature of these modular groups in villages relative to those in large cities. In a real village we are limited to a community that is imposed on us by sheer proximity resulting from its small size, whereas in a city we are freer to choose our own “village” by taking advantage of the much greater opportunity and diversity afforded by a greater population and to seek out people whose interests, profession, ethnicity, sexual orientation, and so on are similar to our own. This sense of freedom provided by a greater diversity across many aspects of life is one of the major attractions of urban life and a significant contributor to rapidly increasing global urbanization.
7. THE REMARKABLY REGULAR STRUCTURE OF MOVEMENT IN CITIES
The extraordinary diversity and multidimensionality of cities has led to a host of images and metaphors that try to capture particular instantiations of what a city is. The walking city, the techno-city, the green city, the eco-city, the garden city, the postindustrial city, the sustainable city, the resilient city. . . and, of course, the smart city. The list goes on and on. Each of these expresses an important characteristic of cities, but none captures the essential feature encapsulated in the rhetorical Shakespearean question “What is the city but the people?” Most images and metaphors of cities conjure up their physical footprint and tend to ignore the central role played by social interaction. This critical component is captured in a different kind of metaphor such as the city as a cauldron, a crucible, a mixing bowl, or a reactor in which the churning of social interactions catalyzes social and economic activity: the people’s city, the collective city, the anthro-city.
The image of the city as a large vat in which people are being continually churned, blended, and agitated can be viscerally felt in any of the world’s great cities. It is most apparent in the continuous, and sometimes frenetic, movement of people in downtown and commercial areas in what often appears to be an almost random motion much like molecules in a gas or liquid. And in much the same way that bulk properties of gases or liquids, such as their temperature, pressure, color, and smell, result from molecular collisions and chemical reactions, so the properties of cities emerge from social collisions and the chemistry of and between people.
Metaphors can be useful but sometimes they can be misleading, and this is one of those instances. For despite appearances, the motion of people in cities is not at all like the random motion of molecules in a gas or particles in a reactor. Instead, it is overwhelmingly systematic and directed. Very few journeys are random. Almost all, regardless of the form of conveyance, involve willful travel from one specific place to another: mostly from home to work, to a store, to a school or cinema, and so forth . . . and back again. Furthermore, most travelers seek the fastest and shortest route, one that takes the least time and traverses the shortest distance. Ideally, this would mean that everyone would like to travel along straight lines but, given the obvious physical constraints of cities, this is impossible. There is no choice but to follow the meandering roads and rail lines, so, in general, any specific journey involves following a zigzagging route. However, when viewed at a larger scale through a coarse-grained lens by averaging over all journeys for all people over a long enough period of time, the preferred route between any two specific locations approximates a straight line. Loosely speaking this means that on average people effectively travel radially along the spokes of circles whose center is their specific destination, which acts as a hub.
With this assumption it is possible to derive an extremely simple but very powerful mathematical result for the movement of people in cities. Here’s what it says: Consider any location in a city; this could be a “central place” such as a downtown area or street, a shopping mall or district, but it could just as well be some arbitrary residential area such as where you live. The mathematical theorem predicts how many people visit this location from any distance away and how often they do it. More specifically, it states that the number of visitors should scale inversely as the square of both the distance traveled and the frequency of visitation.
Mathematically, an inverse square law is just a simple version of the kinds of power law scaling we’ve been discussing throughout the book. In that language the prediction of movement in cities can be restated as saying that the number of people traveling to a specific location scales with both the distance traveled and the visitation frequency as a power law whose exponent is −2. Thus if the number of travelers is plotted logarithmically against either the distance traveled keeping the visitation frequency fixed, or vice versa, against the visitation frequency keeping the travel distance fixed, a straight line should result in both cases with the same slope of -2 (recall that the minus sign simply means that the line slopes downward). I should emphasize that as with all of the scaling laws, an average over a long enough period of time, such as six months or a year, is presumed, in order to smooth over daily fluctuations, or the differences between weekdays and weekends.
As can be readily seen from Figure 47, these predictions are spectacularly confirmed by the data. Indeed, the observed scaling is remarkably tight, with slopes in excellent agreement with the prediction of −2. Particularly satisfying is that the same predicted inverse square law is observed across the globe in diverse cities with very different cultures, geographies, and degrees of development: we see an identical behavior in North America (Boston), Asia (Singapore), Europe (Lisbon), and Africa (Doha). Furthermore, when each of these metropolitan areas is deconstructed into specific locations, the same inverse square law is manifested at each of these within the city, as shown, for example, in Figures 48 and 49 for a sampling of locations in both Boston and Singapore.
Let me give a simple example to illustrate how the theorem works. Suppose that on average 1,600 people visit the area around Park Street, Boston, from 4 kilometers away once a month. How many people visit there from twice as far away (8 km) with the same frequency of once a month? The inverse square law tells us that ¼ (= ½2) as many make the visit, so only 400 people (¼ × 1,600) visit Park Street from 8 kilometers away once a month. How about from five times as far away, 20 kilometers? The answer is 1⁄25 (= 1/52) as many, which is just 64 people (1⁄25 × 1,600) visiting once a month. You get the idea. But there’s more: you can likewise ask what happens if you change the frequency of visitation. For instance, suppose we ask how many people visit Park Street from 4 kilometers away but now with a greater frequency of twice a month. This also obeys the inverse square law so the number is ¼ (= ½2) as many, namely 400 people. And similarly, if you ask how many people visit there from the same distance of 4 kilometers away but five times a month, the answer is 64 people (1⁄25 × 1,600).
Notice that this is the same number that visit Park Street from five times as far away (20 km) with a frequency of just once a month. Thus the number of people visiting from 4 kilometers away five times a month is the same as the number visiting from five times farther away (20 km) once a month (64 in both cases of our specific example). This result does not depend on the specific numbers I chose for the illustration. It is an example of an amazing general symmetry of mobility: if the distance traveled multiplied by the frequency of visits to any specific location is kept the same, then the number of people visiting also remains the same. In our example we had 4 kilometers × 5 times a month = 20 in the first case and 20 kilometers × once a month = 20 in the second. This invariance is valid for any visiting distance and for any frequency of visitation to any area in any city. These predictions are verified by the data and manifested in the various graphs of Figures 48 and 49 where you can explicitly see that the pattern of visitation remains unchanged when the product of distance times frequency has the same value.



Here and here: (47) (a) Flux of people visiting from varying distances to a specific location in Boston with different but fixed frequencies (f times a month) showing agreement with the inverse square law. (b) Same data as in (a) but showing how all of the different frequencies and distances collapse to a single line when plotted against the single variable frequency × distance. (c) Similar plot to (b) showing how the visitor flux obeys the same predicted inverse square law in very different cities around the globe. (48) Similar plot to (c) but at multiple locations in Boston and (49) Singapore; the solid lines are the predictions from the theory.
I want to emphasize just how remarkable and unexpected this prediction is, given the extraordinary complexity and diversity of movement and transport in cities. When one thinks of the seemingly chaotic random and diverse movement and mobility of people in cities like New York, London, Delhi, or São Paulo, it’s hard not to view this extremely simple picture of a hidden order and regularity as being most unlikely and even absurd. Each individual’s random decision to travel to and from a specific location via an optimal route regardless of whether they walk, take the subway, ride the bus, drive their car, or even do all of the above, is predicted to result in a coherent collective flow just as the random motion of trillions of individual water molecules results in a smooth, coherent flow when you turn on the tap in your kitchen.
As I explained above, cell phone data provide detailed information not only about who you talked to and for how long, but also where you were and when you did it. In effect, each of us is carrying a device that is keeping track of where we are at any time. It’s as if we were able to put a tag on every molecule in a room and thereby know its location, how fast it’s moving, who it bumps into, and so forth. Because there are more than ten thousand trillion trillion (1028) molecules in a modest-size room, this would represent the mother of all big data. However, this information is actually not very useful, especially for gases in equilibrium—it’s massive overkill. The powerful techniques of statistical physics and thermodynamics have been successfully developed to understand and describe macroscopic properties of gases, such as their temperature, pressure, phase transitions, and so on, without needing to know the gory details of the motion of all of their constituent molecules. In cities, on the other hand, such information is extremely valuable not only because we ourselves are the molecules, but also because, unlike gases, cities are complex adaptive systems with intricate network structures exchanging both energy and information. Mobile phone data provide us with a powerful tool for determining the structure and dynamics of these networks and, consequently, for quantitatively testing theoretical predictions.
This is potentially a powerful tool for planning and development because it provides a framework for estimating the flux of people to and from specific areas of a city. Building a new mall or developing a new housing project requires accurate, or at least credible, estimates of the flow of traffic and people to ensure sufficient and efficient transport needs. Much of this is done using computer models, which are certainly very useful, but the simulations tend to be locally focused, ignoring the relationship to a bigger, integrated systemic dynamic of the city, and are rarely based on fundamental principles.
The analysis of these massive data sets of mobile phone calls used to test the theory was brilliantly carried out by a Swiss engineer, Markus Schläpfer, working with the Hungarian physicist Michael Szell, two of the bright young postdocs hired by Carlo Ratti at MIT. Markus later joined us at the Santa Fe Institute in 2013, where we began this particular collaboration. Of the many projects he worked on, a particularly interesting one was with Luis on analyzing how the heights and volumes of buildings relate to city size. Markus has since moved on to the prestigious ETH in Zurich, his hometown, where he is engaged with a large collaborative program called the Future Cities Lab, which is based in Singapore and supported by their government.
8. OVERPERFORMERS AND UNDERPERFORMERS
Most of us find rankings intriguing whether they’re for cities, schools, universities, corporations, states, or countries, not to mention football teams and tennis players. Basic to this is, of course, the choice of metrics and methodologies used to make the rankings. How questions are posed and what segment of the population is sampled can strongly determine the outcome of surveys and polls, which can have significant consequences in politics and commerce. Such rankings play an increasingly influential role in decision making by individuals, planners, and policy makers in government and industry. How a city or state ranks on the world or national stage in health, education, taxes, employment, and crime can have a powerful influence on how it is perceived by investors, corporations, and vacationers.
In sports, a question that’s perennially debated is who was the greatest player or team of all time, a question that is obviously unanswerable from any objective viewpoint. The problem is not just what metrics are reasonable proxies for “greatness,” but that it typically involves comparing apples with oranges, often over different periods of time. In this context let’s briefly revisit the discussion on weight lifting introduced in chapter 2 and recall Galileo’s seminal insight that the strength of the limbs of animals should scale sublinearly as the ⅔ power of their body weight. This prediction is confirmed by data on champion weight lifters, as shown in Figure 7. I introduced the idea that this scaling curve should be viewed as the baseline about which performance should be measured: it tells us how much an idealized champion weight lifter of a given body weight should lift. In a similar fashion, the ¾ power scaling law for metabolic rates shown in Figure 1 tells us what the metabolic rate of an idealized organism of a given size “should” be. “Idealized” in that case is understood to mean a system that is “optimized” in terms of the energy use, dynamics, and geometry of network structures, as was explained in chapter 3.
This framework was used as a point of departure to give a science-based measure of performance. Four of the six champions lifted loads they should have, given their body weights and the expectations from the scaling law. On the other hand, the middleweight overperformed relative to the expectations for his size, whereas the heavyweight underperformed. So despite the heavyweight lifting a greater load than anyone else, from a scientific perspective he was actually the weakest of all the champions while the middleweight was the strongest.
In situations like this where we are able to develop a quantitative scientific framework for performance based on scaling, we can also construct meaningful metrics for rankings and for comparison across different competitions. More mechanical sports such as weight lifting, rowing, and even running potentially lend themselves to this methodology, whereas team sports like football and basketball are considerably more challenging. Deviations from scaling therefore provide a principled metric for individual performance and a quantitative point of departure for investigating why, as in the weight lifting case, the middleweight overperformed and the heavyweight underperformed relative to their size.
This strategy of ranking performance effectively levels the playing field by removing the dominant variation arising simply from differences in size to reveal the essential individual skill of each competitor. Below I will apply this idea to cities, but before doing so I want to use it in conjunction with the mobility analysis in cities to indicate how it can potentially be used as an important planning and development tool.
As exemplified in Figures 48 and 49, the data for travel to specific locations in cities fits the theoretical prediction extremely well. However, if you look closely at the graphs for Boston you can see that there are two particular locations, the airport and the football stadium, where there are significant deviations and the fits aren’t quite as good. Given the special role of both places, this is perhaps not so surprising precisely because they draw on a relatively narrow subset of people who use them for very specific reasons: either for taking a trip or for going to a football game.
Although the data for the airport still cluster reasonably well around the prediction, the greatest deviations occur in the number of people traveling either from short distances away or relatively infrequently. This subset actually constitutes the majority of people using the airport. In contrast, those coming from farther away or who use the airport most frequently conform very well to the predicted scaling curve, though they constitute the minority of users. Knowing and understanding these patterns of usage both in the general trend and in their variance is clearly important for planning and managing transport flows to and within the airport and how these relate to transport in the metropolitan area as a whole.
In Singapore there is only one such major outlier, namely, Raffles Place, which is the central core of the city-state’s financial district. In addition, it is a major transportation hub and a gateway to a large tourist area. The data on the number of visitors actually scale reasonably well, but the exponent is significantly smaller than in the rest of Singapore’s locations, all of which are in excellent agreement with the predicted value of −2. In addition, it exhibits much larger fluctuations around scaling than in the rest of Singapore. This translates into fewer people coming either from close by or less often than expected, and more people coming from farther away or more often than expected. This may well be because of the special nature of Singapore as a small island nation whose core district, Raffles Place, is not near its geographical center but rather borders on its boundary with the ocean.
As in the case of Boston’s airport and stadium, it’s important for planning, designing, and controlling transport and movement for both this specific special location as well as across the entire city to recognize that Raffles Place is an outlier from the dominant mobility pattern observed in every other location in the city. Equally important is that this can be quantified and understood within the context of the entire urban system.
9. THE STRUCTURE OF WEALTH, INNOVATION, CRIME, AND RESILIENCE: THE INDIVIDUALITY AND RANKING OF CITIES
How rich, creative, or safe can we expect a city to be? How can we establish which cities are the most innovative, the most violent, or the most effective at generating wealth? How do they rank according to economic activity, the cost of living, the crime rate, the number of AIDS cases, or the happiness of their populations?
The conventional answer is to use simple per capita measures as performance indices and rank order of cities accordingly. Almost all official statistics and policy documents on wages, income, gross domestic product (GDP), crime, unemployment rates, innovation rates, cost of living indices, morbidity and mortality rates, and poverty rates are compiled by governmental agencies and international bodies worldwide in terms of both total aggregate and per capita metrics. Furthermore, well-known composite indices of urban performance and the quality of life, such as those assembled by the World Economic Forum and magazines like Fortune, Forbes, and The Economist, primarily rely on naive linear combinations of such measures.6
Because we have quantitative scaling curves for many of these urban characteristics and a theoretical framework for their underlying dynamics we can do much better in devising a scientific basis for assessing performance and ranking cities.
The ubiquitous use of per capita indicators for ranking and comparing cities is particularly egregious because it implicitly assumes that the baseline, or null hypothesis, for any urban characteristic is that it scales linearly with population size. In other words, it presumes that an idealized city is just the linear sum of the activities of all of its citizens, thereby ignoring its most essential feature and the very point of its existence, namely, that it is a collective emergent agglomeration resulting from nonlinear social and organizational interactions. Cities are quintessentially complex adaptive systems and, as such, are significantly more than just the simple linear sum of their individual components and constituents, whether buildings, roads, people, or money. This is expressed by the superlinear scaling laws whose exponents are 1.15 rather than 1.00. This approximately 15 percent increase in all socioeconomic activity with every doubling of the population size happens almost independently of administrators, politicians, planners, history, geographical location, and culture.
In assessing the performance of a particular city, we therefore need to determine how well it performs relative to what it has accomplished just because of its population size. By analogy with the discussion on determining the strongest champion weight lifter by measuring how much each deviated from his expected performance relative to the idealized scaling of body strength, one can quantify an individual city’s performance by how much its various metrics deviate from their expected values relative to the idealized scaling laws. This strategy separates the truly local nature of a city’s organization and dynamics from the general dynamics and structure common to all cities. As a result, several fundamental questions about any individual city can be addressed, such as how exceptional it is relative to its peers, what timescales are relevant for local policy to take effect, what are the local relationships between economic development, crime, and innovation, to what extent is it unique, and to what extent can it be considered a member of a family of like cities.
My colleagues Luis, José, and Debbie carried out such an analysis for the entire U.S. urban system consisting of 360 Metropolitan Statistical Areas (MSAs) for a suite of metrics.7 A sample of the results is presented in Figure 50), where the deviations from scaling for personal income and patent production for cities in the United States in 2003 are plotted logarithmically on the vertical axis against the rank order of each city. We called these deviations Scale-Adjusted Metropolitan Indicators (SAMIs). The horizontal axis across the center of these graphs is the line along which the SAMI is zero and there is no deviation from what is predicted from the size of the city. As can be seen, every city deviates to some extent from its expected values. Those to the left denote above-average performance, whereas those to the right denote below-average performance. This provides a meaningful ranking of a city’s individuality and uniqueness beyond what is effectively guaranteed just because it’s a city of a certain size. Without delving into details of this analysis, I want to make a few salient points about some of the results.
First, compared with conventional per capita indicators, which place seven of the largest twenty cities in the top twenty in terms of their GDPs, our science-based metrics rank none of these cities in the top twenty. In other words, once the data are adjusted for the generic superlinear effects of population size, these cities don’t fare so well. Mayors of these cities who take credit and boast that their policies have led to economic success as evidenced by their city’s being near the top of the per capita GDP rankings are therefore giving a misleading impression.
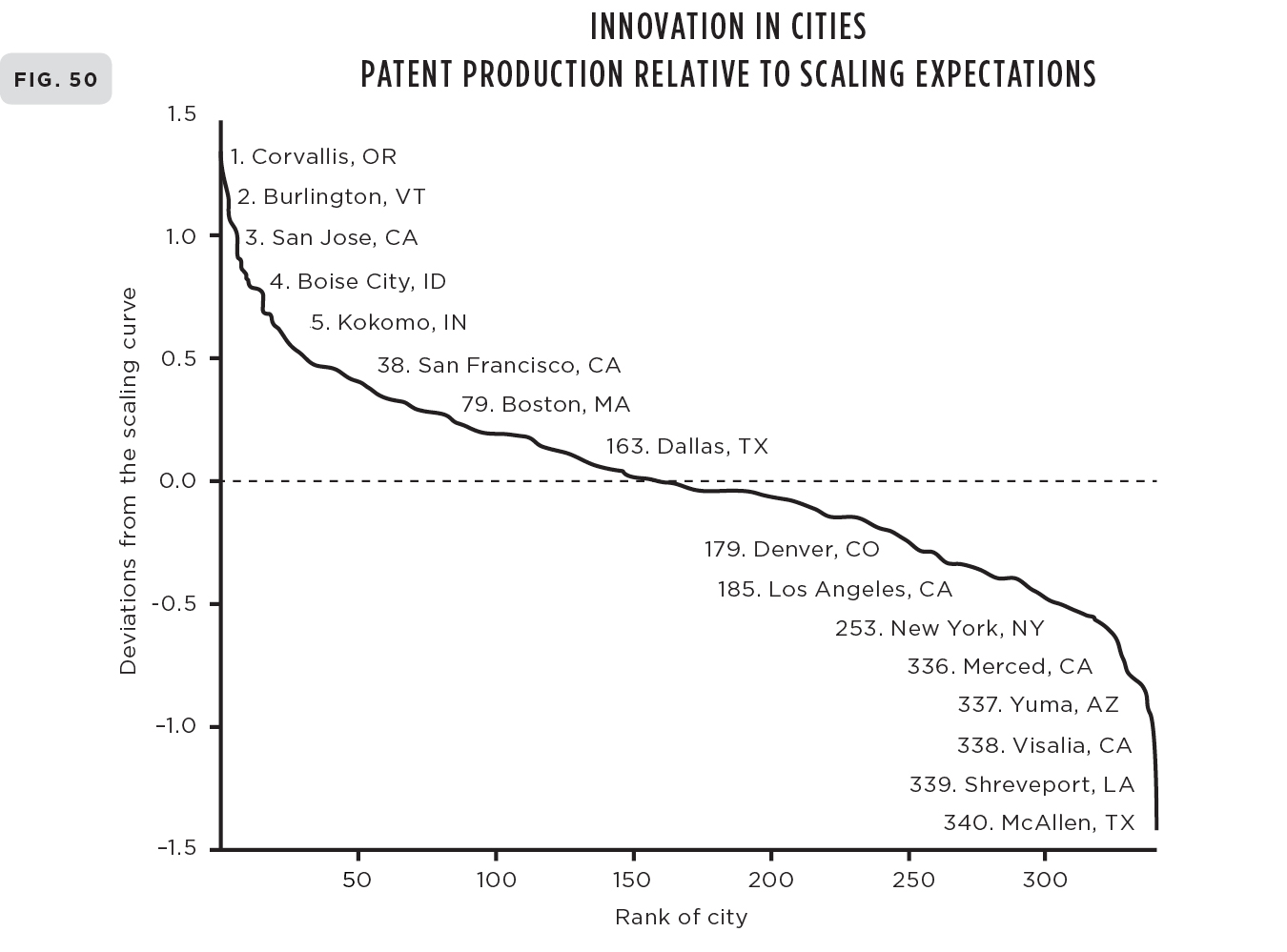
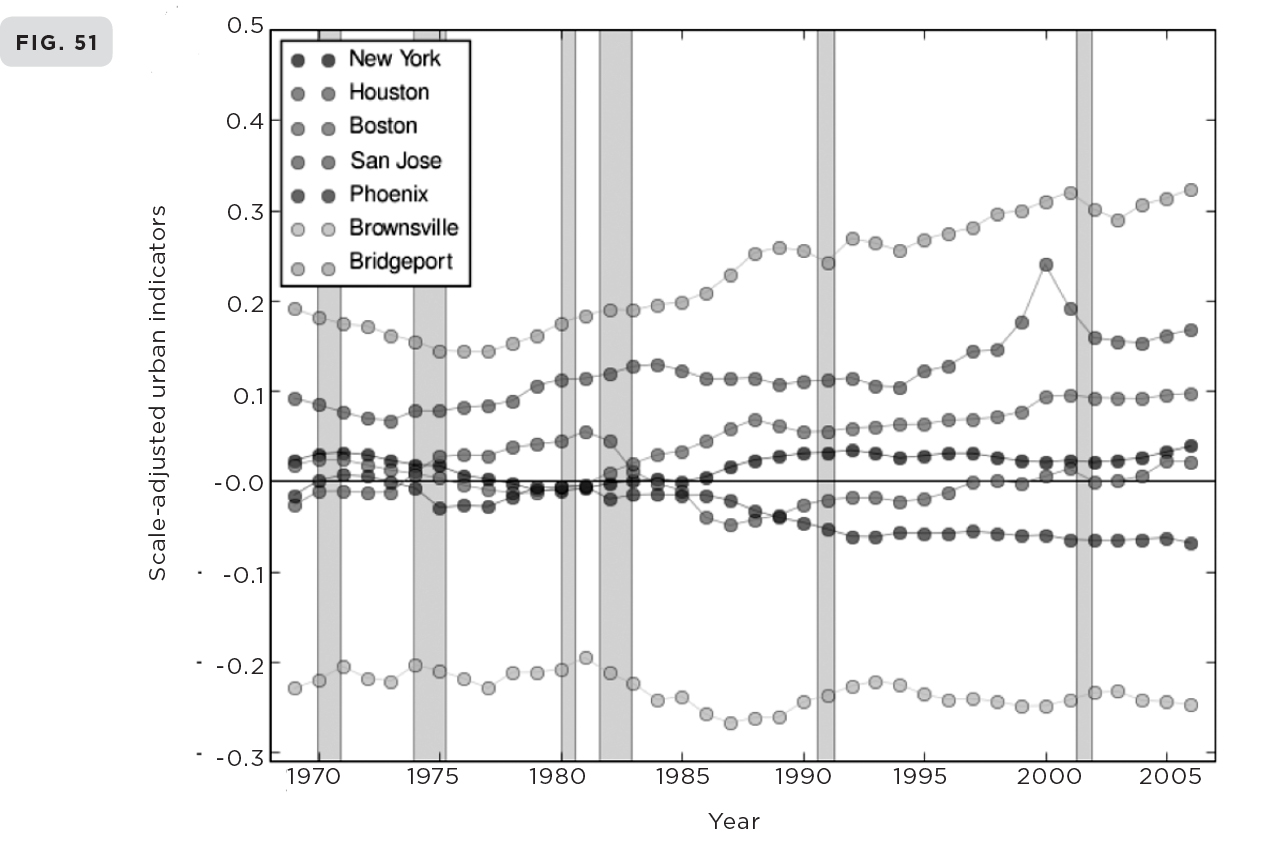
(50) Deviations in the number of patents produced in U.S. cities in 2003 relative to the expected number from scaling laws given the size of the city, plotted against their rank. Those to the left are overperformers with Corvallis being ranked first, whereas those to the right are underperformers with McAllen being ranked last. (51) The time evolution of these deviations (SAMIs) showing their long persistence time.
Amusingly from this point of view, New York City as a whole turns out to be quite an average city, marginally richer than its size might predict (rank 88th in income, 184th in GDP), not very inventive (178th in patents), but surprisingly safe (267th in violent crime). On the other hand, San Francisco is the most exceptional large city, being rich (11th in income), creative (19th in patents), and fairly safe (181st in violent crime). The truly exceptional cities are typically smaller, such as Bridgeport for income (due to all those bankers and hedge fund managers from New York City living in the suburbs), Corvallis (home of Hewlett-Packard research lab and a respectable university, Oregon State), and San Jose (which encompasses Silicon Valley—what more need be said?) for patents, and Logan (the Mormon culture?) and Bangor (who knows?) for safety.
This is just for a single year (2003), and it is natural to ask how any of this changes with time. Unfortunately, readily accessible data on all of these metrics are hard to come by prior to about 1960. However, an analysis covering data over the last forty to fifty years reveals some very intriguing results, as illustrated in Figure 51, where the temporal evolution of deviations for personal income in a few typical cities is shown. Perhaps the most salient feature is how relatively slowly fundamental change actually occurs. Cities that were overperforming in the 1960s, such as Bridgeport and San Jose, tend to remain rich and innovative today, whereas cities that were underperforming in the 1960s, such as Brownsville, are still near the bottom of the rankings. So even as the population has increased and the overall GDP and standard of living have risen across the entire urban system, relative individual performance hasn’t changed very much. Roughly speaking, all cities rise and fall together, or to put it bluntly: if a city was doing well in 1960 it’s likely to be doing well now, and if it was crappy then, it’s likely to be crappy still.
Once a city has gained an advantage, or disadvantage, relative to its scaling expectation, this tends to be preserved over decades. In this sense, either for good or for bad, cities are remarkably robust and resilient—they are hard to change and almost impossible to kill. Think of Detroit and New Orleans, and more drastically of Dresden, Hiroshima, and Nagasaki, all of which have to varying degrees survived what were perceived as major threats to their very existence. All are actually doing fine and will be around for a very long time.
A fascinating example of persistent advantage is San Jose, which includes Silicon Valley, the place everyone wants to be. It’s hardly a surprise that this is a major overperformer in terms of wealth creation and innovation. But what is a surprise is that San Jose was already overperforming in the 1960s, and almost to the same degree as it is now, as graphically illustrated in Figure 51. This also demonstrates that this overperformance has been sustained and even reinforced for more than forty years despite the short-term boom and bust technological and economic cycle in 1999–2000, at the end of which the city relaxed back to its long-term basal trend. Put slightly differently: apart from a relatively small bump in the late 1990s, the continued success of San Jose was already set well before the birth of Silicon Valley. So rather than seeing Silicon Valley as generating the success of San Jose and lifting it up in the conventional socioeconomic rankings, this suggests that it was the other way around and that it was some intangible in the culture and DNA of San Jose that helped nurture the extraordinary success of Silicon Valley.8
It takes decades for significant change to be realized. This has serious implications for urban policy and leadership because the timescale of political processes by which decisions about a city’s future are made is at best just a few years, and for most politicians two years is infinity. Nowadays, their success depends on rapid returns and instant gratification in order to conform to political pressures and the demands of the electoral process. Very few mayors can afford to think in a time frame of twenty to fifty years and put their major efforts toward promoting strategies that will leave a truly long-term legacy of significant achievement.
10. PRELUDE TO SUSTAINABILITY: A SHORT DIGRESSION ON WATER
In the developed world we take much of our infrastructure for granted and rarely appreciate the scale and cost that goes into providing amenities like clean, safe drinking water each time we turn on the faucet in our kitchens. This is a huge privilege and, as I discussed in an earlier chapter, is a prime reason why our longevity made such a huge leap beginning in the late nineteenth century. Providing such basic services for all people across the globe is an enormous challenge as we urbanize the planet. Safe water is progressively becoming a source of increased social friction, especially as the climate changes and produces unpredictable periods of severe drought or massive floods, both of which compromise supply and delivery systems. This is already a major issue in many developing countries and hints of it have begun to be seen even in the United States with serious problems arising in supply systems, as in Flint, Michigan, and severe water shortages occurring throughout many of the western states.
I live in the small city of Santa Fe, New Mexico, whose population is about 100,000, in what is usually identified as a semiarid high desert climate where only about 14 inches of rain falls each year. Appropriately, water is very expensive and there are high penalties for overuse. The city boasts one of the highest costs for water of any city in the United States—about two and a half times above the national average and about 50 percent higher than the next most expensive city, which, surprisingly, is drizzly Seattle with almost 40 inches of rain a year. But equally surprising is that it is six times higher than one of the cheapest cities, Salt Lake City, which gets only 16.5 inches of rain a year. Even more bizarre is that the cost of water in the desert cities of Phoenix, whose population is 4.5 million, and Las Vegas, whose population is almost 2 million, is barely higher than in Salt Lake City, even though Phoenix gets only 8 inches of rain a year and glitzy Las Vegas only a measly 4 inches. Go figure!
This kind of profligacy is everywhere. For instance, most people don’t realize that even California megalopolises like Los Angeles and San Francisco with almost one hundred times the population of Santa Fe, or fancy leafy-green towns with luxurious vegetation like Palo Alto, the home of Stanford University, or Mountain View, the home of Google, get pretty much the same amount of rainfall as Santa Fe, namely, about 14 inches a year. And much of their water use goes to keeping their lawns and gardens looking as if they were growing in Singapore, whose annual rainfall is 92 inches.
The good news is that most urban communities in the United States and across the globe are becoming much more sensitive to these issues, recognizing that clean water is a precious commodity that is being depleted at an alarming rate and that it cannot be taken for granted. Most are beginning to implement policies to significantly reduce water consumption but, like many “green” conservation measures, these may be too little too late.
The point is that in all of these communities enormous resources have been put into the engineering infrastructure to artificially provide them with abundant water transported over great distances and/or from very deep aquifers, with the implicit assumption that these sources are inexhaustible and forever cheap—questionable, at best. As urbanization and questions of sustainability become ever more pressing, the politics and economics of water will progressively become ever more contentious, much like that of oil and other sources of energy in the twentieth century. And, as in the case of oil, major conflicts may eventually be fought over its access and ownership.
Curiously, however, it is worth bearing in mind that in contrast to oil, the planet has more than enough water, just as it has more than enough solar energy to support the entire mass of humanity essentially forever. Adapting our technological and socioeconomic strategies to this simple fact is critical to our long-term survival—a mind-set that we should have adopted long ago by promoting renewable solar energy and desalinization. Have we been so shortsighted and parochial that we are doomed like the sailors in Samuel Taylor Coleridge’s famous poem “The Rime of the Ancient Mariner” to a collective nightmare of thirst?
Water, water, every where,
And all the boards did shrink;
Water, water, every where,
Nor any drop to drink.
Before returning to science and the city I want to give a sense of the scale of a major city’s water system and what it entails. New York City is rightly famous for being a trendsetter in almost everything, but one of its achievements that is not often appreciated is its water system. Its quality and taste are often considered to be superior not just to water from other municipalities, but to fancy bottled water and at a fraction of the cost without the absurd waste of throwaway plastic containers. Next time you’re in New York you can save yourself a few bucks and at the same time get a superior product by simply filling your water bottle from the tap.
Water is supplied to the city from watersheds that are up to one hundred miles north of the city and primarily fed by gravity flow, thereby saving huge energy costs in pumping. The water system has a storage capacity of 550 billion gallons (about 2 billion cubic meters), which provides more than 1.2 billion gallons a day (about 4.5 million cubic meters) of clean drinking water to more than 9 million residents. These are huge numbers, and to appreciate their size note that they are equivalent to delivering about 100,000 of those silly little 16-ounce or 500-millileter plastic bottles of water every second. To accomplish this astonishing feat, water leaves the reservoirs through massive “pipes” that are actually deep underground concrete tunnels. A new $5 billion project is presently under way to build a new tunnel to augment two older ones. It will eventually span sixty miles in length at a depth of up to eight hundred feet, and its diameter when leaving the reservoir is twenty-four feet (bigger even than Godzilla’s aorta). This steps down in progressive sections as water is distributed through the network hierarchy to the entire New York metropolitan area, eventually feeding the main pipes buried beneath streets whose diameters are anywhere from four to twelve inches depending on the building density (obviously the largest pipes are in downtown Manhattan). Water is distributed from these mains to individual homes through one-inch pipes that are then further downsized to half an inch before they reach kitchen sinks and toilets.
This hierarchical geometry of New York’s water system is typical of all urban water systems across the globe, except, of course, that the overall scale varies depending on the size of the city. This template is quite similar to our own circulatory system, even to the extent that both networks are space filling and the terminal units in both systems are approximately invariant. Santa Fe’s water system is very much smaller than New York’s, but the size of the one-inch pipes delivering water to my house and the half-inch ones delivering water to my toilet are the same as those in New York in much the same way that the size of our capillaries is pretty much the same as those of mice or blue whales. This fractal-like behavior is reflected in the total length of all of the pipes in New York’s water network system: added together from the reservoir down to the street mains they stretch for approximately 6,500 miles (10,500 km). In other words, put end to end the total length of all of the pipes in the system would run from New York to Los Angeles and back again. This is pretty impressive, but it pales in comparison to the length of all of the vessels in your circulatory system: if you put all of them end to end it, too, would also stretch from New York to Los Angeles and back, yet all of it fits inside your body.
11. THE SOCIOECONOMIC DIVERSITY OF BUSINESS ACTIVITY IN CITIES
Like resilience and innovation, diversity has become a much overused buzzword commonly employed to characterize a successful city. Indeed, the ever-changing admixture of individuals, ethnicities, cultural activities, businesses, services, and social interactions is a defining characteristic of urban life. A major socioeconomic component of this is the abundance of different types of businesses in cities. While all cities necessarily have a similar essential core of businesses—lawyers, doctors, restaurants, garbage collectors, teachers, administrators, and so on—only a very few have specialized subcategories such as maritime lawyers, tropical disease doctors, blacksmiths, chess store proprietors, nuclear physicists, and hedge fund managers.
Consequently, quantifying the diversity of business types is potentially problematic because any systematic classification scheme is subject to an arbitrary designation of specific categories; any business type can be further subdivided as long as a defining distinction can be made. Restaurants, for example, can be decomposed into fine dining, fast food, et cetera, as well as into multiple levels of cuisine, price, quality, and so on. There are broad categories such as Asian, European, and American, but Asian, for instance, can be divided into Chinese, Indian, Thai, Indonesian, Vietnamese, et cetera, and Chinese itself can be further subdivided into Cantonese, Szechuan, dim sum, and so on. The lesson is clear: urban diversity is scale-dependent in the sense that it depends on the resolution with which it is perceived. This is not so different in spirit from the problem first recognized by Lewis Fry Richardson when he tried to measure the length of various coastlines and boundaries, and which led Benoit Mandelbrot to invent the concept of fractals.
Luckily, the challenge of formally categorizing businesses has been addressed, at least in North America, by the compilation of an extraordinary data set that includes the records of almost all business establishments in the United States (more than 20 million). This is the result of an impressive collaboration between the United States, Canada, and Mexico, and is called the North American Industry Classification System (NAICS).9 An establishment is just any single physical location where business is conducted. Consequently, individual businesses that are part of a national chain, such as a Walmart store or a McDonald’s franchise, would be counted as separate establishments. Establishments are often viewed as the fundamental units of economic analysis because innovation, wealth generation, entrepreneurship, and job creation all manifest themselves through the formation and growth of such workplaces. The NAICS classification scheme employs a six-digit code at the most detailed industry level. The first two digits designate the largest business sector, the third digit designates the subsector, and so on, thereby capturing economic life at an extraordinarily fine-grained level.
My colleagues Luis, José, and Debbie carried out an analysis of these data with our postdoc Hyejin Youn taking the lead role. Hyejin was trained in statistical physics in Seoul, South Korea, and had joined SFI to finish her doctorate. She first worked on the origin and structure of languages before joining our collaboration. She has now established herself as an expert on innovation in technology and is currently a fellow of the Institute of New Economic Thinking (INET) at Oxford University—a new program funded by the financier George Soros.
As we saw in the analysis of other urban metrics, the data reveal surprisingly simple and unexpected regularities. For instance, the total number of establishments in each city regardless of what business they conduct turns out to be linearly proportional to its population size. Double the size of a city and on average you’ll find twice as many businesses. The proportionality constant is 21.6, meaning that there is approximately one establishment for about every 22 people in a city, regardless of the city size. Or to put it slightly differently, on average a new workplace is created each time the population of a city increases by just 22 people, whether in a small town or a large metropolis. This is an unexpectedly small number and usually comes as quite a surprise to most people, even those dealing in business and commerce. Similarly, the data also show that the total number of employees working in these establishments also scales approximately linearly with population size: on average, there are only about 8 employees for every establishment, again regardless of the size of the city. This remarkable constancy of the average number of employees and the average number of establishments across cities of vastly different sizes and characters is not only contrary to previous wisdom, but also rather puzzling when viewed in light of the pervasive superlinear agglomeration effects that underlie all socioeconomic activity including per capita increases in productivity, wages, GDP, and patent production.10
To get a deeper understanding of this and to reveal the business character of a city, it’s illuminating to ask how many different types of businesses there are in a city. This is like asking how many different species of animals there are in an ecosystem. The simplest coarse-grained measure of economic diversity of a city is obtained by just counting the number of distinct types of establishments it has as a function of its population size. The data confirm that diversity systematically increases with population size at all levels of resolution, as defined by the NAICS data set. Unfortunately, the classification scheme is unable to capture the full extent of economic diversity in the largest cities because it is unable to differentiate among very closely related types of establishments such as, for instance, between a northern and southern Italian restaurant. However, an extrapolation of the data strongly suggests that if we could measure diversity to the finest possible resolution it would scale logarithmically with city size.
Compared with the usual canonical power law behavior that most metrics obey, this represents an extremely slow increase with population size. For instance, an increase of the population by a factor of one hundred from, say, 100,000 to 10 million results in the addition of one hundred times as many businesses but an increase of only a factor of two in their diversity. To put it slightly differently: doubling the size of a city results in doubling the total number of establishments, but only a meager 5 percent increase in new kinds of businesses. Almost all of this increase in diversity is reflected in a greater degree of specialization and interdependence involving larger numbers of people, both as workers and as clients. This is an important observation because it shows that increasing diversity is closely linked to increasing specialization, and this acts as a major driver of higher productivity following the 15 percent rule.
A more detailed way of assessing economic diversity is to dig deeper and examine the specific component types of establishments that constitute the business landscape of individual cities. How many lawyers, doctors, restaurants, or contractors are there in each city, and how many of these are corporate lawyers, orthopedic surgeons, Indonesian restaurants, or plumbing contractors? As an example of such an analysis, Figure 52 shows the abundances of the one hundred leading business types for a selection of cities in the United States. These are plotted in the classic rank-size format that was used when discussing Zipf’s law for the frequency distribution of words in a language and cities in an urban system. When giving a talk, I preface the showing of this graph by asking the audience what they think is the most abundant business type in New York City. So far, no one has yet come up with the correct answer, including audiences of business and corporate gurus operating in New York City itself. It’s amazing what you can learn from taking a simple analytic, principled approach to problems.
Well, in New York the most abundant business type is offices of physicians. Weird, especially because physicians are ranked only fifth in Phoenix, which has a huge retirement community of decrepit old farts like me, and seventh in San Jose, which is possibly less surprising given all those young obsessive-compulsive California joggers and health enthusiasts. Less surprising is that after physicians, the next highest ranked in New York are offices of lawyers, followed by restaurants. In fact, restaurants rank high in all cities, being first, for example, in Chicago, Phoenix, and San Jose. Eating out, whether at a fancy Four Seasons restaurant or at a McDonald’s fast-food stop, is clearly a major component of the socioeconomic activity of Americans. More generally, it’s interesting to speculate what these sorts of rankings say about a city. For instance, after restaurants Phoenix ranks real estate second, which is perhaps not surprising in a rapidly growing city, whereas San Jose, the home of Silicon Valley, predictably ranks computer programming second. It’s obvious why lawyers and restaurants would rank high in New York, but what is it about New York that there should be such a large abundance of doctors? Is life in the Big Apple that stressful and unhealthy? If you find this intriguing, you can see the analogous decomposition of economic activities in your favorite city in the supplementary material to our paper posted on the Web. Clearly, for those running a city or thinking about its future or investing in its development, knowing these sorts of details about the composition of their business landscape provides an important input.

(52) The number of establishments ranked in descending order of their frequencies (from common to rare) for New York City, Chicago, Phoenix, and San Jose. Establishment types are referred to by their NAICS classification. (53) Universal per capita rank-abundance curve of establishment types for all 366 metropolitan statistical areas of the United States; shown explicitly are New York City, Chicago, Phoenix, Detroit, San Jose, Champaign-Urbana, and Danville. The inset shows the first 200 types plotted logarithmically, obeying an approximate Zipf-like power law behavior.
In contrast to the inherent universal properties of cities that are manifested in the scaling laws, these rank-size distributions of business types reflect the individuality and distinctive characteristics of each specific city as exhibited by the composition of its economic activities. They are the hallmark of each city and obviously do depend on its history, geography, and culture. It is therefore all the more remarkable that, despite the unique admixture of business types for each individual city, the shape and form of their distribution is mathematically the same for all of them. So much so, in fact, that with a simple scale transformation inspired by theory their rank abundances collapse onto a single unique universal curve common to all cities, as shown explicitly in Figure 53. When one considers the vast range of income, density, and population levels, let alone the uniqueness and diverse cultures that vary so widely in cities across the United States, this universality is quite surprising.
What is particularly satisfying is that this unexpected universality, as well as the actual form of the universal curve and the logarithmic scaling of diversity, can all be derived from theory. The universality is driven by the constraint that the sum total of all the different businesses in a city scales linearly with population size, regardless of the detailed composition of business types or of the city. The snakelike mathematical form of the actual distribution function in Figure 53 can be understood from a variant of a very general dynamical mechanism that has been successfully used for understanding rank-size distributions in many different areas, ranging from words and genes to species and cities. It goes under many different names including preferential attachment, cumulative advantage, the rich get richer, or the Yule-Simon process. It is based on a positive feedback mechanism in which new elements of the system (business types in this case) are added with a probability proportional to the abundances of how many are already there. The more there are, the more of that type are going to be added, so more frequent types get even more abundant with increasingly higher probability than less frequent types.11
A couple of colloquial examples may help: successful companies and universities attract the smartest people, resulting in their becoming more successful, thereby attracting even smarter people, leading to even greater success and so on, just as wealthy people attract favorable investment opportunities that generate even more wealth which they further invest to get even more wealthy. Hence the catchphrase the rich get richer and its implied, but usually unstated, corollary the poor get poorer to characterize this process. Or, as so articulately put by Jesus according to the Gospel of Matthew in the New Testament:
For everyone who has will be given more, and he will have an abundance. Whoever does not have, even what he has will be taken from him.
This surprising declaration has been used by some fundamentalist Christians and others as justification for rampant capitalism—a sort of anti–Robin Hood slogan supporting the idea of taking from the poor to give to the rich. But while Jesus’s remarks are a good example of preferential attachment, the quote is, not surprisingly, taken out of context. It is often conveniently forgotten that Jesus was actually referring to knowledge of the mysteries of the kingdom of heaven and not to material wealth. He was expressing a spiritual version of the very essence of diligent study, knowledge accumulation, and research and education as expressed by the ancient rabbis: He who does not increase his knowledge decreases it.
The first serious mathematical consideration of preferential attachment was made by Udny Yule, a Scottish statistician who in 1925 used it to explain the power-law distribution for the number of species per genus of flowering plants. The modern socioeconomic version of preferential attachment, or cumulative advantage, is due to Herbert Simon and is consequently nowadays referred to as the Yule-Simon process. Simon, by the way, was an extraordinary polymath and one of the most influential social scientists of the twentieth century. His research ranged across the fields of cognitive psychology, computer science, economics, management, philosophy of science, sociology, and political science. He was a founding father of several important scientific subdisciplines whose influence has gained great prominence in recent years, including artificial intelligence, information processing, decision making, problem solving, organization theory . . . and complex systems. He spent almost his entire academic career at Carnegie Mellon University in Pittsburgh and received the Nobel Memorial Prize in Economics for his seminal work on decision-making processes in economic organizations.
The empirical and theoretical analyses of business diversity presented above show that all cities exhibit the same underlying dynamics in the development of their business ecology as they grow. Initially, small cities with a limited portfolio of economic activities need to create new businesses and functionalities at a fast rate. These basic activities constitute the economic core of every city, big and small; every city needs lawyers, doctors, shopkeepers, tradesmen, administrators, builders, et cetera. As cities grow and these basic core activities become saturated, the pace at which new functionalities are introduced slows down dramatically but never completely ceases. Once the set of individual building blocks is large enough, the resulting combination of talents and functions is sufficient to generate novel variations that expand the business landscape, giving rise to specialized establishments such as exotic restaurants, professional sports teams, and luxury stores, leading to greater economic productivity.
Although the theory cannot predict how specific business types rank in individual cities (why, for instance, doctors are first in New York but seventh in San Jose), it does predict how their rankings change as cities grow. The general rule is that business types whose abundances scale superlinearly with population size systematically rise in their rankings, whereas those that scale sublinearly systematically decrease. For instance, at the coarsest level of the NAICS classification scheme traditional sectors such as agriculture, mining, and utilities scale sublinearly; the theory predicts that the rankings and relative abundances of these industries decrease as cities get larger. On the other hand, informational and service businesses such as professional, scientific, and technical services, and management of companies and enterprises, scale superlinearly and are consequently predicted to increase disproportionally with city size, as observed. As a concrete example, consider the number of lawyers’ offices. This scales superlinearly with an exponent close to the canonical 1.15, meaning that there are systematically more lawyers per capita in larger cities. The preferential attachment model predicts that as a city grows the ranking of lawyers should increase as an approximate power law with an exponent of about 0.4, as observed.12 Such predictions can be made for any business type at any level of granularity.
Thus the scaling exponents that relate how the abundances of each business category scale with city size capture the disproportionate growth of different business sectors and parameterize them in a more systematic way than simple counts of businesses, or “expert” judgments on the nature of sectors, which are very often quite subjective. A critical aspect of this approach is that cities and businesses are complex adaptive systems and should consequently be viewed as an integrated system and not as isolated individual agents. By looking at all cities and the complete set of business sectors that constitute the entire urban economy in a country, this analysis couples the economic fabric of each city with that of the entire system of cities.
12. GROWTH AND THE METABOLISM OF CITIES
A major theme running throughout this book is that nothing grows without the input and transformation of energy and resources. This was the fundamental basis for the comprehensive theory that I presented in chapter 4 for quantitatively understanding the growth of biological systems, whether of individual organisms or communities. Recall the basic idea: Food is consumed, then digested and metabolized into a usable form that is transported through networks to supply cells, where some is allocated to the repair and maintenance of existing cells, some to replace those that have died, and some to create new ones that add to the overall biomass. This sequence is the basic template for how all growth occurs whether for organisms, communities, cities, companies, or even economies. Roughly speaking, incoming metabolized energy and resources are apportioned between general maintenance and repair, including replacement of what’s already there and has decayed and the creation of new entities, whether cells, people, or infrastructure, that add to the system and increase its size. Thus the energy available for growth is just the difference between the rate at which energy can be supplied and the rate that is needed for maintenance.
On the supply side, metabolic rate in organisms scales sublinearly with the number of cells (following the generic ¾ power exponent derived from network constraints) while the demand increases approximately linearly. So as the organism increases in size, demand eventually outstrips supply because linear scaling grows faster than sublinear, with the consequence that the amount of energy available for growth continuously decreases, eventually going to zero resulting in the cessation of growth. In other words, growth stops because of the mismatch between the way maintenance and supply scale as size increases. The sublinear scaling of metabolic rate and the associated economies of scale arising from optimizing network performance are therefore responsible for why growth stops and why biological systems exhibit the bounded sigmoidal growth curves that were shown in Figures 15–18 of chapter 4. The same network mechanism that underlies sublinear scaling, economies of scale, and the cessation of growth is also responsible for the systematic slowing down of the pace of biological life as size increases—and for eventual death.
I now want to apply this framework to the growth of social organizations, beginning with cities. Because of its generality it can be readily extended to companies and entire economies, which I shall discuss in the next chapter. As was explained in chapter 7 cities are comprised of two generic components: their physical infrastructure, manifested as buildings, roads, et cetera, and their socioeconomic dynamics, manifested as ideas, innovation, wealth creation, and social capital. Both are networked systems, and their tight interconnectivity and interdependence result in the approximate complementarity between the corresponding sub- and superlinear scaling laws, namely, that the 15 percent savings with every doubling of size in the former are approximately equal to the 15 percent gain in the latter.
It is the first of these, the physical infrastructural component, that has close analogies to biology and provides the metaphor of the city as an organism. But as I have persistently emphasized, the city is much more than its physicality. Consequently, the concept of metabolic rate as the supply-side input that fuels growth and sustains a city has to be expanded to include socioeconomic activity. In addition to the electricity, gas, oil, water, materials, products, artifacts, and so on that are used and generated in a city, we have to add wealth, information, ideas, and social capital. At a more fundamental level all of these, whether physical or socioeconomic, are driven and sustained by the supply of energy. In addition to heating buildings, transporting materials and people, manufacturing goods, and providing gas, water, and electricity, every transaction, every dollar gained or lost, every conversation and meeting, every phone call and text message, every idea and every thought has to be fueled by energy. Furthermore, just as food must be metabolized into a form that is useful for supplying cells and sustaining life, so the incoming energy and resources digested by a city must be transformed into a form that can be used to supply, sustain, and grow socioeconomic activities such as wealth creation, innovation, and the quality of life. No one has articulated this more eloquently than the great urbanist Lewis Mumford13:
The chief function of the city is to convert power into form, energy into culture, dead matter into the living symbols of art, biological reproduction into social creativity.
This extraordinary process, which can be thought of as the social metabolism of a city, is responsible for increasing our conventional biological metabolic rate derived from the food we eat from just 2,000 food calories a day or 100 watts to about 11,000 watts, the equivalent of 2 million food calories a day. Thus the actual energy content of the food input to the total energy budget of a city is a tiny portion of its overall consumption—less than 1 percent—and that’s why I didn’t include it in the above discussion even though it is obviously a critical component of urban life. This may seem paradoxical since we saw in the last section that food establishments are the most abundant business type in most cities, even exceeding lawyers. The point is that the overwhelming energy cost associated with food is not in the food itself (the 2,000 food calories a day per person) but in its production, transportation, distribution, and marketing through the supply chain from farms to stores to your house and ultimately to your mouth.
When one contemplates the huge number of different contributions to the total metabolism of a city it becomes clear that determining its value, whether in dollars or watts, becomes a major challenge that as far as I know has never been attempted in detail.14 This is quite surprising given that this is fundamental to how cities and more generally economies function and grow. In addition to the need for collecting and analyzing huge amounts of data across a broad spectrum of diverse activities, there is the issue as to what should actually be counted as part of the social metabolism of a city. What are the independent contributions? Should we include, for instance, the energy costs of crime, police, patents, construction, investments, and research as independent contributions, or will we be double counting if we do as there are clear overlaps and interconnections among and between them?
For the purposes of understanding growth, however, this challenge can be elegantly finessed using the conceptual framework of our scaling theory. The critical point is that all socioeconomic contributions to social metabolism that underlie growth, including wealth creation and innovation, scale in approximately the same way following the classic superlinear power law with a common exponent of approximately 1.15. Because all of its subcomponents scale this way, the total social metabolic rate of a city must likewise scale superlinearly with an exponent of 1.15. This is the beauty of the scaling perspective—we don’t need to know the details of what the individual contributions to the metabolism of a city are in order to determine its growth trajectory. This is because they are all interconnected and interrelated through the same integrated unifying dynamics of the social and infrastructural networks that constitute urban life.
The superlinear scaling of metabolism has profound consequences for growth. In contrast to the situation in biology, the supply of metabolic energy generated by cities as they grow increases faster than the needs and demands for its maintenance. Consequently, the amount available for growth, which is just the difference between its social metabolic rate and the requirements for maintenance, continues to increase as the city gets larger. The bigger the city gets, the faster it grows—a classic signal of open-ended exponential growth. A mathematical analysis indeed confirms that growth driven by superlinear scaling is actually faster than exponential: in fact, it’s superexponential.
Even though the conceptual and mathematical structure of the growth equation is the same for organisms, social insect communities, and cities, the consequences are quite different: sublinear scaling and economies of scale that dominate biology lead to stable bounded growth and the slowing down of the pace of life, whereas superlinear scaling and increasing returns to scale that dominate socioeconomic activity lead to unbounded growth and to an accelerating pace of life.


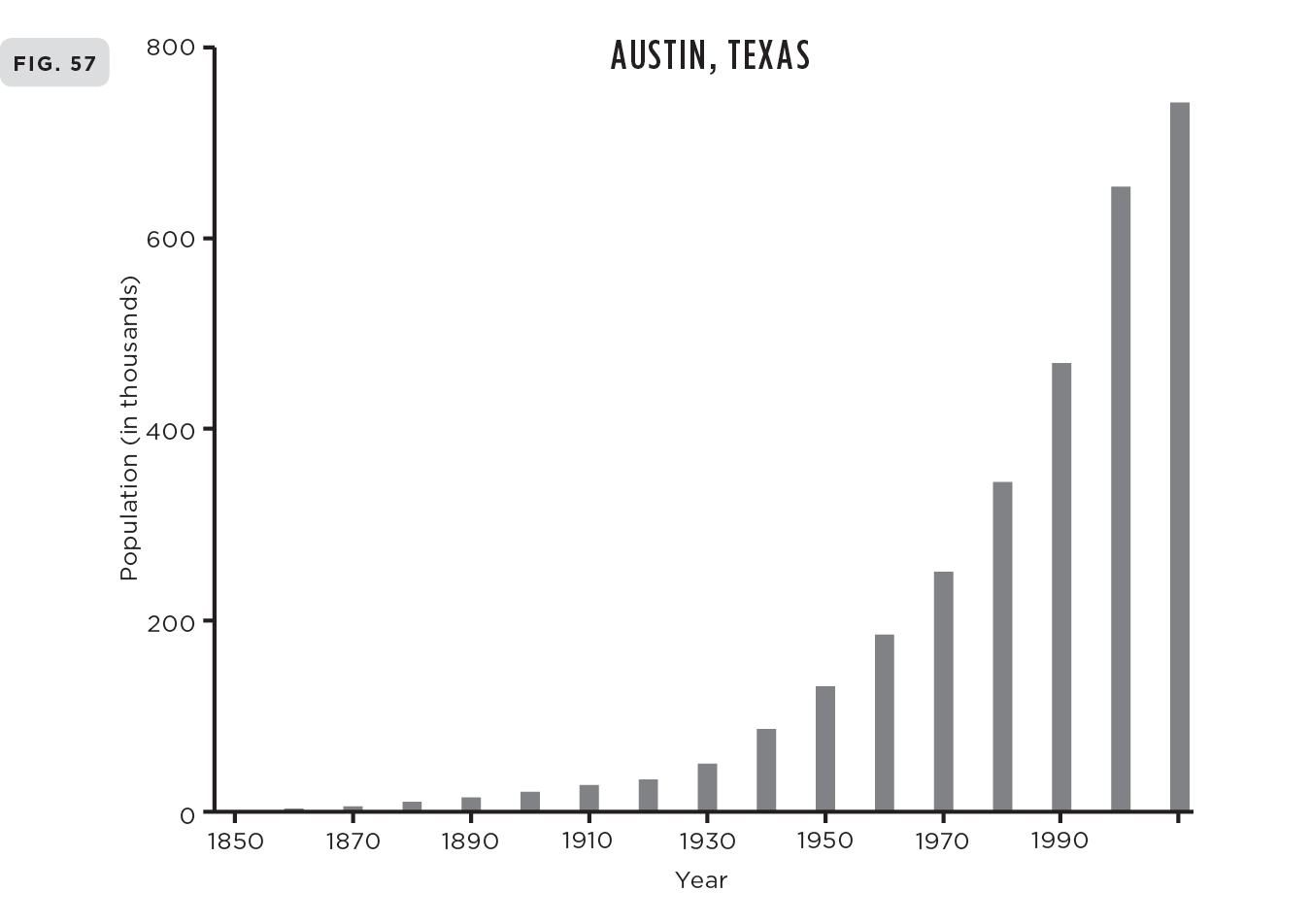

Here: Growth curves for various cities across the globe illustrating the ubiquity of open-ended superexponential growth; in order, they are Bombay, Mexico City, London, Austin, the New York City metropolitan area, and the Los Angeles metropolitan area. Credible data do not exist before about 1850.
The continuous positive feedback mechanisms inherent in social networks that are responsible for the multiplicative enhancement of social connectivity and superlinear scaling lead naturally to open-ended superexponential growth and concomitantly to an increase in the pace of life. This is what has evolved over the past couple of hundred years as cities have exploded on the planet. Some examples from across the globe are shown in Figures 54–59; they include Old World cities (London), New World cities (New York, Austin, several California cities, and Mexico City), and Asian cities (Bombay). The major point I want to stress here is that the growth equation driven by superlinear scaling leads to a mathematical formula whose predictions are consistent with the generic superexponential growth seen in these graphs.
Notice, however, that both London and New York show periods of contraction and stagnation. I will return to discuss these effects in chapter 10, where I’ll pick up the story on open-ended growth in a larger context by relating it to the role of innovation cycles and the accelerating pace of life and how these affect the critical question of sustainability.