I take the early Pythagoreans to cover roughly to the time of Plato and the key figures I want to look at in this chapter are Pythagoras (c. 570–c. 495) himself, Philolaus (c. 470–c. 385) and Archytas (428–347 bce).1 In terms of issues for this chapter, the Pythagoreans have been associated with a number of ideas that might be thought to involve the non-natural. We will need to look at the nature of Pythagorean metempsychosis, the idea that the soul survives the death of the body and moves on to a new body at the death of the old, perhaps an animal body. We will need to look at Pythagorean theology, alleged mysticism and the notion that Pythagoras might have been in some sense a shaman. With Philolaus, there is also an issue about astrology. There are also many issues concerning Pythagorean numerology, which I will deal with in a separate chapter, as they raise significant questions about the nature of numerology and of the extent of Pythagorean belief. As we will see, those generally held to be early Pythagoreans had quite a diverse range of beliefs. I will begin with Pythagoras himself. Clearly one can make a case that Pythagoras held non-natural beliefs, but on the evidence we have, it is surprisingly difficult to be specific on exactly what those beliefs were and there are natural belief alternatives. Much here depends on how we take the idea of metempsychosis, and to what extent it is proper to describe Pythagoras as a shaman, as some recent literature has. I will then look at Philolaus, where it is possible to make a case for non-natural belief based on possible beliefs in metempsychosis and astrology, but in fact the case for Philolaus having entirely natural beliefs is quite strong. I will finally deal relatively briefly with Archytas as from the evidence we have, there is no indication of any interest in metempsychosis, numerology, astrology or mysticism in his work. I will make a point here which I will return to later on. I do not wish to present Pythagoras to Philolaus to Archytas as a linear progression of increasing rationality. I take them rather as the three early Pythagoreans we know most about, taken in chronological order and as examples of Pythagorean diversity of views. Here we have a microcosm of the question of how many presocratics were naturalists. How many Pythagoreans were naturalists?
Pythagoras was born in Samos c. 570 bce and died c. 490 bce. Around 530 bce he relocated to Croton, which became an important centre for the Pythagoreans. The great difficulty for generating an accurate picture of Pythagoras is that Pythagoras himself wrote nothing and if his contemporaries wrote anything about him nothing of this has survived.2 A further difficulty is that those who associated with Pythagoras may have kept a silence about his key views.3 All we know of Pythagoras comes from significantly later sources, many of which are unreliable. There was a strong tendency after Plato and Aristotle for Pythagoras to be aggrandised as a semi-divine or a divinely inspired figure and visionary and for the views of later thinkers to be attributed to him, especially those of the later Pythagoreans and aspects of Plato’s metaphysics and cosmology. This poses the ‘Pythagorean question’, of the extent to which we can reconstruct the historical views of Pythagoras from the information we have available.4
Walter Burkert’s Lore and Science in Ancient Pythagoreanism,5 has proved a critical turning point in studies of Pythagoras. Burkert sifted the wide range of material available and concluded that to find out about Pythagoras, we must look to the earliest and least corrupt sources on him, which meant looking at Plato and Aristotle. In this general strategy he has been followed by the work of Carl Huffman and Leonid Zhmud.6 While I disagree with Burkert on the issues of shamanism and numerology in Pythagoras and early Pythagoreanism, I follow his general methodology for dealing with the material.
The older picture of Pythagoras is that of a rational philosopher who first saw the importance of number in a proper description of the cosmos.7 So Pythagoras was an expert in mathematics and geometry, proved Pythagoras’ theorem, made important discoveries on harmonics and mathematised harmonic theory. In astronomy Pythagoras believed there was a harmony of the spheres, believed the world was in some way constituted from numbers and that mathematics was the key to understanding the cosmos. It is notable though that while both Plato and Aristotle talk of presocratic natural philosophy, they do not give Pythagoras any significant role in this, nor do they recognise any Pythagorean cosmology prior to Philolaus.8 Plato for instance says that:
Such was Pythagoras, who was particularly beloved in this way, and his followers have a reputation for a way of life they call Pythagorean even down to this day.9
The picture that then emerges from looking just at Plato and Aristotle is radically different. It is of someone whose key beliefs were in the immortality of the soul and reincarnation and whose expertise was in the fate of the soul after death and in the nature of religious ritual. Pythagoras’ major achievements are seen as the advocacy and founding of a way of life based on stringent dietary regulations, strict self-discipline and the keen observance of religious ritual. Pythagoras is not credited with a proof of Pythagoras’ theorem, nor seen as a significant mathematician or geometer by Plato and Aristotle. Nor is Pythagoras seen as important by early histories of Greek mathematics. Pythagoras is not associated by Plato and Aristotle with any harmonic theory.10 Tales that Pythagoras discovered the mathematical ratios underpinning harmonics are often demonstrably corrupt. The most popular of these tales has Pythagoras discovering these ratios when passing a blacksmith’s shop and noticing that different-sized hammers produced different notes. However, the size/weight of a hammer has no direct relationship to the note produced when it hits something. Nor can Pythagorean musical ratios be found by comparing the sizes/weights of bells, by comparing how much water is in similar-sized glasses or by tensioning strings with weights in the Pythagorean ratios. The last sounds most plausible, but string tension does not relate to pitch in this way and only by stopping strings and listening to the pitch produced can the ratios be generated.11
There is no need to choose absolutely between these two accounts on the basis that ‘rational science’ cannot or ought not to be associated with religious or magical ideas.12 An account of Pythagoras largely as a religious figure does not preclude him having some interest in cosmology or harmonic theory. There is no need, and indeed there are no grounds, for treating all of Pythagoreanism as a monolithic set of beliefs deriving from a strict adherence to the views of Pythagoras himself. The balance of religious and scientific ideas may have been seen very differently by many of his followers.
There is evidence that Pythagoras was aware of something related to Pythagoras’ theorem without having generated a proof himself. Possibilities here are an awareness of what are known as ‘Pythagorean triples’ (integer side lengths for Pythagorean triangles such as 3, 4, 5), which were known to the Babylonians, perhaps a significant diagram, perhaps the theorem but not the proof or perhaps he simply celebrated someone else generating the proof.13 There is also evidence that Pythagoras valued mathematics in education. Given the current state of the evidence, it is very difficult to determine with any certainty what Pythagoras’ attitude to mathematics was, what his knowledge of mathematics was or what his contribution to mathematics was. My own view, for what it is worth, is that it is unlikely that Pythagoras proved what we know as Pythagoras’ theorem. On the other hand I do find it likely that Pythagoras, or some early associate, did something significant in relation to Pythagoras’ theorem. The often quoted tale that Pythagoras sacrificed oxen on discovering the theorem looks unlikely on the grounds of vegetarianism related to views on metempsychosis. I also find it likely that Pythagoras was to some extent interested in number and passed this interest on to his followers, without having discovered or been interested in the later, more ramified theories of the Pythagoreans.14
I agree with Zhmud15 and Huffman16 that neither Pythagoras, nor any known Pythagorean held the view that the world is actually constituted from numbers. This view of the early Pythagoreans seems likely to have originated with Aristotle.17 There is no trace of this view in the attested fragments. For Philolaus this seems demonstrably false as he believed the cosmos is in the first instance constituted from limited things and unlimited things.18 Aristotle’s evidence seems to be confused and contradictory, saying in different places that numbers are the material basis of the world, that the Pythagoreans liken numbers to things and that the elements of numbers are the elements of things.19 One might also draw parallels with Aristotle’s treatment of Thales and Anaximander where he attributes a single material substance to them where their account is rather more complex.20 As I will discuss later, it is likely that the Pythagoreans investigated various ideas about how number might relate to the world and there is an important sense in which it is proper to say that they have an arithemetical approach to cosmology rather than the geometrical approach pioneered by Plato in the Timaeus.
It may well be the case that the notion of the tetraktys can be traced back to Pythagoras. The tetraktys is the first four numbers and their sum is the Pythagorean perfect number, 10. They are often arranged in this manner:

Pseudo-Plutarch records a Pythagorean oath as:
No, I swear by he who gave to our heads the tetraktys,
The origin and root of immortal nature.21
There is evidence that the tetraktys was in some way related to the harmony sung by the Sirens, which in turn may be related to the notion of the harmony of the spheres.22 The harmony of the spheres is something of a misnomer when applied to the Pythagoreans, as we have no evidence they believed in celestial spheres. I will come back to this idea when I discuss Philolaus and numerological ideas later on. In relation to ideas on musical theory, Barker has commented that:
What we know, reasonably securely, about Pythagorean harmonics around 400 BC certainly presupposes an earlier tradition which may have gone back to Pythagoras himself.23
While Zhmud is somewhat more optimistic:
Given an unbiased approach to the fifth- and fourth-century sources, we can state with justifiable confidence that Pythagorean harmonics must go back to Pythagoras himself.24
Porphyry tells us that:
As Xenocrates says, Pythagoras also discovered that musical intervals do not come apart from number, for they are a comparison of a quantity with a quantity.25
It has been argued that the early Pythagoreans could not have discovered the basic ratios of musical theory from Greek stringed instruments because there were no suitable instruments.26 If we are thinking of the ratios generated by stopping strings, then that is so as early Greek stringed instruments did not have fingerboards. However, it is possible to generate the notes and length ratios using what are known as harmonics or flageolet tones.27 This can be done in two ways. One can sound an open string and then lightly touch it half way along, when the octave will be heard. Alternatively one can touch the string half way along and then pluck the string. On a modern guitar, harmonics can easily be produced above the 5th, 7th and 12th frets and at other places as well. This would be enough to at least begin on the idea that there is a mathematical basis to music. Whether the Pythagoreans discovered this, or it was well known to musicians but then developed into something more mathematical by the early Pythagoreans is a question we are not in a position to answer.
The current state of the Pythagorean question then is that while Pythagoras was not the important mathematician, cosmologist and harmonic theorist of legend, he did have an interest in mathematical and related issues and that the tradition he fostered facilitated later Pythagoreans such as Philolaus and Archytas who developed many of the views that were later attributed to Pythagoras.28 Exactly what is attributed to Pythagoras, even within this general structure, still remains a matter of controversy though and that relates to the issue of how much we consider Pythagoras to be within the mainstream of presocratic natural philosophy. One can emphasise the shamanic aspects of Pythagoras, with important new teaching on the fate of the soul and strict rules governing behaviour and ritual, as Dodds and Kingsley have done and push Pythagoras outside this tradition. Which account is chosen by modern scholars has tended to reflect a broader philosophical agenda on their part.29
One can try as Kahn and Riedweg have done, to give Pythagoras some role as a cosmologist, through the relation of musical theory via the harmony of the spheres to the nature of the cosmos, when Pythagoras is brought into the presocratic cosmological tradition again.30 It is difficult on the evidence we have available to come down conclusively on either side of this debate. All the more so since despite the advances made by Burkert there is still considerable dispute over which evidence should be accepted as genuine and agendas to push Pythagoras out of the mainstream of presocratic natural philosophy or to draw him into it often determine which evidence is accepted.31
Metempsychosis
The key passage for the idea of metempsychosis,32 the transmigration of the soul from one body to another at death, comes from Xenophanes:
On the subject of reincarnation, Xenophanes tells a tale which begins: Now I turn to another account and I will show the way. He says this about Pythagoras: Once he passed a young dog which was being mistreated, and taking pity he said: ‘Stop, do not beat it, that is the soul of a man who was my friend, I recognised it when it cried aloud.’33
How reliable in detail this report is may be open to question as Xenophanes was an opponent of Pythagoras and probably does not cast this anecdote in a favourable manner. That Pythagoras and some later Pythagoreans believed in metempsychosis is generally agreed though. Whether this is something original to Pythagoras, or is influenced by Orphic or Egyptian ideas is also contentious.34 There is though some consensus that this is a significant move away from the Homeric conception of the fate of the soul. The standard passage for comparison in Homer is where Achilles says:
I would rather be above ground still and labouring for some poor and portionless man, than be lord over all the lifeless dead.35
We have very little definite information about the nature of metempsychosis. One problem is that we have very little on Pythagoras’ account of the soul and we do not know if the entire soul or only part of it was supposed to transmigrate. We have nothing at all on the nature of the actual transmigration, of how the soul moved from its previous host body to the next host body. We do not know if every soul underwent transmigration, we do not know the extent of how many living things could participate (animals other than dogs, plants?) and we do not know if there was eventually an escape from the sequence of transmigration, either by death of the soul or escape to some heaven or state which did not involve embodiment.36
This uncertainty makes it very difficult to say whether anything non-natural was involved in metempsychosis. Clearly that is one view of metempsychosis, but it is entirely possible to construct others as well. Huffman, for instance, has argued that both Philolaus and Pythagoras had material conceptions of the soul and that only part of this soul, that to do with the seat of the emotion and sensation is transmitted in metempsychosis.37 The soul is drawn in at first breath and expelled with the last breath. As the seat of this part of the soul is the heart, only other living things which have hearts can take part in metempsychosis. This is in many ways an attractive view, not least because one might then draw parallels with the origins of humans and the origins of the cosmos. So there is evidence that for the Pythagoreans:
Directly after birth an animal, whose body is mainly hot, will draw in a breath from the outside, which is cold, and then expels it as if of necessity.38
On the issue of the cosmos, Stobaeus tells us that:
In the first book of ‘On the Philosophy of the Pythagoreans’, he (Aristotle) writes that the heavens are one, and that from the unlimited are drawn time, breath and the void, It is the void which distinguishes the nature of each thing.39
This may be a biological analogy, certainly it can be compared with the Pythagoreans on the birth of animals. Finally, there is the view of Barnes on metempsychosis, who believes that there is a serious philosophical analysis of personal identity behind this theory:
Metempsychosis is no rough dogma: it is a rational theory, capable of rigorous statement and implying a respectable account of the nature of personal identity; it was advocated by Pythagoras on solid empirical grounds. We are far from mystery-mongering.40
Barnes is notoriously sceptical and critical of some aspects of Pythagorean thought, notably numerology, so this is an interesting assessment, both in itself and in the idea that there is some serious philosophy behind Pythagorean ideas, a thought I will return to later in relation to numerology.
Heraclitus on Pythagoras
Heraclitus was a critic of Pythagoras and could be quite acerbic. His most famous saying is that:
Much learning does not teach intelligence – if it did, it would have taught Hesiod, Pythagoras as well as Xenophanes and Hecateus.41
There are two other passages which are significant in producing a picture of Pythagoras independent of anything that Plato or Aristotle have to say. Heraclitus says that:
Pythagoras, son of Mnesarchus, practiced enquiry far beyond all other men and selecting these made them his own, wisdom, polymathy, malpractice (kakotechnien).42
This is interesting in confirming the view of Pythagoras as a polymath though the attribution in the hands of Heraclitus here may be double-edged as in the previous fragment. The final word in this passage, kakotechnia, is very interesting. LSJ give ‘base artifice, malpractice, as law-term, fraudulent or malicious conspiracy, false artifice.’ It is unclear precisely what Heraclitus meant by this word.43 Some sort of (perceived) organised fraud is a possibility, as is criticism of practices that failed in their claims or were malicious in their intent. I don’t see any evidence though that we should see parallels with the word ‘maleficia’, evil doing, often associated with a pact with the devil and commonly used during the European witch hunt. Heraclitus also describes Pythagoras as ‘kopidôn archêgos’,44 which can be translated in several ways, such as ‘original chief of wranglers’45 or ‘prince of imposters’46 or ‘the chief of swindlers’.47 As LSJ give ‘prater, liar, wrangler’ for kopis and ‘beginning, originating; primary, leading, chief’ for archêgos, we may have to slip outside scholarly language here to get the full force of this expression and I would suggest ‘the original bullshitter’ or ‘the chief bullshitter’ as crude but probably accurate and carrying the pejorative sense that Heraclitus may well have intended. It is notable that Heraclitus, a great proponent of cosmic order, does not criticise Pythagoras for any suggestion that the cosmic order might be broken or manipulated.
Pythagoras as a shaman?
Was Pythagoras some form of a shaman? In the twentieth century Dodds has argued that he was,48 Burkert49 accepted this to some extent as did Cornford,50 Kingsley has argued strongly for this view,51 while more recently Huffman,52 Bremmer,53 and Zhmud have rejected the idea.54 The Kirk, Raven and Schofield view is that:
It is doubtful how far a historical case can be made for an influence upon Archaic Greece from Central Asian shamanistic cultures, or to what extent an institution central to the life of politically primitive nomadic peoples could in any case illuminate the activities of a Greek sage in the more complex society of a rich and powerful city state.55
However, this does little to address what is perhaps the key question posed by Dodds:
Why should we attribute to the ancient Greeks an immunity from ‘primitive’ modes of thought which we do not find in any society open to our direct observation?56
It is possible to make the case for influence, as Kingsley has done, citing a path through ancient Iran.57 Zhmud though has now cast considerable doubt on the view of Meuli, that there was a route of transmission via the Scythians on the Black Sea coast, by showing that it is highly doubtful that the Scythians were in any proper sense of the word shamanic.58 It is also possible to take the view that shamanism is a ubiquitous phenomenon, whose clearest expression may be Siberian, so doing away with the need for a path of influence.59 I see nothing in the nature of a Greek sage nor in the nature of Greek society, however complex or wealthy it is perceived to be, which would preclude an ancient Greek being a shaman, at least in the looser sense of claiming to enter into ecstatic states, claiming to communicate with spirits and having a retinue of followers believing in their abilities. A great deal here depends on whether one wants to assert that Pythagoras was indeed a shaman and so had all the characteristics of a shaman, or whether he could reasonably be likened to a shaman. It is quite possible to accept that Pythagoras had some traits in common with shamen without accepting that Pythagoras was a shaman. So for instance, one might happily accept that Pythagoras was a charismatic leader of a religious grouping that took part in rituals.60 The Oxford English Dictionary gives this definition of a shamen:
A person regarded as having access to, and influence in, the world of good and evil spirits, especially among some peoples of northern Asia and North America. Typically such people enter a trance state during a ritual, and practise divination and healing.61
In his paper ‘What is a Shaman? Definition, Origin and Distribution’, Walsh says that:
The term itself comes from the word saman of the Tungus people of Siberia, meaning ‘one who is excited, moved, raised.’62
Shirokogoroff, who was one of first to investigate the shamen of the Siberian Tungus people said that:
In all Tungus languages this term (saman) refers to persons of both sexes who have mastered spirits, who at their will call and introduce these spirits into themselves and use their power over the spirits in their own interests, particularly helping other people, who suffer from the spirits; in such a capacity they may possess a complex of special methods for dealing with the spirits.63
Walsh offers this definition of shamanism:
Shamanism might be defined as a family of traditions whose practitioners focus on voluntarily entering altered states of consciousness in which they experience themselves, or their spirit(s), travelling to other realms at will and interacting with other entities in order to serve their community.64
More recently, discussions on the definition of shamanism have shifted in focus from the individual shamen to the cultures they are part of. Jolly, in his paper ‘On the Definition of Shamanism’, says that:
The following could perhaps serve as a definition: cultures that can be classified as shamanic are those which, as a minimum requirement, possess religious functionaries who draw on the powers in the natural world, including the powers of animals, and who mediate, usually in an altered state of consciousness, between the world of the living and that of the spirits including the spirits of the dead.65
The notion of a trance, or some form of ecstatic state leading to access to a spirit world is the key part of shamanism. There is though no reliable evidence that Pythagoras entered trances or ecstatic states and the notion of entering a spirit world is contrary to the principles of metempsychosis.66 If souls do not enter into some sort of afterlife, but transmigrate to other bodies, what spirit world is there for Pythagoras to enter via some form of ecstatic state? It is perhaps significant that within shamanism proper there is no trace of any view like metempsychosis. One could perhaps construct some sort of view where they are compatible (if one ultimately escapes reincarnation to a spirit realm, for instance) but they are not easily or naturally reconciled, there is no evidence for such a reconciliation in Pythagoras and no historical record of their reconciliation anywhere else.
There are some affinities between Pythagorean ideas and those of the Orphics, but this line of enquiry is unlikely to lead us very far. The exact nature of Orphism and Orphic practice remains obscure and it is by no means clear how Pythagoreanism or individual Pythagoreans related to Orphism or indeed individual Orphics. There are similarities, though they are probably not exact, in that the Orphics held that the soul is a prisoner in the body until the soul makes recompense. They believed that they could speed this process by purification and ritual. Whether Pythagoras or later Pythagoreans believed that the soul could escape the cycle of reincarnations is not known. Here I follow the view of Kirk, Raven and Schofield who suggest that the Orphics and the Pythagoreans were two separate religious movements with certain affinities and differences who may well have borrowed ideas from each other.67 It is virtually impossible to decide on the evidence we have who borrowed what from whom.
Pythagoras and meteorology
One of the key themes of this book has been the attitude of the presocratics to meteorological phenomena. We have little information from Pythagoras and the Pythagoreans on these issues, but what we do have indicates that Pythagoras and at least some Pythagoreans did not treat all meteorological phenomena as entirely natural. So Aristotle says that:
If it thunders, then if what the Pythagoreans say is true, then this is to threaten those in Tartarus, in order that they will fear.68
Aristotle also tells us that Pythagoras said:
The origin of earthquakes was nothing but the gathering of the dead, while the rainbow was the gleam of the sun and the echo which often falls upon our ears is the voice of more powerful beings.69
Porphyry informs us that Pythagoras:
Said some things in a mystical and symbolic manner and Aristotle has written many of these down; he considered the sea to be the tear of Kronos, the Bears to be the hands of Rhea, the Pleiades to be the Muses’ lyre, the planets to be Persephone’s dogs and the ringing sound of the bronze to be due to a daimon imprisoned in the bronze.70
Aristotle on Pythagoras
In contrast to this evidence on meteorology, we have some other evidence from Aristotle:
The ‘Pythagoreans’ treat of principles and elements stranger than those of the physical philosophers (the reason is that they got the principles from non-sensible things, for the objects of mathematics, except those of astronomy, are of the class of things without movement); yet their discussions and investigations are all about nature; for they generate the heavens, and with regard to their parts and attributes and functions they observe the phenomena, and use up the principles and the causes in explaining these, which implies that they agree with the others, the physical philosophers, that the real is just all that which is perceptible and contained by the so-called ‘heavens’.71
If it is true that the Pythagoreans’ ‘discussions and investigations’ are indeed ‘all about nature’ and that what is real is ‘perceptible and contained by the so-called heavens’ then there seems to be no room for anything other than the natural. Aristotle also tells us that:
Contemporaneously with these philosophers and before them, the so-called Pythagoreans, who were the first to take up mathematics, not only advanced this study, but also having been brought up in it they thought its principles were the principles of all things. Since of these principles numbers are by nature the first, and in numbers they seemed to see many resemblances to the things that exist and come into being.72
Whether number is all things or is part of the explanation of all things need not concern us here. The key point is that all things are dependent on number. That again makes it difficult to see how there could be anything beyond the natural. One might want to say that this applies only to the later Pythagoreans and not to Pythagoras himself, but even then it is quite an important statement about early Pythagoreanism. It is worth noting that Aristotle does not criticise Pythagoras for having non-natural beliefs.
Pythagoras’ powers?
Pythagoras was associated with many strange powers and deeds. Those mentioned by Aristotle are that he was seen in two different places at exactly the same time, that once when he stood up at the theatre he revealed that one of his thighs was golden and that when crossing the river Kosas the river spoke to him and many people heard this.73 So too he is supposed to have prophesied the coming of a white, female bear, to have killed a dangerous snake by biting it and to have prophesied to his followers approaching political strife.74 Two unknowns here are the attitudes of Aristotle and Pythagoras to these claims. Given Aristotle’s attitude to nature, one would expect that Aristotle is reporting these tales about Pythagoras without believing them. What of Pythagoras though? Did he claim any prophetic or non-natural ability? That we simply do not know.
Kingsley has argued that Pythagorean food prohibitions and abstinence have considerable similarities with Greek ritual and magic, as well as with the preparations to receive dream oracles.75 Doubtless that is so, but what follows from it is another matter. Can we then infer that the Pythagoreans had the same aim in their prohibitions and abstinence? It is possible that at least some of them had similar aims, but there are other explanations here as well. It is by no means clear that the early Pythagoreans refused to eat different foods for the same reason. They may not have eaten meat, or at least some meats, for reasons related to metempsychosis while refusing to eat beans either because they are hard to digest or cause flatulence.76 The extent to which the early Pythagoreans adhered to these taboos is unknown.77 As for Pythagoras himself, again we simply do not know.
On the issue of Pythagoras’ supposed golden thigh, I agree with Kingsley that we cannot dismiss the evidence that there was such a legend and that the legend was early. The evidence is in Aristotle and if we accept, with due reservation, the evidence of Aristotle as fundamental for our picture of Pythagoras and the early Pythagoreans, then we have to accept the evidence that there was the tale of the golden thigh.78 Exactly what we make of that is another matter. We do not know who first attributed a golden thigh to Pythagoras or why. It may be, as Kingsley has argued, that this has considerable significance in terms of magic, ritual and access to the realm of the dead.79 How widespread such a view was among the early Pythagoreans though remains unknown.
Kingsley has an interesting cumulative case that there is a good deal of varied evidence which points to the early Pythagoreans being interested in magic, ritual and access to the realm of the dead. My view in relation to this goes back to the quote from Zhmud at the beginning of this chapter. The early Pythagoreans seem to have held a great diversity of views with seemingly little in the way of a central doctrine. Indeed, we still debate what it is that is central to Pythagoreanism and what views are common to all the Pythagoreans. I am quite happy to accept that some early Pythagoreans were interested in magic, ritual and access to the realm of the dead, and that may well have involved them in belief in the non-natural. The problem is that on the evidence we have, we do not know and have no way of knowing how widespread such views were among the early Pythagoreans. Much the same can be said about the two supposed groups of Pythagoras’ immediate followers, the akousmatikoi and the mathematikoi, the listeners and the learners. I say ‘supposed groups’ here as a sharp division of this kind between the early followers of Pythagoras may be a later imposition.80 The classic statement of the division between the followers of Pythagoras is Cornford, who says:
Tradition points to a split between the Acousmatics, who may, perhaps, be regarded as the ‘old believers’ who clung to the religious doctrine, and the Mathematici, an intellectualist or modernist wing, who, as I believe, developed the number doctrine on rational, scientific lines, and dropped the mysticism.81
However, I would, as I have done throughout this book, caution against such a bipolar split between religion and science and at least leave open the possibility that early Pythagoreanism was more of a broad church where some may have felt happy with a mix of what Cornford categorises here as religious and scientific views.
This section on Pythagoras may seem non-committal, but that I hope is a fair reflection of the evidence we have about Pythagoras. It is difficult on that evidence to give a precise and concrete picture of his thought. It is possible, as we have seen, to draw Pythagoras outside of the presocratic philosophical tradition by emphasising the religious and shamanic nature of his thought. It is possible to draw him back in by attributing the basics of the tetraktys, music theory and the harmony of the spheres to him. A balanced view, I suspect, is that Pythagoras is on the margins of the presocratic investigation of nature tradition, neither definitively in it nor outside it. There is nothing conclusive which attributes a belief in the non-natural to Pythagoras. Metempsychosis could be construed naturally and while there may be some affinities with shamanism, there is no evidence that Pythagoras entered into ecstatic states in order to access a supposed spirit realm. The meteorology is of a different tenor to that of the mainstream of presocratic philosophy, but whether we can attribute that to Pythagoras himself is another issue. Some Pythagoreans may have gone in for non-natural explanations of meteorological phenomena, but that does not commit either Pythagoras or the rest of the Pythagoreans to them.
Philolaus
Philolaus of Croton lived from around 470 bce to around 385 bce. Philolaus wrote one book, On Nature, which if Pythagoras indeed wrote nothing, is probably the first book of the Pythagorean tradition, of which a few fragments survive. He worked on astronomy, cosmology and cosmogony, on harmonic theory and medical theory. As On Nature was the standard title for presocratic works on the natural world, Philolaus immediately places himself in that tradition. In terms of general principles, there is nothing problematic in what Philolaus has to say. Philolaus Fr. 1 says that:
Nature in the cosmos was fitted together out of unlimited and limited things, both the whole cosmos and the things in it.82
Philolaus Fr. 2 tells us that:
It is necessary that all the things that are are limiting, or unlimited or limiting and unlimited. As it is evident that they are not constituted entirely from limited things or from unlimited things it is clear that the cosmos and the things in it were fitted together by limited and unlimited things. This is clear from things in their actions.83
The character of the unlimited and the limited things may not be entirely evident, but it is clear that this conception of the cosmos does not require anything non-natural. Philolaus’ epistemology is also based on the idea of limit and number. Philolaus Fr. 3 runs:
According to Philolaus, there will not be anything that is going to know if everything is unlimited.84
While Philolaus Fr. 4 tells us that:
All things which are known have number. Without this, it is not possible for anything at all to be understood or known.85
Again, while the details of this may be obscure, there seems to be no reference to and indeed no room for anything non-natural here.
Philolaus and metempsychosis
Did Philolaus believe in metempsychosis? It is perfectly viable simply to deny that Philolaus believed in metempsychosis.86 There is no direct evidence in the fragments that he had such a belief. If, quite rightly, we are rejecting the idea that Pythagoreanism was a monolithic entity then the fact that Pythagoras believed in metempsychosis does not entail that all of his followers did too. Here we need to ask an important question. As Netz has put it: ‘What made the Pythagoreans Pythagorean?’87 One hypothesis on what makes someone a Pythagorean is that they have a belief in metempsychosis. That though is one hypothesis among many and not, in my view, the most plausible. One problem for the metempsychosis hypothesis is that while Archytas is widely accepted, both by ancients and moderns as a Pythagorean, there is no trace of any belief in metempsychosis in his work. Much more plausible, as a single defining characteristic of what it is to be a Pythagorean is a belief that number is fundamental to understanding and interacting with the cosmos. This works well with the modern view of Pythagoras, which while it does not consider Pythagoras to be a mathematician, does trace an interest in the tetraktys back to him and does allow him a role in fostering the investigation of number. This works for the akousmatikoi, who again were not mathematicians per se, but were again interested in the tetraktys and used number in their rituals. It will of course work well for the mathematikoi and for Philolaus and Archytas. It is also worth considering what Aristotle meant when he said that ‘Plato always Pythagoreanises.’ Does he mean that Plato always applies ideas related to the notion of metempsychosis? I would suggest that Aristotle is more likely to have meant that Plato always applies number or always thinks in terms of mathematics as the key discipline. Whether the number hypothesis for identifying Pythagoreans is fully adequate though is open to some doubt, as I think is the idea that the Pythagoreans can be characterised by any single defining characteristic. More probable for the ancients (and here I have Plato and Aristotle in mind) and more useful for us moderns is the idea that there were a group of ideas for the Pythagoreans and one could be, or be considered to be Pythagorean if one bought into at least some but not necessarily all of those ideas, or bought into all the ideas but some much more fully than others. One could then have Pythagoreans interested in number but not in metempsychosis, or interested in metempsychosis with no great interest in number. That I think is important in accounting for the breadth of interest among the akousmatikoi and the mathematikoi .
Plato in the Phaedo attributes a ban on suicide to Philolaus,88 but no reason is given for that ban. The idea that the soul is an attunement is also discussed in the Phaedo but rejected on the basis that if this were so, the soul would die with the body.89 However, it is by no means clear that the theory being discussed is that of Philolaus, or if it was whether Philolaus, believing the soul to be a harmony, could believe in metempsychosis or not. This is what Philolaus has to say about intellect and soul:
There are four principles of rational animals, as Philolaus said in his On Nature: brain heart, navel and genitals. The head for the intellect, the heart for soul and sensation, the navel for formation and first growth, the genitals for sowing seed and generation. The head has the principle of man, the heart of animals, the navel of plants and the genitals of all. For all things propagate and grow from seed.90
It has been suggested that Philolaus believed in some form of ‘occult soul’ or ‘mysterious daimon’, which underwent transmigration.91 If we take it that Philolaus believed in metempsychosis, then there is a need to suppose something which transmigrates. If that is not the ordinary soul, then it must be some occult soul or daimon. Fragment 13 tells heavily against that as it seems to give a catalogue of the key parts of rational animals but makes no mention of any extra soul. It is easiest simply to take the view that Philolaus did not believe in metempsychosis.
Even if Philolaus believed in metempsychosis, as we saw with Pythagoras this does not in itself entail a non-natural belief. Huffman has argued a similar position on a material soul for Philolaus with the same notion of the soul being drawn in with the first breath and being exhaled with the last breath.92 We simply do not have enough information on Pythagoras and the early Pythagoreans to determine how widespread the belief in metempsychosis was or whether it involved any non-natural belief. If asked for an opinion I would say that Philolaus did not believe in metempsychosis and that if he did, given the nature of the rest of his thinking, it is likely that nothing non-natural was involved.
Philolaus and harmony
Philolaus’ theory of music is a form of what is known today as just intonation, or Pythagorean intonation, as it is based on ratios of small integers.93 Who discovered the basic relationships between musical notes and the length a string on an instrument is stopped at is now lost, though as we saw with Pythagoras there are many apocryphal stories on this issue. Whoever discovered this, Philolaus produced the first extant theoretical account.94 If the length of a string is halved, then the note it sounds is an octave above the first note, and ratio of the string lengths is 2:1. If the ratio is 4:3 we get a musical fourth and if the ratio is 3:2 we get a musical fifth. Both of these notes sound harmonious when played with the original note. A fourth and a fifth make an octave (4/3 x 3/2 = 12/6 = 2/1). The difference between a fourth and a fifth is 9/8 (4/3 x 9/8 = 3/2). The ratio used to generate one whole tone is 9:8. So if the root note is taken as 1, the first note in the scale will be 9/8. The second note will be 9/8 x 9/8 = 81/64. The Philolean semitone is generated by 256:243. The third note in the scale is 81/64 x 256/243 = 4/3 (a musical fourth). The following note is 4/3 x 9/8 = 3/2 (a musical fifth), then 3/2 x 9/8 = 27/16, then 27/16 x 9/8 = 243/128 and finally 243/128 x 256/243 = 2, which gives the octave as a ratio of 2:1.95 The Philolean scale is mathematically very pure, using only powers of 2 and 3. The ratio 256/243 initially looks obscure, but in fact is, in modern notation 28/35.
Philolaus and astronomy
With Philolaus we have a surviving Pythagorean cosmology, depicted in this diagram:
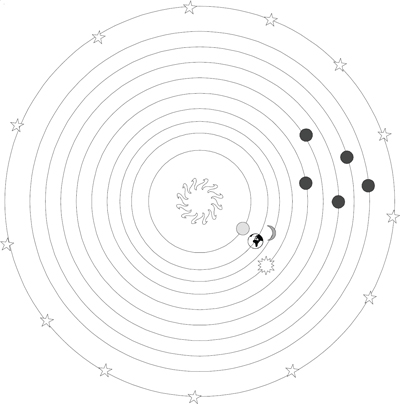
The Italian philosophers known as Pythagoreans take the contrary view. At the centre, they say, is fire, and the earth is one of the stars, creating night and day by its circular motion about the centre. They further construct another earth in opposition to ours to which they give the name counterearth. In all this they are not seeking for theories and causes to account for observed facts, but rather forcing their observations and trying to accommodate them to certain theories and opinions of their own.96
Working outwards from the middle, there is a central fire, a counter-earth, the earth, the moon, the sun, the five naked eye planets (Mercury, Venus, Mars, Jupiter, Saturn) and the stars. This cosmology is notable for being almost unique in antiquity in displacing the earth from the center of the cosmos. Instead there is a central fire (not the sun) with the earth and sun orbiting around it. No reason has been passed down to us as to why the earth was placed in motion. How well this model could account for the phenomena is still open to debate, as is whether accounting for the phenomena or some form of religious/eschatological symbolism was its main function. Huffman has made a very good case that this is a serious piece of astronomy/cosmology from the presocratic period,97 and is joined in that estimation by Kahn98 and Graham.99 On this I would agree and would add something which I have argued in the context of Plato’s astronomical model in the Timaeus.100 Is it the case that for every model of the heavens we have from antiquity, that the author believed it covered all of the phenomena known to them? The answer to that is a clear no, as Simplicius, quoting Sosigenes, tells us that:
These [unrolling spheres] of Eudoxus’ school do not save the phenomena, not only those that were found later, but also those known before (ta proteron gnôthenta) and recognised by them.101
So even if Philolaus’ model could not reproduce all the phenomena and even if he was aware of that, those are not grounds for supposing that the main importance of the model was eschatological rather than astronomical. Philolaus’ model does include some important ideas, not least the notion of perfectly regular circular motion and an ordering of planets in relation to period.102 It is interesting to note that the phenomena that Simplicius refers to as problematic for Eudoxus are not, at least in principle, problematic for Philolaus – variations in the distance of planets from the earth, variations in the apparent size of the moon, variations in type of eclipse from full to annular.103 One problem with determining some sort of religious/eschatalogical significance from this cosmology is that we do not know Philolaus’ views here and he does not seem to have a belief in metempsychosis. Aristotle is critical of Philolaus on slightly different lines, saying that the reason Philolaus supposed there to be 10 heavenly bodies was that 10 was the perfect Pythagorean number.104 We will look at this a little more closely in a moment, in relation to numerology among the Pythagoreans.
One explanation of why there is a central fire in Philolaus’ cosmology is his cosmogony. Fragment 7 has a hearth in the centre of the sphere as the first thing to be generated as the cosmos is fitted together. The cosmos comes to be from the unlimited and limiters. The outline of Philolaus’ view of unlimited and limiters is clear enough even if we lack enough information to say much in detail about this view. It would seem that fire is first limited in the centre of the cosmos and then other unlimiteds are drawn in. There is some debate on exactly what these are, but it is likely they include breath, space and time. There is also debate concerning whether number is generated with the cosmos and whether the central fire is in some sense the number one or whether being the first unity, one describes the central fire. In common with other presocratic cosmogonies, limited and unlimited are seen as existing prior to the organization of the cosmos so there is no creation ex nihilo.
Philolaus and astrology
Did the early Pythagoreans, and in particular Philolaus, have any belief in astrology? There are several passages which might suggest they did, of which the following from Proclus is typical:
With the Pythagoreans we find different angles dedicated to different gods, as Philolaus did, giving the angle of the triangle to some and the angle of the square to others.105
Huffman and Kingsley have disagreed on whether this cluster of fragments are genuine in relation to Philolaus and whether they refer to some form of astrological practice.106 The basic idea is that either three squares or four triangles can be inscribed in a circle, offset at the same angle, when the twelve points lying on the circle can then be interpreted as parts of the zodiac, with the squares or triangles being interpreted as seasons or as elements. There have been several attempts to flesh this basic idea out into something more detailed, without any of them being convincing. Older authorities such as Bouch-Leclerq and Neugebauer date the development of Greek astrology to the third century bce, post dating Philolaus.107 More recent work has allowed for an earlier knowledge of Babylonian sources and a recognition that Babylonian astronomy was hardly separable from Babylonian astrology, so if the former were known at least something would be known of the latter. Huffman argues that these fragments do not go back to Philolaus but originate from the early academy as part of attempts at commentary on the Timaeus.108
Even if these fragments are genuine and do refer to some form of astrological practice (personally I have doubts on both counts), does that commit at least some of the Pythagoreans to a belief in the non-natural? There is nothing here to indicate that it does. It is possible that the angles and gods material here refers to some form of astrology, but it is by no means certain and there are other plausible possibilities. As Huffman has suggested, the 12 point arrangement may merely indicate the 12 months of the year.109 Without further detail of how the alleged astrology is supposed to work though, we cannot assume that it required anything non-natural.
One parallel here might be with Johannes Kepler, the great astronomer of the late sixteenth and early seventeenth centuries, who was interested in astrology as well as astronomy and cosmology. In On the More Certain Fundamentals of Astrology,110 Kepler begins by discussing the physical causes by which astrological influence is transmitted111 and then moves on to the geometrical causes.112 The geometrical causes relate to how the heavenly bodies form angles relative to us on earth and how we perceive these. However, Kepler is adamant there is nothing non-natural or mystical in his views and says in Harmonices Mundi:
Whoever wants to nourish his mind on the mystical philosophy … will not find in my book what he is looking for.113
Even if we take the passages above to be genuine and to be about astrology, there is no need to attribute any non-natural belief to Philolaus.
I have argued that there is no credible evidence that Philolaus subscribed to the theory of metempsychosis. There is little to suggest that he was interested in astrology and nothing to suggest that if he was, this involved any non-natural belief. There seems to be nothing that is mystical in Philolaus’ thought. The real issue here is that of numerology, in both music theory and in cosmology. That we will look at in some more detail once we have looked at the nature of numerology and its historiography more generally.
Archytas
Archytas of Tarentum was born around 428 bce and lived to around 347 bce. He was important for his work in mathematics, cosmology and music theory and was also active as a political leader. We have no work that has survived as a whole, with only a few fragments having come down to us, though they are important and there is a good deal of significant testimonia.114 There has been some question on whether Archytas should be treated as a Pythagorean, as there is nothing in his work about metempsychosis, but Plato clearly does treat Archytas as a Pythagorean when he says:
As our eyes are suited to astronomy, so our ears are suited to harmony, for these are sister disciplines, as the Pythagoreans say and we, Glaucon, agree.115
Apart from a similar grouping of the sciences to Archytas, Plato uses the term adelphos to express their relationship, as does Archytas in fragment 1. There is also a question of whether Archytas should be treated as a presocratic in the strictest sense as the historical evidence is that he was a contemporary of Plato.
I will pass over Archytas’ work in mathematics and cosmology relatively rapidly. Excellent accounts of these can be found in Huffman.116 We will look at his work on music in a little more detail as there is an important contrast to be drawn with the work of Philolaus. In what follows, several things are of importance. Firstly, there is no trace in Archytas of the idea of metempsychosis. Not only is there no direct mention of this idea, there are no passages or fragments which might be thought to allude to it either. It is quite simply absent from Archytas on the evidence we have. Second, there is no hint of mysticism in Archytas’ work either. Indeed, Archytas is concrete in everything he says and he regards logistic as the key science. So in Fr. 1 we find him saying things like:
It seems to me that those concerned with the science make distinctions well and it is by no means surprising that they understand individual entities as they are. Having made good distinctions concerning wholes they are also able to see well how things are according to their parts. Concerning geometry, arithmetic and sphaerics they gave clear distinctions and not least concerning music. These sciences seem to be akin.117
In Fr. 4 we find him saying:
It seems that logistic is far better than the other crafts in respect of wisdom and deals with its topics more concretely than geometry. In those ways in which geometry is lacking, logistic utilises demonstration.118
Third, there are no criticisms of Archytas like those of Heraclitus or Pythagoras, there are no stories of strange powers or deeds associated with Archytas and no one has suggested that Archytas was a shaman. Finally, I will argue that numerology is also absent from Archytas’ thought.
Archytas, mathematics and cosmology
We have a very interesting thought experiment concerning the finite nature of space from Archytas.119 What would happen if someone standing at the limit of a finite cosmos thrust a staff beyond the limit of the cosmos? If he can, and our intuition would seem to be that he can, then this is not the limit of space, and we have a new limit. The thought experiment though is replicable, so wherever a new limit is supposed we can imagine someone thrusting a staff beyond it. Therefore space is unlimited. This argument was much discussed in antiquity and there are replies, such as that it is impossible to stand at the edge of the cosmos, or more subtly, outside the cosmos there is neither time nor space so there is nowhere to thrust the staff. All I want to point out here is there is no sense of mysticism or an extended world in Archytas’ work here. His comments on cosmology are also free from any sense of numerology.
Archytas produced a solution to the Delian problem, of doubling the volume of a cube.120 Archytas built on the work of Hippocrates of Chios. If L is the length of the original cube, it is possible to set up a series of ratios such that L:a :: a:b :: b:2L.121 It is then possible to derive the relation L:2L = L3:a3. As L3:a3 is in the ratio of 1:2, a3 is twice L3, and the cube can be built with sides of length a. Archytas’ solution, which is too complex to give in full here, involved constructing four similar triangles in the proportions suggested by Hippocrates by an imaginary rotation of triangles and calculation of their points of intersection.
Archytas demonstrated one very important property of what are known as superparticular ratios, which were important in Pythagorean musical theory. These superparticular ratios were of the type where n+1:n. Now if x bears the same proportion to y as y does to z, then y is the mean proportional of x and z (if x:y :: y:z). This is important for Pythagorean musical theory, as a double octave (4:1) can be split into two octaves with a mean proportional as 4:2 is the same proportion as 2:1. Archytas though managed to demonstrate that there is no mean proportional for numbers in superparticular ratios. This means that critical musical ratios, such as 3:2, 4:3 and 9:8 (which all have the form n+1:n) have no mean proportional and cannot be split into two equal parts.
I offer this snapshot of Archytas’ mathematical work to give a sense of the sort of problems he worked out and the way he went about solving these problems. These are specific mathematical problems to which Archytas has concrete solutions and there is no sense of anything mystical or non-natural in this work
Archytas and music theory
Archytas’ work on music theory builds on that of Philolaus. Archytas also had a physical theory of pitch.122 The pitch of a sound on this theory is related to how quickly it travels, a sound travelling more quickly being of higher pitch.123 Archytas produced a variation on Philolaus’ diatonic musical scale, using 9:8, 8:7 and 28:27 to determine the notes up to the fourth (9/8 x 8/7 x 28/27 = 4/3). Archytas also worked on two other types of scale, known as the chromatic and the enharmonic. A chromatic scale includes all twelve semi-tones.124 The key ratios for Archytas’ chromatic scale are 32:27, 243:224 and 28:27 (32/27 x 243/224 x 28/27 = 4/3). In the chromatic scale, A# = Bb. In an enharmonic scale this is not so, and what we would call A# differs from Bb. The key ratios for Archytas’ enharmonic scale are 5:4, 36:35, 28:27 (5/4 x 36/35 x 28/27 = 4/3).
|
Diatonic |
9:8 |
8:7 |
28:27 |
|
Chromatic |
32:27 |
243:224 |
28:27 |
|
Enharmonic |
5:4 |
36:35 |
28:27 |
In contrast to Philolaus, who seems to be generating in some ways an ideal scale, using only numbers directly related to the tetraktys, Archytas is now generally agreed to have been describing the scales in use during his time.125 He may be the target of Plato’s criticism at Republic 531aff. that some people
Seek to find numbers in these heard concordances, but they do not ascend to problems and thinking about which numbers are concordant and which not and in each case why.126
I agree with Huffman that Archytas is a reasonable target for Plato here as Plato will want more in terms of relation to some ultimate good than Archytas will be able to supply, even if Archytas has some mathematical reasoning behind the ratios he uses.127
There is no hint of the idea of metempsychosis in any of Archytas’ work. There is no suggestion of any mysticism and indeed the whole set up of his thinking with ‘logistic’ as the master science would militate against that.128 Archytas would also seem to be immune from any accusation of numerology. Certainly there is no trace of numerology in his thinking about cosmology. Nor, in distinction to Philolaus, is there any numerology in his thinking about musical theory either.
Cleansing Pythagoras and Pythagoreanism?
One issue that needs to be addressed before I close this chapter is whether, in the words of Kingsley, I have attempted to
Clean up the image of early Pythagoreanism and present Pythagoras himself as a philosopher who is more or less respectable in modern terms.129
Certainly that is not the intention of this chapter. As I said in the introduction to this book, it is not the aim of this work to attempt to cleanse the orthodox canon of presocratic philosophers of any taint of magic or the non-natural. Rather, I am interested in the evidence and how we analyse it. For Pythagoras himself, I think the evidence is inconclusive. I am not convinced that Pythagoras was a philosopher at all on the evidence of Plato or Aristotle, though perhaps that is better put as Pythagoras not being primarily a philosopher. One can certainly make the case that some Pythagoreans believed in an extended world with a possible realm of the dead and souls previously incarnated in humans now incarnated in animals. I think Kingsley makes an interesting case for magic, ritual and access to the realm of the dead among the early Pythagoreans. How deeply held and how widespread that was among such a diverse group as the early Pythagoreans is difficult to tell. However, as we saw with Philolaus and Archytas this does not apply to all the early Pythagoreans. How many, we simply have no way of telling.
Conclusion
The state of the evidence concerning Pythagoras makes it very difficult to draw any precise and concrete conclusions about him. In the post-Burkert era, the picture of the master originator in mathematics, cosmology and music theory has gone, replaced by someone more interested in the fate of the soul and ritual. The new picture need not exclude elements of mathematics, cosmology and music from Pythagoras though but it is still an open question how much Pythagoras contributed to these areas and how much he fostered or inspired research into these areas. Whether Pythagoras himself believed in anything non-natural must also remain an unresolved question. Metempsychosis may involve a belief in the non-natural but does not necessitate it. Pythagoras may well have been a charismatic religious leader and as such might be compared to a shaman, but his belief in metempsychosis seems to rule out the idea of an accessible spirit realm for him. What should hopefully be evident is the truth of Zhmud’s comment about the early Pythagoreans, ‘how unique they all were’.130 There seems to be no body of doctrine for the early Pythagoreans. Quite possibly some held non-natural interpretations of what they thought were Pythagoras’ ideas while others did not.
What I think we can say quite categorically is that on the evidence we have, Archytas had no belief in the non-natural. There is nothing in his views on mathematics or science to indicate such a belief, there is no trace of metempsychosis in his views and his approach to musical theory seems to avoid even numerology. Philolaus is in some ways the most interesting case. The evidence for a belief in metempsychosis and astrology is thin and even if he did have such beliefs there are plausible natural interpretations of those beliefs.
In looking at Pythagoras, Philolaus and Archytas I do not want to present a linear development of Pythagoreanism from the primitive, non-natural views of Pythagoras through to the rational, mathematical science of Archytas.131 To begin with, I am not convinced that we can ascribe those sorts of ideas to Pythagoras with any confidence given the current state of the evidence. Second, I do not take Philolaus or Archytas to be representative of the Pythagoreanism of their period or even to be typical Pythagoreans of their period. I have little doubt that there were Pythagoreans of their times who believed in the non-natural and certainly there were Pythagoreans after them who believed in the non-natural. I have talked about them here partly because they are the people we have the most information on and partly because they are good examples for the purposes of this chapter and book. If we accept Archytas as a Pythagorean and accept that his work had no non-natural element to it at all, which is what the evidence would seem to indicate, then we cannot move from ‘x was a Pythagorean’ to ‘x held non-natural beliefs’. Philolaus too is an interesting battleground where the balance of the evidence is that he held no non-natural beliefs either. So this chapter is in a sense a microcosm of this book. Where this book asks how many presocratics held entirely natural beliefs, this chapter has effectively asked the same question about the Pythagoreans.