Chapter 2
Making tides
Early maritime civilizations knew that the Moon was important for making tides but a plausible explanation of how this worked, exactly, was slow in coming. An early Arabic idea was that the tide was caused by the thermal expansion of seawater warmed by moonlight. In the 16th century in Europe, serious thought was given to the possibility that the tide was relevant to the new ideas placing the Sun at the centre of the solar system. Galileo Galilei (1564−1642) developed a theory which would allow tides to be created by the movement of the Earth about its own axis and about the Sun. Johannes Kepler (1571−1642) appears to be one of the first to suggest that the Moon is able to attract the waters of the ocean, although this idea on its own is not enough to explain why there are two tides each day.
In 1687, Isaac Newton presented, in the Principia, the inverse square law of gravity which, together with his three laws of motion, provided—for the first time—a coherent explanation of the movement of the planets and moons of the solar system. In modern language, the Law of Universal Gravitation can be stated:
Every object in the universe attracts all other objects with a force directly proportional to the product of their masses and inversely proportional to the square of their distance apart.
Newton’s ideas met some resistance at the time (how can objects exert a force on each other when there is no apparent link between them?)—but they explained the workings of the solar system so well that they soon became accepted. Newton devoted some of the Principia to an explanation of the ocean tide. The theory didn’t help immediately with the practical problem of predicting tides but it did explain many features that had been difficult to account for previously, including the fact that there are two tides a day. Newton also showed how the interaction of the Sun and the Moon, and the lunar declination are important to the tide.
The tide-generating force
The trick to understanding how the Moon raises tides in the ocean is to appreciate that the Earth moves, once a month, around its common centre of gravity with the Moon. This is not an easy concept to grasp; intuition tells us that the Earth remains still while the Moon moves around us. But, it is the nature of bodies held together by gravity that they orbit about each other in such a way that their mutual gravitational attraction provides the necessary centripetal force (or if you prefer, balances the centrifugal force) arising from the motion.
In the case of the Earth and the Moon, the common centre of gravity—the barycentre—lies much closer to the centre of the Earth than to that of the Moon; in fact it lies within the body of the Earth about three-quarters of the way from the Earth’s centre to its surface. Once a month, the centre of the Earth completes a circle about the barycentre keeping a position such that the Moon always lies on the opposite side of the barycentre. For the next few paragraphs, forget that the Earth is rotating about its own axis and concentrate on this monthly motion of the Earth, which we have sketched in Figure 5.
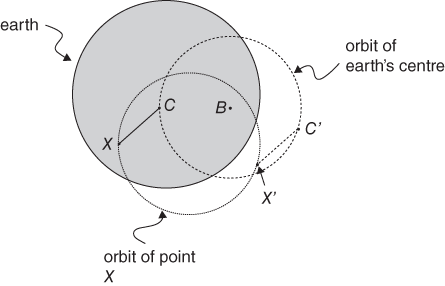
5. The monthly motion of the Earth about the barycentre.
This figure shows the centre of the Earth, C, moving in a circle about the barycentre, B. We have drawn a line from C to an arbitrary point, labelled X, within the Earth. Because the Earth is not rotating, the line XC keeps the same orientation during the month. We can imagine that X and C are joined by a solid bar which always points in the same direction. As C moves round its orbit it drags X with it: for example, when C has moved to position C’, X has moved to X’. The point X goes around the same sized circle as C; because the position of X is arbitrary, it follows that all points on and in the Earth go around the same sized circle once a month.
Centrifugal force depends just on the radius of the circular motion and the time taken to complete the circle. Since each part of the Earth moves in the same sized circle in one month, the centrifugal force is the same everywhere. It is directed away from the Moon, parallel to a line connecting the Earth and Moon centres.
The gravitational pull of the Moon, however, varies over the Earth, becoming weaker with increasing distance from the Moon. The Moon’s gravity and the centrifugal force balance exactly at the centre of the Earth but at other points there is an imbalance: a residual force acting towards the Moon in the Earth hemisphere closest to the Moon and away from the Moon in the opposite hemisphere (see Figure 6). At P, for example, the Moon’s gravity is a little stronger than the centrifugal force and at Q it is not quite so strong.
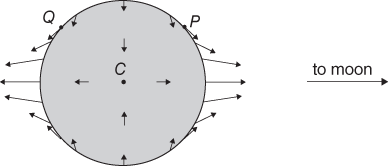
6. The tidal forces created on the surface of the Earth by the Moon.
These residual forces are the tidal forces of the Moon on the surface of the Earth; at each point the tidal force is equal to the difference between the Moon’s gravity at that point and the Moon’s gravity at the centre of the Earth. The maximum size of the Moon’s tidal force is very small—about one-ten-millionth of Earth’s own gravity at its surface. It seems incredible that such a small force can create the large tides we observe in the ocean. But, as we shall see, the ocean is very good at responding to a small force applied regularly at just the right interval of time.
The tidal forces can be divided into a component acting perpendicularly to the Earth’s surface (which adds or subtracts a little from the Earth’s own gravity) and a component that acts parallel to the surface. It is this latter component that moves the ocean and creates tides. This horizontal component is called the tide-generating force, or the tractive force. As the Earth spins on its axis once a day, these tractive forces act first one way and then another, creating an oscillating force acting on each piece of the Earth and its ocean.
The orbit of the Earth about the Sun generates an equivalent set of tide-generating forces converging on points directly below the Sun and on the far side of the Earth to the Sun. Although the Sun is much more massive that the Moon, it is also a lot further away. Tidal forces depend on the mass of the attracting body and the inverse cube of its distance (this inverse cube rule arises because tidal forces depend on the rate of change of gravity with distance). As a result, the Sun’s tidal forces on Earth are a little less than half as strong as those of the Moon. The tidal forces exerted on the Earth by other planets in the solar system are negligible.
Despite its smallness, it is possible to measure the tide-generating force. A pendulum bob suspended on a string 10 metres long will be pulled aside by less than one-thousandth of a millimetre by the Moon’s tractive force. Observed deflections of a carefully designed pendulum are actually somewhat smaller than those predicted theoretically, by a factor of about 0.7. This reduction is caused by the response of the solid Earth to the tidal force. The earth changes its shape (and the surface tilts) under the influence of tidal forces, an effect known as the Earth tide. As the surface tilts, a component of Earth’s gravity acts parallel to the surface and is able to cancel out, in part, the tide-generating force.
The equilibrium tide
If the Earth was covered completely with ocean, the Moon’s tide-generating force would cause the water to flow to a point directly below the Moon and another point on the far side of the Earth from the Moon. Bulges in the ocean surface would be created at these places. Newton anticipated intuitively the shape of such an ocean and, in 1740, the Swiss mathematician Daniel Bernoulli derived the exact shape mathematically. The shape is that of an ellipse rotated about its long axis: roughly the shape of an egg (see Figure 7). The sloping water surface creates a horizontal pressure gradient which balances the tide-generating force: the ocean comes into equilibrium with the tidal force applied to it. The size of the bulges required to balance the tide-generating force is not great—the ocean is stretched about a quarter of a metre above the no-tide level.
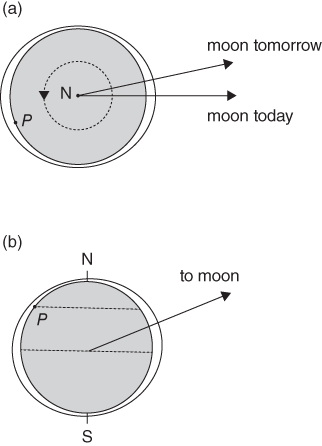
7. The equilibrium tide viewed from (a) above the north pole and (b) above the equator.
If we now start the Earth spinning about its own axis (Figure 7(a)) and the ocean maintains its position relative to the Moon, there will be two high tides each day as a point P on the Earth’s surface passes through the tidal bulges in the ocean. Furthermore, during the time it takes the Earth to turn once on its axis, the Moon moves about one-thirtieth of the way about its orbit. The Earth takes a further one-thirtieth of a day, or fifty minutes, to catch up with the Moon. There are therefore two high tides in a period of twenty-four hours and fifty minutes—or one tide every twelve hours and twenty-five minutes.
The Sun will create additional tidal bulges in the ocean pointing towards and away from the Sun. When the Sun, Moon, and Earth are in line (at times of a new and a full moon), these bulges overlap and create a large spring tide. When the Sun and Moon make a right angle with the Earth, the Sun’s equilibrium tide tends to cancel that of the Moon to some extent (the Moon’s wins out because it is larger) and smaller neap tides result.
In Figure 7(b) (in which we are now looking at the Earth from the side), the Moon is shown at its maximum declination. For the point labelled P, the high tide when the Moon is overhead will be greater than the next (or previous) high tide when the Moon is underfoot. There will be two high tides and two low tides in a day, but one of the high tides will be higher than the other. This effect creates the diurnal inequality which we came across in Chapter 1.
The equilibrium tide model explains, in a qualitative way, many of the observed features of the ocean tide. Unfortunately, it fails in two important respects. First, the range of the equilibrium tide is small: just half a metre or so as the Earth turns through the bulges and the spaces between. This accords with the tidal range at oceanic islands but is much smaller than the tide observed at many coasts. Second, high water in the equilibrium tide always occurs when the Moon crosses the meridian at a particular place. We know that this is not the case: the time of high tide varies from place to place on the same meridian. It is not surprising that the theory fails (Newton acknowledged its weaknesses and knew what needed to be done to correct them), but it is a shame that it fails so spectacularly on these particular points which are the most important for tidal prediction.
The response of the oceans to the tide-generating force
Every point in the ocean experiences a tide-generating force changing in strength and direction with rhythms set by the motions of the Earth, Moon, and Sun. In general, this force will have east–west and north–south components, and each of these will change in different ways with time. These forces act on ocean basins which are connected to each other and bounded by continents. Each ocean will respond to the tide-generating force acting on it and also influence (and be influenced by) what happens in adjacent oceans. It’s a complicated business. How will the tide behave in such a world ocean?
An accurate answer to this question had to wait until computers became powerful enough to solve, for the whole globe, the equations that govern the flow of water on a rotating Earth. These equations were first written down by the French mathematician Pierre-Simon Laplace in 1775. They allow Newton’s second law of motion (acceleration is proportional to applied force) and the principle of conservation of mass to be applied to the ocean. The solution shows that the tide behaves as a series of waves, with the same periods (or rhythms) as the tidal forcing, sweeping around the outside of the ocean basins in great circular movements. The amplitude of the waves diminishes to zero at points near the centre of the oceans, and the waves travel around these points, mostly in an anti-clockwise sense in the northern hemisphere and in a clockwise sense in the southern hemisphere. This picture of the world ocean tide agrees with modern observations which can be made from Earth-orbiting satellites equipped with instruments (called altimeters) that can measure the height of the ocean surface.
To understand how this comes about, we will examine the various processes that lead to this behaviour one at a time until we can build up the whole picture. The tide-generating force varies with several rhythms but the most important of these is that set by the spinning Earth within the Moon’s orbit; this force has a period of oscillation of half a lunar day or twelve hours and twenty-five minutes. (To see how this works, imagine we are looking down on the Earth in Figure 6 from above the north pole. Starting at a point directly beneath the Moon and following it as the Earth makes a half turn anti-clockwise, the horizontal part of the tidal force is zero, maximum towards the west at P, zero again, maximum to the east at Q, and returns to zero after half a lunar day.)
The response of a body of water to an oscillating force can be seen, in miniature, in a kitchen sink. Partly fill a sink or basin, and then move your hand gently back and forth in the water. You will create a sloshing motion called a standing wave which will look something like Figure 8 (in fact, it’s hard not to create higher frequency oscillations in the sink which complicate the picture, but the simplest motion is the one shown).
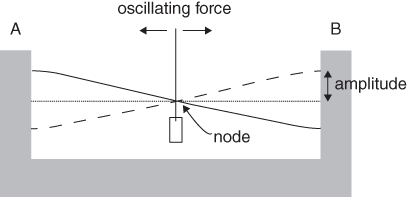
8. A standing wave created in a basin by an oscillating force.
The time taken for the water to slosh from one end of the basin to the other and back again is called the period of the wave. Starting at a time when the water level is high at one end, A, the current is everywhere zero. Water then flows from A to B, reaching its maximum speed one quarter of a wave period later; at this time, the surface is flat. One half period after high water at A, it is high water at B and the currents are again everywhere zero. Water now starts to flow back towards A, reaching maximum speed a quarter of a period after high water at B. A further quarter period later it is high water at A, and the cycle is complete.
The water surface oscillates about a line, called a node, across the middle of the basin. At the node, there is no vertical movement of the water surface but the horizontal currents are fastest. Other kinds of standing wave are possible with more nodal lines, but the single node standing wave illustrated in Figure 8 is the simplest and most common.
If you time the movement of your hand just right, you can create large oscillations with little effort: the water can slop right out of the sink. You have found the resonant period of your sink. The movement of the wave across the sink proceeds at exactly the same pace as your hand. The force of your hand, acting on the flowing water, continually feeds energy into the wave, which consequently grows. If your hand moves at a different speed to the wave, you will create oscillations in the water which match the speed of your hand, but they will not be so large. The wave now travels ahead of your hand, or gets left behind, and you have to make a new wave. You can feel that your hand has to work harder when you are off the resonant period.
The speed of a water wave in a shallow basin is equal to √(gd) where g is the acceleration due to gravity and d the water depth. The condition for resonance is that one back and forth motion of the applied force (the forcing period) should match the time it takes for the wave to travel backwards and forwards across the basin. The forcing period, T, required for resonance is therefore T = 2L/√(gd) where L is the width of the basin. For a sink 60 centimetres wide with water 15 centimetres deep, the required forcing period to produce a resonant wave is about one second.
Applying the same rule to an ocean basin tells us that, in order to be in resonance with the semi-diurnal tidal forcing, a wave should cross the basin in six lunar hours (a lunar hour is one-twenty-fourth of a lunar day). The speed of a shallow water wave in water 4 kilometres deep (the average depth of the ocean) is 713 kilometres per hour: about the speed of an airliner. Travelling at this speed for six lunar hours, the wave will cover a distance of 4,427 kilometres which is the required basin width for an ocean 4 kilometres deep to be in resonance with the semi-diurnal tide. It’s difficult to be sure about ocean widths because coastlines are uneven, but this figure is not so far off the width of major ocean basins such as the North Atlantic. We can therefore expect this, and other oceans, to be close to resonance with the semi-diurnal tidal force.
Laplace’s equations can be applied to an ocean-sized basin to see how it will respond, in theory at least, to a small applied oscillating force. This is a familiar problem in classical physics called the forced, damped, harmonic oscillator. To keep things simple, we will just consider one dimension (east to west, let us say): the force acts forwards and backwards along the width of the ocean in the same way as the hand in the kitchen basin. Figure 9 shows the response of an ocean 4 kilometres deep and of varying widths to an oscillating tide-generating force of maximum strength one-ten-millionth of Earth’s gravity and period twelve hours and twenty-five minutes. The amplitude of the tide in the ocean rises sharply as the width approaches the resonant width and the tide wave becomes most efficient at taking energy from the tidal force. Theoretically, the amplitude grows infinitely large at resonance, but in reality friction prevents this from happening. We have included a small frictional damping force in the equations used to produce this figure; more about this later.
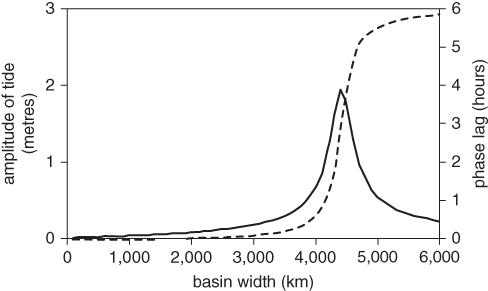
9. The response of an ocean basin 4 kilometres deep and of different widths to the Moon’s tide-generating force. The solid curve shows the amplitude of the tide and the dashed curve the phase lag, expressed as the time of maximum elevation at the coast after the time of maximum force directed towards that coast.
Seeing a resonant response on a graph doesn’t really tell us exactly what is happening at resonance. How can the tides in the ocean grow so large when the applied force is so small? If you struggle with this concept, try pushing a child on a swing. A small push, applied at just the right regular interval, results in a large swinging motion and a happy child. We find the resonant period of the swing instinctively, to save ourselves from too much work. The applied force of our arms is required only to overcome the friction. The motion actually drives itself, in the same way that a frictionless pendulum, once released, will oscillate forever.
There are three forces acting on the basin: the tide-generating force, the pressure gradient force (see Box 2) and friction. The sum of these three forces, according to Newton’s second law of motion, gives the acceleration of a unit mass (1 kilogram, for example) of water in the basin.
Box 2 The pressure gradient force
Water pressure at a point below the ocean surface depends on the height of water above that point. When a water surface slopes the pressure is greater under the high part of the slope than it is under the low part. The difference in pressure creates a horizontal force, the pressure gradient force, which acts to drive water down-slope. Alternatively, in steady state, the pressure gradient force can balance other horizontal forces such as the tide-generating force. The pressure gradient force acting on 1 kilogram of water is equal to the gradient of the surface times Earth’s gravity.
For a small basin in which the wave crosses too quickly to remain in synchronization with the forcing, the wave, the acceleration, and friction force are relatively small. The tide-generating force mostly balances the pressure gradient force. High water at the eastern end of the basin occurs at the same time as the maximum tide-generating force in that direction. The size of the tide can be calculated by matching the pressure gradient force to the tidal force. A tidal force one-ten-millionth of gravity will create a surface slope of one in ten million, or 1 centimetre in 100 kilometres. A basin 100 kilometres across and 4 kilometres deep would have tides of just 1 centimetre. This is the kind of tide we could expect in a large deep lake. Tides have been measured in many lakes, but they are always small.
As the size of the basin increases and resonance is approached, the tide becomes bigger, and large accelerations and slopes in the water surface are created. The pressure gradient force now drives the acceleration of the water and the tide-generating force is required only to overcome the frictional drag on the flow. The maximum velocity from west to east in the basin coincides with the maximum tidal force in that direction, and high tide at the east end of the basin occurs one quarter of a cycle, or three lunar hours, after this time.
As the width of the basin continues to increase beyond the resonant width, the slopes and accelerations decrease, and the tide-generating force provides the acceleration. At the time of maximum west-to-east tidal force, the velocities are zero and the water surface slopes down from west to east with low tide at the eastern end of the basin. This is exactly the opposite situation to that in a basin which is narrower than the resonant width.
The effect of Earth rotation
The motion of the tide wave in the real ocean is further complicated by the effect of Earth rotation. Moving objects on a spinning Earth appear to be deflected—to the right in the northern hemisphere and to the left in the south. This effect is called the Coriolis effect, after the French mathematician Gaspard-Gustave Coriolis. There is a minimum scale for processes to be affected by Earth rotation: the motion has to continue in the same direction for a significant part of one day. Tide waves, in which the current flows in the same direction for six hours, are affected, whereas the water in a sink is not. Sadly, despite popular belief, the motion of the water down a plughole is not affected by the rotation of the Earth. Instead, the direction of spin down the plughole depends on the residual angular momentum the water retains after the sink was filled. This, in turn, depends on how the taps were used. You can prove this by filling a sink with one tap, leaving the water to settle for a while and then pulling the plug. Repeat with the other tap and you will see the water turns in the opposite direction.
Figure 10(a) shows a hypothetical enclosed ocean basin (in the northern hemisphere) in which there is a semi-diurnal tidal standing wave. High tide occurs at lunar hour 0 on the south shore and at lunar hour 6 on the north shore. At hour 3, the water is flowing at its maximum speed from south to north. The Coriolis effect deflects this flow to the right, creating a slope upwards from west to east. At this time, it is high tide on the eastern shore and low tide on the western shore. At lunar hour 9, the water is flowing at its maximum speed from north to south. The Coriolis effect now makes the surface tilt such that it is high water on the western shore (and low water on the east coast) at this time. The overall effect is that the high water travels around the outside of the basin, anti-clockwise, taking twelve lunar hours to complete the journey.
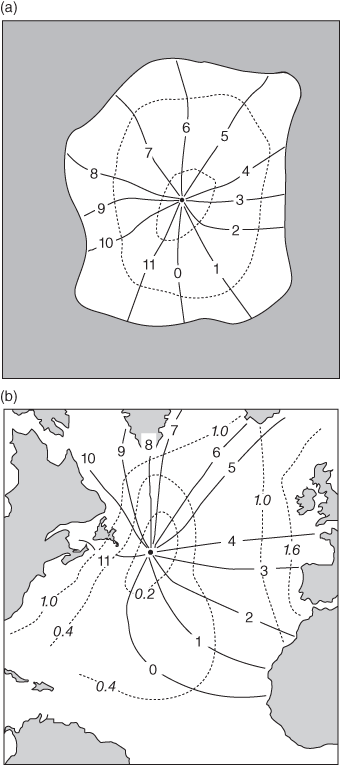
10. (a) A sketch of a forced semi-diurnal tidal wave in a closed ocean basin in the northern hemisphere on a rotating Earth, represented as a co-tidal chart. Continuous lines show the position of the wave crest at different times, in lunar hours. Dashed lines are contours of tidal range, decreasing towards the amphidromic point in the centre. (b) A co-tidal chart of the Moon’s tide in the North Atlantic Ocean, with times of high water expressed in lunar hours after the Moon’s transit at Greenwich and co-range lines in metres.
We can represent this movement, as we have done in Figure 10(a), by drawing lines marking positions along which high water occurs at the same time. These sweep around the ocean basin, like the hands of a clock, in an anti-clockwise sense in the northern hemisphere. The nodal line pivots about a mid-point as the Coriolis effect tilts the surface first one way and then the other. There is now just a single point of no tide and the amplitude of the tide increases radially outwards from this point, reaching a maximum at the shore. Lines, called co-range lines, can be drawn to represent this and we have sketched a few of these on Figure 10(a).
The tide wave sweeping around a central point of no vertical tide is called an amphidromic system and the point of no tide is an amphidromic point. Computer models of the tide show that there are amphidromic systems in all the world’s oceans. Generally the movement of the tide wave about the amphidromic point is as expected: clockwise in the southern hemisphere and anti-clockwise in the northern hemisphere. As an example, Figure 10(b) shows a co-tidal chart of the North Atlantic which has an amphidromic point located to the east of Newfoundland.
We have made much in this chapter about the importance of resonance to tides in the ocean. It has to be acknowledged, however, that in the main oceans themselves, tides are not, actually, that large; the tide at oceanic islands is rarely more than the half-metre or so we would expect from the equilibrium theory. What is happening is that the near-resonant oceans are leaking energy into the shelf seas around their margins. As their name implies, these shelf seas lie on the submerged shelves at the edge of the continents. They are shallow and dissipate tidal energy through friction between tidal flows and the seabed. It is mostly the energy loss in shelf seas which places the frictional damping on tides in the ocean.
The age of the tide
We will return to the effect of friction later in this book. We can say here, however, that tidal friction is the main cause of something mentioned in Chapter 1—that maximum tidal range, or spring tides, occurs a day or two after the time of new or full moon. This ‘age of the tide’ effect was reported early on (by Pliny the Elder in 77 ad) but it eluded a proper explanation until much later.
To make a spring tide it is necessary for the tides created by the Sun and Moon to coincide, producing a maximum in the tidal range. The Sun’s tide-generating force has a slightly higher frequency than the Moon’s (it repeats in a period of exactly twelve hours compared to twelve hours and twenty-five minutes for the Moon). If the frequency of the tide-generating force is increased, the tide wave has less time to cross the ocean basin if it is to keep up with the forcing. We could, if we liked, re-draw Figure 9 for an ocean basin of constant width and with the frequency of the oscillating tidal force on the x-axis. The curves would look the same, with a peak in the amplitude of the tide at the resonant frequency of the basin and a phase lag increasing with frequency, most rapidly when the ocean is close to resonance. The exact shape of the curves depends on the frictional damping.
Because the phase lag between the applied force and high tide increases with the frequency of the force, the delay is greater for the Sun’s tide than it is for the Moon. When the Earth, Moon, and Sun are in line (at new or full moon) the maximum tidal force of the Sun and Moon occurs at the same time but, because of the different phase lags, the sun’s high water is later than that of the Moon. Spring tide cannot therefore occur on the day of a new or full moon.
Let’s say that on the day of a new moon, the Sun’s high tide occurs one and a quarter hours after that of the Moon. Each day after new moon, the time of the Moon’s high water advances by fifty minutes and the time of the Sun’s high water stays exactly the same (since it has a period of twelve hours). After a day and a half, the Moon’s high water has advanced by one and a quarter hours (1.5 x 50 minutes); the two high waters now coincide and maximum tidal range will occur one and a half days after new moon. The exact delay between new or full moon and spring tides will depend on the phase difference between the Sun and Moon tides at a given location.