Chapter 6
Tides and the Earth
The energy in tides comes, ultimately, from the spin of the Earth. This may surprise you, but it is the Earth turning within the pattern of lunar and solar tidal forces that drives the daily and semi-daily tidal motion. Tidal streams, rubbing against the seabed, lose energy through friction and, to make up for this loss, energy is transferred into the tide from the Earth’s spin. As a result, our planet’s rotation is gradually slowing and the day is lengthening. Most tidal friction happens in shelf seas, where the currents are strongest and the water is shallow, but there is an additional loss of energy in the body of the deep ocean, through the creation of waves called internal tides.
The slowing planet
Evidence for the slowing of the Earth’s rotation comes from a number of sources, including the fossil record. Fine microscopic analysis of growth bands in fossilized marine corals shows that 400 million years ago there were 400 days in a year. If the length of the year was the same then as now, the daylength at that time must have been 21.9 hours. The length of an Earth day has therefore increased by 2.1 hours in 400 million years. This is equivalent to adding 1.9 milliseconds to the length of the day each century.
A further source of evidence for increasing daylength is the historical record of solar eclipses. Eclipses were (and are) important events and have been recorded by several ancient civilizations. The oldest known recording of a total solar eclipse took place in Babylon in 720 bc. As we go back through historical time, the speed at which the Earth was spinning increases enough to have a measurable effect on the position of places relative to the fixed stars.
To see how this works, imagine two planet Earths, one of which spins at a constant speed and the other with a speed which increases as we move back in time. A place on the Earth which speeds up as we turn back the clock will move ahead (that is eastwards) of its equivalent position on the constant-speed Earth. If we know that, at a particular time, a total solar eclipse was observed at (say) Babylon, it is possible to fix the position of Babylon, relative to the Sun and Moon, at that time. In the case of the 720 bc eclipse, we know that the accelerating Earth must have made a further quarter-turn, compared to its steady-speed counterpart, for Babylon to catch the eclipse. A quarter-turn in 2,700 years is equivalent to an increase of daylength of 1.8 milliseconds per century.
An accurate way of measuring the present deceleration of the Earth’s spin is through the change in the distance to the Moon. As the Earth’s spin slows, the conservation of angular momentum of the Earth–Moon system requires that the Earth’s angular momentum is transferred to the Moon. The mean distance to the Moon and the length of the month are both gradually increasing. Laser ranging (using reflectors left at the time of the Moon landings) gives an accurate measurement of the distance to the Moon: the distance is increasing at a rate of just under 4 centimetres per year. The rate of loss of Earth’s angular momentum that this implies equates to an increase in daylength at the present time of 2.4 milliseconds per century.
The observations of the Moon’s increasing orbital radius tell us that the Earth is losing kinetic energy at a rate of 3.7 × 1012 watts, or 3.7 terawatts. If this energy is used to replace frictional losses by the tide, this figure should match what observations at sea tell us about tidal friction.
Tidal friction in shelf seas
The obvious place to look for the effects of tidal friction is in the resonant shelf seas, where the currents are fastest and friction is greatest. The first person to do this correctly was the British physicist Sir Geoffrey Ingram Taylor. Taylor realized that any analysis of tidal friction would have to allow for the fact that tidal currents are turbulent, and the turbulence will increase the effect of seabed friction on the flow.
In a tidal current in a shallow shelf sea, the water directly in contact with the sea floor is slowed down by friction. This water then slows down the water immediately above it and so on towards the surface, creating a profile of velocity increasing with height (Figure 29). A flow in which layers of water slide over each other at different speeds in this way (the flow is said to be sheared) is inherently unstable in water depths greater than a few centimetres. Some of the energy in the flow is used to create turbulence.
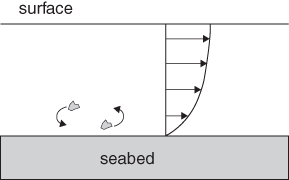
29. Turbulent exchange of parcels of water between layers in a tidal flow transfers momentum, increasing the height at which bed friction is felt and creating a velocity profile.
The turbulent eddies created by the tide move, in general, in three dimensions. The vertical eddies move water between the seabed and the surface. A way to picture this is that, each second, a parcel of water is transferred from one horizontal layer into an adjacent layer and, at the same time, an equal sized parcel is transferred in the opposite direction (we have sketched this exchange in Figure 29). There is no change in the volume of water in each layer but there is a sharing of momentum (and other water properties). The parcels of water from a faster moving layer speed up a slower layer and vice versa.
In the case of a tidal stream flowing over the seabed, the vertical exchange of horizontal momentum by turbulent eddies increases the height to which the friction of the seabed is felt. In a shallow sea with fast tidal streams it is not unusual to see an apparent ‘boiling’ motion at the surface caused by friction at the seabed.
In turbulent flows (in the atmosphere and the sea) the frictional force between the flow and a solid object depends on the square of the flow speed (a rule known as the quadratic friction law). The rate of energy loss from the flow equals the frictional force multiplied by the flow speed and so depends on the cube of the speed. A current flowing at 1 metre per second will lose energy one million times faster than one flowing at 1 centimetre per second. For this reason we would expect most energy losses due to bottom friction to occur in the resonant shelf seas (where speeds are of order 1 metre per second) rather than the deep ocean (where the speeds are of order 1 centimetre per second).
G. I. Taylor calculated the loss of tidal energy using the quadratic friction law with observed current speeds. His estimate of the energy lost by the tide in the Irish Sea, using a mean current speed of 1.17 metres per second, was 5x1010 watts, about 1.3 per cent of the total global energy dissipation rate of 3.7 terawatts predicted from astronomy.
Taylor checked his figure by calculating the flux of tidal energy flowing into the Irish Sea from outside. A progressive tidal wave carries energy; the flux of energy depends on the height and speed of the wave. Taylor realized that it was possible to calculate the net flux of tidal energy entering a semi-enclosed water body using measurements of currents and tidal elevations at the entrance. He used tidal diamonds to provide information about currents and shore-based tide gauges for the elevations. His estimate of the flux of tidal energy into the Irish Sea agreed (within the limits of experimental error) with his calculations of energy loss from bottom friction.
In the decades that followed Taylor’s work, tidal frictional losses were calculated for a growing catalogue of shelf seas. As expected, the main areas in which energy is lost are those shelf seas close to resonance with the tidal forcing. Tidal friction is greatest, per unit area of sea, in Hudson Bay and the Labrador Sea of Canada, the north-west European Shelf, the Yellow Sea in China, the North Australian Shelf, and the Patagonian Shelf of South America. In total, for all shelf sea areas, the current estimate of the rate of energy loss through tidal friction is 2.5 terawatts.
This figure falls short of the 3.7 terawatts estimated from astronomy. If we are to match tidal friction to energy loss from the spinning Earth there must be a further drain on tidal energy which does not rely directly on bottom friction.
Internal tides
Oceanographers measure the structure of the ocean with an instrument called a CTD, which stands for conductivity-temperature-depth probe. The CTD is lowered using the ship’s winch from the surface to as near the seabed as the operator cares, or dares, to go. To allow the sensors time to adjust to the environment through which they are descending, the CTD is lowered slowly: half a metre per second is the recommended speed. At a deep ocean station it can take well over an hour to profile from the surface to the bottom. On a long research cruise, the CTD soon becomes part of the routine work pattern, but for the first few profiles, scientists will gather round the computer screen to watch the plots of temperature, salinity, and other water properties unfold.
In a typical CTD profile in the deep ocean, there is a surface layer of uniform temperature, 10−100 metres deep, in which the Sun’s heat is uniformly mixed by wind and waves. Below this, water temperature falls with increasing depth, rapidly at first and then more slowly. The steeper vertical gradient of temperature in the ocean marking the transition between warm water on top and cold water below is called the thermocline. As the ocean floor is approached, temperatures drop close to 0 degrees Celsius even in the tropics. Because warm water is less dense than cold water, the ocean thermocline is generally stable: the water density increases downwards. Occasionally, changes in salinity will contribute to the stratification (fresh water is less dense than salty), but in a stable state, density always increases from the surface down.
This density structure can be disturbed. If a parcel of water is displaced vertically in the thermocline it will experience a restoring force as it moves into water less or more dense than itself. The water parcel will oscillate about its equilibrium depth, making waves in the interior of the ocean known as internal waves. Internal waves may be generated by changes in the discharge of a major river into the sea, and by variable wind and atmospheric pressure effects on the surface of the ocean. They can also be made by tidal currents flowing over mountains on the sea floor. Internal waves with semi-diurnal or diurnal tidal periods are called internal tides. In the simplified case of an ocean with two layers of different density, these internal tides travel along the interface between the layers. If the vertical density variation is continuous over depth, internal waves can form at all depths and travel in directions at an angle to the horizontal.
It is fairly easy to make a small-scale internal wave in a drinking glass with salt water at the bottom and fresh water on top. You can stir some milk into either layer to make the density difference visible. The tricky part is making the layers without mixing them too much: it’s best to put the light, surface water in first and then gently pour the denser water into the bottom through a drinking straw or small funnel. If you now tilt the glass and then set it straight, simulating the flow of the tide over an underwater hill, you will create an internal wave on the interface between the layers.
Internal tides travel slowly compared to surface tidal waves. This is because the difference in density, and hence the restoring force, between the layers in the stratified water is small compared to the difference in density between water and air at the ocean surface. Internal tidal waves travel at speeds of order 1 metre per second. The vertical movement in an internal tide wave can be large, however. The amplitude of internal tides in the ocean is typically tens of metres: several orders of magnitude greater than that of the surface tide. In a two-layer ocean, these vertical motions are largest at the density interface and decrease rapidly in amplitude with vertical distance from it. Near the sea surface, oscillations associated with a passing internal tidal wave are almost (but not quite) undetectable.
The earliest measurements of internal tides that we are aware of were made in the Kattegat by the Swedish oceanographer Otto Pettersson. In the Kattegat, salty water from the North Sea lies underneath fresher water from the Baltic, creating a sharp density interface. Pettersson fashioned a sinker which was dense enough to fall through the lighter upper layer but not dense enough to penetrate the heavier deep layer. The sinker therefore sat on the interface between the layers. Internal tidal waves then made the sinker move up and down, and the movements could be observed by fixing a light pole, long enough to stick out of the surface, to the sinker. The amplitude of the internal tide in the Kattegat was as great as 5 metres, much larger than the surface tide in these waters.
The horizontal currents generated by an internal tide produce alternating zones of convergent and divergent flow. These make patches of surface roughness which can be seen by eye. In some cases, particularly in coastal areas, natural and anthropogenic surface oils are swept together in the convergence zones to form ‘slicks’ that damp short surface waves (i.e. those which have surface tension as their restoring force—oceanographers call these capillary waves). More commonly, the interaction of capillary waves and the horizontal currents associated with internal tides concentrates these short waves in the convergence zones, locally increasing surface roughness (Figure 30(a)). In both cases, under light wind conditions the result is similar: clear, alternating bands of rough and smooth water.

30. Internal tides seen in sea surface roughness (a) and internal tide wave packets in astronaut photography (b).
The surface expressions of internal tides are visible in satellite radar images and astronaut photography (Figure 30(b)) as alternating bright and dark bands. Internal tides are observed to be generated in packets each tidal cycle and they travel large distances across oceans. Today, there are a number of innovative ways of studying internal tides, some of which have led to important scientific discoveries.
By combining satellite altimeter measurements of tidal amplitudes with model results for tidal currents, American oceanographers Gary Egbert and Richard Ray have calculated and mapped the global distribution of the rate at which energy from the surface tide is transferred to internal tides. Their method is an extension of that used by G. I. Taylor in the Irish Sea a century ago. The input of energy from the tide-generating force working on the current in a section of ocean is calculated. The net rate at which energy enters or leaves that section is determined from the elevations and currents on the boundary. The difference is the loss of energy from the surface tide.
The geographical distribution of the dissipation of surface tidal energy in the ocean leaves little doubt that it is being converted into internal tides. Most energy is dissipated at mid-ocean ridges and the continental shelf edge, where there are sudden changes in the depth of the ocean and where we would expect internal tides to be generated. The rate at which energy is put into the creation of internal tides is estimated to be at least 1 terawatt. The internal tide ultimately loses that energy by breaking at the edge of the ocean and by mixing the interior of the ocean.
And so we can balance the tidal energy budget of our planet. The Earth’s spin is losing energy at a rate of 3.7 terawatts. Of this, 2.5 terawatts are lost through bottom friction in shelf seas. A further 1 terawatt is lost through the creation of internal tides. That leaves 0.2 terawatts which we can reasonably suppose are lost through frictional effects in the tidal flexing of the solid Earth.
The Earth’s heat engine
Because our planet is a sphere, the Sun’s rays fall more obliquely on the surface at high latitudes than they do at the equator. There is more solar heating per unit area at low latitudes, and the atmosphere and ocean are working constantly to re-distribute this heat. Without these fluid heat pumps, the temperature gradient from the equator to the poles would be more extreme and the Earth’s climate more hostile to life.
Present estimates have it that the atmosphere and ocean work about equally hard in re-distributing heat to high latitudes, but the comparison is a difficult one to be sure of. There is no doubt, however, that ocean currents make a vital contribution to moderating global temperatures. The Sun warms the global ocean at the equator, and this warm water flows towards the poles, driven largely by the wind. For dynamical reasons to do with the conservation of angular momentum (as first reasoned by the US oceanographer Henry Stommel in the 1940s), these poleward flows hug the western boundaries of the oceans (in both hemispheres).
The western boundary currents have familiar names, for example the Gulf Stream in the North Atlantic and the Agulhas in the southern Indian Ocean. As the currents flow towards colder latitudes, surface winds carry heat from the ocean to the land, providing warmth for the continents and gradually cooling the sea. The cooled water that reaches high latitude then returns to the equator by two routes. One is as weak surface currents down the eastern boundaries of the oceans. The other is as a deep bottom flow forming part of the thermohaline circulation of the ocean (so-called because it is driven by differences in temperature and salinity).
We have sketched a simple picture of the thermohaline circulation in Figure 31. The Sun warms a relatively thin surface layer; heat is carried polewards in this layer by the wind-driven western boundary currents. As these currents approach polar regions, the water has lost enough heat to be very cold and very dense. If—in addition—sea ice forms, salt is excluded from the ice, increasing the salinity of the remaining water and further increasing its density. In a few places surface water at high latitudes in winter becomes dense enough to sink to great depths in the ocean. This happens primarily on the continental shelves of Antarctica and in the Greenland and Norwegian Seas.
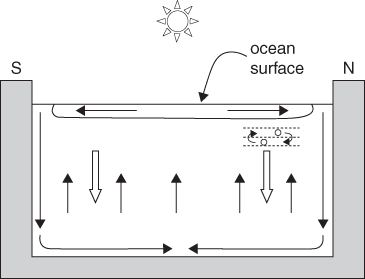
31. Sketch of the ocean thermohaline circulation. The Sun’s heat, put into the surface of the ocean at low latitudes, travels polewards in surface, largely wind-driven, currents. Water sinks at high latitudes and fills the bottom of the ocean, gradually upwelling back to the surface (thin vertical arrows). To maintain this circulation, it is necessary for heat to diffuse downwards (fat vertical arrows), a process thought to be driven by vertical turbulent exchange associated with internal tides.
Oceanographers measure the size of ocean currents in units called sverdrups (or Sv). The sverdrup, named after the Norwegian oceanographer Harald Sverdrup, is a flow of one million cubic metres of water per second. To place this in context, the flow in all the rivers in the world adds to about one sverdrup. The rate at which water is added to the deep ocean in the high latitude cooling zones is thought to be in the range 25−30 sverdrups.
The sinking water mixes a little with surrounding water as it falls, but reaches the ocean floor with temperature close to 0 degrees Celsius. It then spreads throughout the ocean basins filling the bottom of the ocean, as far as the equator, with cold water. The water filling the deep ocean returns to the surface as an upwelling current throughout the world’s ocean. The speed of the upwelling flow can be estimated by dividing the rate at which bottom water is created (25−30 sverdrups) by the surface area of the global ocean. This works out to be about 1 centimetre per day.
To keep the thermohaline circulation going, the cold water formed at the surface at high latitudes must be dense enough to sink to the ocean floor. This presents a problem because the bottom water has been made from the cold polar surface water: if nothing else is happening they will have the same density. The deep ocean will eventually fill with water of this density and the circulation will stop.
The problem can be solved by making the bottom water, after it has been formed, less dense. This can be achieved by mixing heat down to the bottom of the ocean from the Sun-warmed surface layer. Mixing warm, buoyant, surface water downwards into the ocean requires energy, in the same way that energy is needed to push a beach ball into the sea (the idea that we need a source of energy to maintain the thermohaline circulation was first proposed by Johan Sandström. It is now known as Sandström’s theorem). A possible (and indeed probable) source of this energy is the internal tide. The currents at different depths in the internal tide slide over each other at different speeds and generate turbulence.
The turbulent eddies, moving in the vertical, transfer parcels of water between different depths in the thermocline. An upward moving parcel of water will bring cold water from the deeps and a downward moving parcel will carry warm water to a deeper layer. The exchange of water parcels between layers produces a net transfer of heat downwards. The turbulent mixing created by internal tides can provide the necessary mechanism for the vertical mixing of heat needed to maintain the ocean’s thermohaline circulation. It is, indeed, difficult to see what else could provide this mechanism.
The power required to warm the deep ocean and maintain the thermohaline circulation is surprisingly small: around 10-3 watts for a column of water of surface area 1 square metre and stretching from the surface to the floor of the ocean (this could be provided by one kitchen food mixer whirring away in each cubic kilometre of ocean). Multiplying this power requirement by the surface area of the ocean gives the total power needed to maintain the thermohaline circulation as 0.4 terawatts. The rate at which energy is being put into the internal tide is reckoned as 1 terawatt, so it is possible for the internal tide to provide the necessary mixing energy if it runs at 40 per cent efficiency. The efficiency of conversion of mechanical energy to vertical mixing is likely not as high as this, though (it is thought to be just 20 per cent). The difference might be accounted for by allowing for some wind stirring of the deep ocean. An input of wind power of 1 terawatt, coupled with internal tide power of 1 terawatt, both acting at an efficiency of 20 per cent would provide the necessary mixing.