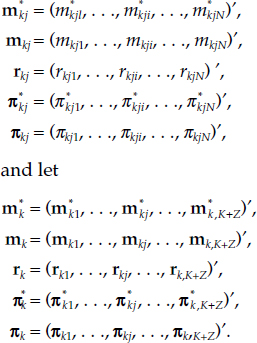
Appendix A provides the fundamental theory needed to measure monetary services flows within a country. In that theory the distribution effects of policy over regions of the country are not considered. But in an economic union, such as the European Monetary Union (EMU), the central bank cannot ignore differential distribution effects over countries. In a single country, the central bank can argue that residents of disadvantaged states, provinces, or regions could move to geographical areas that benefit from the monetary policy. In a multicountry economic union, countries seek to protect their cultures and rarely favor evolution of a uniform homogeneous population throughout the union. When there is a need to track distribution effects over countries, as well as the aggregate effects over the economic union, there is a need to extend the single country theory of appendix A to multilateral aggregation. Multilateral aggregation theory permits aggregation within countries and then aggregation over countries, with the ability to monitor second-moment dispersion of policy over countries. This appendix provides the extension of monetary aggregation theory to multilateral aggregation.
This appendix derives the fundamental theory for measuring monetary service flows aggregated within and then over countries for a multi-country area. The appendix develops three increasingly restrictive approaches: (1) the heterogeneous-agents approach, (2) the multilateral representative-agent approach, and (3) the unilateral representative-agent approach. These results were produced at the request of the European Central Bank (ECB) for the purpose of supporting construction of its Divisia monetary aggregates database, with convergence from the most general to the more restrictive approaches that is expected as economic convergence within the area proceeds. This theory permits monitoring the effects of policy over a multicountry area, while also monitoring the distribution effects of policy among the countries. The theory is equally as relevant to constructing a multilateral Divisia database for other multicountry economic union. This appendix is based on the ECB Working Paper, Barnett (2003), and the subsequent published article in the Journal of Econometrics, Barnett (2007).
With the growth of “free trade” economic and political unions, such as the North American Free Trade Agreement (NAFTA) and the European Union, and more profoundly the growth of economic monetary unions, such as the EMU, an increasing amount of research effort has focused on index-number-theoretic measurement problems associated with economic modeling and the conduct of macroeconomic policy in such economic unions.1 The need for internally consistent recursive aggregation over monetary data within and over countries is central to the objectives of that research. For those purposes this research, unlike prior research on this subject, was conducted in a manner that produces direct, multilateral extensions of the available closed-economy results.
The purpose of this appendix is to extend the theory of appendix A to the multicountry case in a form that would be applicable to economic unions, both prior to and after the introduction of a common currency. Progress toward convergence within economic unions occurs gradually. For that reason the results are produced under a sequence of increasingly strong assumptions, beginning with (1) a heterogeneous-agents approach applicable to the past under reasonable assumptions, and then progressing to (2) a new multilateral representative-agent approach applicable to an economic union under reasonable convergence assumptions, and finally to (3) a unilateral representative-agent approach requiring very strong assumptions, perhaps relevant to the very distant future, if at all.
At some date following the introduction of a common currency, the heterogeneous-agents approach could become mathematically equivalent to the multilateral representative-agent approach, since the assumptions necessary for equivalence of the two approaches are reasonably related to the long-run objectives of economic monetary unions. But the far more restrictive unilateral representative-agent approach requires very strong assumptions. In particular, the unilateral representative-agent approach would require convergence of inflation rates and interest rates across countries and would imply demographic convergence to a homogeneous population, such that the country of residence of a consumer would become irrelevant to the unilateral representative agent’s decisions. In the case of the EMU, the unilateral representative-agent approach could represent full convergence to a “United States of Europe.” The unilateral representative-agent approach is strictly nested within the multilateral representative-agent approach, while the multilateral representative-agent approach is strictly nested within the heterogeneous-agents approach having the weakest assumptions of the three approaches.
This appendix’s extensions of my earlier work produced a number of unexpected innovations, including the need for simultaneous use of two different consumer price indexes for internal consistency of the theory. The current appendix is intended to solve the central theoretical problems associated with monetary aggregation over countries.
The purposes and objectives of this research in the multicountry case are analogous to the purposes and objectives of monetary and financial aggregation and index number theory in the single country case. Data construction and measurement procedures imply the theory that can rationalize those procedures. Unless that implied theory is internally consistent with the theory used in applications of those data in modeling and policy, the data and its applications are incoherent. Such internal inconsistencies can produce the appearance of structural change, when there has been none.2
We define an “economic union” to be any multicountry area within which multilateral measurement and policy are relevant. Whether or not a common currency exists within the area is not part of this definition, but is relevant to the choice among assumptions we introduce. In practice, the identification of an economic union is usually by political treaty. But in economic theory, existence of such an area can be defined by a weak separability clustering condition, which need not imply the existence of a political treaty or an “optimal currency area.”3 All results are in continuous time. Certainty equivalence is assumed within the decisions of each consumer, as would be attained under risk neutrality by replacing contemporaneously random rates of return by their expectations. Appendix D develops the theory for extension of appendixes A, B, and C to the case of risk aversion, which becomes particularly relevant when there is exchange rate risk, as between different country’s interest rates within an economic union not having a single common currency. Examples would be the European Union, since only the EMU countries have the euro, or the EMU countries prior to their acquiring the euro.
Let K be the number of countries in the economic union. We let p*k = p*k(pk) be the true cost of living index in country k? {1,. . ., K], where pk = pk(t) is the vector of prices of consumer goods at time t and Xk = xk(t) is the vector of per capita real rates of consumption of those goods in country k at time t. Let Hk = Hk(t) be the population of country k at time t, and let mkji be the nominal per capita holdings of asset type i located or purchased in country j but owned by economic agents in country k. The holdings are per capita relative to country k’s own population, Hk. We present all results in per capita form, since the per capita variables are the ones that are needed in demand functions at the aggregate level. In addition the correlation with inflation tends to be in terms of per capita flows, since increases in monetary services that produce no change in per capita monetary services just accommodate population growth.
Assume that asset holders within the economic union also sometimes hold assets in Z countries that are outside the economic union. Let Nj be the number of asset types available within country, j, and let N be the total number of asset types available within all of the relevant countries, j? {1, . . ., K + Z}, where clearly N ≥ Nj for all j e {1, . . ., K + Z}. Then the subscripts of mkji have range k ? {1,. . ., K}, j ? {1,. . ., K + Z}, i e {1, . . ., N}. We are not limiting i to be within {1, . . ., Nj}, since we wish to associate a unique numerical value of i to each asset type, regardless of country ƒ within which the asset is located. As a result for each (k, j) there will necessarily be zero values of mkji for N - Nj values of i. If countries j and k do not share the same currency, then nominal holdings are converted to units of country k’s currency using the exchange rate between country k s and country j’s currencies.4 Then m*kji = mkji/p*k is the real per capita holdings of asset i located or purchased in country j but owned by economic agents in country k.
Let rkji = rkji(t) be the holding period after-tax yield on asset i located or purchased in country j and owned by an economic agent in country k at instant of time t, where all asset rates of return are yield-curve adjusted to the same holding period (e.g., 30 days).5 It is important to recognize that the subscript k identifies the country of residence of the asset holder, and not necessarily the country of location of the asset. Rates of return on foreign denominated assets owned by residents of country k are understood to be effective rates of return, net of the instantaneous expected percentage rate of change in the exchange rate between the domestic and foreign currency. At some time following the introduction of a common currency, the dependency of rates of return on k can be expected to end, and the dependency on j will be relevant only to holdings within the economic union of assets located in the Z countries outside the economic union. Hence at some time after the introduction of a common currency, it follows that rkji will be independent of(j,fc)for all j,kf? {1,. . ., K}.
Let Rk = Rk(t) be the benchmark rate of return in country k at instant of time t, where the benchmark rate of return is the rate of return received on a pure investment, providing no services other than its yield.6 Then π*k]i{t) = Rk(t) - rkji(t) is the real user-cost price of asset i located or purchased in country j and owned by residents of country k at time t, and πkji = p*kπ*kfi is the corresponding nominal user cost.7 It does not matter whether real or nominal interest rates are used, since the inflation rate conversion between nominal and real applies to both terms in the user-cost formula and hence cancels out between the two terms.
Technically speaking, whenever mkji is zero, as often will happen when a particular asset type i is not available within country j, the user-cost price should be the asset’s reservation price in country j. But, in practice, terms containing assets having zero quantity will drop out of all of our formulas, except when the asset’s quantity becomes nonzero in the next period. In such cases the reservation price must be imputed during the period preceding the innovation, and the new goods introduction procedure must be used.8 Since such innovations are infrequent, it usually will not be necessary to impute a reservation price or interest rate to asset holdings for which mkji = 0.
We now define
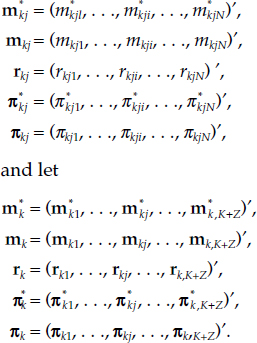
Aggregation within countries uses the existing theory presented in appendix A and developed by Barnett (1980a, b, 1987). That theory uses the economic approach to index number theory and assumes the existence of a representative agent within each country. To avoid the unnecessary imputation of reservation prices to assets not being held by residents of country k, we will restrict most of our computations to the index set Sk = {(j, i): mkji > 0, j ? {1,. . .,K + Z}, i e {1,. . .,N }} for all k e {1,. . .,K}.
Definition 1 Within each country k ? {1,. . ., K}, define the monetary real user-cost price aggregate, Π*k, the monetary nominal user-cost price aggregate, nk, the real per capita monetary services aggregate, M*k, and the nominal per capita monetary services aggregate, Mk, by the following Divisia indexes:
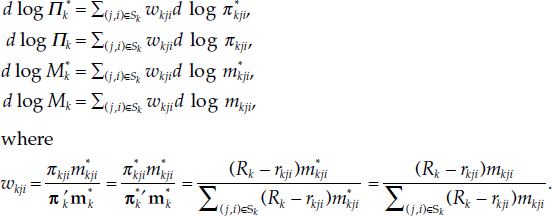
Observe that 0 ? wkji ? 1 for all k e {1,. . ., K},j ? {1,. . ., K + Z}, and i e {1, . . ., N}. Also observe that Σ(j,i)?sk wkji = 1 for all k ? {1,. . ., K}. Hence the shares, wkji, have the properties of a probability distribution for each k e {1,. . ., K}, and we could interpret our Divisia indexes above as Divisia growth rate means. But since it is convenient to assume the existence of a representative agent within each country, the statistical interpretation as a mean is not necessary. We instead can appeal to the Divisia index’s known ability to track the aggregator function of the country’s representative consumer.
The following result relating nominal to real values follows immediately.
Lemma 1 Mk = M*kp*k and Πk = Π*kp*k..
Proof The proof follows from the known linear homogeneity of the Divisia index.
Our heterogeneous-agents approach to aggregation over countries is based on the stochastic convergence approach to aggregation, championed by Theil (1967) and developed further by Barnett (1979a, b, 1981, ch. 2). This approach not only can be used to aggregate over heterogeneous consumers but also jointly over consumers and firms. Hence the approach is not only a heterogeneous-consumers approach, but more generally is a true heterogeneous-agents approach. See section A.9 of appendix A to this book along with Barnett and Serletis (2000, ch. 9). By assuming the existence of a representative agent within each country, and treating those representative agents as heterogeneous agents, we produce a heterogeneous-countries approach to aggregation over countries.
In aggregating within an economic union, this approach implies that the countries’ characteristics, such as cultures, tastes, and languages,, were sampled from underlying theoretical populations consistent with the climates, histories, resources, geographies, neighboring population characteristics, and so forth. All time-varying variables then become stochastic processes. Each Divisia index aggregating over component stochastic processes becomes the sample mean of realizations of those stochastic processes, and thereby an estimate of the mean function of the underlying unknown population stochastic process. The distributions of those stochastic processes are derived distributions induced by the random sampling from country characteristics. The derived empirical distributions of the countries’ solution stochastic-process growth rates impute probabilities to countries equal to their relevant expenditure shares in expenditure within the economic union.
Let ek be the exchange rate of country k’s currency relative to a market basket of currencies, such as the ecu (European currency unit), where ek is defined in units of the market basket currency per unit of country k’s currency. When extending the data backward to before the introduction of a common currency, the exchange rates can play an important role in our results.
The stochastic convergence approach to aggregation over heterogeneous agents has traditionally been based more on statistical theory than on economic theory. But a rigorous connection with economic theory has been provided by Barnett (1979a). We use that interpretation in our heterogeneous-agents approach, as we now explain.
Consider a possible country with representative consumer c, having utility function, Uc = Uc[uc(m*c),gc(xc)]. Assume that the differences in tastes across possible countries can be explained in terms of a vector of taste-determining variables, Φc. The dimension of the vector of taste-determining variables must be finite, but otherwise is irrelevant to the theory.9 Then there must exist functions U, u, and g, such that
for all possible countries’ tastes, ?c. Although U, u, and g are fixed functions, the random vector ?c of taste-determining variables causes Uc, uc, and gc to become random functions, reflecting the possible variations of tastes and their probabilities, conditionally on their given environmental, demographic, historical, resource, and other factors in the economic union.
Assume that each possible country c’s representative consumer solves the following decision problem for (m*c, xc) at each instant of time t:
maximize U[u(m*c, ?c), g(xc, ?c), ?c]
subject to m*c’ ?c + x’cpc = Ic.
Assume that the countries and their representative agents are about to be drawn from the theoretically possible populations, but have not yet been drawn. Assume that there is an infinite number of possible countries in the economic union, so that there exists a continuous joint distribution of the random variables (Ic, pc, ec, πc, ?c) at any time t. We assume that ?c is sampled at birth and does not change during lifetimes, so that ?c is not time dependent. But {Ic(t), pc(t), ec(t), πc(t)} are stochastic processes. Hence at any time t we can write the theoretical population distribution function of {Ic(t), pc(t), ec(t), πc(t), ?c} at t as Ft. With distributions derived from Ft, it follows that at any t, the following are random variables:
d log(p*cec), d log(Mcec), d log(Mc*), d log(Πcec), and d log(Πc*).
Using the derived distribution of those random variables, we can define their theoretical population means by θ1 = E[d log(p*cec)], θ2 = E[d log(Mcec)], θ3 = E[d log(Mc*)], θ4 = E[d log(Πcec)]/ and θ5 = E[d log(Πc*)], where (θ1, θ2, θ3, θ4, θ5) = (θ1(t), θ2(t), θ3(t), θ4(t), θ5(t)) is a nonstochastic function of time. Now consider sampling from the theoretical population K times to draw the k? {1,. . ., K} actual countries. The countries are assumed to have representative consumers having characteristics that are produced from the continuous theoretical population distribution, Ft, at t.
Definition 2 Let sk = Hk/Σkk=1 HK be country k’s fraction of total economic union population. Define the kth country’s expenditure share, Wk, of the economic union’s monetary service flow by
The fact that this definition is in terms of total national expenditure shares, rather than per capita shares, is evident from the fact that
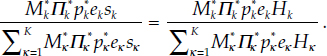
Observe that 0 ≤ Wk ≤ 1 for all k, and Σkk=1 Wk=1 We thereby can treat {Wlr . . ., WK} as a probability distribution in computing the following Divisia means by our stochastic heterogeneous-countries approach to aggregation over countries.
Definition 3 Aggregating over countries, define the monetary-sector-weighted Divisia consumer price index, p* = p*(t), by
Definition 4 Define the economic union’s nominal, M, and real, M*, per capita monetary service flows by
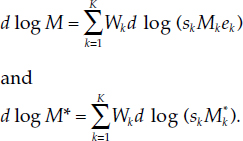
Definition 5 Define the economic union’s nominal, Π, and real, Π*, monetary user-cost prices by
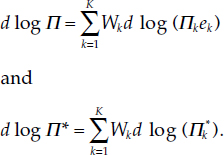
When we draw from the derived population distributions, the frequency with which we draw the growth rates, d log p*kek, d log(skMkek), d log(skM*k), d log(Πkek), and d log(Π*k), is Wk. From Khinchine’s theorem, assuming independent sampling, we find that d log p*, d log M, d log M*, d log Π, and d log Π* are sample means of distributions having population means equal to θ1(t), θ2(t), θ3(t), θ4(t), and θ5(t), respectively. In addition, d log p*, d log M, d log M*, d log Π, and d log Π* converge in probability as K ? 8 to θ1(t), θ2(t), θ3(t),θ4(t), and θ5(t), respectively It is this convergence to theoretical population properties that accounts for this aggregation approach’s name, “the stochastic convergence approach,” in Barnett (1979a).
Observe that there is no assumption that a representative agent exists over countries. We assume in this heterogeneous-agents approach only that representative agents exist within countries. Aggregation over countries is defined to be estimation of the moments of the stochastic processes generated by sampling from the underlying theoretical population that produces the countries’ representative agents. When in later sections we consider the existence of multilateral and unilateral representative agents over countries, we add strong assumptions about the realized tastes after sampling from the theoretical population.
In summary, the perspective from which our heterogeneous-agents approach is produced is prior to the drawing from the theoretical distribution, so that random variables have not yet been realized and all dynamic solution paths are stochastic processes induced by the randomness of {Ic(t), pc(t), ec(t), πc(t), ?c}. No assumptions are made about the precise form in which realized tastes relate to each other across countries. The heterogeneous-agents approach tracks aggregator functions within countries. But this approach does not require assumptions sufficient for the existence of microeconomic aggregator functions over countries. After aggregating over countries, this approach tracks moments of aggregate stochastic processes and is interpreted relative to the underlying population distributions.
In contrast, our multilateral and unilateral representative-agent approaches add assumptions regarding the functional relationship among realized tastes of countries already in existence, and seek to track the realized aggregator function over countries. Under those additional assumptions producing the existence of an aggregator function over the economic union, the heterogeneous-agents approach reduces to the multilateral representative-agent approach as a special case. Although the two approaches have different interpretations, because of the difference in perspective regarding prior versus post sampling, the multilateral economic-agent approach is nevertheless mathematically a nested special case of the heterogeneous-agents approach.
It is important to recognize the following proof’s dependence on the definition of p* in equation (C.2), with the share weights determined by definition 2. If any other weights, such as consumption-expenditure share or GDP weights, had been used in defining p*, then theorem 1 would not hold.
Theorem 1 M = M*p* and Π = Π*p*.
Proof The method of proof is proof by contradiction. First consider M, and suppose that M ?M*p*. Then
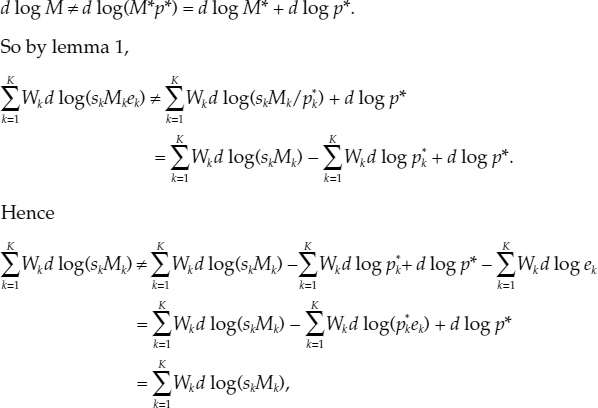
which is a contradiction. The last equality follows from equation (C.2) in definition 3.
Now consider Π, and suppose that Π? Π*p*. Then
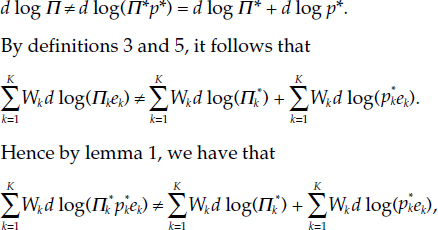
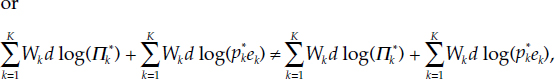
The following theorem proves Fisher’s factor reversal property for the monetary quantity and user-cost aggregates over countries. In particular, we prove that total expenditure on monetary services aggregated over countries is the same, whether computed from the product of the economic union’s quantity and user-cost aggregates or from the sum of the products within countries. The multiplications by sk convert to per capita values relative to total economic union population, while the within-country aggregates, M*k, remain per capita relative to each country’s own population.
We now consider some special cases of our results. First we consider the case of purchasing power parity. While the purchasing power parity assumption is not applicable to many economic unions, this special case is useful in understanding the forms of the more general formulas we have derived without purchasing power parity and could be useful in applying this theory to other economic unions in which purchasing power parity may apply
Definition 6 We define E = {e: k = 1,. . ., K} to satisfy purchasing power parity, if Pj* / Pi* = eit/ ej for all countries i, j? {1,. . ., K}. Under this definition, it equivalently follows that there exists a price, p°, such that p° = P*iei = P*jej for all i,j ?{l, . . .,K}.
Theorem 3 If E satisfies purchasing power parity, then
Proof See the ECB working paper, Barnett (2003).
Theorem 4 If E satisfies purchasing power parity, then
for all countries, k? {1,. . ., K}.
Proof See the ECB working paper, Barnett (2003).
Compare (C.3) with (C.1), and (C.4) with (C.2), to see the sources of the complications in (C.1) and (C.2) caused by violations of purchasing power parity.
This section defines the concept of a multilateral representative agent. The next section defines a unilateral representative agent over countries to be a representative agent who considers the same goods in different countries to be perfect substitutes, regardless of the country of residence of the purchaser or the country within which the good or asset is acquired. The existence of a unilateral representative agent has been implicit in the existing studies using the “direct method” of aggregation over monetary assets in the euro area. As I will show, the existence of a unilateral representative agent requires extremely strong assumptions. Without a homogeneous culture and the vast population migrations that could produce that uniformity, this assumption will not apply The existence of a multilateral representative agent requires far more reasonable assumptions.
If tastes across countries do converge in the distant future, the convergence is more likely to be toward a homogeneous multilateral representative agent, rather than toward a unilateral representative agent. A homogeneous multilateral representative agent recognizes the existence of country specific tastes but equates those tastes across countries. A unilateral representative agent does not recognize the relevancy of countries at all and thereby does not recognize the existence of country specific tastes. Country specific utility functions cannot be factored out of the economic union’s tastes (i.e., weak separability of country tastes fails); and the country subscripts, j and k, disappear from the decision of the unilateral representative agent. The allocation of goods across countries is indeterminate in that case.
We begin by defining relevant assumptions and produce the theory of a multilateral representative agent. We show that the existence of a multilateral representative agent is a special case of our heterogeneous-countries theory. We further show that a homogeneous multilateral representative agent exists under stronger assumptions.
As described in the previous section, our representative-agent approach for aggregating over countries treats countries as already realized, so that variables and functions no longer are random. Hence we can consider realized functional structure aggregated over realized countries. The following assumption is needed, and begins to become weak only after the introduction of a common currency.
Assumption 1 Suppose that there is convergence over the economic union in the following sense. Let there exist R = R(t) such that Rk = R(t) for all k? {1, . . ., K} and all t.
The existence of a representative agent is necessary and sufficient for the nonexistence of distribution effects.10 Distribution effects introduce second moments and possibly higher order moments into demand functions aggregated over consumers. The existence of such second and higher order moments in the macroeconomy can cause policy to influence distributions of income and wealth across consumers. Assumption 1 rules out certain possible distribution effects. Additional assumptions ruling out other sources of distribution effects will be needed as we consider further special cases.
By its definition, the benchmark asset, unlike “monetary” assets, provides no services other than its investment rate of return, and hence cannot enter the utility function of an infinitely lived representative agent.11 Therefore differences in tastes across countries play no role in decisions regarding benchmark asset holdings by a representative agent within the economic union. For that reason the existence of a common benchmark rate for all countries is necessary for a representative agent over countries. A representative agent within the economic union would hold only the highest yielding of the possible benchmark assets. This conclusion is not necessary in our (thereby more general) heterogeneous-countries approach.
By assumption 1, we also can consider the following stronger assumption. We assume that all K countries have already been drawn from their theoretical population of potential countries. Then the tastes of the representative consumers in each country are realized and are no longer random. The following assumption produces the existence of aggregator functions, (U, V, G), over the individual realized countries’ tastes, (uk, gk) for k ? {1,. . ., K}.
Assumption 2a Suppose that there exists a representative consumer over the economic union. Within that representative agent’s intertemporal utility function, assume that (m1*(t),. . ., m*K(t), x1(t), . . ., xK(t)) is intertemporally weakly separable from (m*1(t),. . .,m*K(t), x1(t), .. .,XK(T)) for all t ? t, and also assume that monetary assets are weakly separable from consumer goods.
As defined in section C.1, xk is the vector of instantaneous per capita goods consumption rates in country k relative to the population of country k. Then skXk is the per capita real consumption vector relative to total economic union population, H = Σkk=1Hk. Since contemporaneous consumption of goods and services is weakly separable from future consumption, a contemporaneous category utility function exists of the form
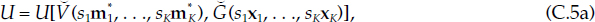
where V and G are linearly homogeneous.
Assumption 2b Suppose further that consumption of monetary assets and goods are weakly separable among countries, so that the contemporaneous utility function has the blockwise weakly separable form
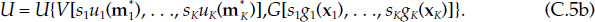
Assume that the functions V, G, uk, and gk do not change over time and are linearly homogeneous for all k? {1,. . ., K}.12
The dependency of uk and gk on k permits heterogeneity of tastes across countries. In the next subsection, we will explore the special case of homogeneity of tastes across countries. As in our heterogeneous-agents approach, the subscript k identifies the country of residence of the owner of the asset and not necessarily the country within which the asset is purchased or located. Hence equation (C.5b) requires that the tastes which determine the utility functions, uk and gk, are those of the residents of country k, regardless of the country within which the residents have deposited their assets. Note that equation (C.5a) does not require that tastes of consumer’s residing in country k exist independently of the tastes of consumers residing in other countries. The existence of stable country-specific tastes, uk and gk, exist only under the stronger assumption (C.5b).
Equation (C.5b) could equivalently be written as because of the linear homogeneity of the utility functions, uk and gk. But the form of equation (C.5b) is preferable because it makes clear our ability to aggregate first within countries to acquire the within-country monetary aggregates, M*k = uk(m*K), and the within-country consumer goods aggregates, Xk = gk(xk). Note that M*k and Xk are in per capita terms relative to country k’s population. We then can aggregate over countries to acquire the economic union’s monetary aggregate over countries, M* = V[s1u1(m*1), . . ., sKuK(m*K)] = V[s1M*1,. . ., sKM*K], and the economic union’s consumer goods aggregate over countries, X = G[s1g1(x1), .., SkgK(xK)] = G[s1X1,. . ., sKXK]. Note that M* and X are in per capita terms relative to total economic union population. Our proofs below demonstrate the capability to aggregate recursively in that manner.
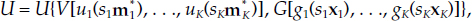
By assumptions 1, 2a, and 2b, we let I = I(t) be the instantaneous rate of expenditure. It is budgeted to t by the representative consumer in a prior stage intertemporal allocation. Then we can define the following contemporaneous, conditional decision at instant of time t.
Decision 1a Choose (m*1,. . ., m*K, xlr. . ., xK) to maximize u{v[s1u1(m1*),. . ., sKuk(m*K)], G[s1g1(x1),..., SKgK(xK)]} subject to
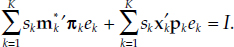
Definition 7 We define a multilateral representative consumer to be an economic agent who solves decision 1 by assumptions 1, 2a, and 2b.
Note that our definitions of real and nominal money balances have not changed from those in section C.1. Nominal balances owned by residents of country k are deflated by p*k to acquire real balances, where p*k is the unit cost function dual to the consumer goods quantity aggregator function, gk(xk.), within country k. We are not yet accepting assumptions that would be sufficient for existence of a single consumer price index that could be used to deflate nominal balances within all countries in the economic union to real balances in those countries. Hence p*k is not independent of k. Our economic union consumer-goods price aggregate, p*, is relevant to deflation of monetary balances only after monetary balances have been aggregated over countries.
Observe that assumption 1 does not require convergence of rates of return on all monetary assets across countries. To produce the multilateral representative consumer, assumption 1 requires only that consumers in all countries of the economic union have access to the same benchmark rate of return on pure investment. We now consider the implications of a multilateral representative agent. In the next section we then focus on the case of a unilateral representative agent, requiring the adoption of very strong assumptions.
The following lemmas now are immediate:
Lemma 2 By assumptions 1, 2a, and 2b, the representative consumer’s allocation of I(t) over goods and monetary services will solve decision 1.
Proof Follows from known results on two-stage budgeting, where the first stage is intertemporal. One need only redefine the variables in the continuous time analogue to sections A.2.1 and A.2.2 of appendix A. ?
Lemma 3 By assumptions 1, 2a, and 2b, let Xk = gk(xk) be the exact consumer goods per capita quantity aggregate over xk for country k, relative to the population of country k, and let X = G(s1X1, . . ., sKXK) be the exact consumer goods per capita quantity aggregate over countries, relative to total economic union population. Then p*k is the exact price dual to Xk, and P* is the exact price dual to X, where P* is defined such that
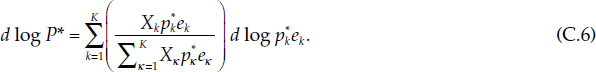
Proof The result regarding p*k follows, since it was defined in section C.1 to be the true cost of living index of Xk. The result on P* follows by a proof analogous to that of theorem 2, since duality of P* and X implies, from factor reversal, that
This equation accounts for the form of the share weights in equation (C.6).
Note that P*, defined by equation (C.6), and p*, defined by equation (C.2), are not the same. Both consumer price indexes are needed for different purposes, as we will discuss further below. Now consider the following decision, within which aggregation over consumer goods has already occurred:
Decision 2 Now choose (m*1, . . ., m*K, X) to maximize U{V[s1u1(m*1), . . ., sKuK(m*K)], X} subject to
The following theorem establishes the connection between decisions 1 and 2:
Theorem 5 By assumptions 1, 2a, and 2b, we let (m*1,. . ., m*k, xl. . ., xK) solve decision 1, and let X and P* be defined as in lemma 3. Then (m*1,. . ., m*k, X) will solve decision 2.
Proof The proof follows from lemma 3 and well-known results on two-stage budgeting.
Theorem 5 permits us to concentrate on aggregation over monetary assets within countries and then over countries, while using a quantity and price aggregate for consumer goods. Theorem 5 also demonstrates our need for the P* price index in the prior aggregation over consumer goods.
In decision 3 we next define a “second-stage” decision by which funds preallocated to monetary-services expenditure within the economic union are allocated over countries. In decision 4, we define a “third-stage” decision, by which funds preallocated to monetary-services expenditure within the each country are allocated over assets in the country.
Let Πk for each k ? {1,. . ., K} be as in definition 1. We can then define the following decision:
Decision 3 For given value of X, choose (M*1.., M*K) to maximize V(s1M1, . . ., sKM*K) subject to
Decision 4 For each k ?{1,. . ., K} choose m*k to maximize uk(m*k) subject to m*’kπk = M*kΠk.
The following two corollaries to theorem 5 relate to decisions 3 and 4.
Corollary 1 to theorem 5 By assumptions 1, 2a, and 2b, let (m*1,. . ., m*k, X) solve decision 2. Define P* as in equation (6) and the vector of user costs Π = (Πl’ . . ., ΠK) as in definition 1. Then (M*1, . . ., M*K) will solve decision 3, where M*k = uk(m*k) for all k ? {1,. . ., K}.
Proof The proof follows from well-known results on two stage budgeting.
Corollary 2 to theorem 5 By assumptions 1, 2a, and 2b, let (m*1,. . ., m*k, X) solve decision 2, and let M*k = uk(m*k) for all k ? {1,. . ., K}. Define Πk as in definition 1. Then mk also will solve decision 4 for all k ? {1,. . .,K}.
Proof The proof follows from well-known results on two-stage bud geting and a simple proof by contradiction. Suppose that M*k = uk(m*k) but m*k does not solve decision 4 for all k e {1,. . ., K}. Then (m*1,. . ., m*k, X) cannot solve decision 2.
Decision 4 defines the representative consumers assumed to exist within countries in section C.3.2. By the assumptions in definition 7 for the existence of a multilateral representative consumer, corollary 2 to theorem 5 proves that the decisions of the representative consumers in section C.3.2 are nested as conditional decisions within the decision of the multilateral representative-consumer. Hence our results in section C.3.2 can be used to aggregate within countries, regardless of whether aggregation over countries is by our heterogeneous-countries approach or by our multilateral representative-consumer approach.
After the aggregation within countries is complete, corollary 1 to theorem 5 demonstrates that decision 3 can be used to aggregate over countries, if we accept the assumptions necessary for the existence of a multilateral representative agent. The monetary quantity aggregator function for aggregation over countries then is V, and a Divisia index can be used to track V in the usual manner. Observe that decision 4 would be unaffected, if the vector of within-country user costs πk and the aggregate within-country user cost Πk were changed to real user costs, since all that would be involved is the division of each constraint by P*k. Hence that constraint would continue to hold, if all values in the constraint were in real terms.
But observe that in decisions 2 and 3, the consumer price index, P*, on the right-hand side of equation (C.8) is not the same as the consumer price index, p*k, needed to deflate the user costs on the left-hand side to real value. In addition the consumer price index, P*k, used to deflate each term on the left-hand side is different for each k ? {1,. . ., K}. Hence the constraint would be broken, if all variables on both sides of the constraint were replaced by real values. This would amount to dividing each term by a different price index. Also recall that conversion of m*kto nominal balances requires multiplication by P*k, which is different for each country, k.
The following illustration can further clarify the need for two price indexes in modeling. Consider the following decision using the exact aggregates both over monetary assets and goods within the economic union.
Decision 5 Choose (M*, X) to maximize U(M*, X) subject to M*Π + XP* = 1.
The solution will be of the form
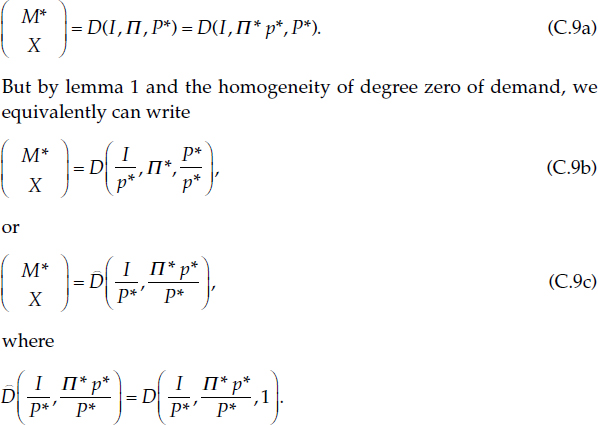
As can be seen from equations (C.9b) and (C.9c), there is no way to remove the simultaneous dependence of the solution demand function systems on the two price indexes, P* and p*. The form of the demand system in (C.9a) is in terms of nominal total expenditure (“income”), I. The form of the demand system in (C.9b) is in terms of real income relative to p* aggregate prices. The form in (C.9c) is in terms of real income relative to P* aggregate prices. None of the three possible forms results in either p* or P* canceling out. In addition lemma 1 requires that conversion of M* to nominal balances must be relative to p* prices.
The following theorem establishes the relationship between our heterogeneous-countries approach and our multilateral representative-agent approach.
Theorem 6 Under assumptions 1, 2a, and 2b, let (M*1,. . ., M*K) solve decision 3, and let M* be as defined in definition 4. Then
d log M*=d log V(s1M*1,. . . skM*k).
Proof The proof follows from the exact tracking of the Divisia index in continuous time.
Our multilateral representative-agent theory produces conditions under which an economic (rather than statistical) monetary aggregate exists over countries. When an economic monetary aggregator function, V, exists over countries, theorem 6 shows that our quantity index number, M*, introduced in definition 4, will exactly track the theoretical aggregate. In particular, we have demonstrated that our heterogeneous-agents approach for aggregating over countries reduces to the multilateral approach under assumptions 1, 2a, and 2b, since both approaches then produce the same monetary aggregate, M*, over countries. In addition Πk and Πk* defined in definition 5 will remain dual to M*, since the proofs of theorems 1 and 2 remain valid by assumptions 1, 2a, and 2b.
We have demonstrated at all stages of aggregation that our multilateral representative-agent approach is nested within our heterogeneous-countries approach as a special case of assumptions 1, 2a, and 2b. Theorem 6 is the result at the level of aggregation over countries, while corollary 2 to theorem 5 is the result for aggregation within countries.
Also observe that since the proofs of theorems 1 and 2 remain valid under our additional assumptions in this section, it follows that we must continue to deflate nominal M aggregated over countries to real M* using p*, not P*. The correct dual to aggregate real consumption X is P*, which should be used to deflate nominal to real consumption expenditure. Regarding the computation of P* and its possible use as an inflation target, see Diewert (2002). It is important to recognize that p* and P* both play important roles in this theory, and neither is an acceptable substitute for the other.13 These conclusions hold in both our heterogeneous-countries approach and in the multilateral representative-agents special case acquired when the benchmark rate is the same for all countries in the economic union.
Let us now proceed to the far more restrictive case of a homogeneous multilateral representative agent who imputes identical tastes to the residents of all countries in the economic union. An initial necessary assumption is assumption 1. As shown by theorem 7 below, the seeming paradox of the existence of two consumer price indexes—p* to deflate nominal money balances to real balances and P* to deflate nominal consumption expenditure to real aggregate consumption—disappears under the following additional important assumption.
Assumption 3 Suppose that there is convergence over the economic union in the following strong sense. Let there exist P = P(t) such that
for all k ? {1,. . ., K} and all t.
The following theorem is immediate:
Theorem 7 By assumption 3, the following equation holds for all non-negative (e1r. . ., eK) and all nonnegative (p*1,. . ., p*K):
d log P*(p1e1,. . . p*ek) =d log p*(p*1e1,. . ., p*ek)
Proof By equation (C.10), d log(p*kek) = d log P for all k e {1,. . ., K} and all t. Hence d log p* = d log P by equation (C.2), and d log P* = d log P by equation (C.10). So d log p* = d log P*.
We now consider further the case of a homogeneous multilateral representative agent, but first we need the following lemma:
Lemma 4 By assumptions 1, 2a, 2b, and 3, there exists g such that gk = g for all k ? {1, . . ., K}, so that tastes for consumer goods are identical across countries.
Proof From equation (C.10) it follows that d log [p*k(t)ek(t)] = d log P[pk(t)ek(t)] for all k ? {1,. . ., K}. Hence the same consumer-goods price aggregator function, P, applies for all k ? {1, . . ., K}. But the consumer-goods quantity aggregator function, gk, is dual to the consumer-goods price aggregator function. So the consumer-goods quantity aggregator functions, gk, must also be independent of k.
To move further toward the existence of a homogeneous multilateral representative consumer, we also need the following assumption, which is analogous to assumption 3:
Assumption 4 Suppose that convergence over the economic union results in the existence of Π such that
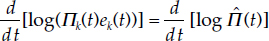
for all k ? {1,. . .,K} and all t.
Clearly, by this assumption, it follows from definition 5 that Π(t) = Π(t) for all t. The following lemma depends heavily on assumption 4:
Lemma 5 By assumptions 1, 2a, 2b, and 4, there exists u such that uk = u for all k ? {1, . . ., K}, so that tastes for monetary services are identical across countries.
Proof The proof is analogous to the proof of lemma 4.
The form of decision 1 now is as follows:
Decision la Choose (m*1,. . ., m*k, x1, . . ., xK) to maximize U{V[s1u(m*1),. . ., sKu(m*K)], G[s1g(x1),..., SKg(xK)]} subject to
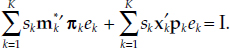
Observation 1 By assumptions 1, 2a, 2b, 3, and 4, the solutions to decisions 1 and 1a will be the same, as is evident from lemmas 4 and 5. Because of the homogeneity of tastes across countries in decision la, we have the following definition.
Definition 8 We define a homogeneous multilateral representative agent to be an economic agent who solves decision 1a by assumptions 1, 2a, 2b, 3, and 4.
Observe that despite the homogeneity of tastes across countries, the decision remains multilateral, as a result of the assumption of block-wise weak separability of tastes across countries. That separability assumption produces existence of within-country tastes, u, independent of consumption in other countries. The fact that the tastes are identical for all countries in the economic union does not negate the existence of those tastes, u.
In econometric studies there could be reason to investigate convergence of the general multilateral representative consumer toward the homogeneous multilateral representative agent. But for data construction purposes we see no advantage to adopting the homogeneous multilateral representative-agent model. The general multilateral representative-agent model can be used to construct aggregates recursively, first within countries and then across countries. When producing the aggregates within countries, there is not benefit to imposing uniformity of tastes across countries.
The next section explores the unilateral representative-agent model that would produce a large gain in data construction simplification, but only under a very strong assumption that is not likely to be reasonable within the near future, if ever.
A unilateral representative agent considers the same goods and assets to be perfect substitutes, regardless of the country within which the goods and assets are purchased and regardless of the country within which the purchaser resides. By this assumption, our subscripts j and k will be irrelevant to the tastes of the unilateral representative agent. Only the subscript i will matter, since countries, and thereby country subscripts, will be irrelevant to the decision.
We no longer can accept assumption 2b; we will instead have to make a much stronger, but nonnested, assumption. Assumption 2b assumed weak separability among countries of residence of consumers. But a unilateral representative agent neither recognizes the country of residence of a consumer nor the country within which a good or asset was acquired. Hence tastes specific to a country no longer exist. It is important to recognize the fundamental difference between the homogeneous multilateral representative consumer and the unilateral representative consumer. The former imputes identical tastes to each country’s residents but does recognize the existence of different countries and the existence of the identical tastes, u, within each country. But the unilateral representative consumer does not impute existence of weakly separable tastes to the residents of any country in the economic union.
Since we no longer can assume weak separability among countries, we will have to rewrite decision 1 as follows:
Decision 1b Choose (m*1.., m*K, x1. . ., xK) to maximize U[V(s1m*1.., sKm*K), G(s1x1,. . .skxK)] subject to
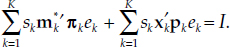
Hence we now replace assumption 2b with the following much stronger assumption, which is neither necessary nor sufficient for assumption 2b:
Assumption 5 Let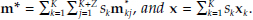 
.Suppose that there exists linearly homogeneous 
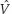such that (m*) = (s1m1* . . ., sKm*k), where V is as defined in equation (C.5a). Then for any i, all monetary assets of that type are perfect substitutes, regardless of the country within which they are located or the country in which the owner resides. Analogously for consumer goods, assume there exists Ĝ such that Ĝ(x) = Ğ(s1x1,. . ., sKxK), where G is as defined in equation (C.5a). Hence for any i, all consumer goods of that type are perfect substitutes, regardless of the country within which they are located or the country in which the owner resides. Further assume that there exist n(t) and pit) such that πkj(t)ek(t) = π(t) and pk(t)ek(t) = p(t) for all k ? {1,. . ., K}, j ? {1, . . ., K + Z}, and all t.
The assumptions πkj (t)ek(t) = π(t) and pk(t)ek(t) = p(t) are needed to avoid corner solutions allocating no consumption to residents of some countries. Otherwise, with perfect substitutability across countries of residence, all consumption of each good by the unilateral representative agent would be allocated to residents of the country having the lowest price of that good. By assumption 5, decision 1b now becomes decision lc, defined as follows:
Decisionlc Choose (m*, x) to maximize U[V(m*), Ĝ(x)]
subject to m*’π + x’p = I.
The following theorem demonstrates that decision 1 c is the decision of a unilateral representative consumer for the economic union:
Theorem 8 Let (m*1,. . ., m*k, xl. . ., xK)solve decision lb, and let m* and x be as defined in assumption 5. By assumptions 1, 2a, and 5, it follows that m* and x will solve decision 1c.
Proof Observe that there is no need to include assumptions 3 or 4 in this theorem, since assumption 5 implies assumptions 3 and 4. The result follows directly from the theorem’s assumptions and the definitions of m* and x.
We thereby are led to the following definition:
Definition 9 By assumptions 1, 2a, and 5, we define a unilateral representative consumer to be an economic agent who solves decision 1c.
Note that a unilateral economic agent recognizes no differences in tastes among countries, either for the owner’s country of residence or for the country within which the asset or good is located or purchased. But in a more fundamental sense, observe that in general, it is impossible to factor out of (m*) or Ĝ(x) the consumption or asset holdings of residents of any country. Hence country-specific separable subfunction, uk or gk, does not exist, and hence separable tastes of residents of a country do not exist. In fact for any solution for (m*, x) to decision lc, the allocation of asset holdings and consumption expenditure to countries is indeterminate. Assumptions 3 and 4 have been omitted from theorem 8, because of redundancy with assumption 5. But assumption 2b, which also has been omitted, is not redundant but rather is omitted since it contradicts assumption 5. The unilateral representative agent exists under much stronger assumptions than the multilateral representative agent. But the unilateral representative agent is not a nested special case of the multilateral representative agent, whether in its general or homogeneous form.14
The multilateral representative-agent model of decision 1 is far more reasonable, requiring only assumptions 1, 2a, and 2b. But we see from theorem 6 that our heterogeneous-agents approach would produce the same results as the multilateral representative-agent theory, if the necessary conditions for existence of a multilateral representative agent were satisfied.
Since interest rates play important roles in policy, it could be useful to compute the interest rate aggregate that is dual to the Divisia monetary quantity index. We show that the correct interest rate aggregate is not the one in common use by central banks, and we view the commonly used interest rate aggregates to be unacceptable. In particular, we provide the correct formula for aggregating interest rates jointly over monetary assets and over countries.
Let rk be the dual aggregate interest rate for country k. It follows from definition 1 and the definition of the vector of component user-cost prices, π*k, that Rk—rk = Π*k where Πt* = n*k(π*k). Hence rk easily can be computed from rk =Rk– Π*k. In discrete time when n*ki= (Rk – rki) + Rk), it follows that (Rk – rk)/(l + Rk) = Π*k, with rk being computed by solving that equation.
After aggregating over countries, the interest rate dual to M* is similarly easy to compute, if the same benchmark rate applies to all countries. In that case, which we believe not likely to be applicable prior to the introduction of a common currency, our heterogeneous-agents approach to aggregating over countries becomes mathematically equivalent to our multilateral representative-agent approach.
Let R = R(t) be the common benchmark rate applying to all countries in the economic union, and let 
= (t) be the interest rate aggregate dual to M*. In continuous time, it follows that R - r = Π*, where Π* = n*(t) =Π* (Π*1,. . ., Π*k). Hence easily can be computed from k=R–Π*. Analogously in discrete time, it follows that (R – k)/(l + R) = Π*, with k being computed by solving that equation.15
Note that our aggregation-theoretic interest rate aggregates are not the interest rate weighted averages often used in this literature.
Use of the stochastic approach to aggregation lends itself naturally to the computation of Divisia second moments, although in the sections above we have provided only the Divisia first moments. In this tradition the “Divisia index” is synonymous with the Divisia growth rate mean. The Divisia growth rate variance could be especially useful for exploring distribution effects of policy within an economic union and progress toward convergence. Some potentially useful Divisia growth rate variances are proposed below. Conversion of the continuous time formulas to their discrete time version is analogous to that available for the within-country Divisia quantity and user-cost growth rate variances in Barnett and Serletis (2000, p. 172, eqs. 4 and 7).
The Divisia growth rate variances could be especially useful when computed about the Divisia means of the following growth rates: (1) the monetary quantity growth rates, d log M and d log M*, in definition 4, (2) the Divisia means of the user-cost price growth rates, d log Π and d log Π*, in definition 5, and (3) the inflation growth rate, d log p*, in equation (C.2) or the inflation growth rate, d log P*, in equation (C.6). Repeating those Divisia mean formulas and producing the analogous Divisia variances, we have the following formulas:
The Divisia growth rate means are in definitions 3, 4, and 5 and equation (C.6). The analogous Divisia growth rate variances are
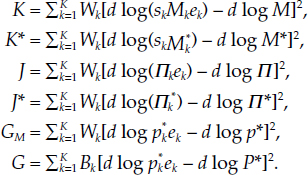
An additional potentially useful Divisia growth rate variance is that of the monetary expenditure share growth rates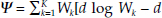 
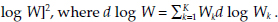
The Divisia monetary services growth rate variances, J and J*, and the Divisia monetary-services expenditure-share growth rate variance, ψ, are measures of the dispersion of monetary service growth rates across countries in nominal and real terms, respectively, while the Divisia inflation rate variances, G and GM, are measures of the dispersion of inflation rates across countries. Increasing values of K, K*, ψ, and G over time are indications of growth in the distribution effects of monetary policy over the countries of the economic union. Decreases in K, K*, ψ and G over time are indications of convergence toward more uniform effects of policy over the economic union. If variations in K, K*, and ψ tend to precede those of G, then there is an implication of causality. The converse could indicate that policy is accommodating other causal factors.
The Divisia growth rate variances, ƒ and ƒ*, are measures of the progress of harmonization of financial markets over countries and hence are less directly connected with monetary policy and more directly connected with structural progress in the unification of money markets over the economic union.
The approach in appendix A applies to Divisia aggregation within countries and then the heterogeneous-countries approach to aggregation over countries. The stochastic approach to aggregation over countries lends itself naturally to computation of Divisia second moments. Computation of Divisia variance growth rates about the Divisia means is advocated across countries. Those Divisia second moments could provide useful information about the distribution effects of policy and about progress toward convergence over an economic union, such as the EMU.
This appendix also defines and produces the theory relevant to a third very restrictive case, called the unilateral representative-agent approach. This approach, which is implied by some early studies of euro area monetary aggregation, may be relevant to aggregation over states or provinces of a single country, but not likely for aggregation over different countries within an economic union.
With the heterogeneous countries or multilateral representative-agent approach, there is the need for two different consumer price indexes: one for use in deflating nominal to real monetary balances after aggregation over countries, and one for deflating nominal to real consumer-goods expenditure. The imputation of either index to both uses would produce a serious specification error. Only under the very restrictive homogeneous multilateral representative-agent assumptions or the even more restrictive unilateral representative-agent assumptions do the growth rates of the two consumer price indexes become equal.
The choice among the nested assumption structures for aggregation must be consistent with the assumptions made in producing the models, within which the data is to be used. In fact attainment of that internal consistency is the primary objective of index number and aggregation theory. Without that coherence among aggregator function structure and the econometric models within which aggregates are embedded, stable structure can appear to become unstable.
1. See, for example, M. M. G. Fase and C. C. A. Winder (1994), Spencer (1997), Wesche (1997), Fase (2000), Beyer, Doornik, and Hendry (2001), Stracca (2001), and Reimers (2002). Two approaches to international aggregation have been proposed and applied by other researchers. One has been called the direct approach and the other the indirect approach. We show that the direct approach implies the existence of our most restrictive, unilateral representative agent, which requires assumptions that we consider to be very strong. The alternative indirect approach uses Divisia aggregation within countries and then ad hoc weighting of those within-country indexes to aggregate over countries. The indirect approach produces a result that is disconnected from theory and does not produce nesting of the multilateral or unilateral representative-agent approaches.
2. This phenomenon has been called the “Barnett critique” by Chrystal and MacDonald (1994) and Belongia and Ireland (2010).
3. See Swofford (2000) and Drake, Mullineux, and Agung (1997).
4. Similarly we assume that prices of consumer goods are converted to units of country k’s currency. Since aggregation over consumer goods is not the primary subject of this appendix, our notation for consumer-goods quantities, expenditures, and prices is less formal than for monetary assets.
5. In most cases below, the adjustment for taxation will have no effect, unless the marginal tax rate is not the same on assets appearing in the numerator and denominator of the shares. See equations (A.5a) and (A.5b) in appendix A. The yield curve adjustment of rates of return of different maturities is acquired by subtracting from the asset’s yield the country’s Treasury security yield of the same maturity and then adding that yield differential onto the Treasury security yield of the chosen holding period. The same holding period should be used for all assets.
6. See the appendix and footnotes 17 and 28 to Barnett (2003), regarding construction of a proxy for the benchmark rate.
7. In discrete time it is necessary to discount to the beginning of the period all interest paid at the end of the period. This requires dividing nominal and real user costs by 1 + Rk. This is the multilateral analogue of equation (A.5) in appendix A.
8. For the new goods introduction procedure, see Anderson, Jones, and Nesmith (1997, pp. 77–78) and footnote 6 in Appendix A of this book.
9. The assumption of finite dimensionality of ?c is only for notational convenience. Without that assumption, ?c could not be written as a vector. A sequence or continuum of taste-determining variables would not alter any of our conclusions, but would complicate the notation.
10. See Gorman (1953).
11. See equation (A.7) in Appendix A. In the finite planning horizon case, the benchmark asset enters utility only in the terminal period to produce a savings motive to endow the next planning horizon.
12. The assumption that the functions do not move over time does not preclude subjective discounting of future utility within the integrand of the intertemporal utility integral.
13. Although perhaps somewhat surprising, the need for two different consumer price indexes is not entirely without precedent. The theory that produces the relative price version of Theil’s (1971, p. 578, eq. 6.19) Rotterdam consumer demand system model also requires two consumer price indexes: the Divisia price index with average share weights to deflate nominal income to real income and the Frisch consumer price index with marginal budget share weights to deflate nominal to real relative prices. But that Rotterdam model phenomenon has a different source.
14. Decision lc is the representative-agent model previously used in some studies to aggregate within the euro area. But the required convergence conditions, assumptions 1, 2a, and 5 and the implied assumptions 3 and 4, are clearly very strong, since they imply decision independence of the country of residence of purchasers and of the country of location of the purchase. Rather than requiring identical tastes of consumers among all countries in the economic union, as in the homogeneous multilateral representative-agent case, the unilateral representative-agent case implies nonexistence of separable tastes or cultures for any country, through irrelevancy of the location of the purchaser or of the purchased good or asset.
15. In the heterogeneous-agents approach, there does not exist a common benchmark rate, which can be imputed to all countries. Under those circumstances, the aggregation theoretic method of producing the interest rate aggregate can be found in Barnett (2000, p. 278, eq. 5).
