Deep neural network–based models are gradually becoming the backbone for artificial intelligence and machine learning implementations. The future of data mining will be governed by the usage of artificial neural network–based advanced modeling techniques. One obvious question is why neural networks are only now gaining so much importance, because it was invented in 1950s.
Borrowed from the computer science domain, neural networks can be defined as a parallel information processing system where all the input relates to each other, like neurons in the human brain, to transmit information so that activities like face recognition, image recognition, and so forth, can be performed. In this chapter, you learn about the application of neural network-based methods on various data mining tasks, such as classification, regression, forecasting, and feature reduction. An artificial neural network (ANN) functions in a way that is similar to the way that the human brain functions, in which billions of neurons link to each other for information processing and insight generation.
Recipe 4-1. Working with Activation Functions
Problem
What are the activation functions and how do they work in real projects? How do you implement an activation function using PyTorch?
Solution
Activation function is a mathematical formula that transforms a vector available in a binary, float, or integer format to another format based on the type of mathematical transformation function. The neurons are present in different layers—input, hidden, and output, which are interconnected through a mathematical function called an activation function. There are different variants of activation functions, which are explained next. Understanding the activation function helps in accurately implementing a neural network model.
How It Works
All the activation functions that are part of a neural network model can be broadly classified as linear functions and nonlinear functions. The PyTorch torch.nn module creates any type of a neural network model. Let’s look at some examples of the deployment of activation functions using PyTorch and the torch.nn module.
The core differences between PyTorch and TensorFlow is the way a computational graph is defined, the way the two frameworks perform calculations, and the amount of flexibility we have in changing the script and introducing other Python-based libraries in it. In TensorFlow, we need to define the variables and placeholders before we initialize the model. We also need to keep track of objects that we need later, and for that we need a placeholder. In TensorFlow, we need to define the model first, and then compile and run; however, in PyTorch, we can define the model as we go—we don’t have to keep placeholders in the code. That’s why the PyTorch framework is dynamic.
Linear Function

Bilinear Function


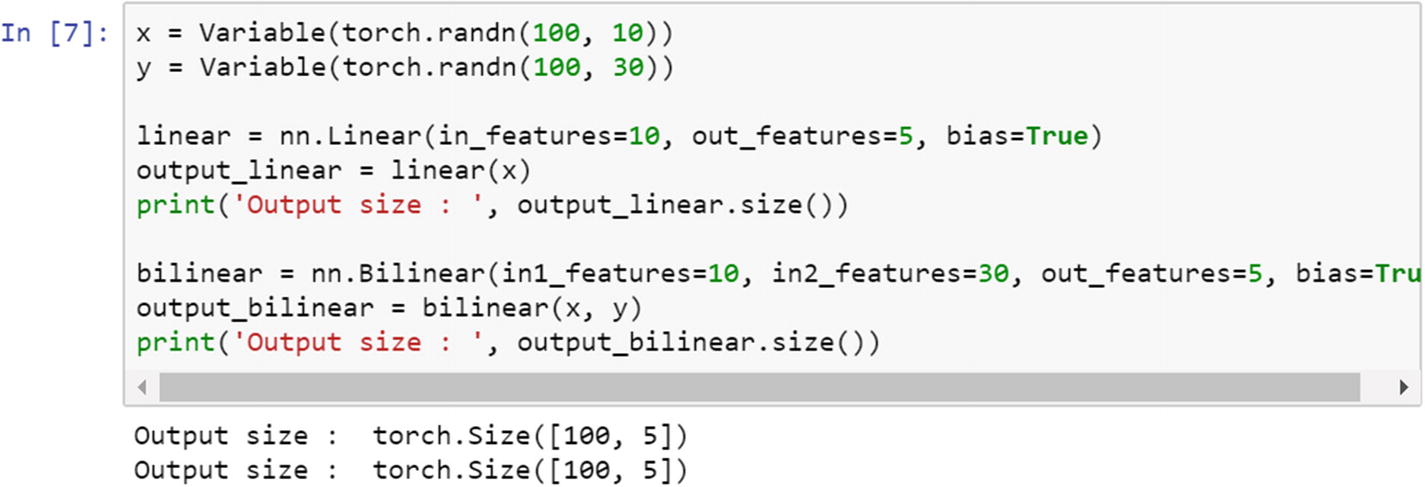
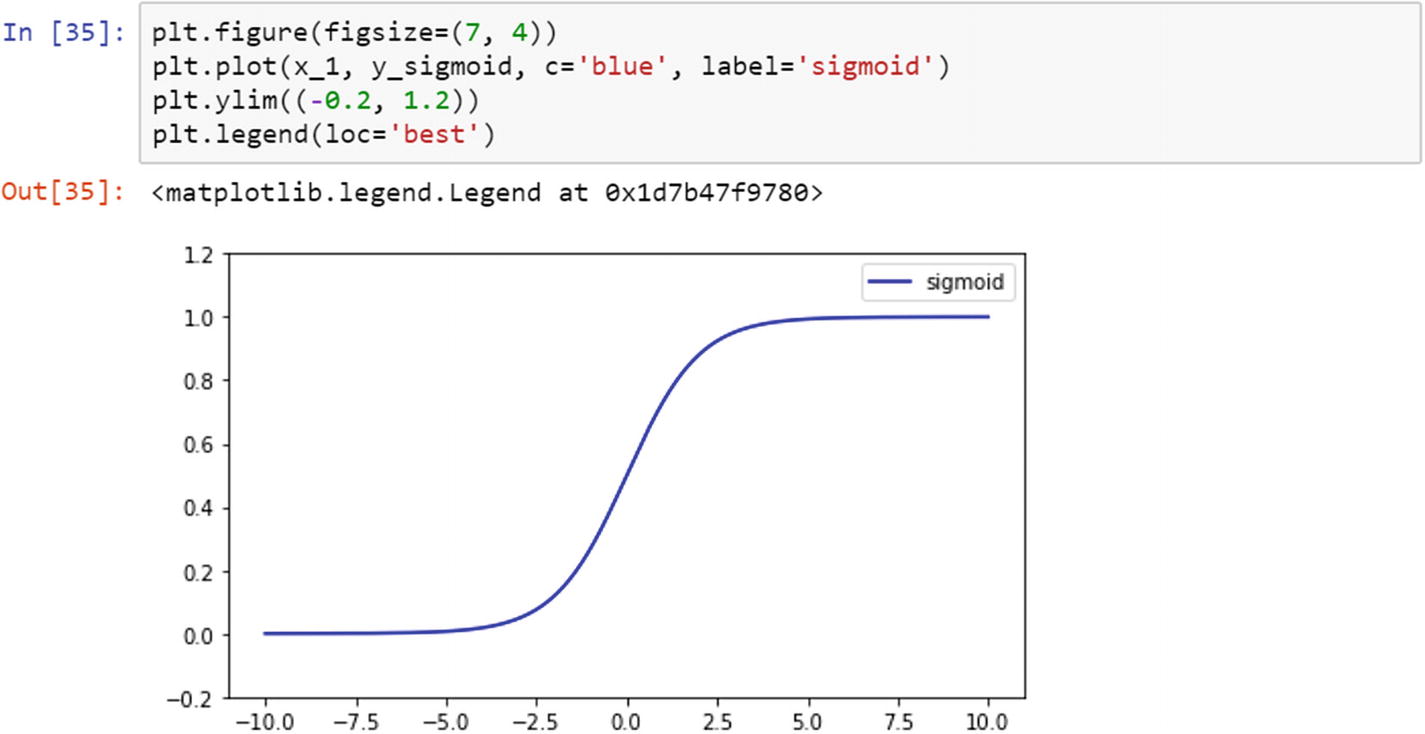
Sigmoid Function
A sigmoid function is frequently used by professionals in data mining and analytics because it is easier to explain and implement. It is a nonlinear function. When we pass weights from the input layer to the hidden layer in a neural network, we want our model to capture all sorts of nonlinearity present in the data; hence, using the sigmoid function in the hidden layers of a neural network is recommended. The nonlinear functions help with generalizing the dataset. It is easier to compute the gradient of a function using a nonlinear function.


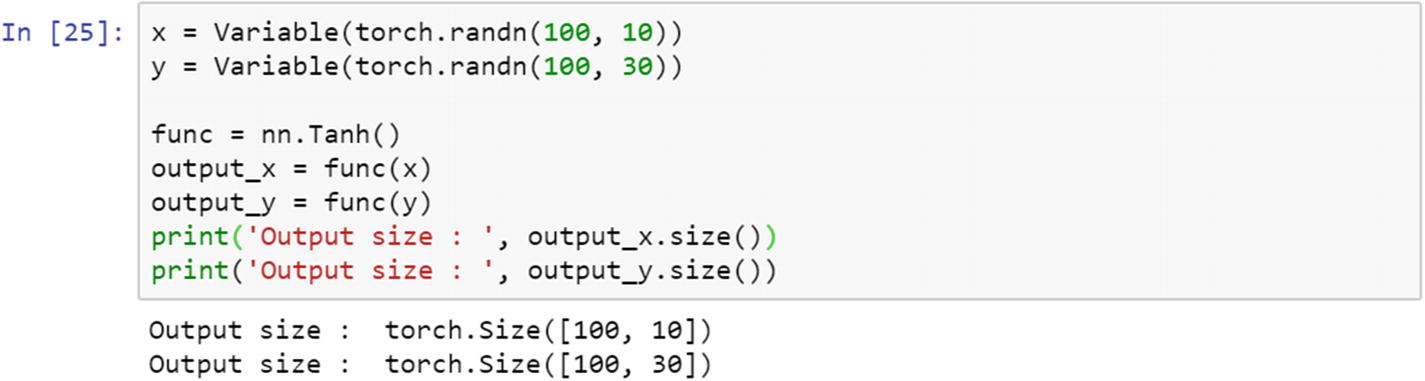
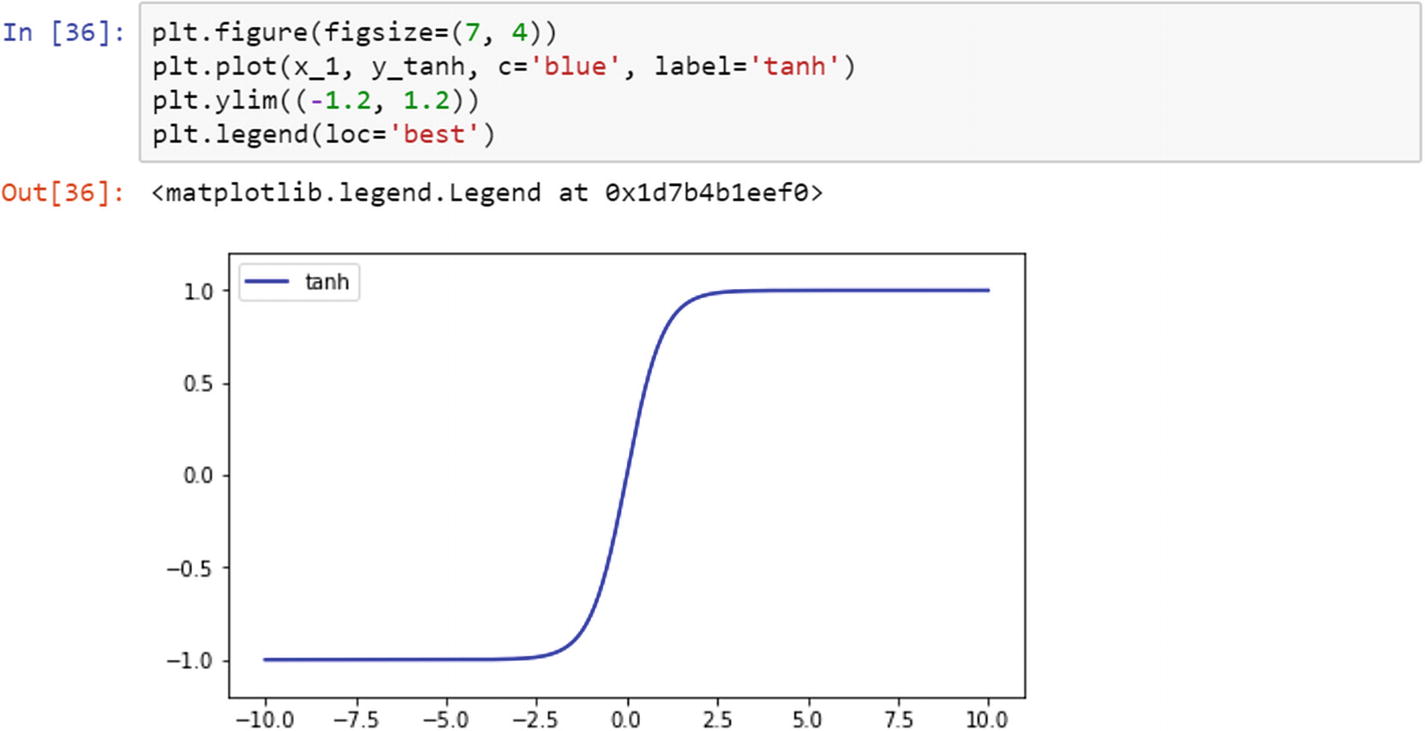
Hyperbolic Tangent Function


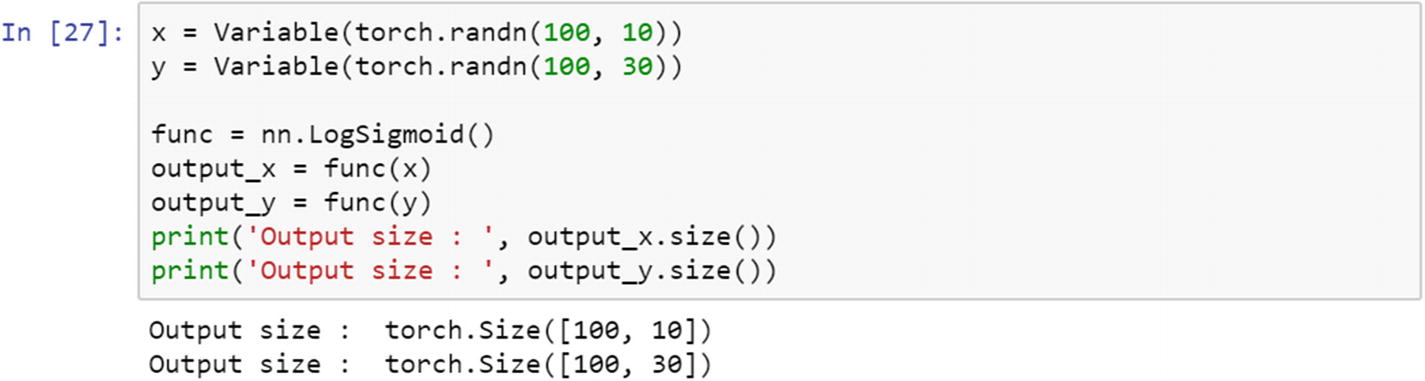
Log Sigmoid Transfer Function
The following formula explains the log sigmoid transfer function, which is used in mapping the input layer to the hidden layer. If the data is not binary, and it is a float type with a lot of outliers (as in large numeric values present in the input feature), then we should use the log sigmoid transfer function.

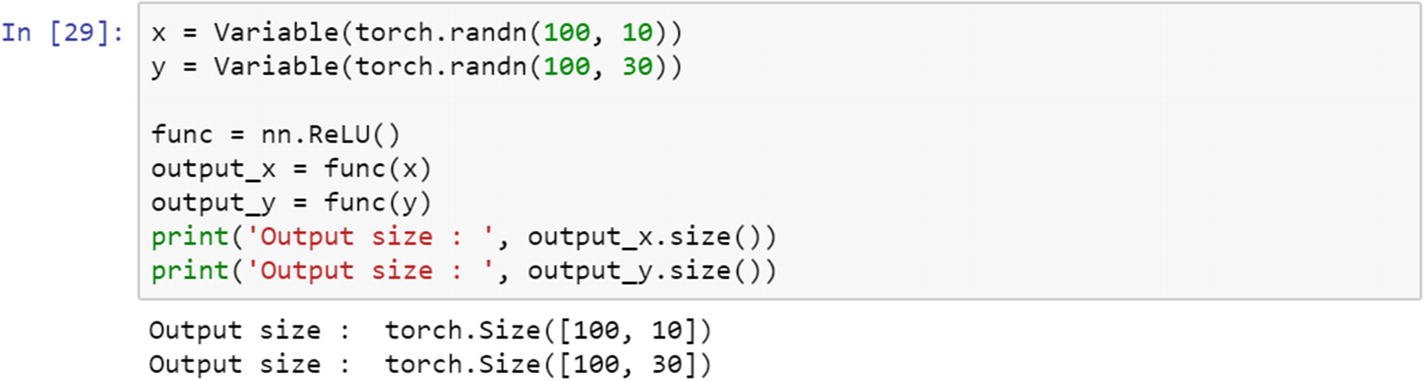
ReLU Function
The rectified linear unit (ReLu) is another activation function. It is used in transferring information from the input layer to the output layer. ReLu is mostly used in a convolutional neural network model. The range in which this activation function operates is from 0 to infinity. It is mostly used between different hidden layers in a neural network model.

The different types of transfer functions are interchangeable in a neural network architecture. They can be used in different stages , such as the input to the hidden layer, the hidden layer to the output layer, and so forth, to improve the model’s accuracy.
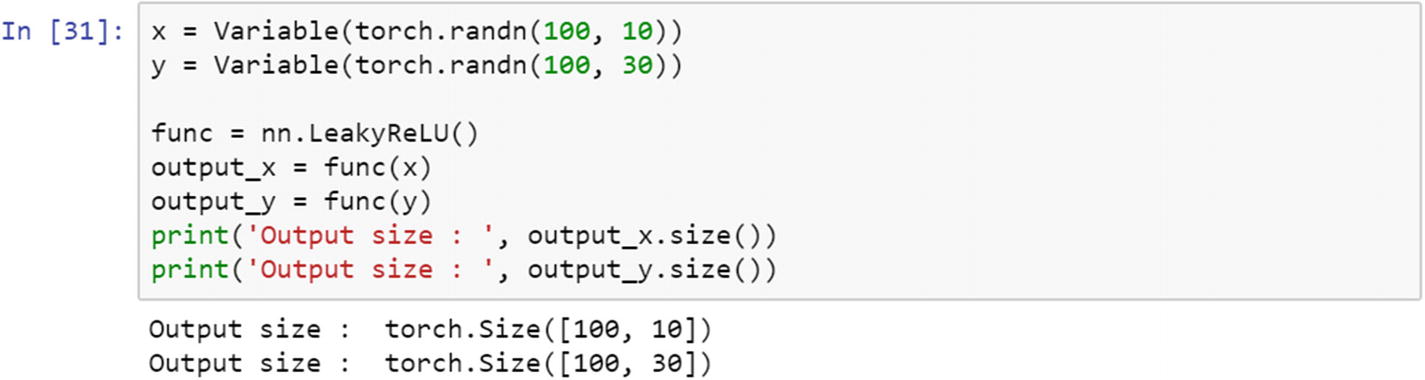
Leaky ReLU
In a standard neural network model, a dying gradient problem is common. To avoid this issue, leaky ReLU is applied. Leaky ReLU allows a small and non-zero gradient when the unit is not active.

Recipe 4-2. Visualizing the Shape of Activation Functions
Problem
How do we visualize the activation functions? The visualization of activation functions is important in correctly building a neural network model.
Solution
The activation functions translate the data from one layer into another layer. The transformed data can be plotted against the actual tensor to visualize the function. We have taken a sample tensor, converted it to a PyTorch variable, applied the function, and stored it as another tensor. Represent the actual tensor and the transformed tensor using matplotlib.
How It Works
The right choice of an activation function will not only provide better accuracy but also help with extracting meaningful information.

In this script, we have an array in the linear space between –10 and +10, and we have 1500 sample points. We converted the vector to a Torch variable, and then made a copy as a NumPy variable for plotting the graph. Then, we calculated the activation functions. The following images show the activation functions.


Recipe 4-3. Basic Neural Network Model
Problem
How do we build a basic neural network model using PyTorch?
Solution
A basic neural network model in PyTorch requires six steps: preparing training data, initializing weights, creating a basic network model, calculating the loss function, selecting the learning rate, and optimizing the loss function with respect to the model’s parameters.
How It Works
Let’s follow a step-by-step approach to create a basic neural network model.

To show a sample neural network model, we prepare the dataset and change the data type to a float tensor. When we work on a project, data preparation for building it is a separate activity. Data preparation should be done in the proper way. In the preceding step, train x and train y are two NumPy vectors. Next, we change the data type to a float tensor because it is necessary for matrix multiplication. The next step is to convert it to variable, because a variable has three properties that help us fine-tune the object. In the dataset, we have 17 data points on one dimension.

The set_weight() function initializes the random weights that the neural network model will use in forward propagation. We need two tensors weights and biases. The build_network() function simply multiplies the weights with input, adds the bias to it, and generates the predicted values. This is a custom function that we built. If we need to implement the same thing in PyTorch, then it is much simpler to use nn.Linear() when we need to use it for linear regression.
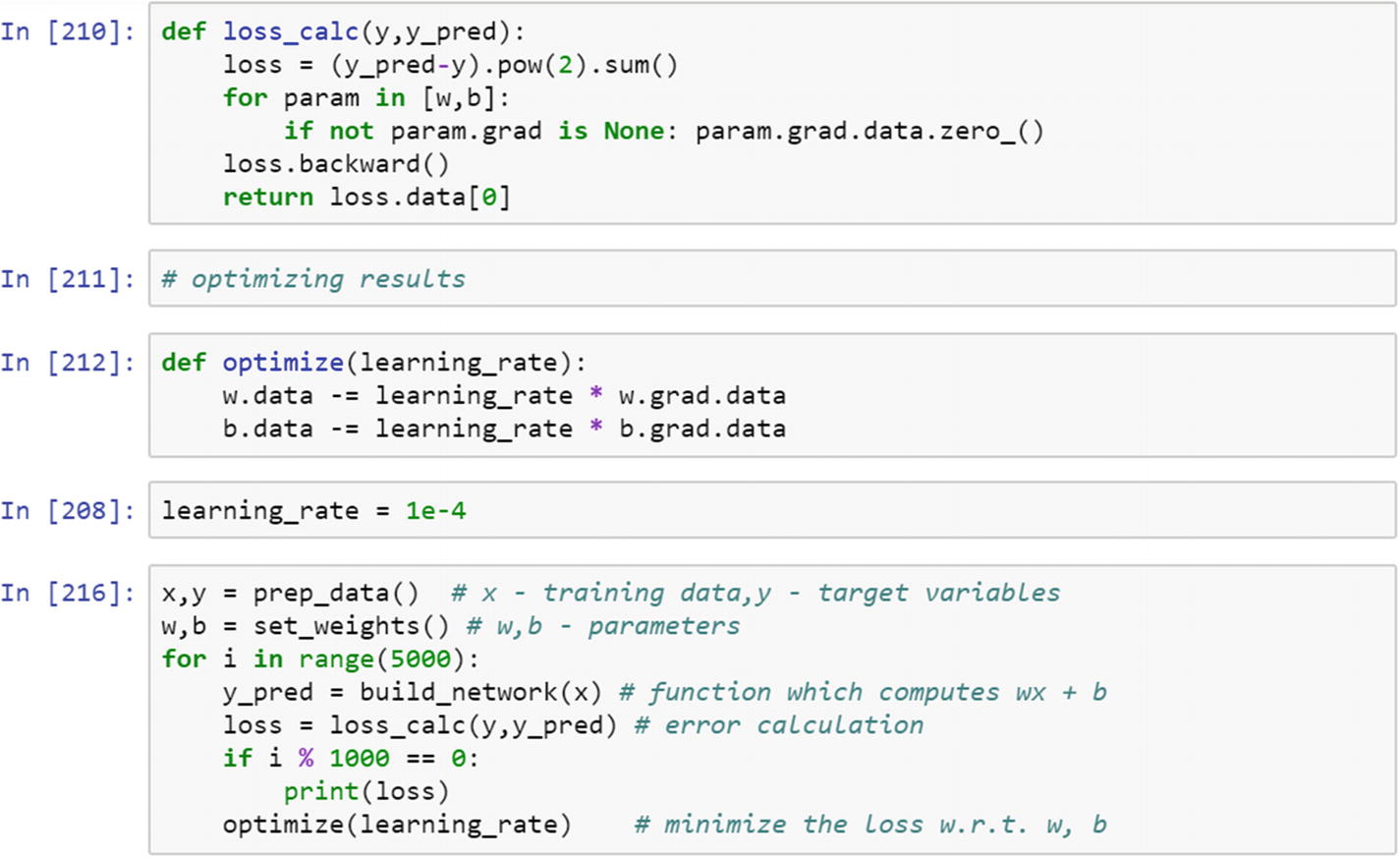
Once we define a network structure, then we need to compare the results with the output to assess the prediction step. The metric that tracks the accuracy of the system is the loss function, which we want to be minimal. The loss function may have a different shape. How do we know exactly where the loss is at a minimum, which corresponds to which iteration is providing the best results? To know this, we need to apply the optimization function on the loss function; it finds the minimum loss value. Then we can extract the parameters corresponding to that iteration.
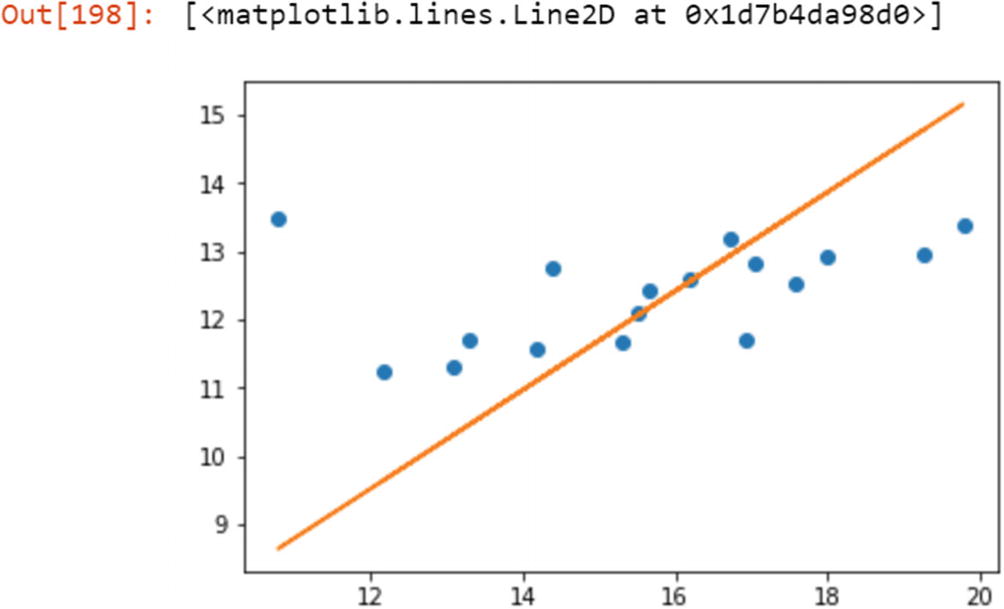
Median, mode and standard deviation computation can be written in the sa
Standard deviation shows the deviation from the measures of central tendency, which indicates the consistency of the data/variable. It shows whether there is enough fluctuation in data or not.
Recipe 4-4. Tensor Differentiation
Problem
What is tensor differentiation, and how is it relevant in computational graph execution using the PyTorch framework?
Solution
The computational graph network is represented by nodes and connected through functions. There are two different kinds of nodes: dependent and independent. Dependent nodes are waiting for results from other nodes to process the input. Independent nodes are connected and are either constants or the results. Tensor differentiation is an efficient method to perform computation in a computational graph environment.
How It Works
In a computational graph, tensor differentiation is very effective because the tensors can be computed as parallel nodes, multiprocess nodes, or multithreading nodes. The major deep learning and neural computation frameworks include this tensor differentiation.
Autograd is the function that helps perform tensor differentiation, which means calculating the gradients or slope of the error function, and backpropagating errors through the neural network to fine-tune the weights and biases. Through the learning rate and iteration, it tries to reduce the error value or loss function.
To apply tensor differentiation, the nn.backward() method needs to be applied. Let’s take an example and see how the error gradients are backpropagated. To update the curve of the loss function, or to find where the shape of the loss function is minimum and in which direction it is moving, a derivative calculation is required. Tensor differentiation is a way to compute the slope of the function in a computational graph.

In this script, the x is a sample tensor , for which automatic gradient calculation needs to happen. The fn is a linear function that is created using the x variable. Using the backward function, we can perform a backpropagation calculation. The .grad() function holds the final output from the tensor differentiation.
Conclusion
This chapter discussed various activation functions and the use of the activation functions in various situations. The method or system to select the best activation function is accuracy driven; the activation function that gives the best results should always be used dynamically in the model. We also created a basic neural network model using small sample tensors, updated the weights using optimization, and generated predictions. In the next chapter, we see more examples.