
In Chapter 4 you learned how Joe Bloggs, our model average student, can help you avoid trap answers on the Critical Reading sections of the SAT. Well, that’s not all he can do. In this chapter you will see that we can learn from Joe on the Math sections of the test too. By keeping in mind what Joe is likely to do on difficult math questions, you can avoid those same mistakes and maximize your math score.
Joe Bloggs has already been a big help to you on the Critical Reading section of the SAT. By learning to anticipate which answer choices would attract Joe on difficult questions, you know how to avoid careless mistakes and eliminate obvious incorrect answers.
You can do the same thing on the SAT Math section. In fact, Joe Bloggs answers are even easier to spot on math questions. ETS is quite predictable in the way it writes incorrect answer choices, and this predictability will make it possible for you to zero in on its answers to questions that might have seemed impossible to you before.
As was true on the SAT Critical Reading section, Joe Bloggs gets the easy questions right and the hard questions wrong. In Chapter 3, we introduced Joe by showing you how he approached a particular math problem. That problem, you may remember, involved the calculation of total miles in a trip. Here it is again:

20. Graham walked to school at an average speed of 3 miles an hour and jogged back along the same route at 5 miles an hour. If his total traveling time was 1 hour, what was the total number of miles in the round trip?
(A) 3
(B) 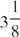
(C) 
(D) 4
(E) 5
When we showed this problem the first time, you were just learning about Joe Bloggs. Now that you’ve made him your invisible partner on the SAT, you ought to know a great deal about how he thinks. Your next step is to put Joe to work for you on the Math sections.
This problem was the last in a 20-question Math section. Therefore, it was the hardest problem in that section. Naturally, Joe got it wrong.
The answer choice most attractive to Joe on this problem is D. The question obviously involves an average of some kind, and 4 is the average of 3 and 5, so Joe picked it. Choice D just seemed like the right answer to Joe. (Of course, it wasn’t the right answer; Joe gets the hard ones wrong.)
Because this is true, we know which answers we should avoid on hard questions: answers that seem obvious or that can be arrived at simply and quickly. If the answer really were obvious and if finding it really were simple, the question would be easy, not hard.
Joe Bloggs is also attracted to answer choices that simply repeat numbers from the problem. This means, of course, that you should avoid such choices. In the problem about Graham’s going to school, you can also eliminate choices A and E, because 3 and 5 are numbers repeated directly from the problem. Therefore, they are extremely unlikely to be ETS’s answer.
We’ve now eliminated three of the five answer choices. Even if you couldn’t figure out anything else about this question, you’d have a fifty-fifty chance of guessing correctly. Those are excellent odds, considering that we really didn’t do any math. By eliminating answer choices that we knew were wrong, we were able to beat ETS at its own game. (ETS’s answer to this question is C, by the way.)

Generally speaking, the Joe Bloggs principle teaches you to
The rest of this chapter is devoted to using Joe Bloggs to zero in on ETS’s answers to difficult questions. Of course, your main concern is still to answer all easy and medium questions correctly. But if you have some time left at the end of a Math section, the Joe Bloggs principle can help you eliminate answers on a few difficult questions, so that you can venture some good guesses. And as we’ve already seen, smart guessing means more points. (In Chapter 15, you’ll learn how he can help you with grid-ins.)
Let’s take a look at some common situations you will come across on the SAT and find out how best to handle them.
As we’ve just explained, hard questions on the SAT simply don’t have correct answers that are obvious to the average person. Avoiding the “obvious” choices will take some discipline on your part, but you’ll lose points if you don’t. Even if you’re a math whiz, the Joe Bloggs principle will keep you from making careless mistakes.
Here’s an example:

18. A 50-foot wire runs from the roof of a building to the top of a 10-foot pole 14 feet across the street. How much taller would the pole have to be if the street were 16 feet wider and the wire remained the same length?
(A) 2 feet
(B) 8 feet
(C) 14 feet
(D) 16 feet
(E) 18 feet
Here’s How to Crack It
Which answer seems simple and obvious? Well, if the wire stays the same length, and the street is 16 feet wider, then it seems obvious that the pole would have to be 16 feet higher.
What does that mean? It means that we can eliminate choice D. If 16 feet were the correct answer, then Joe Bloggs would get this problem right and it would be an easy question, not one of the hardest in the section.
Choice C repeats a number from the problem, which means we can be certain that it’s wrong too.
If you don’t know how to do this problem, working on it further probably won’t get you anywhere. You’ve eliminated two choices; guess if you need the question to reach your pacing goal and then move on. (ETS’s answer is B. Use the Pythagorean theorem—see Chapter 14.)

Joe Bloggs doesn’t usually think of difficult mathematical operations, so he is attracted to solutions that use very simple arithmetic. Therefore, any answer choice that is the result of simple arithmetic should be eliminated on hard SAT math questions.
Here’s an example:

17. A dress is selling for $100 after a 20 percent discount. What was the original selling price?
(A) $200
(B) $125
(C) $120
(D) $80
(E) $75
Here’s How to Crack It
When Joe Bloggs looks at this problem, he sees “20 percent less than $100” and is attracted to choice D. Therefore, you must eliminate it. If finding the answer were that easy, Joe Bloggs would have gotten it right. Joe is also attracted to choice C, which is 20 percent more than $100. Again, eliminate.
With two Joe Bloggs answers out of the way, you ought to be able to solve this problem quickly. The dress is on sale, which means that its original price must have been more than its current price. That means that ETS’s answer has to be greater than $100. Two of the remaining choices, A and B, fulfill this requirement. Now you can ask yourself these questions:
(A) Is $100 20 percent less than $200? No. Eliminate.
(B) Is $100 20 percent less than $125? Could be. This must be ETS’s answer. (It is.)


16. The length of each side of a cube is doubled to create a second cube. The volume of the second cube will be how many times the area of the original cube?
(A) 2
(B) 4
(C) 8
(D) 16
(E) 64
Here’s How to Crack It
The problems asks for how much larger the volume of the new cube is than the original. What’s the Joe Bloggs answer here? Since each side doubled, Joe Bloggs would guess that the volume doubles as well. That’s too easy for a difficult question such as this one. Eliminate A.
You may have also noticed that you can eliminate E, 64, because it is too large.
The problem never gives you an actual cube, right? In that case, you can always make one up. This is a Hidden Plug In question, which we’ll talk more about later. Say that each side of the cube is 3. That makes the current volume 3 × 3 × 3 = 27. The second cube has sides which are twice as long, so each side is 3 × 2 = 6. The volume of the second cube is therefore 6 × 6 × 6 = 216. Now, go back and reread the question. Since the questions asks how many times larger the second cube is than the first, divide 216 by 27, to find that the second cube is 8 times larger than the first one, and the answer is C.

Occasionally on the Math section, the fifth answer choice on a problem will be
(E) It cannot be determined from the information given.
The Joe Bloggs principle makes these questions easy to crack. Why? Joe Bloggs can never determine the correct answer on difficult SAT problems. Therefore, when Joe sees this answer choice on a difficult problem, he is greatly attracted to it.
It means that if “it cannot be determined” is offered as an answer choice on a difficult problem, it is usually wrong.
Here’s an example:

19. If the average of x, y, and 80 is 6 more than the average of y, z, and 80, what is the value of x – z ?
(A) 2
(B) 3
(C) 6
(D) 18
(E) It cannot be determined from the information given.
Here’s How to Crack It
This problem is the next-to-last question in a section. It looks absolutely impossible to Joe. Therefore, he assumes that the problem must be impossible to solve. Of course, he’s wrong. Eliminate choice E. If E were ETS’s answer, Joe would be correct and this would be an easy problem.
Choice C simply repeats a number from the problem, so you can eliminate that choice also. Because you already eliminated two answer choices, the odds are in your favor if you need to guess.
ETS’s answer is D. Don’t worry about how to solve this problem right now. It’s only important that you understand how to eliminate Joe Bloggs answers to get closer to ETS’s answer. If you have to guess, that’s okay. Besides, that was a hard question; you should be concentrating on answering all the easy and medium questions correctly.
