
1. ábra, A gőzgép őse, az „áolipil”
Dr. Fülöp Zsigmond
GONDOLAT KIADÓ 1958
Előszót írta és a szerkesztésben közreműködött
ZEMPLÉN JOLÁN
Szakmailag ellenőrizték:
ELEK ÉVA
KUTASNÉ PÉTER ÁGNES
ZEMPLÉN JOLÁN
ÖVEGES JÓZSEF
TARTALOM
A kísérletezés szerepe a természettudományok történetében
MÉRFÖLDKÖVEK A FIZIKA ÚTJÁN
1. Néhány elvetélt kísérlet az ókorban
2. A kísérleti kutatás megindulása a reneszánsz korában: Gilbert tanulmányozza a mágneses erő természetét
3. Galilei megalapozza a kísérleti fizikát
4. Archimedes újra felfedezője: Simon Stevin
5. A Kísérleti Akadémia és a légnyomás problémája
6. Otto Guericke, a kísérletező magdeburgi polgármester
7. A Boyle—Mariotte-törvény
8. Kísérletek a gőz feszítőerejével: Papin
9. Newton felfedezi a színszórást
10. Franklin felfedezi a légköri elektromosságot
11. További elektromos kutatások a XVIII. században: Coulomb
12. Galvani felfedezi az érintkezési villamosságot
13. Volta, az elektromos áram felfedezője
MÉRFÖLDKÖVEK A VEGYTAN ÚTJÁN
1. Az első nagy kísérletező a vegytan terén
2. Mayow és a tűzlevegő
3. Boerhave kísérletei megcáfolják az alkimisták néhány tévedését
4. A porcelángyártás felfedezése
5. Priestley végre felfedezi az oxigént
6. Az oxigén másik felfedezője: Scheele
7. Lavoisier megalapítja a tudományos kémiát
MÉRFÖLDKÖVEK A BIOLÓGIA ÚTJÁN
1. Az első élettani kísérlet sikere és kudarca
2. A parányi élőlények eredete
3. Folytatódik a vita az ősnemzésről
4. Egy Newton-tanítvány növényélettani kísérletei
5. Réaumur nemcsak a hőmérőt osztja be
6. Aki apróra vagdalt alsórendű állatokat
7. Ingenliousz felfedezi a növények gázcseréjét
8. Saussure folytatja Ingenhousz munkáját
9. Tisztázódik a növények megtermékenyítési módja
A KÍSÉRLETEZÉS SZEREPE A TERMÉSZETTUDOMÁNYOK TÖRTÉNETÉBEN
Az emberiség ismert történetének, sőt a tudomány történetének évezredeihez képest a modern természettudomány aránylag rövid, legjobb esetben mintegy négyszáz esztendős múltra tekinthet csak vissza. Míg a képzőművészetek, irodalom, filozófia éppúgy virágoztak a legrégibb keleti kultúrnépeknél, mint a régi görögöknél és rómaiaknál, addig modern értelemben vett természettudományos kutatásról csak a reneszánsz óta beszélhetünk. Ennek oka elsősorban az, hogy a modern természettudományt csak a középkori feudalizmus és az egyház uralma alól fokozatosan felszabaduló polgári osztály hozta létre. A polgárságnak ugyan csak a XVIII. sz. végén, a francia forradalom győzelme után sikerült politikailag is véglegesen hatalomra jutni, de a harc lényegében már a középkor végén elkezdődik, amikor a városi élet kialakulása, a kereskedelem és ipar fejlődése és a pénzgazdálkodás előtérbekerülése során a polgárság kezébe egyre nagyobb gazdasági erő összpontosul. A megváltozott gazdasági módszerekhez már szükség van fejlett természettudományra, fizikára, kémiára, de ezeknek fejlődését gátolja a középkor merev, a természettudománynak nem kedvező felfogása: a skolasztikus filozófia, amely egyedül a teológiát ismeri el tudománynak, minden egyéb, így a filozófia is, amelynek a fizika, kémia, biológia egyelőre csupán egy-egy fejezete, a teológia szolgálatára van rendelve.
A küzdelem tehát nemcsak gazdasági és társadalmi, hanem ideológiai téren is folyik: felszabadítani először a filozófiát a teológia gyámsága alól és kiszabadítani, önálló, a filozófiától független tudományokká tenni az egyes szaktudományokat.
Ennek az ideológiai harcnak az első része tehát még a filozófia síkján zajlik le: a reneszánsz haladó természetfilozófusai élükön Francis Bacon-nel ezt a célkitűzést igyekeznek megvalósítani: ne a tekintély szava legyen a döntő tudományos kérdésekben, mint volt az egész középkoron át, amikor az egyház mellett Aristotelesnek, a legnagyobb görög filozófusnak a nézete volt kizárólag az irányadó, hanem az igazság. Az igazság felismerésének kérdésében pedig elsősorban magát a természetet kell tanulmányozni.
Ez a program azután felvetette a legfontosabb kérdést, a módszer kérdését. Már a XIII. században akadt olyan gondolkodó — Roger Bacon —, aki sürgette a természettudományok módszerének és célkitűzéseinek gyökeres megváltoztatását, azt, hogy a természet kutatásának alapja ne a tekintély, hanem a tapasztalat legyen, célja pedig nemcsak a természet megismerése, hanem a természetnek, a természet erőinek az ember jobb boldogulása érdekében való felhasználása.
Ma sem fogalmazhatnánk meg világosabban a természettudomány célkitűzését, de még hosszú időnek kellett eltelnie, míg Roger Bacon programjából valóság lett. A programot utána az említett haladó filozófusok a XV. és XVI. században átvették, kibővítették, de még mindig hiányzott a programnak tényleges és általános alkalmazása. Ez a fordulat lényegében csak a XVII. században történt meg, amikor Galilei nemcsak kidolgozta az egész módszert, hanem a gyakorlatban is megmutatta milyen eredményeket lehet annak alkalmazásával elérni. A fizikának, mint önálló tudománynak a megszületése azután maga után vonta a többi természettudománynak, kémiának, biológiának stb. önálló tudomány rangjára való emelkedését.
Engels nyomán Kopernikus fellépésétől, illetve Kopernikus művének megjelenésétől, 1543-tól szoktuk számítani az újkori természettudomány megszületését. Kopernikus műve valóban az első döntő lépés volt abban az irányban, hogy a tudomány felszabaduljon a teológia uralma alól, de hatása tulajdonképpen csak a következő században mutatkozott meg igazán: éppen Galilei csillagászati felfedezései állították a kopernikusi világrendszert az érdeklődés középpontjába. Másrészt mint csillagászati mű — természetesen — megfigyelésekre támaszkodott, de a tárgy természetéből következőleg nem tartalmazhatta az új természettudományos módszer másik alapvető tényezőjét, a kísérletet. Ha voltak is Galileinek — mint látni fogjuk — elődei ezen a téren, joggal nevezhetjük őt a kísérleti fizika és így a kísérleti természettudomány igazi megteremtőjének mind a módszer kidolgozását, mind eredményeinek tartalmát tekintve.
A vázlatosan érintett okok következtében tehát néhány ezer évig eltartott, míg eljöhetett az első kutató, aki felismerte a természettudományok egyedüli helyes módszerét. Hogy ez a módszer milyen eredményes volt, azt mutatja az a fejlődés, amelyet az utolsó három és fél század alatt elértünk a tudományban éppúgy, mint a technikában.
Most nézzük kissé közelebbről ezt a döntő szerepet játszó módszert. A legalapvetőbb különbség a régi, skolasztikus felfogás és az új felfogás között elsősorban ott volt, hogy míg az elsőnél bizonyos előre lefektetett alapelvekből kiindulva, spekulatív úton akartak eljutni helyes tételekhez, de úgy, hogy maguk az alapelvek sem támaszkodtak általában a tapasztalatra, addig az új felfogás szerint mindenféle megismerés első és legfontosabb kiindulási pontja a tapasztalat.
Hogyan teszünk szert tapasztalatra? Elsősorban megfigyelés útján. Ez annyira természetesnek hangzik, hogy még az eddig elmondottak után is meglepő, hogy egyáltalában vita tárgya lehetett. Valóban, Aristoteles és követői sem becsülték le teljesen a tapasztalat szerepét, sőt Aristoteles hangoztatja is, hogy vitás esetekben a tapasztalatnak kell döntenie, csak egyrészt nem biztosította a tapasztalat elsőbbségét, másrészt a középkorban meggyökeresedett tekintélytisztelet lehetővé tette, hogy évszázadokon keresztül helyesnek fogadják el ellenőrzés nélkül az esetleges téves megfigyeléseket, illetve az ezekből levont téves következtetéseket. Ilyen volt például a szabadesés kérdése is. A felületes szemlélet valóban azt mutatja, hogy a különböző súlyú testek nem egyforma sebességgel esnek. Ha egyszerre ejtünk le egy tollat és egy ólomgolyót, nem egyszerre érnek a földre. Tehát, vonta le a következtetést Aristoteles, a szabadon eső testek sebessége a súlytól függ. És erre építette fel egész mechanikáját. Vagy: a fémek elégetésénél súlyuk megnövekedik. Csak a XVIII. században gondoltak rá, hogy ugyanakkor a levegő mennyisége ugyanannyival csökken. Aristoteles szerint például a vérkeringés középpontja az agy, és csak a XVI. században fedezte fel Harvey, boncolással, hogy ez nem igaz.
És itt következik a másik döntő módszertani mozzanat: a tények puszta — bármily pontos — megfigyelése még nem vezet el szükségképpen a jelenség helyes ismeretéhez. A természet nem nyújtja mindig készen a megfigyelendő jelenségeket. Ha az elektromosságot csak a villámlásban tanulmányozhatjuk, korlátozva vagyunk azokra az időpontokra, amikor zivatar van. Ha a növények életét csak a természetben vizsgáljuk, esetleg évekig kell várni, míg a feltételek megváltoznak. A másik nehézség a puszta megfigyelések esetében, hogy egy-egy jelenség a természetben szinte kizárólag összetetten, más jelenségekkel együtt fordul elő, tehát lehetetlen csupán néhány tényező összefüggését vizsgálni. Ezért van szükség arra, hogy a természeti jelenséget magunk állítsuk elő, azaz kísérletezzünk.
A kísérleteknél a megfigyelni szándékozott jelenséget a természettudós maga állítja elő, mégpedig oly módon, hogy minden zavaró vagy pillanatnyi célja szempontjából felesleges tényezőt kiküszöböl, és hogy az adott kísérleti feltételeket tetszése szerint változtathassa, illetve állandóan tarthassa. Ha például azt akarja megállapítani, hogy milyen összefüggés van egy gáz nyomása és térfogata között, kísérletei során ügyelnie kell arra, hogy megfigyelés közben a hőmérséklet ne változzon, mert az észlelt térfogat vagy nyomásváltozás minden hőmérsékleten más és más lesz (Boyle—Mariotte-törvény). Ha ezzel szemben éppen azt akarja megfigyelni, miképpen változik a gáz térfogata, ha a hőmérséklet változik, arra kell ügyelnie, hogy a nyomás maradjon állandó (Gay-Lussac első törvénye). A kémikusnak, ha pontos adatokhoz akar jutni, a fémek elmeszesítését (oxidálását) zárt edényben kell végeznie, amint azt Lomonoszov és Lavoisier tették, mert különben nem tudja ellenőrizni, milyen szerepe van itt a levegőnek. A biológusnak sok megfigyelést kell végeznie az élő természetben, mert az élő világ jelenségei még bonyolultabbak, mint a fizikai vagy kémiai folyamatok, és szinte végtelen sok különböző tényező egymásra hatásából jönnek létre. Egy-egy fontos probléma tehát csak kísérlettel dönthető el, mert így megvalósítható, hogy pl. a növények életében csak a víz, vagy csak a napfény szerepét vizsgáljuk.
Az eredményes kísérletezéshez tehát nagy gondosság, ügyesség, körültekintés és türelem szükséges. Egyetlen kísérletből általában nem lehet és nem szabad általános következtetést levonni, a kísérletet nagyon sokszor meg kell ismételni azonos és módosított feltételek között, míg eredményét helyesnek lehet elfogadni. De még ez sem elegendő. Nem elég megállapítani, hogy pl. a gáz nyomása a térfogattal úgy változik, hogy ha növeljük a nyomását, a térfogata csökken. Vagy a zárt térben égő gyertya csökkenti a levegő térfogatát. Az első lépés természetesen mindig egy tájékozódó, kvalitatív (minőségi) megállapítás. A következőkben azonban már arra keressük a feleletet, milyen pontos kvantitatív (mennyiségi) összefüggés áll fenn a két (vagy több) mennyiség között. Azaz, ha kétszeresére növelem a nyomást, hányszorosára csökken a térfogat? A levegőnek hányad része használódik el az égéssel? Sok mérés elvégzése után azután megállapítható a mennyiségi (rendszerint matematikai alakban is kifejezhető) összefüggés: a gáz nyomása állandó hőmérsékleten a gáz térfogatával fordított arányban változik. Ezt már felírhatom arányosság vagy matematikai egyenlet alakjában, és az így nyert összefüggés neve természeti törvény, minden természettudományos kutatás végcélja.
Nem jelenti ez természetesen azt, hogy az egyes természettudományoknak ne lenne több vagy kevesebb leíró része. Ebből a szempontból a leg„egzaktabb” tudomány a fizika, ahol lehetőleg csak mérhető, számokkal kifejezhető fogalmakkal dolgozunk. A kémia is a történeti fejlődés során egyre inkább egzakt tudománnyá vált: ma már minden kémiai folyamatban a szereplő anyag pontos mennyiségét meg lehet és meg kell adni, bár az egyes anyagok ismertetésénél szükségképpen vannak leíró, kvalitatív részek: az egyes anyagok íze, szaga, színe stb., de már például a keménységet szintén számadatokkal lehet jellemezni. A biológia, természeténél fogva — éppúgy mint az élettelen világ anyagaival foglalkozó ásványtan — szükségképpen nagymennyiségű leíró részt tartalmaz: az egyes növény- és állatfajok pontos ismertetését, rendszerezését stb., szükség van igen nagyszámú, sokszor csak kvalitatíve végezhető kísérletekre is, de a biológus sem nélkülözheti az egzakt méréseket.
A természettudósnak tehát általában nemcsak kísérleteznie kell, hanem mérnie is. A fizikus és kémikus számára elsősorban azok a fogalmak használhatók, amelyek számszerűen kifejezhetők, mérhetők. Csak így tudja a megtalált természeti törvényben kísérlete tényezőit matematikai alakba önteni, és ezzel a meglelt oksági összefüggést kifejezni. A mérés, mint követelmény további igényeket jelent: szükség van mértékegységekre és pontosan működő, megbízható mérőeszközökre. A fent tárgyalt Boyle—Mariotte-kísérletnél, ahol arányosságokat mérünk, még aránylag egyszerű a dolog, mert a kiinduló térfogat és nyomás tetszés szerinti lehet. Általában ez azonban nem így van.
A fizikai jelenségek térben és időben folynak le, és mindig testeken, anyagokon játszódnak le. Ezért a fizikus elsősorban három alapvető mennyiségnek a mértékegységét határozza meg önkényesen: a hosszúságét (evvel tájékozódik a háromméretű térben), az időét és a tömegét, a szóban forgó test anyagmennyiségének a mérésére. Ma az általánosan elfogadott három fizikai alapegység a centiméter, a secundum és a gramm. Minden fizikus ezeket használja, és a világ bármely táján élő fizikusok ezek segítségével meg tudják magukat értetni egymással. A többi fizikai mennyiség mértékegységét közvetlenül vagy közvetve szintén ezek adják. A térfogatot és a felületet a hosszegységgel, a sebességet a hosszegységgel és az idővel stb. fejezzük ki. Természetesen a kémikusnak vagy biológusnak is szüksége van ezekre a mértékegységekre, pontos hosszúság, tömeg, idő, térfogat stb. mérésére, de az egységes és következetesen felépített mértékrendszer a fizikus számára a legfontosabb.
Ne gondoljuk azonban, hogy ez az egységes mérték-rendszer túlságosan régi keletű. A hosszegység számára a métert, a tömegegység számára a kg-ot, amelyeket nemzetközileg is elfogadtak, csupán a francia forradalom idején állapították meg. Addig például a hosszegység vagy a súlyegység nemcsak országonként, hanem városonként változott. Nem volt jobb a helyzet az időegység terén sem. Bár a nap, óra, perc, másodperc több ezeréves egységek, nem lévén pontos időmérő eszközök, rendszerint valamilyen önkényesen választott időegységet kellett használni.
Ez veti fel a másik, említett követelményt: a pontos, megbízható mérőeszközöket. Nemcsak megbízható órák nem voltak még a XVII. és XVIII. században, de nem rendelkeztek precíziós hosszmérő műszerekkel vagy érzékeny mérleggel sem. Nem is beszélve a hőmérőről, barométerről, elektrométerről stb. A kísérletezés úttörőinek nemcsak az egyes tudományok alaptörvényeit kellett kísérletezéssel megállapítani, de meg kellett teremteniük éppen a felsorolt mérőeszközöket is, hogy egyre pontosabb méréseket végezhessenek, olyan korban, amikor a technika még gyermekcipőben járt kezdetleges volt az üvegcsiszolás éppúgy, mint hajszálfinom rugók vagy mutatók készítése. Hiszen ennek a technikának az alapjait is lényegében ők vetették meg.
Még egy további nehézség: ha a kísérlet sikerült, ha sikerült a rendelkezésre álló kezdetleges mérőeszközökkel a mennyiségi kapcsolatot is megtalálni, nehézséget okozott az elért eredménynek a kifejezése, szavakba öntése is. Hiszen új fogalmakkal dolgoztak, ezek számára nekik kellett a megfelelő kifejezést megtalálniuk. És bizony sokszor előfordult, hogy a különböző kutatók ugyanazt a dolgot többféleképpen fejezték ki, vagy két különböző fogalomnak ugyanazt a nevet adták. Jóformán csak a XIX. század végén mondhatjuk el, hogy megszületett az egységes fizikai mértékrendszer és az egyes szaktudományok terminológiája (szakkifejezései). Látni fogjuk például, hogy az oxigént hány különböző elnevezéssel illették (deflogisztizált levegő, tűzlevegő, jó levegő stb.), míg azután az oxigén kifejezést egységesen elfogadták.
Az eddig mondottakat összefoglalva: a kísérletezés úttörőinek nem csekély nehézségekkel kellett megküzdeniük, hiszen úgyszólván a semmiből kellett felépíteniük a természettudomány új világát. Ideológiailag ellenséges környezetben, állandó harcban a meggyökeresedett előítéletekkel, a legkezdetlegesebb kísérleti feltételek között: megfelelő műszerek, mértékegységek és terminológia nélkül. És mégis: sikerrel jártak. Az ilyen körülmények között megtalált természeti törvények: a szabadesés törvényei, a színszórás törvénye, Boyle—Mariotte-törvény, a Coulomb-törvény, az anyag megmaradásának elve, a növények anyagcseréjének megismerése stb. ma is érvényes, helyes törvények. Az általuk feltalált és ma már tökéletesített és egyre tökéletesedő eszközök: az ingaóra, a hőmérő, a barométer, a villamozó gép, a galvánelem, az elektrométer a legérzékenyebb mérlegek stb., mindmegannyi fontos műszere a modern kutatásnak is. Alkotásaik jelentősége azonban még ennél is nagyobb. Mert igaz, hogy a természettudományos kutatás egyetlen helyes kiindulópontja a tapasztalat, a kísérlet, de a kísérlet eredményeinek értékelése, egybefoglalása és az ezeken alapuló újabb, messzebbre mutató kísérletek kigondolása már elméleti éleslátást, matematikai tudást is követel. Galilei és társai ezen a téren is megállták a helyüket és megmutatták a továbbhaladás útját utódaiknak is. Sőt, ha nem is jutott el mindegyikük odáig, sokan megtették a következő lépést is: az eredményeknek az ember céljaira való alkalmazását. Papint például már közvetlenül ez a cél vezette, Franklin a légköri elektromosságra vonatkozó kutatásait azonnal hasznosította a gyakorlatban, Böttger — miután éveket töltött hiú ábrándok kergetésében — tudatosan alkalmazta tapasztalatait egy olyan gyakorlatilag fontos anyagnak, mint a porcelánnak előállítására. Ugyanakkor azonban a Papin kezdetleges gőzgépével vagy a Franklin villámhárítójával szerzett tapasztalatok tovább ösztönözték a tudományos kutatást is. A természettudomány első két századának a kiemelkedő alakjai tehát olyan példát mutattak elmélet és gyakorlat elválaszthatatlanul összefonódó egységére, hogy a ma tudósa egyre tökéletesebben felszerelt laboratóriumában, precíziós műszerek tömegével ellátva, az előző századok minden jelentős ismeretének birtokában is mint követendő mintaképekre tekinthet fel rájuk.
MÉRFÖLDKÖVEK A FIZIKA ÚTJÁN
I. NÉHÁNY ELVETÉLT KÍSÉRLET AZ ÓKORBAN
Akármennyire nem volt is tisztában az ókori tudomány a kísérletezés jelentőségével, mégis végeztek néhány kísérletet, hiszen az igazi fizikát szinte nem is lehet művelni enélkül. Persze ezek az első kísérletek nem is lehettek mások, mint kezdetleges próbálkozások.
Íme Aristoteles-nek egyik fizikai kísérlete: megmért egy állati hólyagot, mégpedig először üresen, kinyomva, másodszor felfújt állapotban. Hogy mi volt a mérés módja, azt nem tudjuk, de eléggé finom lehetett, ha úgy találta, hogy felfújt állapotban a hólyag nehezebb. Aristoteles úgy vélte, hogy ekként a levegő súlyát mérte meg. Sokkal érdekesebb ennél az a kérdés, amit ezzel kapcsolatban fölvet: hogy van az, hogy a kinyomott hólyag alásüllyed a vízben, de a fölfújt hólyag nem süllyed le, pedig nehezebbnek kell lennie, hiszen most levegő van benne. Nem találta meg a feleletet a kérdésre, mert még nem ismerte a fajsúly fogalmát.
Archimedes (i. e. 287—212) volt az ókor legnagyobb fizikusa, aki egyben mint igen kiváló matematikus ismeretes. Nevét jól ismeri a ma embere is, hiszen mindenki tanulja az iskolában, hogy „minden vízbe mártott test annyit veszít súlyából, amennyi az általa kiszorított víz súlya”; ezt a törvényt pedig Archimedes fedezte föl, méghozzá kísérleti úton.
Fennmaradt művei, amelyekben a súlypont számítással, az emelők, csigák, szóval egyszerű gépek törvényszerűségeivel foglalkozik, azt sejtetik, hogy sokat kísérletezett, de csak egy néhány kísérletének részletes leírása maradt ránk, az se az ő írásaiban, hanem Vitruvius latin fizikus egyik könyvében. Vitruvius érdekesen adja elő, hogyan jött rá Archimedes híres hidrosztatikai törvényére, s hogyan alkalmazta ezt először gyakorlatilag. Archimedes rokona volt Hieronnak, Szirakúza fejedelmének. Hieron egyszer lemért mennyiségű aranyat adott át egy aranyművesnek, hogy koszorút készítsen belőle. A mester szállította a megrendelt koszorút, de valaki megsúgta az uralkodónak, hogy az átadott arany egy részét az iparos elsikkasztotta, és ezüsttel pótolta. Az uralkodó Archimedes tanácsát és segítségét kérte ahhoz, hogy bebizonyíthassa a csalást és megbüntethesse a gonosztevőt. „Archimedes éppen ezzel a dologgal foglalkozott — írja Vitruvius —, amikor fürödni indult. Belépve a teli kádba, észrevette, hogy a víz olyan mértékben folyik ki belőle, amilyen mértékben a kádba ereszkedik teste. Elgondolkozott a dolgon, és amint rájött a jelenség okára, nem időzött tovább a fürdőben, hanem örömmel ugrott ki belőle, meztelenül szaladt háza felé és hangosan kiáltozta: heuréka, heuréka! (megtaláltam).” A továbbiakban elmondja Vitruvius, hogyan alkalmazta Archimedes ezt a fölfedezést a rábízott probléma megoldására, vagyis, hogyan dolgozta ki az úgynevezett koronaszámítást: „Akkor Archimedes erre a fölfedezésre támaszkodva, két ugyanolyan súlyú tömböt állított elő, mint amennyit nyomott a koszorú, egyet aranyból, egyet ezüstből. Erre egy tág edényt a legfelső széléig megtöltött vízzel s belesüllyesztette az ezüsttömböt, mire a víz ugyanolyan mértékben folyt ki, mint amilyen mértékben a tömb belemerült az edénybe. Ekkor kivette a tömböt az edényből, pótolta a kiszorított vizet s megmérte, mennyivel kellett pótolni. Ebből kiderült, mekkora súlyú víz felel meg bizonyos térfogatú ezüstnek. Miután ezt megtudta, az aranytömböt süllyesztette bele a teli edénybe, s egy űrmérővel utána töltötte a kiszorított vizet. Kiderült, hogy ez alkalommal annyival kevesebb szorítódott ki a vízből, amennyivel kisebb térfogatú volt az aranytömb a hasonló súlyú ezüsttömbnél. Most újból megtöltötte az edényt, s magát a koszorút süllyesztette a vízbe és úgy találta, hogy a koszorú több vizet szorított ki, mint a hasonló súlyú aranytömb, s ebből a többletből kiszámította, mennyi ezüstöt kevertek hozzá, tehát bebizonyította a sikkasztást.”
Archimedes kísérlete főleg azért gyönyörködtet bennünket, mert ez már tiszta természettudományos gondolkodás terméke volt. Talán azért is mondotta Leibniz, a XVII. század nagy bölcselője: „Aki behatol Archimedes műveibe, már nem csodálkozik annyira az újabb felfedezéseken.” Az ókor hajszálnyi közelségben járt ahhoz, hogy fölfedezze a gőz feszítő erejét, munkavégző képességét, azt a természeti erőt, amelynek felfedezése majdnem kétezer évvel később elindította a gépkorszakot. Az időszámításunk előtti 100. év körül élt Alexandriában, az ókori tudomány akkori székhelyén néhány kiváló fizikus, akik közül különösen Heron emelkedett ki, mint rendkívül ügyes kísérletező és technikus. Nagyon találékonynak kellett lennie, mert „Pneumatica" című művében nem kevesebb mint 78 olyan készüléket írt le, amelyeket levegő vagy gőz hajt. Hogy a valóságban elkészítette-e mindezt, azt nem tudjuk, de az bizonyos, hogy valóban megszerkesztette és működésbe is hozta a mai gőzgép nagyon kezdetleges ősét, amelynek szerkezetét mindmáig ismerteti minden fizikai tankönyvünk. A híres „áolipil” ez a gép, mely kétségtelenül az első gőzzel hajtott gép volt (1. ábra). Amint látható, az áolipil alkatrészei a vízforraló kazán, ebből két cső nyúlik függőlegesen fölfelé. A két cső között fémlabda van forgó ízülettel, belőle szintén két rövid cső nyúlik ki, a végeik egy irányban meghajlítva, Ha az egyik függőleges csövön át gőz hatol be a kazánból a labdába, akkor a golyó meghajlított csövei forgó mozgásba hozzák a golyót, mivel a kitóduló gőz nyomása ilyen forgást okoz. Rendkívül egyszerű szerkezet, gyakorlati célokra ebben a formában nem is használható, de jó volt annak bebizonyítására, hogy a hőenergia mozgási energiává alakítható át.

1. ábra, A gőzgép őse, az „áolipil”
Jóval később (i. sz. 150 körül) újabb ügyes kísérletezővel találkozunk ugyancsak Alexandriában, Claudius Ptolemaios-szal, akinek a nevét a tudomány története mint a geocentrikus világrendszer kidolgozójáét őrizte meg. Nemcsak kiváló csillagász és matematikus volt, hanem fénytani kísérleteket, sőt méréseket is végzett. (Ptolemaios világrendszere szerint, amely egészen a XVI—XVII. századig általánosan elfogadott volt, a világmindenség közepén mozdulatlanul áll a Föld és körülötte koncentrikus gömbökön forognak a bolygók, a Nap és az állócsillagok. A XVI. században Kopernikus (1543) hirdette elsőnek, hogy a világ középpontja nem a Föld, hanem a Nap, de ennek az új elméletnek az elfogadását sokáig akadályozta mind az egyház, mind a szakmai körök ellenállása. Általánosan elfogadott tulajdonképpen csak a XVIII. században lett.)
Közismert jelenség, hogy ha a fénysugár például levegőből egy más közegbe, vízbe vagy üvegbe hatol, irányát megváltoztatja. Ptolemaios ennek a jelenségnek törvényszerűségét próbálta megállapítani. Ügyes szerkezetet készített, amelynek

2. ábra. Fénytörés mérésére szolgáló berendezés
segítségével megmérte, hogy a fénysugár különböző beesési szögeihez milyen törési szögek tartoznak (2. ábra). Helyesen állapította meg, hogy ha fény levegőből vízbe megy, a beesési szög (az a szög, amelyet a beeső sugár iránya a beesés pontjában emelt merőlegessel bezár) mindig nagyobb, mint a törési szög, és megsejtette azt is, hogy az egymáshoz tartozó szögpárok között valamilyen pontos mennyiségi összefüggésnek kell lennie. Ezt az összefüggést azonban még nem találta meg, mert ehhez trigonometriai ismeretek szükségesek. A törés pontos törvényét a XVII. században fedezte fel a holland Snellius és Descartes, a nagy francia filozófus.
Az alexandriai tudósok kísérleteivel a görög tudomány elérte tetőpontját. A keresztény középkor első századaiban az érdeklődés elfordult a természettudománytól, sőt a korai egyházatyák álláspontja egyes esetekben kimondottan tudományellenes volt. A görög tudósokat, mint pogányokat, veszedelmesnek tartották, munkásságukat nem sokra becsülték. Jelentősen változott a helyzet, amikor a VII—VIII. század körül a rövid életű arab birodalom tudósai újra felfedezték, lefordították és részben tovább fejlesztették a régi görögök főképpen Alexandriában feltalált munkáit. Az araboknak ez a rendkívül fontos kulturális tevékenysége azonban elsősorban Aristoteles munkáinak lefordítására és magyarázatára szorítkozott, úgyhogy az európai keresztény kultúra tulajdonképpen az arabok közvetítésével ismerkedett meg újra Aristotelesszel, és rajtuk keresztül vált — néhány száz évig tartó ellenzés után — Aristoteles a kereszténység hivatalos filozófusává. Ugyanakkor azonban az arab tudósok nemcsak az elméleti spekulatív filozófia iránt érdeklődtek, hanem a gyakorlatibb, természettudományos kérdések is foglalkoztatták őket. Így a kémia, orvostudomány és a fizika terén is jelentős munkásságot fejtettek ki. A fizikában elsősorban a fénytanban értek el eredményeket, a fizikai kísérletezés terén pedig különösen Al Khazini „A bölcsesség mérlege" című XII. sz.-beli könyve méltó említésre, amelyben először találkozunk a fajsúly pontos fogalmával (Archimedes még nem határozta meg pontosan), mint a súly és térfogat hányadosával és az erre a célra szolgáló különleges mérleg leírásával.
A bölcsesség mérlege a leírás szerint közönséges, kétkarú mérleg, de nem két mérlegserpenyő tartozik hozzá, hanem öt. Ezek közül legalább az egyik eltolható. Erre a célra a mérlegkarokon beosztások vannak, úgyhogy a mérleg, mint ún. római vagy gyorsmérleg is használható (ilyen egyenlőtlen karú mérleget használnak ma is a vándorló árusok) (3. ábra). Ilyen módon súlysorozat nélkül is meghatározható két test súlyának viszonya. Az egyik serpenyőt azonkívül a másik alá lehet erősíteni, úgyhogy testek súlyát vízben is meg lehet mérni, ha a harmadik serpenyő eltolásával a mérleget kiegyensúlyozzuk.
Al Khazini szerint ennek a mérlegnek a következő előnyei vannak: 1. Olyan pontos, hogy 1000 súlyrész megterhelés esetén még 1 súlyrész túlsúlyt is kimutat. (Ma ezt úgy mondjuk, hogy az érzékenysége 1/1000). 2. Segítségével meg lehet különböztetni a tiszta fémeket az utánzatoktól (nyilván vízbemerítéssel, ahogy Archimedes tette). 3. Fémkeverékek összetételét röviden és egyszerűen meg lehet vele határozni és általában a fémek, de más anyagok súlyára és fajsúlyára vonatkozó méréseket lehet vele végezni, amelyeknek ebben a korban megvolt a maguk gyakorlati jelentősége.

3. ábra. Római vagy gyorsmérleg
Al Khazini dicsekedése mérlege pontosságáról nem volt üres szóbeszéd, ezt mutatja a könyvében ugyancsak fennmaradt fajsúlytáblázat, amely szerint Al Khazini értékei meglepően kevéssé térnek el a mai pontos mérésekkel meghatározott adatoktól. Csak néhány példa:

2. A KÍSÉRLETI KUTATÁS MEGINDULÁSA A RENESZÁNSZ KORÁBAN:
GILBERT TANULMÁNYOZZA A MÁGNESES ERŐ TERMÉSZETÉT
Mind az alexandriai tudósok, mind az arabok kísérletei kivételeknek tekinthetők azokban a századokban, amelyekben az érdeklődés inkább a spekulatív tudomány felé fordult. A középkor társadalmi-gazdasági berendezkedése éppoly kevéssé volt alkalmas a kísérleti természettudomány létrehozására, mint az ókor rabszolgatársadalmai. A kivételek sora azonban nem zárul le az arabokkal. A XII., XIII. században is találkozunk haladó tudósokkal, akik sürgetik a természetnek kísérletek alapján való kutatását, sőt esetleg ők maguk is végeznek kísérleteket. Az ilyen emberek azután könnyen kerülnek boszorkányság hírébe, mint Albertus Magnus (valószínűleg 1207—1280), vagy összeütközésbe az egyházi hatóságokkal, mint Roger Bacon (1212—1296). Különösen Roger Bacon volt erős szószólója a kísérleti kutatásnak, ő maga is tett néhány fontos felfedezést, valószínűleg kísérleti úton (parabolikus tükrök), de fő érdeme, hogy teljes mértékben felismerte, milyennek kell lennie a természettudomány módszerének, ha azt akarjuk, hogy segítségével ne csak megismerjük a természetet, hanem szolgálatunkba is állíthassuk. A helyes módszer felismerése tette lehetővé számára, hogy olyan mértékben a „jövőbe lásson", mint kortársai közül kevesen. Műveiben számos helyen találkozunk hasonló kijelentésekkel: „Lehet készíteni úszó járműveket, amelyek evezősök nélkül haladnak, folyami és tengeri hajókat, amelyek egyetlen ember kormányzásával gyorsabban úsznak, mintha evezősökkel lennének megtömve. Ugyancsak lehet készíteni ló nélküli hintókat, amelyek rendkívüli sebességgel mozognak... lehet készíteni repülő szerkezeteket: az ember, a szerkezet közepén ülve, egy bizonyos szerkezet segítségével mozgatja annak szárnyait... az átlátszó testeket meg lehet munkálni úgy, hogy a távoli testek közelieknek tűnnek és megfordítva, hogy elképzelhetetlen távolságból is el tudjuk majd olvasni a legkisebb betűket s meg tudjuk különböztetni a legparányibb tárgyakat, valamint módunk lesz úgy szemlélni a csillagokat, ahogyan óhajtjuk.”
A Roger Bacon által megálmodott kor akkor még messze volt, de a következő századok során egyre többen akadtak, akik sürgették a tudomány megújulásának szükségességét. Az egyre fejlődő és erősödő városi polgárságnak szüksége volt új technikára, de ennek az igénynek először a filozófusok adtak hangot, egyelőre a régi, spekulatív tudomány bírálatával.
Az első igazán jelentős kísérleti kutató William Gilbert (1540—1603) angol orvostudós volt, aki a mágnes természetét kutatta. Hogy jobban megértsük a munkáját, látnunk kell, mi volt kutatnivaló ezen a téren, vagyis mit tudtak az ő koráig a mágnességről.
Thales az i. e. VI. században élt görög bölcs írja le elsőnek bizonyos vasérceknek azt a tulajdonságát, hogy magukhoz ragadnak kisebb vasszilánkokat meg vasdarabkákat. Lydiában Magnesia helység mellett találtak ilyen vasérceket, azért is nevezték el ezeket mágneseknek. Magát a mágneses erőt „léleknek" nevezi Thales. Nagyon érdekes, hogy a régi hinduk előbbre lehettek a mágneses erő ismeretében, mert az 500-ból eredő „Ayur-Véda" című orvosi könyvükben a Susruta nevű szerző nagyon alkalmasnak találja a mágneses vasércet arra, hogy segítségével kihúzzák a testből a beléhatolt acél nyílhegyet, ha ez nem túl mélyen fúródott be a húsba. Lehet, hogy Susrutának ezt a javaslatát vette figyelembe századokkal későbben (1256-ban) Halifa aleppói arab orvos, aki azt ajánlja, hogyha érvágásnál a lancetta finom hegye letörnék, mágnes segítségével lehet kihúzni a sebből. 1320-ban Mondeville francia orvos már lövedékeket húz ki a testből mágnes segítségével. Ugyancsak ismeretes volt az a jelenség is, hogy a vízszintes síkban felfüggesztett mágnestű mindig észak—déli irányban helyezkedik el. Kínában már i. e. a III. században használták az iránytűt tájékozódásra, Európában pedig 1190 óta terjedt el.
1269-ben végzi Maricourt az első kísérleti kutatásokat a mágnesség körül. Ő már ismeri a két sarkot és a mágnes megosztó hatását, tudja azt is, hogy a különböző nemű sarkok vonzzák, az egyneműek taszítják egymást, sőt egy mágnességen alapuló perpetuum mobile ötletét is felveti. 1530-ban az olasz Fracastoro említi először a Föld mágneses sarkait. Ötven évvel később Sanuto már a Föld két mágneses sarkáról beszél. 1580-ban Sarpi Paolo már tudja, hogy ha mágnest érintünk egy vasrúdhoz, ez maga is mágneses lesz. 1589-ben Della Porta már többet tud a mágnesről. „Magia naturalis" (Természetes mágia) című művében azt írja le, hogy a mágnes magához vonzza a vasreszeléket, ez szakáll módjára tapad hozzá, és ha nem mozdítják a mágnest, meg is marad ebben a helyzetben, de ha a reszeléket lerázzák a mágnesről, megszűnik a vasreszelék mágnessége.
A tizenhatodik század végén Gilbert orvos és természet-tudós alapos vizsgálat alá veszi a mágnességet. 1600-ban jelent meg fő műve „A mágnesről, mágneses testekről és a nagy mágnesről, a Földről”. Amit könyvében mond és megállapít, abban sok a tévedés, de egészen új világot, új kutatási területet tár föl tudóstársai számára, és először végez kutatást olyan módszerrel, amilyet megkívánt nagy kortársa, Verulami Bacon. És tőle származik néhány szak-kifejezés, amelyeket ma székében használunk, de még fizika- és földrajztudósaink sem igen tudják, hogy Gilbert-től erednek, így pl. az „északi sarok”, „déli sarok”, „elektromosság” kifejezések.
Két körülmény késztette arra Gilbert-t, hogy a mágnességgel foglalkozzon. Az egyik, hogy olvasta Porta említett könyvét a „Természetes mágiá”-ról. A másik az, hogy amióta Kolumbus felfedezte Amerikát (1492), a hajózás erősen fellendült és a hajósoknak igen nagy szükségük lett volna az addiginál tökéletesebb iránytűre. Gilbert jó nagy és erős mágnesköveket használt a kísérleteihez, mégpedig úgy, hogy gömb alakúra formálta őket. „Az ilyen alakú kő — mondja — hűséges mása a Földnek, nevezzük hát Terellá-nak” (földecske).

4. ábra. Gömb alakú mágneskő
Hogy a gömb alakú mágneskő pólusait megtalálja, Gilbert a kezébe vette és vékony vasdrótot helyezett a kőre. Ahol a drót megtapadt, ott krétával jelölte meg a mágneskövet. Aztán második, harmadik stb. helyre tette a drótot, s irányát mindig megjelölte krétával. „A Terellán kapott ilyen vonások hasonlók a délkörvonalakhoz és világosan látszik, hogy ezek összefutnak a mágneskő sarkainál" — írja Gilbert. Így találta meg a mágneskő pólusait, de talált erre más módszert is. Mágnestűt vett elő, amelynek közepén kis mélyedés volt, s úgy helyezte ezt egy tű hegyére, hogy szabadon mozoghasson. Jól látható ez az A—B kövön a C-nél (4. ábra), ahol a mágnestű egyensúlyi helyzetben van a mágneskő fölött. Ha most Gilbert a tű irányát megjelölte krétával a mágneskövön s többször megismételte a dolgot, úgy a vonalak megint csak A és B pontban futottak össze, délkörök módjára, mint az előbbi kísérletnél.
Gilbert rájött arra is, hogyha apró darabokra tördelünk egy mágnestűt, minden darabka teljes mágnes lesz. Ehhez a kísérletéhez hosszúkás mágneskövet használt, amelynek két sarka A-nál és D-nél volt. A követ fatálba helyezve vízre tette oly módon, hogy ez minden irányban szabadon mozoghatott. Észrevette, hogy az A északi sarok mindig dél felé, a D déli sarok mindig észak felé mutat. Ha pedig kettétöri a mágneskövet, akkor B-nél és C-nél új sarkok képződnek. A B déli sarok mindig vonzódik az új C északi sarokhoz (5. ábra). „Ha nem volt akadály és az egész súly úszott, akkor ezek a sarkok közeledtek egymáshoz, majd egyesültek. De ha az A sarkot a C sarokhoz közelítettem, ezek taszították egymást."

5. ábra. Egy mágnes feldarabolása
A mágnestűvel számtalan kísérletet végzett Gilbert és így állapította meg, hogy a mágnestű a golyó alakú mágneskő sarkainál függőlegesen lehajlik.
Akkor már ismerték a mágnestűnek azt a tulajdonságát, hogy minél közelebb fekszik egy vidék az Északi-sarkhoz, annál inkább lehajlik ott a mágnestű a vízszintes irány alá, ezt nevezték inklináció-nak. Az inklinációt 1544-ben a német Hartmann fedezte fel, és elsőnek az angol Norman mérte meg 1580-ban Londonban és 71° 50'-nek találta. Ezeket a felfedezéseket Hudson erősítette meg, aki fölfedezte Észak-Amerikának azt a nagy öblét, amelyet róla neveztek el. Hudson 1608-ban észrevette, hogy a 75. északi szélességi fok alatt már majdnem függőlegesen hajlott lefelé a mágnestű. Ez nem nagyon vágott avval, amit Hudson olvasott Gilbert-nek pár év előtt megjelent munkájában, mert Gilbert még úgy vélte, hogy a mágneses sarok egybeesik a földrajzi sarokkal.
Gilbert szerint — ez a jelenlegi felfogás is, melyre ma már számtalan kísérleti bizonyítékunk is van — a Föld óriási mágneses golyó két sarokkal. Régebben azt hitték, hogy az iránytű északi végének a vonzása az égtől származik. Ezt a nézetet Norman cáfolta meg. Másik felfogás szerint az Északi-sarkon óriási vastömegek vannak felhalmozva, ezért áll be az iránytű észak—déli irányba. Gilbert úgy próbálta magyarázni a jelenséget, hogy az iránytű északi vége mindig a nagyobb földtömeg felé mutat, mert az óceánt nem tartotta mágnesesnek, csak a szárazföldet. Azt is tanította Gilbert, hogy a többi égitestnek is van mágneses ereje, így a Napnak és a Holdnak. Gilbert már ekkor elfogadta Kopernikus hipotézisét és mint oly sok tudós e korban, a gravitációt és a mágnességet azonos eredetű erőknek tartotta, saját elméletével erősíteni vélte a kopernikusi tant.
Említsük még meg Gilbert kísérleteit a „fegyverzett" mágnesekkel (6. ábra). Ezeket úgy állította elő, hogy a természetes mágnes sarkait vaskupakokkal födte be.

6. ábra. Gilbert fegyverzett mágnesei
Kiderült, hogy ez a „fegyverzés" erősen emeli a mágnesek teherviselő képességét. Így az ő kísérleteinél egy mágnes a fegyverzés előtt kettő, fegyverzés után 12 uncia vasterhet bír el. (1 uncia = 28,38 gramm.)
Mágneses vizsgálatai során Gilbert az elektromos jelenségekhez is eljutott. Az ókorban és középkorban még csak a borostyánról és egy általunk jelenleg nem ismert féldrágakőről, a lynkurionról tudták, hogy a dörzsöléstől valamilyen erő lép fel bennük, amivel magához vonzanak könnyebb tárgyakat.
Gilbert volt az első, aki más anyagok dörzsölésével is megpróbálkozott. Dörzsölt gyémántot, rubint, opált, zafírt, ametisztet, berilt, hegyikristályt, ként és gyantát. Kikísérletezte, hogyha megdörzsölik ezeket az anyagokat, nemcsak papírszeletkéket és szalmafoszlányokat vonzanak magukhoz, hanem minden fémet, fát, száraz leveleket, kövecskéket, földet, sőt még vizet és olajat is, egyszóval mindent, „amit érzékszerveink észrevehetnek". Úgy végezte a kísérleteket, hogy mindegyik fémből készített egy-egy 8—10 cm hosszú mutatófélét, rátette egy tű hegyére, amelyen könnyen elfordulhatott, mint az iránytű. Ha most közelítette a mutatóhoz a megvizsgálandó elektromozott anyagot, a mutató mindjárt elfordult.
Ez a szerkezet tehát a mai elektrométerek őse.
Kísérletei során Gilbert felfedezte az egyes anyagok között azt a különbséget, amit ma úgy fejezünk ki, hogy vannak vezetők és szigetelők. Az előbbiekről Gilbert megállapította, hogy dörzsöléssel nem elektromozhatók (fémek), illetve nem előnyösek az elektromosság megmaradása szempontjából, mert azt elvezetik (nedves levegő és még néhány folyadék). A ma szigetelőknek nevezett anyagokat Gilbert dörzsöléssel elektromozhatóknak találta; a felsorolt anyagokon kívül a száraz levegőnek és az olajnak szigetelő tulajdonságát is észrevette. Nem figyelte meg azonban az elektromos taszítóerő felléptét, csupán a vonzóerőt észlelte, és így nem tudott a kétféle elektromosság pozitív (üveg) és negatív (gyanta) — létezéséről sem.
Természetes az is, hogy Gilbert ennek az addig úgyszólván ismeretlen területnek a felfedezésénél a mágnesség és elektromosság közötti különbséget látta meg inkább, mint a hasonlóságot, illetve rokonságot.
Ezeket a különbségeket a következőkben foglalta össze: „1. A villamosság dörzsölés által keletkezik, a mágnes vonzó hatása megvan dörzsölés nélkül is. 2. A nedves levegő megsemmisíti a villamosságot, a mágnességnek nem árt. 3. Egy villamos test nagyon sokféle anyagot vonz, a mágneses az acélt és a vasat vonzza. 4. A villamos test csak kicsi testeket hord, a mágnes nagyokat is."
Ezek voltak azok az elemi ismeretek a villamosságról, amelyeket Gilbert-nek köszönhetünk. Utána egyelőre nem akadt senki, aki folytatta volna az ő kísérleteit; a XVII. században történt a tulajdonképpeni fizika megalapozása, és csak ezután kerülhetett sor a fizika egyes részletterületeinek feltárására. Gilbert ebből a szempontból tehát messze megelőzte korát, és még több mint száz esztendőnek kellett eltelnie, hogy az elektromos kísérleteket sikerrel folytatni lehessen.
(William Gilbert 1540-ben született Angliában, Essex grófságban. Oxfordban és Cambridge-ben tanult orvos-tudományt. 1573-ban mint orvos telepedett le Londonban, hamarosan nagyhírű orvos lett belőle, Erzsébet királynő udvari orvosának nevezte ki, és évjáradékot biztosított számára, hogy tudományos kutatásainak élhessen. 1600-ban jelent meg a mágnességről szóló nagy műve. Első volt a tudománytörténelemben, aki rendszeresen végzett fizikai kísérleteket. Külföldön is nagy híre volt.)
3. GALLILEI MEGALAPOZZA A KÍSÉRLETI FIZIKÁT
Gilbert kétségkívül úttörő munkássága rendkívül jelentős volt, de lényegében a fizikának egyik részletterületére vonatkozott. Mindaddig azonban, amíg a legalapvetőbb fizikai jelenségre, a mozgásra vonatkozólag, a többé-kevésbé téves aristotelesi nézetek uralkodtak, nem lehetett szó arról, hogy a természet megismerésére vonatkozó törekvések teljes sikerrel járjanak. A mozgástan, a dinamika minden fizikai ismeret alapja. A spekulatív aristotelesi fizika a mozgásra vonatkozólag megállapított bizonyos alapelveket, és ezeket — mivel a tudományban főképpen a tekintély és nem a valóság uralkodott — mintegy kétezer esztendőn keresztül elfogadták, mint ahogy elfogadták a ptolemaiosi, geocentrikus világrendszert is. Ez utóbbi esetben azonban mentségül szolgálhat, hogy a Nap és a csillagok keleten való „felkelése" és nyugaton való „lenyugvása", valamint a Föld mozdulatlan volta a mindennapi szemléletnek valóban megfelelt. Így volt ez kissé Aristotelesnek a szabadesésről szóló tanításával is. Szerinte a „súlyos" testek annál nagyobb sebességgel esnek, minél nagyobb a súlyuk, míg a „könnyű" testek (füst, tűz, gőzök) igyekeznek a földtől eltávolodni. Nagyon éles elme és sok kísérletezés kellett ahhoz, hogy valaki a fenti állítások téves voltát kielemezze, és hogy sok kísérlettel és helyes következtetéssel megállapítsa a szabadesés törvényeit. Ilyen volt Galileo Galilei olasz tudós, akit munkássága nyomán méltán nevezünk nemcsak a kísérleti fizika, hanem az egész fizika megalapozójának. Galilei nemcsak a szabadesés helyes törvényeit állapította meg, és ezáltal alapot adott Newton ugyancsak korszakalkotó felfedezéseinek, hanem hozzájárult a kopernikusi világrendszerről szóló tanítás elterjedéséhez is, amennyiben csillagászati felfedezéseivel megerősítette Kopernikusnak néhány elméleti következtetését. Mindezek mellett Galilei megmutatta a fizika művelésének egyetlen helyes módszerét: a kísérletekből, tapasztalatból kiindulva méréssel és a matematika felhasználásával jutni el egy-egy természeti törvényhez. Ha a mai fizikus rendelkezésére álló eszközök és műszerek tökéletesebbek is, mint Galilei korában voltak, a ma fizikusa pontosan úgy jár el kísérletei végzésénél és kiértékelésénél, ahogy annak idején — a fizika történetében elsőnek — több mint 300 esztendővel ezelőtt Galilei.
Galileinek már pisai tanárkodása alatt kételyei támadtak az aristotelesi dinamika helyességét illetően. Mint mondottuk, Galilei idejéig dogmaként fogadták el Aristoteles tanításait, hogy két szabadon eső test közül az ér hamarabb a földre, amelyik nehezebb, vagyis, ha egy vasdarabot és egy tollat ejtünk el, a vas ér a földre előbb. Látszólag így is van, és Aristoteles nem gondolt arra, hogy azért van ez így, mert a levegő erősen visszatartja a nagyfelületű tollat. De nemcsak a toll és a vas, hanem a nem egyenlő súlyú kövek esetében is így van ez. Aristoteles tudtunkkal soha nem ellenőrizte a dolgot kísérlettel, de elméletileg úgy gondolta el, hogyha egyszerre ejtünk két követ, amelyek közül az egyik tízszer nehezebb a másiknál, akkor az esési idő aránya is 1: 10 lesz, vagyis a nehezebb kő tizedrésznyi idő alatt ér a földre.
Nem Galilei volt az első, aki kételkedett ebben. Már ezer évvel előbb Philoponos alexandriai tudós nemcsak kételkedett Aristotelesnek ebben az állításában, hanem kísérletet is végzett a megcáfolására. Legalábbis ezt írja: „Ha a testek azonos közegben esnek lefelé, Aristoteles szerint az esési idők úgy aránylanak egymáshoz, mint az ejtett testek súlyai. Ez azonban teljesen hamis, mint ezt minden logikai bizonyításnál jobban mutatja a kísérlet. Ha ugyanis két eltérő súlyú testet egyszerre ejtünk le ugyanolyan magasságból, akkor láthatjuk, hogy az esési idők nem arányosak a súlyokkal, hanem az esési idők csak nagyon kevéssé térnek el egymástól."
Galilei két éven át volt tanár Pisában, amely város már akkor híres volt ferde tornyáról. Viviani nevű tanítványa szerint Galilei különböző súlyú golyókat ejtett le egyszerre a toronyból. A nehezebb csak néhány hüvelykkel előzte meg könnyű társát. Ezt a kis eltérést pedig Galilei a levegő ellenállásával magyarázta. Azt mondta, hogyha ki tudnánk küszöbölni ezt az ellenállást (vagyis ha légüres teret tudnánk előállítani, s abban végezni ilyen kísérletet), „akkor minden test egyenlő sebességgel esne le". Akkor még ott tartott a fizika, hogy nemcsak nem ismerték a légüres teret, hanem létrehozását elvileg is lehetetlennek tartották. (Magát a kísérletet, tollnak és vasdarabnak légüres térben való leejtését Newton végezte el elsőnek, és ezzel igazolta Galilei feltevését.) Viviani szerint Galilei kísérleteit tanártársai nem fogadták túl nagy lelkesedéssel. (A legújabb történeti kutatások nem erősítik meg Viviani leírását, aki nem lehetett szemtanú, mert jóval fiatalabb volt (1622-ben született, a kísérlet pedig még a XVI. században történt!), de ez talán nem is lényeges: a lényeg, hogy Galilei már Pisában foglalkozott Aristoteles mozgástanának cáfolatával.)
Galilei más kísérleteket is végzett a szabadeséssel, hogy megállapítsa annak törvényeit. Közismert tapasztalat ugyanis, hogy a leeső test mozgása folyton gyorsul. Bizonyosra vehette tehát, hogy a sebesség szabályosan növekedik, és meg akarta nézni, milyen viszonyban van a leeső test által megtett út az esési idővel. De a szabadesés túl gyors mozgás, és az akkori gyatra mérőeszközökkel nem lehetett az esési időket pontosan megmérni. Elhatározta, hogy méréseit nem szabadeséssel fogja végezni, hanem lejtőn, vagyis ferde síkon történő eséssel. Majd megállapítja, mennyivel változik meg ugyanannak a testnek az esési sebessége, ha a lejtő enyhébb vagy meredekebb. Hogy van különbség a kétféle lejtő esetében, az már közismert dolog volt, csak addig még nem végeztek mérést erre vonatkozóan.
Maga Galilei így írja le ezt a kísérletsorozatot. Elővett egy 12 könyök (1 könyök = 50 — 60 cm.) hosszú deszkát, ebbe fél hüvelyk (1 hüvelyk kb. 2,5 cm.) széles csatornát vájt; a kisimított falú csatornát még bevonta pergamennel. A deszka egyik végét felemelte mintegy hétkönyöknyi magasságra. Most simára csiszolt rézgolyót vett elő, végig guruitatta az árokban és megmérte, mennyi idő alatt szaladt végig a golyó, aztán úgy rendezte, hogy a golyó csak az ároknak egy negyedét járja meg. Megint megmérte az esési időt, s úgy találta, hogy ehhez felényi idő kellett. Matematikailag így lehetne kifejezni ezt az arányt: az utak hossza úgy aránylik, mint 1:4, az esési idők pedig úgy aránylanak, mint 1: 2. Egészen matematikai formában úgy mondanánk ezt, hogy az utak úgy aránylanak egymáshoz, mint az idők négyzetei. Galilei aztán több módosításban végezte el ezt a kísérletet. Hol ferdébb, hol enyhébb volt a lejtő, hol hosszabb, hol rövidebb a golyó útja, de az eredmény mindig ugyanaz volt, tehát Galilei a fizikának egy általános érvényű törvényét találta meg. Galilei érdemeit akkor tudjuk különösen értékelni, ha meggondoljuk, hogy mai szemmel nézve természetesen a legkezdetlegesebb eszközökkel végezte kísérleteit. Henlein nürnbergi mester ugyan már a XVI. század legelején feltalálta a zsebórát, de ez még teljesen alkalmatlan volt tudományos mérésekre. Abban az időben tudományos kísérleteknél — és így Galilei is — a következőképen mérték az időt: nagyobb edényt megtöltött vízzel, ennek fenekén szűk nyílás volt, amelyen finom sugárban folyt ki a víz. Ezt a vizet kisebb edényben fogta fel. Az így felfogott folyadékmennyiséget nagyon finom mérleggel megmérte. A különböző mérésekből adódott a súlyok aránya. Ez olyan pontosan megfelelt az esési idők arányának, hogy a sok megfigyelés között alig mutatkozott valami eltérés. Abban az időben tehát nem is perceket és másodperceket — ezek túl kis egységek voltak — hanem időtartamokat mértek, és ezeket hasonlították össze.
Galilei a fizika más területein is végzett kísérleteket. Ezek közül igen jelentős az, amellyel lényegében ugyancsak Aristoteles mozgástanának egy állítását cáfolta meg. Az ókori kísérletek között láttunk egyet, ahol Aristoteles megméri a levegő súlyát, illetve úgy találja, hogy a levegőnek van súlya. Filozófiájában viszont azt tanította, hogy a tűz meg a levegő abszolút könnyűek, igyekeznek minél távolabbra kerülni a Föld középpontjától. Galilei észrevette, hogy itt ellentmondás van és így okoskodott: ha igaza volna Aristotelesnek, akkor ebből az következnék, hogyha valamely edényben megsűrítik a levegőt, az fokozná a könnyűségét, és az edény még jobban törekednék fölfelé.
Ez is olyan tétel, aminek végére lehet járni kísérlettel. És valóban sikerült is bebizonyítani, hogy az ókori tudós itt is tévedett. Galilei elővett egy nagy üvegretortát és fecskendő segítségével levegőt sajtolt belé. Utána pontos mérlegre tette az üvegballont és kiegyensúlyozta. Most kinyitotta az edényt. Az összesajtolt levegő természetesen kitódult belőle. A mérleg most felbillent, mert az üvegedény könnyebb lett, el kellett venni a tara-súlyokból, hogy helyreálljon az egyensúly. A kísérlet eredményét ebben a mondatban foglalja össze Galilei: „Kétségtelen, hogy az elvett tara súlya pontosan megfelel ama levegő súlyának, amelyet erőszakkal sajtoltam az edénybe."
Ez a kísérlet tehát annyit bebizonyított, hogy a levegő igenis súllyal bíró test. Olyan tudós elme, amilyen a Galileié volt, nem elégedhetett meg ennyivel. Fölvetette a kérdést, mennyi a levegő súlya más anyagok súlyához — például a vízéhez — képest? Galilei ennek megállapítására is kigondolt egy szellemes kísérletet. Közbe meg kell jegyeznünk, hogy a természettudománnyal is foglalkozó Leonardo da Vinci is tudta már, hogy a levegőnek is van súlya, de nem jött rá, mihez lenne célszerű viszonyítani. Cardano viszont félszázaddal Galilei előtt már így fogalmazta meg a problémát: „Mérés által megtalálni, hogyan viszonylik a víz sűrűsége a levegőéhez." De ő se jött rá, hogyan lehetne végrehajtani ezt az összehasonlító mérést. Galilei elmés kísérlete ez volt: vizet sajtolt egy levegővel töltött üvegedénybe mindaddig, amíg a víz háromnegyed részét foglalta el a térfogatnak. Most pontosan lemérte ennek az edénynek a súlyát. Erre átszúrta a hártyát, amely elzárta az összesajtolt levegőt, s most kiszabadult az a levegő, amely azelőtt az edény űrtartalmának háromnegyed részét elfoglalta. Ezután Galilei újból megmérte az edényt, és akkora különbséget talált a súlyban, amely megfelelt a kiszabadult levegő súlyának. Ez persze elég kezdetleges módja volt a fajsúlymérésnek, de annyi mindenesetre kiderült belőle, hogy a levegő sokkal könnyebb, mint a víz. Hogy mennyire pontatlan eredményt adott ez az eljárás, látszik abból, hogy Galilei 400-szor könnyebbnek találta a levegőt a víznél, pedig valójában 773-szor könnyebb, tehát majdnem 50 százalékot tévedett.
E néhány ismertetett kísérlet Galilei munkásságának csak egyik oldalát mutatja. Csillagászati felfedezéseiről életrajzában számolunk be röviden.
Galilei Pisában született 1564-ben. Apja kedvelte a zenét és a matematikát, fiából mégsem akart tudóst nevelni, hanem a jövedelmezőbb posztókereskedői pályára szánta. Tanulmányai kezdetén azonban Galilei már olyan tehetségesnek mutatkozott, hogy apja mégis a pisai egyetemre küldte, hogy orvos legyen. A matematika és fizika iránti érdeklődés azonban csakhamar elvonta orvosi tanulmányaitól. Életrajzírói feljegyezték róla, hogy 19 éves korában a pisai dómban függő csillár lengéseinek megfigyeléséből állapította meg, hogy az ingalengések ideje független a kilengések nagyságától. Időmérőnek itt a saját érverését használta fel. Galilei már huszonhat éves korában a matematika professzora lett Pisában. Igaz, hogy nevetségesen csekély fizetéssel (évi 60 scudi, kb. 500 Ft), de ebben az állásában nem maradhatott meg soká, mert tanártársai rossz szemmel nézték nyílt kritikáját Aristoteles filozófiájával szemben. A velencei szenátus meghívására a páduai egyetemen lett a matematika és csillagászat professzora. Itt érte az a hír, hogy Hollandiában távcsöveket készítenek. A leírás alapján 1608-ban maga is szerkesztett távcsövet, és segítségével olyan felfedezéseket tett, amelyek egyrészt megcáfolták Aristotelesnek az „égről" tanított tételeit, másrészt megerősítették hitét Kopernikus elméletének helyességében, amellyel már évek óta foglalkozott. A távcső megmutatta, hogy a Hold nem tökéletesen sima gömbfelület — mint Aristoteles tanította —, hanem azon hegyek és völgyek váltakoznak, a Napnak foltjai vannak; nem igaz az sem, hogy csak 7 bolygó van, mert a Jupiternek 4 holdja is van, a Szaturnusz sem egyszerű, hanem összetett csillagkép (a gyűrűt Galilei távcsövével még nem lehetett kivenni, ezt csak Huyghens fedezte fel 1656-ban), a Venus pontosan olyan fényváltozásokat mutat, mint a Hold; ez következett is Kopernikus elméletéből, de Kopernikus távcső nélkül még nem tudta állítását igazolni.
Galilei felfedezései óriási feltűnést keltettek. Híre Rómába is eljutott. Időközben Galilei elhagyta Páduát és Firenzében Toscana nagyhercegének udvari matematikusa lett. Ez biztosította ugyan számára az anyagilag független kutató munkát, de Firenze már a római inkvizíció hatáskörébe tartozott, amelynek tagjai között Galileinek sok személyes ellensége is volt. Ezek elérték, hogy az inkvizíció 1616-ban indexre tette Kopernikus könyvét, Galileinek pedig megtiltották, hogy a Föld forgásáról szóló tant akár szóban, akár írásban tanítsa. Nagy csapás volt ez, mert Galilei már évek óta tervezett egy nagy művet Kopernikus elméletének ismertetésére és bizonyítására. Nem is tudott e tervről lemondani és úgy próbálta a tilalmat megkerülni, hogy a művet párbeszédes formában írta meg melyben csak az egyik szereplő képviseli Kopernikus álláspontját és azt a vita végén feladja. (Párbeszéd a két legnagyobb világrendszerről: a ptolemaiosiról és a kopernikusiról. Firenze 1632.)
1632-ben meg is jelent a könyv, de megjelenése után néhány hónappal betiltották, a 70 éves Galileit pedig Rómába idézték: adjon számot róla, miért szegte meg a tilalmat. A hosszú és kínos per természetesen Galilei elítélésével végződött. Galilei csak úgy menekülhetett meg az eretnekeknek kijáró máglyahaláltól, hogy esküvel kellett megtagadnia a kopernikusi tant, mint a szentírással ellenkezőt. Hátralevő éveit Galilei — félig, majd teljesen megvakulva — az inkvizíció állandó felügyelete alatt töltötte. Mindez azonban nem tudta megtörni a nagy tudós szellemét. Ezekben az években foglalta össze egy másik remekműben a szabadeséssel kapcsolatban végzett kísérleteit és egyéb mechanikai, fizikai felfedezéseit. (Beszélgetések két új tudományról, amelyek a mechanikára és a szabadesésre vonatkoznak. Leyden 1638.) A mű 1638-ban jelent meg Hollandiában. Ez a műve Galileinek az, amellyel lényegében elindította a fizikát a további fejlődés útján. 1642-ben halt meg a Firenze melletti Ancetriben.
4. ARCHIMEDES ÚJRA FELFEDEZŐJE: SIMON STEVIN
Galilei idősebb és sokkal kevésbé ismert kortársa volt a holland Simon Stevin, aki Archimedes vizsgálatait ismételte meg és fejlesztette tovább. Stevin, éppúgy mint Galilei, már teljes mértékben az új korszak tudósa; kutatásaiban kizárólag a kísérletekből kiinduló matematikai következtetésekre támaszkodott.
Míg Galilei kísérleteivel megállapította, hogy a lejtőn

7. ábra. Stevin könyvének címlapja
legördülő test gyorsulása a lejtő hajlásszögétől függ, Stevin ezt a következtetést a lejtőn mozgó testre ható erőkre mutatta ki, ugyanakkor elsőnek fogalmazta meg pontosan az erők összetevésének, az ún. erőparallelogrammának a tételét.
A 7. ábra Stevin könyvének címlapján szerepel. A holland felírás azt jelenti, hogy csoda, és mégsem az. A lejtőn átvetett lánc ugyanis egyensúlyban van, mert a lejtő keresztmetszetét alkotó háromszög két rövidebb oldalán átvetett lánc súlya éppen annyi, mint az alsóé. A háromszög oldalaival párhuzamos és azokkal arányos nagyságú erők tehát egymással egyensúlyban vannak. Vagyis — mint mondtuk — ez a kísérlet egyrészt megmutatta, hogy a lejtőn mozgó test nem teljes súlyával nyomja a lejtőt, másrészt azt, hogy miképpen lehet meghatározni két egymással szöget bezáró erő eredőjét.
Foglalkozott azután Stevin Archimedes csigasoraival is; ezen a téren szintén valamivel messzebbre jutott, mint a nagy ókori tudós. Archimedes ugyanis annak idején sikeresen megállapította, hogy csiga, illetve csigasor segítségével aránylag kis erővel nagy munkát lehet végezni. Erre utal legalábbis az ugyancsak Vitruvius által feljegyzett kijelentése Archimedesnek, hogy: „Adjatok nekem egy fix pontot és kimozdítom sarkaiból a világot." A reális ok erre — Vitruvius szerint — az volt, hogy Archimedes csigasor segítségével sajátkezűleg szárazra húzott egy hajót, amely munkához egyébként több ember vagy igavonó állat erejére lett volna szükség.
Ma már tudjuk, hogy egyetlen mozgó csiga alkalmazása felére csökkenti az emeléshez szükséges erőt, ha tehát több, pl. 3 csigát alkalmazunk, az erő a súly 1/6-ára csökken. Stevin korában azonban ennek a tapasztalatnak a tudományos megfogalmazása különleges éleslátást jelentett. Stevin ugyanis kísérletei során megmérte azt is, hogy mekkora a terhet húzó és az erőt kifejtő kötél elmozdulása. Megállapította, hogy míg a teher útja — mondjuk — egy egység, addig három csigából álló csigarendszer esetén a megtett út az előbbinek hatszorosa. Nem volt még ebben az időben lerögzítve a munkának mint az erő és elmozdulás szorzatának e fogalma. Annál figyelemre méltóbb Stevinnek ez a felismerése, amely szerint a végzett munka (út szorozva elmozdulás) semmiféle gépnek az alkalmazásával nem csökken, mert ha a munka elvégzéséhez kisebb erőt alkalmazunk, a megtett út szükségképpen nagyobb lesz. Ezt ma úgy is szoktuk fogalmazni, hogy a perpetuum mobile, azaz az örökmozgó készítése lehetetlen. Vagyis lehetetlen olyan gépet szerkeszteni, amely munka (energia) befektetése nélkül működik. Stevin lejtő kísérlete lényegében ezt is megmutatta. Ha ugyanis a lejtőn átvetett láncnak csak egy szeme elmozdulna, akkor attól kezdve a lánc örökös forgást végezhetne, éppen azért, mert az egyensúly nyugalom esetén éppen úgy fennáll, mint egyenletes mozgásnál.
Stevin nemcsak az egyszerű gépek egyensúlyi viszonyai terén volt Archimedes követője, hanem a folyadékok egyensúlyi viszonyait is az ő nyomán vizsgálta és Archimedes felfedezéseit tovább fejlesztette. Számos, érdekes kísérlete közül csak kettőt említünk meg, amelyek eléggé közismertek, mivel az iskolai kísérletek között általában szerepelnek, rendszerint anélkül, hogy felfedezőjükről, Stevinről megemlékeznének. A két kísérlet lényegében szorosan összefügg egymással: egyik az ún. hidrosztatikai paradoxon, a másik a közlekedőedények törvénye.

8. ábra. Hidrosztatikai paradoxon
A hidrosztatikai paradoxon tétele a következőképpen fogalmazható meg: ha veszünk különböző alakú, de egyenlő keresztmetszetű edényeket és ezeket egyenlő magasságig megtöltjük vízzel, akkor az edényekben levő vízoszlop súlya az edény alakjától függetlenül egyenlő (8. ábra). A kísérletet Stevin úgy végezte el, hogy az edények alja leszerelhető volt; ezt összeköttetésbe hozta egy kis mérleggel, amelynek egyik karja az edényt elzáró lemez volt, a másikon egy súly tartott egyensúlyt az edényben levő vízoszloppal. A mérleg egyensúlya bármelyik edény esetén ugyanannál a vízoszlop magasságnál billent meg. Ez a kísérlet lényegében Archimedes elvének tovább fejlesztése: a folyadékban a nyomás minden irányban: lefelé, felfelé és oldalt egyenletesen terjed el. Amit a folyadékoszlop súlyának észlelünk a mérlegen, az a háromféle irányú nyomóerő eredője. A felfelé szűkülő edénynél az oldalnyomás növeli, a felfelé tágulónál pedig csökkenti a súlyt, míg az Archimedes által felfedezett súlycsökkenés, a felhajtóerő mindegyik esetben felfelé mutat és csak az edény alapterületétől és a vízoszlop magasságától függ.
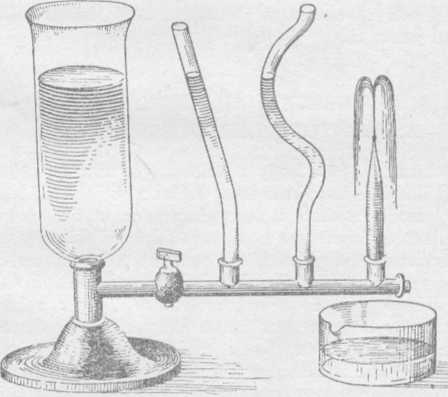
9. ábra. Közlekedőedények
A fenti kísérletnek egy további, Stevin által történt általánosítása az ún. közlekedőedényekre vonatkozik. Stevin kísérlettel és számítással igazolta ezt a tételt, hogy „egy font víz vagy 100 000 font víz ugyanazt a nyomást fejti ki“, mert ha két teljesen különböző keresztmetszetű közlekedőcsőbe ugyanazt a folyadékot öntjük, a folyadékoszlopok magassága egyenlő lesz, mert ez csak a nyomástól, azaz a felületegységre ható nyomóerőtől függ. Ha a két szárban különböző folyadék van, a folyadékoszlopok magassága fordítottan arányos a folyadékok fajsúlyával. A nagyobb fajsúlyú folyadék annyiszor fog alacsonyabban állni, mint a kisebb fajsúlyú, ahányszor nagyobb a fajsúlya a másikénál (9. ábra).
(Simon Stevin — (1548 — kb. 1630) a leydeni egyetemen volt professzor. A maga korában azért nem ismerték érdemeinek megfelelően, mert műveit — az akkoriban szokásos latin helyett — anyanyelvén írta. Galilei sem ismerte, és az egyszerű gépek egyensúlyára vonatkozó több tételhez tőle függetlenül jutott el.)
5. A KÍSÉRLETI AKADÉMIA ÉS A LÉGNYOMÁS PROBLÉMÁJA
Galilei megmutatta, hogy a tudományos kutatási módszerek közül a kísérletezéssel lehet elérni a legjobb és legbiztosabb eredményeket a természettudományok terén. Néhány lelkes és tehetséges tanítványa folytatni akarta ezt a kutatási módszert, főleg Viviani és Torricelli; utóbbinak nevét még ma is gyakran emlegetik mint a higanyos barométer föltalálóét. Buzgóságuk és a mester iránti hűségük abban nyilvánult meg, hogy Galilei halála után kis tudományos egyesületet alapítottak, amelynek tagjai kötelezték magukat, hogy kísérleti módszerrel végzik kutatásaikat. Ennek megfelelő nevet is adtak az egyesületnek: Kísérleti Akadémia (eredeti olasz neve Accademia del Cimento volt). Tagjai kiváló olasz tudósok voltak, így Borelli, aki az izmok működését, a járás-futás mechanikáját tanulmányozta kísérleti úton; Steno, a modern geológia egyik megalapozója; Redi, aki biológiai kísérleteket végzett; Cassini csillagász, aki a párizsi csillagvizsgáló igazgatója lett stb. Ez a nagyszerű egyesület sajnos csak tíz évig működött, 1657-től 1667-ig. Tagjai sok alapvető fizikai és élettani kísérletet végeztek, amelyek közül néhányat alább ismertetünk.
Ez alatt a tíz év alatt az Akadémia tagjai foglalkoztak a fizikának majdnem minden olyan ágával, ahol a kísérletezés lehetséges volt. Megpróbáltak néhány alapvető mérőeszközt megszerkeszteni, például hőmérőt, nedvességmérőt, sűrűségmérőt, s ők alkalmazták először az ingát mint időmérő eszközt; foglalkoztak a légnyomással, és először végeztek különféle kísérleteket légüres térben. Készítettek hűtőkeveréket. Ők végeztek először kísérleteket sugárzó meleggel a következő módon: nagyobb jégdarabot helyeztek el egy homorú tükör közelében. A tükör gyújtópontjába érzékeny hőmérőt állítottak, a hőmérő alacsonyabb hőmérsékletet mutatott, mint a környező levegő hőmérséklete.
A Kísérleti Akadémia tagjai kísérleteztek a mágnességgel és villamossággal is, de ezen a téren nem értek el Gilbert kutatásaihoz képest újabb eredményeket.
A Kísérleti Akadémiának egyik legszebb és legértékesebb munkája volt a légnyomás és légüres tér kutatása. Az Akadémia tagjai tovább haladtak a Torricelli által megkezdett úton. Meg kell tehát előbb ismernünk Torricelli nagy felfedezését a légnyomás mérésére, azaz a higanyos barométert.
A XVII. században még Aristoteles tanítása nyomán azt gondolták, hogy a szívókutakban azért nyomul fel a víz, mert a természet „irtózik" a légüres tértől. Ez volt az ún. „horror vacui" elmélet. Ebben Galilei sem kételkedett, feltűnt neki azonban, hogy ez az irtózás csak 20 könyöknyi, azaz 10 m magasságig tart, ennél magasabbra nem lehet vizet szivattyúzni. Torricellinek különös ötlete támadt: miután a higany 14-szer súlyosabb a víznél (mai mérések szerint 13,6-szer), vajon milyen magasra emeli ezt a szivattyú? Mivel azonban nem volt elegendő higanya, barátja Viviani végezte el a kísérletet az ő utasításai szerint. Az eredmény igazolta Torricelli felfogását: a higany annyival kisebb magasságra emelkedett, ahányszor súlyosabb a víznél. Erre mindketten elvégezték a kísérletet a következő módon (1643-ban): két könyök (1 m) hosszú üvegcsövet töltöttek meg higannyal színültig; most ujjukkal befogták a cső szabad végét, belefordították higannyal telt edénybe s elvették az ujjukat onnan; amint ez megtörtént, a higanyoszlop alásüllyedt l 1/2 könyöknyi (76 cm) magasságra, és meg is maradt ott akkor is, ha rázták. Lényegében itt egy olyan közlekedőedényről volt szó, amelynek egyik szárában a 76 cm-es higanyoszloppal, a másikban a több ezer km-es levegőoszlop tartott egyensúlyt. A higanyoszlop fölött légüres tér keletkezett, amely a mai napig a Torricelli-űr nevet viseli. Ez volt az első barométer, vagyis légsúlymérő, amelyet azóta tökéletesítettek, de lényegében ugyanaz maradt (10. ábra). A készülék hosszú időn át állott a helyén, olykor ingadozott a magassága. Torricelli ezt helyesen a légnyomás változásával magyarázta, de úgy, hogy megmaradt a horror vacui elmélete mellett. Még néhány évtized múlt el, amíg ez a téves feltevés eltűnt a fizikából, főleg Pascal és Guericke hatására.

10. ábra. Torricelli kísérlete, a barométer őse
(Evangelista Torricelli 1608-ban született, nem tudjuk, hol. Húszéves korában került Rómába, ott matematikát tanult Castellitől, Galilei barátjától. Mikor Galilei megvakultan sínylődött az inkvizíció fogságában, szüksége volt egy fiatal tudósra, akinek diktálhassa a műveit. Castelli Torricellit ajánlotta, így került a nagy mester mellé. Ennek halála után a matematika tanára lett Firenzében. De már 1647-ben, nagyon fiatalon meghalt.)
Blaise Pascal francia tudós baráti levelezés útján értesült Torricelli kísérletéről. Megismételte a kísérletet vízzel is meg higannyal is: a vizet negyven (kb. 14 m) láb hosszú csőbe zárta. Ezzel azonban nem elégedett meg, hanem azt a kérdést akarta kísérletileg ellenőrizni, mennyiben van befolyással a tengerszín fölötti magasság a higanyoszlop állására. Ezért csinálta a következőt: ugyanazon a napon többször is előállította a Torricelli-féle űrt ugyanazzal a csővel és ugyanazzal a higannyal, mégpedig hol egy hegy tövénél, hol a hegy tetején. Így akarta megtudni, vajon azonos-e a higanyoszlop magassága a hegy tövében és a hegy tetején. Mert ha a higanyoszlop a hegy tetején rövidebb, akkor csakugyan nem lehet mással magyarázni a jelenséget, mint a levegő nyomásával. Hogy Pascal milyen nagyon fontosnak találta ezt a kísérletét, az kiderül annak a dolgozatának címéből, amelyben beszámol róla: Beszámoló a folyadék egyensúlyára vonatkozóan végzett nagy kísérletről. Párizs 1648. Nagyon érdekes az ebben közölt végkövetkeztetése: „Könnyen belátható, hogy a hegy tövénél a nagyobb tömeg levegő nagyobb nyomást fejt ki, mint a csúcson, viszont semmi okunk föltenni, hogy az alsóbb tájakon a természet irtózása az űrtől nagyobb volna, mint a felső tájakon."
Pascal nem egyedül végezte első kísérletét, Périer nevű, tudós sógora volt a kivitelező. Périer a 4300 láb magas, Párizs melletti Puy de Dome nevű hegyen végezte a kísérletet, a következő módon. A hegy tövénél, Clermont-ban, két üvegcsőben állított elő vákuumot. Mind a két higanyoszlop 26 hüvelyk, 3,5 vonal magasságú volt. Most az egyik csövet otthagyta a helyén, megjelölte az üvegen a higanyoszlop magasságát, és megkérte az egyik bámészkodót, maradjon egész nap a készülék mellett és figyelje, mutatkozik-e valami változás, de persze ne nyúljon a csőhöz.
Ő maga fogta a másik csövet és több tanú kíséretében fölvitte a Puy de Dome csúcsára. Ott 500 toise-zal az első hely magassága fölött újabb légüres teret állított elő a higanyoszloppal. Ennek magassága most 23 hüvelyk és 2 vonal volt, míg lent Clermont-ban, ugyanebben a csőben 26 hüvelyk 3,5 vonal magasságban állott a higanyoszlop; a különbség tehát a két higanyoszlop magassága között 3 hüvelyk és l 1/2 vonal volt (8,5 cm körül), ami igen tekintélyes eltérés. (Ha a hegy magassága 1000 m körül volt, durva számítással a légnyomás csökkenése kereken 100 mm, azaz 10 cm körül kellett hogy legyen, mert a föld közvetlen közelében minden 10 cm-es emelkedésnek kb. 1 Hg mm légnyomáscsökkenés felel meg, a Hg fajsúlya ugyanis kereken 1000-szer nagyobb, mint a levegőé. Pascalék mérései egyrészt persze még nem lehettek túl pontosak, másrészt jelentős bizonytalanságot okozott az akkori — egymástól gyakran eltérő — mértékegységek átszámítása.) Mikor lefelé jöttek a hegyről, megismételték a kísérletet: a higanyoszlop magassága erősen csökkent, a magasságváltozásnak megfelelő mértékben. Périer így közölte ezt: „Ez nem csekély elégtételünkre szolgált, mert azt láttuk, hogy a higanyoszlop magassága a hely magasságához igazodik." Mikor pedig visszatért Clermont-ba, a higanyoszlop magassága változatlan volt. A megfigyelő személy azt mondta, hogy egész napon át nem változott.
A városban azonnal híre ment Périer csodálatos kísérletének. A hitetlenkedők megkérték, végezze el a kísérletet Clermont legmagasabb tornyán, mert ők is közvetlenül akarják látni a csodát. Périer kedvükben járt, elvégezte a kísérletet, de persze a higanyoszlop most csak pár vonalnyi szintkülönbséget mutatott, hiszen a magasságkülönbség is csekély volt, de az eltérés mégis megvolt, mutatva az eredeti feltevés helyes voltát.
(Blaise Pascal 1623-ban született Clermont-Ferrand-ban. Már kisgyermek korában feltűnt rendkívüli matematikai képességével. Még nem is kapott matematikai oktatást, mikor rájött, hogy minden háromszögben a szögek összege 180 fok. Tíz éves korában feltűnt neki, hogy egy megcsendített pohár csengése rögtön megszűnik, ha kézzel megfogják; elgondolkozott ezen a dolgon és tudományos értekezést írt a hangról.

Számos fontos matematikai tétel őrzi nevét a számelméletben, geometriában. A fizikában a légnyomás mellett a folyadékok fizikájával is foglalkozott és Stevintől függetlenül hasonló eredményekre jutott. Tizenkilenc éves korában számológépet talált fel, mely nagy feltűnést keltett. Ennek példájára szerkesztett Leibniz, a kor egyik legnagyobb matematikusa és filozófusa olyan gépet, amely már szorzott és osztott is. Sajnos amúgy is rövid életének is csak néhány évét szentelte matematikai és fizikai kutatásainak. 1650 körül betegsége miatt kedélyállapota megromlott, és vallási rajongásban keresett vigasztalást. 1662-ben halt meg.)
11. ábra. Edényes barométer
Így állott a légnyomás problémája, mikor a firenzei fizikusok, a Kísérleti Akadémia tagjai újból kezükbe vették a dolgot. Új fajtájú higanyos légsúlymérőt szerkesztettek, amely alkalmas volt másféle kísérletek végzésére is.
A mellékelt ábra mutatja a készülék szerkezetét; a pontocskák a függőleges üvegcső oldalán apró, hozzáforrasztott üveggyöngyök, ez volt a fokbeosztás (11. ábra).
Az akadémikusok végleges bizonyítékot akartak arra, hogy a légköri levegőnek a CBD higanyfelületre gyakorolt nyomása tartja meg a magasban a higanyoszlopot az A csőben. Egyszerű módosítást csináltak az alsó tág edényen: rövid kis oldalcsövet forrasztottak rá. Ha most ennek a végére légmentesen ráhúzták egy szivattyú csövét és ennek dugattyúját meghúzták, akkor az edényen belül levő levegő megritkult és a higanyoszlop jelentősen süllyedt. Viszont ha a szivattyú segítségével több levegőt nyomtak belé, a légnyomás nagyobb lett, a csőben levő higany magasabbra emelkedett, mert a CBD felületről a nyomás áttevődött a csőben levő higanyra.

12. ábra. Edény vákuumban végzett kísérletekhez
Ennek az egyszerű készüléknek a segítségével még valami fontos dolgot fedeztek föl az akadémikusok: a légnyomás függ a hőmérséklettől is. Nem tudni, melyikük eszelte ki ezt a kis elmés kísérletet. (Az Akadémia tagjai ugyanis megfogadták, hogy eredményeiket közösen, egyének nevének említése nélkül teszik közzé.) Az alsó tág edény kis oldalcsövét légmentesen elzárták és jeget raktak az edény köré, amitől a higany fölötti levegő lehűlt. Ekkor azt észlelték, hogy a higanyoszlop leszállt. Viszont, ha melegítették a higany fölötti levegőt, akkor a légnyomás fokozódott, a higanyoszlop magasabbra emelkedett. Ezeknek az aránylag egyszerű kísérleteknek igen nagy jelentőségük volt a természeti jelenségeknek idáig úgyszólván ismeretlen területén.
Az Akadémia tagjai végeztek kísérleteket légüres térben is. Ez persze elég nehéz volt, hiszen nem tudtak másként előállítani légüres teret, mint a Torricelli-féle űrt a higanyoszlop fölött, ahhoz pedig nem lehetett hozzáférni. Akadt közöttük ötletes ember, aki megoldotta ezt a problémát is (12. ábra). Az ábrán látható módon kiszélesítették a Torricelli-cső felső végét úgy, hogy az fedéllel légmentesen zárható legyen. Belül mindenféle tárgyakat erősítettek erre a fedélre, hogy majd megnézzék, hogyan viselkednek ezek a légüres térben. Például hozzáerősítettek egy állati hólyagot, amelyben csak kevés levegő volt s erősen bekötözték a nyílását. Akkor aztán az ismert módon előállították a Torricelli-űrt. A hólyag légüres térbe került, felfúvódott. Elhelyeztek benne azután apró állatokat is, de nem tudták megállapítani, hogy azok a felszálló higanygőzöktől vagy a levegő hiányától döglöttek-e meg.

13. ábra. A Kísérleti Akadémia által használt hőmérő
Nem ismerjük ugyan bizonyosan a hőmérő igazi feltalálóját, de az bizonyos, hogy a Kísérleti Akadémia tagjainak köszönhetjük a mai értelemben vett első hőmérőt. Már Galilei előállított egy készüléket hőmérséklet mérésére, de nem is nevezte másként, mint thermoskopnak (hőmutató), mert csak azt lehetett megállapítani vele, hogy a hőmérséklet emelkedett vagy süllyedt, de még ezt se bizonyosan, mert a levegő kiterjedésén alapult és így változást mutatott akkor is, ha a légnyomás változott meg, nem pedig a hőmérséklet.
Az Akadémia tagjai úgy szerkesztettek hőmérőt, hogy hosszú és nagyon szűk keresztmetszetű üvegcső végére üres üveggolyót forrasztottak. Ezt folyadékkal töltötték meg, de a légnyomás befolyását kiküszöbölték úgy, hogy eleinte pecsétviasszal zárták el a cső nyílt végét, majd későbben beforrasztották. A csövet és golyót borszesszel töltötték meg, ezzel a folyadékkal mérték a hőmérsékletet. A fokokat parányi ráforrasztott üveggolyócskák jelezték a csövön (13. ábra). A készülék nem is lett volna rossz, de más baj volt: nem voltak határozott kiinduló, illetve alapul szolgáló pontjaik, mint ahogyan ma a víz fagyás- és forráspontját vesszük alapnak. Az egyik fix pont volt az a legalacsonyabb hőmérséklet, amelyet elő tudtak állítani, a másik a Toscanában észlelt legnagyobb meleg.
Az Akadémia feloszlása után a tagok persze folytatták a kísérletezéseiket és akkor történt, hogy az Akadémiának egy Renaldini nevű ötletes tagja rátalált a ma is használt és könnyen ellenőrizhető alap-pontokra: a víz fagyáspontjára és forráspontjára. A Kísérleti Akadémia nyomtatásban megjelent dolgozatai közül egyikben leírást is találunk arra, hogyan kell elkészíteni egy hőmérőt: „Az üvegfúvó először állítson elő alkalmas nagyságú golyót és forrasszon bele csövet. A töltés aztán a következő módon történjék. Föl kell melegíteni a golyót és a cső nyílt végét hirtelen borszeszbe mártani. Az utolsó töltést olyan tölcsérrel végezzük, amelynek nyaka nagyon vékonyra van kihúzva. Előzetesen egyenlő részekre osztjuk be a csövet és minden fokot ráégetett gyöngyökkel jelölünk meg. Akkor lehűtjük a hőmérőt, majd felmelegítjük, így határozzuk meg pontosan a szükséges borszesz-mennyiséget és ha a borszesz elérte a kívánt legmagasabb állást, hermetikusan elzárjuk a csövet."
Mai fizikai órákon gyakran mutatnak be a tanárok egy egyszerű kísérletet annak bizonyítására, hogy a víz kiterjed, amikor megfagy. Üvegedénybe vizet tesznek, megfagyasztják s az edény szétreped. Ezt a kísérletet a toscanai akadémikusok végezték el először egy hűtőkeverékkel, amit salétrommal és szalmiáksóval állítottak elő. Az ő érdemük tehát, hogy először alkalmaztak hűtőkeveréket. Megmérték azt is, mennyire terjed ki a víz, ha megfagy. Úgy találták, hogy a víz és jég térfogatának aránya 8: 9.
A Kísérleti Akadémia tagjainak sokféle kutatásai közül még egyet megemlítünk. Próbálták kísérleti úton megmérni a hang és fény terjedésének sebességét. A hang terjedési sebességét úgy mérték, hogy ágyút sütöttek el, s igyekeztek pontosan meghatározni azt az időt, amely eltelik a tűz felvillanása és a dörgő hang megérkezése között. Az akkori órákkal még nem lehetett ilyen kis időközt mérni, csak ingalengések számolásával (vagy az érverést számolgatta a kísérletező a saját ütőerén). Arról sem tudtak még akkor, hogy a levegő hőmérséklete is befolyásolja a hang terjedését, így ezt nem vették figyelembe. A kísérletek egymástól meglehetősen eltérő eredménye az volt, hogy a hang egy másodperc alatt 1111 párizsi lábnyi* utat tesz meg, ami nem is nagyon messze jár az igazságtól. (361 m/sec lenne, 20°C-os levegőben a hang terjedési sebessége mai mérések szerint 340 m/sec.) Az akadémikusok arra sem gondoltak, hogy a szél befolyásolja a hang terjedési sebességét.
A fény terjedési sebességének megállapításával már Galilei foglalkozott, kísérleteinek alapja fényjelek adása volt, azaz a fényjel adása és észlelése között eltelt időt akarta megmérni. Eredményt az akkori mérőeszközökkel nem érhetett el, hiszen a fény 300 000 km-t tesz meg másodpercenként. A Kísérleti Akadémia tagjai sem tudtak kiokoskodni valami új módszert, amellyel földi távolságok esetében mérni tudtak volna. A XVII. században Olaf Roemer dán csillagász mérte meg először a fény terjedési sebességét csillagászati úton, a Jupiter holdjainak megfigyelése alapján. Földi távolságok esetében csak a XIX. században végeztek sikeres méréseket.
A Kísérleti Akadémia nagyon hasznos, sőt megbecsülhetetlen munkát végzett ama rövid tíz év alatt is, ameddig fennállott. Abban az időben azonban az olasz városállamok politikai hatalma már hanyatlóban volt, és a tudományos kutatás súlypontja lassan áttevődött a nyugati, fejlettebb polgársággal rendelkező országokba. Körülbelül abban az időben már másutt is alapítottak tudományos akadémiákat, így Párizsban és Londonban, ahol a tudósok szabadabban kutathattak, és az egyre fejlődő ipar és kereskedelem részéről támogatásban is részesültek.
6. OTTO GUERICKE, A KÍSÉRLETEZŐ MAGDEBURGI POLGÁRMESTER
Láttuk, hogy a Torricelli-féle űrben végzett kísérletek meglehetősen bonyolultak voltak. Éppen ezért a Torricelli-kísérletnek nem sikerült még véglegesen meggyőzni azokat a természetfilozófusokat, akik az üres tér létezését elvben lehetetlennek tartották. Az első, akinek sikerült légüres teret az általa feltalált szerkezettel előállítania, a XVII. század egyik legjelentősebb kísérletezője, Otto Guericke volt. Sok-sok próbálkozás hozta csak meg az eredményt. Először egy üres hordót töltött meg vízzel és megpróbálta, hogy jól tömített víz-szivattyúval kiszivattyúzza belőle a vizet. Sikerült is kiszivattyúznia egy keveset, de mert a dongák közötti hézagokat nem tudta kellően tömíteni, újra és újra víz szivárgott be a hordóba.
Guericke, szerencsére nem volt az az ember, aki meghátrál a kudarc után. Ha nem tudja tömíteni a hordót, majd fémből készült edénnyel próbálkozik. Rézgömböt készített, amelybe csappal ellátott cső volt forrasztva. Ennek a csőnek segítségével összekötötte a rézgömböt egy közönséges szivattyúval; a gömbből kiszívott levegőt a szivattyú csapján át ki lehetett ereszteni. Ez volt Guericke első légszivattyúja; nagy haladást jelentett a fizikában és a technikában. Később megjavította, egyszerűsítette ezt a készüléket, és sok értékes vizsgálatot végzett vele a levegő tulajdonságaira vonatkozóan. Ő is bebizonyította, hogy a levegőnek is van súlya és hogy a levegő rugalmas.
Nem sokkal a légszivattyú föltalálása után Guericke nyilvános bemutatót rendezett vele. Eleinte könnyen lehetett ide-oda mozgatni a dugattyút, de ez hamarosan mind nehezebb lett. Amikor Guericke azt hitte, hogy most már majdnem minden levegőt kiszivattyúzott a rézgömbből, ez hirtelen nagy pukkanással felrepedt. Guericke hamarosan rájött, mi okozta ezt a bajt: nem volt egyenletesen vastag az a rézlemez, amelyből a gömböt kovácsolták, egyik vékonyabb lemezrész nem bírta el a külső nagy nyomást, és ezért repedt be a gömb. Miután erre figyelmeztette a rézverőmestert, az ezután készült gömbökkel nem történt többé hasonló baj.
Guerickének egyik eredeti légszivattyúját máig megőrizte a müncheni híres tudománytörténelmi múzeum. Szerkezete jól látható a 14. ábrán. Egy háromlábú állványt csavarokkal a padlóhoz erősítettek. A lábak között helyezték el a szivattyú csövét. Két láb között jobbfelé nyúlik ki az a fogantyú, amellyel a szivattyúban a dugattyút tologatják ide-oda. A szivattyú szelepei bőrből készültek. A készülék fölött volt egy csappal ellátott rézgömb. A szivattyú és a gömb között tölcsér látható; az összes alkatrészek tömítése után ezt vízzel töltötték meg, hogy így akadályozzák meg levegő újbóli behatolását. A kép jobb alsó sarkában vödör látható, ezt is vízzel töltötték meg, és a szivattyú csöve alá állították hasonló okokból. Persze akkoriban még nagy nehézségeket okozott a tömítés. A képen még egyes kisebb alkatrészek láthatók külön-külön, melyek mind Guericke ügyességére mutatnak.
Guericke nemcsak a technikai szerkesztésben volt ötletes, hanem új kísérletek kigondolásában is, amelyek a levegőnek, illetve a légnyomásnak valami új tulajdonságát árulták el. Egyszer kiszivattyúzta a levegőt a rézgömbből. De mikor a csapot megnyitotta, nem levegőt engedett bele, hanem összekötve a gömb csapját egy csővel, ennek végét a vízzel telt vödörbe tartotta. Levegő helyett természetesen víz tódult a gömbbe. Akkor újabb ötlete támadt: meg kellene próbálni, milyen magasságba, illetve távolságba lehetne tartani a gömböt a vödörtől. Ezért úgy rendezte el a kísérletét, hogy a vödröt lent állította fel az udvaron, a gömböt pedig felvitte házának középső emeletére. Amit előre elgondolt, bekövetkezett: a víz súlya ellenére is, éppúgy felemelkedett a gömbbe! Miután a kísérlet ilyen jól sikerült, még hosszabb csövet vett elő, s a víz felemelkedett egészen a harmadik emeletig. A negyedik emeletig már nem sikerült felszívni a vizet.

14. ábra. Guericke légszivattyúja
A mellékelt ábra Guericke eredeti könyvéből való (15. ábra). Középen látható az n—m dézsa, fölötte és mellette a négy darabból álló cső (b—g), i a rézgömb. Mindegyik cső el van látva egy kis tányérral, ez is arra való, hogy az összeállítás után vizet öntsenek beléjük tömítés céljából. A ház sarkánál az ablakok előtt látható a teljesen összeállított készülék. De az volt a baj, hogy a csövek rézből készültek, átlátszatlanok voltak, ezért Guericke nem tudta megállapítani, meddig hatol fel a víz. De könnyen segített ilyen csekélységen. Felül közbeiktatott egy üvegcsövet, ezt ablakgittel tömítette és megismételte a kísérletet. Mikor most megnyitotta az üres rézgömb csapját, a víz rohant felfelé, fent még lebegett egy kicsit a szintje, majd megállapodott. Megjelölte a víz szintjét az üvegcsövön, aztán függőónnal megmérte ennek távolságát a föld színétől: 19 magdeburgi könyöknek találta, ami kb. 10 méternek felel meg.
Guericke nem eresztette ki a vizet a csőből, hanem heteken át figyelte. Észrevette, hogy a vízoszlop magassága néha egy-két arasszal magasabb, máskor alacsonyabb. Nagyon bajos volt figyelni a vízoszlop magasságát. A nagy kísérletező ötletessége segített ezen a bajon is. Fából faragott kis emberfigurát tett a víz tetejére, a víz hol feljebb emelte a figurát, hol lejjebb eresztette, amellett a figura keze rámutatott az üvegcsövön alkalmazott beosztásra. Ez a vízbarométer jól látható az ábra baloldalán.
Guericke már pontosan tisztában volt vele, hogy a légnyomás változtatja meg a víz magasságát. Szó szerint ezt mondotta: „Ha a légüres tértől való irtózás okozná a víz emelkedését, akkor a víznek vagy korlátlan magasságig követnie kellene a vákuumot, vagy mindig ugyanazon magasságban kellene állnia. De hogy ez a magasság változik, a legbiztosabb jele annak, hogy nemcsak a víz fölemelkedése, hanem az ingadozás is valami külső ok folytán áll be. Tehát a víz magassága a csőben nem attól van, mert a természet irtózik az üres tértől, hanem ez jelenti az egyensúlyt a vízoszlop súlya és a légnyomás között.”

15. ábra. Guericke-féle víz-barométer
Ez a lángeszű ember talán nem is nagyon sokáig figyel-gette a különös készüléket, amíg rájött arra a végtelenül fontos összefüggésre a légnyomás és időjárás között, amelynek ismeretén alapul részben a mai meteorológia. Már meg tudta jósolni a viharokat! Így ír erről: „Mikor a múlt évben a szörnyű vihar dühöngött, a levegőnek különös, rendkívüli elváltozását észleltem. Mikor ezt láttam, közöltem a körülállókkal, hogy valahol kétségtelenül nagy vihar tört ki. És alig telt bele két óra, mikor a mi vidékünkre is betört a vihar.” Tudjuk, hogy a vízbarométer gyors változása a vízoszlop hirtelen leszállása volt, és pontosan tudjuk a napját is ennek az első híres időjóslásnak: 1660. december 6.
Magától értetődik, hogy ez a ragyogó elme kutatta a légnyomás okát is. Nem fogadta el azokat a kalandos magyarázatokat, amelyeket kortársai vallottak, hanem így nyilatkozott erről: „Egyesek a csillagok minden oldalról érkező sugaraiban keresik az okot... Ha így volna, a földgolyónak is meg kellene kapnia ezt a nyomást és ellen kellene állania ennek. De ha két test nyomja egymást, akkor a köztük levő tárgy is kapja azt a nyomást mindkét oldalról. Ebből szükségszerűen következnék, hogy a levegő felső részei ugyanúgy nyomódnak össze, mint az alsók, de a kísérletek megcáfolják ezt. Miután az alsó levegő erősebb nyomás alatt van, mint a felső, és nemcsak a magas hegyeken észlelhető ez, hanem már a templomok tornyain is, ebből következik, hogy a levegő nem nagyon messzire terjedhet ki a Föld felületétől, hanem a magassága nagyon csekély lehet a csillagok nagy távolságához képest.”
Most pedig írjuk le a magdeburgi féltekék históriáját, azt a jelenetet, amely Guerické-nek véglegesen biztosította a dicsőséget és világhírt, amikor uralkodója előtt mutatta be korának egyik legfényesebb felfedezését.
1654-ben birodalmi gyűlés volt Regensburgban. Felvonultak a német-római birodalom fejedelmei III. Frigyes császár vezetésével. Nagyon díszes és ünnepélyes felvonulás volt, amelyen részt vett minden fejedelem, gróf, püspök stb. A menetet egy egyszerű kocsi zárta be, amelyen különös, még soha nem látott eszközök voltak. A kocsi mögött egyszerűen öltözött férfi lovagolt, Magdeburg polgármestere, leghátul pedig tizenhat nehéz lovat hajtottak. Guericke uralkodójának akart bemutatni néhány csodás kísérletet az általa föltalált légszivattyúval. A bemutatás egyenesen a császár parancsára történt, mert senki sem akart hinni abban, hogy létezhetik „légüres tér”.
Mikor az ünnepség számára kijelölt térre értek, Guericke izmos szolgái két nagy, nehéz, üres félgolyót emeltek le a kocsiról. Guericke egymáshoz illesztette a két félgolyót, amelynek szélei oly kitűnően voltak összecsiszolva, hogy légmentesen zártak. Hozzákapcsolta a légszivattyút, amelynek a rúdját a szolgák verejtékezve húzgálták ide-oda félórán át. Mindkét féltekéhez erős fémkarika volt forrasztva. A szolgák most nyolc-nyolc lovat fogtak a golyó két oldalára, aztán elkezdték kétfelé hajtani a lovakat, nem kímélve az ostorokat. A lovak megvetették a lábaikat és izmaik minden erejével húztak kétfelé, mégsem sikerült a két féltekét szétválasztani, melyeket a roppant légnyomás tartott össze. Ez a légnyomás nagyobb erőt jelentett, mint tizenhat izmos ló ereje. De mikor Guericke megnyitotta a légszivattyú csapját, levegő hatolt a golyóba, és ez rögtön szétesett két darabra.
A császár nagy elismerését fejezte ki. Mikor a tömeg oszlóban volt, egy Valerianus nevű szerzetes-fizikus lépett oda Guerickéhez s elmagyarázta neki, hogy Torricelli egészen másként állított elő légüres teret. Guericke így értesült arról, hogy előtte már foglalkozott valaki a légüres tér és légnyomás problémáival. Abban az időben még gyakran előfordult, hogy egyik tudós véletlenül, és néha évtizedek múlva, értesült mások munkásságáról. A würzburgi püspök mindjárt megvette Guericke készülékét és hazavitte, hogy saját tudósai kísérletezzenek vele, így Caspar Schott, würzburgi tanár, aki jelen volt a féltekék bemutatásánál is, tíz évvel későbben (1658) megjelent „Technikai kuriózumok” című könyvében leírta a híres kísérletet is: „Minden tartózkodás nélkül elismerem, hogy ezen a területen még soha nem láttam csodálatosabb valamit. Sőt úgy vélem, a Nap sem látott még hasonlót, még kevésbé csodálatosabbat, mióta a világ megteremtődött.” Egyébként Schottnak ebből a könyvéből értesült Boyle is Guericke kísérleteiről, mert Guericke csak 1672-ben tette közzé vizsgálatait.
Guericke nem találomra, a jó szerencsében bízva ment neki ennek a kísérletnek. Előzetes számításokat végzett. Miután azt már kikísérletezte, hogy a levegő nyomása akkora, mint egy 19 könyök (10 m) magas vízoszlopé, kimutatta azt is, hogyan lehet kiszámítani egy tetszés szerinti magasságú légoszlop súlyát, illetve nyomását. Kiszámította, hogy ha az oszlop átmérője 2/3 könyök, akkor ilyen levegőoszlop súlya, illetve nyomása 2687 font. E számítás alapján készítette el a két féltekét, kísérlete sikerült is.
A légüres vagy légritkított tér kutatásánál Guericke nem maradt meg ennél a mutatványos résznél, bár nagy dolog volt ez is. A mai fizikatanár a középiskolában minden évben bemutatja a következő kísérletet: ébresztőórát tesz üvegbúra alá, aztán kiszivattyúzza belőle a levegőt, berregteti az ébresztőórát, de ennek éles hangja most nem hallatszik, mert a hang nem terjed légüres térben. Nos, ezt a kísérletet Guericke végezte először. Ugyanezzel a kísérlettel kimutatta, hogy a fény viszont akadálytalanul terjed légüres térben is.
Élettani kísérleteket is végzett ez a lángeszű kutató, amilyeneket a Kísérleti Akadémia tagjai is csináltak. Guericke bizonyította be először, hogy élet nem lehetséges levegő nélkül. Ha kisebb állatokat tett be gömbjébe, s utána kiszivattyúzta a levegőt, a kísérleti állatok gyorsan elpusztultak. Halakkal különös dolgokat tapasztalt, ha az akvárium fölött megritkította a levegőt. Azoknál a halaknál, amelyeknél az úszóhólyagnak kivezető csöve van, a levegő buborékolva tódult ki a hólyagból: az olyan halaknál, amelyeknél az úszóhólyag teljesen zárt, a légritkítás hatására a hólyag levegője is megritkult, ezek a halak erősen felfúvódtak. Guericke azt is kimutatta kísérletekkel, hogy légüres térben a tűz is kialszik, nemcsak az élet. Ő figyelte meg elsőként, hogy az égéshez levegő kell: a következő században hatalmas tudományos vita folyt erről. De ő világos kísérlettel mutatta ki, hogy zárt térben a gyertya már akkor is elalszik, ha a levegőnek csak egy kis része elfogy.
Gilbert volt az első tanulmányozója a villamosságnak, kísérleteit fentebb ismertettük. Ebből tudjuk, hogy a XVII. században még alig tudtak valamit erről a roppant fontos és hatalmas fizikai erőről. Guerickének köszönhetjük, hogy abban a században még egyet-kettőt léptünk előre.
A kénről már Gilbert megállapította, hogy ha megdörzsöljük, elektromos lesz. Guericke is ezt az anyagot választotta kísérletei tárgyául. Nagyobb üveggolyóba olvasztott ként öntött. Amint a kén megszilárdult, az üveget széttörte és így nagy kéngolyót kapott. Ebbe hosszú fapálcát illesztett be tengelynek (16. ábra). A tengely egyik végére forgatót csinált, s a golyó két oldalán kiálló tengelyt alátámasztotta. Ha most a kéngolyót forgatta és közben saját száraz tenyeréhez dörzsölte, a kéngolyó a dörzsöléstől elektromos lett. Kétségtelenül ez volt az első villamozó gép, amelyet valaha készítettek. A megdörzsölt kéngolyó magához vonzott papírszeletkéket, tollat és más könnyű tárgyakat. Guericke addig kísérletezett ezzel az eszközzel, míg végre felfedezte azt, ami elkerülte Gilbert figyelmét: hogy az egynemű villamosságú testek taszítják, a különnemű villamosságú testek vonzzák egymást. Sőt közel járt annak felfedezéséhez is, hogy az elektromosság vezethető! Rájött ugyanis, hogy lenfonál segítségével elvezetheti a kéngolyóban dörzsölés folytán keletkezett elektromosságot. Észrevette azt is, hogy ha a kéngolyó eltaszított egy testet, újból vonzza ezt, ha érintkezésbe jött az ember ujjával vagy a padlóval: például ha egy tollat tett a villamos kéngolyó meg a padló közé, a toll le és föl ugrált.

16. ábra. Elektromos gömbökkel végzett kísérlet
(Otto Guericke 1602-ben született Magdeburgban. 15 éves korában jogot kezdett tanulni, de aztán áttért a matematikára és mechanikára. Hivatalnok lett szülővárosában. Magdeburg elpusztult a harmincéves háborúban, Guericke teljesen elszegényedett és svéd szolgálatba állt mint építész. Majd visszakerült szülővárosába és annak nagyrabecsült polgármestere lett. 1686-ban halt meg.)
7. A BOYLE—MARIOTTE-TÖRVÉNY
A Torricelli által fölvetett légnyomás-probléma az egész XVII. század folyamán nem hagyta nyugodni az európai tudósokat, és újabb és újabb kísérletezésekre ösztökélte őket.
Az előbbi fejezetben említettük, hogy Boyle (1627—1691), a XVII. század egyik legkiválóbb angol kémikusa, Schott könyvéből értesült Guericke kísérleteiről. Ezek nyomán ő is megszerkesztett egy légszivattyút, amelyik jobb volt, mint a magdeburgi polgármesteré. Ezenkívül sok új ötlete is támadt. 1660-ban könyvet adott ki „Új kísérletek” címmel. Ebben részben a magdeburgi kísérleteket írta le, részben új, saját kísérleteit. Ilyen kísérletek folyamán ismert föl egy fontos fizikai törvényt, amelyet a mai gyáripar nagyon kiterjedten alkalmaz: légritkított térben a víz már jóval 100 fok alatt is felforr. Boyle tehát rájött arra, hogy a folyadékok forráspontja függ a rájuk nehezedő nyomástól.
Minden középiskolai tanuló megtanulja a törvényt: a gázok térfogata fordítottan arányos a nyomással. Ezt a törvényt Boyle és tőle függetlenül Mariotte fedezte föl, ezért nevezik ma Boyle -Mariotte-törvénynek. Boyle a következő egyszerű kísérlettel jött rá erre (17. ábra). U alakú üvegcsövet készített, ennek rövidebb ágába 12 köbhüvelyk levegőt zárt be higany segítségével. Aztán higanyt öntött az üvegcső hosszabb nyílt ágába. Minél több higanyt öntött be, annál kisebb térre szorult össze az elzárt levegő, vagyis annál kisebb lett a térfogata. Mikor közelebbről megvizsgálta a dolgot, a térfogat csökkenésének matematikailag kifejezhető szabályszerűségét vette észre: két légköri nyomásnál a 12 köbhüvelyknyi bezárt levegő már csak 6 köbhüvelyknyi térfogatot mutatott, három légköri nyomásnál 4 köbhüvelyknyi térfogatot, ami az eredeti térfogatnak egyharmada. Boyle még így fejezte ki ezt az arányosságot: a levegő az összes nyomó erők arányában sűrűsödik meg. Később Mariotte adta meg a törvénynek a fentebbi, szabályosabb fogalmazást.

17. ábra. Boyle készüléke a nyomás és térfogat közötti összefüggés megállapítására
A francia Mariotte (1620— 1684) is nagyon ötletes kísérleteket végzett a gázok mechanikájának területén. „Értekezés a levegő természetéről” című könyvében írja le ezeket (1679).
Egyik érdekes kísérlete a következő volt: barométert belemártott eléggé mély tiszta vízbe.
Észrevette, hogy 14 hüvelyk magasságú vízoszlop a higanyoszlopnak 1 hüvelyknyi emelkedését okozta. Ebből az egyszerű megfigyelésből mindjárt egy fontos következtetést vont le: „Ez nyilván onnan ered — írja Mariotte —, hogy a higany fajsúlya 14-szer nagyobb, mint a vízé.”
Kimondta továbbá, hogyha a higanyoszlop 28 hüvelyk magasan áll a barométerben, ebből az következik, hogy ez a higanyoszlop éppen olyan súlyú, mint a hasonló alapú légoszlop, amely a légkör külső határáig terjed. Lényegében ezt mutatta a Torricelli-kísérlet is, de ezt az értelmezést Mariotte fogalmazta meg elsőnek.
Boyle és Mariotte bebizonyították, hogy a levegő térfogata fordítva arányos a nyomással.
Mariotte fölvetette a kérdést: vajon érvényes-e a törvény akkor is, ha csökken a nyomás? Döntsön itt is a kísérlet. Mariotte higanyt és levegőt zárt egy barométercsőbe és elvégezte a Torricelli-féle kísérletet. A higany alásüllyedt. Mariotte a következő magyarázatot fűzi ehhez: „Miközben a higany leesik, a csőben levő levegő kiterjed. Ennek következtében kisebb lesz a feszültsége. A higany egy része a csőben marad. Éspedig a higanyoszlop magassága a bezárt levegő sűrűségétől fog függeni, A csőben lebegve maradt higany kiegyenlíti a légnyomás maradékát, úgyhogy egyensúlyi állapot jön létre a légkör nyomása között egyrészt és a higanyoszlop nyomása között másrészt, amit még fokoz a bezárt levegő feszültsége."
A higany nélküli fémbarométer (aneroid) gondolata, amelyet ma általában használnak, Leibniznél, a nagy német filozófusnál merült fel először. Erről ezt írja: „Én azt hiszem, meg lehetne csinálni egy higany nélküli barométert, valami zárt fújtató vagy szivattyú módjára." Egyszer egyik Bernoulli-hoz, a nagy matematikushoz írott levelében megint visszatér a gondolatra. „Olykor elgondolok valami hordozható barométert, amely órához hasonló kis tartályba volna zárva. Ennél nem szerepelne higany, hanem valami fújtató-féle, amelyet a légnyomás igyekszik összenyomni, de valami elasztikus rugó ellenáll ennek."
Leibniz jó elgondolása csak lassan valósult meg. Zeiher 1760-ban megszerkesztett valami rugós barométert, de nem vált be. Végül Vidi készítette el 1848-ban a mai fémbarométert, amelynek fő alkatrésze vékony, hullámos fémlemezből készült kis zárt doboz, amelyben erősen megritkítják a levegőt.
Mariotte még az optika terén is tett egy nagyszerű felfedezést: ő fedezte fel a szem vakfoltját. Ez a vakfolt az a pici része a szem belső felületének, ahol a látóideg belép a szembe; a szemnek ez a része a fényre érzéketlen, ott nem tud fölvenni fényingereket.
(Edme Mariotte életéről keveset tudunk. 1620-ban született Bourgogne-ban, Dijon mellett volt pap, 1666-ban választotta tagjául a párizsi Akadémia. Párizsban halt meg 1684-ben. Optikai vizsgálatai a látás problémája mellett kiterjedtek az ún. hold- és napudvar értelmezésére, valamint a színek természetére, ahol ellentétbe került Newton elméletével. Foglalkozott még az ütközés kérdésével is, amely a XVII. századnak egyik sokat vitatott mechanikai problémája volt.)
8. KÍSÉRLETEK A GŐZ FESZÍTŐEREJÉVEL: PAPIN
Láttuk, hogy már az alexandriai tudósok felfedezték a gőz feszítőerejét, de ennek a felismerésnek gyakorlatban való hasznosítására még az ókori rabszolgatársadalomban vagy a feudális középkorban nem kerülhetett sor. A XVII. században azonban az iparosodás fejlődésével egyre sürgetőbben kezd felmerülni új energiaforrások szükségessége. Különösen két területen lép fel ez az igény. Az egyik a fejlődő manufaktúrák területe: a kézierő egyre kevésbé válik elegendővé az ipar igényeinek kielégítésére; a másik a szénbányászat, ahol az egyre mélyebbről kibányászandó szén felszínrehozásánál több és több problémát okoz a minden szénbányában fellépő nagy vízmennyiségnek emberi, illetve állati erővel való eltávolítása. Ez az a nehézség, amely az első gépnek, a gőzgépnek a felfedezését elősegítette. A fejlődés természetesen igen lassú folyamat volt és csak a XVIII. században James Watt (1736—1819) gőzgépe hozta meg a gyakorlatban a döntő változást, amit az emberi civilizáció szempontjából a gépesítés jelent. Addig azonban számos tudományos és technikai próbálkozás történt, amelyek egyaránt hozzájárultak a hőtannak mint tudománynak a fejlődéséhez és a gyakorlatban használható gőzgép technikai megvalósításához. Ezen a területen a XVII. században különösen Denis Papin ezirányú kísérletei említésre méltóak.
Papin mint a nagy holland fizikus, Huyghens (1629—1695) asszisztense kezdte pályafutását. Huyghens megjavította többek között a távcsövet és néhány fontos csillagászati felfedezést tett vele, feltalálta az ingaórát, s feltalálta a zsebóra billegőjét, rájött, hogyan lehet óra segítségével meghatározni a tengeren a földrajzi hosszúságot, megjavította a barométert, hullámelméletet állított fel a fény természetéről, fölfedezte a kettős törést, a centrifugális erőt stb. Papin kísérleteihez is Huyghens egy gondolata adta az alapot.
Mikor Franciaországba is eljutottak a hírek Guerickének a légnyomással kapcsolatos kísérleteiről, ugyanakkor egy helyi szükséglet is lépett fel Párizsban. XIV. Lajos király pompás szökőkutakat építtetett Versailles-ban. Ehhez valami erőmű kellett, amely a Szajna vizét belenyomja a szökőkútba. Az ötletes Huyghens arra gondolt, hogy a légnyomást használja fel erre a célra. Gépet épített, amelyet lőpor robbantása hajtott. A robbanás dugattyú alatt történt, ereje felnyomta a dugattyút, de amikor a henger lehűlt, a belsejében levő gázok kisebb térfogatot foglaltak el, és a külső légnyomás ismét lenyomta a dugattyút, melyet aztán az újabb robbanás ismét felnyomott. Az alapelv ugyanaz volt, mint a jóval később feltalált robbanómotoré, amelynek ősi feltalálója tehát Huyghens volt. Huyghens a gép megszerkesztésével asszisztensét, Papint bízta meg. El is készítette a gépet, működött is valahogyan. Csak évek múlva, amikor Papin Németországban dolgozott, jött arra a gondolatra, hogy nem lőporral idézi elő a légritkított teret a dugattyú alatt, hanem megpróbálkozik a vízgőz feszítőerejével. Egy kevés vizet tett a hengerbe, elgőzölögtette, s természetesen a vízgőz nyomása is magasba hajtotta a dugattyút; ha a henger lehűlt, a gőz megint vízzé sűrűsödött, de mert a víz sokkal kevesebb helyet foglal el, mint a gőz, megint csak légritkított tér támadt a dugattyú alatt, a légnyomás tehát lenyomta a dugattyút. Ez az első, ún. atmoszférikus gőzgép, amelynél a dugattyút a külső légnyomás nyomja vissza (18. ábra).

18. ábra. Papin első „gőzgépe”
Papin bámulatos szorgalommal évekig dolgozott gépe tökéletesítésén, és sikerült is jobb gépet előállítania. De csodálatos kitartás kellett ehhez. Papin a saját kis kovácsműhelyében barkácsolta, kalapálgatta és reszelgette össze gépét. Hogy milyen bizonyos volt dolgában, mennyire bízott a sikerben, ez kiderül egyik leveléből, amelyet Leibnizhez írt, kora legnagyobb filozófusához, akivel jóbarátságban volt, és aki nagyon érdeklődött kísérletei iránt.
„Biztosíthatom róla, minél előbbre jutok gépemmel, annál többre értékelem ezt a találmányt, amely elméletben a végtelenségig fokozhatja az ember erejét. Ami pedig a gyakorlati oldalát illeti, talán túlzás nékül állíthatom, hogy gépem segítségével egyetlen ember talán száz ember munkáját végezheti el. Persze elismerem, hogy idő kell hozzá, amíg majd ennyire tökéletesítem. Legyen meggyőződve, minden tőlem telhetőt el fogok követni, hogy jól és közmegelégedésre sikerüljön a dolog, bár itt nagyon nehéz kapni csak kissé is használható munkásokat. Mégis remélem, hogy le tudok majd győzni minden nehézséget."
Papin jól látta: gépe már nem száz, hanem sok millió ember munkáját végzi. De nem tudta legyőzni a nehézségeket, nem tudta használhatóvá tenni a gépet. 1706-ban megrendelésre készített egy gépet (szivattyúzásra), és be kellett mutatnia ezt a Hessen-Casseli fejedelemnek. A próba abban állott, hogy bizonyos magasságra kellett felszivattyúznia vizet. Ám az egyes alkatrészek tömítése olyan rossz volt, hogy a víz kicsurgott minden illeszkedési helyen. Maga Papin mondja el egy levélben ennek a sikertelen bemutatásnak sajnálatos történetét, amelyet szintén Leibnizhez írt (1706. aug. 19.):
„Mikor a kísérletre került a sor, azt láttuk, hogy a víz valóban kicsurog minden illeszkedési helyen, a legalsónál olyan nagy erővel, hogy őfensége kimondotta: a kísérlet nem sikerült. Erre alázatosan megkértem, várjon még egy kicsit, mert hiszem, hogy a gép elég vizet fog szolgáltatni, a jelentékeny veszteségek ellenére is, a vízoszlop felszáll a magasba. És valóban, mikor folytattuk a kísérleteket, négyszer-ötször is láttuk, hogy a víz felszállott egészen a cső végéig.”
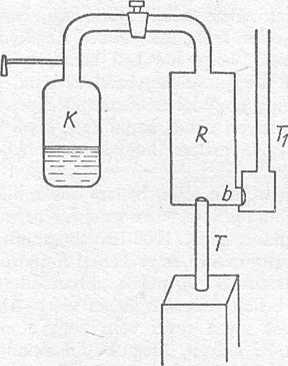
19. ábra. Savery-féle vízemelő gép
Papin tovább fejlesztette elgondolásait. Az előbbinél tökéletesebb gép tervét írja le abban a könyvben, amelyet 1707-ben adott ki Casselben francia nyelven: „Nouvelle maniere pour lever l'eau par la force de feu” (Új módja annak, hogy a tűz erejével vizet emeljünk). Ennek alapján őt tekinthetjük a korszakalkotó találmány szellemi apjának, bár egy Savery nevű angol már 1698-ban megszerkesztett egy gépet, amely a gőz erejével vizet emelt (19. ábra). De Savery gépében a gőz ereje a vizet nyomja fel, míg Papiné-ben a gőz a dugattyút hajtja. Nem tudjuk, hogy Papin valóban megcsinálta-e a könyvében leírt gépet, de valószínű, mert amikor visszaköltözött Londonba, műhelye volt a mai híres újság-utcában, a Fleet Streeten.