APPENDIX B

GOLDEN CONSTRUCTIONS

In the time of Euclid, geometric constructions were restricted to the use of a compass and straightedge only. These “pure” constructions are what appeared in the ancient Greek mathematician’s famous book The Elements, which laid the cornerstone for mathematics education for the next two millennia. As it turns out, there are a lot of ways to derive the golden ratio using only the simple tools mentioned above. Here are two of the most common constructions that can be made with a ruler and compass:

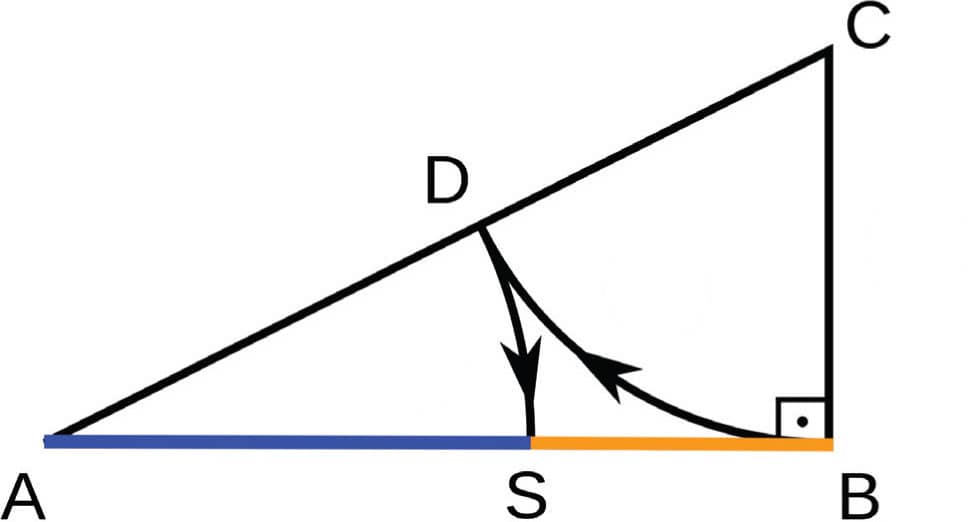
1. Draw a line AB.

2. Draw a perpendicular vertical line BC that is half the height of AB.

3. Draw a line AC to complete the triangle.

4. Draw an arc at point C from point B to point D on the hypotenuse.

5. Draw an arc at point A from point D to point S on line AB.

In this construction, AB/AS = Ф

Here’s another golden ratio construction that can easily be done with a compass and ruler:

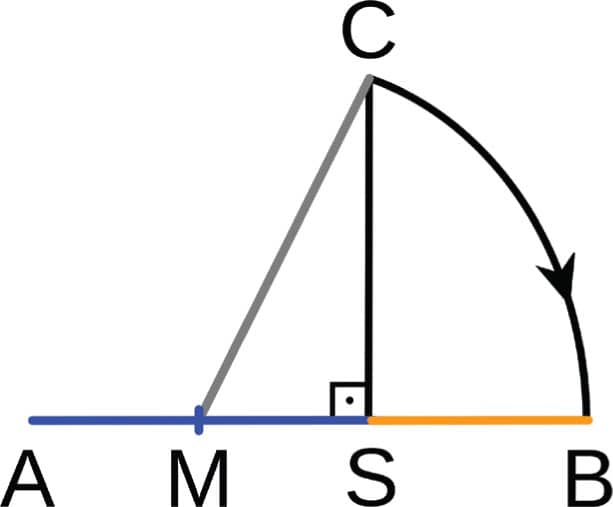
1. Draw a line AS.

2. Draw a vertical line SC that is equal in length to AS.

3. Divide line AS at its midpoint M.

4. Draw an arc at midpoint M from point C to point B on the extension of line AS.

In this construction, AB/AS = Ф.

A Geometric Expression of (1 + √5) / 2

Shown here, we saw that the mathematical expression of the golden ratio is (1 + √5) / 2. Geometer Scott Beach developed a way to represent this expression geometrically:

To construct this, follow these steps:

1. As you did in the first construction of this appendix, create right triangle ABC with the length of side AB equal to 1 and the length of side AC equal to 2. (The Pythagorean Theorem can be used to determine that the length of side BC is √5.)

2. Extend side BC by 1 unit of length to establish point D.

3. Bisect line segment CD to establish point E.

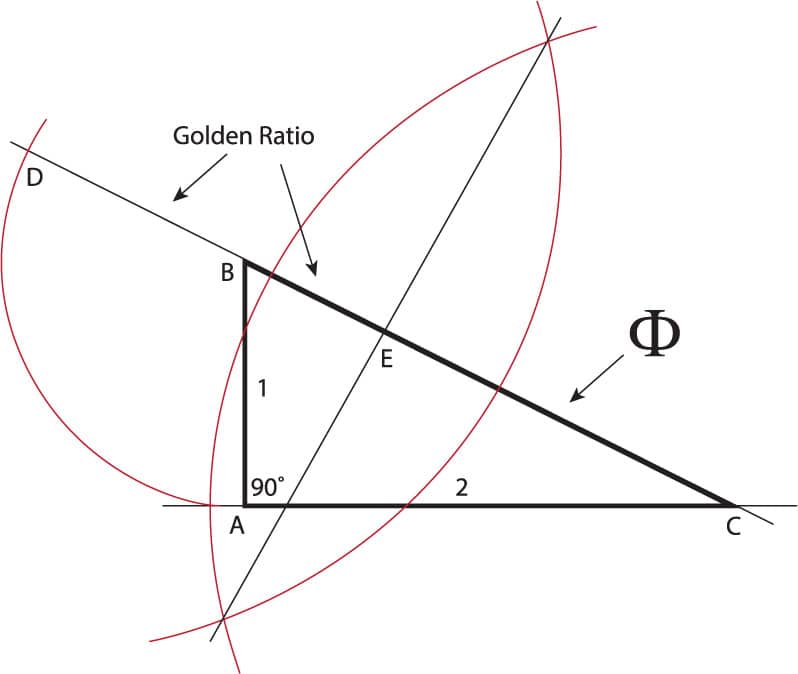
In the resulting graphic representation of (1 + √5) / 2, the segment CD represents 1 + √5, which means that the length of segment CE is equal to (1 + √5) / 2, or Ф. Furthermore, DB/BE = Ф.

Circle Constructions

Among mathematicians, there’s a bit of a competition to see how few lines can be used to create a golden ratio, or how many golden sections can be created with the least number of lines. (Okay, so as competitions go, it’s not exactly the Super Bowl, but then on the other hand nobody will be pondering the winning teams of the NFL two thousand years from now.) Below you’ll find a few ingenious constructions involving circles.

Three adjacent circles

1. Using a compass, draw three 1-inch circles on top of a line, making sure that they touch one another but do not overlap. The segment extending between the bottom of the first and third circles is AC, with a length of 2.

2. Draw a line that connects the top of the first circle to the bottom of the third circle, forming segment BC.

3. Complete the triangle by connecting point B to point A.

4. Add point D where BC intersects with the left side of the second circle.

5. Add point E where BC intersects with the right side of the second circle.

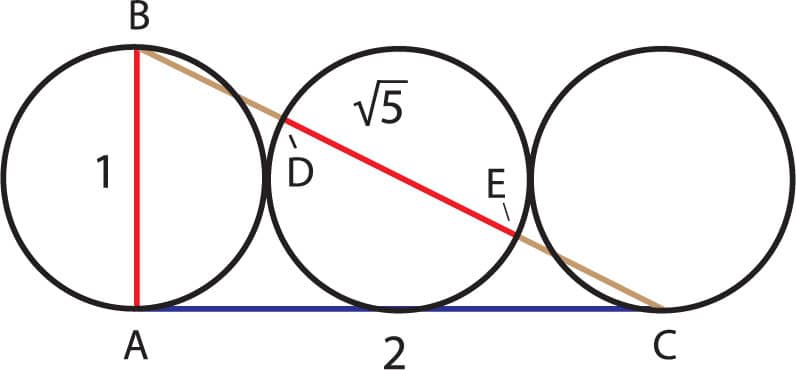
In this construction, both DE/BD and DE/EC = Ф.

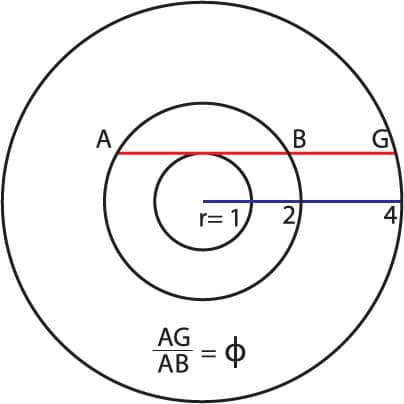
Three concentric circles

1. Draw three concentric circles whose radiuses are in a ratio of 1 : 2 : 4.

2. Draw line AG tangent to the top of the inner circle that connects the middle circle to the outer circle.

Overlapping circles

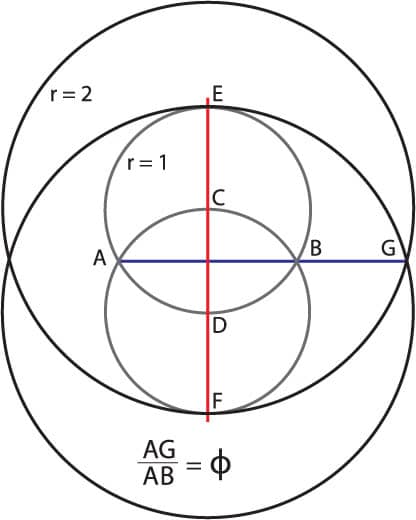
In 2002, Austrian artist and composer Kurt Hofstetter published this construction, involving only four overlapping circles and a line, in Forum Geometricorum:

1. Using a compass, draw two overlapping circles such that the center of each circle (points C and D) defines the radius of the other.

2. Center two larger circles on points C and D, with radii that are twice that of the small circles.

3. Draw a line AG from the left-most intersection points of the two smaller circles (A) to the left-most intersection point of the two large circles (G), as shown.

Below is another construction by Hofstetter:

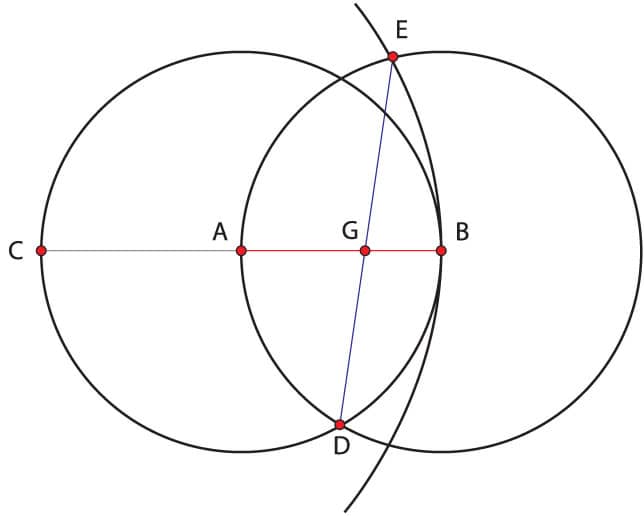
1. Draw a circle around center point A.

2. Draw a point B on the right-most edge of this circle. From center point B, draw a circle that passes through point A.

3. On the left-most point of the first circle, draw a point C.

4. From point C, draw an arc that passes through point B.

6. Where the arc intersects the top half of the second circle, draw a point E. Extend a line from this point to the bottom intersection point of the two circles (D) to form line ED.

7. Finally, draw line AB between points A and B, and then draw a point G at the intersection of AB and ED.

In this construction, AB/AG = Ф.

ORTHOGONS

The above construction of a golden section is the most commonly known of twelve orthogons (aka “dynamic rectangles”) which in essence are rectangular geometric structures that are constructed from a square using only a compass and straightedge. Among orthogons, the one that yields a golden rectangle (ratio: 1/2 + √5/2) is known as the auron, coming from the Latin root aur, meaning “gold.”

Orthogons provide a system of design that, for centuries, has allowed artists and artisans to create consistent, harmonious figures without the need for complicated calculations or measuring devices. Examples of orthogons, with their height to width ratios, include the diagon (√2), quadriagon (1/2 + √2/2), and hemidiagon (√5/2). Information on the application of orthogons to the principles of design is available at www.timelessbydesign.org, a website run by professional artist Valrie Jensen.

The auron.

The diagon is shown top, center, in this scan of this 1575 edition of the first German translation of Vitruvius’s work, Vitruvius Teutsch.