Performance of Digital Signature Schemes on Mobile Devices
D.Y.W. Liu*; G.Z. Xue†; Y. Xie†; X.P. Luo*; M.H. Au* * The Hong Kong Polytechnic University, Kowloon, Hong Kong
† Xiamen University, Fujian, China
Abstract
Exchanges of information (with various types of documents, images and movies) among mobile devices are very common nowadays because these devices have been widely used in people’s daily lives. The fact that the information being handled may be sensitive and valuable has increased people’s awareness in the need for mobile security. In the context of digital communications, the common security requirements include authentication integrity and nonrepudiation. The standard solution is a technique from the cryptographic community known as digital signature. In practice, the solution is quite adequate, since the personal computers of today are perfectly capable of signature generation and verification. In this chapter, we plan to investigate the situation in which everything goes mobile. The main difference is that mobile devices are limited by their computational power and battery capacity. Specifically, we conduct performance evaluations on two digital signature schemes. We examine the computation time and energy consumption in the signature generation and verification process on two mobile devices. Our results show that modern mobile devices are capable of handling digital signatures.
Keywords
Digital signatures; Pairing-Based Cryptography; Energy consumption; Computation cost; Android devices
Acknowledgments
We acknowledge the support from the National Natural Science Foundation of China (No. 61271242, 6137915), the Scientific Research Fund of Sichuan Provincial Department Science and Technology (No. 2015GZ0333), the Innovation Method Fund of China (No. 2015IM020500).
1 Introduction
Mobile devices such as smartphones, PDAs, and tablets are so popular that they are indispensable to humans these days. Large amounts of digital information are being exchanged among the devices. The malicious access or utilization of this information might result in financial loss or the loss of other advantages. Particularly, people are concerned about the authentication, integrity, and nonrepudiation of the information. Authentication ensures that the communicating entity is legitimate, meaning that the entity is the one that he/she claims to be. Data integrity ensures that the information being received is the same as the one sent by an authorized entity, while nonrepudiation ensures that the parties in a communication cannot deny their participations in the process.
Inspired by handwritten signatures, cryptographers invented the term “digital signatures” to fulfill the authentication, integrity, and nonrepudiation requirements of digital communications. As an analogy to handwritten signatures, digital signatures provide a clue to the origin of a piece of digital information or a commitment of a piece of digital information by the sender (signer). Digital signatures also provide an integrity guarantee of a piece of digital information since the piece of digital information is “signed.”
The idea of a “digital signature” first appeared in Diffie and Hellman’s seminal paper, “New Directions in Cryptography,” Diffie and Hellman (1976). A signer, say A, would like to protect his/her digital information, say m, against threats to authentication, integrity, and nonrepudiation. Two keys are being generated, namely a “public key” (pk) and a “private key” (sk). sk is kept secretly by A, who uses this key to produce signatures on messages. pk is used to verify the validity of a given digital signature σ on m, signed by A. pk is therefore accessible by public users. Here, validity refers to two concepts, namely, (1) the signature is created by A (authentication and nonrepudiation) and (2) the integrity of the message is maintained. The public key is normally derived from the private key and thus, the two keys are correlated. However, it is not feasible to derive the private key when only the public key is known. Besides, it is impossible to forge signatures without the knowledge of sk. The study of digital signature schemes is an important subfield of public-key cryptography, initiated by Rivest et al. (1978). Since the signing key (sk) and the verifying key (pk) are different, this kind of cryptosystems is also known as asymmetric cryptosystems. We remark that being asymmetric is a necessary condition for a cryptosystem to provide nonrepudiation. The reason is that for any symmetric cryptosystems, the same key is used for both signing and verification processes. Consequently, both the signer and the verifier can be the origin of the signature and in this sense, both parties can deny having participated in the process. In other words, the signer must hold some “secret” information to achieve nonrepudiation.
One drawback of public-key cryptosystems is that they usually involve computations that are relatively heavy (e.g., modular exponentiations). The reason is that the security of these schemes relies on the difficulty of solving certain number-theoretic problems. Many digital signature schemes in practice fit the description. Well-known examples include the schemes, whose difficulties depend on the hardness of the Integer Factorization Problem (e.g., Rabin (1979)) and the Discrete Logarithm Problem (e.g., ElGamal (1985), Schnorr (1991), Pointcheval and Stern (1996), and DSS (National Institute of Standards and Technology, 1991, 1992)). Such intensive computations might not be desirable in mobile devices, in which the computational capability and battery capacity are limited.
1.1 Our Contribution
We present a performance analysis of two well-known digital signature schemes from pairing-based cryptography on mobile devices with Android (Google, 2016) platform. The two schemes are from Boneh et al. (2004b) (BLS) and Paterson and Schuldt (2006) (PS). The efficiency of these schemes is evaluated in terms of computation time and energy consumption during signature generation and verification, as well as the time to generate the message digest. Various types of information which reflect the practical settings, in terms of size and information type, are adopted in our experiments. We present the results and discuss their implications.
2 Related Work
Digital signature is the de facto way to ensure the authentication, integrity, and nonrepudiation requirements. The Guidelines for Managing the Security of Mobile Devices in the Enterprise (Souppaya and Scarfone, 2013), developed by National Institute of Standards and Technology (NIST), suggested that digital signatures should be adopted for two purposes, namely, to ensure that only applications from trusted entities can be installed and to protect the integrity of the codes of these applications. A digital signature variant called mobile signature was defined by the European Telecommunications Standards Institute (ETSI) (2003). A number of models are proposed for the generation of digital signatures in the mobile environment. Specifically, digital signatures can be generated either on a mobile phone or on a SIM card on a mobile phone (Samadani et al., 2010). Digital signatures can be adopted in various mobile applications, including payment platforms (Wu et al., 2016), file transfer systems (Sayantan et al., 2015), and location proofs (Saroiu and Wolman, 2009). A survey of electronic signature solutions in mobile devices was carried out by Ruiz-Martínez et al. (2007), which discovered that mobile clients were able to generate digital signatures.
Recently, pairing-based cryptography (Paterson, 2005) has gain considerable attention thanks to its efficiency and improved security guarantees. For instance, Boneh et al. (2004a) introduced a short signature scheme (BLS) based on the Computational Diffie-Hellman (CDH) assumption on certain elliptic and hyper-elliptic curves. The signature length is half the size of a DSA signature (National Institute of Standards and Technology, 1992) for a similar level of security. Paterson and Schuldt (2006) proposed an efficient identity-based signature scheme (PS) based on Bilinear Decision Diffie-Hellman (BDDH) and Decision Linear (DL) assumptions with short signatures. This scheme enjoys the advantage that it is secure without relying on the so-called random oracle assumption (Bellare and Rogaway, 1993). In this chapter, we choose to investigate the practicality of these two well-known signature schemes on mobile devices.
3 The Experiment
We experimented with the BLS and PS schemes on the Android (Google, 2016) platform. We adopted the Java Pairing-Based Cryptography Library (JPBC) (De Caro and Iovino, 2011) to develop the performance testing application on the Android platform.
3.1 Cryptographic Settings
In our experiment, we adopted Type A pairings, which is a standard bilinear pairing setup for cryptosystems. Type A pairings are constructed on the curve y2 = x3 + x over the field 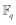 for some large prime q satisfying the constraint that q mod 4 ≡ 3. Both
for some large prime q satisfying the constraint that q mod 4 ≡ 3. Both 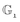 and
and 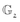 are group of points on the elliptic curve
are group of points on the elliptic curve 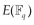 having the same group order, say r. It is also required that r is a prime factor of q + 1. In other words, q + 1 is divisible by r. For a security level comparable with 1024-bit RSA encryption, q and r should be large prime numbers of 512 and 160 bits, respectively. For more information about this setting, please refer to PBC Library (Lynn, 2006).
having the same group order, say r. It is also required that r is a prime factor of q + 1. In other words, q + 1 is divisible by r. For a security level comparable with 1024-bit RSA encryption, q and r should be large prime numbers of 512 and 160 bits, respectively. For more information about this setting, please refer to PBC Library (Lynn, 2006).
3.2 Testing Environment
We examined the computation time (in terms of milliseconds) and energy consumption (in terms of joules) of information with diverse types and sizes reflecting practical scenarios. Table 1 shows the details of the data file being signed in the test application. For each type, we test the time on (1) signature generation, (2) signature verification, and (3) message digest generation based on SHA-256 algorithm (NIST FIPS PUB 180-2, 2001). For each test, one of the information types (text string, document, image, or movie) was used. Each involved 10 trails, and the number presented for each type was the average of these 10 trails.
Table 1
Information Type and Size
| Type | Size (kB) |
| Text string | 0.144 |
| Document (.docx) | 14a |
| Image (.jpg) | 2547 |
| Movie (.mp4) | 40217 |
a This corresponds to a one-page text document of about 400 words on Microsoft Word version 15.22.1.
These tests were carried out on an experimental testbed which measures the computation time and energy consumption of two Android devices with specifications shown in Table 2. Device 1 has a more powerful hardware configuration in terms of processing power and memory than Device 2.
Table 2
Testing Platform Specifications
| Device 1 | Device 2 | |
| Operating system | Android OS, v5.0.1 | Android OS, v4.1 |
| Chipset | Qualcomm MSM8974AC Snapdragon 801 | TI OMAP 4470 |
| CPU | Quad-core 2.5 GHz Krait 400 | Dual-core 1.5 GHz |
| GPU | Adreno 330 | PowerVR SGX544 |
| Memory (internal) | 32 GB and 2 GB RAM | 16 GB and 1 GB RAM |
| Card slot | microSD | microSD |
| Standard voltage | 3.8 V | 3.8 V |
| Battery capacity | 3000 mAh | 2100 mAh |
| Max energy | 41040 J | 28728 J |
As shown in Fig. 1, the testbed consists of three elements: (1) power monitor, (2) Android device, and (3) laptop computer. As a core element, the power monitor (Monsoon FTA22D) connects the Android device and the computer laptop (Intel i5-2560M processor, 2.5 GHz, 3 MB cache, and 4 GB memory). The power monitor provides the DC electrical source with 3.8 V to the Android device, which avoids the influences of the unstable voltage when the battery continuously discharges. It also records the read-time voltage and current of the Android device at an interval of 0.2 ms. The power trace, including the time and the instant power, is sent to the laptop computer via USB interface communication in real time. A customized software is executed on the laptop computer to calculate the energy computation according to the measured data from the power monitor and the timestamps from applications.

As an integral preparation for the measurement, a testing app is designed to test the BLS and PS schemes which supports three processes, signature generation, signature verification, and message digest generation, in the sequence of i = 1, 2, 3. The app provides these functions: (1) record the beginning time t0 of each test, and simultaneously send a signal packet to the laptop, (2) record the beginning time t2i−1 and the ending time t2i of each process, which are used to calculate the computation time, (3) sleep for 30 s after each process to make sure that the device voltage returns a stable value.
The testing steps are as follows:
1. Carry out one test by executing the testing app after the voltage values of the device are stable for 5–10 s.
2. Upon receiving the signal packet, the laptop records the current time 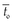 of the power monitor, which is used to synchronize the power trace.
of the power monitor, which is used to synchronize the power trace.
3. The app records the timestamps of three processes. The power monitor measures the energy trace during the whole test.
4. The customized software in the laptop collects the timestamps from the app and the power trace from the power monitor. The computation time and energy consumption of the device in each process can be calculated after combining the two sets of measurements.
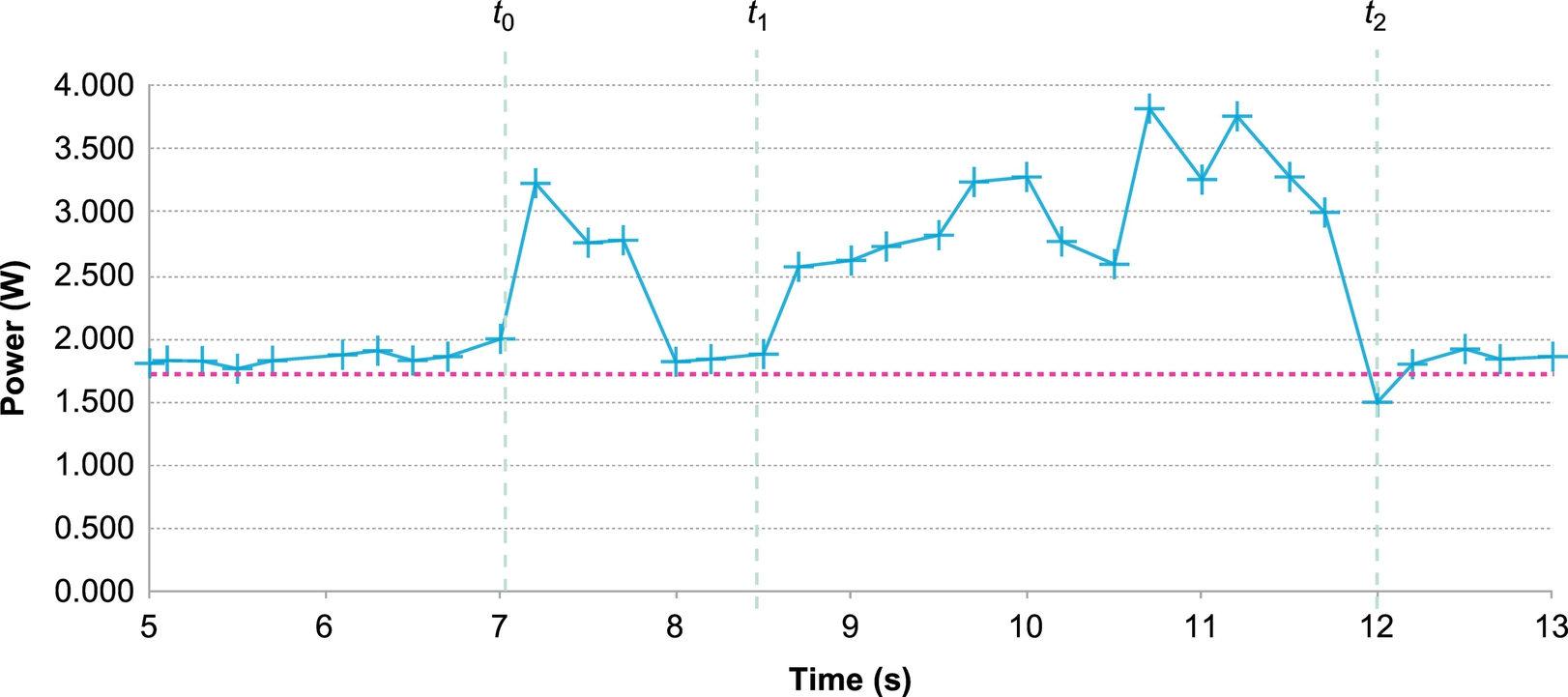
First, the computation time Ti of three processes can be obtained by Ti = t2i − t2i−1, i = 1, 2, 3. Next, the energy consumption of the device caused by the BLS and PS schemes is obtained after eliminating the basic energy consumption, which is caused by the screen and OS. The power trace of the device is shown as Fig. 2. Here, the basic power consumption is computed as the average of the power values before each test for a few seconds, shown as the red base line with 1850 mW in Device 1 (which is 2250 mW in Device 2). Then the energy consumption during signature generation/signature verification/message digest generation can be computed from the area between the power curve and the base line during the computation time from 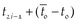 to
to 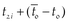 , i = 1, 2, 3.
, i = 1, 2, 3.
3.3 Experiment Results and Observations
The experimental results are shown in Tables 3 and 4. We would like to highlight a few observations.
Table 3
Testing Results of Device 1
| BLS | PS | |||
| Signature generation (time—millisecond) | String | 569.5 | String | 518.1 |
| Document | 400.9 | Document | 395.1 | |
| Image | 520.5 | Image | 502.2 | |
| Movie | 447.7 | Movie | 428.6 | |
| Signature verification (time—millisecond) | String | 1096.3 | String | 887 |
| Document | 1020 | Document | 915.8 | |
| Image | 1143.5 | Image | 1150.2 | |
| Movie | 955.6 | Movie | 932.1 | |
| Message digest generation (time—millisecond) | String | ∼0 | String | ∼0 |
| Document | 1.6 | Document | 1.8 | |
| Image | 305.7 | Image | 291.9 | |
| Movie | 4057.2 | Movie | 4186.9 | |
| Signature generation (energy consumption—joule) | String | 0.824 | String | 0.721 |
| Document | 0.766 | Document | 0.623 | |
| Image | 0.722 | Image | 0.648 | |
| Movie | 0.644 | Movie | 0.59 | |
| Signature verification (energy consumption—joule) | String | 1.271 | String | 1.033 |
| Document | 1.344 | Document | 1.214 | |
| Image | 1.346 | Image | 1.212 | |
| Movie | 1.373 | Movie | 1.263 | |
| Message digest generation (energy consumption—joule) | String | ∼0 | String | ∼0 |
| Document | ∼0 | Document | ∼0 | |
| Image | 0.337 | Image | 0.341 | |
| Movie | 4.197 | Movie | 3.988 | |
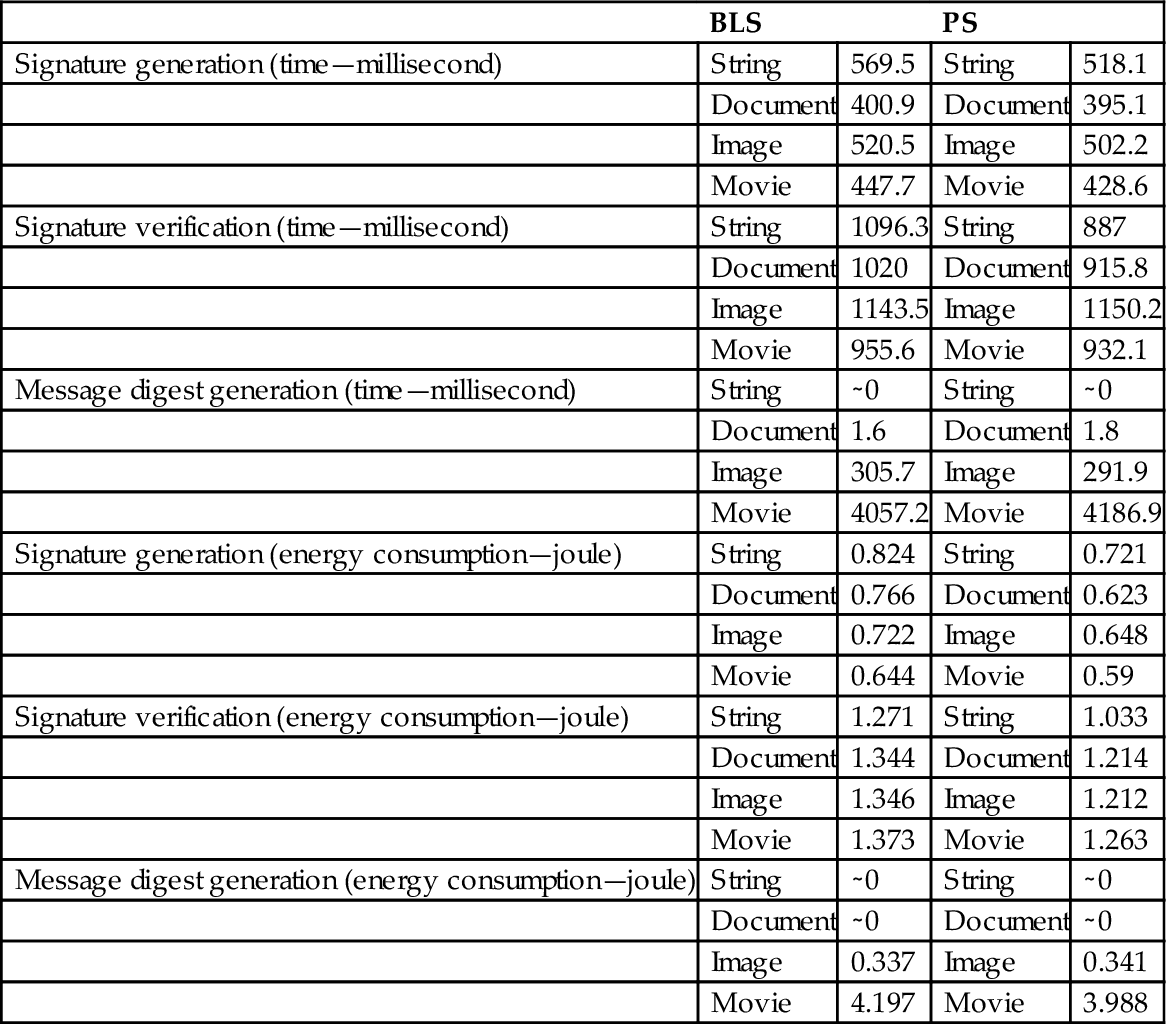
Table 4
Testing Results of Device 2
| BLS | PS | |||
| Signature generation (time—millisecond) | String | 850 | String | 582.4 |
| Document | 724.2 | Document | 543.6 | |
| Image | 532.8 | Image | 342 | |
| Movie | 603.4 | Movie | 378.4 | |
| Signature verification (time—millisecond) | String | 1901.2 | String | 2511.8 |
| Document | 1582.8 | Document | 2663.6 | |
| Image | 1259.2 | Image | 1997.2 | |
| Movie | 1246.6 | Movie | 1826.8 | |
| Message digest generation (time—millisecond) | String | 0.2 | String | ∼0 |
| Document | 5 | Document | 10.4 | |
| Image | 988.6 | Image | 1005.6 | |
| Movie | 15420 | Movie | 15543.6 | |
| Signature generation (energy consumption—joule) | String | 0.836 | String | 1.033 |
| Document | 0.825 | Document | 1.037 | |
| Image | 0.548 | Image | 0.968 | |
| Movie | 0.656 | Movie | 1.021 | |
| Signature verification (energy consumption—joule) | String | 2.69 | String | 2.273 |
| Document | 2.142 | Document | 1.705 | |
| Image | 1.712 | Image | 1.364 | |
| Movie | 1.868 | Movie | 1.42 | |
| Message digest generation (energy consumption—joule) | String | ∼0 | String | ∼0 |
| Document | ∼0 | Document | ∼0 | |
| Image | 1.095 | Image | 1.137 | |
| Movie | 16.858 | Movie | 17.51 | |
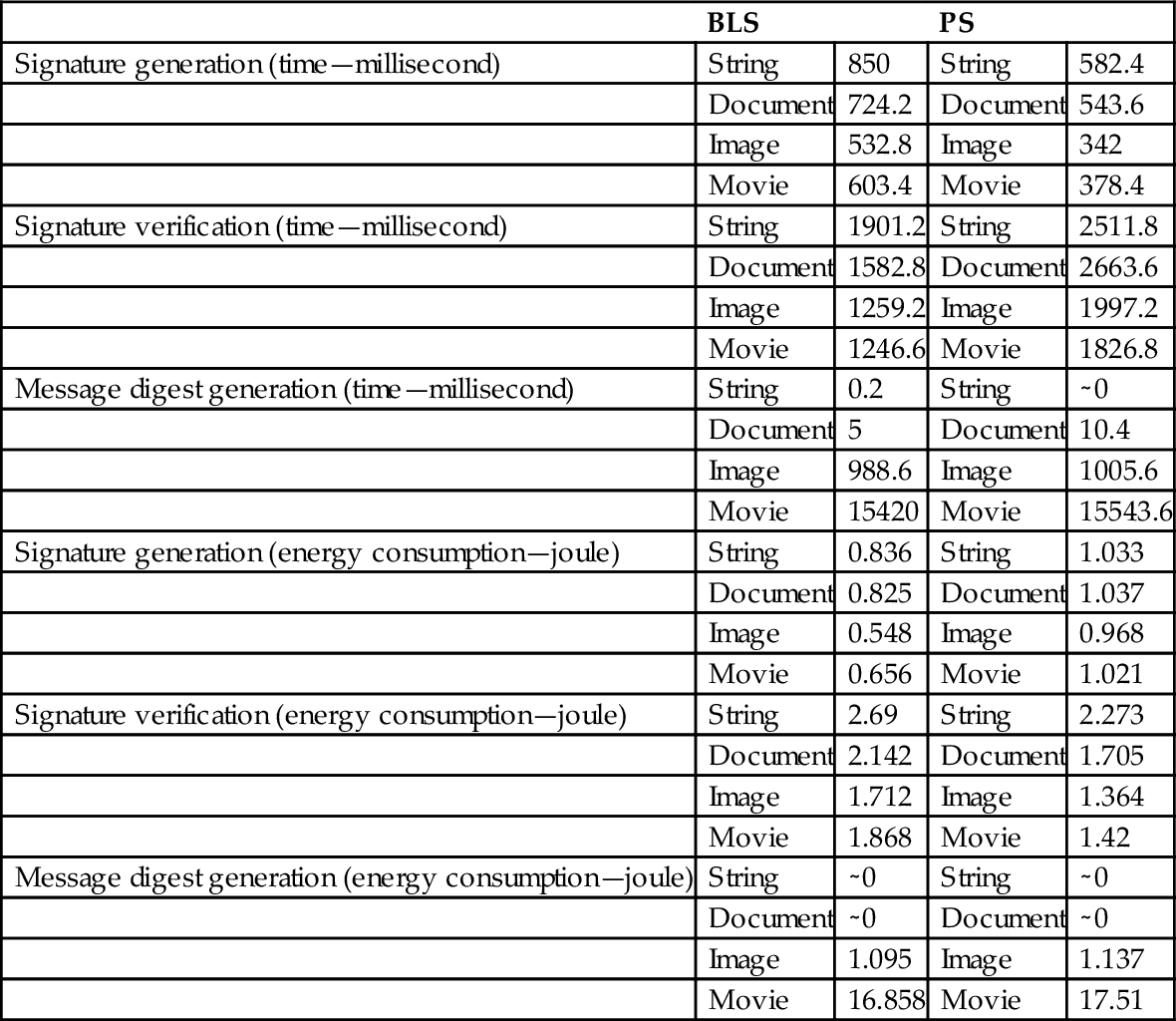
• Signature scheme BLS is more efficient than PS in both signature generation and verification. This is natural because BLS assumes the existence of a PKI, while PS is purely identity-based. Secondly, PS is proven to be secure in the standard model, while BLS’s security analysis relies on the random oracle heuristic.
• The size of data affects the time in message digest generation but not signature generation nor verification. This is because we adopt the common practice that the signature is generated and verified with respect to the message digest instead of the original message. As the message digest has a constant size (256 bits), the time spent on signature generation and verification for all types of data is similar in our experiment.
• The time required for message digest generation cannot be ignored. For a movie file of approximately 40 MB, 4 and 15 s are required in the message digest process in Devices 1 and 2, respectively. This is reasonable because a message digest is merely the hash value of the data while the computation of the hash for large data files is time consuming (Sravan Kumar and Saxena, 2011).
• We note that signature verification is more expensive than signature generation in general. Both devices take more time and energy to complete the process of signature verification.
Discussion. It is fair to say mobile devices nowadays possess comparable processing power to desktop/laptop computers. Incorporating cryptographic features into mobile applications does not impose too much of a burden on the computation time and energy consumption. Even though operations like hashing for relatively large files are still time consuming, such operations are not frequent for mobile agents. Our experiments show that it is feasible for mobile application developers to incorporate cryptographic techniques.
4 Conclusion
In this chapter, we provide a performance analysis of two well-known digital signature schemes on Android mobile devices. The efficiency of these schemes is evaluated in terms of computation time and energy consumption in signature generation and verification, as well as message digest generation. Our experiments involve various types of information, including text string, document, image, and movie files, which simulate realistic application scenarios. We realize that the main cost in applying digital signatures is in fact the generation of the message digest. Nonetheless, we have demonstrated that it is feasible to execute pairing-based signatures on mobile devices. Therefore we feel comfortable concluding that the use of cryptographic techniques in mobile applications is feasible to enhance security.