An Agent Based Model of Vague Beliefs in Games
This chapter discusses the way that three distinct fields, decision theory, game theory and computer science, can be successfully combined in order to optimally design economic experiments. Using an example of cooperative game theory (the Stag-Hunt game), the chapter presents how the introduction of ambiguous beliefs and attitudes towards ambiguity in the analysis can affect the predicted equilibrium. Based on agent-based simulation methods, the author is able to tackle similar theoretical problems and thus to design experiments in such a way that they will produce useful, unbiased and reliable data.
In this chapter, our aim is to explore how Agent-Based Simulation techniques can act as a complement to a relatively new field of the experimental economics literature, that of preferences towards ambiguity. As experimental techniques in economics constitute an indispensable part of the applied and empirical research, with scholarly research getting published in the top journals of the profession, it is of paramount significance for the implemented experimental protocols to be carefully designed so as to provide by minimizing the number of possible flaws. Moreover, advances in the field of decision theory, combined with the numerous available datasets of experimental observations, pose a huge challenge to the ‘rational’ agent paradigm1. As a result, empirics have rendered the use of more realistic modelling of human behaviour as well as the interdisciplinary research to be more than necessary. Due to this, several new scientific fields have emerged such as the field of ‘Behavioral’ economics (where elements from psychology and biology are coalesced with the economic theory) or the field of neuroeconomics (where advances of neuroscience are applied) to name but a few. In addition to the latter, crucial improvements have been made to the literature of decision making under ambiguity, or stating it in a different way, improvements on how to model agents’ behaviour in situations where they lack useful information. This fact can be explained by the increased frequency of research papers published that either focus on similar theoretical issues or on the application of theory to real life. Consequently, every single field in economics now takes advantage of these advances augmenting the ability to explain data and behaviour in a more realistic way (e.g. macroeconomics, game theory, environmental economics). Similar applications can be found in the present volume by Trindade, Magessi, and Antunes (2014) and Arciero et al. (2014).
In this chapter, we show how three distinct fields can be brought together enabling us to design and conduct more effective experiments that will generate useful and unbiased data. Our aim is to use advances of the literature of decision making under ambiguity that centres on individual choice, in order to predict behaviour in strategic interaction environments. The commonest way to model interaction in economics is game theory. There are several other different ways to model social interaction such as using the public choice approach (for a similar approach, see Lucas and Payne (2014) and Trigo (2014) or principal- agent models to name but a few. Incorporating the theoretical advances into the game theoretical models enables us, on the one hand, to solve puzzles that the standard assumption of the rational choice produces and, on the other, to obtain better predictions of how agents will react in similar interactions. The next step, after having derived the theoretical predictions, is to test this theory in the lab. The role of agent-based simulation becomes apparent at the step before entering the lab. Thus, what we provide is an intuition of how decision theory, game theory and computer science can be combined for the optimum design of economic experiments. As this chapter is addressed to readers of multifarious scientific backgrounds, careful consideration has been taken as regards the fact that they may not be familiar with the tools and methods that are employed in economic analysis to model individual behaviour. Henceforth, effort has been made to keep mathematics and definitions to the lowest formal level possible. A mathematical as well as a technical appendix with the code for the simulation is attached at the end of this chapter.
Agent-Based Simulation in Economics
As was described in the introduction, we focus on the use of agent based modelling in order to design and implement economic experiments. Before proceeding to this, it is instructive to outline other cases as well in which agent-based modelling can be useful in economic research. It is well-known that economics is a science heavily based on mathematics, making it one of the most essential tasks when conducting research. The range of applications is enormous. Starting from complex optimization programs that need to be solved, testing theoretical models or writing estimation routines to simulate evolutionary systems, agent-based modelling can be proved to be the optimal way to do so. Tesfatsion (2006) provides a nice definition of Agent Based Computational Economics (ACE) as the “computational study of economic processes modelled as dynamic systems of interacting agents.”
In economics, there are various reasons where simulation techniques can be exploited for research. Van Dinther (2008) discusses one of the major benefits in agent based modelling, namely that of controlling all the parameters of interest in order to adapt them to the specific problem under investigation. This offers to the researcher a unique flexibility in the modelling process that allows comparative statics analysis but also is a powerful prediction and testing tool.
Why should one use agent-based models in economics? Starting with the most simple, the main reason to program the behaviour of agents is to tackle complex mathematical problems that the theoretical model under consideration demands. When the mathematics allows, closed form expressions that represent the optimal decisions that a decision maker takes can be derived. In a similar case, agent-based models are useful for conducting comparative statics exercises and seeing how the results change when some of the key variables fluctuate. But as the complexity of the problems increases and as more variables are added in order to capture extra elements of the reality (e.g. extend model to dynamic dimension), it becomes harder and harder to obtain analytical solutions in an efficient way. In addition, there are cases where an analytical solution is impossible to be calculated and, thus, the researcher seeks assistance to numerical methods that make extensive use of simulations (e.g. Monte Carlo simulations).
Van Dinther (2008) lists the most common approaches that are used in economics for carrying out simulations. More analytically, these include:
Epstein (1996, 2008) has extensively described the alternative modelling opportunities that the agent based simulations offer. More specifically, he provides 16 reasons of why ABM is helpful not only for predictions but also for explanation, to seek new questions and to support decision analysis, to name but a few. Another field in economics where simulation plays a significant role is that of experimental economics. Duffy (2006) perfectly illustrates the connections between agent-based models and human-subject experiments by stating that the two methodologies should be complementary rather than rival as the one can compensate for the weaknesses of the other. Yet, most of the effort has been devoted to how simulations can be used so as to interpret behaviour and analyze the data of an already completed experiment. A role of agent-based modelling that is often omitted is its usefulness as a tool to design the experiments. As mentioned earlier, in order to guarantee the reliability of the data, an experimenter should be quite careful when designing the experiment. As the decisions are made by human beings, noise in the data should not be taken for granted and appropriate assumptions should be imposed. Consequently, to minimize the biases, extensive simulations can be carried out to pick up the suitable tasks that the subjects are asked to undergo. Hauser et al. (2009) present the weaknesses of both scientific approaches. On the one hand, there are the restrictions that simulation models impose on agents’ behaviour that usually depart from reality. On the other hand, it is vagueness that characterizes experimental methods. The latter is a common problem in experimental methods as the participation time is limited and does not allow for sufficient learning and adaptation, the use of simple and interesting experimental frameworks becomes obligatory. These difficulties can be bypassed by making the best use of both methods.
Hommes (2006) gives an account of the various benefits of the agent-based modelling. The most significant seems to be the ability to model agents that have heterogeneous preferences. In economics, and especially in fields that try to deviate from the mainstream analysis (e.g. Behavioural Economics), the latter is of outmost significance. Accepting that “people are different” in many aspects such as preferences, experience or culture to name but a few, it is crucial to capture similar differences in the analysis.
Decision Making under Ambiguity
Traditional decision theory, and thus game theory analysis as well, dogmatically rely on the mainstream microeconomic model that is used in the literature, that of the homo economicus. This is a well-established theory on how people make decisions which is based on the ‘rational’ agent model of the individual that maximizes her own utility subject to the various constraints2. Nevertheless, in the last decades, the extensive use of experimental methods has provided rich evidence on why this model cannot always capture the way people behave. Using experiments in the same manner as physics scientists do (by isolating the environment where agents act and observe only the parameters of interest), economists have obtained important input on how people make decisions and whether they abide by the neoclassical model of economic behaviour or not. As expected, most of the evidence shows that participants in these experiments often violate the rationality criteria that are imposed by the theoretical models. As a result, a new field of economics has been emerged, that of Behavioural Economics. In this alternative field of economic theory, researchers aspire to conduct interdisciplinary research and combine findings from distinct at first sight sciences (some characteristic examples include evolutionary economics and neuroeconomics). The importance of all this evidence lies in that it buttresses the power of experimental methods leading to an excessive demand for more robust protocols in both the design of experiments and the high quality of experimental data.
Extending this model to more complex situations such as in cases of risk, the famous Expected Utility model is set into action. However, in order to be able to represent the preferences in the way that the theory predicts, there is a number of axioms than need to be satisfied3, an issue that in the recent years has started to be seriously challenged. Before introducing ambiguous beliefs, it would be useful to sketch some key decision theory elements that enable us to understand the main concepts of economic modelling. Additionally, this is a crucial issue in economic theory as it constitutes the main criticism against the mainstream ‘rational’ way of modelling economic behaviour.
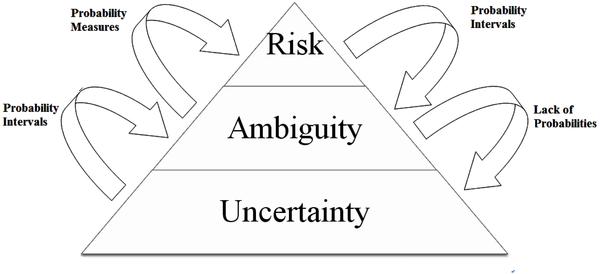
Firstly, it is useful to discriminate between risk and ambiguity as it is a common mistake that many researchers not acquainted with the decision literature make when they model similar situations. Risk refers to the case where the possible probabilities for the future state of the world are well-defined, are known ex-ante and sum up always to 1. A standard illustration of risk in all introductory courses of statistics is that of throwing a die. The possible states of the world are six and assuming that this is a fair die, then the probability of receiving each state of the world, is the same for each side and equal to 1/6. Moreover, these probabilities are well-known to the decision maker and she is also fully aware of them. On the contrary, in the case of ambiguity, as Knight (1921) described it, the probabilities for the future states of the world are not well-defined, or at least the decision maker is not fully aware of the real chances, and do not necessarily add-up to 1 (we will return to this issue later on). Finally, another typical mistake that is usually made is to use the terms ambiguity and uncertainty interchangeably. Even though the essence of these two terms resembles in nature, we could think of uncertainty as being a subset of ambiguity. If we can think the probability space as an interval, where on the one extreme there is uncertainty and on the other risk, then ambiguity is somewhere in the middle. In Figure 1, A conceptual map presents the relationship among the three.
| Figure 1. Relationship among risk, ambiguity, and uncertainty |
|---|
 |
In our case, we are going to focus on ambiguity for two reasons. Firstly, a practical reason for testing experimentally similar assumptions is that ambiguity must be implemented in the lab and this must be done using some suitable device. On the other hand, it is quite reasonable to think of ambiguity as a more realistic characteristic of the daily economic life, where probabilities can be attached to the various events albeit with no accuracy.
In the cases of decision making under risk, the standard model employed by the literature is the Expected Utility model. This is simply the probability weighted sum of the utilities that an agent receives. Imagine, for instance, that we are offered two options. Either we can win for sure $50 or we can flip a coin where if it lands heads, we win $100 otherwise zero. Making the assumption that we are risk neutral4. In this case, the expected Utility from flipping the coin is Pr(Heads)U(50) + Pr(Tails)U(0) and this amount is the compared to U(50). In ambiguous situations where the formation of beliefs is not quite straightforward, Savage (1954) showed that the decision makers can always formulate subjective beliefs, which are always additive and precise. This notion is quite appealing and furthermore offers mathematical elegance. However, Ellsberg (1961) showed that this is not always true and that agents do not form correct beliefs for the various effects (Table 1). He suggested a simple thought experiment, the main idea of which was that due to the presence of ambiguity aversion, the subjects experience preference reversals. The Ellsberg's three-colour urn paradox suggests:
There is an urn with 90 balls of which 30 are black (B) and the rest 60 are red (R) and yellow (Y) (unknown proportions) and could be any number between 0 and 60. A ball is drawn from the urn and the decision maker has to bet on the colour she thinks it is, based on the amounts below (let us say in dollars):
Table 1.Ellsberg paradox
| Bet | RED | BLACK | YELLOW |
|---|---|---|---|
| f | 100 | 0 | 0 |
| g | 0 | 100 | 0 |
| f’ | 100 | 0 | 100 |
| g’ | 0 | 100 | 100 |
This means that if she chooses f and a Red ball is drawn, she wins $100 otherwise 0. The decision maker firstly has to choose between the bets f and g and then between f’ and g’. Empirically, subjects prefer f to g and g’ to f’ which is a violation of the axioms that Subjective Expected Utility (SEU) assumes5. If f is preferred to g, then this shows that the subject believes that Prob(Red)>Prob(Black). Similarly, if g’ is preferred to f’, this shows that the subject thinks that Prob(Red)+Prob((Yellow)<Prob(Yellow)+Prob(Black) which leads Prob(Red)<Prob(Black) and apparently results lead to a contradiction and thus to decisions incompatible with the SEU.
Camerer (1992, 1995) summarizes the main experimental results that show deviation from Expected Utility preferences. Following this line of research, there is a considerable amount of experimental evidence that confirms that human subjects do not conform to the behaviour that the rational agent model requires. Nevertheless, in the literature there are plenty of alternative ways that one can use in order to model ambiguous beliefs. Ranging from simple heuristics to fancy mathematical objects, still there is no consensus on which model is the most suitable. For our example, we are going to use the Choquet Expected Utility model, which is based on Choquet integrals (Choquet, 1953) and was axiomatized as a theoretical model by Gilboa (1987) and Sarin and Wakker (1992). This model is appealing as it has some nice descriptive properties. Beliefs are not represented by subjective probabilities anymore but by capacities. This allows the incorporation of ambiguity aversion in the analysis. Imagine, for example, that someone is offered a bet by flipping a coin and wins one dollar if it comes heads or pays one dollar otherwise. When the agent is sure that the coin is a fair one, then there is no reason to believe that one of the sides has more chances to turn out than the other. In that case, the agent is indifferent to which one to choose and plays each with probability 50% which is exactly the probability that she attaches to each of the outcomes. Imagine now a situation where the agent does not trust that the coin is unbiased. In this case, she is not able to attach 50-50 chances. And since she is ambiguity averse, she attaches probabilities 40% to each side. This is exactly the notion of non-additive capacities, as, according to this definition, p(tales)+p(heads)=0.8≠1. There is a 0.2 missing, which in this model expresses the lack of confidence in the subjective probabilities. Contrary to expected utility, this model is a rank-dependent model which means that the agent ranks the several different outcomes and attaches different weights according to her preferences6. In the experimental literature of testing choices under ambiguity, there is robust empirical evidence that the Choquet Expected Utility performs considerably better than Subjective Expected Utility and thus outperforms as a model of ambiguous beliefs (Hey et al., 2010, 2011; Hanany, 2007).
Game Theory with Strategic Ambiguity
A standard way to extend individual decision making to interactive environments with two or more participants is game theory. In this extension, it does not suffice to assume that each player behaves in the same way as in the individual decision making model but we need to take into consideration that the actions of the one player affect the decisions of the other. The notion of Nash equilibrium constitutes a cornerstone for game theory and this is why thousands of papers and books cite the idea of the ‘Beautiful Mind’, John Nash. This idea is quite attractive in both normative and positive aspects. As an informal definition, Nash equilibrium shows all those combinations of strategies that players have at their disposal that make them lose any incentive from deviating of playing such strategies. The latter requires that agents satisfy two requirements at the same time. On the one hand, they always play their best strategy and, on the other, they hold firm beliefs about the opponent.
Camerer (2003) introduces the idea of Behavioural game theory by collecting a series of experiments that show deviation from the Nash equilibrium and effort is made to find the psychological reasons that can explain this. In our example, we are going to use a standard game with known equilibria and see how they can be affected by introducing ambiguous beliefs.
The Game
As an example we will use a standard cooperative game that was inspired by Jean Jacques Rousseau (1755). The idea of cooperative game theory, in contrast to the non-cooperative, is that the players of the game are better off when they cooperate. A variation of such a game is the Stag Hunt game. The story is quite simple. Two hunters meet in the woods. There are also only two kinds of preys that they can look for, Stags and Rabbits. Stags are the big preys and catching one suffices to feed both hunters. Rabbits, conversely, can be captured one at a time and are adequate only for one person. As the Stag is quite strong, more than one person are needed to catch it. On the contrary, a Rabbit is much easier to catch, so only one person is needed. Both hunters are hungry so it is to their benefit to leave the woods in a successful way. They start discussing and they conclude that they can cooperate and focus on catching the Stag. In this case both will receive the maximum payoff. Although, since this decision it is not binding, each of the hunters may be indulged, and when a Rabbit passes by, they can forget their mission to catch the Stag and go for a Rabbit. In this case, one of the hunters takes a payoff which is lower than what she would get by catching the Stag and the other gets zero. Finally, it is likely that both go for the Rabbit and each results with positive payoffs but always less than the payoff that the Stag offers. In this kind of games, the optimal result is obtained when both of the players coordinate. Having each player to choose between two available strategies {cooperate, defect} or {c, d}, we can represent this game using a payoff matrix which states the returns of each of the strategies. The payoffs are show in Table 2.
Table 2. Payoff matrix 1
| Player 2 | |||
|---|---|---|---|
| c | d | ||
| Player 1 | C | 9, 9 | 0, 8 |
| D | 8, 0 | 7, 7 | |
This game depicts the beliefs that each player attaches on the other player’s strategy. It has two Nash equilibria, one when both cooperate (c, c) and one when both defect (d, d). So if Player 1 thinks that Player 2 is going to cooperate for sure, then the optimal thing to do is to cooperate as well. On the contrary, if we expect that the other player is going to defect, then in order to avoid the zero outcome, it is better to defect as well. When the players are sure about the behaviour of the fellow player, then the two Nash equilibrium will emerge. If we want to think this in terms of probabilities, it is as if we have two different types (cooperative, non cooperative) and we attach prior probability equal to 1 to the type on which we are sure. This leads us to the notion of mixed-Nash equilibrium. In this case, we are not sure on the type of each player so we need to form some beliefs. In the appendix, we show that when Player 1 attaches probability 7/8 or more to the fact that Player 2 is cooperative type, then she always cooperates. If her beliefs are less than 7/8, then it is better for her to defect and go for the Rabbit.
In order to illustrate the previous result, we run a series of simulations. Using the payoff matrix given by table(payoff 1), we simulate a 2x2 game (2 players, 2 strategies). We assume that both players are identical in their preferences and are risk neutral. Nonetheless, they differ in the subjective beliefs each holds on the strategies of each player. As it holds in lab experiments and even more in real life, there are legitimate reasons why one can hold diverse beliefs. Past experiences, cultural background, social status, religious motives, anything can affect the way that agents form their subjective beliefs on others. As our scope is to examine how different beliefs affect the equilibrium, we will not focus on any of these “environmental variables” as Myerson (1991) calls them7. Hence, in order to model the beliefs of the agents, we use a random number generator that generates numbers from a uniform distribution in the space [0,1]. We range the number of iterations from 10 to 1000 and we simulate three different rounds with 10, 100 and 1000 iterations. The results are summarized in Table 3.
Table 3. Simulation game 1
| Strategy | N_iter=10 | N_iter=100 | N_iter=1000 |
|---|---|---|---|
| (c, c) | 0.00% | 0.02% | 0.01% |
| (c, d) | 0.10% | 0.16% | 0.10% |
| (d, c) | 0.20% | 0.13% | 0.12% |
| (d, d) | 0.70% | 0.69% | 0.77% |
| Avg Pay | 6.50, 5.70 | 6.05, 6.29 | 6.44, 6.30 |
In this example, roughly 75% of the games resulted in the Pareto dominated8 equilibrium and each of the players gained on average something less than 6.5 units of utility when they could have won 9 units each. In this game, Rousseau wanted to show how attitudes inside a group affect the result. In other words, depending on the beliefs of the players and whether the player is optimistic or pessimistic, we may have cooperation or not.
A crucial issue here is the payoff matrix. Playing the same game but with a different payoff matrix, which keeps the same form of the game (coordination always gives the best outcome), may produce significantly different results. Consider now the payoff matrix in Table 4.
Table 4. Payoff matrix 2
| Player 2 | |||
| C | D | ||
| Player 1 | C | 3, 3 | 0, 2 |
| D | 2, 0 | 1, 1 | |
Solving for the Mixed Strategies Nash Equilibrium, it is easy to show that the probability where we observe a switch in the beliefs is ½. So if Player 1 believes that there is more than 0.5 chances that Player 2 will cooperate, she cooperates as well, otherwise she defects. The same holds for Player 2 regarding his beliefs for Player1. Running again three different simulations with 10, 100 and 1000 iterations, we obtain the results shown in Table 5.
Table 5. Simulation game 2
| Strategy | N_iter=10 | N_iter=100 | N_iter=1000 |
|---|---|---|---|
| (c, c) | 0.1% | 0.26% | 0.242% |
| (c, d) | 0.3% | 0.2% | 0.241% |
| (d, c) | 0.2% | 0.25% | 0.25% |
| (d, d) | 0.4% | 0.29% | 0.267% |
| Avg Pay | 1.1, 1.3 | 1.57, 1.47 | 1.49, 1.47 |
Changing the payoff matrix and keeping the same game structure, the impact on the way that the game is played is significant. In Figure 1, the relative frequency of the strategies is depicted. The difference in the two equilibria is apparent due to the change in the payoffs.
As interesting it may be a similar result, it is still quite restrictive on the assumptions that standard decision making makes. In the examples above, it is required that the players have full information and they always form the correct probabilities on the strategies that the other player is going to play. Nevertheless, in real life, similar occasions are very rare, hence we need to extend the analysis to incomplete information.
In the analysis before, we made two explicit assumptions. We required that both the players are rational and identical concerning their attitudes towards ambiguity and we also assumed that they can always form subjective beliefs that are always precise and additive (agents are always able to set p and 1–p for each of the other player’s strategies). In the remainder of the chapter we introduce the same game but with capacities instead of probabilities. In this case the chances that the other player, let’s say Player B, will coordinate or defect are not anymore p and 1–p but vB(c) and vB(d) which are not necessarily additive (they do not sum up to 1). The advantage of using capacities is that now we can count for ambiguity as well. Furthermore, the use of ambiguity attitudes helps us to distinguish between different types of agents. In this case, we can define as an optimistic agent the one that always focuses on the biggest payoffs, while the pessimist type always focuses on the lowest payoff (Marinacci, 2000). In the appendix we provide the ways that each of the agents behave.
Let us now see how the results change when we allow for non-additive beliefs. Prior to this, we need to define a new term, the measure of vagueness which differentiates the additive and non-additive beliefs. Let Ψ to represent this measure. Let also vB(c) and vB(d) the beliefs that Player A attaches to each of the strategies of player B. Then the measure of vagueness is simply given by . It is easy to show that in the case of additive beliefs,
. Let us now introduce different levels of vagueness (in a lab experiment this can be done by using a random device and virtual players. The subjects are playing against a virtual player whose strategies are defined by this device). As is illustrated in the appendix, the two different types focus on different parameters. The pessimistic player cares for her beliefs that the other player will cooperate while the optimistic in the beliefs that the other will defect. This means that in our simulation we need again two different sources of ambiguity, each that represents the vague beliefs of each player. In the simulation we are running 1000 games in three different treatments, two optimistic players, two optimistic players and one optimistic against one pessimistic. We assume that both players face the same ambiguity and attach the same beliefs to each of the strategies. Using the payoffs of Table 2, as was stated earlier, we know that each player cooperates when the probability that the other player will cooperate is more than 0.5. Let us assume that each player attaches beliefs equal to 0.45 at each strategy, creating in this case a measure of vagueness equal to 0.1. The results are summarized in Table 6.
Table 6. Simulation 3
| Strategy | Optimistic Vs Optimistic | Pessimistic Vs Pessimistic | Optimistic Vs Pessimistic | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ψ | .10 | .30 | .70 | .10 | .30 | .70 | .10 | .30 | .70 |
| (c, c) | 0.293% | 0.423% | 0.719% | 0.218% | 0.11% | 0.031% | 0.239% | 0.227% | 0.115% |
| (c, d) | 0.254% | 0.213% | 0.132% | 0.229% | 0.228% | 0.111% | 0.323% | 0.447% | 0.731% |
| (d, c) | 0.268% | 0.227% | 0.121% | 0.241% | 0.224% | 0.125% | 0.197% | 0.108% | 0.02% |
| (d, d) | 0.185% | 0.137% | 0.028% | 0.312% | 0.438% | 0.733% | 0.241% | 0.218% | 0.134% |
| Avg Pay | 1.6, 1.572 | 1.86, 1.832 |
2.427, 2.449 | 1.448, 1.424 | 1.216, 1.224 | 1.076, 1.048 | 1.352, 1.604 | 1.115, 1.793 |
0.519, 1.941 |
Defining the two different types of behaviour is exactly the idea that Rousseau wanted to support when he was talking for optimism in the group. According to this idea, coordination maybe the equilibrium if there are optimistic types in the game. Three observations emerge from the results of the simulation. Firstly, when the population consists only of optimistic agents, then the most frequent equilibrium we observe is the coordination. The opposite holds for the pessimistic agents. In addition, when the level of vagueness (Ψ) increases, this result becomes more robust. So as ambiguity goes up, the optimistic agent always coordinate while the pessimistic defects. In the case of mixed players, the result converges to the pure strategy of each of the players. Lastly, we obtain different results in the case we allow for different types compared to the ones we obtained in simulating the game using expected utility and additive beliefs (simulation 2). It is easy to deduce that the results changed not only due to the different payoff matrix, but also due to the introduction of ambiguous beliefs to the modelling process.
Issues, Controversies, Problems
The literature is dispersed with several explanations on why we see different equilibrium to emerge.. Two of those focus on the payoff-dominant equilibrium (Harsanyi & Selten, 1988; Andrenlini, 1999) and the risk-dominant equilibrium (Carlsson & Van Damme, 1993; Harsanyi & Selten, 1995)9. In our experiment, we diverge from this line of research and suggest both the introduction of ambiguity in the strategies played and also the introduction of ambiguity attitudes. These results have not been tested experimentally yet, so using agent-based modelling is a quite useful way to design an appropriate experiment10.
These simulations remained only to a simple level. We cannot reach fully-fledged conclusions with only these examples. Our objective, is to show how simulations can be helpful and, in fact, should constitute an indispensable part during the design of an economic experiment. From the examples described above, if someone remained on the assumption that different payoffs lead to different equilibrium, by incorporating ambiguity it can be easy to refute her.. When designing an experiment, it is vital to choose the payoff matrices as well as the questions that the subjects will be asked, in such a way that the experimenter will be sure that they cover all the possible aspects that can unpredictably affect behaviour. Then, on the basis of these observations, we will be able to both design the experiment in an optimal way and to provide the subjects with the suitable incentives that will lead to the elicitation of preferences and beliefs. Then, after having obtained the data from the experiment, a new model can be created that will assist the replication of the subjects’ strategies and will simultaneously provide insights of human behaviour that can contribute to the refinements of the theory (Duffy, 2006).
The previous examples focus on a series of one shot games. This can be thought as a tournament where each player plays once against another player and they never meet again. This game has been extended to its repeated form, where players have the chance to learn and adapt from past experience. This kind of problems requires the introduction of learning models. In the game theory literature, one can find several models that have been suggested such as the fictitious play, the partial best response dynamic, the replicator dynamic, reinforcement learning, belief based learning (Camerer, 2003, pp. 235-365; Fudenberg & Levine, 1998). However, none of them involves the existence of ambiguous beliefs. Since similar models are an ideal candidate for agent-based modelling methods, a natural way to extend the previous experiments is to combine learning models, cooperation and ambiguous beliefs, an issue that seriously challenges the standard model, based on Bayesian updating and maximization of Expected Utility.
In this chapter, we focused on the formation of ambiguous beliefs and how the possession of non-additive beliefs can change the equilibrium during game play. As the objective was to show how the introduction of subjective beliefs can affect the results, all the simulations remained simple and focused only on the one-shot games where the individuals played once and did not have any opportunity to learn and adapt their behaviour. As most of the problems include time dimensions, we can benefit from the power the agent-based modelling gives and extend the models to their dynamic form. In addition, as the literature in decision making under ambiguity has been developed quite satisfactorily, it is more than imperative to include these advances in most of economic research. This has a cost in the difficulty that it adds but the payoff of getting more realistic and accurate predictions and models does compensate well.
This research was previously published in Interdisciplinary Applications of Agent-Based Social Simulation and Modeling edited by Diana Francisca Adamatti, Graçaliz Pereira Dimuro, and Helder Coelho, pages 125-142, copyright year 2014 by Information Science Reference (an imprint of IGI Global).
Andrelini, L. (1999). Communication, computability and common interest games. Journal of Games and Economic Behaviour , 27, 1–37. doi:10.1006/game.1998.0652
Arciero, L., Picillo, C., Solomon, S., & Terna, P. (2014). Building ABMs to control the emergence of crisis analyzing agents' behavior . In Adamatti, D., Dimuro, G., & Coelho, H. (Eds.), Interdisciplinary applications of agent-based social simulation and modeling . Hershey, PA: IGI-Global.
Binmore, K. (2009). Rational Decisions. Gorman Lectures in Economics . Princeton, N.J.: Princeton University Press.
Camerer, K. (1995). Individual decision making . In Kagel, J. H., & Ross, A. E. (Eds.), Handbook of experimental economics . Princeton, NJ: Princeton University Press.
Camerer, K. (2003). Behavioural game theory: Experiment in strategic interaction . Princeton, NJ: Princeton University Press.
Camerer, K., & Weber, M. (1992). Recent developments in modelling preferences: Uncertainty and ambiguity. Journal of Risk and Uncertainty , 5(4), 325–370. doi:10.1007/BF00122575
Carlsson, H., & Van Damme, E. (1993). Global games and equilibrium selection. Econometrica , 61, 989–1018. doi:10.2307/2951491
Choquet, G. (1953). Theory of capacities. Ann. Inst. Fourier (Grenoble) , 5, 131–295. doi:10.5802/aif.53
Coehlo, H., Rocha Costa, A. C., & Trigo, P. (2014). On agent interactions governed by morality . In Adamatti, D., Dimuro, G., & Coelho, H. (Eds.), Interdisciplinary applications of agent-based social simulation and modeling . Hershey, PA: IGI-Global.
Dubois, D., Willinger, M., & Van Nguyen, P. (2011). Optimization incentive and relative riskiness in experimental stag-hunt games. International Journal of Game Theory , 41, 369–380. doi:10.1007/s00182-011-0290-x
Duffy, J. (2006). Agent-based models and human subject experiments . In Tesfatsion, L., & Judd, K. (Eds.), Handbook of computational economics (Vol. 2). Amsterdam, The Netherlands: Elsevier.
Eichberger, J., & Kelsey, D. (2011). Are the treasures of game theory ambiguous? Economic Theory , 48, 313–339. doi:10.1007/s00199-011-0636-4
Ellsberg, D. (1961). Risk, ambiguity and the savage axioms. The Quarterly Journal of Economics , 75, 643–669. doi:10.2307/1884324
Epstein, J. M. (2008). Why model? Journal of Artificial Societies and Social Simulation , 11(4), 12.
Epstein, J. M., & Axtell, R. (1996). Growing artificial societies . Cambridge, MA: MIT Press.
Fudenberg, D., & Levine, D. (1998). The theory of learning in games . London: MIT Press.
Gibbons, R. (1992). Game theory for applied economists . Princeton, NJ: Princeton University Press.
Gilboa, I. (1987). Expected utility with purely subjective non-additive probabilities. Journal of Mathematical Economics , 16, 65–88. doi:10.1016/0304-4068(87)90022-X
Gilboa, I. (2009). Theory of decision under uncertainty (Econometric Society Monograph Series) . New York: Cambridge University Press. doi:10.1017/CBO9780511840203
Halevy, Y. (2007). Ellsberg revisited: An experimental study. Econometrica , 75(2), 503–536. doi:10.1111/j.1468-0262.2006.00755.x
Harsanyi, J., & Selten, R. (1995). A general theory of equilibrium selection for games . Cambridge, MA: MIT Press.
Harsanyi, J., & Selten, R. (1998). A general theory of equilibrium selection for games with complete information. Journal of Games and Economic Behavior , 8, 91–122. doi:10.1016/S0899-8256(05)80018-1
Hauser, F., Huber, J., & Kirchler, M. (2009). Comparing laboratory experiments and agent-based simulations: The value of information and market efficiency in a market with asymmetric information . In Hernández, C., Posada, M., & López-Paredes, A. (Eds.), Artificial economics: The generative method in economics (pp. 199–210). Berlin: Springer-Verlag. doi:10.1007/978-3-642-02956-1_16
Helbing, D., & Balietti, S. (2012). Agent-based modeling . In Helbing, D. (Ed.), social self-organization (Understanding complex systems) (pp. 25–70). Berlin: Springer. doi:10.1007/978-3-642-24004-1_2
Hey, J. D., Lotito, G., & Maffioletti, A. (2010). The descriptive and predictive adequacy of theories of decision making under uncertainty/ambiguity. Journal of Risk and Uncertainty , 41(2), 81–111. doi:10.1007/s11166-010-9102-0
Hey, J. D., & Pace, N. (2011). The explanatory and predictive power of non two-stage-probability theories of decision making under ambiguity (Discussion Papers 11/22) . Department of Economics, University of York.
Hommes, C. H. (2006). Heterogeneous agent models in economics and finance . In Tesfatsion, L., & Judd, K. (Eds.), Handbook of computational economics (Vol. 2). Amsterdam, The Netherlands: Elsevier.
Isaak, A. G. (2008). Simulating evolutionary games: A Python-based introduction. Journal of Artificial Societies and Social Simulation , 11(3), 8.
Knight, F. H. (1921). Risks, uncertainty and profit. Boston: Houghton-Mifflin.
Lucas, P., & Payne, D. (2014). Usefulness of agent-based simulation to test collective decision-making models . In Adamatti, D., Dimuro, G., & Coelho, H. (Eds.), Interdisciplinary applications of agent-based social simulation and modeling . Hershey, PA: IGI-Global.
Macal, C. M., & North, M. J. (2010). Tutorial on agent-based modeling and simulation. Journal of Simulation , 4, 151–162. doi:10.1057/jos.2010.3
Marinacci, M. (2000). Ambiguous games. Games and Economic Behavior , 31(2), 191–219. doi:10.1006/game.1999.0739
Myerson, R. B. (1991). Game theory . Cambridge, MA: Harvard University Press.
Rousseau, J. J. (1755). Discourse on inequality . Holland: Marc-Michel Rey.
Sarin, R., & Wakker, P. (1992). A simple axiomatization of nonadditive expected utility. Econometrica , 60, 1255–1272. doi:10.2307/2951521
Savage, L. J. (1954). The foundations of statistics . New York: Wiley.
Shoham, Y., & Leyton-Brown, K. (2009). Multiagent systems . New York: Cambridge University Press.
Tesfatsion, L. (2006). Agent based computational economics: A constructive approach to economic theory . In Tesfatsion, L., & Judd, K. (Eds.), Handbook of computational economics (Vol. 2). Amsterdam, The Netherlands: Elsevier. doi:10.1016/S1574-0021(05)02016-2
Trigo, P. (2014). Multi-agent economically motivated decision-making . In Adamatti, D., Dimuro, G., & Coelho, H. (Eds.), Interdisciplinary applications of agent-based social simulation and modeling . Hershey, PA: IGI-Global.
Trindade Magessi, N., & Antunes, L. (2014). Agent’s risk relation on strategic tax reporting game . In Adamatti, D., Dimuro, G., & Coelho, H. (Eds.), Interdisciplinary applications of agent-based social simulation and modeling . Hershey, PA: IGI-Global.
Van Dinther, C. (2008). Agent-based simulation for research in economics handbook on information technology . In Detlef, S., Weinhardt, C., & Schlottmann, F. (Eds.), Finance international handbooks information system . Berlin: Springer. doi:10.1007/978-3-540-49487-4_18
Fudenberg, D., & Tirole, J. (1991). Game Theory . Cambridge, Mass.: MIT Press.
Game Theory Binmore. Ken. 1992. Fun and Games: A Text on Game Theory. Lexington, Mass.: D. C. Heath.
Gibbons, R. (1992). Game Theory for Applied Economists . Princeton, N.J.: Princeton University Press.
Gilboa, I. (2010). Rational choice . Cambridge, Massachusetts: MIT Press.
Hernández, C., Posada, M., & López-Paredes, A. (Eds.). (2009). Artificial Economics: the Generative Method in Economics. Springer-Verlag Berlin Heidelberg . Springer. doi:10.1007/978-3-642-02956-1
Kreps, D. M. (1988). Notes on the Theory of Choice . Boulder, Colo: Westview Press.
Matthieu, P., Beaufils, B., & Brandouy, O. (Eds.). (2006). Artificial Economics. Agent-Based Methods in Finance, Game Theory and their Applications. Springer-Verlag Berlin Heidelberg . Springer.
Myerson, R. B. (1991). Game Theory: Analysis of Conflict . Cambridge, Mass.: Harvard University Press.
Osborne, M. J., & Rubinstein, A. (1994). A Course in Game Theory . Cambridge, Mass.: MIT Press.
Tesfatsion, L., & Judd, K. (Eds.). (2006). Handbook of Computational Economics (Vol. 2). Netherlands: Elsevier.
Ambiguity: The case where there are no available exact measures of the probability that some events will happen.
Games: A methodology used in social sciences in order to model strategic interaction among agents.
Non-Additive Additive Capacities: When our beliefs on the probabilities that some events will happen do not add up to unit.
Optimism: When an agent focuses on the high payments of the payoffs.
Pessimism: When an agent focuses on the low payments of the payoffs.
Stag Hunt: A game that Rousseau used to explain social cooperation and optimism.
1 According to rational choice theory, an agent always has well-defined preferences and always maximizes her utility with respect to these preferences subject to the various constraints in her environment (income, institutional, etc).
2 A familiarity of the reader with basic economic theory is assumed. For more information on choice theory and utility maximization, see Binmore (2009).
3 In order to represent the agent’s preferences with a utility function, there are several axioms that must be satisfied. These axioms are either behavioral or axioms that guarantee the existence of such preferences. Most of the times they are normative axioms (what people should do).
4 This means that the agent faces no risks.
5 For more on decision making under ambiguity see Gilboa (2009).
6 The main properties of capacities are presented in the appendix.
7 Similar issues are discussed in the present volume by Coelho et al. (2014).
8 Pareto dominated outcome is one which is reached when another outcome that makes at least one of the two players better off without hurting the other is available.
9 For an extended literature review and experimental results, see Dubois et al. (2001).
10 For further references on the issue, see Eichberger and Kelsey (2011).
11 For an excellent tutorial on how to write Python programs for simulations in games, see Isaak (2008).
Mixed Strategies Nash Equilibrium (MSNE)
In order to find the MSNE, we attach probabilities to the various strategies of the players. For example, we assume that Player 1 plays c with probability p and d with probability 1-p. Similarly, for player 2 we assume that she plays c with probability q and d with 1-q. In order to calculate the level of the probabilities where agents switch strategies, we use the following procedure:
For Player 1, we want to find the reaction of the opponent that makes her to be indifferent to playing either strategy. The expected utility of Player when she cooperates is:
EU1(c) = qU1(c,c) + (1–q)U1(c,d) = 9q
Similarly, when she decides to defect:
EU1(d) = qU1(d,c) + (1–q)U1(d,d) = 8q – (1–q)7 = q – 7
Player 1 is indifferent to either strategies when EU1(c) = EU1(d) which leads to
This gives three different cases:
Choquet Expected Utility (CEU)
Let X be a finite set and 2X its power set. Then a capacity v on 2X which satisfies:
A capacity v is convex if . As this model is a Rank Dependent Model, contrary to the Expected Utility model, in CEU the ranking of the outcomes plays significant role. If we assume that we have three different events {s1,s2,s3} which respectively lead to consequences {x1,x2,x3}, then the decision maker makes a rank of the utility that she obtains from the three consequences. So if, for example, u(x1)>u(x2)>u(x3), then the decision maker maximizes the weighted expected utility. Thus, instead of probability, now the agent uses capacities which are weighted depending on the ranking. So in this case the Choquet Expected Utility to be maximized can be written as:
In the case of additive beliefs, this equation is simply the Expected Utility. Marinacci (2000) shows that when the capacities are convex (agent is ambiguity averse), then more weight is out on the worst outcome. This is exactly the way that a pessimistic agent forms her CEU. On the contrary, an optimistic decision maker maximizes the following:
Pessimistic Player: A pessimistic player focuses on the ‘bad’ outcome. Take, for example, the payoff matrix of game 2. In this case, the pessimistic player focuses on the payoff when she and the opponent both defect, thus 1. This is the outcome that is overweight. When she decides which strategy to play, she solves:
U1(c)=3vb(c); U1(d)=1+vb(c)
Player 1 decides to cooperate when U1(c)>U1(d) and this holds when vb(c)>1/2.
Optimistic Player: Similarly, an optimistic player decides as:
U1(c)=3–3vb(d); U1(d)=2–vb(d)
Player 1 decides to cooperate when U1(c)>U1(d) and this holds when vb(d)<1/2.
| Figure 2. Simulation code 111 |
|---|
 |
| Figure 3. Simulation code 211 |
|---|
 |