Game theory has been variously described as the science of strategy or that of conflict resolution. At its core, it has the characteristics of a mathematical construct: a clear set of concepts and assumptions, fundamental theorems, and applications to real world issues. The fact that the issues in question are mostly the domains of the social sciences, however, places game theory in a peculiar position compared to other mathematical and scientific disciplines. Following von Neumann and Morgenstern’s book, it is customary to analyze what we call game situations by using parlor games—already existing ones or ones specially constructed for this very purpose—as analytical models. This chapter does this.
The past decade has witnessed a huge explosion of interest in issues that intersect network design and game theory. In recent times, algorithmic game theory has been one of the most high-profile growth areas in theoretical computer science and telecommunication (Wooldridge, 2012). Game theory is the mathematical theory of interactions between self-interested agents. In particular, it focuses on decision making in settings where each player’s decision can influence the outcomes of other players. In such settings, each player must consider how each other player will act in order to make an optimal choice. In game theory, ‘game’ means an abstract mathematical model of a multi-agent decision making setting (Wooldridge, 2012).
In game theory, a modeling situation is defined as a game to predict the outcome of complex interactions among entities. Usually, a normal game form () can be formulated with three parameters: the players, a strategy or action space for each player (i.e., strategy set), and consequences of the actions (i.e., a set of payoffs). Mathematically,
can be defined as ∈ {, {Si}i∈, {ui}i∈}.
The utility function of player i (ui) can be represented as the degree of satisfaction received by player i as the function of the strategy it chooses, si, and the action of other players:
s-i = (s1,…,si-1, si+1,…,sN).
Players are decision makers, who choose how they act. A player, such as a company, a nation, a wireless node, or even a biological species, may be independent and has to make specific actions that have mutual, possibly conflicting, consequences. Usually, players are assumed to be individually rational and act in a rational manner and try to ensure the best possible consequence according to their preferences. Strategy set is the collection of various actions available to the player. Each player has a number of possible actions and can choose an action to determine the resulting outcome of the game. Any kind of action of a player should be expressed with a suitable utility function, which maps every action to a real number. A payoff (or utility) function quantifies the satisfaction that a player can get from a particular action. Usually, utility of a player corresponds to the received payment minus the incurred cost. Based on the payoff, the outcome to the different players can be evaluated. Therefore, individual decision makers (i.e., players) try to find the best actions.
The most classic game theory example is the Prisoner's Dilemma (“Prisoner's dilemma,” n.d.). The prisoner's dilemma is a canonical example of a game analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interests to do so. To put it simply, two prisoners are getting charged for a crime that they most likely did together, but the police aren't sure. So, they set up a deal where they question each suspect privately, and they can choose to cooperate (i.e., claim they did not commit the crime) or betray (i.e., admit to committing the crime). The punishments are as follows:
If we were to draw a matrix to represent the prisoners' payoffs, it would resemble Table 1.
Table 1. Sample matrix for the prisoners' payoffs
| Prisoner B Stays Cooperates | Prisoner B Betrays | |
|---|---|---|
| Prisoner A Stays Cooperates | Each serves 1 year | Prisoner A: 10 years Prisoner B: goes free |
| Prisoner A Betrays | Prisoner A: goes free Prisoner B: 10 years |
Each serves 3 years |
If the other prisoner chooses to cooperate, betraying gives a better reward, and if the other prisoner chooses to betray then betraying also gives a better reward. Because betrayal always rewards more than cooperation, all purely rational self-interested prisoners would betray each other. Therefore, collaboration is dominated by betrayal in the classic version of the game. The interesting part of this result is that pursuing individual reward logically leads the prisoners to both betray, even though they would get a better reward if they both cooperated. In this situation, the only rational choice for a sentence-minimizing prisoner is to betray, since this gives it a better outcome, whatever the other does. Hence both are worse off if both are rational than if both are irrational. Specifically, each individual gets a lighter sentence if both try to maximize their sentences than if both try to minimize them. Therefore, it is so-called ‘prisoner’s dilemma’.
Far from being mere curiosities, game-theoretic dilemmas occur throughout social life. Therefore, the concept of prisoner's dilemma is an interesting issue in the social sciences such as economics, politics and sociology, as well as to the biological sciences such as ethology and evolutionary biology (Howard, 1971). The arms races during Cold War period can be modeled as a Prisoner's Dilemma situation. Although the best strategy is for the Western and Eastern sides to disarm, the rational course for both sides is to arm. This is indeed what happened in real world, and both sides poured enormous resources in to military research and armament.
Initially, game theory assumes that games are represented in a flat form, as a matrix or tree. It also assumes that players have no resource limitations in terms of time or space, so that they can keep the entire game tree in memory, and can calculate all the possible consequences of each move. Given these assumptions, and as long as we could conceive an algorithm which played the game perfectly in finite time, the game would be effectively trivial. This means that the finite two-player perfect-information game (i.e., chess) is considered trivial to this field. However, when we take into account the resource limitations of the players, it is obvious that a player could never maintain the entire game tree (for a big game) in memory, nor consider all possible consequences of each action. Thus a player must consider possibilities and outcomes selectively, and make decisions based on less-than perfect information. As the player cannot in general see the exact influence of a move on the final goals of the game, it follows that her reasoning must be heuristic (Pell, 1993).
Learning can be defined as the capability of drawing intelligent decisions by self-adapting to the dynamics of the environment, taking into account the experience gained in past and present system states, and using long term benefit estimations. Learning is adamantly driven by the amount of information available at every game player. As a result, learning algorithmic game theory has become an increasingly important part of algorithmic research in recent years. In particular, machine learning has made continued progress in developing methods that can generalize from data, adapt to changing environments, and improve performance with experience, as well as progress in understanding fundamental underlying issues. There has recently been increasing interest in research at the intersection of game theory and learning algorithm. Such work is motivated by the observation that whilst these two fields have traditionally been viewed as disparate research areas, there is actually a great deal of commonality between them that can be exploited within both fields. By integrating over the distribution of opponent strategies rather than taking a simple empirical average, recent research work shows how insights from game theory can be used to derive a novel learning algorithms (Blum, 2008).
Most game-learning algorithms are designed to improve a program based on watching or playing against knowledgeable opponent players. Although it is certainly important to understand how a program (or player) could learn from good players, it is equally important to know how those good players became good in the first place. A much smaller proportion of learning work has considered how programs might become strong players while relying neither on active analysis nor on experience with experts. Most of these approaches can be considered as self-play, in which either a single player or a population of players evolves during competition on large numbers of contests. A related technique, which can also be viewed as a form of self-play, is that the basic playing program which learned to predict the expected-outcome of positions if played by random players. This was shown to be effective for constructing evaluation functions for some games (Pell, 1993).
To interpret game theory, descriptive and normative interpretations exist. These two interpretations present very different criteria for the question of whether game theory works (Wooldridge, 2012). Under a descriptive interpretation, we can view game theory as attempting to predict how game players will behave in strategic settings. Therefore, the descriptive interpretation suggests that we should look for whether game theory successfully predicts how people will make choices in settings that we can model as games. Some scholars believe that by finding the equilibria of games they can predict how actual human populations will behave when confronted with situations analogous to the game being studied. This descriptive interpretation of game theory has come under recent criticism. Game theorists assume players are Homo economicus and always act rationally to maximize their payoffs (“Homo economicus,” n.d.). Moreover, they respond by comparing their assumptions to those used in physics. Thus while their assumptions do not always hold, they can treat game theory as a reasonable scientific ideal akin to the models used by physicists. However, real game players, e.g., human beings, often act either irrationally, or do not play equilibrium strategies. Therefore, the fundamental assumptions made by game theorists are often violated, and the question of how players reach an equilibrium remains open. Under a normative interpretation, we can view game theory as prescribing courses of action for players. That is, game theory tells players how they ought to act. Therefore, the normative interpretation suggests that we should examine whether we can obtain outcomes that are better than what we might otherwise have obtained (Wooldridge, 2012). Some scholars in the normative view see game theory not as a predictive tool for the behavior of human beings, but as a suggestion for how people ought to behave. Since a Nash equilibrium of a game constitutes one's best response to the actions of the other players, playing a strategy that is part of a Nash equilibrium seems appropriate. However, this normative interpretation for game theory has also come under criticism. First, in some cases it is appropriate to play a non-equilibrium strategy if one expects others to play non-equilibrium strategies as well. Second, some cases, e.g., Prisoner's Dilemma, each game player pursuing his own self-interest leads all players to be worse off than if they had not pursued their own self-interests. Some scholars believe that this demonstrates the failure of game theory as a recommendation for behavior.
Games can be classified according to certain significant features and properties. Usually, games can be divided as two different groups based on various two-binary criteria; whether a game is a symmetric or not, or whether a game is a static game or not, or whether a game comprises perfect information or imperfect information, and so on. In this subsection, we study how to classify the games (“Game theory,” n.d.).
Non-Cooperative Games vs. Cooperative Games
Typically, games can be divided into non-cooperative and cooperative games whether players are cooperative or non-cooperative. A game is non-cooperative if the players make decisions independently and are not able to form binding commitments. Therefore, players are in conflict and do not communicate or collaborate with each other. So, players try to ensure the best possible consequence according to the utility function. The prisoner’s dilemma and the battle of the sexes are well known non-cooperative games.
Cooperative games, also called coalition games, are games in which players make binding commitments and find it beneficial to cooperate in the game. Therefore, legal systems or strict rules are required to adhere to players’ promises. In cooperative games, the joint actions of groups are analyzed, i.e. what is the outcome if a group of players cooperate. Therefore, the main interest in cooperative games is to fairly distribute the outcome to each player according to their contributions. In non-cooperative games this is not possible. Shapley value and Nash bargaining solution are well known cooperative games. Table 2 shows the main features of non-cooperative and cooperative games.
Table 2. Main features of non-cooperative and cooperative games
| Game Model | Key Objective | Solution Concept | Type |
|---|---|---|---|
| Noncooperative game | Individual players act to maximize their own payoff. | Nash equilibrium Correlated equilibrium Bayesian Nash equilibrium Subgame Perfect Nash Equilibrium Evolutionary stable strategy Stackelberg equilibrium Wardrop Equilibrium Pareto Equilibrium α-Equilibrium |
Static game Dynamic game Repeated game Evolutionary game, Markovian game, Stackelberg game, Auction game Public goods game Contention game Intervention game Supermodular game Security game, etc., |
| Cooperative game | Coalitions of players are formed and players have joint actions to gain mutual benefits | Nash bargaining solution Kalai-Smorodinsky Bargaining Solution Egalitarian Bargaining Solution Rubinstein Bargaining Solution |
Coalitional game Bargaining game Matching game Voting game, etc., |
However, this two-binary classification has been questioned. Therefore, considerable efforts have been made to link the two type game models. Recently, hybrid games are proposed in a semi-cooperative manner. These games contain cooperative and non-cooperative elements. For instance, coalitions of players are formed in a cooperative game, but these play in a non-cooperative fashion.
Static Games vs. Dynamic Games
Static games are also called strategic, one-shot, single stage or simultaneous games. In static games, all players make decisions (or select a strategy) simultaneously, without knowledge of the strategies that are being chosen by other players. Even though the decisions may be made at different points in time, the game can be called a simultaneous game because each player has no information about the decisions of others. Static games are represented by the normal form and solved using the concept of a Nash equilibrium. Nash equilibrium is a solution concept of a non-cooperative game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally. If each player has chosen a strategy and no player can benefit by changing his or her strategy while the other players keep their strategies unchanged, then the current set of strategy choices and the corresponding payoffs constitute a Nash equilibrium (Osborne & Rubinstein, 1994).
Dynamic games, also called sequential, extensive or repeated games, define the possible orders of the events and players iteratively play a similar stage game. Unlike static games, players have at least some information about the strategies chosen on others and thus may contingent their play on earlier actions. This could not be perfect information about every action of earlier players. Therefore, the players observe the outcome of the previous game round and make decisions for the next game round. Therefore, players can react adaptively to other players’ decisions. For reasoning dynamic games, equilibrium concept for static games is insufficient. Therefore, a sub-game perfect equilibrium is adopted as a solution concept in extensive sequential dynamic games. If a strategy profile represents a Nash equilibrium in every sequence sub-game of the original game, it is defined as a sub-game perfect equilibrium, which is a refinement of a Nash equilibrium.
Dynamic games are also divided finite extensive games and infinite extensive games. Generally, dynamic games are finished in finite actions. Every finite dynamic game has a sub-game perfect equilibrium. It may be found by backward induction, which is an iterative process for solving finite extensive form. Some pure mathematical game models based on the set theory last for infinitely many actions. Since backward induction no more works on infinite games, logicians have proposed a tool, which they call ‘coinduction’ to reason on infinite sequential games (Lescanne & Perrinel, 2012).
Discrete Games vs. Continuous Games
Some game models are concerned with finite, discrete games that have a finite number of players, strategies and outcomes. Therefore, game players choose from a finite set of pure strategies. These games are called discrete games. Most classical game models are discrete games. Discrete game concepts can be extended as continuous games. The continuous game allows games to include more general sets of pure strategies, which may be uncountably infinite continuous strategy set. Differential game and Cournot competition game are well-known continuous games. In differential games, the evolution of the players' state variables is governed by differential equations. By using the optimal control theory, optimal strategy is selected. Cournot game is used to describe an industry competition model in which companies compete on the amount of output they will produce.
Zero-Sum Games vs. Positive-Sum Games
According to player’s payoff structures, games can be categorized into zero-sum and positive-sum (or non zero-sum) games. In particular, zero-sum games are a special case of constant-sum games. If the total sum of all players’ benefits is always zero for every combination of strategies, these games are called as zero-sum games. It means that whatever gained by one player is lost by the other players. Therefore, zero-sum games are strictly competitive. Typical zero-sum games are gambling (i.e., Poker game) and most sporting events. All other games excluding zero-sum games are positive-sum games. Positive-sum games are non-strictly competitive, because such games generally have both competitive and cooperative elements. In positive-sum games, a gain by one player does not necessarily correspond with a loss by another player.
For a zero-sum game, an optimal solution can always be found. However, there is no universally accepted solution for positive-sum games. Since players in a positive-sum game have some complementary interests, there is no single optimal strategy that is preferable to all others. Many game models in network design are positive-sum games (Spangler, 2003).
n-Player Games vs. Population Games
The most common way for game classification is based on the number of game players (i.e., how many players in the game). Game is the formal model of an interactive situation. It typically involves several players. When a game has only 1 player, it is usually called as an individual decision problem with stochastic outcomes. In 1-player games, one player is faced with an optimization problem. It is equal to optimal decision process. Therefore, it can be viewed as optimal-control games. Usually, 1-player games can be divided as static 1-player games and dynamic 1-player games. Static 1-player games are formulized by using mathematical programming. Dynamic 1-player games are modeled based on the optimal control theory over a period of time. Differential games can be viewed as extensions of optimal-control theory. With two or more players, a problem becomes a theoretical game. The formal definition of a game specifies the players, their preferences, their information, the strategic actions available to them, and how these influence the outcome. Modern game theory began with the 2-player games (i.e., two-person zero-sum games). The normal strategic form of 2-player games is usually represented by a matrix which shows the players, strategies, and pay-offs. Games with an arbitrary, but finite, n (n ≥1) number of players are often called n-player games.
Population games are considered to involve a population of players where strategy selections can change over time in response to the decisions made by all individual players in the population. Evolutionary game is a well-known population game (Sandholm, 2007).
Perfect Information Games vs. Imperfect Information Games
If each player knows every strategy of the other players that performed before that player at every point, this game is called a perfect information game. Therefore, the players are fully informed about each other player’s strategy. Usually, extensive games can be games of perfect information. Card and chess games are well-known perfect information games. In addition, on the contrary, players in strategic games do not know exactly what strategies of other players took up to that point. In this case, players have to infer from their likely strategies. These games are called imperfect information games. Most game models studied in game theory are imperfect-information games. Furthermore, an imperfect information game model is a good framework in network design because the users of a network seldom know the exact actions of the other users (Leino, 2003).
Complete Information Games vs. Incomplete Information Games
Complete information game is a game if all factors of the game are common knowledge. Therefore, each player is aware of all other players and the set of strategies and payoffs for each player. Complete information game is a model of the theoretical pre-conditions of an efficient perfectly competitive market. In a sense, it is a requirement of the assumption also made in economic theory that market participants act rationally. All other games are games of incomplete information games. In an incomplete information game, at least one player is uncertain about another player’s preferences. A sealed-bid auction is a well-known incomplete information game. A player knows his own valuation of the merchandise but does not know the valuations of the other bidders.
Perfect information game is often confused with complete information game, which is a similar concept. However, there is a tiny difference between the notions of complete information games and perfect information games. The notion of complete information is concerned with the information of the elements of the game, such as the strategy space, the possible payoffs, and so on. Therefore, complete information game requires that every player know the strategies and payoffs available to the other players but not necessarily the actions taken. However, the notion of perfect information is concerned with the information of the strategies taken by the other players or their sequence (Han, Niyato, Saad, Başar, & Hjørungnes, 2011).
Pure Strategy Games vs. Mixed Strategy Games
A pure strategy game provides a complete definition of how a player will play a game. In particular, it determines the strategy that a player will make for any game situation. Therefore, a player's strategy set is the set of pure strategies available to that player. In a mixed strategy game, a strategy may be random, or drawn from a probability distribution, which corresponds to how frequently each strategy is to be played. Therefore, there are infinitely many mixed strategies available to a player, even if their strategy set is finite. In particular, a mixed strategy game in which the player assigns a strictly positive probability to every pure strategy is called a totally mixed strategy game.
The prisoner’s dilemma and the Stag hunt game are well-known pure strategy games. Rock-paper-scissors game is a good example of mixed strategy game. John Nash proved that there is an equilibrium for every finite pure strategy or mixed strategy game. If all players are playing pure strategies, pure strategy Nash equilibrium exists. If at least one player is playing a mixed strategy, there exists a mixed strategy Nash equilibrium (“Strategy,” n.d.).
Unitary Games vs. Hybrid Games
Nowadays, a new viewpoint of game theory has been developed to understand complicated circumstances. Game designers try to mix two different type games and propose a new hybrid game model, which contains cooperative and non-cooperative features, simultaneously. All the traditional games excluding hybrid games can be called unitary games. Most traditional games are unitary games.
In hybrid games, players act competitively to maximize their profits. However, sometimes, the competition among players is transformed into a cooperative competition. Well-known hybrid game is biform game and co-opetition game (Brandenburger, & Stuart, 2007). Biform game is a hybrid non-cooperative and cooperative model to formalize the two-stage decision problem. Co-opetition game (co-opetition is a neologism coined to describe cooperative competition) is designed to provide an effective solution under cooperative and competitive situations. For example, co-opetition occurs when players interact with partial congruence of interests. They cooperate with each other to reach a higher payoff creation, and then, struggle to achieve better advantage in competitive manner.
Egalitarian Games vs. Hierarchical Games
Most classical games are designed based on the assumption that the players are symmetric, that is to say, when no single player dominates the decision process. However, there are other types of games wherein one of players has the ability to enforce his strategy on the other players. In these games, some hierarchy exists among players. Some players’ decision priority is higher/lower than the others. Following the original work of H. von Stackelberg, the player who holds the higher priority and powerful position is called the leader, and the other players who rationally react to the leader's decision are called the followers.
Without loss of generality, all the games with symmetric players can be called egalitarian games. In egalitarian games, there are no hierarchical levels among players. On the other hand, some games including the hierarchy concept in decision making process are called hierarchical games. There can be multiple levels of hierarchy with many asymmetric players. Stackelberg games have been widely known as a good example of hierarchical games.
Symmetric Games vs. Asymmetric Games
A game is called a symmetric game if all players have the same strategy set, and the payoff to playing a given strategy depends only on the strategies being played, not on who plays them. Therefore, each player earns the same payoff when the player selects the same strategy against similar strategy of his competitors. In symmetric games, the identities of the players can be changed without changing the payoff to the strategies. Many well-known games are symmetric, for example, the prisoners’ dilemma, the battle of the sexes, the stag hunt game and the chicken game. Symmetric games may naturally arise from models of automated-player interactions, since in these environments, the players may possess identical circumstances, capabilities, and perspectives by design (Cheng, Reeves, Vorobeychik, & Wellman, 2004). Asymmetric games are games where there are different strategy sets for players. The examples of asymmetric games are ultimatum game, Stackelberg game and the dictator game.
CLASSIFICATION OF GAME SOLUTIONS
Game theory puts forward a number of solution concepts that are typically intended to formulate some notion of rational choice in a game-theoretic setting. Therefore, solution concepts are thus at the heart of game theory (Wooldridge, 2012). A solution of a game is a set of the possible strategies and obtained when the players act rationally and intelligently. Generally, a solution is an outcome from which no player wants to deviate unilaterally. Solutions from each game model can be classified into different types according to their certain features and properties.
Equilibria are the most famous concept of solutions in non-cooperative games. If each player has chosen a strategy and no player can benefit by changing his or her strategy while the other players keep their strategies unchanged, the set of current strategy selections constitute a equilibrium. Bargaining solutions, core, Shapley value, nucleolus are well-known solutions for cooperative games. Bargaining solutions provide predictions about how the profit will be shared, or what division is fair, which may depend on the player utility functions. Various bargaining solutions have been proposed based on slightly different assumptions about what properties are desired. Core, Shapley value and nucleolus are solutions for coalitional cooperative games. The following subsection focuses on solutions in game models and explains the fundamental ideas.
Solutions for Non-Cooperative Games
Fundamental problem in game theory is determining how players reach their decisions. In particular, the question of how can players select their strategies is of ultimate importance. In recent years, there has been a proliferation of solutions for non-cooperative games. A typical research mainly focuses on the modeling an environment or strategic interaction, which is the relevant consequence of rational behaviors by all players. Equilibrium is a state that every player will select a utility-maximizing strategy given the strategies of every other player. This concept is very momentous and there are different types of equilibrium in non-cooperative games.
Nash Equilibrium
A Nash equilibrium, named after John Nash, is a well-know and classical solution concept in non-cooperative games. It is a set of strategies if each represents a best response to the other strategies. So, if all the players are playing the strategies in a Nash equilibrium, they have no unilateral incentive to deviate, since their strategy is the best they can do given what others are doing. A game in normal form may have either unique, multiple or no Nash equilibrium.
Formally, a Nash equilibrium of a strategic game G = {, {Si}i∈, {ui}i∈}, is defined as a vector of strategies s* = where
= S1 × S2 ... × Sn is the set of strategy profiles. Therefore, no unilateral deviation in strategy is profitable for any single player, that is
(1)
where s-i = (s1,…,si-1, si+1,…,sN) is a vector of strategies, one for each player, except the player i.
Nash Equilibrium can be classified either a pure-strategy Nash Equilibrium or a mixed-strategy Nash Equilibrium. A pure strategy Nash equilibrium is a Nash equilibrium in which each player uses a pure strategy. If both players use the same strategy in the equilibrium, this kind of equilibrium is called a symmetric equilibrium. For example, the Nash equilibrium of the Prisoner's Dilemma game is a symmetric equilibrium, since both players use the same strategy (i.e., betray). Under mixed-strategy Nash Equilibrium, a pure strategy is chosen stochastically with a fixed frequency. Nash proved that every game with a finite number of players, who can dynamically choose from pure strategy set, has at least one mixed-strategy Nash equilibrium (“Nash equilibrium,” n.d.).
For non-cooperative games, the strategy of a player at Nash equilibrium is the best response to the strategies of the other players. However, there are some disadvantages. First, the main weak point of Nash equilibrium is inefficiency. The solution of Nash equilibrium frequently does not coincide with a point that yield high utility values to all players. Therefore, the Nash equilibrium may sometimes appear non-rational in a perfect rational perspective. Second, there could be multiple Nash equilibria in a game, and if a player is restricted to adopting only pure strategies, the Nash equilibrium may not exist. Third, in the scenario of the Nash equilibrium, the players are assumed to be rational. That is, a player will always be able to maximize his payoff, which is consistent with his preferences among different alternative outcomes. This rationality of the player requires complete information and a well-defined and consistent set of strategies. However, in reality, this assumption rarely holds. Occasionally, game players make decisions irrationally due to the limited information about available strategies. Fourth, the idea of Nash equilibrium has mostly been developed in a static setting. Therefore, this approach cannot capture the adaptation of players to change their strategies and reach equilibrium over time. In addition, computing the mixed-strategy Nash equilibrium of a n-player game is generally very difficult. It requires arduous endeavors to solve multiple high-order polynomial equations (Wang, Han, & Liu, 2009).
Pareto Equilibrium
Pareto equilibrium is the concept of Nash equilibrium with efficiency. It is a set of strategies such that there is no other set of strategies where all players receive a higher payoff. Formally, a Pareto equilibrium of a strategic game {, {si}i∈, {ui}i∈} is a vector of strategies s* ={si}i∈, one for each player, such that there is no s∈{si}i∈ that satisfies ui (s) > ui(s*) for all player i∈.
The idea of Pareto equilibrium is strongly related to the concept of Pareto optimality.
Subgame Perfect Nash Equilibrium
A subgame perfect Nash equilibrium is an equilibrium such that players' strategies constitute a Nash equilibrium in every subgame of the original game. In game theory, a subgame is any part (a subset) of the base game. A subgame perfect Nash equilibrium may be found by backward induction technique, which is an iterative process for solving finite extensive sequential games. It proceeds by first considering the last time a decision might be made and choosing what to do in any situation at that time. Using this information, one can then determine what to do at the second-to-last time of decision. By iteratively repeating the backward induction technique, the best action for every possible situation can be obtained.
Sometimes, implausible Nash equilibria arise in games, such as incredible threats and promises. Such equilibria might be eliminated in perfect and complete information games by applying subgame perfect Nash equilibrium. However, it is not always possible to avail oneself of this solution concept in incomplete information games. Therefore, imperfect and incomplete information games, these implausible equilibria cannot always be eliminated.
Bayesian-Nash Equilibrium
In game theory, Bayesian game is an incomplete game with the probabilistic analysis, and a probability distribution is updated according to Bayes’ rule. Following John C. Harsanyi’s framework, Bayesian game is used to analyze imperfect information scenarios. In a non-Bayesian game, a strategy profile is a Nash equilibrium if every strategy in that profile is a best response to every other strategy in the profile; i.e., there is no strategy that a player could play that would yield a higher payoff, given all the strategies played by the other players. However, in a Bayesian game, rational players are seeking to maximize their expected payoff, given their beliefs about the other players (Cox, 2006).
A Bayesian Nash equilibrium is defined as a strategy profile and beliefs specified for each player about the types of the other players. In dynamic games, this solution concept yields a lot of equilibria when no further restrictions are placed on players' beliefs. Especially, Bayesian Nash equilibrium results in some implausible equilibria, where players take turns sequentially rather than simultaneously. Due to this reason, Bayesian Nash equilibrium is thought as an incomplete tool to analyze dynamic games of incomplete information.
ε-Equilibrium
ε-equilibrium is a strategy profile that approximately satisfies the condition of Nash equilibrium (Han, 2011). When a player has chosen a strategy and it is impossible to gain more than ε in the expected payoff, the current set of strategies and the corresponding payoffs constitute a ε-equilibrium. That is formally formulated as
(2)
ε-equilibrium is a near-Nash equilibrium, and ε is a real non-negative parameter. Every Nash Equilibrium is equivalent to a ε-equilibrium where ε = 0.
Correlated Equilibrium
In 1974, Robert Aumann introduced a solution concept - correlated equilibrium, which is more general than the Nash equilibrium. In the correlated equilibrium, each player chooses his strategy according to the player’s observation and a strategy profile is chosen randomly according to a certain distribution. If no player would want to deviate from the recommended strategy while assuming the others don't deviate, the distribution is called a correlated equilibrium (Kunnumkal, 2004). To mathematically express, let p(si, s-i) be the joint distribution of players to perform a specific strategy (si). If the strategy of the different players is independent, p(si, s-i) is a product of each individual player's probability for different strategies. Given the recommended strategy (si), a correlated strategy s = (si, s-i) is said to be a correlated equilibrium if we have as follows.
(3)
where si, , and s-i∈S-i for all players i∈. If the player i is to choose the recommendation strategy si, then choosing strategy
instead of si cannot result in a higher expected payoff to the player i (Han2011).
Nash equilibrium corresponds to the special case of correlated equilibria. Therefore, Nash equilibrium is a point inside the correlated equilibria set. Usually, there are multiple correlated equilibrium. Therefore, which one is the most suitable should be very carefully considered in practical design (Wang, 2009). To satisfy this goal, the concept of correlated optimal is developed. A multi-strategy sall is correlated optimal if it satisfies the following conditions.
(4)
and ∀i∈N
where Ep(∙)is the expected average utility with p. The correlated optimal is the solution concept to achieve the highest social welfare. Even though the correlated optimal is a notion of efficiency, it does not necessarily result in a socially desirable distribution of resources: it makes no statement about equality, or the overall well-being of a society (Barr, 2012).
Wardrop Equilibrium
In 1952, John G. Wardrop developed the concept of Wardrop equilibrium in the context of road traffic. Initially, Wardrop considered the scenario of roads and a large number of vehicles traveling though the roads from an origin to a destination. The vehicles are interested in minimizing their travel time, which is dependent on each road’s characteristics and the number of vehicles using it. This situation can be modeled by using a non-cooperative game, with the players being the vehicles attempting to find a shortest-path route while minimizing their travel time from origin to destination. Therefore, the main concept of Wardrop equilibrium can capture key features of a minimization problem among many selfish players and it is related to the idea of Nash equilibrium (Han, 2011), (Altmana, Boulognea, El-Azouzia, Jiménezb, & Wynterc, 2006).
In roads at the Wardrop equilibrium, two principles are assumed, i) all used path from a source to a destination have equal mean latencies, and ii) any unused path from a source to a destination has greater potential mean latency than that along the used paths. To formally express the Wardrop equilibrium, define ‘class i’ as all individual vehicles in belonging to population that have a given origin s(i) and a given destination d(i). Let u be the vector of strategies of all vehicles and Si is the strategy set of vehicles in the class i. Therefore, Si is identified with all the available paths in roads between s(i) and d(i). The path j’s delay is defined as Dj(u), . Then, letting
be the subset of paths actually used by the vehicles in the class i, u* is a Wardrop equilibrium if and only if it satisfies
(5)
The Wardrop equilibrium has been applied to many problems in transportation and communication networks (Correa and Stier-Moses, 2010). However one drawback of Wardrop's user equilibrium is that it requires deterministic inputs of travel demand and supply. This assumption is not applicable in real world situations (Altmana, 2006).
Evolutionary Stable Strategy
Game theory developed to study the strategic interaction among rational self-regarding players. However, in the early 1970’s, the theory underwent a transformation into evolutionary game theory. An important concept of evolutionary game theory is that of Evolutionarily Stable Strategy (ESS), which was defined and introduced by John Maynard Smith. Its aim is to investigate the effect of each individual behaving in a selfish manner, on a large population of such individuals, given that the best strategy to use for itself depends on the collective behavior of the population, which itself is composed of many of these same selfish individuals. Therefore, ESS is evolutionarily stable and cannot be invaded by any alternative strategy (“Evolutionarily Stable Strategies,” n.d.). ESS solution can be obtained by repeating a symmetric game with comparing in an infinite population. If all the players play strategy x and x is stable in the sense that a mutant playing with a different strategy y cannot successfully invade, then x is an ESS. More formally, x is an ESS if U(x, z) > U(y, z) where the payoff for playing x against another playing z is greater than that for playing any other strategy y against z.
ESS is an equilibrium refinement of the Nash equilibrium and sometimes, it is associated with mixed strategy equilibriums. Equilibrium in Hawk-Dove game and in a biology oriented version of Chicken game is a very famous example of ESS. The main concept of ESS has been used widely in behavioural ecology, economics, anthropology, evolutionary psychology, philosophy, and political science (Krebs, & Davies, 1997). In addition, this approach also allows to increase our understanding of dynamical systems in biology and, more recently, in the social sciences with significant ramifications for philosophy.
| Figure 1. Equilibria for non-cooperative games |
|---|
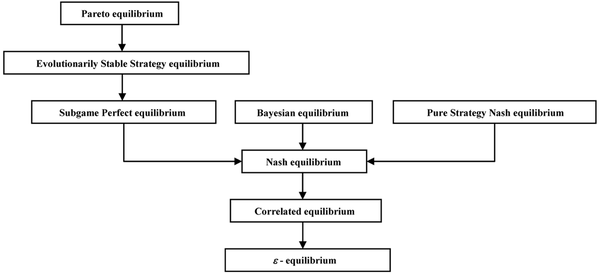 |
Non-cooperative games constitute an important branch of game theory, and Nash equilibrium has been regarded as a general solution for non-cooperative games. Since the development of the Nash equilibrium concept, game theorists have proposed many related solution concepts, which refine the Nash equilibrium to overcome perceived flaws in the Nash concept. However, subsequent refinements and extensions of the Nash equilibrium concept share the main insight of Nash’s concept. All equilibrium concepts analyze what choices will be made when each player takes into account the decision-making of others. Finally, we can draw the equilibria diagram for non-cooperative games. Figure 1 shows the relationship among different kinds of equilibria.
Solutions for Cooperative Games
Nowadays, cooperative games become a hot research topic and have received a generous concern. Cooperative games are games where groups of players (i.e., ‘coalitions’) may enforce cooperative behaviors. Therefore, players choose their strategies through a consensus decision-making process. The key issue in cooperative games is how to divide the total payoffs of players. Many solution concepts have been proposed to answer this problem, each kind of which satisfies a certain rational behavior and reasonable principle. The aim of subsection is to study classical solutions for various cooperative games.
Pareto Optimality
Named after Italian economist Vilfredo Pareto, Pareto optimality (or Pareto efficiency) is a measure of efficiency. In Pareto optimality, no player can be made better off without hurting, or decreasing the payoffs of other players. To formally express the Pareto optimality (v*), let vector v* is preferred to a vector v if each element of v is not strictly greater than the corresponding parameter of v* and at least one parameter is strictly less: that is, for each element i and
for some element j. It is expressed as v∞v*.
An outcome of a game is Pareto dominated if some other outcome would make at least one player better off without hurting any other player. A strategy change process can make at least one player better off without making any other player worse off, it is called a Pareto improvement. Therefore, a solution is defined as Pareto optimal when no further Pareto improvement can be made (“Pareto Optimality,” n.d.).
Weak Pareto optimality is also a solution concept, which nominally satisfies the same standard of Pareto optimal status. However, the conditions are weaker than Pareto optimal. A weak Pareto optimal is an allocation for which there are no possible alternative allocations whose realization would cause every individual to gain with the new allocation. In other words, a new allocation is only considered to be a Pareto improvement if it is strictly preferred by all individuals. Therefore, the set of Pareto optimal solutions is a subset of the set of weak Pareto optimal solutions, because a Pareto optimal solution satisfies the stronger requirement that there is no allocation that is strictly preferred by one individual player and weakly preferred by the rest players. When contrasted with weak Pareto optimal, a standard Pareto optimality may be referred to as a strong Pareto optimal.
The notion of Pareto optimal is very useful in economics and many other fields. However, the concept of Pareto optimality does not necessarily result in a socially desirable distribution of resources. Since there is no fairness consideration in Pareto optimality, some more refined fairness concept is required for the overall well-being society (Barr, 2012).
Core
Core is one of solution concepts for n-person cooperative games. Even the idea of the core already appeared in the work of Edgeworth in 1881, the modern definition was introduced by Donald B. Gillies in 1959. Core is the set of feasible allocations under which no subset (a coalition) has a value greater than the sum of its players’ payoffs. Let the vector x = [x1,...xi,...xn] be the received payoffs for players (={1,2,…,n}). This payoff vector is group rational if
In particular, the highest total payoff can be achieved by forming a coalition among all players. Also, the payoff vector is individually rational if xi≥ν ({i}). It means that a player will not agree to receive payoff less than that the player could obtain without coalition. If the payoff vector x is both group rational and individually rational, it is defined as ‘imputation’ like as.
(6)
An imputation x is unstable with coalition if
. Specifically, if the imputation is unstable, there is at least one player who is unsatisfied. The core is defined as the set of imputations in which no coalition
has an incentive to reject the proposed payoff allocation, and to deviate from the grand coalition of all players while forming coalition
instead. Mathematically, core (
) is expressed as follows:
(7)
The core, sometimes it is called as a cooperative Nash equilibrium, is useful to obtain the stability condition of the coalitional cooperative game. However, it may contain several points and in some cases it could be empty. Therefore, the solution that provides the most preferable distribution strategy is required (Han, 2011).
To avoid the emptiness of core, L. Shapley and M. Shubik introduced the generalized concept for the core solution, named strong ε-core, in 1966 (Shapley, & Shubik, 1966). The strong ε-core for some number ε is the set of payoff vectors
(8)
The strong ε-core is the set of allocations where no coalition can improve its payoff by leaving the grand coalition, if it must pay the ε penalty for leaving. The value ε can be negative. In this case, the strong ε-core represents a bonus for leaving the grand coalition. Clearly, regardless of whether the core is empty, the strong ε-core will be non-empty for a large enough value of ε and empty for a small enough (possibly negative) value of ε (Shapley, 1966).
The strong ε-core solution can avoid the empty problem. However, the core can be quite large, so selecting a suitable core allocation can be difficult. Moreover, in many scenarios, the allocations that lie in the core can be unfair to one or more players (Han, 2011).
Shapley Value
In 1953, Lloyd Shapley proposed a new cooperative solution concept, Shapley Value. It assigns a unique distribution (among the players) of a total surplus generated by the coalition of all players. Shapley also proved that the Shapley Value can satisfy efficiency, symmetry and additivity. Main feature of Shapley Value is to provide a unique solution of a n-person cooperative game. For example, a coalition of players cooperates, and obtains a certain overall gain from that cooperation. Since some players may contribute more to the coalition than others, it is important to decide the final distribution of generated surplus among the players (Shapley value, n.d.). The Shapley value can provide one possible answer under the cooperative game situation.
To compute Shapley value, let us define the value function (v) over the real line like as with
, and characterize unique mapping ϕ = [ϕ 1…, ϕi,…, ϕn] that is the Shapley Value; ϕi is the payoff given to the player i by the Shapley Value ϕ. The Shapley Value is characterized by a collection of desirable properties or axioms described below (Han, 2011),(Cai, 2004).
Shapley showed that there exists a unique mapping, the Shapley value, from the space of all coalitional games to , that satisfies these four axioms (Han, 2011). Based on these properties, the Shapley Value can be obtained by considering the payoff depending on the order that player joins the coalition. In particular, the Shapley Value is the average payoff to a player if the players enter into the coalition in a completely random order. The Shapley Value ϕ = [ϕ1…,i,…,n] can be computed as follows:
(9)
where indicates the number of players in the set
. ν(
) is the minimum payoff which the coalition S can guarantee its members (i.e., players), and ν(
–{i}) is the payoff secured by a coalition with the same members in
except the player i. In the Shapley Value, all the coalitions are regarded equal which means they have the same probability to appear. The first part of the formula can be interpreted as the probability of a coalition containing the player i with the size of
. The second part is the payoff difference between the coalitions with and without the player i, which measures the contribution of the player i to the coalition. The bigger the difference, the more the player contributes to its coalition, then the more payoff he should earn (Han, 2011), (Cai, 2004).
The Nucleolus
In 1969, Schmeidler introduced the idea of nucleolus, which is a solution concept for cooperative games. The basic motivation of the nucleolus is to provide an allocation that minimizes the dissatisfaction of the players with the allocation they can receive in a given cooperative game. The nucleolus is quite an interesting concept, since it combines a number of fairness criteria with stability.
Usually, the model of cooperative game has two basic elements: the set of players and the payoff function. The set of players is expressed as . The meaning of payoff function (v) is a real function of set
; any possible subset S of players (a coalition
) would produce the payoff v(S). If coalition S and T are independent (i.e.,
), then
. In this cooperative game
, there are two important issues, i) how the coalitions are formed amongst the players, and ii) how the payoff from a player is allocated. These two issues are strongly interrelated.
Instead of applying a general fairness axiom for finding a unique payoff allocation, the goal of nucleolus solution is to find a way to fairly allocate the payoff that is jointly created by players. Suppose x={x1,x2,…,xn} (i.e., ) is the set of each player’s payoff, Y={y1,y2,…,yn} is the set of the profit allocation imputation. As mentioned earlier, imputation is a payoff vector that is both individually rational and group-rational. The measure of dissatisfaction with an allocation x for a coalition y∈Y is defined as the excess value like as
If an allocation x can ensure that all excess values (or dissatisfaction indexes) are minimized, it is of particular interest as a solution for coalitional cooperative games. This is the main concept of nucleolus (Han, 2011), (SongHuai, Xinghua, Lu, & Hui, 2006).
Now, let ψ(x) be the set of all excess values in a game (, v) arranged in non-increasing order. In other words, ψi(x)≥ψj(x), ∀i<j. Notice that x is in the core of v if it is an imputation and ψ1(x)≤0 To define the nucleolus, we consider the lexicographic ordering of sets. For example, For two payoff sets u, w, it is said that ψ(u) is lexicographically smaller than ψ(w) if for some index c, we have ψi(u)=ψi(w), ∀i<c and ψc(u)<ψc(w). The nucleolus of v is the lexicographically minimal imputation. Hence, the nucleolus minimizes the excess vales in a non-increasing order starting with the maximum excess value.
The nucleolus is group and individually rational (since it is an imputation), and unique in the game. If the core is not empty, the nucleolus is in the core. The process steps for computing the nucleolus are, i) to find the imputations that distribute the payoff of the grand coalition in such a way that the maximum excess value is minimized, ii) If this minimization has a unique solution, it is the nucleolus, iii) If not, searching for the imputations that minimize the second-largest excess value, iv) this process is repeated for all subsequent excess values, until a unique solution (i.e., the nucleolus) found. The applications of the nucleolus are numerous in cooperative game theory. One of the most prominent examples is the marriage contract problem that first appeared in the Babylonian Talmud (0-500 AD) (Han, 2011.
Even though the nucleolus is quite an interesting concept, and provides an optimal and fair solution to many applications, the main drawback is its computational complexity. Therefore, the applications that utilize the nucleolus remain scarce.
Nash Bargaining Solution
In 1950s, John Nash proposed a simple cooperative game model, which predicted an outcome of bargaining based only on information about each player’s preferences. His bargaining game model is formulated by an expected utility function over the set of feasible agreements and the outcome which would result in case of disagreement.
Nash gave six axioms to provide the concept of efficiency and fairness for desirable bargaining solutions - Individual rationality, feasibility, Symmetry, Pareto optimality, Independence of irrelevant alternatives and Invariance with respect to utility transformations. If a solution can fulfill these six axioms, it is called as the Nash Bargaining Solution (NBS), which is a unique and fair Pareto optimal solution (“Bargaining problem,” n.d.).
To formally express these axioms, we need to introduce some terminology. An agreement point is any strategy vector (s1,…,sn) ∈ where
is the set of strategy profiles. It is a possible outcome of the bargaining process. A disagreement point is also a strategy that is expected to be the result of non-cooperative actions; it means a failure of the bargaining process. Each player i has its own utility function (Ui(si)) and it has also a minimum desired utility value (
), which is the disagreement point. Assume
is a feasible payoff set that is nonempty, convex, closed, and bounded. Let d=(d1,…,dn)=
be the disagreement point, and F be a function F(S,d)→
. If the following Nash’s six axioms are satisfied, X*=
=F(S,d) is said to be an NBS (Han, 2011), (Park & Schaar, 2007), (Han, Ji, & Liu, 2004).
In the cooperative payoff region , all individually rational and Pareto optimal payoff pairs can be called the bargaining set; the NBS is located in the bargaining set. The axioms Individual rationality, feasibility, and Pareto optimality define the bargaining set. The other axioms are called axioms of fairness. The axiom Invariance with respect to utility transformations assures that the solution is invariant if affinely scaled. The axiom Independence of irrelevant alternatives states that if the bargaining solution of the larger set is found on a smaller domain, the solution is not affected by the domain size. The axiom Symmetry states that if two players have the same disagreement utility and the same set of feasible utility, then they will achieve the same NBS payoff (Han, 2011), (Park, & Schaar, 2007), (Han, Ji, & Liu, 2004).
The NBS is an effective tool to achieve a mutually desirable solution with a good balance between efficiency and fairness. However, NBS has focused on problems with convex feasible sets. This extreme assumption might be too strong; the convexity assumption has been questioned and caused some technical difficulties. Usually, the feasible set for real world control problems may be non-convex.
Kalai-Smorodinsky Bargaining Solution
In 1975, Ehud Kalai and Meir Smorodinsky introduced the fundamental solution concept of bargaining games. To get the desirable bargaining solution, they also gave six axioms - Individual rationality, Feasibility, Symmetry, Pareto optimality, individual monotonicity and Invariance with respect to utility transformations. In compare with NBS, the axiom Independence of irrelevant alternatives is substituted with the axiom individual monotonicity. A solution, which would satisfy these axioms, is called the Kalai-Smorodinsky Bargaining Solution (KSBS) (Han, 2011), (Park, & Schaar, 2007).
Individual monotonicity axiom means that the increasing of bargaining set size in a direction favorable to a specific player always benefits that player. For example, let (,d) and (
,d) be two bargaining problems where
If the maximum achievable payoffs of all players are the same except the player i, the player i gains more payoff in (
,d) than in (
,d) through the KSBS. Formally, if
, d=d´ and
for all k∈{1,...,Ν}\{i}, then Fi(
,d) ≥ Fi(
,d) (Park, & Schaar, 2007).
Like as the NBS, the KSBS also provides a fair and optimal solution. In addition, KSBS can be used when the feasible payoff set is not convex. It is the main advantage of KSBS over the NBS. Due to this appealing property, the KSBS approach has been practically implemented in various resource management problems in economics and telecommunications (Davila, 2009).
Egalitarian Bargaining Solution
In 1977, E. Kalai and R. Myerson developed another interesting bargaining solution. It is the Egalitarian Bargaining Solution (EBS). Unlike other bargaining solutions, the egalitarian solution enjoys even stronger monotonicity requirements while satisfying independence conditions. Without using the Nash's axiom of Invariance with respect to utility transformations, the EBS attempts to grant equal gain to players. In other words, it is the point which maximizes the minimum payoff among players. This characterization can be extended to a large class of solutions including the α-proportional bargaining solution (Bossert, 1995).
Let (,d) be a two-person bargaining problem where
is the feasible set of payoff vectors and
is the disagreement point. The ideal point of a bargaining problem is simply defined by
(10)
The egalitarian bargaining solution is defined by letting the unique point (x1, x2) = X∈ such that
x1 – d1 = x2 – d2 (11)
A generalization of the egalitarian solution is the class of α-proportional (or weighted egalitarian) bargaining solution. It is also defined as the unique point X∈ such that
x1 – d1 = α(x2 – d2) (12)
Clearly, α=1 leads to the egalitarian bargaining solution.
The main feature of EBS is a monotonicity with respect to expansions of the feasible set. The monotonicity axiom imposes an invariance condition under decomposition of the bargaining process into several stages. Therefore, the monotonicity axiom can be replaced by step-by-step negotiation (Bossert, 1995). There are at least two advantages in the step-by-step negotiation. First, it makes it easier to implement a solution since the negotiation can be broken up into several stages. Second, the players do not have incentives to change the order of the negotiations. This process is likely to be observed in actual negotiations.
Rubinstein Bargaining Solution
In 1982, Israeli economist Ariel Rubinstein built up an alternating-offer bargain game based on the Stahl’s limited negotiation model; it is known as a Rubinstein-Stahl bargaining process. This game model can provide a possible solution to the problem that two players are bargaining with the division of the benefits.
In Rubinstein-Stahl bargaining model, players have their own bargaining power (δ). The division proportion of the benefits can be obtained according to the bargaining power, which can be computed at each player individually. A more bargaining power player benefits more from the bargaining. Players negotiate with each other by proposing offers alternately. After several rounds of negotiation, they finally reach an agreement as following (Rubinstein, 1982).
(13)
and 0≤δ1,δ2≤1
It is obvious that and
. That is to say, there is a first-proposer advantage in the bargaining process. Traditionally, the bargaining power in the Rubinstein-Stahl's model is defined as follows.
δ = e-ξ×∆, s.t., >0 (14)
where Δ is the time period of negotiation round. Given the △ is fixed (i.e., unit_time), δ is monotonic decreasing with the ξ. ξ is an instantaneous discount factor to adaptively adjust the bargaining power.
Especially, Rubinstein bargaining model provides a solution of a class of bargaining games that features alternating offers through an infinite time horizon. For a long time, the solution to this type of bargaining game was a mystery. Therefore, Rubinstein’s solution is one of the most influential findings in cooperative game theory. Sometimes, it is considered as a non-cooperative implementation of the NBS, and is a solution for non-cooperative games. However, in this book, we treat it in the category of cooperative games.
| Figure 2. Solutions for cooperative games |
|---|
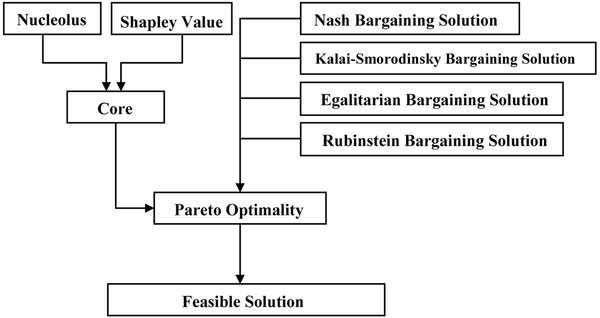 |
For cooperative games, a solution concept is a vector that represents the allocation to each player. Researchers have proposed different solution concepts based on different views. Figure 2 shows the relationship among different kinds of solutions.
This research was previously published in Game Theory Applications in Network Design edited by Sungwook Kim, pages 21-43, copyright year 2014 by Information Science Reference (an imprint of IGI Global).
Altmana, E., Boulognea, T., El-Azouzia, R., Jiménezb, T., & Wynterc, L. (2006). A survey on networking games in telecommunications. Computers & Operations Research , 33, 286–311. doi:10.1016/j.cor.2004.06.005
Bargaining Problem. (n.d.). Retrieved from http://www.answers.com/topic/bargaining-problem
Barr, N. (2012). Economics of the Welfare State . Oxford, UK: Oxford University Press.
Blum, A. (2008). Online Learning, Regret Minimization, and Game Theory. Retrieved from http://videolectures.net/mlss08au_blum_org/
Bossert, W., & Tan, G. (1995). An arbitration game and the egalitarian bargaining solution. Social Choice and Welfare , 12, 29–41. doi:10.1007/BF00182191
Brandenburger, A., & Stuart, H. (2007). Biform Games. Management Science , 53, 537–549. doi:10.1287/mnsc.1060.0591
Cai, J. (2004). Allocate fair payoff for cooperation in wireless ad hoc networks using Shapley Value. In Proceedings of Parallel and Distributed Processing Symposium (pp. 26-30). Academic Press.
Cheng, S. F., Reeves, D. M., Vorobeychik, Y., & Wellman, M. P. (2004). Notes on Equilibria in Symmetric Games. In Proceedings of International Workshop on Game Theoretic and Decision Theoretic Agents, (pp. 23-28). Academic Press.
Correa, J. R., & Stier-Moses, N. E. (2010). Wardrop equilibria. Retrieved from http://www.columbia.edu/~ns2224/papers/WEsurveyRev2public.pdf
Cox, J. C. (2006). Perfect Bayesian Equilibrium. Retrieved from http://www.econport.org/content/handbook/gametheory/useful/equilibrium/perfect.html
Davila, J. (2009). Kalai - Smorodinsky solution to bargaining problems. Retrieved from http://cermsem.univ-paris1.fr/davila/teaching/BargTh/Bargaining%20slides%20-%202%20-%20Kalai-Smorodinsky.pdf
Evolutionarily Stable Strategies. (n.d.). Retrieved from http://ess.nbb.cornell.edu/ess.html
Game Theory. (n.d.). Retrieved from http://en.wikipedia.org/wiki/Game_theory
Han, Z., Ji, Z., & Liu, K. J. R. (2004). Low-complexity OFDMA channel allocation with Nash bargaining solution fairness. IEEE Global Telecommunication Conf., 6, 3726–3731.
Han, Z., Niyato, D., Saad, W., Başar, T., & Hjørungnes, A. (2011). Game Theory in Wireless and Communication Networks . Cambridge University Press. doi:10.1017/CBO9780511895043
Homo Economicus. (n.d.). Retrieved from http://rationalwiki.org/wiki/Homo_economicus
Howard, N. (1971). Paradoxes of Rationality . MIT Press.
Krebs, J. R., & Davies, N. B. (1997). Behavioural Ecology: An Evolutionary Approach. Wiley-Blackwell.
Kunnumkal, S. (2004). Algorithmic Game Theory. Retrieved from http://www.cs.cornell.edu/courses/cs684/2004sp/feb20.pdf
Leino, J. (2003). Applications of game theory in ad hoc networks . Academic Press.
Lescanne, P., & Perrinel, M. (2012). Backward coinduction, Nash equilibrium and the rationality of escalation. Acta Informatica , 49(3), 117–137. doi:10.1007/s00236-012-0153-3
Nash Equilibrium. (n.d.). Retrieved from http://economics.about.com/cs/economicsglossary/g/nashequilibrium.htm
Osborne, M. J., & Rubinstein, A. (1994). A Course in Game Theory . Cambridge, MA: MIT Press.
Pareto Optimality. (n.d.). Retrieved from http://www.economyprofessor.com/pareto-optimality-1906
Park, H. G., & Schaar, M. V. D. (2007). Bargaining Strategies for Networked Multimedia Resource Management. IEEE Transactions on Signal Processing , 55(7), 3496–3511. doi:10.1109/TSP.2007.893755
Pell, B. D. (1993). Strategy Generation and Evaluation for Meta-Game Playing. (Ph.D dissertation). University of Cambridge, Cambridge, UK.
Prisoner's Dilemma. (n.d.). Retrieved from http://en.wikipedia.org/wiki/Prisoner's_dilemma
Rubinstein, A. (1982). Perfect equilibrium in a bargaining model. Econometrica , 50, 97–109. doi:10.2307/1912531
Sandholm, W. H. (2007). Evolutionary Game Theory. Retrieved from http://www.ssc.wisc.edu/~whs/research/egt.pdf
Shapley, L. S., & Shubik, M. (1966). Quasi-cores in a monetary economy with non-convex preferences. Econometrica , 34(4), 805–827. doi:10.2307/1910101
Shapley Value. (n.d.). Retrieved from http://www.answers.com/topic/shapley-value
SongHuai, D., Xinghua, Z., Lu, M., & Hui, X. (2006). A novel nucleolus-based loss allocation method in bilateral electricity markets. IEEE Transactions on Power Systems , 21(1), 28–33. doi:10.1109/TPWRS.2005.860932
Spangler, B. (2003). Positive-Sum, Zero-Sum, and Negative-Sum Situations. Retrieved from http://www.beyondintractability.org/essay/sum
Strategy. (n.d.). Retrieved from http://en.wikipedia.org/wiki/Strategy_(game_theory)
Wang, B., Han, Z., & Liu, K. J. R. (2009). Peer-to-Peer File Sharing Game using Correlated Equilibrium. In Proceedings of Annual Conference on Information Sciences and Systems, (pp. 729-734). Academic Press.
Wooldridge, M. (2012). Does Game Theory Work? IEEE Intelligent Systems , 27(6), 76–80. doi:10.1109/MIS.2012.108
Best Reply: A pure strategy for one player is a best reply to a given opponent's pure strategy if it yields his best possible payoff among all his available strategies, provided that his opponent sticks to the given strategy.
Game States: As a game proceeds, various states of the world it is describing can be achieved.
The Normal Form: The normal form of a game is a list of pure strategies for each player and the specification of an outcome (in utility terms) for each pair of pure strategies (one strategy per player).
Payoff: A development of the game that the players value for itself according to their respective preferences.
Players: Independent decision-makers who influence the development of a game through their decisions.
Pure Strategies: A pure strategy for a player is a complete contingency plan (a game plan) that specifies in advance what he will do in any development of the game.