4
Community Referendum Model

The Community Referendum Model (Abelson and Bernstein, 1963) simulates how citizens’ attitudes change as a result of the communication in a community referendum campaign: the individuals change their attitudes as a consequence of their exposure to the mass media campaign messages, and also as an effect of the discussions with peers in the networks of interpersonal relations. The model is as general as to cover a large class of both non‐political (community referenda on social issues) and political processes (electoral campaigns) (Abelson and Bernstein, 1963: 93–94).

Computational and simulation modelling has some theoretical similarities with McPhee’s model (1963): the model is a computational construction of the political campaign on a particular issue in a social community. This artificial construction consists of a ‘miniature’ dynamic system which is implemented as a symbolic replication of a real campaign. While a single simulation run takes a few minutes on a computer (IBM 7090), it represents a real time of 1 week. Several runs thus cover as many weeks, simulating the campaign time. The outcomes of the simulations are interpreted as group phenomena, showing how the polarization of attitude positions on the referendum issue depends on the individual’s political interest and on that of their friends.

The simulation model consists of a set of artificial individual agents representing 500 citizens (Abelson and Bernstein, 1963: 94), a set of rules which the agents use for assertion, evaluation, and for the campaign message processing, and a set of rules for attitude change.

Conceptual Aspects: The Individual Agent

The individual citizen is represented in the model as a complex computational entity (individual agent) with an internal sophisticated structure with several attributes (see Figure 4.1): (i) social status and other relevant characteristics of each individual; (ii) initial settings of the individual interest, issue position and evidence of previous voting and experience with referendum campaign issues, like knowledge and attitudes toward such issues as acceptance/rejection positions (pro and con); (iii) exposure to the news channels supporting the referendum campaign and frequency of exposure to each such channel; (iv) individual attitude toward campaign key persons (i.e. influencers).

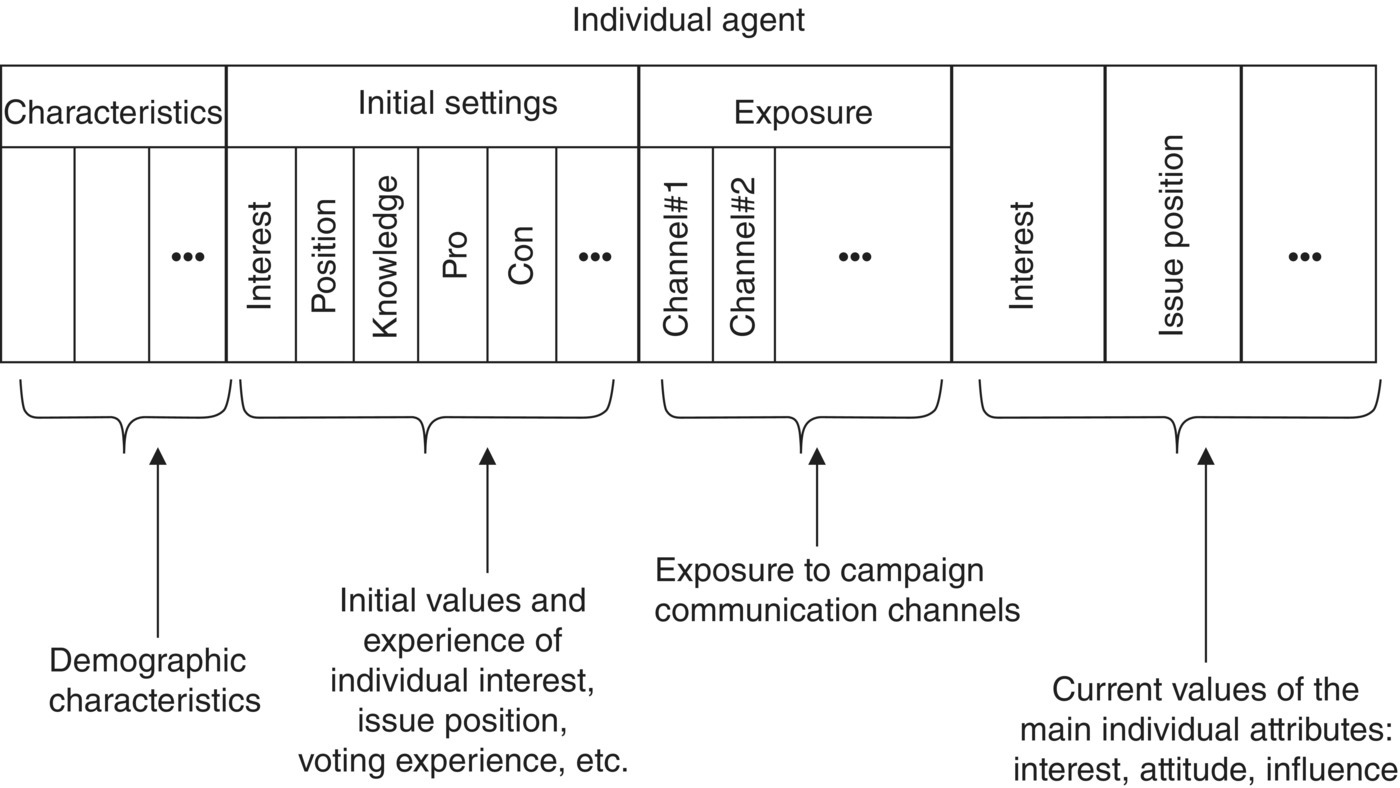
Figure 4.1 Individual agent’s internal representations of the electoral campaign.

The agents are subjected to two sources of influence: mass media public communication channels and personal interconnections. Each agent is characterized by issue positions, political interest for the referendum issue and the capacity to process the information provided by both public channel and the citizens in the network of interpersonal connections.

The message consists of an assertion about the referendum issue with which an agent could agree or disagree. The agreement/disagreement is subject to a set of rules which are initiated according to the type of assertion and its source.

Political Influence and Political Attitude Change

The individual agent is able to evaluate incoming assertions on the referendum issue: the agent has an attitude with respect to each assertion which has been evaluated (pro and con). This issue position is changing as the agent receives more messages from the media. A major role is played by the persons in the network of interpersonal relations, that is, citizens in the community that are considered pivotal for the referendum campaign (Abelson and Bernstein, 1963: 95). The individual agent has a position toward such influencers, and her position is changing as more discussions are engaged in with peers in the different networks – for example, at home or at the work place. The agent is characterized by a specific degree of interest in the referendum issue. This interest is also changing as the individual is exposed to the news media messages in the campaign and to the different issues of the influencers. The model is aimed at providing predictions for group phenomena.

An attitude (issue position) is changed if the source is liked, if there is content consistency, if there is consistency with the individual’s value system and previous experience with campaign issues or voting preferences. Individual agent interactions are simulated discussions and consist of assertion communication. Once communicated, an assertion is evaluated on the basis of the appropriate rule set.

Operational Model

The simulation model has a modular architecture which consists of mainly two modules (see Figure 4.2): the computational agents (population) and the computational structures, which consist of a pool of simulation variables and data structures, mechanisms and processes aimed at enhancing the individual interactions in a large population of individual agents.

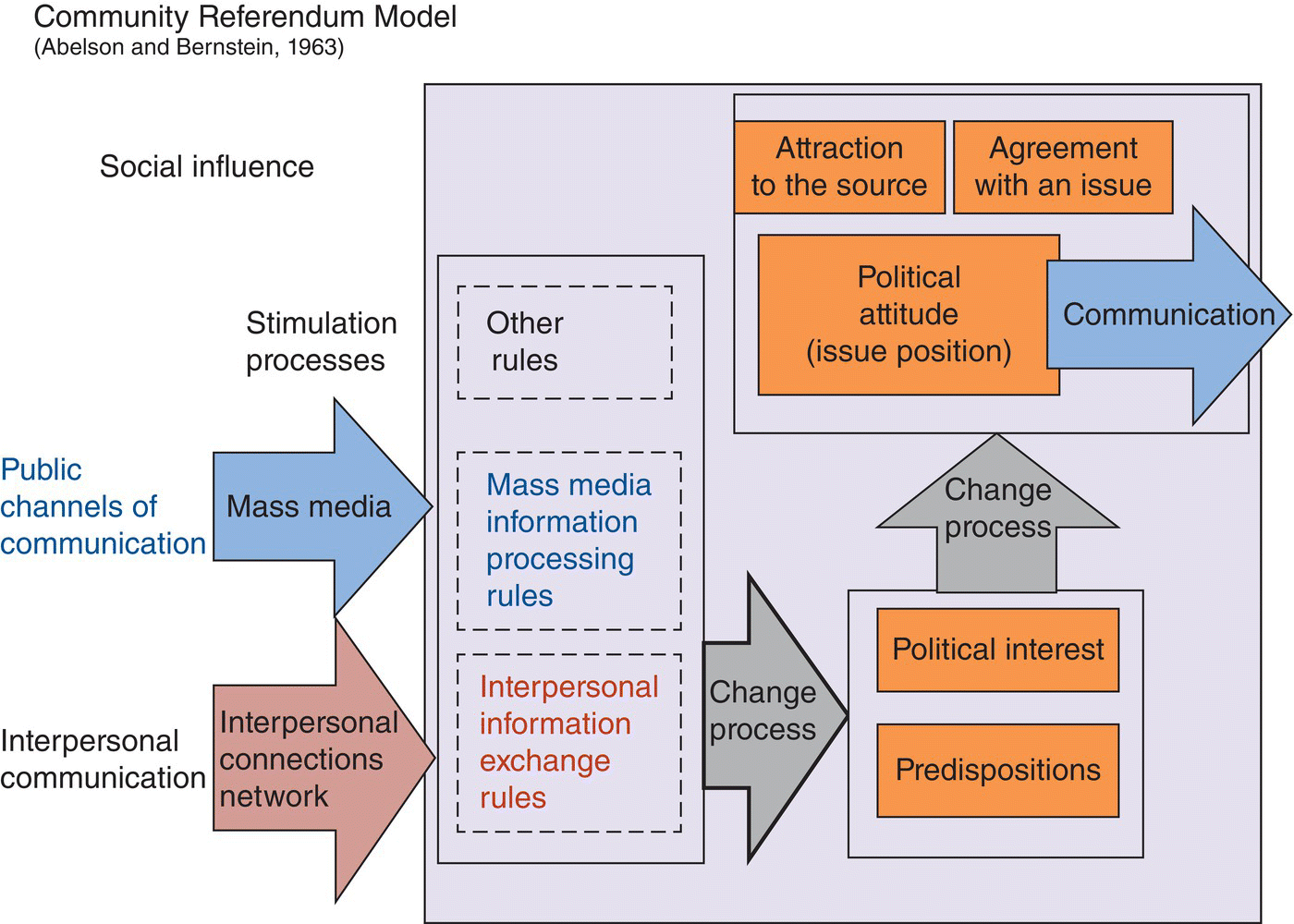
Figure 4.2 Community referendum simulation model: structure and processes.

The individual agent has a very sophisticated description. This includes both social structure (demographic characteristics, sociometric data) and attributes like political interest and attitude position toward the referendum issue, and a considerable number of measures of the agent’s capacity to interact, goal of interaction, internal predispositions, consistency of beliefs, extremity of issue positions and values associated with her interest toward the campaign messages and the conversations with peers in the networks of interpersonal relations.

Each individual agent is subjected to a classic sequence of phases: stimulation phase (achieved through campaign messages), influence phase (by assertions accepting/rejecting assertions) and learning phase (by assertions memorizing/forgetting). However, this classic scheme is employed in a specific way: corresponding mechanisms and processes in each phase are triggered by rules describing nearly each possible situation which an individual agent could encounter during simulation runs.

Stimulation Phase

The stimulation process is based on communication channels. At the operational level, the influence exerted on the individuals by means of communication channels and discussions with peers is controlled by the levels of resistance to influence, which define the attitude extremity levels. The campaign influence is successful when an individual agent has a mild position toward campaign issue(s) and her degree of interest in such issue(s) is sufficiently high as to make the agent sensitive to campaign stimulation (messages). The model covers situations in which almost all individual agents are influenced to some degree (Abelson and Bernstein, 1963: p. 98).

Influence Phase

Rules

The individual agent is able to change her attitude toward the referendum issue as the effect of the influences exerted by the sources in the communication channels and the peers in the interpersonal networks. The change processes are triggered by rules which are based on probability updates.

In each simulation run, the main variables – interest, issue position and experience – are updated in a cycle: during the first half of this cycle (A), the individual agents activate the rules which guide the evaluation of exposure to a source internal to a communication channel (A‐rules), while the evaluation of their exposure to the discussions in the dyadic networks is performed during the second half of the cycle (B) by the activation of another set of rules (B‐rules).

There are three sets of rules (Abelson and Bernstein, 1963: 98–112) involved in the appropriate processes which converge toward the changes in political interest, political attitude and vote choice.

There are 22 A‐rules (A1–A22) for evaluating the probability of individual exposure to different sources of campaign messages. The model defines various direct and reverse measures of exposure, like (1) attractiveness of a communication channel and attraction toward a particular issue, (2) receptivity to a particular source, (3) credibility of a certain source, a concept inspired by the work of Hovland and collaborators (Hovland, Janis and Kelley, 1953) and (4) attitude change factors, like the degree of change and direction of change. The model also includes the coupling of variables whose relationship and variability provide the means to evaluate additional factors like, for example, the ‘attention value’ (i.e. ‘low’ or ‘high’), ‘assertion match’ (i.e. ‘positive’ in case of agreement, ‘negative’ in case of disagreement), individual interest as a function of assertion match, individual satisfaction as a function of the degree of consistency between assertion and individual predispositions toward particular campaign issues (Abelson and Bernstein, 1963: 101).

There are 27 B‐rules (B1–B27) for evaluating the probability of individual exposure to conversations with peers in the dyadic networks of interpersonal relations. These rules are parallel to several A‐rules as their role is to transfer what has been defined in terms of exposure to campaign messages into terms of exposure to conversational interactions with peers. The B‐rules work on conditionals defined by concepts like:

• receptivity of an individual agent to another agent as a function of the extremity of attitude position of the latter;
• assertion match, which describes how much the assertions accepted by one agent are also accepted by the conversation partner;
• number of exposures to conversational interactions – the higher this number, the more the attitude position will change;
• interest in the campaign issue increases with the increase of the number of exposures to both conversations and communication through campaign channels;
• degree of forgetting (also used by McPhee in the learning process) – applies only to inconsistent assertions, and is used to keep within realistic limits the assertions involved by any individual agent at a given moment of time during the conversation with another agent.

The rules evaluating the probability of exposure to the conversations with peers in the dyadic networks are operating under the fundamental principle of homophily (as formulated in B27), which induces, in the long run, the effect of general consensus generated by the selection criteria of the peers from the network of interpersonal contacts. The authors make explicit that the attitude change occurs as the result of selective exposure to conversations with peers, and not as an effect of the experience‐based reactions to the messages transmitted by the sources in the campaign communication channels (Abelson and Bernstein, 1963: 94). The issue is especially relevant to the political persuasion within networks of interpersonal relations, an area addressed by McPhee with his collaborators (McPhee, 1961; McPhee and Smith, 1962), and which will be further ‘inherited’ by the approaches developed almost half a century later, two of them comprised here: Latané and collaborators (Nowak et al., 1990) and Huckfeldt et al. (2004).

This issue is particularly relevant since it concerns the problem of universal agreement in modelling democratic societies. It was developed by Abelson in a subsequent paper (Abelson, 1964), and especially by Robert Huckfeldt and collaborators in their diversity survival model. In his exquisite mathematical modelling theories in social psychology, Abelson (1967) developed a differential equation‐based mathematical model of the processes of individual interactions in small worlds. He succeeded in emphasizing in a particular formal way that the modelling of political attitude change as the outcome of the individual interactions in dyadic networks should be approached from the perspective of dynamic processes: it is only by considering the dynamics of individual interactions that the issue of diversity survival can be simulated in a believable way, that is, replicated by simulation models which do not reach universal agreement. Believable simulation models would remain stable in spite of new attitude positions which might be introduced by means of dyadic conversations and compete in the social space of an interpersonal network. The idea will strongly influence the modelling approaches developed much later by Bibb Latané and collaborators (Nowak et al., 1990), Robert Axelrod (1997) and by Robert Huckfeldt and his collaborators (Huckfeldt et al., 2004).

Variables

The interest, issue position (attitude) and the assertion‐acceptance variables are coupled so that their correlation can be evaluated during the simulations.

Mechanisms

The individual agent uses an assertion‐acceptance mechanism which allows for the evaluation of the influencer’s credibility, where the influencer could represent both the sources internal to the communication channels and discussion partners. This mechanism is useful in evaluating the degree of inconsistency between an individual’s issue position and the acceptance of an incoming assertion; if there is consistency, then the individual agent will accept the assertion, otherwise the agent will support increased pressure toward attitude change. Moreover, the spread of the degrees of acceptance/rejection of a particular assertion can thus be traced in the networks of interpersonal relations of each individual agent.

The model has never been tested against empirical data at the parameters described in the theoretical model, which is based on a population of 500 individual agents and a huge number of detailed descriptions for each agent, channel, source, rules and interpersonal networks. The richness of the model is sometimes overwhelming, and Abelson and Bernstein (1963: 115) admitted that the test simulations were performed with a very simplified set of manufactured data for only a set of 50 individual agents and a reduced set of assertions, channels, sources and conversational partners.

Philosophy of Simulation

The Community Referendum Model uses computer simulation with the explicit goal of unifying the theories of individual and group behaviour (Abelson and Bernstein, 1963: 93). Simulation modelling allows for the explanation of group behaviour by the interactions among individuals. One of the justifications provided by Abelson and Bernstein concerns the reduced capacity of statistical modelling to cover the individual attitude change and group behaviour issues. The static characteristic of statistical models based on variables and linear relationships among them has only limited ability to describe and explain the processes of behaviour and attitude change at both individual and group level. In order to overcome such limitations, they employ the computer simulation technique in constructing a dynamic model able to describe and explain the political processes which develop in a community during electoral or social campaigns. Such a simulation model consists of complex sets of variables (Abelson and Bernstein, 1963: 94) and computer programs which are meant to mimic the real structure and the dynamics of the community’s voting preferences by symbolically reproducing the dynamics of change in the individual agents’ attitudes and voting choices as they are exposed to a communication campaign.

Abelson and Bernstein published their model after a previous major experience in studies of electoral behaviour. At that time, the issue was one of the (if not the most) relevant subjects in political science. Their approach was not the only one: other than the computer simulation model developed by William McPhee and his collaborators (McPhee, 1963; McPhee and Smith, 1962), the issue was previously approached by Ithiel de Sola Pool and Robert Abelson (1961) in the Simulmatics project. It was also approached from a psychological perspective involving the psychology of personality as well as the psychology of voting (Lipset et al., 1954). Along with these social psychological and political science approaches, some of the most advanced approaches of that time in the area of artificial intelligence (AI) and problem‐solving models were developed, aimed at replicating the thought processes in humans by means of computer programs (Newell et al., 1958) which further inspired Robert Abelson and Alex Bernstein.

Trying to assess the philosophical idea behind the computer simulations, Abelson and Bernstein make a technical distinction between two types of simulations which are used by the various approaches of the time: one is a simulation type aimed at predicting (‘prognostic simulation’) the final outcomes of a computer simulation model (for example, predicting the winner in the presidential elections¹) and the other type is concerned with the simulation of the processes involved in a situation at hand (‘process simulation’) aimed at studying and tracing the detailed characteristics of the processes involved.The first type should be based on a detailed description of the agents involved in the scenarios. For example, de Sola Pool and Abelson identified 480 types of voters by cross‐classifying demographic characteristics and survey data. This was further oriented toward defining classes of agents and their types of attributes. The study of the individual agent thus becomes a fundamental dimension of research.The second type of simulation should be based on the detailed description of the processes: mechanism involved, variable descriptions, relationships between variables and coupled variables, and so on. This orientation has finally resulted in a second fundamental dimension of research which is that of process simulation. Prognostic simulation is based on large amounts of empirical data and achieves a description of future possible situations (outcomes) like, for example, the polarization of voting preferences.

When such large amounts of empirical data are not available, survey data could support and enhance the study of processes by detailed descriptions of the variables involved and their continuous transformations (Abelson and Bernstein, 1963: 120–121). This dimension of research will later on inspire Latané and collaborators in the design of the dynamic social impact model. It will also inspire Huckfeldt and collaborators in their agent‐based approach of the diversity survival model (Huckfeldt et al., 2004).

Conclusions

The two computer simulation models were developed almost in parallel, they nevertheless show some basic difference in their conceptual backgrounds: McPhee’s model (McPhee, 1961; McPhee and Smith, 1962; McPhee, Smith and Ferguson, 1963) is strongly influenced by Lewin’s concept of social forces (Lewin, 1952, 1959), while Abelson and Bernstein’s model is more oriented toward achieving aggregate mass behaviour from rule‐based interactions at the micro level.

McPhee’s approach is fundamentally oriented toward the achievement of a computer simulation system which could appropriately represent predispositions’ content and their relevant attributes, and mimic the predispositions’ change, a process which he describes as basically depending on political campaign stimulation and dyadic network persuasion.

Abelson and Bernstein’s approach is much more oriented toward the achievement of a computer simulation system which could appropriately represent and mimic the interactions among a large number of individual actors.

Though both models have to cope with the problem of universal agreement in dyadic interaction networks in which the selection of discussants is driven by the homophily principle (‘likes attract’) (Lazarsfeld and Merton, 1954), McPhee’s model addresses the aspects of content‐based roots of agreement, while Abelson and Bernstein model the individual interactions as the engine of reaching agreement.

Abelson and Bernstein’s Community Referendum Model often constitutes a basic reference in the history of simulation modelling and agent‐based models (Troitzsch et al., 1996; Uhrmacher and Weyns, 2009: 57; Troitzsch, 2013). Agent‐based systems and models are extensively used in social simulation (Gilbert and Troitzsch, 2005) and computational sociology (Squazzoni, 2012) to create artificial societies (Epstein and Axtell, 1996) and simulate complex, self‐organizing social processes (Edmonds and Meyer, 2013).

References

1. Abelson, R.P. (1964) Mathematical models of the distribution of attitudes under controversy. In N. Frederiksen and H. Gulliksen (eds), Contributions to Mathematical Psychology . Holt, Rinehart and Winston, New York.
2. Abelson, R.P. (1967) Mathematical models in social psychology. In R. Berkowitz (ed.), Advances in Experimental Social Psychology , vol. 3. Academic Press, New York; pp. 1–49.
3. Abelson, R.P. and Bernstein, A. (1963) A computer simulation model of community referendum controversies. Public Opinion Quarterly , 27(1), 93–122.
4. Axelrod, R. (1997) The dissemination of culture: a model with local convergence and global polarization. Journal of Conflict Resolution , 41(2), 203–226.
5. De Sola Pool, I. and Abelson, R.P. (1961) The Simulmatics project. Public Opinion Quarterly , 25, 167–183.
6. De Sola Pool, I., Abelson, R.P. and Popkin, S. (1965) Candidates, Issues and Strategies . MIT Press, Cambridge, MA.
7. Edmonds, B. and Meyer, R. (eds) (2013) Simulating Social Complexity . A Handbook, Understanding Complex Systems Series, Springer‐Verlag, Berlin Heidelberg.
8. Epstein, J.M. and Axtell, R.L. (1996) Growing Artificial Societies. Social Science from the Bottom Up , M.I.T. Press.
9. Gilbert, N. and Troitzsch, K.G. (2005) Simulation for the Social Scientist , Open University Press: Milton Keynes, UK.
10. Hovland, C.I., Janis, I.L. and Kelley, H.H. (1953) Communication and Persuasion . Yale University Press; Chapter 2.
11. Huckfeldt, R., Johnson, P.E. and Sprague, J. (2004) Political Disagreement. The Survival of Diverse Opinions within Communication Networks , Cambridge Studies in Political Opinion and Political Psychology. Cambridge University Press.
12. Lazarsfeld, P.F. and Merton, R.K. (1954) Friendship as a social process: a substantive and methodological analysis. In M. Berger, T. Abel and C.H. Page (eds), Freedom and Control in Modern Society . Van Nostrand, New York; pp. 18–66.
13. Lewin, K. (1952) Frontiers in group dynamics. In D. Cartwright (ed.), Field Theory in Social Science . Social Science Paperbacks: London (article first published in 1947).
14. Lewin, K. (1959) Group decisions and social change. In T.M. Newcomb and E.L. Hartley (eds), Reading in Social Psychology . Henry Holt, New York (article first published in 1947).
15. Lipset, M., Lazarsfeld, P.F., Barton, A. and Linz, J. (1954) The psychology of voting: an analysis of political behavior. In G. Lindzey (ed.) Handbook of Social Psychology , vol. II. Addison‐Wesley, Cambridge, MA; pp. 1152–1162.
16. McPhee, W.N. (1961) Note on a campaign simulator. Public Opinion Quarterly , 25(2), 184–193.
17. McPhee, W.N. (1963) Note on a campaign simulator. In W.N. McPhee (ed.), Formal Theories of Mass Behavior . Free Press, Glencoe, IL; Chapter 4.
18. McPhee, W.N. and Smith, R.B. (1962) A model for analyzing voting systems. In W.N. McPhee and W.A. Glaser (eds), Public Opinion and Congressional Elections , Free Press. New York; pp. 123–154.
19. McPhee, W.N., Smith, R.B. and Ferguson, J. (1963) A theory of informal social influence. In W.N. McPhee (ed.), Formal Theories of Mass Behavior . Free Press, New York.
20. Newell, A., Shaw, J.C. and Simon, H.A. (1958) Elements of a theory of human problem solving. Psychological Review , 65, 151–166.
21. Nowak, A., Szamrej, J. and Latané, B. (1990) From private attitude to public opinion: a dynamic theory of social impact. Psychological Review , 97(3), 362–376.
22. Squazzoni, F. (2012) Agent‐Based Computational Sociology , Wiley.
23. Troitzsch, K.G. (2013) Historical introduction. In B. Edmonds and R. Meyer (eds), Simulating Social Complexity, Understanding Complex Systems . Springer‐Verlag, Berlin; pp. 13–21.
24. Troitzsch, K.G., Mueller, U., Gilbert, N. and Doran, J.E. (eds) (1996) Social Science Microsimulation . Springer, Berlin.
25. Uhrmacher, A.M. and Weyns, D. (2009) Multi‐Agent Systems: Simulation and Applications . CRC Press.

Note

1 See more details in the book by de Sola Pool et al. (1965).