6
Dynamic Social Impact Theory and Model

Dynamic Social Impact Theory (DSIT) (Nowak et al., 1990) was initially meant to extend the original static impact theory to the general case in which all three factors – strength, immediacy and number – would be allowed to vary simultaneously, scaling up the mathematical model to a population of individuals being influenced and influencing each other in a fully reciprocal persuasion scenario. This scenario is much closer to the reality of political attitude change phenomena and more helpful for making plausible predictions about political preferences and variations in public opinion. However, adapting the original social impact mathematical model to more variability in the combined effect of the three factors brings forth a requirement which the original model fails to cope with: the nonlinear dynamics of political attitude change.

While the original social impact theory relies on a causal model‐invariant explanatory law of how the three factors would affect the individual’s response to group persuasive influence, the new model, adapted to include more variability, would need to go far beyond the traditional deterministic frame in order to scale up to a large population of interactive individuals. Since initially only the number factor was varied as the other two factors were kept constant, introducing full factor variability increases the complexity of the original mathematical model up to a certain limit where both conceptual and methodological approaches need to be changed: a nonlinear dynamic approach and the reductive simulation paradigm have replaced the initial model‐invariant causal approach and the mathematical modelling paradigm (Nowak et al., 1990: 362–364).

And this is just the tip of the iceberg.

The original social impact theory took the author almost two decades of intensive empirical research. Though it took one more decade to work out the new dynamic model, things went far from what, originally, had been expected: the original mathematical model actually turned into a computational simulation model with self‐organizing forms, which fascinated both the social psychology and the political science communities. It succeeded in changing paradigms, astonishing the audience, updating the history of mathematical modelling of political attitude change, and breaking up a tabu! Continuing diversity, as it had been modelled by Latané and his collaborators, finally succeeded in breaking up the universal agreement tabu, while several other authors couldn’t escape it,

And things did not stop here, either. The model was further modified so as to include a catastrophic theory approach on political attitudes’ extremity: the cusp. Nonlinearity of social impact in political attitude extremity proved once again that the model is able to identify the thin shape of dynamic attitude change. No other model of political attitude change has ever gone as far as Latané’s did. What did it need to turn the static social impact theory into the dynamic one? What it needed was actually a huge paradigm change.

It would be worth taking a close look at this notable and most fascinating experience in the computational modelling and simulation of political attitude change phenomena.

What Does It Take To Change a Static Theory Into a Dynamic One?

Social impact theory models the individual’s response to the persuasive presence of others (group persuasion) as depending on the simultaneous effect of three moderating factors: the strength of the attitudes held by the others (‘authority’ in social psychological terms), their immediacy (‘closeness’ in terms of physical space) and their number (group size). Characterized as one of the relevant ‘main‐effects’ models (Martin and Hewstone, 2003: 318) in the theoretical research on the majority–minority influence, it uses a single equation to specify a functional dependency between the social impact and the multiplicative effect of three variables representing contextual objective and subjective factors.

In its original version (Latané, 1981), social impact theory provides empirical evaluations of the dependence of the social impact’s magnitude on the number variable only. It identifies a power function as best describing the increase in the social impact with an increasing number of others as well as the decreasing marginal effect of many additional others. The other two factors, the strength and the immediacy, were introduced in the model as constant values. As the individual is considered the passive receiver of the social influence without the capability to interact and become a source of influence for the others, the original version of social impact theory has been considered a static theory (Nowak et al., 1990: 364).

Generalizing it to a social setting with many individuals, each individual holding a different political attitude and withstanding the persuasive presence of others, became for Latané and his collaborators a most challenging endeavour. The solution to the many difficult problems, however, required a computer simulation model instead of the mathematical one used before.

While preserving a strong explanatory power like its predecessor, the DSIT model differs in the explanation construction paradigm. The computer simulation model offers an explanation of the political change phenomena in other terms than social impact theory does. Both the static and dynamic models rely on the same fundamental mathematical equation of the social impact, but the difference between the static and the dynamic versions is that the former calculates numerical values of a power function describing the outcome of the abstract system in numerical terms, while the latter lets the system self‐organize during the reiterated simulation runs and reach stable or dynamic equilibrium configurations, which are graphically observable, and which make the emergent phenomena observable.

However, this paradigm shift from a model‐invariant explanatory approach to a context‐dependent dynamic one, although not surprising, was not an obvious paradigm choice given that some of the simulation methodologies were still in their infancy when the original social impact theory was published, and even much later when the DSIT showed its first, nevertheless impressive results.

Let us take a brief look at the history, as it will depict the scientific context of this issue.

Historical Context of Nonlinear Models in Social Psychology

In developing the DSIT, Latané and co‐workers make reference to two relevant attitude research paradigms in social psychology.

One of them assumes the cognitive dimension of attitudes and concerns the study of attitude change from the perspective of the relationships between an attitude’s structural internal components. Persuasion and involvement have been studied for their role in attitude formation and change (Petty and Cacioppo, 1980; Petty et al., 1981, 1983) as fundamental dimensions of social influence. One of the most notable approaches on attitude change belongs to Petty and Cacioppo ([1986]2011), who developed the model of the two routes of persuasion: central and peripheral. If an individual does not have a position with respect to some particular issue and, moreover, they are not involved or the issue does not have a particular relevance to them, then the peripheral route of persuasion combines with the hypothesis of the persuasive presence of the others. The individual response to the group persuasion is more sensitive to the social environmental persuasive influence. In this case, the individual could easily be persuaded by the media and/or by close others. Internalized or not, ¹ the wish to comply with the others is at work, and it works even better when the others are numerous, are in the individual’s proximity and their attitude’s strength is high.

DSIT does not argue on this. Moreover, it reinforces the idea that the persuasive influence of the others on the individual works much easier on the peripheral route, especially if this influence has the arguments of number, spatial proximity and strength of attitude (Nowak et al., 1990: 364). The common belief justified in the social psychology literature is that, unless deviant, and under increasing persuasive pressure from the others, the individual’s attitude change goes in the direction of more compliance with the others. And this compliance tendency might go on until uniformity of attitude prevailed. The most notable social psychology approaches on explaining uniformity are those of Moscovici (1976, 1985), Moscovici and Zavalloni (1969) and Isenberg (1986), who analysed attitude change in the relationship between majority–minority and drew the conclusion that attitude change goes toward compliance with the majority reaching, therefore, a final state of universal agreement. One main characteristic of the social psychology research in this period of time was the focus on the ‘milieu’ of interpersonal relations of the individual, which provides the means for communication and persuasion. The same focus on the individual’s interpersonal relations is characteristic of the political science research on the role of persuasion in political attitude formation and change (Lazarsfeld et al., 1944; Katz and Lazarsfeld, 1955).

The other attitude research paradigm concerns the study of attitude change from the perspective of the relationships between attitudes in some external context, thus dominating the area of mass beliefs (Converse, 1964). Converse’s idea that the political attitudes in a large population prove low consistency, lack of structure and instability was very influential (Zaller, 1992) until very late. Converse’s model represents the only individual‐based political attitude formation and change empirical model which has been extensively tested against a huge volume of empirical data. The social psychological research on social attitudes (ideology) has been dominated by structure and measurement models. It has been oriented towards the role played by personality traits and habitual opinions, values and social role, moral and pragmatic beliefs in the structural aggregation of attitudes (Eysenck, 1954; Kerlinger, 1972; Wilson, 1973; Middendorp, 1978).

Though different from both of them, Latané’s approach on dynamic social impact could be considered to belong to the second paradigm, insofar as it is a meta‐theory concerned with the social influence in the attitudinal change phenomena in a large population, and not with the structural components of single attitudes. It might be considered to belong to the second paradigm as far as the DSIT is concerned with the factors involved in the operation of the political attitude change processes and in the emergent phenomena associated with this. However, we should also notice that the DSIT explicitly relies on the former paradigm to assume the cognitive background of the strength factors. As regards the latter paradigm, the simulation models based on the DSIT reach quite opposite conclusions than most other previous modelling approaches.

In the argument presentation, the authors of the DSIT make reference to several mathematical linear models of attitude change using spatial functions. Social attitudes have been modelled in the Asch paradigm by Cohen’s (1963) static model of social influence, using a Markov model with four states to describe the influences of the social environment on the single individual. Hägerstrand (1965) modelled innovation diffusion as conditioned by the probability that target individuals come into contact with innovation sources. Abelson and Bernstein (1963) created a simulation model able to predict opinion change in a community referendum. The conclusion drawn by Abelson (1968), supported by his previous research on mathematical models in psychology (Abelson, 1964), was that mathematical linear models always end up in uniformity of agreement as they usually study a functional linear relationship between the amount of change and the degree of social pressure: as the latter increases, the former increases too.

One of the questions DSIT aimed to answer regards, therefore, the aspect of the end state in the vast majority of the social influence models of attitude change among the individuals exposed to group persuasion. Taking as argument the diversity of human society in general, and the opinion diversity of a democratic society in particular, the DSIT contradicts these models and provides a possible answer for modelling the ways of preserving real‐life continuing diversity: spatial contextuality.

It is at this point that Latané was supposed to make a research paradigmatic choice. One reason to leave the traditional longstanding assumptions of classical deterministic modelling was the need to afford an argument against the almost unanimous belief that, under the compliance condition, social influence makes political attitudes finally converge toward universal agreement.

Before Latané, Abelson and Bernstein (1963) identified a solution to the problem of uniformity of agreement in their microsimulation model of community referendum results. They noticed that, in social influence processes, the conditions for maintaining extremity of attitudes would prevent the system from reaching uniformity (Abelson and Bernstein, 1963: 106).

After obtaining encouraging empirical results of his own, Bibb Latané and collaborators must have taken Bernstein’s conclusion as a guideline (Nowak et al., 1990: 371). There was a long way to go, but this is how they made the paradigmatic choice by adopting a nonlinear dynamic political attitude change model. It is this choice that requested the DSIT rely on a computer simulation model in order to study the complex dynamics of political attitude change. While the original social impact theory is a theory about the individual’s response to the persuasive influence of the group, DSIT is a theory about the response to social persuasive influence of the individuals interacting in a complex social setting, which has three basic characteristics: individual interactions, reciprocity of persuasive influence, and recurrence of persuasive processes.

Modelling this kind of social setting in a social influence scenario under the psychosocial law defined by social impact theory requires different concepts of ‘social system’, ‘physical space structure’, ‘individual interaction’, ‘strength’ and ‘immediacy’.

Conceptual Model

DSIT starts from the hypothesis of a social setting in which many individuals interact with each other. The social setting includes an abstract social space and an associated finite physical space. In this social setting, each individual is assumed to hold a political attitude with respect to some public issue, such that the population can be characterized by a distribution of the individual attitudes toward this issue. It is also assumed that each individual might change their attitude with time as a result of the persuasive presence of the others in the social space.

The origins of change reside in both the individual’s interpersonal network of relations, which works as a means of communication, and also in the interactive nature of the relations between individuals. As each individual is embedded in a global ‘milieu’ representing the entire network of interpersonal relations, each individual is exposed to the persuasive presence of the others: each individual may be influenced by the others and may influence the others. As persuasive influence may be exerted in this social setting by any individual on any other, multiple parallel persuasion processes would simultaneously unfold. Moreover, at the operational level, these processes would interact with one another. In a certain period of time, as persuasive interactions among individuals will be reiterated, we can imagine multiple recurrent persuasion processes interacting with one another as the individuals interact with each other.

From this short description, the social setting already proves to have several of the relevant characteristics of a complex social system.

First, there is a physical space and, as the interpersonal network suggests, a spatial unfolding of the individual interactions. Second, there is a considerable number of individuals, possibly a large population, which makes this scenario quite complicated. Besides the spatial unfolding of the individual interactions, the time unfolding of the recursive persuasive influence processes makes a dynamic picture. Both spatial and time unfolding of the social influence processes involve the idea of bidirectional causality in a dynamic social system made up of many interactive individuals.

The individuals are assumed fixed in the physical space underlying the social space. They communicate through their interpersonal relations network. It is further assumed that each individual exercises their persuasive power with the explicit goal of modifying the attitude of the other. The dynamic outcome of this social system at a particular moment of time would look like a (graphical) ‘map’ of the individual attitudes in the population.

The aspects which make this social setting work as a dynamic social system with self‐organizing characteristics are (1) the bidirectional causality, (2) the representation of political attitude value and the attitude change rule, (3) the distinction between two different types of persuasive influence and (4) the physical space geometry and structure.

The problem of social impact, originally formulated in social impact theory, changes into: How do the individuals’ attitudes change under the persuasive influence of the others in the social settings described above?

What would the answer look like? Two of the above‐mentioned aspects are presented in the following sections: the first concerns bidirectional causality, and the second concerns the political attitude value and the attitude change rule.

Individual Interactions and Bidirectional Causality

Groups have been described in the sociologic and social psychology literature as complex social systems with specific dynamics and self‐organizing capabilities (McGrath et al., 2000: 95–99), which are manifest in the emergence of group‐level phenomena and in their causal power over individuals (Sawyer, 2005). Groups have often been used to model the dynamics of larger and more complicated social systems, by making it easier to pursue distinction between the level of the individual actions and goal‐directed behaviours (micro level) and the behaviour at the group level (macro level) (Coleman, 1986: 1312).

Bidirectional causality is a term denoting the causal power attributed by the researchers to individual‐level and system‐level behaviours to determine each other. It concerns both the ways in which individual goal‐directed actions and behaviour bring about system‐level behaviour, and the ways in which the group behaviour has consequences on the individual behaviours. This reciprocity of action and behaviour between the actors at different group levels is described as a complex effect following from the reciprocal interactivity among the individuals in the group (Sherif, 1936; Hackman, 1992). Sometimes, an equivalent and even older syntagm is used to describe the relations between the individual actions and behaviours, and the system behaviour: the dual terms downward causation and upward causation are often used in the psychological and social–psychological emergentist literature to describe the macro‐to‐micro and the micro‐to‐macro phenomenology respectively (Sawyer, 2005).

Bidirectional causality in small groups has been associated with number (Simmel, 1902) as an essential explanatory factor. Combined with the spatial distribution of the individuals in the social space and taking into consideration the persuasive influence exerted by virtually any individual on the others, the social system concept in DSIT defines a complex social system with a self‐organizing capability concerning the clustering of similar attitudes. In the conceptual model of the dynamic social impact, bidirectional causality would refer to an (abstract) complex social system and to the nonlinear dynamics of the attitude change in this system.

The unidirectional causality model based on social impact theory, where a single individual’s attitude changed as an effect of the persuasive and numerous presence of the others, is now replaced with a model based on complexity of social interactions and emergence of attitude change macro‐level phenomena. Bidirectional causality would, therefore, denote the complicated dynamics of the political attitude change in a social system in which all individuals influence each other and are exposed to the persuasive presence of others, and this influence is dependent on the physical closeness of the others: the closer they are, the greater their influence.

Political Attitude Values and Rule of Change

With regard to the political attitude value, the theory works with political attitudes represented as binary‐valued elements: any individual can hold one of two exclusive positions with regard to a specific issue (‘like/dislike’, ‘accept/reject’). The representation of political attitude as a variable with binary values might seem too reductionist a hypothesis. It might also appear as inconsistent with the theories of attitude measurement, which assume a gradual variation of the attitude value on a bipolar scale. However, the assumption that (political) attitude is a dichotomous variable does not contradict the representation of attitude values as continuous, as the attitude measurement scales suggest. In the limit, even measured on such a scale, the attitude is finally perceived in binary terms, since it is meant to express the preference for a certain object (Nowak et al., 1990: 365).

In order to achieve dynamics of change, the attitudes are defined as being recursively updated after each step of social impact (Lewenstein et al., 1992: 765):

(6.1)

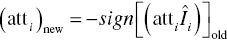
where att _i is the attitude value for the individual i at two consecutive moments of time and Î _i is the social impact for the same individual i. The ‘sign’ function helps to make it obvious if there is an attitude change from one moment of time to the next during the simulation run.

Supportive and Opposing Persuasive Influence

The third is the distinction the theory makes between two types of persuasive influence. As the social impact can be ultimately viewed as a sensitive indicator of the overall change induced by the group influence on each individual’s political attitude, this change has been defined by comparing persuasive opposing and persuasive supporting social impact on the basis of the psychosocial law described in social impact theory.

While social impact theory specifies a unique strength factor, DSIT introduces two strength factors, thus dividing the influencers (the others) into two groups (dichotomous preference space): those who hold an opposite attitude than the individual, and those who share the individual’s attitude. Persuasiveness is a concept which models the persuasion for inducing attitude change in the individual. It measures the strength of social pressure for change when an individual subject is surrounded by others who do not hold the same attitude. Persuasiveness describes the persuasive power of the source to make the individual change their attitude. This type of strength factor is evaluated with a specific type of social impact, called persuasive impact and denoted by .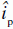

The other type of strength, supportiveness, describes the solidarity of the others with an individual with whom they share the same attitude and whom they help resisting the persuasion of those with opposite attitudes. The second type of strength factor is evaluated with a specific type of social impact, called supportive impact and denoted by 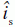. Supportiveness is a concept which models the solidarity of those who hold the same attitude with an individual and make them resist the social influence coming from those who hold an opposite attitude.

Together, the persuasive 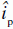and the supportive 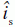social impact provide for the total social impact to which an individual is subjected:

(6.2)

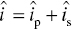
A self‐organizing characteristic is introduced in this system by allowing a nonlinear dynamic attitude change process. It actually compares two different types of persuasive influence: the supportive and the opposing one (see Figure 6.1). The attitude value at each moment of time depends on the previous attitude value and on the social impact value. As the value of persuasive influence opposing the attitude of the individual exceeds the value of the supportive influence of the others, the attitude will change.

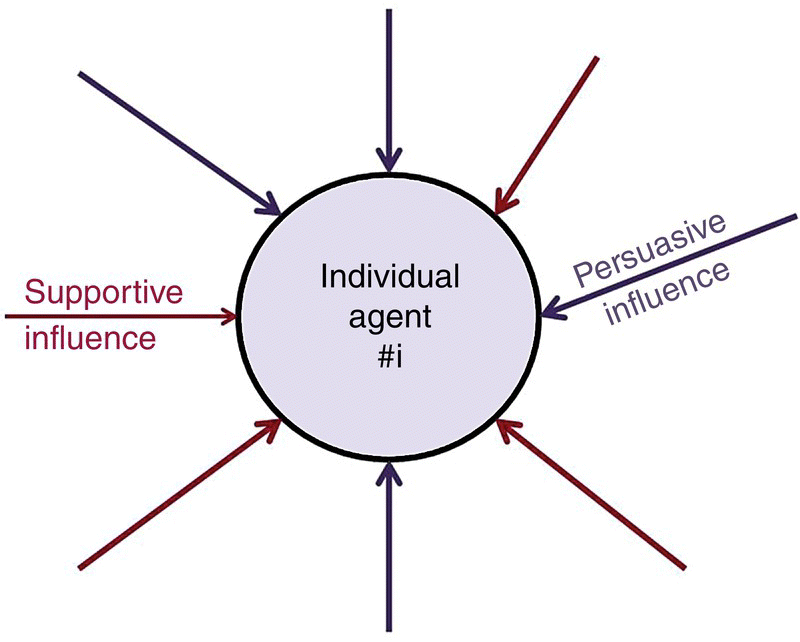
Figure 6.1 The dynamic model of social impact. There are two types of social persuasive forces: supportive and persuasive.

Both strength and immediacy factors are dependent on the geometry and structure of the physical space. Modelling the social impact as dependent on the physical proximity modifies the original social impact equation.

Dynamic Social Impact

The physical space and the geometry of the social space are determinant for the immediacy factor, which expresses the notion of ‘closeness’ to the source of influence in terms of the physical location of an individual in the social space. The social space has been designed following several geometric configurations so as to allow for the study of the variability of social impact as dependent on the type of the physical space: (a) fully connnected model, based on homogeneous (equal) distances between individuals; (b) hierarchical geometry model, based on hierarchy of groups in which the distances between individuals are dependent on the hierarchical levels in the group to which the individuals belong; (c) strong diluted model, based on a random connectedness between an individual and the others; and (d) the Euclidean two‐dimensional space (Lewenstein et al., 1992: 764).

Though all these alternatives have been investigated and their performances compared (Lewenstein et al., 1992), the mathematical model underlying DSIT will be presented here in the Euclidean geometry version for calculating the immediacy for each individual.

Inspired by the gravity model in physics, the immediacy factor models the inverse proportionality of the social impact with the square of distance for each pair of individuals. As both strength factors, the supportiveness s _i and the persuasiveness p _i , vary with the inverse of the squared distance between a source i and an individual target, a mean degree of social influence is calculated for each.

The persuasive impact of the group on a single individual is modelled as the mean effect of a persuasive force exerted by multiple sources (group) on a single individual. The mean persuasive impact 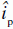is defined for each source i by cumulating the persuasiveness of each source i and then dividing the sum total by the number of persuasive sources in the group N ₀:

(6.3)

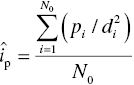
where d is the distance between the source i and an individual target.

The social impact of the persuasive opposition exerted by N ₀ sources on a single individual Î _p is given by

(6.4)

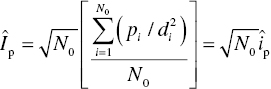
where Î _p, p _i , d and N ₀ are as previously described.

Similarly, the supportive impact of a group who share the same attitude as an individual is modelled as the mean effect of the forces exerted by multiple sources (group) on a single individual. The supportive impact 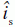is defined by cumulating the supportiveness of each source i and then dividing the sum total by the number of supportive sources in the group N _s:

(6.5)

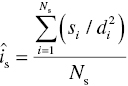
where d is the distance between the source i and an individual target.

The supportive effect diminishes as the supporters are farther from the subject and many in number. The social supportive impact exerted by N _s sources on a single individual Î _s is given by

(6.6)

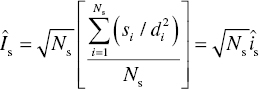
where Î _s, s _i , d and N _s are as previously described.

The total social impact cumulates the supportive and the opposing impact so that the result will produce (or not) an attitude change: if the persuasive opposition impact is greater than the supportive one, 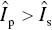, then an attitude change occurs for the individual.

Computer Simulation Model

In political attitude formation and change modelling research, Latané’s experimental research on social impact was pioneering work, for it used a new philosophy of experimental modelling: the computer simulation.

The philosophy of the DSIT computer simulation was characteristic of a wave of revived interest in the computer simulations of the late 1960s which dominated the 1990s decade, along with the advances in dynamic systems and complexity theory (Latane, 1996b). We should keep in mind that social impact theory was developed and reported long before social networks or cellular automata theories reached the simulation power they got soon after the mid‐1990s. Only by situating it in the right historical context can one appreciate the real value of Latané’s endeavour and its excellent potential of application and further development.

By the mid‐1960s, when Latané began his early research work on the bystander effect and political attitude change modelling (Latané and Darley, 1968; Latané and Harkins, 1976), experimental research in social psychology, widely open to the model‐invariant paradigm and mathematical modelling, was still fighting the prejudices against computer simulations. Political methodology was even less penetrated by the new modelling paradigm and, undoubtedly, more resistant to change; some, otherwise very few, scholars in this experimental research area were complaining about the old‐fashioned model‐invariant paradigm (Tilly, 1995).

In social psychology, at least, computer models and simulations were developed on two main paradigmatic dimensions: (a) the explanative, and (b) the generative paradigm.

In the explanative paradigm, the computer model is used to perform the operations and get the outcomes predicted by a preliminary mathematical model (Coleman, 1964: 528–529). This view has been promoted mainly (Troitzsch, 2013: 13–16) by the early microsimulation model of election outcomes in a referendum campaign developed by Abelson and Bernstein (1963) in the Simulmatics project (de Sola Pool and Abelson, 1961).

This kind of approach has evolved towards the idea of using computer simulation modelling in theory construction. It was this view which later provided the basis for the generative paradigm (Troitzsch, 2013: 16).

This new paradigm in experimental social psychology started to be systematically introduced during the 1960s, by authors like Robert Abelson (1968). This first decade of early approaches on computer simulations in social psychology is summarized in the seminal work of Oström (1988), who succeeds in disentangling the meaning of the new paradigm (Oström, 1988: 383–384). Identifying the computer simulation’s huge potential in tackling the dynamical complexities of social behaviour – namely, (1) intrinsic variability of the latent variables, (2) qualitative cognitive structure of attitudinal processes, (3) modelling the interdependence relationships between the latent variable and the observable variables, (4) multiple interdependencies among structural processes and (5) time – Oström describes the general research tendencies of the time, making a strong prediction about the capacity of the new paradigm to provide solutions to most complex phenomena studied in social psychology. In less than one decade his prediction had been fulfilled by the incredible advance in computer simulation theories, modelling methodologies and their performance typologies.

Latané’s view of computer simulation seems to fit in the former paradigm, as the reductive simulation procedure (Nowak et al., 1990: 362) has been essentially used in DSIT for proving the outcomes defined and predicted in the social impact mathematical model. Though it has been associated with advances in the cellular automata and compared with Schelling’s (1971) seminal work on segregation, DSIT makes reference to more popular approaches, the so‐called ‘computer recreations’ explained in technical detail by Dewdney (1987) in his articles and books.

The DSIT model has been compared with a two‐dimensional cellular automaton model and with a social network (Fink, 1996), but also with a neural network model (Eagley and Chaiken, 1993).

The cellular automata theory has its origins in one of von Neumann’s (1951) works on system replication inspired from biology, and has been developed mostly after John Conway elaborated his Game of Life (Gardner, 1970). By the end of the 1960s, the most relevant experimental research work is Schelling’s (1971) segregation model, intensively promoted at the time. The model was usually called ‘checkerboard’ instead of ‘cellular automaton’, and has similarities with another simulation paradigm, what we know today as an agent‐based simulation model. At the beginning of the 1990s, John Casti (1992) turned it into a new appealing theory of complexity, and Wolfram advanced it to what we know today (Wolfram, 1983, 1986, 2002).

The cellular automaton is a finite automaton, which is defined as an abstract computational device with finite input alphabet, a finite number of predefined states and a state‐transition function which provides for the next state by defining and describing it as a function of the actual state and input (Casti, 1992: 189). Usually, it is a one‐ or two‐dimensional ² grid of fixed cells in which each cell is identified with an individual agent, which interacts locally only with the direct neighbours. The local area of interaction could be, therefore, a four‐neighbour area, the so‐called von Neumann neighbourhood, or an eight‐neighbour area, called a Moore neighbourhood. The simulation consists of applying to this grid a simple rule of interaction between cells, such that cells’ states are updated simultaneously at each iteration. The complexity of cellular automata does not reside in their structure or rules, which are quite simple, but in the iterative application of a few simple interaction rules to a large population of individual agents (cells). In this case, the state transitions prove emergent properties. Such emergent phenomena show, for example, how the micro‐to‐macro link works in a self‐organizing social system. Groups have often been considered and studied as small social systems with specific dynamics and self‐organizing properties.

The type of simulation model used in DSIT has many similarities with a cellular automaton; however, it has some relevant dissimilarities too. Like a cellular automaton, a grid representation is used in the computer simulation, so that each individual has a spatial location (cell) and neighbours, and a simple rule guides the attitude change. Each cell has initially assigned an attitude value (binary value) and a state transition function. The group influence on the individual is simulated by the interactions between cells (Fink, 1996: 8). The individuals are kept immobile but, unlike the classic cellular automata, each individual can be influenced by distant others, and not only by the direct neighbours.

From this latter point of view, DSIT has some similarities with social networks. Though no reference is made in the text, Latané’s simulation model bears similarities with Schelling’s model of segregation, at least in the philosophy of approach. Like Schelling, Latané proves interest in the emergent phenomena connected to the relationships between the individual and the group (persuasion, conformity, minority influence). Unlike Schelling, Latané makes a strong point in bringing forth the relevance of personal interconnections, making everything resemble more closely social networks.

A social network consists of actors (nodes) and links (relationships or social structures) between actors. What makes the DSIT computer simulation model similar to a social network is the group modelling as a social network. The computer simulation model takes as the basic level of interaction the dyad and focuses on the micro‐level interactions in the physical space. The agents are interconnected by links which represent physical distances between individuals. In a social network, the nodes represent individual actors, and the connections represent communication links. Each individual (node) communicates with virtually all the others in the network: the connections (i.e. distances between two individuals), the nodes (i.e. the individuals) and the strength of individual attitudes are identified by well‐defined variables. Unlike Schelling’s model of social influence based on segregation, and similar to a social network, in the DSIT simulation model the attitudes are ‘moving’ in the social space, looking for a convenient attribute context, and not the individuals, which are fixed. Besides structural and interaction similarities, complexity similarities can be identified in the convergence of attitudes and in the emergence of majority–minority group patterns (Fink, 1996: 9).

The similarities with neural networks are also relevant: the input and the output of the network are predefined, the nodes (i.e. individual attitudes) are interconnected, their number and their associated values (e.g. attitude values, strength values, immediacy values) are specified, as is the function of transfer (i.e. the social impact, which describes the aggregation of others’ influence for each individual) and of node activation (i.e. attitude change). Also similar to a neural network is the idea of using several levels of persuasive influence processing, which in DSIT correspond to the persuasive and supportive social impact, and which aggregate the influence to the output node, working much like the hidden nodes in a neural network (Eagley and Chaiken, 1993: 101–103, 142–143). Unlike neural networks, the DSIT computer simulation model is not a learning system. Its behaviour is not trained, but emerging on a context‐dependence principle.

Simulation Modelling

The fundamental components of the computer simulation model in DSIT are social space, individual (agent), social impact factors and political attitude change rule.

The fundamental assumptions are twofold: conceptual and operational.

From a conceptual perspective, the computer simulation model is used to implement Latané’s psychosocial law of social impact. Social impact is the combined effect of three factors: group size, physical locations of individuals in the group and the distribution of their attitudes with respect to a public issue. Social influence works mainly on the peripheral route (persuasion and non‐involvement at personal level) and binary attitude values (pro and con).

From an operational perspective, the computer simulation model is used to identify the macro‐level (group‐level) consequences of the iterative application of the simple rules of social impact and political attitude change at the micro level (individual level). Four kinds of emergent phenomena are visualized and analysed: consolidation, clustering, correlation and continuing diversity.

Social Space

The simulated social space is modelled as a collection of social agents which interact with each other in a finite (abstract) physical space. This makes ‘spatiality’ a dimension of the social interaction, since each agent has a sense of physical space associated with the social space, although not equivalent to it.

The representation of this social space is a grid with n × n cells (Figure 6.2), each cell representing a social agent. The agents are fixed and they interact with their neighbours. The neighbours may be closer (direct neighbours) or distant: virtually, each individual is assumed to perceive the persuasive presence of all the other individual neighbours. To limit the number of distant neighbours whose presence is persuasively relevant, the system takes into consideration all neighbours within a specified radius around the current individual.

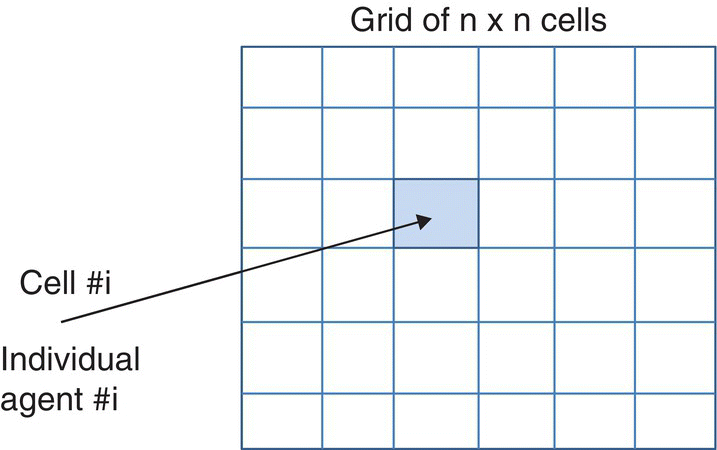
Figure 6.2 The social space is a squared grid of n × n cells, each cell representing an individual.

Though the agents do not move from one cell to another, the model assumes that they know the attitudes of each other. The model assumes that, either by their simple presence or by means of media communication, all individuals know about the attitudes of all the others and that they exercise their persuasive influence (either supportive or opposing) on each other.

Euclidean geometry is assumed. For each pair of individuals, a Euclidean distance is calculated. The individual locations in the physical space make the model predictive with regard to the spatial configuration of subgroup aggregation in the social space. The individuals are distributed in the physical space such that supportive and opposing aggregations of individuals may emerge as distinct spatial configurations.

Individual Agent

The individual agent is represented as a string of four parameter values: attitude value (binary), two types of attitude strength identifying either a supportive or an opposing attitude value, and the immediacy value (Figure 6.3).

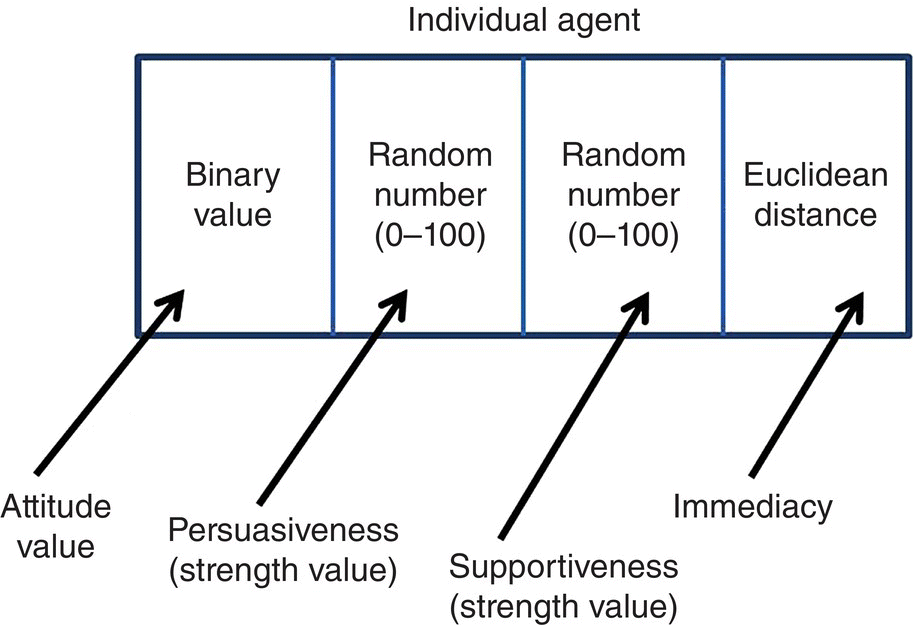
Figure 6.3 The individual agent.

The attitude value is a binary value; it can take one of two values, ‘1’ (pro) or ‘0’ (con), representing a ‘like/dislike’ position toward a public issue (attitudinal object). Each attitude is described as a two‐state variable which takes either the pro or the con value, with graphical signs associated, respectively ‘I’ for ‘pro’ and ‘–’ for ‘con’.

The persuasiveness p _i is a random number between 0 and 100, as is the supportiveness value s _i . The values of persuasive impact and supportive impact are calculated iteratively for each individual during a simulation run.

The immediacy factor should prove that the social impact (either supportive or opposing) decreases as the others (supportive or opposing others respectively) have a more distant location in the physical space with respect to the individual target. The ratio between the supportiveness s _i of the source i and the Euclidean distance d _i between the source i and an individual target provides for a formula of immediacy which shows that the supportive impact decreases as the squared distance increases. And this is the same for the persuasive opposing impact p _i and its corresponding immediacy formula. As the social impact rule is a multiplicative formula of three factors, parallel processing is required. Synchronous processing of the persuasive influence is achieved by simulating a parallel updating of the grid cells on a serial computer; the computer simulation model works with two matrices which are updated at two consecutive discrete time steps during a simulation run, such that all cell updates are done simultaneously.

Number, attitude strength and immediacy are defined as global variables; their dynamic variability is modelled as the generative mechanism for attitude self‐organization and emergence of attitude change phenomena. The complexity of the system and its self‐organizing features reside in the differentiated representation of persuasive influence as supportiveness and persuasiveness variables, and in the set of simple update rules for (a) attitude change and (b) social impact as either supportive or persuasive impact.

The attitude change rule is a decision rule, which compares the supportive and the opposing persuasive impact for each individual. Whenever the persuasive influence for changing an attitude is greater than the support for keeping it, an attitude change occurs; the attitude value is updated and the other attribute values are changed as well (i.e. the persuasiveness and supportiveness values are updated). The following attitude change procedure summarizes the main steps for simultaneously updating all grid cells at each run: ³

Attitude Change Procedure

repeat for all cells

       Initialization:
       Selection of values from random distributions:
              attitude strength att is assigned a random value from distribution of values between 0 and 1;
              supportiveness s is assigned a random value from distribution of values between (0 and 100);
              persuasiveness p is assigned a random value from distribution of values between (0 and 100);
       Communication session:
       communicate attribute values: load current values in the old values matrix;

main loop

         cell i:

         calculate social impact:

                  ;

         apply political attitude change rule:

                  if ()

                  then
                       mark cell_i in the grid;
                       update attitude value: ;

                       update s and p for the marked cells;
                       load values in the new values matrix;
                       communicate new attribute values;

The procedure continues until no more attitude changes occur. At this moment the simulation run stops. Statistics are calculated and (numerical and graphical) results are displayed.

Emergent Phenomena

The most interesting and appealing part of the DSIT is represented by the emergent phenomena observed as outcomes of the simulation runs.

There are four types of emergent phenomena: consolidation, clustering, correlation and continuing diversity. Definition, measurement and interpretation of these self‐organizing social forms are at the heart of DSIT, which aims to explain their meanings in political attitude change phenomena emerging in large dynamic social settings. They are not derived as a result of calculating the solutions of the equations in the mathematical model of social impact theory, but are observable as visual dynamic outcomes of the repeated application of the simple rule of social impact to individual interactions in large social settings over a long period of time. They show that the social impact rule has a strong dependence on the context, on the initial conditions and on the spatiality and group size factors. The DSIT, while developed within the social psychologic cognitive paradigm, succeeds in shifting the focus from internal factors characterizing the cognitive abilities of the individual to the number (size) and immediacy (closeness in terms of physical location and spatial geometry and geography of a social space) factors describing political attitude change phenomena. These four emergent phenomena represent robust results of DSIT: they have been obtained from both empirical experimental settings (laboratory and field experiments) and as computer simulation program outcomes.

Clustering

Clustering emerges from the attribute spatial self‐organization (Figure 6.4). It is the macro‐level effect of large, repeated individual interactions at the micro level: neighbouring individuals tend to share similar opinions, behaviours and attitudes. Clusters as islands of people sharing the same attributes (i.e. attitude value, spatial neighbourhood) offer protection against the persuasive influence of opposing others. Inside clusters, therefore, other phenomena might emerge; namely, consolidation and correlation.

Figure 6.4 Clustering phenomena in the simulations performed with SITSIM. (SITSIM is a software program on the Modeling Social Dynamics website. It has been developed by James Kitts, Michael Macy and Martina Morris under NSF Grant SES‐0433086. http://socdynamics.org/index.html (See Web Resources).)

Correlation

Correlation is an effect of the social persuasive influence of the others on the individual; it consists of the attributes of neighbouring individuals becoming increasingly related after repeatedly exercised persuasive influence than they were before. Latané’s understanding of the issue in DSIT makes reference to a typical social influence situation in which individuals belonging to a particular dynamically evolving cluster (subgroup) have their membership conditioned by their increasing willingness to become similar to their co‐members. As members of a cluster they are eventually (unless the cluster lies at the border of the group) surrounded by like‐minded others and therefore less or not at all exposed to the counter‐persuasion of the opposing others. Consequently, they start behaving like members of their subgroup, and not as independent individuals within the group. This results in increasing correlation between subgroup members’ identical or similar attributes.

Though not further developed beyond statistical correlation coefficients used to emphasize the emergent spatial clustering effects, the idea that ideologies could arise from spatial correlation only has been questioned. However, asking this question could be, at least, a sign of misunderstanding, if not a malicious reading of the text itself, since Latané is suggesting how ideology formation is facilitated by spatial factors influencing the self‐organizing social forms, and not generated by them only. But, sometimes, questions betray the malicious more than answers do.

Spatial correlation of attitudes has been studied as an issue of ideology formation in sociology, social psychology and political science. However, we should briefly emphasize the difference in the approaches on correlation of attitudes as ideology in social psychology and in political science research. In Converse’s model of mass beliefs, political attitudes are characterized by instability, lack of correlation and lack of structure. In order to explain (lack of) correlation, Converse starts from theoretical assumptions and characterization criteria based on the level of cognitive abilities of the individuals and the role their mass beliefs play in their political choices. His approach answers a why? question on the (lack) of correlation in political attitudes. Latané’s approach answers a how? question on the emergence of correlation. It is a meta‐theoretical approach to a complex social setting in which spatiality and physical location play an important role in the operation of the social influence processes; namely, in the spatial clustering of individual attributes. Spatial clustering of attributes fosters correlation of initially unrelated attributes, a phenomenon studied in geography, culture and in political science as spatial auto‐correlation.

Consolidation

Consolidation concerns a tendency inside the minority groups toward reducing diversity (Huguet et al., 1998: 832) by strengthening the similarity within the group. The reason is that minorities are subjected to the adverse persuasive pressure of the majority. As a consequence, minority members have a tendency to reinforce their similarity within the group in order to withstand the majority influence. On the other hand, while being exposed to an increasing persuasive influence of the majority, minority members might be convinced to accept the majority attitude. The majority increases its influence, therefore, by increasing its size (Harton and Bullock, 2007: 527). As minorities (factions) are diminishing in size, they are often ‘absorbed’ by the majority. However, this does not always happen. If their size does not diminish more than 30% of the group size, then they have good survival chances. Nevertheless, this is not the only condition of minority (faction) survival.

Continuing Diversity

Continuing diversity is a hard challenge, withstanding the sword for almost a century. It was initially formulated in political attitude terms by Robert Abelson (1963), but has been approached with equal interest in various research areas, from biology to culture, from economy to sociology, from ecology to political science and, last but not least, to computer science and the sciences of the artificial, computational simulation included. The end of the 1990s witnessed a revived interest in continuing diversity approaches in culture emergence and dissemination (Axelrod, 1997) as well as in political science (Huckfeldt et al., 1998). The complex social systems theory and the availability of computational and simulation modelling methodologies and software enabled this revived interest to become quite high. It soon exceeded expectations, and the field got revolutionarily extended. New disciplines emerged, social simulation and computational political science being but two of them. New paradigms appeared, like agent‐based ones. This is the reason why we have included all political science aspects at the beginning of this chapter. Before the boom in artificial societies, Latané had quietly prepared us for the shock of change: his impressive research work is just an elegant and rich preamble, and he is a forerunner of all this social science deep paradigmatic changes.

Latané suggests three types of approaches to this issue: one is a social psychology approach based on social influence and the role of spatial proximity in persuasion; the second one is a physics‐inspired approach based on the force field model and Euclidean space; and the third one is a computational simulation approach based on the nonlinear dynamics of both the change rule and of the spatially self‐organizing social forms.

From a social psychology perspective, continuing diversity in scenarios of social persuasion concerns the survival of a minority’s attitudes in spite of the persuasive pressure of an opposing majority. Clustering, consolidation and even correlation might converge in making a small‐size minority survive within a large majority. On the one hand, the small size is a disadvantage if compared with the majority size. However, spatial clustering shields the (small) minority from the majority pressure, since minority members are more influenced by like‐minded others inside their subgroup and, therefore, less or not at all exposed to the opposing persuasive influence of the majority. (The problem still remains at the borders, where members have to resist higher pressure, and sometimes they do not.) For the minority kernel, however, the pressure to stay (minority exerted) is likely to be higher than the pressure to change (majority exerted); hence, the rate in attitude change decreases and the minority survives, making the whole group achieve continuing diversity. It is more reinforced and secured, Latané noticed, when personalities with high attitude strength anchor the borders and secure the members inside by making them resist the change (Latané, 1996a: 23).

From a mathematical and computational perspective, continuing diversity is a matter of nonlinearity and complex social systems. As Abelson demonstrated, linear models which exploit the linear proportional relation between increasing social influence and attitude strength decreasing end up in ubiquitous agreement, which sets these models rather apart from real‐life situations. Instead, nonlinear models which exploit an attitude change rule based on the relation between supportive and opposing social impact succeed in preserving diversity in spite of the presence of noise. If, moreover, nonlinear rule change (at the operational level) combines with nonlinear variability in the individual resistance to change (at the individual attribute level), then the social systems achieve dynamic equilibria in which majority and minority coexist for longer.

Generations of Computer Simulations

There have been several generations of computer simulation programs which have been developed by Latané and his collaborators: SITSIM (Nowak and Latané, 1994), GROUPSIM (Rockloff and Latané, 1996) and CAPSIM (Latané and Bourgeois, 2001a).

The fundamental characteristic of these computer simulation models is that their outcomes (either numerical or graphical) have been permanently compared with empirical experiment outcomes (i.e. empirical data and results).

SITSIM

SITSIM (Nowak and Latané, 1994) was the first computer model developed for the simulation of DSIT. SITSIM has an n × n grid representing the social space of the experiment, and each cell in the grid represents an individual agent. It is used in iterative simulations and tested against empirical data for validation and confirmation of the results (Latané and Nowak, 1997: 53).

Social space: a grid of n × n cells is used to represent a physical space for a group of individual agents. Each agent corresponds to one cell; the space is characterized by the Euclidean distance between any two agents (Lewenstein et al., 1992).

Individual agent: the agent does not move in the grid space. An agent is characterized by a set of four attributes: attitude value (binary), two strength parameters (supportiveness and persuasiveness) and immediacy value.

Attitude change rule: an agent will change their attitude toward a specific issue if the pressure from opposing others is greater than the support from the individuals sharing the same attitude.

Emergent macro‐level phenomena: consolidation, clustering, correlation, continuing diversity (Figure 6.5).

Figure 6.5 Simulations performed with the NetLogo SITSIM model. The configurations obtained show (a) emergence and (b) polarization phenomena. NetLogo implementation of the SITSIM model follows the original model (Nowak et al., 1990). The NetLogo SITSIM model has been implemented by Nigel Gilbert and can be found in the public domain at http://ccl.northwestern.edu/netlogo/models/community/Sitsim (see Web Resources).

Several series of simulations have been performed with SITSIM. The purpose of the extensive testing was the necessity to check whether the outcomes of the simulations indeed represent the properties of the system under the social impact rules. SITSIM allowed for the factorial combination of 20 variables (Latané, 1996a: 20) designed to affect certain dynamic characteristics of the system under group social influence so that their role and effect could be observed and quantified. To this aim, a set of test variables was chosen, including (a) the methods to simulate the parallel processing of the factors’ influence on the operation of social influence processes, (b) population size (number of sources), (c) initial minority–majority proportions in the population and their distribution, (d) strength, (e) using borders to the physical space, or let the space wrap around, and several other parameters. Results proved to be extremely robust and easily identified in the empirical data.

SITSIM simulations show that consolidation emerges only when minorities have a critical mass (30%). For lower proportions, the minority groups are overwhelmed by the majority.

SITSIM defines specific measures for evaluating and comparing self‐organizing social forms and their characteristics (Latané and Nowak, 1997: 51–53).

Self‐Organizing Social Forms: Measurement Indexes

Clustering measurement uses a numerical index based on the probability that closer others are less influenced by individuals holding opposing attitudes and, therefore, have less chances to change their own attitudes under the persuasive influence of the others. The individuals most exposed to persuasive influence would be those at the borders of the physical space, since they are not surrounded by people sharing the same views. Consolidation measurement uses a numerical degree of consolidation which is calculated for two cases: (a) if majority prevails; (b) if minority prevails. Continuing diversity measurement uses an index of the dynamic quality of the social interaction.

GROUPSIM

GROUPSIM (Rockloff and Latané, 1996) is a computer simulation program which further extends the capabilities of the SITSIM program to predict the post‐discussion individuals’ choices, and the degrees of consolidation and clustering. The difference from SITSIM is that the agents are constrained to have a reduced number of direct interconnections (four interconnections) and a single interconnection with an individual outside the current ‘family’ subgroup. GROUPSIM has been tested empirically in 24 discussion sessions in which individuals answered questions before and after discussing the topics with the other members of the subgroup.

During the simulations, the number of supporters/oppositions is varied so as to make evident the dependence of the emergence phenomena on the number of others.

Social space: each agent can communicate with a four‐person subgroup (von Neumann neighbours). Borders: wrapping around is allowed, so that the physical space becomes a torus (no borders).

Individual agent: does not move in the physical space.

Attitude change rule: the number of others will decide if the individual agent will change their attitude. GROUPSIM is able to predict individuals’ choices on changing their attitudes as influenced by the number of persons holding a specific attitude in the subgroup.

Emergence phenomena: GROUPSIM is able to predict the emergence of consolidation (reduction in diversity), clustering, correlation and continuing diversity, and to predict the extent (degree) of consolidation and clustering. Attributes of the individuals in the same subgroups tend to become more similar and more representative as they are repeatedly discussing a specific topic. Attributes are spatially self‐organizing as a result of the persuasive presence of others. And this self‐organization takes individuals’ adjacency as a criterion.

CAPSIM

CAPSIM (Latané and Bourgeois, 2001a) is a computer simulation program which advances the features of GROUPSIM by introducing different change rules dependent on the topics discussed by the individual agents. The model includes attitude change probabilities, which moderate the individual’s choice for changing the attitude, depending on the number of others. CAPSIM’s outcomes are probabilistic simulations in comparison with SITSIM’s, which are considered deterministic.

CAPSIM predicts three different levels of self‐organization in dependence on (1) the different types of discussion topics, (2) different topics of discussion among individuals within a subgroup and (3) for different groups.

Social space: has an underlying physical space as a grid with n × n cells; von Neumann neighbour; no borders (torus).

Individual agent: each agent is characterized by a set of attributes; a probability of change is assigned to each discussion topic. The simulation modelling was tested against empirical experimental evidence for self‐organizing forms of social influence. To this end, the authors developed an experimental framework called Computer Administered Panel Study (CAPS) which recruited and managed participants in 10 groups of 24 persons each (Latané and Bourgeois, 2001a: 65–66).

Attitude change rules: change probabilities – a probability of attitude change is assigned to each discussion topic. Three scenarios were simulated: (1) conformity game, (2) deviation game and (3) attitude toward a political issue. For each scenario, a different attitude change rule was introduced in the simulation program. Numerical measures (degrees) of self‐organization forms for consolidation, clustering and continuing diversity were defined so that empirically obtained and simulated results could be compared.

Consolidation score is represented as a measure of the reduction in size of minority as a consequence of social influence (Latané and Bourgeois, 2001a: 70). Clustering score is a clustering index represented as a measure of the increasing similarity of neighbouring individuals as a consequence of social influence. Continuing diversity index (numerical index) is calculated as a percentage of the groups which maintain diversity in spite of social influence (Latané and Bourgeois, 2001a: 70–71).

The Relevance of Social Impact Theories for Political Attitude Modelling

Social impact theories, in both static and dynamic versions, are relevant for their implications in the study of political attitudes, political culture and polity.

Many authors, however, including Latané himself, explain the relevance of social impact concept and theory by taking as argument the implications of their results from a sociologic perspective. Both concept and theory have a strong social psychological ‘flavour’, guiding the interpretation of results toward the culture emergence and culture dissemination domains.

While the orientation toward social representations and culture dynamic phenomena is identified by many analysts, critics and authors, including Bibb Latané (1996a) himself, what actually matters, with regard to the subject of this book, is rather the consideration that social impact theory is one of the first studies on the political mechanisms and processes underlying the structure of a polity.

To further explain this, we should, before anything else, recall two essential aspects concerning social impact theories.

The first is the classification of the social impact theories as meta‐theories. They are mainly studying how certain factors affect the operation of social influence processes, not defining what social influence is and why it works. The second is the view that the successive generations of computer simulation models (which have been constructed for testing the reliability and validity of the theories) are purposefully constructed as virtual experimental settings for the study of the operation of social influence processes in large social settings characterized by generalized interactive features at the micro level.

Remembering these fundamental characteristics of the social impact theories helps us realize their equally fundamental contribution to the study of social self‐organizing forms emerging from the unfolding of social influence processes.

There are two dimensions, at least, on which their contribution is deeply relevant: (a) self‐organizing forms reveal the micro‐to‐macro and macro‐to‐micro mechanisms which support the relation between the individual, on the one hand, and the social system (society) and political system (polity), on the other hand; (b) the philosophy of simulation: how could a computer simulation model support theory construction?

Mechanisms Connecting the Micro and Macro Levels of a Social System

There is this explanatory dimension of any model, which counts in the first place. In our case, the simulation model underlying the social impact theory has an explanatory relevance for political mechanisms and processes which has to be taken into account; it is one of the first simulation models which explains the mechanisms of downward and upward causation in the case of emergent macro‐level phenomena generated by the operation of recurrent persuasive processes at the micro level of a social system over a period of time. The simulation model applies to as wide a domain as possible, from attitudes, behaviours and beliefs to public opinion. All four self‐organizing forms appear almost constantly in the simulations; namely, consolidation, clustering, correlation and continuing diversity represent themselves or embed as many mechanisms of either top‐down or bottom‐up generation of attitude formation and change phenomena. Few of the current political attitudes simulation modelling methods allow for the construction of downward causation mechanisms: cellular automata, agent‐based modelling and even complex adaptive systems do not solve this problem or could hardly cope with it, making their solutions appear either too expensive in terms of computational resources or too rational and often at odds with the real world. This is the case with the artificial societies, which could be grown up quite easily, but do not include mechanisms which might support the concept of downward causation. Latané instead describes such mechanisms in his dynamic theory of social impact, suggesting several paradigms for which they could be extremely relevant. One of them is the evolutionary paradigm. It might allow for developing mechanisms of top‐down causation in value formation and selection in simulation modelling of political attitude formation and change emergent phenomena: attitudes appear as agents in search of a favourable ‘niche’, where, as soon as they arrive, they start struggling for the opponents’ removal (Rockloff and Latané, 1996: 363–364). The idea of a minority group as a favourable ‘niche’, accommodating sets of attributes and reinforcing their similarities so that, as time passes, they become correlated, gives rise to the idea that spatiality plays a role in consolidation of similarity and enhancing minority survival. The other one is the culture emergence paradigm. Latané (1996a) and others (Harton and Bullock, 2007) wrote extensively about it, identifying a connection between patterns of regional differences and patterns of attitude clustering. Latané’s simulation results on correlation also suggest that ideologies might arise from attribute spatial correlations within and across cultures (Latané and Bourgeois, 2001a: 64). Sustained by empirical and simulated results, the emergence of ideologies as spatial correlation of attributes needs to be further elaborated. Research on political conflict and insurgence (Laitin, 1991; Tilly, 1995; Fearon and Laitin, 2003; Cederman and Girardin, 2006) shows that regional geographical patterns might give rise to ideological positions and conflicts between central and local political power on the background of ethnical regional geographical patterns (upward causation). Moreover, research on political geography shows how political ideologies can affect individual voting behaviour by simply revising geographical borders of electoral field units (downward causation). Since both mechanisms address spatiality‐based political mechanisms, the question on ideology arising from spatial correlation within and across cultures remains an open and challenging issue.

Philosophy of Simulation

The philosophy of simulation underlying Latané’s huge experimental research on social impact combines, on the one hand, the longstanding tradition of providing robust empirical evidence in support of theory construction and demonstration, and, on the other hand, the chance to inform theory construction and validation by means of simulation results. Undoubtedly, the computer simulation model is viewed much as a ‘derivation machine’, or anyway as something which, in Coleman’s tradition, could never have been accepted as a basic means to state a theory. However, Latané used it in this latter sense and, moreover, gave it a high credit in theory construction, and justified it so as to convince even the hard‐believers in the social psychology community. And this is no easy thing.

Static impact theory’s idea is to use mathematical equations in order to discover universal laws which guide attitude change in social influence scenarios. This model‐invariant approach is then used as an explanation of the change phenomena in terms of the variables and their values (see Figure 6.6).

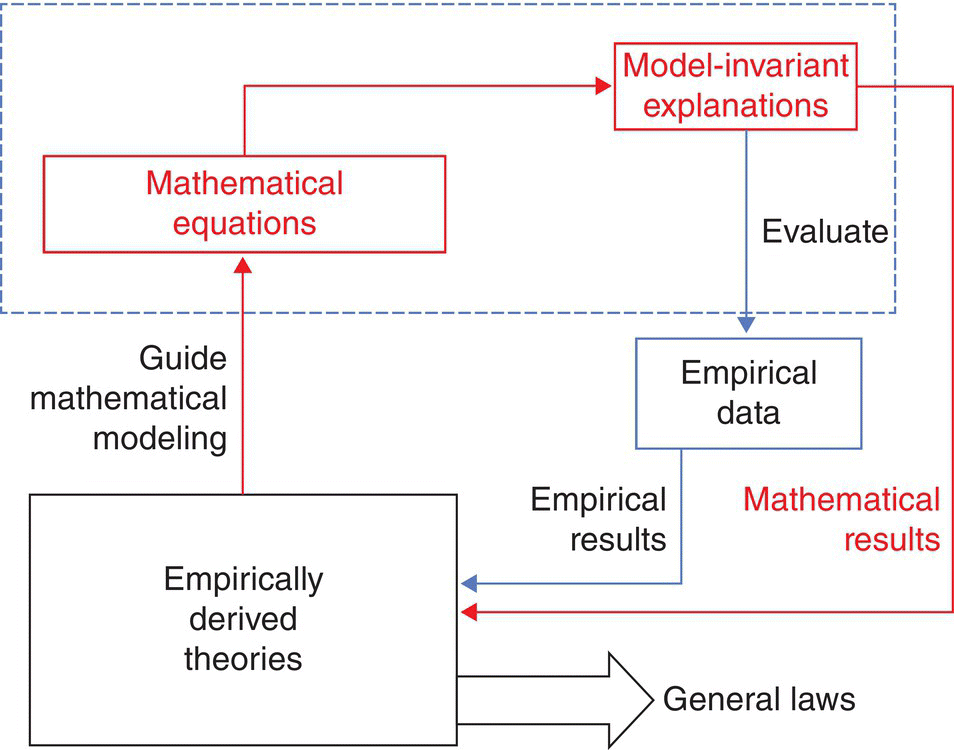
Figure 6.6 Computer simulation model.

DSIT’s philosophy about the use of simulation in the dynamic social impact research is briefly exposed in the so‐called reductive simulation procedure (Nowak et al., 1990: 362), which is used for (1) discovering the macro‐level effects of the individual interaction rules implemented on the micro level, and (2) cross‐validation of empirical data and simulation results so that incompleteness or internal contradictions could be detected during theory testing (Nowak et al., 1990: 374). While the validation of simulation results against empirical data belongs to the classic model‐invariant tradition, when models were both constructed and validated on an empirical basis, the use of computer simulation (Latané and Bourgeois, 2001a,b) for achieving emergence phenomena at the macro level by means of reiteration of update rules at the micro level is a new paradigm introduced as the research on complexity and self‐organization got theoretical support by the end of the 1980s (see Figure 6.7).

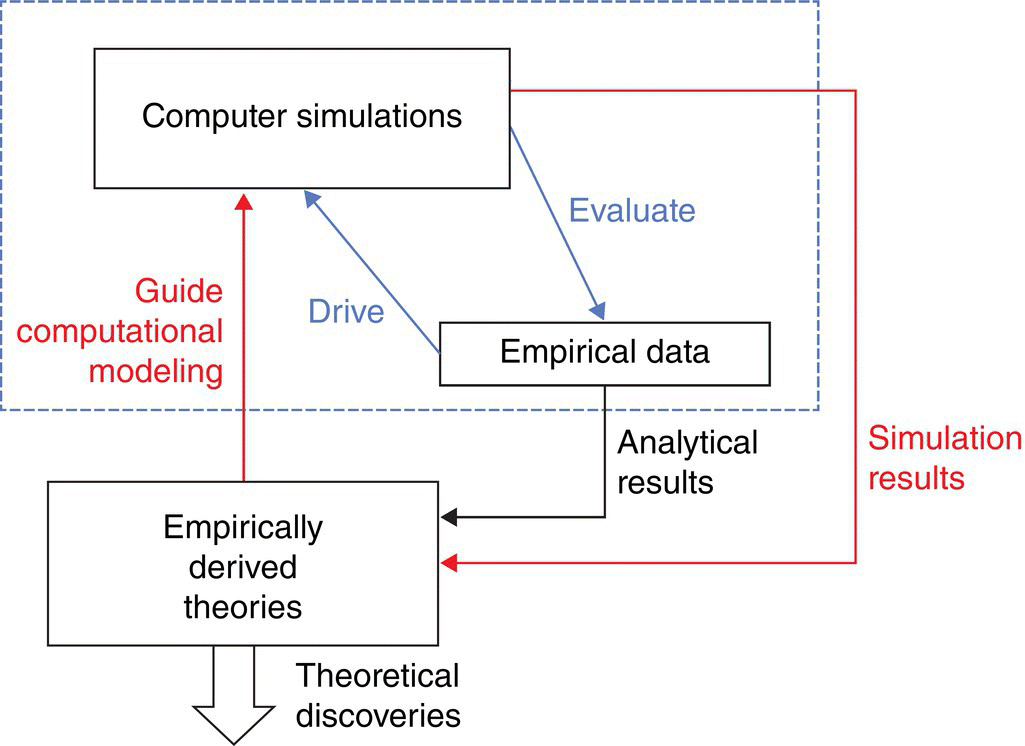
Figure 6.7 SITSIM cycle of theoretical and experimental research. Reductive simulation procedure. Black: empirically derived theories help guide the computer simulations, and use their results to enhance theoretical discoveries. Grey: computer simulations help evaluate the empirical data, while empirical data help in designing computer programs and driving the next rounds in simulations, until the validation of both simulation results and empirical observations is possible.

SITSIM illustrates a conception about how computer simulations and empirical data could stimulate and enforce each other’s performances (Latané and Bourgeois, 2001a: 62). Simple update rules at the micro level of individual influence may provide for the emergence of macro‐level phenomena which are observable by means of simulation only.

Later on, as new generations of computer simulation models were developed for testing DSIT, Bibb Latané (Latané et al., 1994; Nowak and Latané, 1994; Latané, 1996a; Latané and Nowak, 1997; Latané and Morio, 2000) enlarged his view on the use of computer simulation by emphasizing more the complex, self‐organizing nature of social systems, the relevance of social simulation and the need for an enhanced view on the role social simulation plays in our understanding of complex societal dynamics.

Web Resources

Modelling Social Dynamics Website

Site developed by James Kitts, Michael Macy and Martina Morris, under NSF Grant SES‐0433086, at http://socdynamics.org/index.html.

NetLogo Website

User Community Models, SITSIM by Nigel Gilbert, at http://ccl.northwestern.edu/netlogo/models/community/Sitsim.

References

1. Abelson, R.E. and Bernstein, A. (1963) A computer simulation model of community referendum controversies. Public Opinion Quarterly, 27, 93–122.
2. Abelson, R.P. (1964) Mathematical models of the distribution of attitudes under controversy. In N. Frederiksen and H. Gulliksen (eds), Contributions to Mathematical Psychology . Holt, Rinehart and Winston, New York; pp. 141–160.
3. Abelson, R.P. (1968) Simulation of social behaviour. In G. Linzey and E. Aronson (eds), Handbook of Social Psychology , vol. 2. Addison‐Wesley, Reading, MA; 274–356.
4. Abelson, R.E. and Bernstein, A. (1963) A computer simulation model of community referendum controversies. Public Opinion Quarterly , 27, 93–122.
5. Axelrod, R. (1997) The dissemination of culture: a model with local convergence and global polarization. Journal of Conflict Resolution , 41(2), 203–226.
6. Casti, J.L. (1992) Reality Rules. Picturing the World in Mathematics. Volume I: The Fundamentals . John Wiley & Sons, Inc., New York.
7. Cederman, L.‐E. and Girardin, L. (2006) Beyond fractionalization: mapping ethnicity onto nationalist insurgencies. Unpublished paper. Swiss Federal Institute of Technology, Zurich. http://www.icr.ethz.ch/publications/cederman2005beyond.pdf. Accessed: December 11, 2015.
8. Cohen, B.P. (1963) Conflict and Conformity: A Probability Model and its Application . MIT Press, Cambridge, MA.
9. Coleman, J.S. (1964) Introduction to Mathematical Sociology . The Free Press, New York.
10. Coleman, J.S. (1986) Social theory, social research, and a theory of action. American Journal of Sociology , 91(6), 1309–1335.
11. Converse, P.E. (1964) The nature of belief systems in mass publics. In D.E. Apter (ed.), Ideology and Discontent . Collier‐Macmillan, London; pp. 206–261.
12. De Sola Pool, I. and Abelson, R.P. (1961) The Simulmatics project. Public Opinion Quarterly , 25, 167–183.
13. Dewdney, A.K. (1987) Computer recreations: diverse personalities search for social equilibrium at a computer party. Scientific American , 281(July), 112–115.
14. Eagley, A.H. and Chaiken, S. (1993) The Psychology of Attitudes , Harcourt Brace Jovanovich, Fort Worth, TX.
15. Eysenck, H.J. (1954) The Psychology of Politics . Routledge and Kegan Paul, London.
16. Fearon, J.D. and Laitin D.D. (2003) Ethnicity, Insurgency, and Civil War, American Political Science Review , 97(1), 75–90.
17. Fink, E.L. (1996) Dynamic social impact theory and the study of human communication. Journal of Communication , 46(4), 1–12.
18. Gardner, M. (1970) Mathematical Games. The fantastic combinations of John Conway’s new solitaire game “life”, Scientific American , 223 (October 1970), 120–123.
19. Hackman, J.R. (1992) Group influences on individuals in organizations. In M.D. Dunnette and L.M. Hough (eds), Handbook of Industrial and Organizational Psychology , vol. 3, 2nd edn. Consulting Psychologists Press, Palo Alto, CA; pp. 199–268.
20. Hägerstrand, T. (1965) A Monte Carlo approach to diffusion. European Journal of Sociology , 6, 43–67.
21. Harkins, S.G. and Latané, B. (1998) Population and political participation: a social impact analysis of voter responsibility. APA Group Dynamics: Theory, Research, and Practice , 2(3), 192–207.
22. Harton, H.C. and Bullock, M. (2007) Dynamic social impact: a theory of the origins and evolution of culture. Social and Personality Psychology Compass , 1(1), 521–540.
23. Huckfeldt, R., Levine, J., Morgan, M. and Sprague, J. (1998) Election campaigns, social communication, and the accessibility of perceived discussant preference. Political Behavior , 20, 263–294.
24. Huguet, P., Latané, B. and Bourgeois, M.J. (1998) The emergence of a social representation of human rights via interpersonal communication: empirical evidence for the convergence of two theories. European Journal of Social Psychology , 28, 831–846.
25. Isenberg, D.J. (1986) Group polarization: a critical review and meta‐analysis. Journal of Personality and Social Psychology , 50, 1141–1151.
26. Katz, E. and Lazarsfeld, P. (1955) Personal Influence: The Part Played by People in the Flow of Mass Communications . Free Press, New York.
27. Kelman, H. (1958) Compliance, identification, and internalization: three processes of attitude change. Journal of Conflict Resolution , 1, 51–60.
28. Kerlinger, F.N. (1972) The structure and content of social attitude referents: a preliminary study. Educational and Psychological Measurement , 32, 613–630.
29. Laitin, D.D. (1991) The national uprisings in the Soviet Union. World Politics , 44, 139–177.
30. Latané, B. (1981) The psychology of social impact. American Psychologist , 36(4), 343–356.
31. Latané, B. (1996a) Dynamic social impact: the creation of culture by communication. Journal of Communication , 46(4), 13–25.
32. Latané, B. (1996b) Dynamic social impact: robust predictions from simple theory. In R. Hegselmann, U. Mueller and K. Troitzsch (eds), Modelling and Simulation in the Social Sciences from the Philosophy of Science Point of View . Kluwer, Dordrecht; pp. 287–310.
33. Latané, B. and Bourgeois, M.J. (2001a) Successfully simulating dynamic social impact. Three levels of prediction. In J.P. Forgas and K.D. Williams (eds), Social Influence: Direct and Indirect Processes , Sydney Symposium of Social Psychology Series, vol. 3. Psychology Press, Philadelphia, PA; Chapter 4, pp. 61–78.
34. Latané, B. and Bourgeois, M.J. (2001b) Dynamic social impact and the consolidation, clustering, correlation, and continuing diversity of culture. In M.A. Hogg and S. Tindale (eds), Handbook of Social Psychology: Group Processes . Blackwell, Oxford; pp. 235–258.
35. Latané, B. and Darley, J.M. (1968) Group inhibition of bystander intervention. Journal of Personality and Social Psychology , 10, 215–221.
36. Latané, B. and Harkins, S. (1976) Cross‐modality matches suggest anticipated stage fright a multiplicative power function of audience size and status. Perception & Psychophysics , 20, 482–488.
37. Latané, B. and Morio, H. (2000) Maintaining diversity: simulating the role of nonlinearity and discreteness in dynamic social impact. In R. Suleiman, K.G. Troitzsch and N. Gilbert (eds), Tools and Techniques for Social Science Simulation . Springer Physica‐Verlag HD; pp. 196–217.
38. Latané, B. and Nowak, A. (1994) Attitudes as catastrophes: from dimensions to categories with increasing importance. In R. Vallacher and A. Nowak (eds), Dynamical Systems in Social Psychology . Academic Press, New York; pp. 219–249.
39. Latané, B. and Nowak, A. (1997) Self‐organizing social systems: necessary and sufficient conditions for the emergence of consolidation, clustering, and continuing diversity. In G. Barnett and F. Boster (eds), Progress in Communication Science: Advances in Persuasion . Ablex, Norwood, NJ; pp. 43–74.
40. Latané, B., Nowak, A. and Liu, J.H. (1994) Measuring emergent social phenomena: dynamism, polarization, and clustering as order parameters of social systems. Behavioral Science , 39, 1–24.
41. Lazarsfeld, P.F., Berelson, B. and Gaudet, H. (1944) The People’s Choice: How the Voter Makes Up His Mind in a Presidential Campaign . Columbia University Press, New York.
42. Lewenstein, M., Nowak, A. and Latané, B. (1992) Statistical mechanics of social impact. Physical Review A , 45(2), 763–776.
43. Martin, R. and Hewstone, M. (2003) Majority versus minority influence: when, not whether, source status instigates heuristic or systematic processing. European Journal of Social Psychology , 33, 313–330.
44. McGrath, J.E., Arrow, H. and Berdahl, J.L. (2000) The study of groups: past, present, and future. Personality and Social Psychology Review , 4(1), 95–105.
45. Middendorp, C.P. (1978) Progressiveness and Conservatism: The Fundamental Dimensions of Ideological Controversy and Their Relationship to Social Class . Mouton, The Hague.
46. Moscovici, S. (1976) Social Influence and Social Change . Academic Press, London.
47. Moscovici, S. (1985) Social influence and conformity. In E. Aronson and G. Lindsay (eds), Handbook of Social Psychology , vol. 2. Addison‐Wesley, Reading, MA; pp. 347–412.
48. Moscovici, S. and Zavalloni, M. (1969) The group as a polarizer of attitudes. Journal of Personality and Social Psychology , 12, 125–135.
49. Nowak, A. and Latané, B. (1994) Simulating the emergence of social order from individual behavior. In N. Gilbert and J.E. Doran (eds), Simulating Societies: The Computer Simulation of Social Processes . University College of London Press, London.
50. Nowak, A., Szamrej, J. and Latané, B. (1990) From private attitude to public opinion: a dynamic theory of social impact. Psychological Review , 97(3), 362–376.
51. Oström, T.M. (1988) Computer simulation: the third symbol. Journal of Experimental Social Psychology , 24, 381–392.
52. Petty, R.E. and Cacioppo, J.T. (1980) Effects of issue involvement on attitudes in an advertising context. In G.G. Gom and M.E. Goldberg (eds), Proceedings of the Division 23 Program, 88th Annual Convention of the American Psychological Association, Montreal, Canada . American Psychological Association, Minneapolis, MN; pp. 75–79.
53. Petty, R.E. and Cacioppo, J.T. ([1986]2011) Communication and Persuasion: Central and Peripheral Routes to Attitude Change , Springer Series in Social Psychology. Springer (reprint of the original edition).
54. Petty, R.E., Cacioppo, J.T. and Goldman, R. (1981) Personal involvement as a determinant of argument‐based persuasion. Journal of Personality and Social Psychology , 41, 847–855.
55. Petty, R., Cacioppo, J.T. and Schumann, D. (1983) Central and peripheral routes to advertising effectiveness: the moderating role of involvement. Journal of Consumer Research , 10, 135–146.
56. Rockloff, M.J. and Latané, B. (1996) Simulating the social context of human choice. In K.G. Troitzsch, U. Mueller, G.N. Gilbert and J.E. Doran (eds), Social Science Microsimulation . Springer‐Verlag, Berlin.
57. Sawyer, R.K. (2005) Social Emergence . Cambridge University Press, Cambridge.
58. Schelling, T.C. (1971) Dynamic models of segregation. Journal of Mathematical Sociology , 1(2), 143–186.
59. Sherif, M. (1936) The Psychology of Social Norms . Harper & Row, New York.
60. Simmel, G. (1902) The number of members as determining the sociological form of the group: I. American Journal of Sociology , 8, 1–46. https://www.brocku.ca/MeadProject/Simmel/Simmel_1902a.html. Accessed: December 11, 2015.
61. Tilly, C. (1995) To explain political processes. American Journal of Sociology , 100(6), 1594–1610.
62. Troitzsch, K.G. (2013) Historical introduction. In B. Edmonds and R. Meyer (eds), Simulating Social Complexity, Understanding Complex Systems . Springer‐Verlag, Berlin.
63. Von Neumann, J. (1951) Various techniques used in connection with random digits. In A.S. Householder, G.E. Forsythe and H.H. Germond (eds), Monte Carlo Method , National Bureau of Standards Applied Mathematics Series, 12. US Government Printing Office, Washington, DC; pp. 36–38.
64. Wilson, G.D. (1973) The Psychology of Conservatism . Academic Press, New York.
65. Wolfram, S. (1983) Statistical mechanics of cellular automata. Reviews of Modern Physics , 55, 601–644.
66. Wolfram, S. (ed.) (1986) Theory and Application of Cellular Automata . Addison‐Wesley, Reading, MA.
67. Wolfram, S. (2002) A New Kind of Science . Wolfram Media, Champaign, IL.
68. Zaller, J.R. (1992) The Nature and Origins of Mass Opinion . Cambridge University Press, Cambridge.

Notes

1 See Kelman (1958: 53) for an exquisite theoretical presentation.

2 A multidimensional implementation is also possible; see Wolfram (1986).

3 See Latané and Nowak (1997: 49, Table 2.1).