Collective Action Modelling

Political Contagion Model

The Political Contagion Model (Johnson, 1999) employs an agent‐based system, that is, an ALife technology used to build up artificial social systems and artificial societies. As the author mentions in his explanation, the model reveals major problems induced by the use of agent‐based systems in simulating the role of social context and the interdependence of peers in interpersonal communication networks.

One is the problem of data involved in the simulation and regards (i) the empirical versus generated data and (ii) the expected versus obtained relationship between the inputs and the outputs of simulation runs: which one explains the other? and what is explained? The model does not actually use empirical data, nor does it generate output data which are aimed at confirming preliminary empirical observations. Therefore, the questions are essentially concerned with the methodology of the model’s input/output descriptions and explanations, and with the validation of the outputs in computational and simulation modelling of political attitude change phenomena.

A second problem concerns a theoretical research question about the micro–macro link in political models: is the model able to explain the macro‐level phenomena (i.e. political attitude change) by means of the individual interactions at the micro level?

One explanation concerns upward causation: the emergence of macro‐level phenomena (i.e. political attitude change) from individual interactions (i.e. discussions in the dyadic networks).

The other explanation concerns downward causation: the influence (i.e. formation and change) exerted on the individual political attitudes by the aggregate structures and phenomena.

Johnson’s model of political contagion is the only one in the history of political attitude computational and simulation models which addresses this fundamental issue of political science: it employs a modified version of the agent‐based model originally developed by Axelrod’s Culture Dissemination Model to study (i) attitude change emergence as generated by the individual interactions in the dyadic networks (micro‐to‐macro) and (ii) the influence exerted by such phenomena at the macro level onto the individual interactions (macro‐to‐micro).

While the effect of the micro‐to‐macro link is synthesized as the emergence of social order, the effect of the macro‐to‐micro link can be synthesized as the influence exerted by the aggregate structures and phenomena on the individual agents’ behaviours and attitudes. The former framework is intensively studied in social simulation and computational sociology, where agent‐based systems and models offer the appropriate technology and methodology of research. The latter, however, needs a different approach than the bottom‐up one adopted by the former, as agent‐based systems in the methodological individualism paradigm could hardly approach, and even less explain, downward causation.

In Coleman’s classical terms, if approached in the downward causation paradigm, ‘political protest’, ‘authority’ or ‘institution’ could be modelled as aggregate structures which exert influence on the political attitudes of individuals. Johnson chooses to model ‘political protest’ as a macro‐level emergent structure which exerts its influence back to the micro‐level individual behaviours which have generated it in the first place. Thus, the author employs an agent‐based model, which have long been exercised to achieve stable global activity of individual agents at the micro level for studying situations in which emerging (temporarily aggregated) structures (i.e. groups of protesting agents) exert attraction on more individual agents for participating in the protest (i.e. contagion). Political contagion is thus described and explained as a downward causation process.

Conceptual Model

The Political Contagion Model (Johnson, 1999) is an application of an early model of Diversity Survival in democratic societies (Huckfeldt et al., 1995), and it is the first (if not the only!) to formulate the micro–macro problem in political methodology terms of complex systems and also in terms of computational and simulation modelling methodology.

The model deals mainly with political opinion formation and draws on the classic issue of political protest as approached in the political theory literature. It compares two earlier models, Granovetter (1978) and Lohmann (1994), and works out an alternative which includes many of their principles in a more constraint‐relaxed, agent‐based model on a methodological individualism‐based explanation of the emergent outcomes.

Granovetter’s (1978) threshold computational model of protest explains the emergence of social protest as depending on a critical mass of individuals involved in critical evaluations of the government: as the number of these individuals exceeds a certain threshold, the social group of protest emerges. Lohmann’s (1994) game‐theoretical model is based on a similar idea of protest, but in a different theoretical approach which works with the concepts of rationality and political information processing abilities of the individual actor: the rational actor observes the actions of all the other individual actors in the model system. If at time 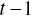images a critical mass of actors 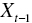images are providing observable signals that they question the desirability of the government, then the individual agent makes the decision to question it itself, thus joining the protest.

Johnson’s model relaxes the requirements on an agent’s rationality and enhances an information processing ability, otherwise present in the former approaches too. His model assumes that the individual agent is a bounded rational agent who takes his personal social condition as a reference and also as a criterion for evaluating the government’s performances. Evaluating its personal condition as unsatisfactory makes the agent acquire a belief about the non‐desirability of the government. This belief further induces an unfavourable attitude toward the government. If the agent’s belief gets reinforced by similar attitudes of agents who protest against the government in the immediate neighbourhoods of the individual agent, then the agent might get influenced and could himself adopt a negative attitude towards the government, thus joining the protest.

Johnson’s model defines political contagion as a political influence generated and sustained by an attitude toward an object (i.e. the government) which is held by many agents. As an individual agent becomes aware of this attitude in the aggregate, it appears like being subjected to political influence while observing the social aggregate. The individual agent observes a political protest against the government as a social aggregate in which a certain political attitude toward the government prevails. These observations are modelled as macro‐level stimuli exerting a political influence on the individual agent. When the individual’s beliefs about the government as the source of discomfort in the agent’s personal condition are congruent with a negative attitude toward the government spread in the aggregate, this congruity reinforces the individual belief concerning the government desirability and makes the individual agent strengthen its beliefs and finally join the protest. The dynamics of the political contagion describe, therefore, a complex social aggregate which appears as the macro‐level output which emerges from the individual decision‐making, beliefs update and conjoint actions of an increasing number of individual agents. The journey from the macro‐level stimuli to the macro‐level output is nevertheless complicated, since the individual beliefs, attitudes, action decision‐making and internal status need to be described and updated in each individual agent.

Operational Model

Political contagion is modelled as collective action with an agent‐based model. The cells in the grid representing the spatial environment of the model system are randomly initialized with a normal distribution of individual agents.

Each agent is characterized by a number of variables describing the ‘personal condition’ with numerical continuous values in the interval (0; 1), such that lower values are associated with low personal condition, and high values are associated with a high personal condition. The higher the values that personal condition takes, the lower is the possibility that the agent is not satisfied with the government. Another variable is the discomfort threshold, which takes continuous values in the interval [0.5; 1]. The individual thresholds are initialized with a normal distribution. As a moving agent, the individual agent is characterized by spatial coordinates which identify its location in the environment such that the individual agent is aware in each moment whether it is close or far from the other agents which protest against the government. These coordinates are then used by the individual agent to either run away from the political protest or to get closer to the political protest and finally join it.

A simulation run develops on a sequence of discrete time steps; at each time step each individual agent takes the same actions: belief update as observing the aggregate, evaluating the conditions for joining (or not) the protest, and choosing a spatial location as close/distant as possible to the protest.

Belief update is accomplished by observing the Moore neighbourhood at each local position with a certain radius: if 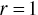images , then the individual agent is able to observe 1‐cell area of Moore neighbours (eight neighbours) in all directions around its own cell; if 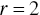images , then the individual agent can observe the Moore neighbours in 2‐cell areas in all directions.

The model succeeds in getting a map of political contagion for a simple scenario in which an individual agent is trying to get spatially closer to other agents with a high level of discomfort associated with low values of personal condition. In this map, the colours indicate how close to the protest area and how strong is the belief of an individual agent that the government is ‘bad’: dark colours indicate distant‐from‐protest cells and low belief strength, while a red colour indicates close‐to‐protest cells and high belief strength.

Collective Action Model of Political Protests

An advanced modelling approach on political protest and political regime change was developed as a collective action model (Johnson and Brichoux, 2002). This approach models the power of commitment in cooperative social action. It achieves various scenarios of emergence and spread of political protests in situations in which activists are (or are not) stimulating the common people to engage in political protests against political leadership. The model is based on theories about individual success motivation. It also builds upon Olson’s theory of collective action (Olson, 1965), and in particular on the theory of critical mass elaborated by Oliver and Marwell (1988) and collaborators (Oliver, Marwell and Teixeira, 1985). As support for the former, the authors employ Kuran’s threshold model of preference revelation (Kuran, 1989, 1995). The model explains the emergence of political protests by running an agent‐based system in which the agents are heterogenous: they represent two types of political actors, common people and political activists. The agents communicate among themselves and are also able to observe other agents and get acknowledged for their beliefs and behaviour.

9
Collective Action Modelling

Political Contagion Model

Conceptual Model

Operational Model

Collective Action Model of Political Protests

Closing Remarks

Web Resources

References