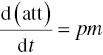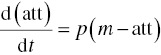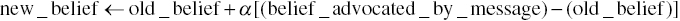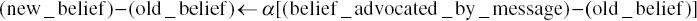10
The System Dynamics Modelling Paradigm
The system dynamics paradigm employed by John Hunter in explaining the attitude change process facilitated its description as a process whose dynamics depends on both the process’s history and on the context in which it develops. John Hunter got famous for his attitude change model. It is the first model which is based on differential equations. It employs the system dynamics paradigm for explaining the attitude change as depending on external (contextual stimuli, messages, influence), and internal (initial attitude, attitude’s strength) factors. The conceptual and operational aspects of this model are explained and further develop by Hunter’s collaborator, Ralph Levine.
Conceptual Aspects
In the system dynamics paradigm, the attitude is defined as a dynamic variable with attributes of magnitude, direction and structure. The system dynamics model takes as variables the receiver’s attitude toward the object (message) and the receiver’s attitude toward the source. Attitude variability is bounded, and it depends on other factors too, like persuasibility, that is the capacity of being persuaded of the person who receives the persuasive message(s).
In a behaviourist model, the attitude change would depend on the message and on the capacity of the person receiving the message to be persuaded, the so‐called persuasibility factor. Using a differential equation and our variable notation, the rule of attitude change reproduces the original model as follows (Levine, 1983: 23/336):
where (att) is the attitude, p is the persuasibility factor, m is the message and d(att)/dt is the first derivative of the attitude variable with respect to time, that is, the attitude’s rate of change.
As initially defined by John Hunter and further refined by his disciple, Ralph Levine (1983), a system dynamics model achieves the attitude change by evaluating a differential equation in which the rate of attitude change is a function of the attitude itself, the message and the persuasibility factor. Adapting the notation used by Levine in defining this equation (Levine, 1983: 24/336), we get the following differential equation:
where p is a persuasibility factor which characterizes the receiver of the message, (att) is the attitude of the receiver toward a particular object, d(att)/dt is the rate of attitude change (i.e. the first derivative of the attitude) and m is the intensity of the message as expressed in attitude units.
Equation 10.1 models attitude change from a behaviourist point of view, emphasizing that attitude is a dynamic process which could be controlled from outside only by sending appropriate messages to the receiver. Equation 10.2 models attitude change by means of the system dynamics paradigm such that the initial attitude held by a person toward a particular object could be changed by sending the person persuasive messages, but the rate of change will depend not only on the message and on the person’s persuasibility, but also on the initial attitude and its strength. In this paradigm, the attitude change is defined as a dynamic recursive process which models both internal and external sources of change and influence factors.
The outcome of this conceptual model should depict the dynamic trajectory of the attitude change process during a given time interval. In order to obtain the results, an operational model is necessary. It transforms the concepts which describe the nature of change in operational terms. The operational model provides for the implementation of a computer simulation version of the conceptual model. System dynamics models have often been used in structural equation modelling such that the advantages of this modelling paradigm have been transferred to the statistical analyses of the results which facilitates the causal modelling (Levine, 1983: 20/334).
Hunter et al. (1984) developed a class of mathematical models for simulating the dynamics of attitude change in the most important paradigms: behavioural, information processing and cognitive dissonance.
Operational Aspects
A system dynamics model is represented as a diagram in which the processes (flows) and variables (stocks) are represented together with their variations (arrows). A negative loop is a feedback loop, in which time is the essential dimension of change. Attitudes are measured on attitude scales in attitude value units. Messages are represented as quantities on the same scales.
A difference between a current value of the attitude toward an object and its value at a subsequent moment of time is described by a differential equation, which quantifies the change in attitude in terms of the dynamics of the rate of change.
Equation 10.2 is a linear differential equation which has a recursive form, such that the rate of attitude change depends on the attitude itself, on the message and on the characteristics of the person who receives the message. As Levine (1983: 24/336) describes it, such a system dynamics model of attitude change includes a feedback loop. The feedback mechanism consists of the difference (denoted as the degree of dissimilarity) between the position advocated by the message and the receiver’s attitude toward a particular object. It is this degree of dissimilarity (measured in attitude units) which determines the change in attitude and its dynamics. The mechanism of evaluating the dissimilarity between a person’s position and the position advocated by a (persuasive) message toward a particular object inspired the Galileo model, which was developed for the measurement of attitude change in multidimensional cognitive spaces.
The dissimilarity‐based mechanism of attitude change in persuasive communication processes at both the individual level and in large populations and the system dynamics modelling paradigm has been addressed by several mathematical models aimed at providing the means to operationalize attitude change. In what follows, three such models are presented. They have been selected for the influential role played in the development of computational and simulation models of attitude change by the teams involved in relevant research projects targeting the modelling of the effects persuasive campaigns might induce in the voting choices of large electorate masses. The models presented in the following sections summarize a long period of social and political attitude modelling research based on the system dynamics paradigm as a distinct research orientation from the orientations based on social influence theories. These latter orientations were reinforced during the late 1980s. They achieved a different computational expression only after the mid‐1990s when the new technologies based on artificial intelligence (AI) and artificial life theories (ALife) took the lead in almost all social and political modelling research areas.
Proportional Change Model
Equation 10.1 could be written to describe a belief change as well. It defines the rule of change in a belief change system dynamics model. The model concerns the belief change which could be observable (measurable) for a person who already has a belief with respect to an object and who accepts a change to this initial belief as recommended by incoming message(s). As such, it is an expression of the Proportional Change Model (Danes et al., 1978: 243), initially formulated by French (1956) and reformulated by Anderson and Hovland (1957) in a recursive form by Equation 10.3:
where the rate of belief change from the old to the new belief depends on the dissimilarity between the positions advocated by the message and the receiver, respectively, and a factor of the receiver’s persuasibility α.
The difference between the new belief and the old one, as reformulated by Equation 10.4,
is defined as directly proportional to the difference between the belief advocated by the message and the initial belief held by the person who receives the message, with α a factor of proportionality.
The model has been very popular ever since Hunter formulated his mathematical model in a fashion which suggested similarities with Newtonian dynamics so as to emphasize its potential application to the dynamics of cognitive objects. The idea was not new, as it had also been inspired by the earlier theories of Kurt Lewin on the issue of force field theory applied to social influence (Lewin, 1952). As emphasized by John Hunter, Jeffrey Danes and Joseph Woelfel in their joint research paper (Danes et al., 1978), linear as well as nonlinear versions of this model have been employed in belief and attitude modelling research in social judgment (Sherif et al., 1965), cognitive dissonance (Aronson et al., 1963) and attitude–behaviour relationship (Fishbein and Ajzen, 1975).
Belief Certainty Model
The degree of certainty with which a person holds a belief about a particular object or an attitude toward it, called the polarity of the belief/attitude, was initially formulated by Osgood and Tannenbaum (1955) in their congruity theory.
The Belief Certainty Model, as initially formulated by John Hunter and S. Cohen1 and reformulated by Danes et al. (1978), is a mathematical model of the polarity principle which has been used for the operationalization of the change in beliefs/attitudes. It states that the change in belief (attitude) is directly proportional to the degree of dissimilarity between a message and a person’s advocated belief (attitude) toward an object, and is inversely proportional to the degree of certainty with which the person holds the initial belief (attitude):
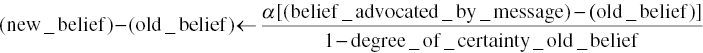
This model has been the subject of long theoretical debates (Danes et al., 1984: 204) on the polarity of attitudes and beliefs and the relationship between polarity and resistance to change in persuasive communication: some authors consider that the polarity of belief and its resistance to change are directly proportional (the so‐called ‘polarity effect’), advocating the idea that extreme beliefs change with great difficulty (if at all) (Sherif and Cantril, 1946). Other authors (Anderson and Hovland, 1957; Hovland, 1972) advocate a different idea, that a belief’s resistance to change is supported by an increased level of information (i.e. a greater amount of information is hypothesized to mean a higher quality of information also, a point of view which, in my opinion, might not get support anymore from one who watches television nowadays, especially during electoral campaigns).
Accumulated Information Model
The Proportional Change Model assumes that the proportionality factor α is constant. Its value could be set up during the model application design for cases in which the message guarantees the truth of the claimed belief and/or attitude toward an object, and the factor α is used for the control of the belief and/or attitude change trajectory. Initially, the model was employed in research on belief and attitude change in persuasive communication scenarios in which old beliefs are held with high degrees of certainty and are, therefore, hard to change (Janis and Hovland, 1959).
If, however, the factor of proportionality α is assumed to vary itself as a function of the person’s accumulated information about a particular object, then the accumulated information model could be formulated so as to account for this hypothesis. The hypothesis, initially formulated by Norman Anderson (1959, 1965) and also by Rosenberg (1968), has been mathematically formulated by Saltiel and Woelfel (1975). In their formulation, the α factor decreases as the number of incoming messages increases significantly:
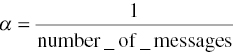
There are two possible interpretations the authors give to this formula. One interpretation would adjust the belief of the receiver after n messages to the average of the belief values conveyed by these messages. However, this interpretation assumes that the number of prior messages is known (or irrelevant). Otherwise, another interpretation would be more appropriate: the receivers make content (value) comparisons each time they receive a new message and assess, among other things, the degree of information they have about the object or the claimed belief or position in each message. If no prior information is found, the receiver accepts the belief or attitude advocated by a new message as no arguments can be found against it.
These ideas were further studied by Woelfel and collaborators in the Galileo Model, which elaborates on the relationship between the mass of attitude and its change trajectory. These theories assume that the message can be viewed as a ‘force’ which ‘moves’ the belief or attitude along one or more dimensions of change in the cognitive space. The intensity of such ‘force’ would depend on the number and concept configuration of the incoming messages.
Advantages and Disadvantages of the System Dynamics Modelling Paradigm
Attitude change is a dynamic process which, in this modelling paradigm, received for the first time a dynamic description and evaluation in terms of system theory. Many of the concepts underlying this modelling paradigm are rooted in Newtonian dynamics. What it has provided for, along with Lewin’s theory about force fields and its applicability to social systems, is an operational description of the attitude and/or belief change trajectory. Evaluating attitude change in persuasion scenarios necessitated an appropriate formalism, which was initially inspired by Forrester’s theory on social dynamics.
However, attitude is very much context sensitive, and its sensitivity requires much more dynamic detail. System dynamics made room for other methodology and technology alternatives in attitude change modelling. The sciences of the artificial soon became relevant in this direction.
However, the orientation Hunter founded has been continued and adapted into a new paradigm: the spatial models of attitude change.
Hierarchical Models
Hierarchical models are a class of spatial models of attitude change. They explain and predict political attitude and belief change in terms of inter‐attitudinal and belief structure theories (Dinauer and Fink, 2005). They are based on the fundamental assumption that attitudes are stored in the memory as part of larger cognitive structures.
Attitude change is approached in many classic attitude theories in terms of the variations of the relationships between structural attitude components: beliefs, affect, cognition and behaviour.
Balance theory (Heider, 1946) describes the attitude structure as a dyad or a triad of cognitive components, namely attitudes and beliefs. Attitude change is associated with a non‐balanced relationship between the components of a dyad/triad, which means conflicting attitudes and/or beliefs. As people prefer balanced relationships within these dyads/triads, the conflict is reduced or eliminated by modifying the attitudes/beliefs. Cognitive dissonance theory (Festinger, 1957) assumes that the structural elements which are in a dissonant relation, like attitudes and beliefs, induce an internal pressure for dissonance reduction. In order to reduce the dissonance, the individual person who experiences it modifies the content and/or relevance of these elements.
Spatial models of attitude change are rooted in the early mathematical models of attitude change developed by John Hunter and collaborators. These approaches are based on Newtonian physics and model the attitudes and their structure with the help of basic physical notions like ‘acceleration’, ‘force’ and ‘mass’, addressing the dynamics issues of an object’s motion in the physical space. These approaches concern attitude change as induced by message communication, and are based on the Hovland–Yale modelling paradigm: ‘source–message–receiver’.
In hierarchical models, inter‐attitudinal change has been approached in terms of hierarchical structures of concepts (Dinauer and Fink, 2005; Dinauer, 2009). In conceptual hierarchies, the connections between concepts (conceptual structure) support the connections between conceptually related attitudes (inter‐attitude structure) and explain how the attitudes change in relation to one another.
Hierarchical models prove that attitude change is constrained by the hierarchy itself (superordinate–subordinate levels), whereas spatial models prove that the change occurs for all linked objects regardless of their hierarchical relationships.
References
- Anderson, N.H. (1959) Test of a model of opinion change. Journal of Abnormal and Social Psychology, 59, 371–381.
- Anderson, N.H. (1965) Primacy effects in personality impression formation. Journal of Personality and Social Psychology, 2, 1–9.
- Anderson, N.H. and Hovland, C.I. (1957) The representation of order effects in communication research. In C.I. Hovland (ed.), The Order of Presentation in Persuasion. Yale University Press, New Haven, CT; pp. 158–169.
- Aronson, E., Turner, J. and Carlsmith, J. (1963) Communicator credibility and communication discrepancy as determinants of opinion change. Journal of Abnormal and Social Psychology, 67, 31–36.
- Barnett, G.A. (1974) Social system homophily as a function of communication. Paper presented at the Annual Meeting of the International Communication Association, New Orleans, 17–20 April. http://files.eric.ed.gov/fulltext/ED097742.pdf. Accessed: December 11, 2015.
- Danes, J.E., Hunter, J.E. and Woelfel, J. (1978) Mass communication and belief change: a test of three mathematical models. Human Communication Research, 4(3), 243–252. http://www.galileoco.com/literature/OCRDanes,%20Hunter,%20Woelfel.pdf. Accessed: December 14, 2015.
- Danes, J.E., Hunter, J.E. and Woelfel, J. (1984) Belief change and accumulated information. In J.E. Hunter, J.E. Danes and S.H. Cohen (eds), Mathematical Models of Attitude Change, vol. 1: Change in Single Attitudes and Cognitive Structure. Academic Press; Chapter 12, pp. 204–216. http://www.galileoco.com/literature/OCRdanes‐1984.pdf. Accessed: December 14, 2015.
- Dinauer, L.D. (2009) Toward a more comprehensive theory of attitude change: the effects of inter‐attitudinal concept structure on attitude dynamics. Advances in Consumer Research, 36, 621–622.
- Dinauer, L.D. and Fink, E.L. (2005) Inter‐attitude structure and attitude dynamics: a comparison of the hierarchical and Galileo spatial‐linkage models. Human Communication Research, 31, 1–32. http://www.galileoco.com/literature/dinauer‐fink.pdf. Accessed: December 14, 2015.
- Festinger, L. (1957) A Theory of Cognitive Dissonance. Stanford University Press, Stanford, CA.
- Fishbein, M. and Ajzen, I. (1975) Belief, Attitude, Intention, and Behavior. Addison‐Wesley, Reading, MA
- Forrester, J.W. (1961) Industrial Dynamics. Productivity Press, Portland, OR.
- Forrester, J.W. (1968) Principles of Systems, 2nd edn. Productivity Press, Portland, OR.
- Forrester, J.W. (1969) Urban Dynamics. Productivity Press, Portland, OR.
- Forrester, J.W. (1973) World Dynamics, 2nd edn. Productivity Press, Portland, OR.
- French, J.A. (1956) Formal theory of social power. Psychological Review, 63, 181–194.
- Heider, F. (1946) Attitudes and cognitive organization. The Journal of Psychology, 21, 107–112.
- Hovland, C.I. (1972) Reconciling conflicting results derived from experimental and survey studies of attitude change. In W. Schramm and D. F. Roberts (eds), The Process and Effects of Mass Communication. The University of Illinois Press, Urbana, IL; pp. 495–516.
- Hovland, C.I., Janis, I.L. and Kelley, H.H. (1953) Communication and Persuasion: Psychological Studies of Opinion Change. Yale University Press, New Haven, CT.
- Hunter, J.E., Danes, J.E. and Cohen, S.H. (eds), (1984) Mathematical Models of Attitude Change, Academic Press.
- Janis, I.L. and Hovland, C.I. (1959) Personality and Persuasibility. Yale University Press, New Haven, CT.
- Levine, R.L. (1983) The paradigms of psychology and system dynamics. In Proceedings of the 1983 International. System Dynamics Society Conference, Chestnut Hill, MA, USA. http://www.systemdynamics.org/conferences/1983/proceed/parallel‐vol1/levin325.pdf. Accessed: December 11, 2015.
- Levine R.L. (2003) Models of attitude and belief change from the perspective of system dynamics. Paper presented at the 2003 International System Dynamics Society Conference. http://www.systemdynamics.org/conferences/2003/proceed/PAPERS/177.pdf. Accessed: December 11, 2015.
- Lewin, K. (1952) Frontiers in group dynamics. In D. Cartwright (ed.), Field Theory in Social Science: Selected Theoretical Papers. Social Science Paperbacks, London (paper first published in 1947).
- Osgood, C. and Tannenbaum, P. (1955) The principle of congruity in the prediction of attitude change. Psychological Review, 62, 42–55.
- Rosenberg, S. (1968) Mathematical models of social behavior. In G. Lindzey and E. Aronson (eds), The Handbook of Social Psychology. Addison‐Wesley, Reading, MA.
- Saltiel, J. and Woelfel, J. (1975) Inertia in cognitive processes: the role of accumulated information in attitude changes. Human Communication, 1, 333–344. http://www.galileoco.com/literature/OCRSaltiel‐Woelfel.pdf. Accessed: December 14, 2015.
- Serota, K.B., Fink, E.L., Noell, J.J. and Woelfel, J. (1975) Communications ideology, and political behavior: a multidimensional analysis. Paper presented to the Political Communication Division of the International Communication Association Convention, 23–26 April, Chicago. Working paper 75‐1, Political Ideology Project. http://www.galileoco.com/literature/SerotaEtAlComIdealogyPolbehICA1975.pdf. Accessed: December 19, 2015.
- Sherif, M. and Cantril, H. (1946) The psychology of ‘attitudes’: part II. Psychological Review, 53, 1–24. https://www.brocku.ca/MeadProject/Sherif/Sherif_1946.html. Accessed: December 14, 2015.
- Sherif, C., Sherif, M. and Nebergall, R. (1965) Attitude and Attitude Change. Saunders, Philadelphia, PA.