15
Ideological Landscapes Model
Generated Versus Empirical Ideological Landscapes
In the Ideological Landscapes Model (Lorenz, 2014), individual agents are assumed to ‘live’ in neighbourhoods where they interact with other agents more or less similar in their ideological opinions with respect to political objects/issues. Ideological opinions are defined as subjective summarizing expressions of structures of attitudes, beliefs, values and emotions about political objects. They are communicated to other agents, thus inducing processes of opinion change. The mechanisms of interaction between agents trigger processes of ideological position change. These changes provide for the emergence of macro phenomena.
The model aims to provide a means to investigate the evolution of ideological landscapes as a result of interactions between individual agents and also as a result of their homophile adaptation.
The model is based on the theoretical and computational background provided by other well‐known models of bounded confidence continuous opinion dynamics (Deffuant et al., 2000; Krause, 2000; Weisbuch et al., 2001; Hegselmann and Krause, 2002). The difference from the bounded confidence opinion dynamics models resides in the study of ideological landscapes’ dynamic evolution as an effect of interaction and adaptation mechanisms which operate at the individual level.
Operational Model
An artificial society is defined as a set of N individual agents which are characterized by personal opinions or attitudes or beliefs (ideological positions) with respect to political issue xi.
The most important aspect is that agents change their ideological positions as they interact with other agents. The interaction process could result in ideology change by means of (i) homophile adaptation of the individual agents and (ii) random reconsiderations of an agent’s ideological issue position.
An ideological distance is defined as the distance between the ideological issue positions of any two agents, i and j, such that their ideological distance is lower than the bound of confidence1 ε:
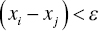
If interacting agents have close ideology issue positions, then the ideology change by homophile adaptation is modelled as a change in the ideology position of agent i, for example, to the mean value of the two ideological positions. Otherwise, the position remains unchanged.
If an individual agent reconsiders its ideology position at some moment of time, it chooses a random position value within [0, 1] with a probability p.
The ideology position of each agent is initialized with a value within the interval [0, 1]. The simulation runs provide for the generated data. The model then compares the ideology landscapes obtained from the European Social Survey and the landscapes obtained from the simulation of the model. The comparison criteria include aspects concerning (i) distributions, (ii) number, location and dimension(s) of peaks and (iii) landscapes’ global shapes.
The conclusion drawn from the analysis of the data patterns in generative model architectures is that the generated data do not achieve full characteristics of the empirical patterns. This has strong implications for the debates about the epistemological value of computational and simulation modelling based on generative technologies.
The model shows that the mechanisms and processes generate different types of agents and polities than the real ones. One reason could be that the agent‐based systems are often biased in the generative processes by the initialization of their agents’ internal structures with normal distributions of attitude values, probabilities and so on. Empirical data such as the ideological landscapes are rarely (if ever) normally distributed.
Another source of bias in agent‐based models identified in the experiments based on the model of bounded confidence opinion dynamics is the reductionist approach of representing attitudes as opinions, and the opinions as variables with numerical values. Ideology as a structure of attitudes and the attitude change in multidimensional spaces is a more enhanced representation which has already proved its own limitations.
The model has the virtues of a model‐to‐model analysis, a computational modelling tradition in agent‐based systems (see a classic approach in: Axtell et al., 1996) and continued by several authors, especially in agent‐based system modelling (ABS), which require a standardized system of evaluation of their design and performances (see a technical report on this issue in: Cioffi‐Revilla (2011). Models are compared on a set of criteria so that performances and validity can be evaluated on a standard basis.
Web Resources
Lorenz, J. (2012) Netlogo model: continuous opinion dynamics under bounded confidence. NetLogo User Community Models. See also http://janlo.de/applets/bc.html.
References
- Axtell, R., Axelrod, R., Epstein, J.M. and Cohen, M.D. (1996) Aligning simulation models: a case study and results. Computational and Mathematical Organization Theory, 1, 123–141.
- Cioffi‐Revilla, C. (2011) On the quality of a social simulation model. Paper prepared for the 2nd Annual Conference of the Computational Social Science Society of America, Santa Fe, NM, 9–12 October. http://computationalsocialscience.org/wp‐content/uploads/2011/10/Cioffi‐QualitySocialSimulation‐CSSSA‐2011.pdf. Accessed: December 19, 2015.
- Deffuant, G., Neau, D., Amblard, F. and Weisbuch, G. (2000) Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87–98.
- Hegselmann, R. and Krause, U. (2002) Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation (JASSS), 5(3). http://jasss.soc.surrey.ac.uk/5/3/2.html. Accessed: December 16, 2015.
- Krause, U. (2000) A discrete nonlinear and non‐autonomous model of consensus formation. In S. Elaydi, G. Ladas, J. Popenda and J. Rakowski (eds), Communications in Difference Equations. Gordon and Breach, Amsterdam; pp. 227–236.
- Lorenz, J. (2014) How clustered ideological landscapes might emerge through opinion dynamics. Paper presented at the ECPR General Conference, 3–6 September. http://ecpr.eu/Events/PaperDetails.aspx?PaperID=20737&EventID=14. Accessed: December 16, 2015.
- Weisbuch, G., Deffuant, G., Amblard, F. and Nadal, J.P. (2001) Interacting agents and continuous opinions dynamics. http://arxiv.org/abs/cond‐mat/0111494. Accessed: December 16, 2015.