Generative Adversarial Networks 101

As shown in the following diagram, the Generative Adversarial Networks, popularly known as GANs, have two models working in sync to learn and train on complex data such as images, videos or audio files:

Intuitively, the generator model generates data starting from random noise but slowly learns how to generate more realistic data. The generator output and the real data is fed into the discriminator that learns how to differentiate fake data from real data.

Thus, both generator and discriminator play an adversarial game where the generator tries to fool the discriminator by generating as real data as possible, and the discriminator tries not to be fooled by identifying fake data from real data, thus the discriminator tries to minimize the classification loss. Both the models are trained in a lockstep fashion.

Mathematically, the generative model  learns the probability distribution 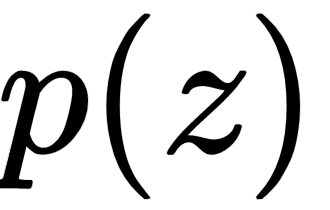 such that the discriminator  is unable to identify between the probability distributions,  and .  The objective function of the GAN can be described by the following equation describing the value function V, (from https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf):

The seminal tutorial at NIPS 2016 on GANs by Ian Goodfellow can be found at the following link: https://arxiv.org/pdf/1701.00160.pdf.

This description represents a simple GAN (also known as a vanilla GAN in literature), first introduced by Goodfellow in the seminal paper available at this link: https://arxiv.org/abs/1406.2661. Since then, there has been tremendous research in deriving different architectures based on GANs and applying them to different application areas. 

For example, in conditional GANs the generator and the discriminator networks are provided with the labels such that the objective function of the conditional GAN can be described by the following equation describing the value function V:

>

The original paper describing the conditional GANs is located at the following link: https://arxiv.org/abs/1411.1784.

Several other derivatives and their originating papers used in applications, such as Text to Image, Image Synthesis, Image Tagging, Style Transfer, and Image Transfer and so on are listed in the following table:

GAN Derivative	Originating Paper	Demonstrated Application
StackGAN	https://arxiv.org/abs/1710.10916	Text to Image
StackGAN++	https://arxiv.org/abs/1612.03242	Photo-realistic Image Synthesis
DCGAN	https://arxiv.org/abs/1511.06434	Image Synthesis
HR-DCGAN	https://arxiv.org/abs/1711.06491	High-Resolution Image Synthesis
Conditonal GAN	https://arxiv.org/abs/1411.1784	Image Tagging
InfoGAN	https://arxiv.org/abs/1606.03657	Style Identification
Wasserstein GAN	https://arxiv.org/abs/1701.07875 https://arxiv.org/abs/1704.00028	Image Generation
Coupled GAN	https://arxiv.org/abs/1606.07536	Image Transformation, Domain Adaptation
BE GAN	https://arxiv.org/abs/1703.10717	Image Generation
DiscoGAN	https://arxiv.org/abs/1703.05192	Style Transfer
CycleGAN	https://arxiv.org/abs/1703.10593	Style Transfer

 

Let us practice creating a simple GAN using the MNIST dataset. For this exercise, we shall normalize the MNIST dataset to lie between [-1,+1], using the following function:

def norm(x):
    return (x-0.5)/0.5

We also define the random noise with 256 dimensions that would be used to test the generator models:

n_z = 256
z_test = np.random.uniform(-1.0,1.0,size=[8,n_z])

The function to display the generated images that would be used in all the examples in this chapter:

def display_images(images):
    for i in range(images.shape[0]):
        plt.subplot(1, 8, i + 1)
        plt.imshow(images[i])
        plt.axis('off')
    plt.tight_layout()
    plt.show()