How puzzling all these changes are! I’m never sure what I’m going to be, from one minute to another.
Lewis Carroll, Alice’s Adventures in Wonderland
I must admit that I am having real trouble with the counterintuitive nature of the quantum world. Apparently, this is a good sign. The quantum physicist Niels Bohr once declared: ‘If quantum physics hasn’t profoundly shocked you, you haven’t understood it yet.’
Richard Feynman went even further, declaring that ‘no one understands quantum physics’. During a keynote address he made in his sixties he admitted: ‘Might I say immediately that we have always had (secret, secret, close the doors!) we have always had a great deal of difficulty in understanding the world view that quantum mechanics represents. I still get nervous with it.’
The mathematician in me hankers after some deterministic mechanism that will tell me when my pot of uranium is going to spit out its next particle. But the probabilistic character of quantum physics really challenges my ability to know what’s going to happen next. Newton’s equations held out the exciting possibility that if I know the momentum and position of a particle then the equations of motion will tell me the complete behaviour of that particle into the future. And if I repeat the same experiment with another particle located at the same point with the same momentum, it will repeat the path of the first particle.
But this hope that we could know the future was fundamentally crushed by the discoveries made by Heisenberg in 1927. He revealed that it doesn’t actually make sense to make the statement: ‘I know the momentum and the position of a particle at the same time.’ There seems to be an elastic relationship between knowing the location of a particle and knowing its momentum. If I measure the position of a particle with increasing precision, it seems to lead to its momentum having a whole range of possible different values. This is the content of Heisenberg’s famous uncertainty principle, perhaps the greatest challenge to what we can know. And as we shall discover, Heisenberg’s uncertainty principle accounts for why the uranium sitting on my desk is randomly chucking out particles.
Heisenberg himself expressed well how important it is to be ready to reset your view of the world in the light of new revelations: ‘Whenever we proceed from the known into the unknown we may hope to understand, but we may have to learn at the same time a new meaning of the word “understanding”.’
Quantum physics isn’t about knowing answers to old questions, but about challenging the questions we are allowed to ask.
At the heart of Heisenberg’s discovery is the following. Suppose I take one of the particles inside my uranium. If I know that the particle is at rest and not moving, it turns out that I can’t know where the particle is located. Indeed, there is a chance that when I look I could find it anywhere across the universe. But in contrast, if I try to pin down exactly where this particle is, I suddenly lose my handle on how the particle is moving. What appeared to be a particle at rest can suddenly find itself moving in any direction.
This seems totally crazy. If I throw my dice through the air, then by watching it carefully as it falls to the table I don’t expect my knowledge of the dice’s location suddenly to cause the dice to fly off in a totally new direction. But this intuition applies only to things with large mass. When the mass is as small as something like that of an electron, this is exactly what can happen. If I pin down the location of the electron to within the radius of an atom, its speed could change by as much as 1000 kilometres per second in any direction.
It’s like trying to fit a strange quantum carpet: every time I pin down the position end of the carpet, the momentum end pops out; try to pin the momentum end down and the position end no longer fits.
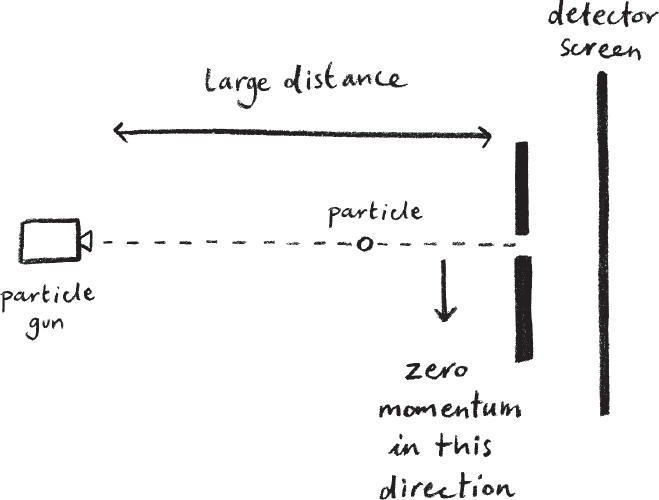
To get a feel for this elastic relation between position and momentum, let’s return to my screen with the slits. I’ve been exploring the strange behaviour of a particle fired at a screen with two slits in it. The strange tension between the position and momentum of a particle has actually already revealed itself in the behaviour of the particle as it passes through a single slit. I noted that I get some diffusion of the particles as they pass through the single slit. But if I think more carefully about this, why should just one electron passing through the slit get deflected at all? If it is a point particle like an electron, why doesn’t it sail straight through the slit? How do I explain the apparent spread of possible locations as it emerges from the slit? It’s this trade-off between knowledge of position versus knowledge of momentum that explains the diffusion I see.
I can arrange for the electron to be fired from a distant source, which ensures that if it passes through the slit then I know that there was no movement in the direction perpendicular to the slit. This means that as the particle enters the slit, I know the momentum in this direction is zero. I know it precisely.

If I think of the electron as a point particle, then it either passes cleanly through the slit or it doesn’t. If it passes through the slit, I have very precise knowledge about its position with an accuracy given by the width of the slit. Surely I can now predict precisely where it is going to hit the screen. The momentum was zero in the direction perpendicular to the slit before the electron entered the slit, so it should hit a region on the detector screen whose width is precisely the width of the slit. So why, as I fire more and more electrons through the slit, do I get the same diffusion pattern that I see for waves hitting the detector plate? Why aren’t they all arriving in a region that is the same width as the slit?
Heisenberg’s uncertainty principle asserts that any measurement that involves determining the precise position of the electron results in a new indeterminacy in the value of the momentum. So, for example, if the electron has passed through the slit, I know the location of the electron within a margin of error given by the width of the slit. As the width of the slit is reduced, that margin of error decreases. But this causes the diffusion pattern to get wider and wider. Why? Because the value of the momentum is affected. While it was zero in the direction perpendicular to the slits as it approached the slit, once the electron emerges with its position narrowed down, the momentum becomes indeterminate. I’ve pulled the quantum carpet down in the position end and caused the momentum end to pop out.
This is a very strange situation. Moreover, the precise way in which the momentum is affected is something I can’t calculate in advance. I can measure it only at a later date. I can know only a range of possible values in which I can expect to find the momentum once observed. Not only that, it now seems that if I repeat the same experiment, the momentum is not determined by the set-up. I have only a probabilistic mechanism to determine what the momentum might be.
Heisenberg’s uncertainty principle isn’t some wishy-washy statement but actually quantifies the loss of knowledge. Once I know the position of the electron with high precision, the momentum of the electron as it emerges is no longer precisely zero but can vary statistically around the average value of 0. I can’t know what value I’ll get when I measure the momentum, since that is still undetermined, but I know that statistically the possibilities for the momentum will be distributed either side of the average value of 0. I can measure the spread of this distribution with something called the standard deviation of the momentum, denoted ∆p. This is a statistical measure of the spread of possibilities. The greater the spread, the larger ∆p and the more uncertain I am of the value of the momentum.
Following Heisenberg’s original 1927 paper detailing this strange inverse relationship between knowledge of position and knowledge of momentum, Earle Kennard and later Howard Robertson mathematically deduced the trade-off in knowledge. If the spread of possibilities of the position has a standard deviation of ∆x, and the standard deviation for the spread of momentum is ∆p, then these two values satisfy the following inequality:
where h is Planck’s constant, the same number that I saw when explaining the energy of a photon of light. The equation says that if the spread of possibilities in the position measured by ∆x is reduced, then to keep the equation correct I have to increase the spread of possibilities for the momentum measured by ∆p. It is a mathematical consequence of quantum physics that the more knowledge you gain of the possible locations of a particle, the more this results in the possibility of the momentum being spread over a larger range of values. This is exactly what happens in the case of the electron passing through the single slit.
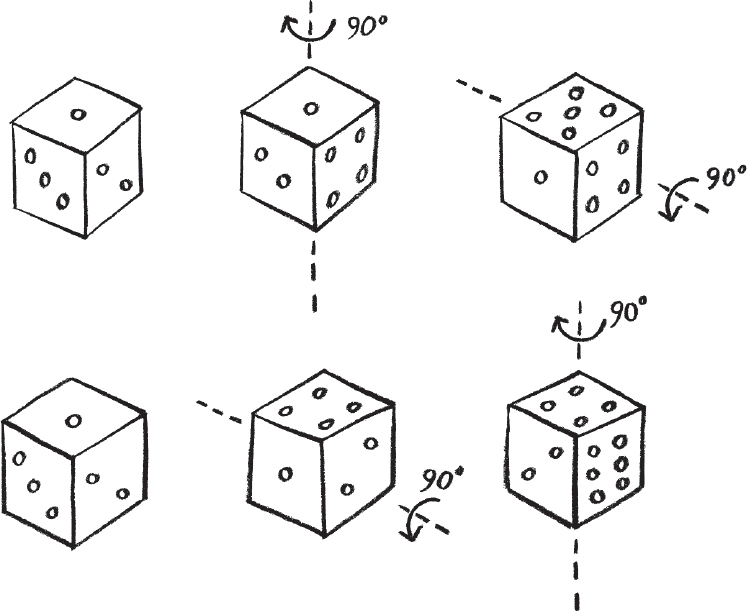
The entwined nature of these two properties is a consequence of the fact that it matters in what order I do my measurements. The acts of measuring position and momentum are described mathematically by two operations that give different answers if you do them in a different order. The idea can be illustrated using my casino dice. Suppose I place my dice on the table with the 1 on top, as illustrated on the next page. Now I am going to rotate the dice by a quarter turn around the vertical axis running through the top face and follow that by a quarter turn through a horizontal axis running through one of the side faces. The top face now has a 5 showing. But if I return the dice to the original position and repeat the moves but in reverse order, horizontal axis spin followed by vertical axis spin, I get a different outcome. Now there is a 4 showing on the top face.
Any measurements that have this property – that when you translate them into mathematical operations it matters what order you do them in – will give rise to an uncertainty principle. This is simply a mathematical consequence of this property called non-commutativity.
It’s the mathematics underlying quantum physics that results in much of its counterintuitive nature. As I’ve buried myself in the books and papers explaining quantum physics, it feels like entering a labyrinth. I thought I knew where I was before I started my journey. Then, using my mathematical skills, I’ve worked my way logically through the twists and turns of the labyrinth. I have to rely on the maths to lead me because the walls are too high for me to intuit anything about the world outside the labyrinth. But once the maths leads me out the other side and I try to make sense of my destination, where I’ve ended up doesn’t look anything like where I started.
I’m happy with the maths – it’s trying to interpret where it’s got me that is tough. It’s almost as if we don’t have the language to reverse-translate what the maths is telling us about reality. Maybe the problems I’m having are not real problems at all but a consequence of the constraints of old language and old stories. Quantum physics is a rabbit hole, and once we’ve fallen through it we need to reset our vision and formulate a new language to navigate this looking-glass world. And, for better or for worse, that language is mathematics.
But can we trust the maths? This theoretically derived behaviour predicted by the mathematics of Heisenberg’s uncertainty principle has been confirmed in experiment. In a paper published in 1969, American physicist Clifford Shull describes the results of firing neutrons at slits of decreasing width. The increased knowledge of the location of the neutrons given by a narrower slit resulted, as theory predicted, in a greater spread of possible values for the momentum. And when the neutrons arrived at the detector plate, they were spread in a distribution whose standard deviation corresponded exactly to that predicted by the equation of Heisenberg’s uncertainty principle.
The simple act of knowing more about the position of the neutron has resulted in a potential change in the momentum. Heisenberg’s uncertainty principle captures in an equation the fact that we can never know it all. An increase in the known must always be traded off against a corresponding increase in the unknown.
As you tighten your hold on one of the values, you lose determinacy in the other. But this indeterminacy can have some unexpected consequences. If I trap an electron in a very tiny box, the position of the electron is known to a high degree of accuracy. But that results in the possible values of the momentum being spread over a huge range. If I try to measure the momentum, the wave function collapses, resulting in a whole range of different values that the momentum might take.
As soon as I have measured the momentum, you might say that I now know both the position and the momentum. But it actually results in the position becoming indeterminate. The possibilities for where I will find the electron are spread out across space, so much so that I get an effect called quantum tunnelling, whereby the particle I thought was trapped inside a box can suddenly appear outside the box. It is this phenomenon which is responsible for the radiation of an alpha particle by the uranium that is sitting on my desk.
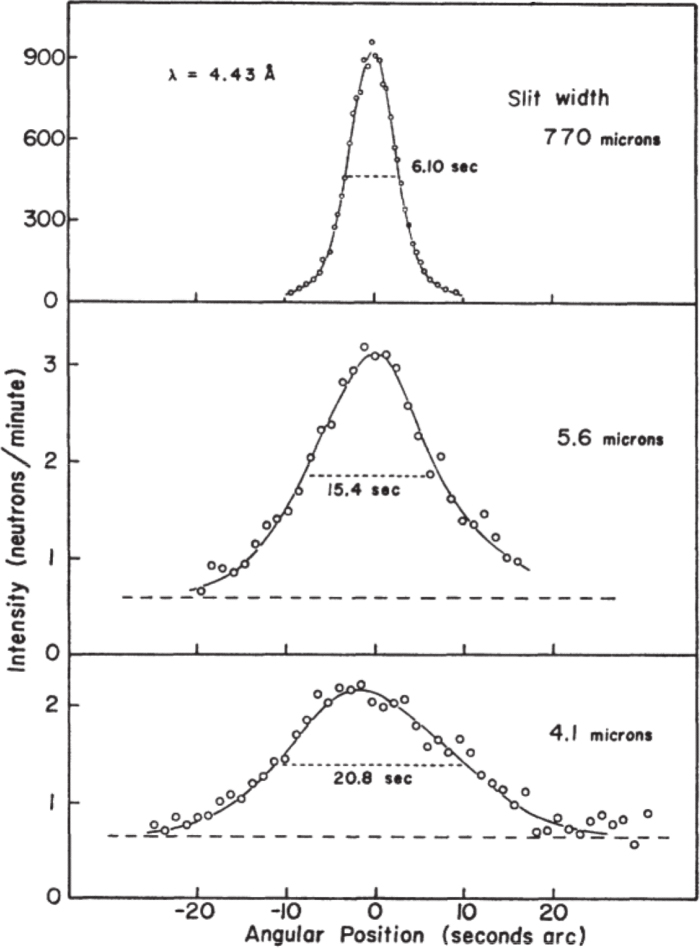
Clifford Shull’s experiment confirmed that as the size of the slit is decreased, the statistical spread of the locations of the neutrons increases.
An alpha particle is part of the nucleus of my uranium and consists of two protons and two neutrons. The nucleus is like the tiny box containing the alpha particle. In general, the particles don’t have sufficient energy to break out of the confines of the nucleus. Since the speed and hence momentum are so confined, it means that I know the momentum with a high degree of accuracy. But by Heisenberg’s uncertainty principle the position of these particles is not so clearly defined. In fact, there is a chance that the position might be located outside the nucleus, in which case the particles can escape. This uncertainty about position is responsible for the possibility of the uranium radiating.
The uncertainty principle not only explains the unpredictability of my pot of uranium but also places limits on the knowledge that I can access as I try to zoom in ever closer on the insides of my dice and see what is going on.
If I try to measure precisely the coordinates of one of the electrons inside my dice, then, as the error in the coordinates goes down, this has to be paid for by an associated uncertainty in the momentum and hence energy. Heisenberg’s equations tell me the mathematical relationship between the trade-off. But there is an extra twist. Since energy and mass are related by Einstein’s equation E = mc2, if the energy is high enough it can lead to the spontaneous creation of new particles. The trouble is that if I am trying to pin down the location of a particle and by doing that I create lots more particles, it significantly muddies any attempt to investigate the location of the original particle. The scale at which this complication starts kicking in is called the Compton wavelength of a particle. For an electron it is about 4 × 10–13 metres.
Things get even more uncertain as I zoom in closer on my particle. There is a point at which the energy uncertainty is so large that the corresponding mass becomes so great that it causes a black hole to materialize. As I shall explore in the Fifth Edge, a black hole by its very nature appears to trap any information within a certain radius of the centre of the hole and prevent it being released.
This means that the uncertainty principle implies an in-built limit to how far I can probe nature. Beyond a certain scale I seem to be denied access to what’s going on. That scale is very small. It is of the order of 1.616 × 10–35 metres, a distance known as the Planck length. This is ridiculously tiny. If I scale up the full stop at the end of this sentence to be the size of the observable universe, then something the size of the Planck length would scale up to look like the full stop before I enlarged it.
In the previous Edge I hit a point when I couldn’t subdivide matter any further, and I’ve now reached a point when I can’t divide space. This seems crazy. Why can’t I just talk about the point halfway between two points that are the Planck length apart? Mathematically it makes perfect sense, but physically it seems that it doesn’t. The physics means that I can’t distinguish any of these points.
The implications are that space at this scale has the appearance of something bitty, grainy and discrete, not continuous as Newton believed. From this perspective, space looks digital, not analogue. This in turn implies that the fractals of the First Edge cannot have any physical reality in quantum physics. A fractal is meant to have infinite complexity at all scales, but quantum physics stops us zooming in beyond the Planck length. Are the fractals of the First Edge only in my mathematical mind? Quantum physics and chaos theory appear to be incompatible with each other. It is possible that quantum physics has the effect of suppressing chaotic systems.
It should be said that this impenetrability beyond the Planck length is under the umbrella of current theory. It is at this scale that quantum physics and general relativity don’t really work. We have to come up with a new theory, which is what has led to all the work in fields like quantum gravity and string theory. In string theory, for example, particles are no longer points but are thought of as finite strings of length of the order of the Planck length with different particles vibrating at different frequencies. Are there rules that apply at this scale that mean I could extract information at even finer scales?
There have been many attempts to explain the uncertainty principle as a consequence of the act of observation affecting the system. If you want to see where a particle is, you have to fire a photon at it, and this will kick the particle, giving it an unknown momentum. Beware of such explanations. They sound attractive but they are misleading. In the description I gave above of the electron passing through a single slit, I did not need to fire any photons at the electron to alter the momentum. It was purely the act of the electron passing through the screen that gave me new knowledge of its location, resulting in a trade-off that meant I lost knowledge about its momentum. There was no direct interaction with the particle that kicked it in one direction or the other.
Apparently this misleading description of photons of light kicking the particle goes back to Heisenberg’s original paper. He needed to include the description in order to persuade the sceptical editors to publish the paper.
Heisenberg’s uncertainty principle really is a challenge to what I mean when I talk about an electron having a position and momentum simultaneously. I just have to avoid making statements like ‘knowing the position and momentum of a particle’. They have no empirical content.
The uncertainty principle is perhaps more than just an expression of what we cannot know. Rather, it represents a limit of the definition of a concept. This ties in with the description of an electron by a wave function which questions whether that the electron really has a location at all before observation. Heisenberg’s approach to this conundrum of what constitutes reality was the following:
I believe that one can formulate the emergence of the classical ‘path’ of a particle pregnantly as follows: the ‘path’ comes into being only because we observe it.
There is a fundamental question about what Heisenberg’s uncertainty principle really tells us. Is it that we can never know the precise location and momentum of an electron at any instant of time? Or is it that such things don’t exist? It’s not that we can’t know them, but that these things don’t make sense to define for the electron. Observation is creation.
For some time I’ve found it very hard to believe that fundamental properties like position and momentum come into existence only once they are measured. The momentum of an electron might change after it emerges through the tiny slit, but surely it has some precise value even before I measure it? I can accept that I might not know what that is until I use my equipment to determine the momentum, but there are lots of things I don’t know before I measure them. Quantum physics, however, is trying to tell me that this belief in the existence of a precise value before measurement is a mistake. It is my interaction with the system that creates the properties of the particle. Can it really be my act of measurement that produces the reality of this particle?
I am in good company. Einstein among others tried to challenge the idea that things like momentum and position are really so indeterminate until they are observed. Surely, he argued, these things really do have explicit values as the particle flies through the vacuum. We might not know what they are, or have a machinery or mathematics to work them out, but they still exist, they still make sense. The argument is that we shouldn’t confuse epistemology with ontology. I may not be able to know both momentum and position (epistemology) but that doesn’t mean they don’t exist (ontology).
However, I had to give up on this intuitive belief in the existence of things before measurement after I read about the remarkable Bell’s theorem, discovered in 1964 by Northern Irish physicist John Bell. His theorem explained why it was impossible for certain properties of a particle to exist prior to a measurement being taken. Try and make them exist prior to measurement and everything ends in a contradiction. Since the system doesn’t know in advance what measurement you might choose to make, Bell showed that it was impossible to assign values to take into account every possible measurement that might be made without creating results that contradicted what theory and experiment are telling us. It’s like trying to do a Sudoku puzzle with a mistake in it. However hard I try to assign values to all the squares, I always get a row or column with the same number twice.
Given that Bell’s theorem is as mathematically robust as they come, I’ve had to concede that my act of measuring seems truly to create the properties of my particle. But I’m still deeply suspicious of whether the outcome of the act of measuring is as random as current theory would have us believe.
Bell’s theorem means that I have to bite the bullet and admit that the quantum dice really isn’t cast until I actually look at it. Measurement is what causes the dice to come to rest and decide how it is going to land. But is the outcome truly random, as quantum physics suggests? I know my casino dice really isn’t random when it comes down to it. There is a physical mechanism at work which finally is responsible for how the dice lands. My feeling is that the same must be true of my pot of uranium and its radiation.
I must admit to a sneaky feeling that quantum physics is a stopgap on the way to a more complete understanding of the behaviour of fundamental particles. Surely, like the dice, there is some mechanism deciding when my lump of radioactive uranium is going to spit out an alpha particle, or that will tell us at what point on the detector screen the electron will hit after passing through the double slits.
Einstein certainly thought so, leading to his famous quote:
Quantum mechanics is very impressive. But an inner voice tells me that it is not yet the real thing. The theory produces a good deal but hardly brings us closer to the secret of the Old One. I am at all events convinced that He does not play dice.
He believed that there must be some objective reality behind this veil that we seem unable to penetrate. Even if we can’t get access to them, he believed that there must be smaller cogs that control the outcomes of measurement.
Again, I’m with Einstein on this. Surely there must be some internal mechanism at work – even if we don’t know it yet – that interacts with the measurement device to determine the outcome. I am happy to concede that the mechanism will produce outcomes that follow a model of randomness, just as the throw of my dice does. But there must be something that determines the outcome. Perhaps the particles inside my pot of uranium have some little internal ticking clock, so that if the second hand is between 0–30 when I measure it, the uranium emits radiation; but if it’s between 30–60, then no radiation is detected.
If it does have an internal ticking clock, then, as I shall explain, it’s a pretty extraordinary mechanism, one that goes counter to another intuition. If it exists, the mechanism should, I feel, be located in the vicinity of the pot of uranium. It could be internal to the particles inside the uranium, and perhaps so tiny that I can’t see it. Maybe I will never be able to explore it. The trouble is that a scenario first dreamt up by Einstein and his colleagues Boris Podolsky and Nathan Rosen revealed that if there is such a mechanism, then part of it can be moved to the other side of the universe and be located nowhere near the uranium on my desk. This may be true, but it is quite surprising that, if there is something like a hidden clock making the decisions about when the uranium spits out an alpha particle, it is a mechanism that spans the entire universe.
The scenario that Einstein, Podolsky and Rosen cooked up involves the idea of quantum entanglement. It is possible to create two particles whose properties are entangled in the sense that if I measure the properties of one particle, this forces the answers to be mirrored by the other particle. It is a bit like having two casino dice, and whenever one lands on a 6, the other must too. It would be pretty difficult to rig up such an entangled pair of cubes, precisely because the mechanism that determines how one dice will land is controlled by its interaction with the local environment, and it seems impossible to see how that could control the behaviour of the other dice. However, in quantum physics it is entirely possible to create such entangled and dependent particles, but these entangled particles reveal the very strange properties of any hidden mechanism that could determine how they will behave when measured.
To demonstrate the weird non-local nature of such a mechanism – if it exists – the experiment sends the two quantum dice in their entangled state off to opposite sides of the universe. If I then measure the first quantum dice, it has to make up its mind which face is showing, and this instantaneously determines which face is showing on the quantum dice at the other side of the universe. Some people, Einstein included, had real problems with this ‘spooky’ action at a distance. He felt that there might be a way for the roll of the dice to be preset before the particles head off to opposite ends of the universe. But that was before Bell proved his theorem, which tells me that it is impossible to preset the properties of a quantum particle in advance of measurement. Remember: measurement is creation.
The real challenge is to understand how creation at one end of the universe can instantaneously create a new state for the second particle at the other end. Because if there is some internal mechanism at work determining the outcome of the second particle, that mechanism has just been altered by something that has happened on the other side of the universe. It cannot be localized. The mechanism is not something that can be neatly packaged up inside the particle.
Einstein already expressed his concerns at this ‘spooky action at a distance’ with the double-slit experiment. How does the photographic plate know not to record an electron in one location if it is to be detected at a second location? There seems to be an instantaneous collapse of the wave function with no cascade effect from the point of observation across the result of the plate.
In this new case I have two particles, but because they are entangled in some sense they are described by one wave function, which makes them not dissimilar to the particle being detected in the double-slit experiment. The two particles must be considered as one holistic unit. Bell’s theorem means that the properties of the particles can’t be preset before they travel to the ends of the universe, which in turn means that any mechanism that determines their properties cannot be localized at the particle, but must span the entire length of the universe.
So if there is a mechanism deciding when my radioactive uranium emits radiation (as my deterministic soul yearns for there to be), it will have to be a mechanism that spans the universe. It can’t just be an internal machine at the heart of the blob of uranium on my desk, because the machine is also potentially controlling the state of particles across the universe that might be entangled with the uranium.
Often these results are trotted out to knock down any attempt to claim that there is a mechanism at work that determines when my pot of uranium spits out an alpha particle. But really these results should be interpreted only as the conditions that a hidden machine must satisfy. There could be a hidden mechanism – it’s just going to be very weird. As Bell, who was responsible for proving that such hidden machines must span the universe, said: ‘What is proved by impossibility proofs is a lack of imagination.’
But there are many who are not as keen as I am to eliminate the possibility that the behaviour of my uranium is random. This is because it might be this small chink in the knowable that allows something many people cherish to enter the scientific picture: free will.
Some commentators have argued that if there is genuine randomness in quantum physics, and the present state of things is not predetermined by past events, then it is evidence of free will at work in the universe. These quantum particles seem free to go one way or the other when deciding what to reveal about themselves when observed. Macro-sized humans may not have free will, but these micro-particles seem able to do what they want … within reason.
Perhaps the free will of these particles is the expression of a greater free will. Some religious thinkers contend that the known unknown of quantum physics allows room for an external agent to act in the world and influence its course. At the moment we have no mechanism for determining the outcome of the measurement of a system in some quantum state of superposition. Provided that the outcomes over the long term are in line with what we’d expect from the random results we observe, there seems room for an agent to determine individual outcomes. This would take advantage of our present inability to explain how the macroscopic world of measurement interacts with the quantum world. So is the unknown of quantum physics home for a theistic God? If I was going to get anywhere in my attempts to understand whether a God could hide in the equations of quantum physics, I needed to talk to someone who was as much at home in a laboratory as in a cathedral. So I made a trip to Cambridge.
John Polkinghorne learned his physics at the feet of Paul Dirac in Cambridge and then with Richard Feynman and Murray Gell-Mann at Caltech. You can’t ask for better teachers than that. His research has, among other things, helped to confirm the existence of the quarks that many believe are the last step as I zoom in on my casino dice.
Polkinghorne is back at his alma mater, so I arranged to meet him at his home in Cambridge. Having done a five-year research stint in Cambridge, I always enjoy a chance to visit even if my heart is with the dark-blue city of Oxford. Polkinghorne’s decision to become an ordained priest, after a quarter of a century of pushing the limits of quantum physics, makes him perfectly placed to explore the theology in the quantum unknowable. To many it seemed a dramatic career change. As he explained:
‘I didn’t leave science because I was disillusioned, but felt I’d done my bit for it after about 25 years. I was very much on the mathematical side, where you probably do your best work before you’re 45.’
Yikes. I hate it when people say that. I’ve always clung to the hope that it is a myth that mathematics is only for the under-forties, that mathematics isn’t some Club 18–30 holiday camp. But then I guess, being the wrong side of that divide, I would say that. Provided that there are still unanswered questions to struggle with, that is what drives me on. And I’ve still got plenty of those unanswered questions on my desk. But I can certainly understand the desire to set yourself new challenges … like my current attempts to understand quantum physics. For Polkinghorne it was getting ordained, and he often jokes about the seemingly contradictory natures of the two professions he has dedicated his life to.
‘People sometimes think that it is odd, or even disingenuous, for a person to be both a physicist and a priest. It induces in them the same sort of quizzical surprise that would greet the claim to be a vegetarian butcher.’
But he himself thinks of the two roles as a harmonious combination.
‘The basic reason is simply that science and theology are both concerned with the search for truth.’
I wondered whether there were any questions that he thought were beyond the reach of either discipline.
‘There are two sorts of questions that science cannot answer. Some of them arise out of science itself. The first is something we’ve learnt from quantum physics, which is that although the world is orderly, it’s also cloudy and fitful in its character and we don’t have access to that clear, unquestionable post-Newtonian world that seems to be sitting there.
‘But there are also questions that by their very nature don’t lie within science’s purview to answer. I think science has been tremendously successful and I have enormous respect for it, but it’s achieved its success by limiting its ambition. Essentially science is asking a single question about how things happen: what is the process of the world? And it deliberately brackets out by its nature questions of meaning and value and purpose.’
That’s not the first time I’ve come across this supposed dividing line: science does the ‘how’ and religion does the ‘why’. It’s an attractive soundbite, but I think it’s a fundamentally flawed take on science.
Science tackles a lot of ‘why’ questions. Why is my pot of uranium radiating alpha particles? Why do the planets orbit the Sun on the same two-dimensional plane rather than at arbitrary angles to each other? Why do bees make their hives in hexagons? Why does the population of lemmings plummet every four years? Why is the sky blue? Why can’t things travel faster than light?
Polkinghorne tried to tease out for me the difference he sees in the two approaches.
‘My favourite homely example is that you come into my kitchen and you see the kettle boiling. If I put on my scientific hat then I explain that it is boiling because the burning gas heats the water, and so on. But I can take off my scientific hat and say the kettle is boiling because I wanted a cup of tea and would you like to have one?’
I decided to take him up on his offer of tea. As it brewed, Polkinghorne continued.
‘I don’t have to choose between those two answers, and if I am to fully understand the phenomenon of the boiling kettle, I have to answer both questions: how it’s happening and why it’s happening.’
I agree with Polkinghorne to some extent that science has limited its ambitions and tackled the easier questions. Fermat’s Last Theorem is frankly easier than trying to understand my cat’s behaviour or the next move Polkinghorne is going to make. But that doesn’t mean that science can’t hope ultimately to understand the complexities of a cat or the vagaries of human desire.
In my view, the science-versus-religion debate has fallen foul of our terrible desire to compartmentalize everything: the silo mentality that says, ‘This is science and this is theology and this is art and this is psychology.’ The exciting thing is that we have developed a multitude of discourses to navigate our environment. The evolution of everything in the universe might be reducible to the solutions of Schrödinger’s wave equation, including Polkinghorne’s decision to boil his kettle, but while it’s a great language for describing the behaviour of my pot of uranium, it isn’t the right language to explain the migration of a flock of birds, the thrill of listening to Mozart, or to discuss the immorality of torture.
Polkinghorne concurred with the dangers of a too reductionist take on reality:
‘Sometimes when I’m having arguments with firmly reductionist friends who say that physics is everything, I say first of all, “What about mathematics?” and secondly, “What about music?” Of course music is just vibrations of the ear, but when you’ve said that you’ve said all that science can say about music, but you certainly haven’t said all that can be said about music. It does seem to me very important that one doesn’t just take a reductionist axe and chop everything down.’
I pushed Polkinghorne on his first example of a question science can’t answer. Does he really believe that quantum physics means that I can’t know when my pot of uranium is going to spit out its next particle? Is it really just chance?
‘It’s very unsatisfactory that there is this sort of lottery going on. A casino in effect. Most quantum physicists who are busy doing the numbers have just got used to that, but I think it is unsatisfactory. The question is whether it is epistemic or ontological.
‘Epistemological problems have an answer, but you don’t happen to know it. But ontological things are situations where you could not know it. And that’s the traditional interpretation of quantum theory: you cannot know.
‘In the casino we know it’s essentially epistemic. There are tiny effects that influence things. My feeling is that if the problems of quantum theory are epistemic, then you need to have some notion of how that epistemological frustration arises, what stops you from doing it. I think it’s sensible to try to push the issue ontologically as far as you can. We haven’t got there yet.’
The majority approach to the problems of quantum physics is that before you observe a particle it is in a superposition of states described by the wave function, and that observation by macroscopic apparatus causes a jump in the behaviour. The particle now has one state and the wave function encodes the probability that you will find the particle in one state rather than another. There is no attempt to explain the jump. This is called the Copenhagen interpretation after the home of its principal proponent, the Danish physicist Niels Bohr. Basically it’s the ‘Shut up and Calculate’ school of quantum physics.
‘Although I sign up to the Copenhagen interpretation of quantum theory, I don’t think it’s intellectually satisfying. At the end of the day all these things come down to someone saying “and then it happens”.
‘It’s somehow produced by the intervention of macroscopic measuring apparatus. End of discussion. But that’s just winning by definition. It is a problem. There are still puzzles.’
Given Polkinghorne’s belief that there is a God acting in the world, I wondered whether he thought the unknown of this collapsing wave function was a window for his God to act.
‘I don’t think that God is on hand to decide whether the nucleus in your uranium decays. There is some sort of mechanism … no, “mechanism” isn’t quite the right word … some sort of influence that sorts this thing out. One of the paradoxes of quantum theory is that here we are 80 years later and we still don’t understand it.’
In the First Edge, exploring chaos theory, I’d read how Polkinghorne believed that God might get involved with the decimal places we can’t know. I wondered why he had chosen chaos theory, rather than his home territory of quantum physics, as the unknown through which his God might act.
‘There was a period of about ten years when the science and theology communities were wrestling with these forms of agency. Of course they didn’t solve the problem, because that would have been a very ambitious project. There were a lot of people, especially on the west coast of America, who put their money on quantum theory explaining everything. That appeared to me just a little too slick. To counterbalance that I lurched a bit too far in the other direction. I don’t think chaos theory is the whole solution. It’s really just the suggestion that the physical universe is orderly but looser in its order than Newton would have thought.’
But he certainly isn’t dismissive of the implications of quantum physics.
‘The discovery of the intrinsic unpredictability in quantum theory shows us that the world certainly isn’t mechanical and therefore we certainly aren’t automata in some trivial and unbelievable sense.’
It’s intriguing that an agent trying to dictate the course of the future using the unknown of quantum physics has the opportunity to act only when measurement is made. Until the measurement causes a phase change, the equations of quantum physics are totally deterministic, rolling along in a linear, non-chaotic fashion with no room for any agent to act. It is one reason why religious physicists like Polkinghorne, who are trying to find a gap for an agent to act, are not particularly enamoured of the unknowable that quantum physics implies.
As I drive back from Cambridge, this question of epistemology versus ontology seems central to navigating what quantum physics tells me about what I cannot know. Is it like my casino dice? Although we can’t know the precise starting conditions for the throw of the dice, we don’t question whether they exist. But quantum physics questions whether I can talk about my pot of uranium having a well-defined initial state.
The current majority interpretation in physics is that we are mistaken to believe that the particles inside my uranium can be said to have simultaneously a precise momentum and position. This interpretation turns epistemology into ontology. Our inability to know is actually an expression of the true nature of things. As Heisenberg put it: ‘The atoms or elementary particles themselves are not real; they form a world of potentialities or possibilities rather than one of things or facts.’
Although Heisenberg’s uncertainty principle seems to create an unknown or gap through which God can slip back in, it may actually fill another gap that is the spark for most people’s belief in a Creator. One of the big unknowns is this: why is there something rather than nothing? My pot of uranium arrived in the post, sent via Amazon from Images Scientific Instruments in Staten Island. But if I keep reaching back, trying to find the ultimate origin of my uranium, I am eventually going to hit an unknown. The need for some explanation of this unknown is at the heart of many cultures’ concepts of God. God is the answer to that question. But what sort of answer is that? Perhaps it just highlights the fact that many people think we can’t know the answer to this.
I think most scientists who talk of a God have in mind something that answers the seemingly unanswerable question of where all this stuff came from. Once the universe is up and running, they are happy to engage their scientific brains to understand how the stuff we’ve got behaves. They are not looking for God to intervene in the world. This is what is often called deism rather than theism. This sort of God is very much one that can be equated with ‘things we cannot know’.
Of course, if we try to describe what this answer actually looks like, we encounter the problem of infinite regress. If you think that something is responsible for creating the universe, then you quickly hit the question of who created that something. Of course, that ‘who’ is part of the problem, because we have a terrible urge to personify this concept.
So this is why many talk about transcendent definitions, things which can’t be articulated: to avoid the problem of infinite regress. They avoid even an attempt to articulate what the answer might look like. It’s just something that is unknown and transcends our attempts to know it. This is the God that the presenter of the Sunday morning programme on BBC Northern Ireland whom I tangled with was trying to formulate.
It is a God that is defined as something that can’t be articulated. But then does it have any potency at all as a concept? If it can’t interfere, if it can’t influence, if it can’t be articulated and described, why do we need it? This is why every myth maker has had to mold their gods into forms that can be articulated, recognized, often personified. A God that is too transcendental loses its potency and fades away. For many early religions this was precisely what happened to the idea of the High God or Sky God. As religious commentator Karen Armstrong writes in her book The Case for God: ‘He became Deus otiosus, a “useless” or “superfluous” deity, and gradually faded from the consciousness of his people.’
As the theologian Herbert McCabe declared: ‘To assert the existence of God is to claim that there is an unanswered question about the universe.’ But he also warned that the fault of religion was always to make this God into a thing rather than a philosophical idea. The problem, he believed, is that religion far too often commits idolatry by trying to engage too personally with this concept of God.
The trouble is that an undefined, unknowable, transcendent concept is too abstract for many to engage with. It can’t offer the sort of consolation that many are after. So perhaps it is inevitable that its potency depends on it becoming a little less transcendent, something tangible, even if that contradicts its original definition and leads to the ‘who created the creator’ paradox.
But the question of why there is something rather than nothing may not be as unknowable as we think. And it is the unknowable of this Third Edge that could provide a way to get something ex nihilo, something out of nothing. As soon as you have a bit of empty space, quantum physics is going to start filling it with stuff. The version of Heisenberg’s uncertainty principle that I have explored so far looks at the relationship between position and momentum. But there are other physical concepts that are similarly entangled.
For example, Heisenberg’s uncertainty principle connects the measurement of energy and time: if I look at what is happening in an apparently empty bit of space, then decreasing the time period in which I examine the space increases the uncertainty of the energy content – which means that empty space can never be truly empty. Over very short periods of time there is the chance of energy fluctuations. Since energy can change into mass, this results in particles spontaneously appearing from the vacuum. Most of the time they annihilate each other and disappear back into the void, but sometimes things survive. And this gives us a mechanism for getting something out of nothing.
But where does this energy come from? Doesn’t its sudden appearance contradict the conservation of energy that physics holds dear? Some propose that the total energy content of the universe is actually zero, and therefore that no one is cheating the system. The key here is that gravity provides a negative energy content. So the universe can emerge from zero energy – from nothing – because what emerges is a combination of positive and negative energy. We are just seeing the equation 0 = 1 – 1 at work. 0 is nothing; 1 plus –1 is matter and gravity pulling that matter.
It might seem a bit bizarre to call gravity negative energy, but think about putting a large mass like an asteroid next to the Earth: as the asteroid falls towards the Earth it gains kinetic energy, but the gravitational pull is also going up because gravity increases the closer two masses are to each other. So to maintain conservation of energy, this gravitational potential energy is negative and balances the increase in kinetic energy.
According to Heisenberg’s uncertainty principle, it follows from the fact that space exists that you will get particles appearing from nothing. You don’t have any need for a creator. Quantum fluctuations mean that we are seeing something appearing from nothing all the time. As I shall discover in the Fifth Edge, this is how Hawking explained why black holes radiate particles. Nothing becomes a particle and an antiparticle: one gets trapped in the black hole and the other radiates away. So quantum physics already provides a partial answer to the something-from-nothing question.
However, you do at least need a stage on which to play this quantum game, and it’s the question of the creation of empty space that in turn becomes the issue. This perhaps is where confusion arises. Some equate empty space with nothing. But that is a mistake. Three-dimensional empty space, a vacuum, is still something. It is an arena in which geometry, mathematics, physics can play out. After all, the fact that you have a three dimensional rather than a four-dimensional empty space already hints at the evidence of something. Nothing does not have a dimension.
There are theories today which could explain how space and time can appear in the same way as particles, as fluctuations in quantum gravity. It’s as if the mathematics is enough to input nothing and show how it can give rise to something – to a universe. It is striking that science is telling us how little we need to get things going. In the end, it might be a bit of mathematics, not Amazon, that is the ultimate source of my pot of uranium.