There is a place where time stands still. Raindrops hang motionless in air. Pendulums of clocks float mid-swing. Dogs raise their muzzles in silent howls. Pedestrians are frozen on the dusty streets, their legs cocked as if held by strings. The aromas of dates, mangoes, coriander, cumin are suspended in the space.
Alan Lightman, Einstein’s Dreams
I’m rather fond of the design of my watch. The face is a simple brown square sitting inside a circular silver case. I like the symmetry of the shape, and yet there is subtle tension between the square and the circle. It’s not expensive, which is a good thing, as I tend to lose watches.
My last watch slipped off my wrist when I was kayaking across a lake next to the glacier on Mount Cook. I tried to rescue the watch but the water was so bitterly cold that I couldn’t leave my hand in it for more than a couple of seconds. Not that I had anything to measure time with anymore. The watch had disappeared below the surface and its mechanism is by now presumably rusted and frozen, its telling of time stopped by the glacial waters flowing off Mount Cook.
If I want an environment to freeze the ticking of my current watch, dropping it into the mathematical singularities that were discovered within Einstein’s equations for general relativity will stop even the most robust of watches. However, I’ll need a spaceship, not a kayak, to explore these singularities known as black holes.
The reason the universe is so fascinating – rather than a uniform spread of matter – is that, thanks to gravity, atoms attract other atoms. And so unless everything is in a perfect balance, we see a movement of matter towards other bits of matter. But the interesting thing about gravity is that the pull that matter exerts on other matter gets stronger as things get closer. This attraction is what leads to the creation of stars like our Sun, but also to the potential for more catastrophic events in space-time.
The simplest atom is hydrogen, which is made up from one electron and one proton held together by the electromagnetic force. If I have two atoms of hydrogen, they are pulled towards each other by the force of gravity. And as the atoms are pulled closer and closer they start to collide with each other. Increase the number of hydrogen atoms and the collisions get more and more energetic until the atoms no longer simply bounce off each other but the conditions for nuclear fusion are satisfied and I get a star. The hydrogen atoms fuse to create helium atoms. In the process energy is given off, creating outward pressure as the energy is dissipated. This is the energy that we depend on for life on Earth. The star remains stable, not collapsing any further, because the gravitational pull inwards is counterbalanced by the outward pressure of the energy released in the process of fusion.
At some point all the hydrogen gets used up. Some stars will continue to fuse helium into atoms further up the periodic table. Many of the atoms we find on Earth, such as iron, oxygen, or even the carbon that is crucial for making life, are all products of this continuing fusion of lighter atoms in stars. Eventually the star isn’t able to sustain this fusion – the fuel is spent. And then, once again, gravity takes over, and as the star contracts, quantum physics comes into play. If I confine particles in a smaller and smaller space then I know a lot about their position. By Heisenberg’s uncertainty principle, this must be balanced by huge uncertainty in the velocity of the particles. The movement of the particles away from each other results in a second period of stability that counteracts the pull of gravity, resulting in what is known as a white dwarf.
But in 1930 the Indian physicist Subrahmanyan Chandrasekhar realized that there is a problem with this. Stuck on a boat sailing from India to do his doctoral studies in Cambridge, Chandrasekhar recognized that special relativity puts a speed limit on how fast these particles can move. So if the mass of the star is great enough, gravity will win out over this speed limit and the star will continue to collapse, creating a region of space of increasingly high density. His calculations made on board ship revealed that any star that was more than 1.4 times the mass of our Sun would suffer such a fate. The supernovae responsible for creating elements like gold and uranium are the result of these cataclysmic collapses.
The space around these points of high density will get severely warped, so much so that the light is trapped inside and can’t get out. One way to get a sense of why things might get ensnared is to consider throwing a ball in the air. On the surface of the Earth it is possible to launch a ball fast enough such that it actually escapes the gravitational pull of the Earth. The speed at which you need to throw the ball is called its escape velocity. But imagine increasing the mass of the Earth more and more. The speed required to escape the gravitational pull also increases. But there will be a point at which the mass of the Earth is so big that the ball would need to be launched at a speed faster than the speed of light in order to escape. At this point the ball is trapped. It cannot go beyond a certain point before it is pulled back to Earth.
This is with our classical pre-Einstein view of gravity. Towards the end of the eighteenth century, Laplace and English physicist John Michell had already flirted with the proposal that light too could get trapped by massive objects. However, Michelson and Morley’s discovery a hundred years later that light always travels at the same speed in a vacuum means that light doesn’t behave like the ball. Gravity isn’t going to slow the light down as Laplace and Michell thought. But Einstein’s conception of gravity as the result of curved space-time can still result in light failing to get away. Einstein’s ideas suggest a region of space that is so curved that even light (which is massless yet still affected by the curvature of space) cannot escape. Space is curved so much that no light can find its way out but is bent back into the region of high density. In 1967 American physicist John Wheeler whimsically referred to these regions as ‘black holes’. Richard Feynman thought the name was obscene: in French, trou noir has other connotations. However, the name stuck.
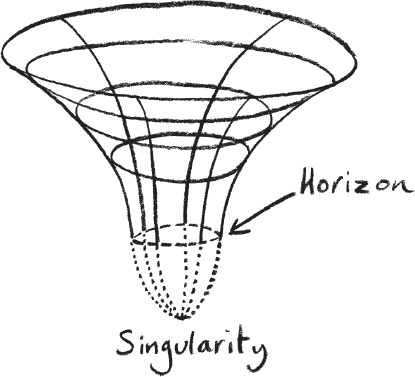
As you move away from the centre of the collapsed star, the effect of gravity decreases. This results in a boundary shaped like a sphere, with the black hole at its centre, that represents a point of no return: outside of this sphere light can escape; but any light or any thing inside this boundary will be trapped because it doesn’t have sufficient speed to escape. This sphere is known as the event horizon of the black hole, because anyone outside the sphere cannot witness the events occurring on the inside.
The mass of the star needs to be sufficiently great for the mass to collapse within the region of this sphere. For example, the mass of the Earth is too small to create a black hole – it would need to be packed into a sphere with a radius of just 1 centimetre. Our Sun is also not massive enough: the radius of its event horizon would be just 3 kilometres. But if the mass of the star is 1.4 times greater than the mass of our Sun, the inward pressure of gravity will counter any outward pressure caused by the high momentum of the trapped matter and it will collapse inside its event horizon.
Black holes have been a subject of hot debate since they were first theoretically proposed following Einstein’s publication of his equations for gravity in 1915. Some believed that stars, as they collapsed, would somehow avoid such no-go regions. Perhaps the star would throw off mass. That is certainly possible, but with a star that is 20 times the mass of the Sun, you’d need 95% of the mass to be thrown off to avoid it becoming a black hole, which is unlikely. Nevertheless, some held on to the belief that these regions of space-time would not occur.
In 1964 the first potential example of just such a high-density region was identified in the constellation of Cygnus. Called Cygnus X-1, by 1971 calculations of its mass and concentration led to the conjecture that it was a black hole. Not everyone was convinced. In fact, there was one notable person who made a bet in 1975 to the effect that Cygnus X-1 was not a black hole: Stephen Hawking. This was somewhat odd, given that he’d dedicated much of his research to probing the nature of black holes. If Cygnus X-1 turned out to be the first example of a black hole, all Hawking’s theoretical musings would have been justified.
As he explained in A Brief History of Time, the bet was an insurance policy. Betting against your football team winning the final of the FA cup is a win–win situation: if your team loses, at least you benefit financially. If it turned out that his life’s work on black holes was a waste of time, then at least he’d won the bet. His prize? A subscription to Private Eye magazine to distract him from the misery of his failed research. He made the bet with fellow cosmologist Kip Thorne. Convincing evidence that proved that Cygnus X-1 was indeed a black hole would win Thorne a subscription to the journal of his choice. He opted for Penthouse magazine.
By 1990 there was much evidence that Cygnus X-1 was indeed a black hole: it is estimated to have a mass of 14.8 times the mass of the Sun and to be too compact to be a star. Cygnus X-1 is believed to have an event horizon of 44 kilometres. Inside this spherical ball, whose diameter stretches the distance between Oxford and Cambridge, no light can escape. Given all the data, Hawking conceded the bet. Thorne has his subscription to Penthouse, much to the chagrin of his wife.
But there is something mathematically disturbing about these black holes, something which contributed to those doubts about whether they could exist. As the stars collapse, creating points of high density, there seemed nothing left to counter the continuing pull of gravity. It seemed like they would continue collapsing, becoming smaller and smaller and more and more dense with nothing to stop the implosion. Would it therefore continue to collapse, creating a singular point of infinite density? There was a lot of hostility to the idea of such physical infinities.
Einstein himself tried to prove the absurdity of such a mathematical conclusion. Eddington could see what the maths was implying but baulked at the implications: ‘When we prove a result without understanding it – when it drops unforeseen out of a maze of mathematical formulae – we have no grounds for hoping that it will apply.’ But in 1964 Oxford mathematician Roger Penrose proved that such singular points were a necessary consequence of the theory of general relativity.
A black hole in two-dimensional space-time. The event horizon is a circle inside of which we cannot know.
In collaboration with a young Stephen Hawking, Penrose went on to prove that the same infinite density is predicted when we rewind the universe back to the Big Bang. Both black holes and the Big Bang are examples in general relativity of a mathematical entity called a singularity. Singularities encompass a whole range of situations where it is impossible to work out what’s happening. A singularity is a point at which our ability to model the scenario breaks down. A place where we have to throw up our hands and declare that we do not know.
Singularities are points at which mathematical functions crash. A function in mathematics is a little like a computer program. You input numbers, the function calculates away and then it spits out an answer. Mathematicians often represent functions visually using graphs. The input is given by a number on the horizontal line, and we mark the output above the horizontal line, and the result is a curve.
For example, consider the function which inputs the distance from a massive object, and, outputs the gravitational pull experienced at that point due to the massive object. Newton realized that the greater the distance from the object, the weaker the pull. He discovered a very precise relationship between the pull and the distance. If I am a distance x from the planet, Newton’s function calculates that the pull of gravity is proportional to 1/x2. This is what we mean by an inverse square law. I can draw a picture of this function.
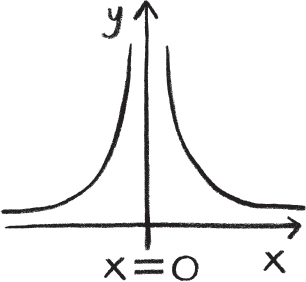
Graph of 1/x2. The function has a singularity at x = 0.
But something interesting happens as I get closer and closer to the object. The force gets bigger and bigger until, when I am at distance x = 0, the output is infinite and the graph doesn’t have a value. Of course, in reality I am measuring the distance from the centre of gravity of the planet, and once I reach the surface of the planet the function and graph change because, as I pass through the surface, parts of the planet start pulling in the other direction. When I hit the centre of gravity, all the pulls balance out and I experience zero gravitational pull. But what if I replace the planet with a black hole, a region in space where all the mass is meant to be concentrated at a single point? Now this point has infinite density, and I can approach it and as I hit the point the gravitational pull is infinite.
The fact that the function doesn’t really make sense at x = 0 is what mathematicians call a singularity. There are different sorts of singularities, but they all have a point at which the function doesn’t give a sensible output, or where there is a sudden discontinuous jump from one value to another.
A very homespun example of a singularity can be realized by taking a coin and spinning it on a table. If there was no friction on the table or air resistance, the coin would spin forever at a constant speed. However, because in fact energy is dissipated, the coin does not spin forever. Instead, the angle of the coin to the table decreases, and, intriguingly, the speed of the rotation increases proportionally. As the angle approaches zero, the speed eventually becomes infinite. The final stages of the spinning result in the coin shuddering as it falls and there is a whirring sound whose frequency rapidly increases until suddenly the coin comes to a juddering halt.
The equations of motion reveal that the speed of the coin’s rotation is increasing at such a rate that after a finite amount of time it hits infinite speed. This is what we hear when the frequency of the sound increases. The spinning coin is an example of a singularity. Of course there are other effects that come into play to stop the full realization of this mathematical infinity, but it does reveal that you don’t have to disappear down a black hole for the equations of physics to produce infinities.
Even Newton’s equations on planetary motion can produce singularities. As I explained at the end of the First Edge, mathematician Zhihong Xia revealed that four planets can be arranged in such a way to cause a fifth planet to be ejected from their midst, so that after a finite amount of time that planet hits infinite speed. The equations have nothing to say about what happens to that planet once it hits this astronomical singularity.
Singularities are typically moments where infinities kick in and beyond which it is impossible to make predictions. It isn’t just in physics that these singularities can emerge. There is a famous example, published in 1960 by Heinz von Foerster, Patricia Mora and Lawrence Amiot, which predicts a serious singularity here on Earth. The rate of population growth, if it followed the pattern of behaviour observed up to 1960, indicated that the population of the planet would become infinite on 13 November 2026. A Friday, it so happens, if you’re at all superstitious.
The simplest model of population growth posits that it is exponential. For example, a species might double in number every 50 years. With such a model the population quickly explodes but never becomes infinite. But the authors’ analysis of previous data indicated that the period of time it takes for the human population to double was getting shorter and shorter.
The population took 1650 years to double from 250 million in AD 0 to 500 million in 1650. It reached a billion 200 years later, in 1850. The next doubling took only 80 years. The population hit 4 billion in 1976, just 36 years later. The rate of growth is faster than exponential. So, in 1960, with the data to hand, the authors estimated that the population of the Earth is due to hit a singularity a decade or so from now.
Another example of this super-exponential growth is the rate of increase of computer power. There is a dictum called Moore’s law, which states that computers double in power every 18 months. With such an increase, computers are powerful but never hit a singularity. But others have suggested that just as the time it takes for the population to double seems to be getting shorter, the same applies to technology. The possibility of a technological singularity has given rise to something called the Singularity movement. Popularized by inventor and futurist Ray Kurzwell in his book The Singularity Is Near, the singularity is due to hit humanity in 2045. At this point, Kurzwell believes, humans will be able to create artificial intelligence that exceeds our own. This moment will be accompanied by a breakdown in our ability to predict what life after such a singularity will be like.
We have to be careful about mathematical equations, because there may be some hidden piece that becomes significant only when we approach the singularity, and which will then play a large role in preventing any physical realization of this infinity. This clearly occurs in the case of population growth, because the finite area of the Earth’s surface will, beyond some threshold, constrain how big a population can be produced.
Similar factors could come into play with the Big Bang and black holes. Some have suggested that the equations of general relativity don’t apply in these extreme settings. For example, it is possible that we need to introduce another term into Einstein’s equations for gravity that impacts on the equations only when we approach the singularity. This will alter what happens as we approach the singularity of the Big Bang – but the extra component is practically undetectable before we hit these extreme conditions. It is like the subtle change that Einstein needed to introduce when considering things travelling near the speed of light: at low speed, we just add speeds; but Einstein realized that close to the speed of light you need to be more careful. As I explained in the previous chapter, the formula for the speed of a man running on a moving train relative to the platform is given by adding together the speed of the man and the train, but then you need to divide by a second formula. At low speeds, this second formula is so close to 1 that it has little effect, which is why scientists pre-Einstein believed that the speeds were simply being added together. But close to the speed of light a different behaviour dominates. The same could apply close to the Big Bang or a black hole. The equations of general relativity might need that extra term that comes into play only in cases of extreme gravity.
But if the universe does contain these singular points of infinite density, what effect do they have on time? Einstein discovered that increased gravity slows time down. So what happens to my watch as I approach these singular points of extreme gravity?
If I throw my watch into a black hole, something strange occurs. If I stay on Earth and observe my watch dropping towards the black hole, there is a moment when time seems to stop. My watch gets slower and slower until it doesn’t tick any more. Eventually the image of my watch is frozen, then fades. The event horizon surrounding a black hole is like a bubble in space beyond which time seems to break down. It can’t continue. From my perspective outside the ‘black hole’, it doesn’t have an ‘after’. Could this be the reverse of what happens to time as we head back to the Big Bang? Time doesn’t have a ‘before’.
But remember, this is from my perspective, as I compare time on Earth to the time I can see on my watch as it heads towards the black hole. How do things look if I wear my watch on my wrist and join it on its trip towards this mathematical singularity? My experience is now very different. From Earth, when my watch hit the event horizon of the black hole it appeared to stop ticking. But from my new perspective, as I cross the event horizon my watch seems to continue ticking with no problem. Indeed, I won’t actually be able to detect when I have crossed this line of no return.
That’s not to say that all is well for me as I fall towards the black hole, because what happens to space-time as I approach this infinitely dense centre is not so easily ironed out. As I head feet first towards the centre of the black hole, gravity pulls harder on my feet than my head, stretching me out until I am spaghettified. Within a finite amount of time, everything is crushed into the singularity, including my watch, and time comes to an end. Like a line drawn across a page, time reaches the edge and there is nowhere for it to go.
It is strange that elsewhere time seems to tick on obliviously. I guess we all have a similar fate waiting for us. When we die, time stops for us, but we know that time will continue on unawares. Just as I cannot experience my own death, I wouldn’t experience arriving at a singularity in space-time.
Just in case I do slip into a black hole, a physicist friend offered me some advice: as with quicksand, the best thing is not to struggle. If I just free-fall towards my destiny, I will survive longer. This sounded very counterintuitive. But my physicist friend reminded me of what happens to my watch under the effects of gravity and acceleration. If I struggle, and try to accelerate away from the singularity, I’ll find time running slower where I am. Increased acceleration, like gravity, slows clocks down. And so I will race into the future of the surrounding space-time – remember my accelerating twin daughter Ina who raced into the future of her sibling Magaly. So if I struggle when I arrive at the singularity I will have aged less. But that’s not much good: I’ll be extinguished in the singularity after having experienced less of life. So it’s much better not to struggle and enjoy as much time as possible before I hit the singularity.
The interesting thing is that someone outside the event horizon will never know what is going on inside. From their perspective, time does appear to stop as soon as I cross the event horizon, and for them there is no telling what comes after, although there is an after for me as I carry on towards spaghettification. So asking what happens next appears to be a sensible question. It has an answer. The only trouble is that if you are outside the event horizon, you are denied access to the answer by the laws of physics.
The same principle was thought to apply to the challenge of knowing what, if anything, happened before the Big Bang. Time comes to an end inside a black hole. But the Big Bang is like the collapse of a star into a black hole played in reverse. So I should also infer that time comes to an end as I head back towards the Big Bang. In other words, I should conclude that time had a beginning, that time itself starts at the Big Bang.
Singularities in space-time are edges, points at which I hit an end and can’t go any further. An edge in space and time is difficult to understand: even though I may be prohibited from going any further, I still feel there should be something beyond that edge.
These black holes offer a challenge not only to our concept of time, but also appear to contradict one of the other discoveries of modern physics: that information is never lost.
There is a rather remarkable consequence of the laws of quantum physics, which is that they are reversible. This means that information is never lost. This is very counterintuitive. For example, if I took a subscription to Private Eye and a subscription to Penthouse magazine and I burned a year’s worth of both, then it seems impossible that I could ever determine which pile of ashes corresponds to which magazine.
But provided I have complete information about all the atoms and photons involved in my bonfire, it is theoretically possible to rewind the process and recover the information contained inside the magazines. It would of course be extremely difficult in practice, but the science asserts that there is nothing about this process that is irreversible. The laws of physics work both ways.
The existence of black holes offers a challenge to this idea. If I throw one magazine in one black hole and the other magazine in another black hole, it is now impossible to find out which magazine went into which black hole. Black holes seem to be the ultimate paper shredders, in which information appears to be genuinely lost.
Black holes are particularly interesting in my search for things we cannot know, because once something has disappeared behind the event horizon – the boundary beyond which light cannot escape – it appears that I actually lose information about what has crossed the horizon. If I take the casino dice that I’ve been carrying with me in my search for things we cannot know and I toss it into the black hole, then once it passes the event horizon it appears that I can never know how it will land. There could be a desk on the other side on which the dice lands and comes up 6. Someone on the other side of the event horizon could see this but never be able to communicate the result because everything is trapped inside.
According to the physics of general relativity, the only things I can know about a black hole from the outside are its mass, its angular momentum and its electric charge. All other information is lost. This is known colourfully as the no-hair theorem, the idea being that any other information would represent hairs on this round bald ball of a black hole. I could chuck my dice, my cello, my wristwatch inside, and once they have passed the event horizon there is nothing about the black hole that gives any hint about what I threw in there. There is no way to rewind events to see what it was that passed that event horizon.
Although it is referred to as a theorem, it should actually be called a conjecture, because there is no conclusive proof that information is truly lost. Indeed, in 1974 the extent to which the event horizon masks what’s going on inside a black hole was queried. This is because, according to Stephen Hawking, black holes are leaking.
Once my dice is thrown into a black hole, there seems to be no mechanism to know how it lands. At least many thought this must be the consequence of such a concentration of mass-warping space-time. But when Hawking applied the second law of thermodynamics to black holes, it turned out that they weren’t as black as everyone had originally thought.
The second law of thermodynamics states that we are moving from a highly ordered universe into one which has disorder. What is changing is something called the entropy of a system. Entropy is a measure of disorder. It essentially measures the number of different possible scenarios, which in turn will be a measure of how likely it is that one of those scenarios will come to pass. And the second law states that the entropy of the universe is increasing.
A classical example of the increase of entropy is to consider a gas trapped inside a container. If the gas is concentrated in one corner (imagine it has been squashed in by internal walls that have been removed), it will, in time, distribute itself across the container. The entropy counts how many different scenarios are possible for the gas. When the gas is trapped in the corner there are fewer possible scenarios than when the walls are removed and the gas can occupy the whole of the container. The entropy increases as the number of possible scenarios increases. The entropy starts low and then rises.
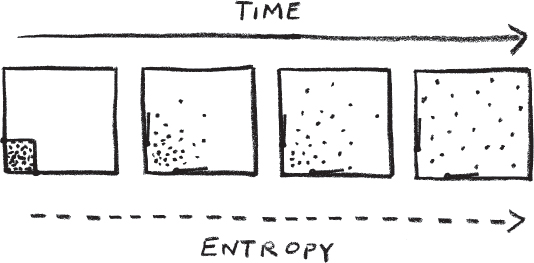
Or consider the everyday example of an egg falling from a table and smashing on the ground. The highly ordered egg becomes a scattered mass of eggshell. There are many more ways for the broken shell to be arranged than when it was in one piece around the egg. Watch a video of this scenario run forwards and backwards and it is clear which direction represents the true flow of time. Increased entropy keeps track of time’s arrow.
And this is why entropy is intimately related to the concept of time. It is one of the few things that helps us to know which way the movie should be playing. Many other laws of physics work perfectly well if I run them forwards or backwards. Although the egg reassembling itself onto the table is physically possible, the decrease in entropy is an indication of how unlikely it is.
Yet there is a curious question about where the order in that egg comes from in the first place. You may feel that this move from order to disorder is not demonstrated on Earth. We have evolved from a messy swamp to a state in which we have life and eggs and order. This seeming violation of the second law of thermodynamics is resolved because the Earth is taking low entropy from another source – there is a trade going on. The incoming photons from the Sun, which are the source of life on Earth, have low entropy. But then, instead of the Earth warming up, the planet radiates heat via electromagnetic waves of lower frequency (and hence energy) but more of them.
So a few high-energy waves from the Sun are changed into many low-energy waves emitted by the Earth. This increase in the number of rays means an increase in the number of possible scenarios for the emission of the rays. The process is a bit like smashing the egg. A single photon of high frequency is absorbed by the Earth like the egg falling to the ground, and then the Earth kicks out many photons of low energy like bits of eggshell. The Earth benefits by a net decrease in its own entropy, and we witness order emerging out of chaos. But consider the whole system of the Earth and Sun, and entropy is indeed increasing just as the second law of thermodynamics demands.
So what happens to a container of gas when it is thrown into a black hole? Or, more intriguingly, what happens to its entropy? Outside the event horizon, I’m meant to lose any knowledge of what goes on inside. Is the entropy lost, in which case entropy would decrease, contradicting the second law of thermodynamics? Perhaps we should regard the black hole as having its own entropy, which would increase as stuff gets chucked in. But since we have no idea what’s going on inside the black hole, it has been suggested that the entropy might be proportional to the surface area of the sphere of the event horizon, something we could know and calculate. That’s all very well, but the physics implies that things with entropy have temperature – and things with temperature radiate heat. So it seemed that black holes should be emitting radiation inversely proportional to the mass contained in the black hole. If they were radiating, they weren’t as black as the name suggests, but should be glowing gently in the night sky.
This didn’t make sense. How can the black hole radiate if everything including light is meant to be trapped inside? There just didn’t seem to be a mechanism for this to happen. That was until Hawking brought a bit of quantum physics to bear. Heisenberg’s uncertainty principle implies that the event horizon is a little fuzzier than the mathematics of general relativity implied. As we saw in the Third Edge, the uncertainty principle means that position and momentum cannot both be known precisely. Similarly, time and energy are related in such a way that I can’t know both simultaneously. Therefore we can’t have a perfect vacuum in which everything is set to zero. If everything was zero, I’d know everything precisely.
The vacuum experiences quantum fluctuations, so that, for example, a particle and an antiparticle can appear, one with positive energy and the other with negative energy. It was possibly this mechanism of something from nothing that got the universe up and running. Usually in the vacuum of space, the particle and antiparticle will very quickly annihilate each other. But if this pair should form in such a way that the particle with positive energy is outside the event horizon of a black hole and the particle with negative energy is trapped inside, something interesting happens.
We get this strange effect: the particle inside gets sucked into the black hole, and since it has negative energy it reduces the mass of the black hole; while the particle with positive energy looks like something being radiated away from the black hole. The black hole is glowing – it has a temperature, just as we would expect if the black hole had positive entropy.
But hold on. Half the time the positive-energy particle ends up on the inside rather than the outside. Wouldn’t that lead to the black hole increasing in mass? The way to resolve this is to understand that a negative-energy particle outside the event horizon doesn’t have the energy to get away, so the net effect of these random fluctuations is an overall decrease in the mass of the black hole over time.
Hawking radiation, as it is known, hasn’t been detected emanating from any of the black holes we’ve identified so far. The trouble is that the mathematics implies that the rate of emission depends inversely on the mass of the black hole. So a black hole with the mass of several suns will be emitting radiation at such a slow rate that it is below the temperature of the cosmic microwave background radiation, meaning that it is impossible to detect against the background noise left over from the Big Bang.
The striking implication of Hawking’s proposal was that it provided a mechanism for black holes to fade away, reducing in mass as time passes. As the mass decreases, the radiation increases, with the result, it’s believed, that black holes will eventually disappear with a pop. Hawking predicted the pop would be pretty grand: equivalent to the explosion of millions of H-bombs. Others believe it to be more on a par with an artillery shell going off.
But this leaves us with something of a puzzle. Where did the information thrown into the black hole go? I could cope with the fact that this information was trapped inside the black hole – at least it still existed. But if the black hole eventually disappears, does the information vanish with it? Or is the information somehow encoded in the radiation coming off the singularity? If I throw my casino dice into the black hole, can I somehow tell how it lands from the particles emitted at the edge of the event horizon? Perhaps, like the magazines being burnt, there is in theory a way to untangle this radiation and retrieve information about everything that disappears behind the event horizon. The puzzle of what happens to the information is called the black hole information paradox.
In 1997 Hawking took out another bet, and this time Kip Thorne sided with him. Their bet was with Caltech theoretical physicist John Preskill. They believed that this loss of information was inevitable. But, given that it contradicted the theory of quantum physics, Preskill wasn’t prepared to concede that information was lost. Rather than magazine subscriptions, the wager this time was an encyclopedia of the winner’s choice. The choice of an encyclopedia captured the idea that if it was thrown into a black hole, could the information contained in the encyclopedia somehow be encoded in the new particles being radiated thanks to the uncertainty principle?
In 2004 Hawking dramatically conceded the bet. Preskill collected Total Baseball: The Ultimate Baseball Encyclopedia. Hawking later joked: ‘I gave John an encyclopedia of baseball, but maybe I should just have given him the ashes.’
Hawking now believes that the information that plunges into a black hole is actually encoded on the surface of the event horizon enclosing the black hole and is then imparted back to the particles that are emitted. Weirdly, this surface is two-dimensional yet seems to encode information about the three-dimensional space inside. It has led to the idea of the holographic universe: the whole of our three-dimensional universe is actually just the projection of information contained on a two-dimensional surface. Although Hawking conceded the bet, Thorne has stood his ground. He still believes that the information is lost.
Roger Penrose, like Thorne, believes that Hawking conceded the bet too quickly. Once a black hole has radiated away, Penrose believes that information and entropy are lost. For Penrose, this is relevant to the question of why the universe started in such a low-entropy state. Why was there order to begin with, which meant that the second law of thermodynamics could get started in the first place? Where did the order come from? If black holes actually destroy entropy, they could provide a mechanism for resetting the universe to a low-entropy state.
Penrose had always been a believer in the Big Bang as a boundary beyond which you couldn’t do physics. As we head back towards the singularity of the Big Bang, the equations of physics break down. If we accept the description of the Big Bang as an infinitely dense point, on many levels it doesn’t make sense to explore the question of what happened before the Big Bang: the laws of physics could do anything on the other side of this singularity. We can’t measure anything that lies beyond this singularity either, so we may as well treat it as if it doesn’t exist. Or should we? Penrose has changed his mind.
There are stories emerging of what might have happened before the Big Bang, and one of the most remarkable is told by Penrose. He proposes that the Big Bang was just one in an infinite cycle of Big Bangs. This isn’t the first time such a possibility has been suggested: when it was thought that the universe would end in a big crunch, it seemed a good idea to turn the crunch into the Big Bang of a new era.
But as I discovered in the Fourth Edge, the universe is not contracting but expanding at an accelerating rate, heading for a cold state where no life, galaxies or even matter will exist, just photons of light. This is what Penrose calls the ‘very boring era’. Even the black holes that will swallow much of the galaxies we see at the moment are believed to leak radiation, so that they too will be spent, disappearing in a final pop and leaving a universe full of photons and gravitons, the hypothetical massless particle thought to mediate the force of gravity.
Penrose admitted to being somewhat depressed by this vision of our universe’s future: ‘Good God, is that what we are in for!’ But then he was struck by the question of who would be around to witness this ‘overpowering eventual tedium’. Certainly not us. The only things around to be bored by events would be the photons and gravitons that alone would make up the universe.
But it turns out that a photon has no concept of time. It lives in a timeless environment. As things approach the speed of light, relativity implies that time slows down, so much so that by the time something hits the speed of light, clocks stop. But hold on. Light travels at the speed of light. So this means that a photon has no concept of time. In fact, in Penrose’s scenario, in which all particles with mass will have decayed to massless photons or gravitons, there will be nothing left to mark time, nothing from which to make a clock. Similarly, since time is essential to measuring space, this future universe will have lost all ability to quantify and measure distance – whether it is big or small will be meaningless.
Rather than giving in to pessimism, Penrose saw an opportunity. Didn’t that sound remarkably like the state of the universe just after the Big Bang? A universe full of energy, but with no matter yet formed. Admittedly, this energy was meant to be concentrated into an infinitely small region, creating the conditions for the Big Bang. But if the universe has lost any sense of scale, then couldn’t the conditions at the end of our universe be the starting point for a new Big Bang, so that the universe that emerges has rescaled to concentrate the energy into a new beginning?
These two scenarios – the universe ending in a boring heat death and the universe starting in an exciting Big Bang – can actually be seamlessly fused together, like two landscapes whose boundaries match up to create one continuous landscape. The sewing together of these scenarios requires that the end of one universe contracts and the beginning of the next expands, so that the two ends fit together, smoothly passing from one to the other. Cold far-away photons become hot close-together photons initiating a new Big Bang.

By rescaling the universe at the end of one aeon with the beginning of another, we can pass seamlessly from one to another.
Penrose’s theory is controversial, and I couldn’t find many scientists who thought it was more than a clever mathematical idea. And yet when Penrose first revealed that the mathematics of general relativity predicted the existence of singularities in space-time, many dismissed the idea as physically impossible. His current theory of the cycles of time may prove to be wrong, but for me there is something exciting about a scientist changing his mind about the possibility of exploring time before the Big Bang.
Penrose calls the period between one Big Bang and the next an aeon, and our aeon is just one of possibly infinitely many aeons that preceded and will follow our own.
One big challenge to this model, and to many cyclical models, is the second law of thermodynamics. How is entropy reset to such a low state that we can run the second law of thermodynamics in each new aeon?
The Big Bang singularity is a state of very low entropy. As the universe evolves, entropy increases – how can we move seamlessly into the next aeon and reset the entropy? This is why Penrose was unhappy that Hawking conceded the bet about black holes. In Penrose’s view, black holes are the mechanism for resetting entropy. All the entropy entering a black hole is lost or subtracted from the whole system, so that by the end of the aeon we are at low entropy again, because all the information has been lost in the plethora of black holes that populate the universe. This sets up the conditions for the next Big Bang.
Even if the theory is correct, how can we ever dig back into the period that preceded our own Big Bang to test this or other theories? Is ‘before the Big Bang’ a no-go area? Penrose thinks not. Given that the two landscapes must match up, things that happened in the previous aeon should impact on our own. He believes that the bumping together of black holes towards the closing stages of the last aeon will have caused gravitational ripples that passed into our aeon. He compares it to a pond into which many pebbles have been thrown. Once the black holes or pebbles have disappeared, we will have a pattern of ripples that results from these interacting expanding circles.
Penrose believes that this is something that we could look for in the cosmic microwave background radiation, the radiation left over after the Big Bang that started our universe. Although the fluctuations across this radiation look random, perhaps some of them are the result of black holes bouncing off each other towards the end of the last aeon.
The trouble is that the cosmic microwave background radiation is notoriously difficult to analyse, partly because there isn’t enough of it. You may consider this crazy, given that it makes up the surface of the sphere enclosing the observable universe. And yet if you are surveying sections of this sphere that surrounds the universe and you need to take sections which span 10 degrees of arc, you are very quickly going to run out of bits you haven’t looked at. Although many are sceptical about seeing evidence of previous aeons in our current aeon, it does raise the exciting prospect that perhaps the question of what happened before the Big Bang is not as unanswerable as we once thought!
I popped into Penrose’s office, which is one floor down from my own in Oxford, to get his take on whether we will ever know what happened before the Big Bang. In his eighties, Penrose is a great example of how the desire to know never fades. Because he wrote a book with the subtitle A Complete Guide to the Laws of the Universe, you may assume that he thinks he knows it all. But Penrose is still asking new questions.
‘I used to say that the Big Bang was a singularity so the notion of time doesn’t mean anything before the Big Bang. ‘Before’ is a meaningless question. Don’t ask that question. I’ve heard Stephen Hawking saying not to do so, and I would have agreed. But the view I take now is that you really are allowed to ask that question.’
Did this mean that Penrose thought there was no beginning to it all?
‘My belief is that it’s an infinite sequence of aeons.’
I challenged him on whether this was an example of something we cannot know. After all, infinity is usually a no-go area for physics.
‘We might be able to increase technology and see a few aeons back. But going back to the beginning of them all? Well, there’s a candidate for something we may never know. People say that the infinite is unknowable, but in mathematics people use it all the time. We feel completely at home. Well, if not completely, then largely.’
When I asked Penrose whether he thought there was any question that by its very nature was unanswerable, he was typically cautious.
‘I slightly worry about the concept that there might be anything that will always remain beyond our knowledge. There may be questions that you might not expect an answer to, I suppose. Problems that you think are unsolvable, but then you think of a way around them and get some handle on them. I don’t like the term “unknowable”. It just means we’re not looking at the thing in the right way.
‘You might not think you could ever know what’s happening in the middle of the Sun, but now people do know what is going on there. Not so long ago, people would have thought of that as an impossible question, I suppose.
‘Can you multiply together two incredibly large numbers when the result has more digits than there are particles in the universe and therefore cannot be written down? Does that count as an unsolvable problem? It just seems a tiresome unsolvable problem.
‘I think I have a bias – although I wouldn’t like to say it’s a position I’m taking – a bias in favour of not having absolutely unknowable things.’ Penrose looked a little concerned. ‘I hope I haven’t disappointed you by saying there are no unknowables.’
I suggested that this could be an important mindset for doing science.
‘A problem may be pretty difficult, but somehow you feel there’s got to be a solution. I do have that feeling, but I don’t know if it is justified. I don’t expect to see answers to the big questions in my lifetime, though it would be nice to see a few of the more immediate ones resolved.’
I wanted to know which problem he would like to see resolved if he could choose one. Since time is on Penrose’s mind, he chose evidence of a time before the Big Bang.
‘I’d like to see signals from the previous aeon. But we’re a long way from that.’
So is doing away with the need for a beginning a threat to those who believe in a God who created everything? Penrose laughs as he recalls how he was worried that his proposal might ruffle ecclesiastical feathers, just as his hero Galileo had.
‘I did this event at the Vatican and I was a little bit nervous. But then I realized they were honouring Galileo and the invention of the astronomical telescope. So I described my theory of cycles of time and I thought they might be a bit uncomfortable about the Big Bang not being the beginning. Their response: “No, that’s fine … God created the whole thing.”’
The Vatican response points to a question that has always intrigued religious thinkers: what is God’s relation to time, especially given our modern revelations about its fluid nature? Einstein’s special theory of relativity asks whether you can talk about one event happening before another. From one perspective, event A happens before event B, but Einstein showed that from another perspective event B can occur first.
For religious commentators this poses an interesting challenge: what is God’s perspective? For God, did A happen before B, or vice versa? One answer is to respond as the Vatican representative had to Penrose: take God outside of time. Just as God is not located at one point in space, there is no need to locate God at one point in time.
An outsider would look at space-time just as someone on top of a mountain might look down on the lie of the land. But this view of space-time would include the past, present and future, all of time, in one take. Although not phrased in terms of four-dimensional Lorentzian geometry, this is actually the position taken by the fourth-century theologian Saint Augustine of Hippo.
Einstein tried to use this perspective on time to comfort the widow of his friend Michele Besso, writing to her: ‘Now he has departed from this strange world a little ahead of me. That means nothing. People like us, who believe in physics, know that the distinction between past, present and future is only a stubbornly persistent illusion.’ We should regard our existence at this point in time like being in London rather than Paris.
But some theologians have a problem with a God outside of time, because it doesn’t leave room for that God to act in the world. If you opt for theism rather than simple deism, then God needs to have a temporal quality to intervene in the world. If God is outside, looking at the whole of space-time, the future is already there in the landscape. Interestingly, although people may argue over the order of events, they won’t argue about their order if they are causally related. This demands a God who steps in and out of time, moulding the geometry of space-time. But a God who acts in the world is a God who acts in time. So it is very difficult to square a timeless God with a God who acts in the universe.
The question remains: what is this thing called God that is meant to be outside of time? Can anything be outside of time? Actually, there is something that I would regard as timeless: mathematics. And as a timeless thing it is well suited to the job of sparking the creation of what we observe around us. It is the creator responsible for the equations of quantum physics that give us space-time and something from nothing. Mathematics has an attractive quality: you don’t need to ask who created the mathematics. It is something that exists outside of time and doesn’t need a moment when it was created. It just is. Perhaps we should reverse the old adage ‘God is a mathematician’. Perhaps mathematics is the god everyone is chasing. If I replace the word ‘God’ with the word ‘mathematics’ in Aquinas’s attempt at a definition, I think it works quite well: ‘Mathematics is to be thought of as existing outside the domain of existents, as a cause from which comes everything that exists in different forms.’
This is close to theoretical physicist Max Tegmark’s idea of the mathematical universe hypothesis, or MUH. He proposes that our physical universe is an abstract mathematical structure. It’s a modern take on the Pythagorean philosophy. In the paper in which he proposes this mathematical universe, he concludes with the following:
‘If the MUH is true, then it constitutes great news for science, allowing the possibility that an elegant unification of physics, mathematics and computer science will one day allow us humans to understand our reality even more deeply than many dreamed would be possible.’
I probably wouldn’t go as far as Tegmark in identifying our physical universe with mathematics. It seems hard mathematically to distinguish between two universes in which positive and negative charges are swapped over. The two universes would be physically different, but the mathematical description would be exactly the same. This is an example of something called quidditism: the idea that there is more to the universe than just the relationship between objects – what they are (the quid is Latin for ‘what’) provides another level of distinction.
If mathematics is eternal and outside of time, you don’t need a creator to begin things. The equations of mathematics are truly outside the universe, so they could play the role of something supernatural and godlike. It is not, however, a God that acts in the world, because this is a deistic vision. The interesting question is then: how many different ways are there to set up a universe out of a set of mathematical equations? The multiverses now arise from multi-mathematical models.
Some argue that simply having an equation that goes from zero unicorns to three unicorns per second doesn’t mean unicorns exist. So having equations that allow for the physics of quarks and their interactions with various fields doesn’t make the quarks any more real than the unicorns. It’s what Hawking refers to as the necessity of understanding how ‘to breathe fire into the equations’. For example, what led to our universe having negative and positive charges set as they are rather than the other way round? Where did the ‘quid’ in ‘quidditism’ come from?
If there was no universe, no matter, no space, nothing, I think there would still be mathematics. Mathematics does not require the physical world to exist. Therefore, for me, mathematics is a very strong candidate for the initial cause. It also explains the ‘unreasonable effectiveness of mathematics’. This is the expression Eugene Wigner coined for the uncanny knack of abstract mathematics to explain physical phenomena. If physical phenomena are a result of mathematics, it should not be surprising that we keep finding mathematical explanations at the heart of the universe we inhabit.
There are those who would have us do away with the need to talk of time at all. My watch has been ticking away. It says it is a little past ten o’clock in the evening. But what does that mean? Put another watch telling the same time in a spaceship, and when it returns it won’t match my watch.
Einstein’s discoveries reveal that the best I can do is to compare the running of clocks. No one clock measures absolute time. Such a thing does not make sense. If you think about it, this was always the case. How did Galileo discover that swinging pendulums are a good way of measuring time? He was sitting in Mass watching the chandelier in the church swinging in the wind. When he compared it with his pulse, he realized that the time it took to swing from one side to the other did not depend on the angle of swing. But here Galileo was comparing one measure of time with another that he assumed was constant. The truth is that all these time-keeping devices are relative to other things.
If we go back to the equations of physics, then, although time appears to play a major role, it is possible to rewrite everything without reference to time at all. It seems that because we have such a strong sense of the passage of time, it was the most obvious window through which to observe the world. Books on mechanics are all about the evolution of the universe with respect to time. The equation for the trajectory of a ball takes time as input and outputs where you will find the ball. But none of these books defines time, and no physicist has satisfactorily pinned down what we mean by time, so perhaps the best strategy is to eliminate it altogether.
This was the aim of physicist Julian Barbour. Working without an academic position, supporting his family by translating Russian, Barbour has developed a theory of physics that removes the need for time at all. His ideas are articulated in his ground-breaking book The End of Time, published in 1999. ‘Nothing happens; there is being but no becoming. The flow of time and motion are illusions.’ A number of physicists within mainstream academia have taken his ideas very seriously.
But why then do I feel that there is something called time flowing along, with me at its mercy? I have the feeling that I can never go back in time, that the future is waiting out there still to happen. I remember the past but not the future. Italian physicist Carlo Rovelli and French mathematician Alain Connes believe that this sensation is a result of incompleteness of knowledge. Called the thermal time hypothesis, it proposes that time is an emergent phenomenon, not a fundamental concept.
If I take any physical system, like the molecules of gas in my room, then generally I don’t have complete knowledge of the microscopic state of these particles, but only some overall macroscopic description that could allow for many possible microscopic states. I am reduced to considering the situation statistically because of my incomplete knowledge. Rovelli and Connes are able to demonstrate mathematically how this incomplete knowledge can give rise to a flow that has all the properties we associate with our sensation of time. They believe that time emerges only from this macroscopic consideration of an unknown microscopic system. If you dig deep enough, time will disappear, rather like the way the idea of surface of a liquid doesn’t make sense when you are at the atomic level. Or consider the fact that you can’t talk about an atom having a temperature or a molecule of water being wet. Time is not fundamental but a similar emergent property.
That’s not to say these things aren’t real. Hotness, wetness, time ticking by. I look at my watch. Staring me in the face is 23:55. Another day drawing to a close. Midnight is about to strike, heralding the end of the party, and the feeling that I am one day closer to the moment when I won’t be able to know anymore. But why do I feel anything: the passage of time, the pain of a stubbed toe, the pleasurable taste of a fine wine, the excitement of listening to Prokofiev? These things are at the heart of one of the biggest unsolved and possibly unanswerable questions on the scientific books, as I will discover in the next Edge.