Number is the ruler of forms and ideas and the cause of gods and demons.
Pythagoras
The statement on the other side
of this card is false
The statement on the other side
of this card is true
Bored of the uninspiring range of Christmas crackers available in the shops, I decided this year to treat my family to my very own home-made mathematical crackers. Each cracker included a mathematical joke and a paradox. My family were of the opinion that the jokes were stronger on the mathematics than the humour. I’ll let you decide … How many mathematicians does it take to change a light bulb? 0.99999 recurring. And if you’re not laughing, don’t worry. My family weren’t either. If you don’t get it, then – although you should never have to explain a joke – the point is that you can prove that 0.9999 recurring is actually the same number as 1.
The paradoxes were a little less lame. One contained a Möbius strip, a seemingly paradoxical geometric object which has only one side. If you take a long strip of paper and twist it before gluing the ends together, the resulting shape has only one side. You can check this by trying to colour the sides: start colouring one side and you soon find you’ve coloured the whole thing. The strip has the surprising property that if you cut it down the middle, it doesn’t come apart into two loops, as you might expect, but remains intact. It’s still a single loop but with two twists in it.
The cracker I ended up with wasn’t too bad, even if I say so myself. Even the joke was quite funny. What does the B in Benoit B. Mandelbrot stand for? Benoit B. Mandelbrot. (If you still aren’t laughing, the thing you’re missing is that Mandelbrot discovered the fractals that featured in my First Edge, those geometric shapes that never get simpler, however much you zoom in on them.) The paradox was one of my all-time favourites. It consisted of the two statements that opened this chapter, one on either side of a card. I’ve always enjoyed and in equal measure been disturbed by word games of this sort. One of my favourite books as a kid was called What Is the Name of This Book? It was stuffed full of crazy word games that often exploited, like the title, the implications of self-reference.
I have learnt not to be surprised by sentences formed in natural language that give rise to paradoxes like the one captured by the circular logic of the two sentences on my cracker card. Just because you can form meaningful sentences doesn’t mean there is a way to assign truth values to the sentences that makes sense.
I think the slippery nature of language is one of the reasons that I was drawn towards the certainties of mathematics, where this sort of ambiguity was not tolerated. But as I shall explain in this Edge, my cracker paradox was used by one of the greatest mathematical logicians of all time, Kurt Gödel, to prove that even my own subject contains true statements about numbers that we will never be able to prove are true.
This desire for certainty, to know – to really know – was one of the principal reasons that I chose mathematics over the other sciences. In the sciences the things we think we know about the universe are models that match the data. To qualify as a scientific theory they must be models that can be falsified, proved wrong. The reason they survive – if they survive – is that all the evidence supports the model. If we discover new evidence that contradicts the model, we must change the model. By its very nature, a scientific theory is one that can potentially be thrown out. In which case, can we ever truly know we’ve got it right?
We thought the universe was static, but then new discoveries revealed that galaxies are racing away from us. We thought the universe was expanding at a rate that was slowing down, given the drag of gravity. Then we discovered that the expansion was accelerating. We modelled this with the idea of dark energy pushing the universe apart. That model waits to be falsified, even if it gains in credibility as more evidence is collected. Eventually, we may well hit on the right model of the universe, which won’t be rocked by further revelations. But we’ll never know for sure that we have got the right model.
This is one of the exciting things about science: it is constantly evolving – there are always new stories. We can feel rather sorry for the old stories that fade into irrelevance. Of course, the new stories grow out of the old. As a scientist you live with the fear that your theory may be flavour of the moment, winner of prizes, and then suddenly it is superseded. Plum pudding models of the atom, the idea of absolute time ticking away, particles having identifiable positions and momentum: these are no longer top of the science bestseller list. They have been replaced by new stories.
The model of the universe I read about as a schoolkid has been completely rewritten. The same cannot be said of the mathematical theorems I learned. They are as true now as the day I first read them and as true as the day they were first discovered. Sometimes that day was as long as 2000 years ago. As an insecure spotty teenager, I found the certainty it promised particularly attractive. That’s not to say that mathematics is static. It is constantly growing as unknowns become known, but those knowns remain known and robust, and become the first pages in the next great story. Why is the process of attaining mathematical truth so different from that faced by the scientist who can never really know?
The all-important ingredient in the mathematician’s cupboard is proof.
There is evidence of people doing maths as far back as the second millennium BC. Clay tablets in Babylon and papyri in Egypt show sophisticated calculations and puzzles being solved: estimates for π; the formula for a volume of a pyramid; algorithms being applied to solve quadratic equations. But in general these documents tell of procedures that can be applied to particular problems to derive solutions. We don’t find justification for why these procedures should always work, beyond the convincing evidence that it’s worked in the thousands of examples that have been documented in the clay tablets to date. Mathematical knowledge was based on experience and had a more scientific flavour to it. Procedures were adapted if a problem cropped up that wasn’t amenable to the current algorithm.
Then around the fifth century BC things began to change as the ancient Greeks got their teeth into the subject. The algorithms come with arguments to justify why they will always do what it says on the tin or tablet. It isn’t simply that it’s worked the last thousand times, so it will probably work the next time: the argument explains why the proposal will always work. The idea of proof was born.
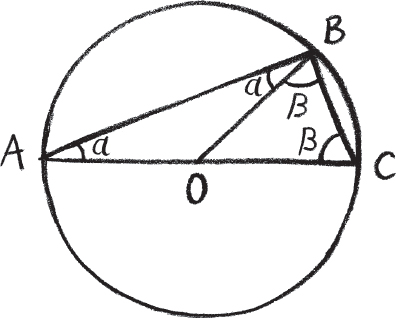
Thales of Miletus is credited with being the first known author of a mathematical proof. He proved that if you take any point on the circumference of a circle and join that point to the two ends of a diagonal across the circle, then the angle you’ve created is an exact right angle. It doesn’t matter which circle you choose or what point on the circle you take, the angle is always a right angle. Not approximately, and not because it seems to work for all the examples you’ve drawn. But because it is a consequence of the properties of circles and lines.
Thales’ proof takes a reader from things they are confident are true and by a clever series of logical moves arrives at this new point of knowledge, which is not one that you would necessarily think obvious just from looking at a circle. The trick is to draw a third line going from the initial point B on the circle to the centre of the circle at O.

Why does this help? Now you have two triangles with two sides of equal length. This means that in both triangles the two angles opposite the centre of the circle are equal. This is something that has already been proved about such triangles. Take the larger triangle you originally drew. Its angles add up to 2α + 2β. Combine this with knowledge that a triangle has angles adding up to 180 degrees, and we know that α + β must be 90 degrees, just as Thales asserted.
When I first saw this proof as a kid it gave me a real thrill. I could see from the pictures that the angle on the circle’s edge looked like a right angle. But how could I know for sure? My mind searched for some reason why it must be true. And then as I turned the page and saw the third line Thales drew to the centre of the circle, and took in the logical implications that flowed from that, I suddenly understood with thunderous clarity why that angle must indeed be 90 degrees.
Note that already in this proof you see how the mathematical edifice is raised on top of things that have already been proved, things like the angles in a triangle adding up to 180 degrees. Thales’ discovery in turn becomes a new block on which to build the next layer of the mathematical edifice.
Thales’ proof is one of the many to appear in Euclid’s Elements, the book which many regard as the template for what mathematics and proof are all about. The book begins with basic building blocks, axioms, statements of geometry that seem so blindingly obvious that you are prepared to accept them as secure foundations on which to start building logical arguments.
The idea of proof wasn’t created in isolation, out of nowhere. Rather, it emerged alongside a new style of writing that developed in ancient Greece. The art of rhetoric, as formulated by the likes of Aristotle, provided a new form of discourse aimed at persuading an audience. Whether in a legal context or political setting, or simply the narrative of a story, audiences were taken on a logical journey as the speaker attempted to convince listeners of his position. The mathematics of Egypt and Babylon grew out of the building and measuring of the new cities growing up round the Euphrates and Nile. This new need for logic and rhetorical argument emerged from the political institutions of the flourishing city-states at the heart of the Greek empire.
Rhetoric for Aristotle was a combination of pure logic and methods designed to work on the emotions of the audience. Mathematical proof taps into the first of these. But proof is also about storytelling. And this is why the development of proof at this time and place was probably as much to do with the sophisticated narratives constructed by the likes of the dramatists Sophocles and Euripides, as with the philosophical dialogues of Aristotle and Plato.
In turn, the mathematical explorations of the Greeks moved beyond functional algorithms for building and surveying to surprising discoveries that were more like mathematical tales to excite a reader.
A proof is a logical story that takes a reader from a place they know to a new, unvisited destination. Like Frodo’s adventures in Tolkien’s Lord of the Rings, a proof is a description of the journey from the Shire to Mordor. Within the boundaries of the familiar land of the Shire are the axioms of mathematics, the self-evident truths about numbers, together with those propositions that have already been proved. This is the setting for the beginning of the quest. The journey from this home territory is bound by the rules of mathematical deduction, like the legitimate moves of a chess piece, prescribing the steps you are permitted to take through this world. At times you arrive at what looks like an impasse and need to take a lateral step, moving sideways or even backwards to find a way around. Sometimes you need to wait for new mathematical characters like imaginary numbers or the calculus to be created so you can continue your journey. The proof is the story of the journey and the map charting the coordinates of that journey. The mathematician’s log.
To earn its place in the mathematical canon it isn’t enough that the journey produce a true statement about numbers or geometry. It needs to surprise, delight, move the reader. It should contain drama and jeopardy. Mathematics is distinct from the collection of true statements about numbers, just as literature is not the set of all possible combinations of words or music all possible combinations of notes. Mathematics involves aesthetic judgement and choice. And this is probably why the art of the mathematical proof grew out of a period when the act of storytelling was flourishing. Proof probably owes as much to the pathos of Aristotle’s rhetoric as to its logos.
While many of the first geometric proofs are constructive, the ancient Greeks also used their new mathematical tools to prove that certain things are impossible, beyond knowledge. The discovery, as we saw, that the square root of 2 cannot be written as a fraction is a striking example.
The proof has a very narrative quality to it, taking the reader on a journey under the assumption that the length can be written as a fraction. As the story innocently unfolds, one gets sucked further and further down the rabbit hole until finally a completely absurd conclusion is reached: odd numbers are even and vice versa. The moral of the tale is that the imaginary fraction representing this length must be an illusion. (If you would like to take a trip down the rabbit hole, the story is reproduced in the box on page 370.)
For those who encountered a number like the square root of 2 for the first time, it must have seemed like something that by its nature was beyond full knowledge. To know a number was to write it down, to express it in terms of numbers you knew. But here was a number that seemed to defy any attempt to record its value.
Let L be the length of the hypotenuse of a right-angled triangle whose short sides are both of length 1 unit. Pythagoras’ theorem implies that a square placed on the hypotenuse will have the same area as the sum of the area of squares placed on the two smaller sides. But these smaller squares each have area 1 while the larger square has area L2. Therefore L is a number which when you square it gives you 2.
Suppose L is actually equal to a fraction L = p/q.
We can assume that one of p or q is odd. If they are both even we can keep dividing both top and bottom by 2 until one of the numbers becomes odd.
Since L2 = 2, it follows that p2/q2 = 2.
Multiply both sides by q2: p2 = 2 × q2.
So is p odd or even? Well p2 is even so p must be even because odd times odd is still odd. So p = 2 × n for some number n. Since p is even that means that q must be the odd number. But hold on …
2 × q2 = p2 = (2 × n)2 = 2 × 2 × n2,
so we can divide both sides of the equation by 2 to get
q2 = 2 × n2.
Remember that we’d worked out that q was the odd number.
So q2 is also odd. But the right-hand side of this equation is an even number! So if L is expressible as a fraction it would imply that odd = even. That’s clearly absurd, so our original assumption that L can be written as a fraction must have been false.
I think this is one of the most stunning proofs in mathematics. With just a finite piece of logical argument we have shown there is a length that needs infinity to express it.
It was an extraordinary moment in the history of mathematics: the creation of a genuinely new sort of number. You could have taken the position that the equation x2 = 2 doesn’t have any solutions. At the time, the numbers that were known could not solve this equation precisely. Indeed, it was really only in the nineteenth century that sufficiently sophisticated mathematics was developed to make sense of such a number. And yet you felt it did exist. You could see it – there it was, the length of the side of a triangle. Eventually mathematicians took the bold step of adding new sorts of numbers to our mathematical toolkit so that we could solve these equations.
There have been other equations that seemed to defy solution, where the answer was not as visible as the square root of 2, and yet we’ve managed to create solutions. Solving the equation x + 3 = 1 looks easy from our modern perspective: x = –2. But for the Greeks there was no number that solved this. Diophantus refers to this sort of equation as absurd. For mathematicians like Diophantus, numbers were geometrical: they were real things that existed, lengths of lines. There was no line such that if you extended it by three units it would be one unit in length.
Other cultures were not so easily defeated by such an equation. In ancient China numbers counted money and money often involved debt. There certainly could be a circumstance in which I add 3 coins to my purse, only to find I have 1 coin left. A debt to a friend could be responsible for swallowing 2 of the coins. In 200 BC Chinese mathematicians depicted their numbers using red sticks; but if they represented debts, they used black sticks. This is the origin of the term going into the red, although somewhere along the line the colours got swapped.
It was the Indians in the seventh century AD who successfully developed a theory of negative numbers. In particular, Brahmagupta deduced some of the important mathematical properties of these numbers: for example, that ‘a debt multiplied by a debt is a fortune’, or minus times minus is plus. (Interestingly, this isn’t a rule, it’s a consequence of the axioms of mathematics. It is a fun challenge to prove why this must be so.) It took Europeans till the fifteenth century to be convinced that there were numbers that could solve these sorts of equations. Indeed, the use of negative numbers was even banned in thirteenth-century Florence.
New numbers continued to appear, especially when mathematicians were faced with the problem of solving an equation like x2 = –1. At first sight, it seems impossible. After all, if I take a positive number and square it, the answer is positive, and, as Brahmagupta proved, a negative number squared is also positive. When mathematicians in the Renaissance encountered this equation, their first reaction was to assume it was impossible to solve. Then Italian mathematician Rafael Bombelli took the radical step of supposing there was a new number that had a square equal to –1, and he found that he could use this new number to solve a whole host of equations that had been thought unsolvable. Interestingly, this imaginary number would sometimes be needed only in the intermediate calculations and would disappear from the final answer, leaving ordinary numbers that people were familiar with that clearly solved the equation at hand.
It was like mathematical alchemy, but many refused to admit Bombelli’s new numbers into the canon of mathematics. Descartes wrote about them in a rather derogatory manner, dismissing them as imaginary numbers. As time went on, more mathematicians realized their power but also the fact that they didn’t seem to give rise to any contradictions in mathematics if they were admitted. It wasn’t until the beginning of the nineteenth century that they truly found their place in mathematics, thanks in part to a picture which helped mathematicians to visualize these imaginary numbers.
The ordinary numbers (or what mathematicians now call the real numbers) were laid out along the number line running horizontally across the page. The imaginary numbers like i, the name given to the square root of –1, were pictured on the vertical axis. This two-dimensional picture of the imaginary or complex numbers was instrumental in the acceptance of these new numbers. The potency of this picture was demonstrated by the discovery that the geometry of the picture reflected the arithmetic of the numbers.
So are there even more numbers out there beyond the edge that we haven’t yet discovered? I might try writing down more strange equations in the hope that I get more new numbers. For example, what about the equation x4 = –1?
Perhaps to solve this equation I’ll need even more new numbers. But one of the great theorems of the nineteenth century, now called the fundamental theorem of algebra, proved that, using the imaginary number i and the real numbers, I can solve any equation I want. For example, if I take
and raise it to the power of 4, then the answer is –1. The edge had been reached beyond which no new numbers would be found by trying to solve equations.
The ancient Greek proof of the irrationality of the square root of 2 was the first of many in mathematics to show that certain things are impossible. Another proof of the impossible was the concept of ‘squaring the circle’. Indeed the mathematical idea of squaring the circle has entered many languages as an expression of impossibility. Squaring the circle relates to the geometric challenges that the ancient Greeks enjoyed trying to crack, using a ruler (without measurements) and a compass (for making arcs of circles). They discovered clever ways to use these tools to draw perfect equilateral triangles, pentagons and hexagons.
Squaring the circle consists of trying to use these tools to construct from a given circle a square whose area is the same as that of the circle you started with. Try as hard as the Greeks could, the problem stumped them. A similarly impossible challenge was posed by the oracle of the island of Delos. Residents of the Greek island had consulted the oracle to get advice about how to defeat a plague that the god Apollo had sent down upon them. The oracle replied that they must double the size of the altar to Apollo. The altar was a perfect cube. Plato interpreted this as a challenge to construct, using straight edge and compass, a second perfect cube whose volume was double the volume of the first cube.
If the second cube is double the volume of the first, this means the sides have lengths which are the cube root of 2 times the length of the first cube. The challenge therefore was to construct a length equal to the cube root of 2. Constructing the square root of 2 was easy since it arises as the diagonal of a unit square; but the cube root of 2 turned out to be so difficult that the residents of Delos could not solve the problem. Perhaps the oracle wanted to distract the Delians with geometry and mathematics as a way of diverting their attention away from the more pressing social problems they faced.
Doubling the cube, squaring the circle, and a third classical problem of trisecting the angle all turned out to be impossible. But it took until the nineteenth century before mathematicians could prove beyond doubt that there was no way to do these things. It was the development of group theory – a language for understanding symmetry that I use in my own research – that held the key to proving the impossibility of these geometric constructions. It turns out that the only lengths that can be constructed by ruler and compass are those that are solutions to certain types of algebraic equation.
In the case of squaring the circle, the challenge requires you to produce, using ruler and compass, a straight line of length √π starting from a line of unit length. But it was proved in 1882 that π is not only an irrational number but also a transcendental number, which means it isn’t the solution to any algebraic equation. This in turn means that it is impossible to square the circle.
Mathematics is remarkably good at proving when things are impossible. One of the most celebrated theorems on the mathematical books is Fermat’s Last Theorem, which states that it is impossible to find any whole numbers that will solve any of the equations
where n is greater than 2. This is in contrast to the case of n = 2, which corresponds to the equation Pythagoras produced from his right-angled triangles. If n = 2, there are many solutions, for example 32 + 42 = 52. In fact, there are infinitely many solutions, and the ancient Greeks found a formula to produce them all. But it is often a much easier task to find solutions than to prove that you will never find numbers which satisfy any of Fermat’s equations.
Fermat famously thought he had a solution but scribbled in the margin of his copy of Diophantus’ Arithmetica that the margin was too small for his remarkable proof. It took another 350 years before my Oxford colleague Andrew Wiles finally produced a convincing argument to explain why you will never find whole numbers that solve Fermat’s equations. Wiles’s proof runs to over one hundred pages, in addition to the thousands of pages of preceding theory that it is built on. So even a very wide margin wouldn’t have sufficed.
The proof of Fermat’s Last Theorem is a tour de force. I regard it as a privilege to have been alive when the final pieces of the proof were put in place.
Before Wiles had shown the impossibility of finding a solution, there was always the prospect that maybe there were some sneaky numbers out there that did solve one of these equations. I remember a great April fool that went round the mathematical community around the same time as Wiles announced his proof. The joke was that a respected number theorist in Harvard, Noam Elkies, had produced a non-constructive proof that such solutions existed. It was a cleverly worded April fool email because the ‘non-constructive’ bit meant he couldn’t explicitly say what the numbers were that solved Fermat’s equations, just that his proof implied there must be solutions. The great thing is that most people were forwarded the email several days after 1 April, when the joke first started its rounds, and so had no clue that it was an April fool.
April fool or not, the mathematical community had spent 350 years not knowing whether there was a solution or not. We didn’t know. But finally Wiles put us out of our misery. His proof means that however many numbers I try, I’ll never find three that make one of Fermat’s equations true.
We are living in a golden age of mathematics, during which some of the great unsolved problems have finally been cracked. In 2003 one of the great challenges of geometry, the Poincaré conjecture, was proved by the Russian mathematician Grigori Perelman. But there are still many statements about numbers and equations whose proofs elude us: the Riemann hypothesis, the twin primes conjecture, the Birch–Swinnerton-Dyer conjecture, Goldbach’s conjecture.
In my own research I have dedicated the last twenty years trying to settle whether something called the PORC conjecture is true or not. This was formulated over fifty years ago by Oxford mathematician Graham Higman, who believed that the number of symmetry groups with a given number of symmetries should be given by nice polynomial equations (which is what the P in PORC stands for). For example, the number of symmetry groups with p6 symmetries, where p is a prime number, is given by a quadratic expression in p: it is p2 + 39p + c (where c is a constant that depends on the remainder you get on dividing p by 60).
My own research has cast real doubts on whether this conjecture is true. I discovered a symmetrical object with p9 symmetries whose behaviour suggests something very different to what was predicted by Higman’s conjecture. But it doesn’t completely solve the problem. There is still a chance that other symmetrical objects with p9 symmetries could smooth out the strange behaviour I unearthed, leaving Higman’s conjecture true. So, at the moment, I don’t know whether this conjecture is true or not, and Higman, alas, died before he could know. I am desperate to know before my finite life comes to an end, and it is questions like this that drive me in my mathematical research.
I sometimes wonder, as I get lost in the seemingly infinite twists and turns of my research, whether my brain will ever have the capacity to crack the problem I am working on. In fact, mathematics can be used to prove that there are mathematical challenges that are beyond the physical limitations of the human brain, with its 86 billion neurons connected by over 100 trillion synapses.
Mathematics is infinite. It goes on forever. Unlike chess, which has an estimated 101050 different games that are possible, the provable statements of mathematics are infinite in number. In chess, pieces get taken, games are won, and sequences are repeated. Mathematics, though, doesn’t have an endgame, which means that even if I get my 86 billion neurons firing as fast as they physically can, there are only a finite number of logical steps that I will be able to make in my lifetime, and therefore only a finite amount of mathematics that I can ever know. What if my PORC conjecture needs more logical steps to prove than I will ever manage in my lifetime?
Even if we turned the whole universe into a big computer, there are limits to what it could ever know. In his paper ‘Computational Capacity of the Universe’, Seth Lloyd calculates that since the Big Bang the universe cannot have performed more than 10120 operations on a maximum of 1090 bits. At any point in time the universe can only know a finite amount of mathematics. You might ask: what is the universe calculating? It’s actually computing its own dynamical evolution. Although this is a huge number, it is still finite. It means that we can prove computationally that at any point in time there will always be things that the observable universe will not know.
But it turns out that mathematics has an even deeper layer of unknown. Even if we had a computer with infinite capacity and speed, there are things it will never know. A theorem proved in the twentieth century has raised the horrific possibility that even a computer with this infinite capacity may never know whether my PORC conjecture is true. Called Gödel’s incompleteness theorem, it shook mathematics to the core. It may be that these conjectures are true, but they will always be beyond our ability to prove within our axiomatic framework for mathematics. Gödel proved that within any axiomatic framework for mathematics there are mathematically true statements that we will never be able to prove are true within that framework. A mathematical proof that there are things that are beyond proof – mathematics beyond the edge.
When I learned about this theorem at university, it had a profound effect on me. Despite the physical limitations of my brain or the universe’s brain, I think I grew up with the comforting belief that at least theoretically there was a proof out there that would demonstrate whether my PORC conjecture was true or not, or whether the Riemann hypothesis was true or not. One of my mathematical heroes, the Hungarian Paul Erdős, used to talk affectionately about proofs from ‘The Book’. This was where Erdős believed God kept the most elegant proofs of each mathematical theorem. The challenge for a mathematician is to uncover the proofs in The Book. As Erdős joked in a lecture he gave in 1985: ‘You don’t have to believe in God, but you should believe in The Book.’ Erdős himself doubted the existence of God, dubbing him the Supreme Fascist responsible for hiding his socks and Hungarian passport. But I think most mathematicians accepted the metaphor of The Book. However, the proof I learned about in my university course on mathematical logic proved that there were pages missing from The Book, pages that even the Supreme Fascist did not possess.
The revelation that there were mathematical statements beyond the limits of proof was sparked by the realization that one of the geometric statements Euclid had used as an axiom was actually not as axiomatic as had been thought.
An axiom is a premise or starting point for any logical train of thought. In general, an axiom is meant to express some self-evident truth that is accepted as true without the need for proof. For example, I believe that if I take two numbers, then no matter in what order I add them together, I get the same answer. If I take 36 and add 43, I won’t get a different answer if I start with 43 and add 36. You might ask how I know that this will always be true. Perhaps something weird happens if I take really large numbers of things and add them together. What mathematics does is to make deductions about numbers which do satisfy this rule. If the way we count things in the universe does something weird, we just have to accept that the mathematics that we have developed from this axiom is not applicable to the way physical numbers work in the universe. We would then develop a new number theory based on numbers that satisfy a different fundamental set of axioms.
Although many of the axioms that Euclid used to deduce his theory of geometry seemed self-evident truths about the geometry of the universe, there was one that mathematicians increasingly thought a bit suspicious.
The parallel postulate states that if you have a line and a point off that line then there is a unique line through the point which is parallel to the first line. This postulate certainly seems obvious if you are drawing geometry on a flat page. It is one of the axioms that is crucial to Euclid’s proof that triangles have angles that add up to 180 degrees. Certainly any geometry in which the parallel postulate is true will give rise to triangles with this property. But the discovery in the nineteenth century of new sorts of geometry with no parallel lines, or with many lines that could be drawn parallel, led mathematicians to the realization that Euclid’s geometry was just one of a whole host of different geometries that were possible.
For example, if I take the surface of a sphere – a curved geometry – then lines confined to this surface are not straight but bend. Take two points on the surface of the Earth, then, as anyone who has flown across the Atlantic knows, the shortest path between these two points won’t match the line you would draw on a flat atlas. This is because the line between these two points is part of a circle like a line of longitude that divides the sphere perfectly in half. Indeed, if one of the points is a North or South Pole then the line would be a line of longitude. All lines in this geometry are just lines of longitude that are moved round the surface so that they pass through the two points you are interested in. They are called great circles. But now if I take a third point off this great circle there is no way to arrange another great circle through the third point that doesn’t intersect the first circle. So here is a geometry that doesn’t have parallel lines.
Consequently, any proof which depends on the parallel postulate won’t necessarily be true in this new geometry. Take the proof that angles in a triangle add up to 180 degrees. This statement depends on the geometry satisfying the parallel postulate. But this spherical geometry doesn’t. And indeed this geometry contains triangles whose angles add up to more than 180 degrees. Take the North Pole and two points on the equator and form a triangle through these three points. Already the two angles at the equator total 180 degrees, so the total of all three angles will be greater than 180 degrees.
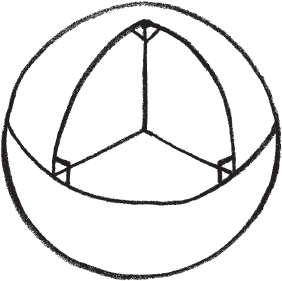
A triangle whose angles add up to more than 180 degrees.
Other geometries were discovered in which there was not just one but many parallel lines through a point. In these geometries, called hyperbolic, triangles have angles adding up to less than 180 degrees. These discoveries didn’t invalidate any of the proofs of Euclid. This is a great example of why mathematical breakthroughs only enrich rather than destroy previous knowledge. But the introduction of these new geometries in the early nineteenth century nonetheless caused something of a stir. Indeed, some mathematicians felt that a geometry that didn’t satisfy Euclid’s axiom about parallel lines must contain some contradiction that would lead to it being thrown out as impossible. But further investigation revealed that any contradiction inherent in these new geometries would imply a contradiction at the heart of Euclidean geometry.
Such a thought was heretical. Euclidean geometry had stood the test of time and not produced contradictions for 2000 years. But hold on … this is beginning to sound like the way we do science. Surely mathematics should be able to prove that Euclidean geometry won’t give rise to contradictions. We shouldn’t just rely on the fact that it’s worked up to this point, therefore we should believe everything’s OK. That’s how the scientists in the labs across the road work. We mathematicians should be able to prove that our subject is free of contradictions.
When, at the end of the nineteenth century, mathematical set theory produced strange results that seemingly led to unresolvable paradoxes, mathematicians began to take more seriously this need to prove our subject is free of contradictions. The British philosopher Bertrand Russell was the author of a number of these worrying paradoxes. He challenged the mathematical community with the set of all sets that don’t contain themselves as members. The problem was whether this new set was a member of itself. The only way you are in this set is if you are a set which doesn’t contain yourself as a member. But as soon as you put the set in as a member, suddenly it is (of course) a set which contains itself as a member. Aargh! There seemed no way to resolve this paradox, and yet the construction was not so far from sets that mathematicians might want to contemplate.
Russell came up with some more prosaic, homely examples of this sort of self-referential paradox. For example, he imagined an island on which a law decreed that the barber had to shave all those people who didn’t shave themselves – and no one else. The trouble is that this law leads to a paradox: can the barber shave himself? No, since he is allowed only to shave those who don’t shave themselves. But then he qualifies as someone who must be shaved by the barber. Aargh, again! The barber has taken the role of the set Russell was trying to define, the set of all those sets that don’t contain themselves as members.
I think my favourite example of all these paradoxes is the puzzle of describing numbers. Suppose you consider all the numbers that can be defined using fewer than 20 words taken from the Oxford English Dictionary. For example, 1729 can be defined as ‘the smallest number that can be written as the sum of two cubes in two different ways’. Since there are only finitely many words in the Oxford English Dictionary and we can use only a maximum of 20 words, we can’t define every number in this way since there are infinitely many numbers and only finitely many sentences with fewer than 20 words. So there is a number which is defined as follows: ‘the smallest number which cannot be defined in fewer than 20 words from the Oxford English Dictionary’. But hold on … I just defined it in fewer than 20 words. Aargh!
Natural language is prone to throw up paradoxical statements. Just putting words together doesn’t mean they make sense or have a truth value. But the worrying aspect to Russell’s set of all sets that don’t contain themselves is that it is very close to the sorts of things we might want to define mathematically.
Mathematicians eventually found ways around this paradoxical situation, which required refining the intuitive idea of a set, but it still left a worrying taste in the mouth. How many other surprises were hiding inside the mathematical edifice? When the great German mathematician David Hilbert was asked to address the International Congress of Mathematicians in 1900, he decided to set out the 23 greatest unsolved problems facing mathematicians in the twentieth century. Proving that mathematics was free of contradictions was second on his list.
In his speech, Hilbert boldly declared what many believed to be the mantra of mathematics: ‘This conviction of the solvability of every mathematical problem is a powerful incentive to the worker. We hear within us the perpetual call. There is the problem. Seek its solution. You can find it by pure reason, for in mathematics there is no ignorabimus.’ In mathematics there is nothing that we cannot know. A bold statement indeed.
Hilbert was reacting to a growing movement at the end of the nineteenth century that held that there were limits to our ability to understand the universe. The distinguished physiologist Emil du Bois-Reymond had addressed the Berlin Academy in 1880, outlining what he regarded as seven riddles about nature that he believed were beyond knowledge, declaring them ‘ignoramus et ignorabimus’. Things we do not know and will never know.
In the light of my attempt to understand what questions may be beyond knowledge, it is interesting to compare my list with the seven riddles presented by du Bois-Reymond:
Du Bois-Reymond believed that 1, 2 and 5 were truly transcendent. The first two are very much still at the heart of the questions we considered in the first few Edges. The teleological arrangement of nature refers to the question of why the universe seems so fine-tuned for life, something that still vexes us today. The idea of the multiverse is our best answer to this riddle. The last three were the subject of the previous Edge, which probed the limits of the human mind. Only the riddle with the origin of life is perhaps one that we have made some headway on. Despite amazing scientific progress in the last 100 years, the other six problems are still potentially beyond the limits of knowledge, just as du Bois-Reymond believed.
But Hilbert was not going to admit mathematical statements to the list of du Bois-Reymond’s riddles. Thirty years later, on 7 September 1930, when Hilbert returned to his home town of Königsberg to be made an honorary citizen, he ended his acceptance speech with the clarion call to mathematicians:
For the mathematician there is no Ignorabimus, and, in my opinion, not at all for natural science either … The true reason why no one has succeeded in finding an unsolvable problem is, in my opinion, that there is no unsolvable problem. In contrast to the foolish Ignorabimus, our credo avers: Wir müssen wissen. Wir werden wissen. [We must know. We shall know.]
However, Hilbert was unaware of the startling announcement that had been made at a conference in the same town of Königsberg the day before the ceremony. Mathematics does contain ignorabimus. A twenty-five-year-old Austrian logician by the name of Kurt Gödel had proved that it was impossible to prove whether mathematics was free of contradictions. And he went even further. Within any axiomatic framework for mathematics, there will be true statements about numbers that you can’t prove are true within that framework. Hilbert’s clarion call – ‘Wir müssen wissen. Wir werden wissen’ – would eventually find its rightful place: on Hilbert’s gravestone. Mathematics would have to face up to the revelation that it too had riddles that we would never be able to solve.
The title of this section is true.
It was self-referential statements like the one I found in my cracker last Christmas that Gödel tapped in to for his devastating proof that mathematics had its limitations.
Although sentences in natural language might throw up paradoxes, when it comes to statements about numbers, we expect a statement to be either true or false. Gödel was intrigued by the question of whether you could exploit the idea of self-reference in mathematical statements. Hilbert’s challenge already had an element of self-reference built in: he wanted to construct a mathematically secure argument to prove that mathematics was without contradictions. The challenge already demanded that mathematics look in on itself to prove that it wouldn’t suddenly give rise to proofs that two contradictory statements were true.
Gödel wanted to show that within any axiom system for number theory there would always be true statements about numbers which couldn’t be proved from these axioms. It’s worth pointing out that you can try to set up different sets of axioms to try to capture how numbers work. Hilbert’s hope was that mathematicians could construct one axiom system from which we could prove all truths of mathematics. Gödel found a way to scupper this hope.
The clever trick that Gödel played was to produce a code that assigned to every meaningful statement about numbers its own code number. A similar idea is already at work as I sit typing. The words that I am using to tell Gödel’s story are being converted into strings of numbers which represent the letters I am typing. For example, in decimal ASCII, Gödel becomes the number 71246100101108. The advantage of the coding Gödel cooked up is that it would allow mathematics to talk about itself.
According to Gödel’s code, any axioms we choose to capture the theory of numbers – the statements from which we deduce the theorems of mathematics – will each have their own code number. For example, the axiom ‘if A = C and B = C, then A = B’ has its own code number. But statements that can be deduced from these axioms like ‘there exist infinitely many primes’ will also have their own code number. Even false statements like ‘17 is an even number’ will have a code number.
These code numbers allowed Gödel to talk in the language of number theory about whether a particular statement is provable within the system. The basic idea is to set up the code in such a way that a statement is provable if its code number is divisible by the code numbers of the axioms. It’s much more complicated than that, but this will be a helpful simplification.
Gödel could now talk about whether a statement is provable or not from the axioms just as a statement about numbers. To express the fact that ‘The statement “there exist infinitely many primes” can be proved from the axioms of number theory’ translates into ‘the code number of the statement “there exist infinitely many primes” is divisible by the code numbers of the axioms of number theory’ – a purely mathematical statement about numbers which is either true or false.
Hold on to your hats as I take you on the logical twists and turns of Gödel’s proof … Gödel decided to consider the statement S: ‘This statement is not provable.’ Statement S has a code number. But if we analyse the content of statement S, it translates into a statement simply about whether the code number of this sentence S is not divisible by the code numbers of the axioms. Let us suppose that the axiomatic system for number theory that we are analysing doesn’t lead to contradictions – as Hilbert hoped.
Thanks to Gödel’s coding, S is simply a statement about numbers. Either the code number of S is divisible by the code numbers of the axioms or it isn’t. It must either be true or false. It can’t be both, or it would contradict our assumption that the system doesn’t lead to contradictions.
Suppose there is a proof of S from the axioms of number theory. This implies that the code number of S is divisible by the code number of the axioms. But a provable statement is true. If we now analyse the meaning of S, this gives us the statement that the code number of S is not divisible by the axioms. A contradiction. But we are assuming that mathematics doesn’t have contradictions. Unlike my Christmas cracker paradox, there has to be a way out of this logical conundrum.
The way to resolve this is to realize that our original assumption is false: we can’t prove S is true from the axioms of number theory. But that is exactly what S states. So S is true. We have managed to prove that Gödel’s statement S is a true statement that can’t be proved true from the axioms.
The proof may remind you of the way we proved the square root of 2 was irrational. First, suppose it isn’t. This leads to a contradiction. So root 2 must be irrational after all. The proofs of both results rests on the important assumption that the axioms of number theory don’t lead to contradictions. One of the striking consequences of Gödel’s proof is that there is no way of rescuing mathematics by adding one of these unprovable statements as an axiom. You may think that if the statement S is true but unprovable, why not just make it an axiom and then maybe all true statements are provable? Gödel’s proof shows why, however many axioms you add to the system, there will always be true statements left over that can’t be proved.
Don’t worry if your head is spinning a bit from this logical dance that Gödel has taken us on. Despite having studied the theorem many times, I’m always left a bit dizzy by the end of the proof – the implications are amazing. Gödel proved mathematically that within any axiomatic framework for number theory that was free of contradictions there were true statements about numbers that could not be proved to be true within that framework – a mathematical proof that mathematics has its limitations. The intriguing thing is that it’s not that the statement S is unknowable. We’ve actually proved that it is true. It’s just that we’ve had to work outside the particular axiomatic framework for mathematics that we have demonstrated has limits. What Gödel showed is that it can’t be proved true within that framework.
Gödel used this already devastating revelation, called Gödel’s first incompleteness theorem, to kill off Hilbert’s hope of a mathematical proof that mathematics was free of contradictions. Gödel proved that ‘this statement is not provable’ is true under the hypothesis that mathematics has no contradictions. If you could prove mathematically that there were no contradictions, this could be used to give a proof within mathematics that the statement ‘this statement is not provable’ is true. But that is a contradiction because it says it can’t be proved. So any proof that mathematics is free of contradictions would inevitably lead to a contradiction. We are back to our self-referential statements again. The only way out of this was to accept that we cannot prove mathematically that mathematics is free of contradictions. This is known as Gödel’s second incompleteness theorem. Much to Hilbert’s horror, it revealed ignorabimus at the heart of mathematics.
But mathematicians believe that mathematics is free of contradictions. If there were contradictions, how could we have come this far without the edifice collapsing? We call a theory consistent if it is free of contradictions. The French mathematician André Weil summed up the devastating implications of Gödel’s work: ‘God exists since mathematics is consistent, and the Devil exists since we cannot prove it.’
Did Gödel’s revelations mean that mathematics was as open to falsification as any other scientific theory? We might have hit on the right model, but just as with a model for the universe or fundamental particles, we can’t know that it might not suddenly fall to pieces under the weight of new evidence.
For some philosophers there was something attractive about the fact that although we cannot prove Gödel’s statement S is true within the axiomatic system for number theory, we have at least proved it is true by working outside the system. It seemed to imply that the human brain was more than a mechanized computing machine for analysing the world mathematically. In a paper called ‘Minds, Machines and Gödel’, read to the Oxford Philosophical Society in 1959, philosopher John Lucas put forward the argument that if we modelled the mind as a machine following axioms and the deductive rules of arithmetic, then, as it churned away constructing proofs, at some point it would hit the sentence ‘This statement is not provable’ and would spend the rest of time trying to prove or refute it; and yet we as humans could see that it was undecidable by understanding the content of its meaning. ‘So the machine will still not be an adequate model of the mind … which can always go one better than any formal, ossified, dead system can.’
It seems a very attractive argument. Who wouldn’t want to believe that we humans are more than just a computational device, more than just an app installed on some biological hardware? In his recent research on consciousness, Roger Penrose used Lucas’s argument as a platform for his belief that we need new physics to understand what makes the mind conscious. But although it is true that we acknowledge the truth of the statement ‘this statement is not provable’ by working outside the system, it is also under a huge assumption, which is that the system we are working within to prove the truth of this Gödel sentence is itself free of contradictions. And this is the content of Gödel’s second incompleteness theorem: we can’t prove it.
The sort of statement that Gödel cooked up that is true but unprovable may seem a little esoteric from a mathematical point of view. Surely the really interesting statements about numbers – the Riemann hypothesis, Goldbach’s conjecture, the PORC conjecture – will not be unprovable? The hope that it would only be tortuous Gödelian sentences that would transcend proof turned out to be a false one. In 1977, mathematicians Jeff Paris and Leo Harrington came up with a bona fide mathematical statement about numbers that they could show was true but unprovable within the classical axiomatic set-up for number theory. But in the next chapter I will discover that, as mathematicians grappled with the idea of infinity, they discovered not only that some statements are unprovable, but also that it is impossible to tell whether they are true or false.
Having read this chapter and the Third Edge, you are now ready for one of the other jokes in my paradoxical Christmas crackers. The only other thing you need to know is that the American linguist and philosopher Noam Chomsky distinguished between linguistic competence (the linguistic knowledge possessed by a culture) and linguistic performance (the way the language is used in communication). The joke goes like this:
Heisenberg, Gödel and Chomsky walk into a bar. Heisenberg looks around the bar and says, ‘Because there are three of us and because this is a bar, it must be a joke. But the question remains, is it funny or not?’
And Gödel thinks for a moment and says, ‘Well, because we’re inside the joke, we can’t tell whether it is funny. We’d have to be outside looking at it.’
And Chomsky looks at both of them and says, ‘Of course it’s funny. You’re just telling it wrong.’