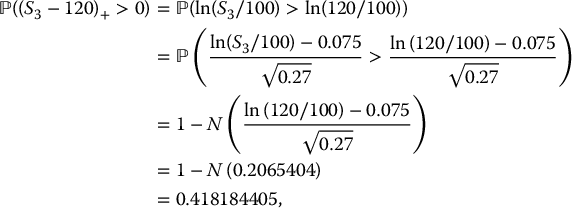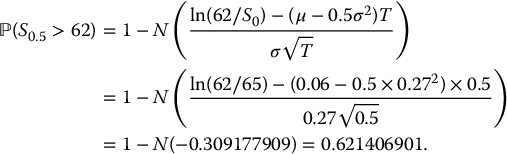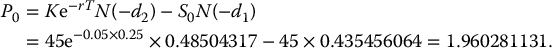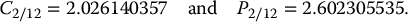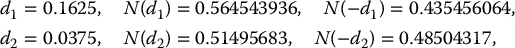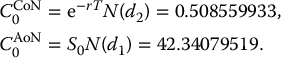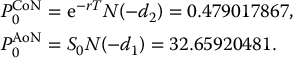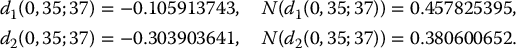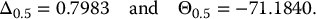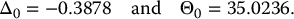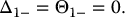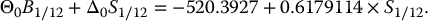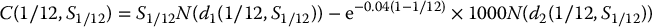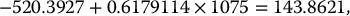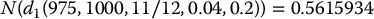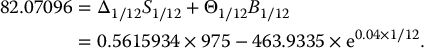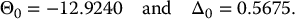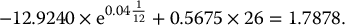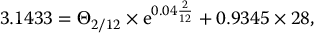16
Introduction to the Black-Scholes-Merton model
The year 1973 shall be remembered as the year of breakthroughs in the history of options and derivatives. First of all, the largest U.S. options market, the Chicago Board Options Exchange (CBOE), was created that year. Moreover, the works from Fischer Black, Myron Scholes and Robert C. Merton, gave birth to modern financial mathematics and thus largely contributed to the shape of today’s derivatives markets.
More precisely, in the paper The Pricing of Options and Corporate Liabilities, published in 1973, Black and Scholes pioneered rational option pricing by dynamically replicating the option payoff until maturity. During the same period, Robert C. Merton published Theory of Rational Option Pricing. He extended Black and Scholes’ approach in several ways, e.g. by pricing options on dividend-paying stocks and down-and-out barrier options. See [] and [].
In his paper, Merton refers to Black and Scholes’ framework as the ”Black-Scholes’ theory of option pricing” and even nowadays the model is widely known as the Black-Scholes’ model. Their work was recognized by the Royal Swedish Academy of Sciences (Nobel Prizes) in 1997.1 The model is still very popular today on the financial markets.
In this chapter, our main objective is to lay the foundations of the famous Black-Scholes-Merton market model and its pricing formula. We will provide a heuristic approach to this formula by linking as much as possible the derivations to the binomial model of Part I using a limiting argument. More specifically, the learning objectives are to:
- understand the main assumptions of the Black-Scholes-Merton model, including the dynamics of the risk-free and risky assets;
- connect the Black-Scholes-Merton model to the binomial model;
- differentiate real-world (actuarial) and risk-neutral probabilities;
- compute call and put options price with the Black-Scholes formula;
- price simple derivatives using risk-neutral probabilities;
- analyze the impact of various determinants of the call or put option price, namely the strike price, stock price, risk-free rate, volatility and time to maturity;
- derive the replicating portfolio for simple derivatives;
- apply the delta-hedging strategy over several periods to hedge simple derivatives.
16.1 Model
As in the binomial and the trinomial models, the Black-Scholes-Merton model (BSM model) is assumed to be a frictionless market composed of two assets:
- a risk-free asset (a bank account or a bond) which evolves according to the risk-free interest rate r;
- a risky asset (a stock or an index) with a known initial value and unknown future values.
Trades in this market can occur at any continuous time t ⩾ 0 and therefore the BSM framework is a continuous-time market model. We assume that time is always expressed in years (even if it is possible to do otherwise) so that parameters are written on an annual basis. We will mostly work on a time horizon [0, T] where T is very often the maturity of a derivative.
16.1.1 Risk-free asset
In the BSM model, there is an asset B = {Bt, 0 ⩽ t ⩽ T} from which investors can earn an interest rate of r. This asset is said to be risk-free because capital and interest is repaid with certainty: there is no default. Thus, r > 0 is known as the risk-free rate and it is assumed to be continuously compounded, i.e. for 0 ⩽ t ⩽ T,
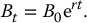
As before, we set B0 = 1. Note that, we could also have fixed BT = 1 instead of B0, in which case B would be modeling a zero-coupon bond.
16.1.2 Risky asset
In the BSM model, the price of the risky asset (often an index or a stock) S = {St, 0 ⩽ t ⩽ T} evolves according to a geometric Brownian motion
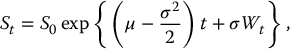
where W = {Wt, 0 ⩽ t ⩽ T} is a standard Brownian motion (with respect to the probability measure  ) and S0 is a known quantity (initial asset price).
) and S0 is a known quantity (initial asset price).
It follows from Section 14.5 that
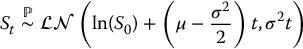
i.e. for each time 0 < t ⩽ T, the random variable St follows a lognormal distribution with parameters  and σ2t (with respect to the actuarial probability
and σ2t (with respect to the actuarial probability 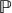 measure).
measure).
Finally, note that the BSM model can be fully specified by four parameters: S0, μ, r and σ > 0.
We can also express the model for the risky asset in terms of log-returns. On any given year, the log-return is such that
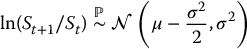
i.e. the continuously compounded annual return is normally distributed with mean 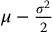 and variance σ2. As a result, σ is called the volatility of the log-return.
and variance σ2. As a result, σ is called the volatility of the log-return.
In many textbooks, μ is interpreted as the expected annual return on the asset. This is because the expected asset price in the BSM model is
However, the expected annual log-return is
To avoid any confusion with other textbooks and unless stated otherwise, we will interpret μ as the mean (annual) real rate of return on the asset.
Usual description of the BSM model
One may wonder why the BSM model is based on a geometric Brownian motion with drift 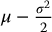 instead of μ. This is because, in the literature, the dynamics of the risky asset is usually given by the following stochastic differential equation:
instead of μ. This is because, in the literature, the dynamics of the risky asset is usually given by the following stochastic differential equation:

More details on stochastic differential equations can be found in Chapter 15. It turns out that the solution to this equation is the process defined in equation (16.1.1), which is a geometric Brownian motion with drift 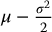 .
.
Moreover, it provides a financial interpretation to parameter μ: it is then the expected asset price is S0eμt.
Recall from the binomial tree model that in order to price derivatives with risk-neutral formulas, we had to contrast between probabilities p and q for each up-move. More formally, we had to distinguish between the real-world or actuarial probability measure  and the artificial risk-neutral probability measure
and the artificial risk-neutral probability measure  obtained as a by-product of an equation rearrangement. A similar situation will occur in the BSM model.
obtained as a by-product of an equation rearrangement. A similar situation will occur in the BSM model.
At this point, it is important to note that the notation 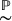 is used to emphasize that at each time t > 0, the risky asset price St really follows a lognormal distribution with parameters
is used to emphasize that at each time t > 0, the risky asset price St really follows a lognormal distribution with parameters  and σ2t. Any computations involving the likelihood that the risky asset price S reaches a given level over the next year, or that it crashes, have to be done with this real-world distribution.
and σ2t. Any computations involving the likelihood that the risky asset price S reaches a given level over the next year, or that it crashes, have to be done with this real-world distribution.
16.1.3 Derivatives
We now introduce a third asset in our market, namely a European derivative, whose value is given by the stochastic process V = {Vt, 0 ⩽ t ⩽ T}. The price of the derivative at inception is given by V0 which is a constant that will be determined later. As the value of the derivative depends upon the underlying asset S, then, for each time 0 < t ⩽ T, the value Vt is random. In particular, the derivative matures at time T, so the random variable VT represents the payoff of this derivative.
One of our main objectives is to compute the no-arbitrage price of derivatives in the BSM model, i.e. to determine Vt, for each time 0 ⩽ t < T, given a payoff VT. In other words, we will compute the initial price V0 and characterize the price Vt, at any time 0 < t < T, using no-arbitrage arguments.
This chapter will focus on simple European derivatives, i.e. derivatives whose payoff only depends on the final asset price ST:
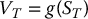
where g( · ) is a function specified in the derivative’s contract. As seen previously in this book, examples include a call option with strike price K, i.e.
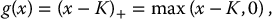
or a put option, i.e.

Exotic path-dependent options, those whose payoff depends on the risky asset price at several times preceding maturity, will be treated later in Chapter 18.
As in discrete-time models, instead of using V = {Vt, 0 ⩽ t ⩽ T}, we will use C = {Ct, 0 ⩽ t ⩽ T} and P = {Pt, 0 ⩽ t ⩽ T} for the price process of a call option and a put option respectively, in which cases we clearly have

when their common strike price is K.
Example 16.1.1 Probability of expiration in the money
A 3-year call option, with a strike price of $120, has been issued on a stock. If the initial stock price is $100 and it is assumed the stock price evolves in a BSM model with mean return of 7% and volatility of 30%, calculate the probability that the call option expires in the money.
We have K = 120 and T = 3 years, so the payoff is given by
The probability that the option expires in the money is
, which in this case is equal to
.
In this BSM model, we also have that μ = 0.07, σ = 0.3 and S0 = 100. Then,
or, equivalently,
Finally, we can write
where we used the fact that
◼
16.2 Relationship between the binomial and BSM models
In this section, we will see how closely related the BSM model is to the binomial model. In fact, the geometric Brownian motion used in the BSM model to represent the evolution of the asset price can be seen as the limit of random walks from binomial trees. Therefore, on many occasions we will be able to compare results from both models.
16.2.1 Second look at the binomial model
Suppose we have a given time horizon [0, T] in mind, with 0 being the initial time and T the end of the investment period (expressed in years). In an n-period binomial tree model, we divide this time interval [0, T] in n periods: (0, T/n), (T/n, 2T/n), …, ((n − 1)T/n, T). Then, there are n + 1 time points: 0, T/n, 2T/n, …, (n − 1)T/n, T. In Chapter 11, we put a significant amount of effort into characterizing the corresponding stock price process
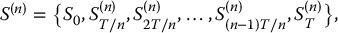
with S(n)0 = S0, as the initial price is not affected by the partition of the interval [0, T]. Here, we have added the superscript (n) to emphasize that we are in an n-period binomial tree model.
For each k = 1, 2, …, n, we can write2

where the random variable Ik keeps track of the number of upward movements in the trajectory after k periods. In other words, Ik can be viewed as the number of successes in k trials. Therefore, Ik follows a binomial distribution with parameters k and p (w.r.t. to  ), and then, for a given j = 0, 1, 2, …, k, we have
), and then, for a given j = 0, 1, 2, …, k, we have

However, note that the random variable S(n)kT/n does not follow a binomial distribution. It is a random variable whose probability mass function is linked to that of a binomial distribution, namely the distribution of Ik. Figure 16.1 illustrates an eight-period binomial tree (left panel) along with the probability mass function of the asset price at time k = 6 (right panel).

Figure 16.1 An eight-period binomial tree (left panel) along with the probability mass function of the asset price at time k = 6 (right panel)
The collection of random variables S = {S0, S(n)T/n, S(n)2T/n, …, S(n)(n − 1)T/n, S(n)T} is a discrete-time stochastic process that can also be written as

for each k = 1, 2, …, n, where Uk ∈ {u, d} (up and down factors) with probability p and 1 − p, respectively. Note that we can also write
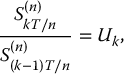
for each k = 1, 2, …, n. These last two equations describe how the asset price evolves over time.
In conclusion, the risky asset price should be viewed as a stochastic process, with each possible path in the tree being a realization of this process. Figure 16.2 illustrates four different paths taken by the asset price in a 20-period binomial tree.
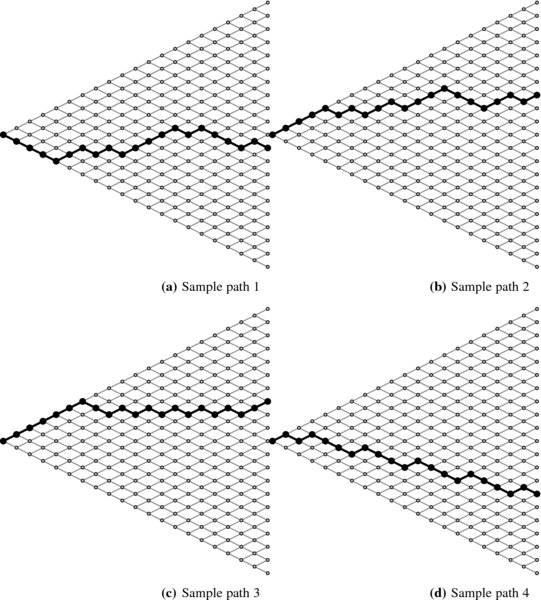
Figure 16.2 Four different sample paths of the asset price in a 20-period binomial tree
16.2.2 Convergence of the binomial model
Suppose we represent the evolution of the price of a financial index over 1 year, using a binomial model with monthly time steps. After each month, the price can take one of two possible values. Thus, after a year, there will be 13 possible values. More generally, after k months, there are k + 1 possible values for the random variable S(12)k/12, where k = 0, 1, …, 12. But what happens if we want to squeeze in additional up and down moves? In other words, what would happen if we were to have daily time steps or even hourly time steps?
Said differently, for a fixed investment horizon [0, T], we will look at what happens if the number of time steps increases, i.e. if we let n go to infinity. If we increase the number of time steps in the binomial model, the mesh of realizations will increase.
For a given investment horizon, i.e. for a fixed T, the probability distribution of the asset price S(n)kT/n, which is a discrete distribution for each n, will slowly converge to a continuous distribution, as n goes to infinity. To what distribution exactly?
Since

taking the log on both sides, we get
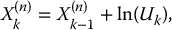
where X(n)k = ln (S(n)kT/n), for each k = 1, 2, …, n. In other words, X(n) = {X(n)k, k = 0, 1, …, n} is given by X(n)0 = ln (S0) and, for each k = 1, 2, …, n, by

The latter process is a random walk because its increments εi = ln (Ui), where i = 1, 2, …, n, are independent and identically distributed random variables taking their values in {ln (u), ln (d)}. However, it is a non-symmetric random walk.
We know from Section 14.2 that a standard Brownian motion is obtained as the continuous-time limit of symmetric random walks. Similarly, non-symmetric random walks will converge to a linear Brownian motion. Consequently, the non-symmetric random walks given by X(n) = {X(n)k, k = 0, 1, …, n} will converge to the linear Brownian motion

used in the BSM model.
Figure 16.3 illustrates how paths in the binomial model resemble paths of a geometric Brownian motion as the number of time steps increases, for a fixed time horizon [0, T].
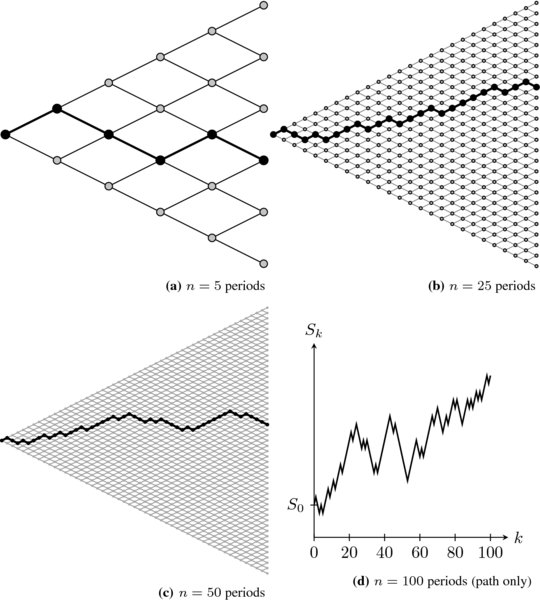
Figure 16.3 Illustration of a path in the binomial tree as the number of time steps increases. The lattice in the lower right plot was removed to highlight the path characteristics
16.2.3 Formal proof
In this section, we show how the distribution of the risky asset price in the binomial model converges to a lognormal distribution as the number of time steps increases. Let us focus on the convergence of the final price S(n)T. The same work would be necessary to prove the convergence of each S(n)kT/n, for k = 1, 2, …, n − 1.
For the convergence to go through, we need to let the up and down factors depend also on n. It would not make sense to increase the number of time steps, for a given time horizon, without adapting the size of the jumps. We did the same thing when proving that some symmetric random walks were converging to a standard Brownian motion. Therefore, the up and down factors are denoted by un and dn, emphasizing that they depend on the number of time steps.
Recall that we can write
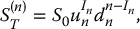
where the random variable In records the number of up moves in the full trajectory of the underlying asset’s price. As discussed above, we can further write
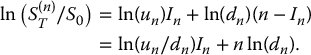
The random variable In follows a binomial distribution with parameters n and pn, i.e.  , where
, where

Hence, by the Central Limit Theorem,3 we deduce that
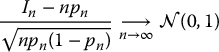
or, more precisely,

for any real numbers a < b.
On the other hand, since  , we have
, we have
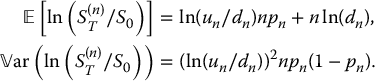
We are interested in the convergence of  , which can also be rewritten as
, which can also be rewritten as
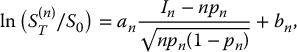
where

With the specifications of the Jarrow-Rudd tree (see Chapter 11), we have

where μ and σ are the BSM model parameters. Then it can be shown that

Consequently,

This means that, at the limit, the final asset price ST follows a lognormal distribution with parameters ln (S0) + (μ − σ2/2)T and σ2T (with respect to the real-world or actuarial probability measure  ).
).
Note that we have obtained the limiting distribution for a single random variable ST. We could repeat the above procedure for any time 0 < t ⩽ T and get

Putting all these random variables together, we get the linear Brownian motion of the BSM model, namely the stochastic process

or, equivalently, the geometric Brownian motion

16.2.4 Risk-neutral probabilities
Recall that in the binomial model, for any given simple derivative, we were able to find its replicating portfolio and then rewrite its value as an expectation using new probability weights q and 1 − q known as risk-neutral probabilities. It is important to emphasize that the risk-neutral (conditional) probability q had nothing to do with the real-world (conditional) probability p: it is only a convenient way to rewrite the value of the replicating portfolio as an expectation.
This approach tells us that whenever we need to find the no-arbitrage price of a derivative, and only then, we are allowed to use the artificial binomial distribution with parameters n and qn in order to write the option price as a discounted (with r) expectation. We should insist that qn has no other actuarial or financial meaning.
As the convergence of the binomial model to the BSM model does not depend on the specific value taken by p, we deduce that the underlying binomial distribution with parameter qn for the log asset price will also converge to a normal distribution, but with slightly different parameters. Following from equation (16.2.1), we summarize the results as follows.
The risk-neutral distributions of the random variables ln (S(n)T/S0), which depend on the (conditional) probability qn of an up-move, converge to the risk-neutral distribution of ln (ST/S0), as n tends to infinity. Therefore,

where we use the notation 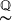 to emphasize that this is a risk-neutral distribution (rather than a real-world distribution). This is the equivalent in the BSM model of using q rather than p in the binomial model.
to emphasize that this is a risk-neutral distribution (rather than a real-world distribution). This is the equivalent in the BSM model of using q rather than p in the binomial model.
We can repeat the above procedure for any time 0 < t ⩽ T and get at the limit

or, equivalently,
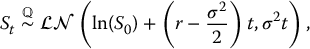
at each time 0 < t ⩽ T.
16.3 Black-Scholes formula
In the binomial model, we first approached the pricing problem with replication. This is the same approach as the one used by Black and Scholes in their pioneering article of 1973. However, now that the underlying asset price follows a geometric Brownian motion, the mathematical arguments needed to obtain option prices by replication are more complicated.5
Therefore, to find the no-arbitrage price of (simple) derivatives in the BSM model, we will take a different approach. Black and Scholes’ original derivation of the replicating portfolio will be presented in detail in Chapter 17, a chapter that requires a stronger mathematical background.
The Black-Scholes formula is a mathematical expression for the no-arbitrage price of a call (or a put) option in the BSM model. We present two methods to obtain this formula: (1) as a limit of prices obtained in binomial models, and (2) as the stop-loss transform of a well-chosen lognormally distributed random variable.
16.3.1 Limit of binomial models
As above, assume the maturity of the call option is T and split the time interval [0, T] into n sub-intervals of length T/n. We want to find the no-arbitrage price of a vanilla call option. Recall from Chapter 11 that in an n-period binomial tree, the initial price of a call option with payoff (S(n)T − K)+ can be written as a binomial sum:
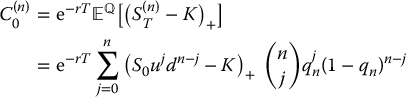
where

See equation (11.3.5) in Chapter 11. In many cases, i.e. when the realization of S(n)T is not big enough, the first terms of this summation are all equal to zero. In other words, if we define

then we can write
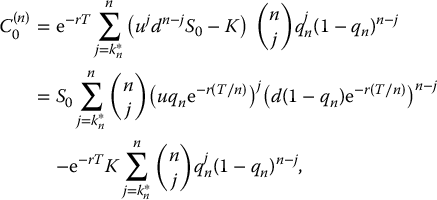
where we have distributed the term  inside the first summation.
inside the first summation.
Then, let us define the incomplete binomial summation, for integers k ⩽ m and real numbers 0 < θ < 1, by

Therefore, the call option price can be written as

where q*n = uqne− r(T/n). It is easy to show that 1 − q*n = d(1 − qn)e− r(T/n) and 0 < q*n < 1.
Intuitively, since the incomplete binomial summation Φ is a (survival) probability for binomial distributions, by the Central Limit Theorem, we expect it to converge to a similar probability for normal distributions.
Letting C0 = limn → ∞C(n)0, then
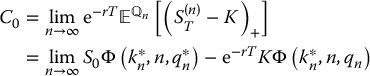
and one can show that we obtain
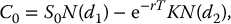
with

This is the classical Black-Scholes pricing formula for the initial price C0 of a European call option in the Black-Scholes-Merton model.
Figure 16.4 illustrates the convergence of the call option price in a Cox-Ross-Rubinstein (CRR) binomial tree as a function of the number of time steps. The plot shows an oscillatory pattern around C0 = 13.26967658, where the wave amplitude goes to 0 as n → ∞.

Figure 16.4 Convergence of a call option price in Cox-Ross-Rubinstein (CRR) binomial trees as a function of the number of time steps. The parameters are σ = 0.2, T = 1, r = 0.1 and S0 = K = 100
Example 16.3.1 Price of a call option
A share of stock currently trades for $65. The mean annual log-return on this stock is 6% and the volatility of the log-return is 27%. Calculate the Black-Scholes price of a 6-month 62-strike call option if the risk-free rate is 3%.
We have S0 = 65, K = 62, T = 0.5, σ = 0.27, r = 0.03. Then
with corresponding probabilities
Using the Black-Scholes formula in equation (16.3.1), the price of this call option is thus
◼
We shall note that μ, the mean (annual) real rate of return on the risky asset, does not appear in the Black-Scholes formula. This is because the Black-Scholes formula can be obtained as the limit of binomial prices which were obtained by first replicating the call option payoff. No matter what is the expected return on the stock, the replicating strategy will replicate the option payoff in any scenario. This parameter is irrelevant for option pricing.
Example 16.3.2 Probability of expiring in the money
Your investment bank has issued the call option of example 16.3.1. Your boss asks about the probability that the option will end up in the money at maturity.
We are thus asked to compute
where S0 = 65. Using the fact that
we have
We have to be careful here: we should not compute
, i.e. using the distribution
This risk-neutral distribution has no real-world meaning and should be used for option pricing purposes only.
◼
Using the put-call parity in equation (6.2.4) of Chapter 6, we have

Substituting the Black-Scholes formula of equation (16.3.1), we get

Since N(x) − 1 = −N( − x) for all  , we get
, we get

Reorganizing yields the desired result:

This is the classical Black-Scholes pricing formula for the initial price P0 of a European put option.
We could also define P(n)0 as the time-0 price of a put option in an n-period binomial tree and verify that

converges to

as n tends to infinity.
Example 16.3.3
In a BSM model, you are given:
- S0 = 45;
- r = 0.05;
- σ = 0.25.
Compute the price of a 3-month at-the-money put option.
We can find:
Using the Black-Scholes formula in equation (16.3.2), the price of this put option is
◼
16.3.2 Stop-loss transforms
The attentive reader will have noticed that the Black-Scholes formulas of equations (16.3.1) and (16.3.2) have a familiar look. Indeed, the call option price is related to the stop-loss transform of a lognormally distributed random variable. In equation (14.1.7) of Chapter 14, we obtained the following identity: for 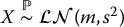 and a real number a > 0,
and a real number a > 0,

Moreover, we know from the binomial model that

converges, as n → ∞, to

In other words, the no-arbitrage price of a call option is the discounted stop-loss transform of ST using its risk-neutral distribution:

or, equivalently,

Using this lognormal random variable with its risk-neutral distribution along with the above formula for the stop-loss transform yields the Black-Scholes formula for the call option, that is

with

The same can be done for a put option; see exercise 14.1 in Chapter 14.
16.3.3 Dynamic formula
As the price of the risky asset changes over time, the prices of call and put options also change. We intend to determine how to calculate those option prices when the underlying asset price moves from S0 to St at time t.
In an n-period binomial tree, the random variable VkT/n is the no-arbitrage price after k steps of a derivative with payoff VT. To find this price, we can compute recursively the risk-neutral conditional expectation
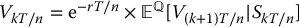
for the corresponding nodes. This is equivalent to applying equation (11.3.1), i.e. it is as if we were issuing, at time kT/n, a derivative maturing one period later with random payoff V(k + 1)T/n, given that the “initial price” of the risky asset is SkT/n. Let us emphasize once more that this risk-neutral expectation was obtained as a rewriting of the value of the replicating portfolio for this derivative. At that point, only elementary algebra was needed.
Furthermore, applying iterated expectations, we find that

We can interpret this expectation as if we were issuing, at time kT/n, a derivative maturing n − k periods later with payoff VT, given that the “initial price” of the risky asset is SkT/n. In other words, when we observe the value SkT/n after k periods, we can determine the value VkT/n by analyzing the sub-tree corresponding to the dates kT/n, (k + 1)T/n, …, T with a root corresponding to the observed value of SkT/n. Figure 16.5 illustrates a 20-period binomial tree conditional upon observing S10T/n: a 10-period binomial sub-tree is highlighted in the figure for a given root.

Figure 16.5 A highlighted sub-tree (in black) of 10 periods in a tree with 20 periods
In the BSM model, the argument is similar. Indeed, suppose now that at any time 0 ⩽ t < T, we observe that the underlying asset price is equal to St. Then, the time interval [t, T] can be split into n sub-periods and the evolution of the asset price is approximated by a binomial tree. We can determine what happens when n tends to infinity using the same arguments as in Section 16.2.2.
We deduce that, in the BSM model, given the value of St, we have the following conditional risk-neutral probability distributions
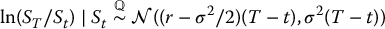
or, equivalently,

Consequently, the time-t Black-Scholes formula, where 0 ⩽ t < T, is thus

where

Note that d1(0, S0) = d1 and d2(0, S0) = d2 as used in formula (16.3.1).
Using the put-call parity relationship at time t, we deduce that the price of a put option at time t is

Example 16.3.4 Call and put prices at intermediate times
For a stock currently trading at $34, you have:
- σ = 0.32;
- μ = 0.09;
- r = 0.04.
In this BSM model, calculate the initial price of 6-month 32-strike call and put options. Determine the price of these options 2 months later, in the scenario that the stock price drops to $31.
Using S0 = 34, K = 32 and T = 0.5 in equations (16.3.1) and (16.3.2), we get
Let us now consider the following scenario. Suppose that, 2 months later, the price of the stock goes down to S2/12 = 31. Using t = 2/12 and T = 0.5 in equations (16.3.3) and (16.3.4), we get
These last two option prices are realizations of the corresponding random variables given that S2/12 = 31. If we were to consider another scenario, i.e. another value for S2/12, then the values of C2/12 and P2/12 would be different.
◼
16.4 Pricing simple derivatives
Now, we will find the price of other simple derivatives, such as forwards, binary options and gap options, i.e. those with a payoff of the form VT = g(ST).
Since, in an n-period binomial tree model, we would have

then at the limit, i.e. in the BSM model, we will have the following corresponding risk-neutral pricing formula:
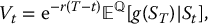
for all 0 ⩽ t ⩽ T. Therefore, to find the no-arbitrage price of a simple derivative, we will use the fact that

to compute the risk-neutral conditional expectation in equation (16.4.1).
Clearly, the Black-Scholes formulas for call and put options can be (re-)obtained using the risk-neutral formula in equation (16.4.1) with g(ST) = (ST − K)+ and g(ST) = (K − ST)+, respectively. In what follows, we will focus on forwards, binary options and gap options.
16.4.1 Forward contracts
We know from Chapter 3 that the payoff of a forward contract on a stock is g(ST) = ST − K. Applying the risk-neutral pricing formula in (16.4.1), we deduce that the value of this forward is given by
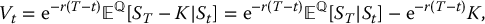
at any time 0 ⩽ t ⩽ T.
Using the fact that

together with formula (14.1.5) for the mean of a lognormal distribution, we get

In conclusion, the price process of a forward contract is given by

for every time 0 ⩽ t ⩽ T. As expected, we have recovered the model-free formula of equation (3.2.2), which was obtained with replication arguments and without any assumption on the distribution of ST.
16.4.2 Binary options
Recall from Chapter 6 that there are two classes of binary options: cash-or-nothing and asset-or-nothing binary options. Binary call options pay whenever ST ⩾ K whereas binary put options pay whenever ST < K.
More precisely, binary call options with maturity date T admit the following payoffs (up to a multiplicative constant): for a strike price K > 0, we have
- cash-or-nothing call:
 ;
; - asset-or-nothing call:
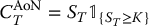 .
.
Let the stochastic process  represent the price process of a cash-or-nothing call option and
represent the price process of a cash-or-nothing call option and 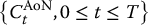 that of an asset-or-nothing call option. Note that if we buy one unit of the asset-or-nothing call and (short-)sell K units of the cash-or-nothing call, then the payoff of our position is equal to
that of an asset-or-nothing call option. Note that if we buy one unit of the asset-or-nothing call and (short-)sell K units of the cash-or-nothing call, then the payoff of our position is equal to
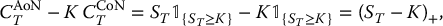
which is the payoff of a vanilla call option. By the no-arbitrage assumption, we have the same relationship regarding time-t prices, that is

for all 0 ⩽ t ⩽ T. As a consequence, it suffices to obtain an expression for  and then, together with the Black-Scholes formula in (16.3.3), we will automatically obtain an expression for
and then, together with the Black-Scholes formula in (16.3.3), we will automatically obtain an expression for 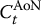 .
.
For a cash-or-nothing call, using the risk-neutral pricing formula (16.4.1), we have

for all 0 ⩽ t ⩽ T. Using the lognormal risk-neutral distribution of ST|St, as given in (16.4.2), together with the c.d.f. of the lognormal distribution as seen in Section 14.1.2, we can write
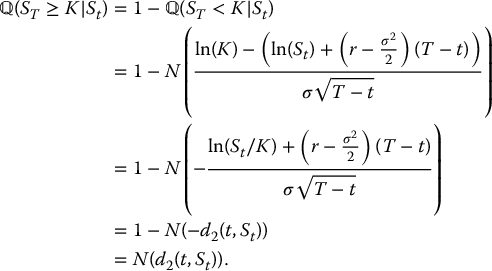
Consequently, the time-t value of this cash-or-nothing call is given by

As mentioned above, since

using the Black-Scholes formula in (16.3.3) together with the pricing formula for a cash-or-nothing call in (16.4.3), we get the following pricing formula for an asset-or-nothing call: for all 0 ⩽ t ⩽ T,

Example 16.4.1 Price of binary call options
In the BSM model, you are given:
- S0 = K = 75;
- r = 0.05;
- σ = 0.25.
Calculate the initial price of 3-month binary call options.
Since we have
then, using the pricing formulas in (16.4.3) and in (16.4.4), we get
◼
Recall that binary put options with maturity date T and strike price K admit the following payoffs:
- cash-or-nothing put:
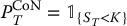 ;
; - asset-or-nothing put:
 .
.
Using parity relationships, it is easy to obtain expressions for the time-t prices of these options (see exercise 16.5). More precisely, for each 0 ⩽ t ⩽ T, we will obtain
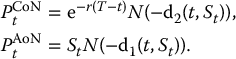
Example 16.4.2 Price of binary put options
In the same BSM model as the previous example, calculate the initial price of 3-month binary put options.
Using the above formulas, we obtain
◼
16.4.3 Gap options
Recall from Chapter 6 that gap call and put options are options to buy or sell an asset for a strike price of K only if the underlying asset price at maturity is greater or less than a trigger price H.
First, a gap call option has a payoff given by

We know this payoff can be decomposed as a long position in one unit of an asset-or-nothing call with strike price H and a short position in K units of a cash-or-nothing call with strike price H. Mathematically,

Therefore, by linearity, and using the pricing formulas in (16.4.4) and in (16.4.3) for the time-t prices of binary call options, we get
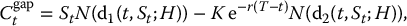
where
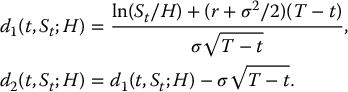
This formula is very similar to the Black-Scholes formula for a vanilla call option as given in (16.3.3). In fact, when K = H, they are equal.
Example 16.4.3 Price of a gap call option
A share of stock currently trades for $35 and the volatility of the log-returns on this stock is 28%. If the risk-free rate is 3%, calculate the initial Black-Scholes price of a 6-month gap call option with strike price $35 and trigger price $37.
We have σ = 0.28, r = 0.03, T = 0.5, S0 = K = 35 and H = 37. If we compute d1(0, S0; H) and d2(0, S0; H) with these quantities, then we get
Therefore, the initial price of this gap call option is
◼
Second, a gap put option has a payoff given by:

In other words, it corresponds to a long position in K units of a cash-or-nothing put with strike price H and a short position in one unit of a cash-or-nothing put with strike price H.
Using this parity relationship together with the formulas for binary put options, the price at time t of a gap put option is

Again, this pricing formula is very similar to the Black-Scholes formula for a vanilla put option as given in (16.3.4) and the two formulas coincide when K = H.
16.5 Determinants of call and put prices
To compute the Black-Scholes formulas for call and put options, we needed to know in advance the model parameters r and σ and the asset-related quantities K, S0 and T. They are the main determinants of call and put option prices and, as such, they are inputs for the Black-Scholes formulas. If the value of one of these quantities changes, then the option price also changes accordingly. In this section, we analyze how such changes affect the value of call and put options in the Black-Scholes-Merton model.
First, recall the Black-Scholes formulas for call and put options, as given in (16.3.1) and (16.3.2) respectively:

where

Note that the notation has been slightly modified to emphasize the dependence on the quantities and parameters of interest. In fact, both C0 and P0 are functions of (S0, K, T; r, σ).
We would like to determine whether C0 increases or decreases if, for example, the value of r increases. If we consider the Black-Scholes formula as a function of r only, keeping all other quantities constant, then differentiating with respect to r will provide an answer to our question. Mathematically, we will compute the partial derivative ∂C0/∂r of the option price with respect to r and determine whether it is positive or negative.
The behavior of each determinant is plotted in Figure 16.6. In words, we computed the Black-Scholes formulas for the call and the put keeping all but one parameter constant.
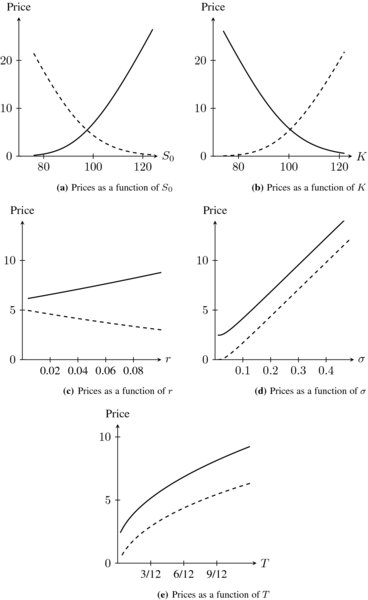
Figure 16.6 Black-Scholes formulas (solid line: call, dashed line: put) as functions of S0, K, r, σ and T. Otherwise, the values are S0 = 100, K = 98, r = 0.03, σ = 0.2 and T = 0.5
16.5.1 Stock price
From a financial point of view, we expect the value of a call option to increase if S0 increases. Indeed, for a fixed strike price K, a greater stock price S0 increases the intrinsic value of the call, which in turn increases the price. It should be the opposite for a put option.
Let us verify this mathematically. We can show that6

and then, using the put-call parity P0 = C0 − S0 + e− rTK, it is easy to deduce that

Since the standard normal c.d.f. N( · ) is a probability, its value lies between 0 and 1 and then we get

and
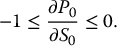
As anticipated, the call option value increases with the initial stock price because 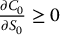 , i.e. C0 is a non-decreasing function of S0. Similarly, the put option value decreases with the initial stock price because
, i.e. C0 is a non-decreasing function of S0. Similarly, the put option value decreases with the initial stock price because  .
.
16.5.2 Strike price
Because it is the price at which we buy or sell the underlying asset at maturity, the strike price K has the opposite effect, compared with the initial stock price, on the up-front premium. Indeed, if K1 ⩽ K2, then

in all possible scenarios, i.e. for any value of the random variable ST. By the usual no-arbitrage arguments, it is easy to verify that this also holds true at any time t prior to maturity.
In conclusion, if we increase the strike price, then we reduce the initial value of the call option and increase that of the put option. Note that we did not use the Black-Scholes formulas, so this conclusion is model-free: it holds in any market model.
16.5.3 Risk-free rate
From a financial perspective, if a long call option ends up in the money at maturity, the holder will pay K (and she will receive a share of the stock). An increase in the risk-free interest rate reduces the present value of K and therefore increases the value of this call option. For a long put option, it is the opposite.
We can verify that
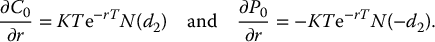
In both cases, as we are multiplying positive quantities, we can further deduce that

In words, an increase in the risk-free rate increases the value of the call and decreases the value of the put.
16.5.4 Volatility
Volatility in general is a measure of the range of outcomes of a random variable. Higher volatility means there is a wider spectrum of scenarios in which call and put options can end up in the money. Therefore, more volatility increases the values of call and put options.
We can also compute the partial derivatives of C0 and P0 with respect to σ to get:

where φ(x) is the p.d.f. of the standard normal distribution. As the partial derivatives are positive, it confirms that increasing the volatility increases both the call and put option prices.
16.5.5 Time to maturity
We want to determine how the time to maturity T affects an option price. Intuitively, the time to maturity impacts at least two elements:
- A longer time to maturity increases the range of outcomes of asset prices. Indeed, it is intuitive to think that the distribution of stock prices after 1 year will be wider than the possible stock prices after 1 month.
- A longer time to maturity decreases the present value of future cash flows. Indeed, one dollar paid in a year is worth less than one dollar paid in a month, or K paid in a year is better than K paid tomorrow.
In the case of call options, those effects add up, thus increasing the call option price. As for the put option, the effects go in opposite directions.
Differentiating C0 with respect to T and then using the put-call parity, we get
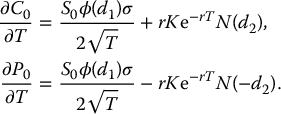
Since ∂C0/∂T is the sum of two positive quantities, we can conclude that the call value increases with T. In other words, a greater time to maturity increases the call option price. For a put option, we cannot make such a definitive conclusion. However, Figure 16.6 suggests that it is also increasing.
16.6 Replication and hedging
In the binomial model, we derived a recursive algorithm to replicate the payoff of any simple derivative. As a consequence, the binomial tree model is a complete market model, meaning that every derivative admits a replicating portfolio (see Chapter 13). By no-arbitrage arguments, the cost of a replicating portfolio has to correspond to the price of the derivative it replicates. Replication is also known as perfect hedging because, at any time during the life of the option, the replicating portfolio and the derivative have the same value.
In the BSM model, now that the asset price follows a geometric Brownian motion, we cannot find an expression for the no-arbitrage price of a derivative using only replication (unless we use Black and Scholes’ original approach through stochastic calculus and partial differential equations). Therefore, in this section, we will discuss replication of a given derivative assuming we already know its no-arbitrage price as studied in Sections 16.3 and 16.4.
In a continuous-time model such as the BSM model, replication of a derivative might require to trade/rebalance continuously. Of course, this is impossible in practice; we will come back to this issue later in the book.
16.6.1 Trading strategies/portfolios
In a continuous-time setup, a trading strategy (or portfolio) on the investment horizon [0, T] is a pair of stochastic processes
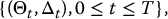
where
- Θt is the number of units of the risk-free asset B held in the portfolio at time t;
- Δt is the number of units of the risky asset S held in the portfolio at time t.
As in the discrete-time setup, (Θt, Δt) can be chosen with specific investment goals in mind. For the rest of this chapter, it will be for replication purposes.
For a given trading strategy {(Θt, Δt), 0 ⩽ t ⩽ T}, its value at time t is given by Πt where

This clearly depends on the risky asset price St and on the (possibly) random number of units Δt and Θt. Therefore, Π = {Πt, 0 ⩽ t ⩽ T} is a stochastic process and it is called the portfolio value process.
In discrete-time financial models, we encountered several times the notion of a self-financing strategy and found many equivalent definitions:
- a strategy that does not involve deposits/withdrawals between inception and maturity;
- the portfolio value resulting from such a strategy is the same before and after rebalancing;
- the variation in the portfolio value comes only from variations in the risky asset and risk-free asset prices.
In a continuous-time model, a self-financing strategy can be defined heuristically as a pair (Θt, Δt) such that
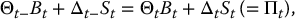
for all t ⩾ 0, i.e. the value of the strategy is the same just before rebalancing (t − ) and just after rebalancing (t). A rigorous definition of a self-financing strategy requires knowledge of stochastic calculus. The interested reader is referred to Section 17.1 for more details.
We seek to replicate the payoff of simple derivatives using a dynamically updated strategy {(Θt, Δt), 0 ⩽ t ⩽ T}. A strategy {(Θt, Δt), 0 ⩽ t ⩽ T} is said to be a replicating strategy for the payoff VT if:
- it is self-financing;
- their final values coincide, meaning that ΠT = VT in each possible scenario.
Since a replicating strategy is self-financing (by definition), which means it generates no cash flows except at time 0 and time T (just like the derivative it replicates), then by the no-arbitrage assumption we can conclude that the corresponding portfolio value process Π mimics the derivative price at each time point t and in each possible scenario. In other words, if {(Θt, Δt), 0 ⩽ t ⩽ T} is a replicating strategy for VT, then we have

for all 0 ⩽ t ⩽ T. In particular, the initial values are equal: V0 = Π0 = Δ0S0 + Θ0B0. In conclusion, the price of the derivative coincides with the value or cost of the replicating portfolio.
In a general continuous-time model, it is not clear whether each payoff admits a replicating portfolio or not. However, as the Black-Scholes-Merton model can be obtained as the limit of binomial trees, it is also a complete market model, i.e. all derivatives can be replicated.
16.6.2 Replication for call and put options
If we want to find the replicating portfolio of a call option, then we must find a self-financing portfolio {(Θt, Δt), 0 ⩽ t ⩽ T} such that

in each possible scenario, at any time 0 ⩽ t ⩽ T.
The Black-Scholes formula is famous for many reasons, one of them being that it yields an explicit representation of the replicating portfolio within the expression for Ct. Indeed, since we have

then, by identification, we directly obtain that

are the number of units of each asset needed to replicate a call option.7
Said differently, at any given time t, in order to replicate the value of the call, we must be
- long N(d1(t, St)) units of S;
- short
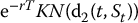 units of B.
units of B.
From the properties of the normal c.d.f., we further deduce that 0 ⩽ Δt ⩽ 1 and thus we should be holding a fraction of the underlying asset to replicate the call option. This is similar to what we obtained in the binomial tree model. Moreover, as the call option gets further into the money (or out of the money), then d1(t, St) increases (or decreases) so that Δt approaches 1 (or 0).
This replicating portfolio for a call option, i.e.
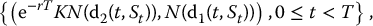
requires to be able to trade continuously. Indeed, the number of units Δt = N(d1(t, St)) and  change continuously with t and St, because d1(t, St) and d2(t, St) change continuously with t and St. In fact, they are never constant for any time interval. Thus, at every instant, the replicating portfolio must be rebalanced to keep matching the call option price.
change continuously with t and St, because d1(t, St) and d2(t, St) change continuously with t and St. In fact, they are never constant for any time interval. Thus, at every instant, the replicating portfolio must be rebalanced to keep matching the call option price.
Example 16.6.1 Replicating portfolio for a call option
Assume a stock, currently trading for $100, behaves according to a geometric Brownian motion with mean return of 6% and volatility of 30%. If the risk-free rate is 3%, find the replicating strategy of a 1-year at-the-money call option:
- at inception;
- after 6 months, in the scenario where S0.5 = 115;
- and just before maturity, in the scenario where S1 − = 107.
At inception, we have d1 = 0.25, d2 = −0.05 and thus, N(d1) = 0.598706326 and N(d2) = 0.480061194. Therefore, the Black-Scholes formula in equation (16.3.1) tells us that this call option price is 13.2833084. The corresponding replicating strategy is given by
at inception. This position is valid at time 0 only and will change immediately after.
In the chosen scenario, the stock price is S0.5 = 115 after 6 months. Then we can compute d1(0.5, 115) and d2(0.5, 115), and find that
Again, this replicating portfolio is only valid at time t = 0.5 (after 6 months) and in this scenario. Note that they will change immediately after.
Moreover, it is interesting to realize that in this scenario, we have Δ0 = 0.5987 < 0.7983 = Δ0.5. This is because the call option is no longer at the money at time 0.5 in this scenario; it is then in the money because we have S0 = K = 100 < 115 = S0.5.
Suppose now that at (or one millisecond prior to) maturity, the stock price is equal to 107. We know that the payoff of the option will be 107 − 100 = 7. Then, the replicating portfolio must have a balance of $7.
To compute the positions slightly prior to maturity, we must look at the behavior of d1 and d2 when t → T. Because S1 > K, then d1 → ∞ and d2 → ∞ when t → T. In this scenario, we get
and the replicating portfolio value just before maturity is
as expected.
◼
Given that the time-t Black-Scholes formula for a put is given by

then again by identification, we get that

are the number of units required in each asset to replicate a put option. In this case, at any given time t, in order to replicate the price of the put, we must be
- short N( − d1(t, St)) units of S;
- long
 units of B.
units of B.
As for the replicating portfolio of a call option, the replicating strategy for a put option requires continuous rebalancing.
Again, from the properties of the normal c.d.f., we deduce that − 1 ⩽ Δt ⩽ 0 and thus we should be selling a fraction of the underlying asset to replicate the put option. Moreover, as the put option gets further into the money (or out of the money), then d1(t, St) decreases (or increases) so that Δt approaches − 1 (or 0).
Example 16.6.2 Replicating portfolio for a put option
Consider a BSM model such that
- S0 = 75;
- σ = 0.25;
- r = 0.04.
A 1-year at-the-money put option is issued. Find the replicating strategy for this put option:
- at inception;
- after 6 months, in the scenario where S0.5 = 72;
- and just before maturity, in the scenario where S1 − = 77.
At inception, using the Black-Scholes formula, we have that the put option price is equal to 5.93699. The corresponding replicating portfolio is
Again, this position is valid at time 0 only and will change immediately after.
In the chosen scenario, 6 months later, the stock price has gone down and the put option is then in the money. Using the formulas in (16.6.3) at time t = 0.5 and in the scenario where S0.5 = 72, we get
As the put option gets more into the money, we must short more stocks: from 0.3878 unit to 0.5117 unit.
Finally, just before maturity, the stock price is worth $77. In this scenario, it is clear the put option expires unexercised as
Therefore, as t gets closer to T = 1, the values of d1 and d2 get closer to ∞, which means that
So, the put option price just before maturity is also equal to zero and in this scenario the option expires out of the money.
◼
16.6.3 Replication for simple derivatives
We now focus on how to replicate simple derivatives, not just call and put options. Unfortunately, finding the replicating portfolio of general simple options will not be as easy as for calls and puts. To help us with this matter, we will relate once more with the binomial model.
Procedure
First of all, let us consider a simple option with payoff VT = g(ST). We know from Section 16.4 that, for all 0 ⩽ t < T, the time-t value of this option is given by Vt = F(t, St), where
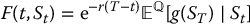
with
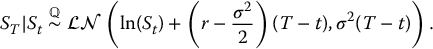
For call and put options, we will now use the notation Ct = C(t, St) and Pt = P(t, St) where

Second, we know from equation (11.2.5) in Chapter 11 that for a derivative with payoff VT,
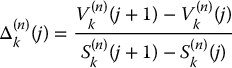
is the number of units of the risky asset that an investor should hold, at time step k and in node j, in order to replicate the derivative value. This formula is very specific to the binomial model because it involves discrete time steps. However, it tells us that the delta of a derivative is the ratio of the variation in the derivative value over the variation in the underlying asset value.
Therefore, we can expect that for a very small quantity ϵ, the delta of a simple derivative will be such that

If we take the limit when ϵ → 0, formally we will obtain the partial derivative of F with respect to its second variable:

Here, the notation ∂F/∂S simply means taking the first-order partial derivative of the deterministic function F with respect to its second variable.8
The formula for Δt given in equation (16.6.4) is known as the delta of the option (see also Chapter 20). It is the number of units of the risky asset S to hold at time t in the replicating portfolio in order to match the value of the simple option with payoff VT = g(ST).
Now that we have the option price Vt and the delta Δt at any time t, we can completely specify the replicating portfolio. Indeed, since we want the replicating portfolio to be such that

then we must have

This is the number of units of the risk-free asset B to hold at time t in the replicating portfolio in order to match the value of the simple option. In conclusion, we now have fully described the replicating portfolio9 for a simple derivative with payoff VT = g(ST).
To summarize, the replicating procedure for a simple derivative with payoff VT = g(ST) is as follows:
- Identify the function of two variables F( ·, ·) such that
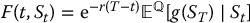 .
. - Compute ∂F/∂S, i.e. the first-order partial derivative of F( ·, ·) with respect to its second variable.
- Set
 .
. - Set
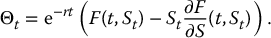
It is important to emphasize that depending on the derivative, this replicating portfolio might need to be continuously rebalanced (or not).
Forward
A forward contract can be considered as a simple derivative with payoff of g(ST) = ST − K. The first step is to identify the function of two variables F( ·, ·) such that 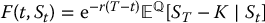 . We have already found that
. We have already found that
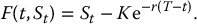
Then, the partial derivative ∂F/∂S with respect to its second variable is constant and equal to 1, i.e.

Consequently,

In other words, the replicating portfolio of a forward contract should always be long one unit of the risky asset, at any time t and in any scenario.
Finally,

for all 0 ⩽ t < T. Since B0 = 1, then at time 0 we should borrow the present value of K (by investing in the risk-free asset) and hold on to this position.
Note that both expressions for Δt and Θt are constant, i.e. they do not depend on the value of t nor of St. In other words, the replicating strategy of a forward contract is a static replicating strategy. Such trading strategies are also called buy-and-hold strategies because no rebalancing is needed. This is consistent with the model-free results obtained in Chapter 3.
Call option
A call option is a simple derivative with payoff g(ST) = (ST − K)+. The Black-Scholes formula for a call option gives us
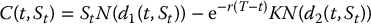
with

Following from Section 16.5.1, we directly get

as obtained in equation (16.6.2).
Finally,

as obtained in equation (16.6.2).
16.6.4 Delta-hedging strategy
The above procedure tells us how to perfectly hedge, i.e. how to replicate, a simple payoff in the BSM model. However, for many derivatives, replication requires continuous rebalancing to maintain the corresponding replicating portfolio, which is obviously impossible in practice. When trading can only occur discretely, i.e. daily, weekly or monthly, then attempting to replicate a payoff will inevitably yield errors for most derivatives. This is the case for vanilla call and put options. Few derivatives can be replicated using a static strategy, as for forward contracts, or a discretely rebalanced trading strategy.
Whenever the objective is to manage as much as possible the risk of a derivative, taking into account the practical constraints of trading, we say we are hedging (rather than replicating) the derivative. We will come back to hedging in Chapter 20.
The discrepancy between the price of the derivative and the value of its hedging portfolio is known as the hedging error. This is illustrated in the following example.
Example 16.6.3 Hedging error over a month
An investment bank sells an at-the-money call option with maturity T = 1 year and exercise price K = $1000. Using a Black-Scholes-Merton model with volatility σ = 0.2 and risk-free rate r = 0.04 for the evolution of the underlying stock price, let us implement a monthly rebalanced hedging strategy for this call option by discretizing the Black-Scholes replicating strategy of equation (16.6.2). Let us also compute the hedging error made over 1 month in each of the following two scenarios:
- if S1/12 = $975;
- if S1/12 = $1075.
Note that S0 = $1000. At time 0, let us compute the number of units as given in (16.6.2). In this case, since
we have
In other words, at time 0, we buy 0.6179114 shares of the underlying stock and short-sell 518.6609 units of the risk-free asset (this also means that we borrow $518.6609 at time 0). Using the Black-Scholes formula, we see that C0 = 99.2505, which coincides with the initial value of this hedging portfolio:
Now, no matter what the value of S1/12 will be, 1 month later our loan will be worth 518.6609 × e0.04/12 = 520.3927. Since no trading is allowed between time 0 and time 1/12, we should not expect the portfolio and the option to have the same value at time t = 1/12 (1 month later). On one side, the portfolio will be worth
On the other side, using the Black-Scholes formula in (16.3.3), we know that the option will be worth
where
Now, if we consider the scenario where S1/12 = 975, then our position in the risky asset would be worth 0.6179114 × 975 = 602.4636, the portfolio value would be
while the option price would be C(1/12, 975) = 79.57933. In this specific scenario, the bank would be lucky: the hedging error will be negative, i.e. there will be an overflow of 82.07096 − 79.57933 = $2.49. The hedging portfolio is worth more than the call option on the market.
In the other scenario, that is if S1/12 = 1075, the portfolio value would be
while the option price would be C(1/12, 1020) = 145.4774. In this case, the hedging portfolio would be worth less than the option price, for an hedging error (loss) of $1.62.
◼
As in the previous example, we will call delta-hedging strategy the trading strategy obtained by discretizing the Black-Scholes replicating portfolio, i.e. whose positions are based upon the procedure of Section 16.6.3. It acknowledges the fact that, in practice, trading can only occur discretely.
The delta-hedging strategy for a call option is defined as follows. Assume that the portfolio can be rebalanced only at the (equidistant) time points t0, t1, t2, …, tn − 1 such that 0 = t0 < t1 < t2 < … < tn − 1 < T. Even if prices {St} and {Bt} are still following the continuous-time Black-Scholes-Merton dynamics, we want to set up a piecewise buy-and-hold trading portfolio. At each of these trading dates ti, we will observe the realization of 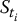 and then choose
and then choose  such that:
such that:
- buy/sell
 units of the risky asset S;
units of the risky asset S; - invest the remaining portfolio balance in the risk-free asset.
In other words, at the beginning of the (i + 1)-th period we must make sure to hold  units of the risky asset. Then, the hedging portfolio’s remaining balance is invested at the risk-free rate.
units of the risky asset. Then, the hedging portfolio’s remaining balance is invested at the risk-free rate.
For each ti, we hold on to the quantities  from time ti (beginning of period) up to time ti + 1 (end of period), and repeat for i = 0, 1, 2, … until ti + 1 = T. Mathematically,
from time ti (beginning of period) up to time ti + 1 (end of period), and repeat for i = 0, 1, 2, … until ti + 1 = T. Mathematically,
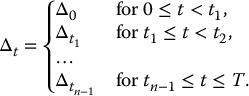
Consequently, the corresponding portfolio value process evolves continuously and is given by
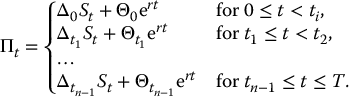
This is indeed a discretization of the Black-Scholes replicating strategy. To delta-hedge any other simple derivative, we only need to replace  by the corresponding
by the corresponding  , as given in (16.6.4).
, as given in (16.6.4).
In this case, the portfolio is self-financing by construction: no funds are injected or withdrawn from the portfolio at any of the trading dates. More precisely, at each of these trading dates ti, we will observe the realization of  and then we will choose
and then we will choose  such that
such that

Since we want  , it implies that
, it implies that

or, equivalently,

for each i = 0, 1, …, n − 1.
The value of the portfolio and the derivative it is tracking are only compared at maturity. In a self-financing hedging portfolio, hedging errors are rolled over until maturity. This is illustrated in the following examples.
Example 16.6.4 Rebalancing a delta-hedging portfolio
Let us come back to example 16.6.3 and see how to rebalance the portfolio after 1 month in the scenario where S1/12 = 975.
We saw, in the previous example, that in this scenario the value of the portfolio after 1 month (before rebalancing) is $82.07096, split into a loan of $520.3927 and 0.6179114 units of the risky asset. This is the amount available for investing over the next month. Recall that this is more than the option price. However, since we are implementing a delta-hedging strategy, we do not withdraw this excess from the portfolio.
Given that the asset price went down to 975, we should trade to make sure we now own
units of the underlying asset. In this scenario, this means selling 0.6179114 − 0.5615934 = 0.056318 unit of this asset for a net income of 0.056318 × $975 = $54.91005.
This amount is then used to partially reimburse the loan: we should now have a short position in the risk-free asset worth 520.3927 − 54.91005 = $465.4826. Since this risk-free asset is now worth
we should be short 465.4826/1.003339 = 463.9335 units.
In conclusion, after rebalancing we have:
We can verify that the portfolio value before and after rebalancing is the same:
◼
It is important to remember that for most derivatives, a delta-hedging strategy is not a replicating strategy: hedging errors will occur. These errors are solely due to discretization because we cannot trade continuously. However, in principle, if we rebalance the portfolio more often, the hedging errors should decrease. We will come back to this issue in Chapter 20.
Example 16.6.5 Delta-hedging until maturity
A 4-month at-the-money European call option is issued. You are using a BSM model with parameters μ = 0.07, r = 0.04 and σ = 0.2. The underlying asset price is S0 = 25 and the call option price is given by the Black-Scholes formula. Calculate the profit or loss resulting from delta-hedging this option monthly until maturity in the following scenario:
At inception
We first need to find the option price at inception. Using the Black-Scholes formula with a maturity of T = 4/12, we get d1 = 0.17 (rounded to two decimals), N(d1) = 0.5675 and thus C0 = 1.2635.
Consequently, over the time interval
, we must hold 0.5675 share of stock for a total value of 25 × 0.5675 = 14.1875. But since we received only $1.2635 from selling the call option, we will borrow the difference, i.e. 14.1875 − 1.2635 = 12.9240 (recall that B0 = 1). The delta-hedging portfolio over the time interval
is
After 1 month
In our scenario, after a month, the stock price will increase to S1/12 = $26 and hence the portfolio value (before rebalancing) will be
Now, we should hold N(d1(1/12, 26)) = 0.7054 share of stocks over the time interval
. After rebalancing, the portfolio value must still be worth 1.7878 since it must be self-financing. Therefore, solving for Θ1/12 in
we find that
in this scenario.
After 2 months
After 2 months, the stock price in this scenario is now $28 and hence the portfolio value (before rebalancing) is
Now, we should hold N(d1(2/12, S2/12)) = 0.9345 share of stocks over the time interval
. After rebalancing, since the portfolio value must still be 3.1433 (self-financing condition), solving for Θ2/12 in
we get
At maturity
Repeating the procedure at times 3/12 and 4/12, we get that the delta-hedging portfolio is worth 3.9004 at the option maturity whereas the payoff is 29 − 25 = 4. In this scenario, there is a hedging error (loss) of 0.1.
The following table summarizes the computations:
t T − t St Bt 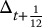
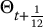
Πt 0 4/12 25 1.0000 0.5675 −12.9240 1.2635 1/12 3/12 26 1.0033 0.7054 −16.4975 1.7878 2/12 2/12 28 1.0067 0.9345 −22.8697 3.1434 3/12 1/12 27 1.0101 0.9222 −22.5409 2.1320 4/12 0 29 1.0134 3.9004 ◼
16.7 Summary
Model
- Risk-free asset price: Bt = B0ert with B0 = 1.
- Risky asset price:
- – it can be obtained as the continuous-time limit of the risky asset price in a binomial tree model;
- – it is a geometric Brownian motion:

- – its time-t value is lognormally distributed (w.r.t. the real-world or actuarial probability
 ):
):

- – the corresponding risk-neutral distribution is also lognormal (w.r.t. the risk-neutral probability
 ):
):
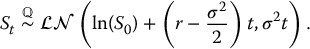
Black-Scholes formula
- Derivation: it can be obtained as the continuous-time limit of the corresponding pricing formula in a binomial tree model or as the stop-loss transform of a lognormally distributed random variable.
- Call option: Ct = StN(d1(t, St)) − e− r(T − t)KN(d2(t, St)) with

- Put option:
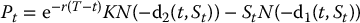 .
.
Pricing simple derivatives
- Payoff: VT = g(ST).
- Risk-neutral pricing formula:
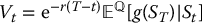 , where
, where

- Binary call options:
- – asset-or-nothing:
 ;
; - – cash-or-nothing:
 .
.
- – asset-or-nothing:
- Binary put options:
- – asset-or-nothing:
 ;
; - – cash-or-nothing:
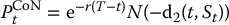 .
.
- – asset-or-nothing:
-
Gap call option:
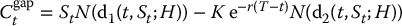 , where
, where

-
Gap put option:
 .
.
Determinants of call and put prices
- Option price increases (+) or decreases (−) when this quantity increases:
- – stock price S0: call (+), put (−);
- – strike price K: call (−), put (+);
- – risk-free rate r: call (+), put (−);
- – volatility σ: call (+), put (+);
- – time to maturity T: call (+), put (cannot be determined).
Replication and hedging
- Portfolio: a pair (Θ, Δ), where Θ = {Θt, 0 ⩽ t ⩽ T} and Δ = {Δt, 0 ⩽ t ⩽ T} are such that:
- – number of units of B held at time t: Θt;
- – number of units of S held at time t: Δt.
-
Portfolio value process: Π = {Πt, 0 ⩽ t ⩽ T}, where

- Self-financing condition: Θt −Bt + Δt −St = ΘtBt + ΔtSt.
- Replicating strategy: self-financing and such that ΠT = VT.
- Replication of a call option:
- – long N(d1(t, St)) units of S;
- – short
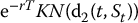 units of B.
units of B.
- Replication of a put option:
- short N( − d1(t, St)) units of S;
- long
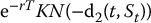 units of B.
units of B.
- Replication procedure for an option with payoff VT = g(ST):
- identify F such that
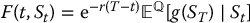 ;
; - compute ∂F/∂S;
- set
 ;
; - set
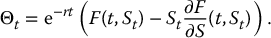
- identify F such that
- In practice, replication cannot be implemented as most replicating portfolios must be continuously rebalanced.
- Hedging strategy: portfolio set up to manage partially the risks of a given derivative.
- Hedging error: discrepancy between the price of the derivative and the value of the hedging portfolio.
- Delta-hedging strategy: discretization of the Black-Scholes replicating strategy.
16.8 Exercises
In the following problems, assume the market is a Black-Scholes-Merton model.
-
Consider a Black-Scholes-Merton model with μ = 0.07, r = 0.04, σ = 0.25 and S0 = 100.
- What is the probability that the stock price will be greater than $120 after 2 years?
- A call option with strike price $110 and a maturity of 2 years is available. What is the probability that this option will mature in the money?
-
For each of the next payoffs, find the initial price and determine the replicating strategy.
- VT = K;
- VT = ST;
 ;
; .
.
For each strategy, determine whether it is static or dynamic.
-
A derivative is introduced whose payoff is $5 whenever the stock price is below 100 or above 115. Otherwise, it pays nothing.
- Express the payoff of this derivative as a function of ST.
- Write the payoff as a combination of binary option payoffs.
- Compute the initial price of this derivative if μ = 0.12, r = 0.04, σ = 0.27, T = 1 and S0 = 100.
- Using the parameters given in (c), what is the probability that the derivative will mature out of the money?
-
A share of stock currently trades for $35 and the volatility of the log-return of this stock is 28%. If the risk-free rate is 3%, calculate the initial Black-Scholes price of a 6-month gap put option with strike $35 and trigger price $34.
-
Using parity relationships between standard and binary options:
- Verify that the price of a cash-or-nothing put option is
 .
. - Verify that the price of an asset-or-nothing put option is
 .
.
- Verify that the price of a cash-or-nothing put option is
-
Find the price and the replicating portfolio of the following payoff:

where n ⩾ 1 is a given integer.
-
Explain briefly (and intuitively) what happens to Δ0 of a call option when S0 is very big/small.
-
You signed an agreement such that you owe 100 if the stock price of ABC inc. ends up above $45 4 months later and 0 otherwise. Note that the current stock price is $50. Assume r = 0.03 and σ = 0.18. You intend to replicate that liability with a portfolio made of shares of ABC inc. and the risk-free asset.
- At time 0, what is the delta-hedging portfolio for this agreement?
- In the scenario that, a month later, the stock price is up to $52, determine the delta-hedging portfolio such that the portfolio remains self-financing.
- In the scenario that, 1 month prior to maturity, the stock price is down to $48, determine the delta-hedging portfolio such that the portfolio remains self-financing.
- In the scenario that, at maturity, the stock price is $47, calculate the hedging error of your preceding strategy.
- Suppose that you approach maturity and the current stock price is close to $45. What happens to Δt whenever the stock price moves a little?
-
Find the initial price of a derivative having payoff:
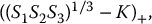
where the maturity is T = 3.
-
Using the chain rule of calculus, verify that, for a call option,
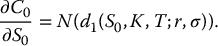
-
A chooser option gives its holder the choice, at time T, between entering a call or a put option (both maturing later). It has the following payoff
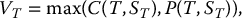
where the call and the put options have a common maturity T⋆ > T, have the same strike price and are both written on the same underlying asset.
- Verify that the chooser option payoff can be rewritten as follows:

- Compute the initial price of this chooser option.
- Verify that the chooser option payoff can be rewritten as follows: