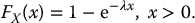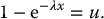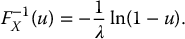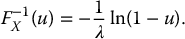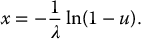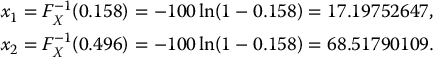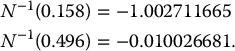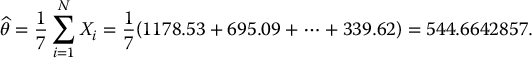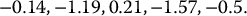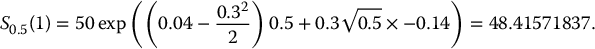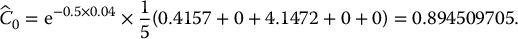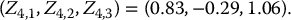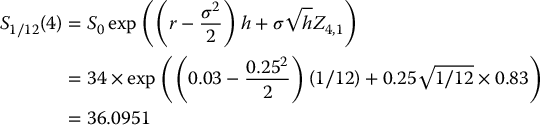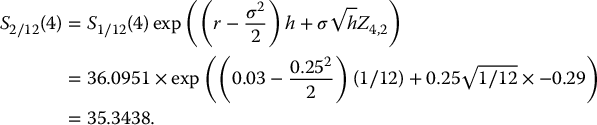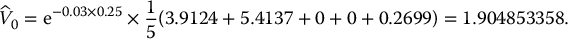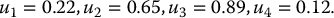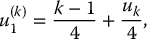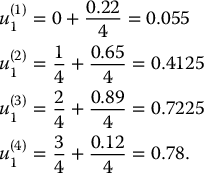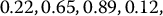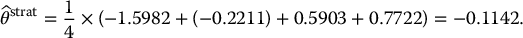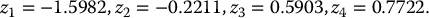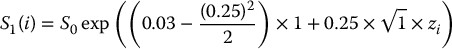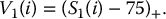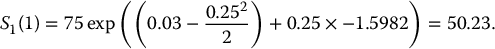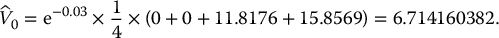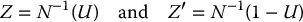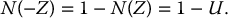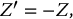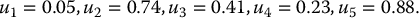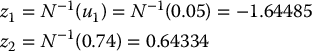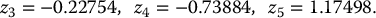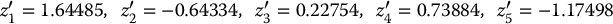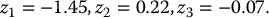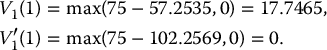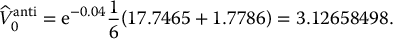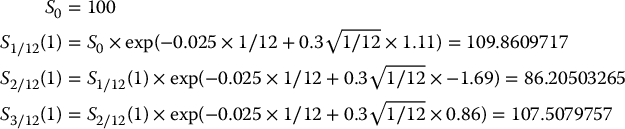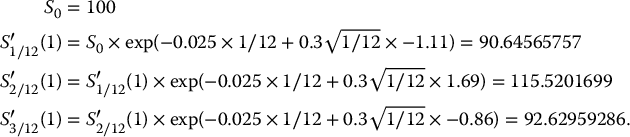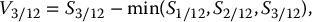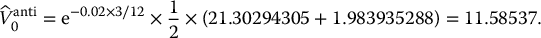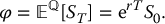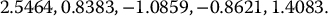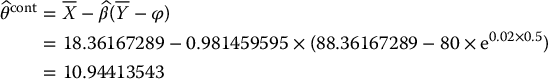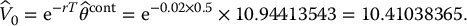19
Simulation methods
As we have seen in Chapter 18, it can be a real challenge to obtain explicit expressions for the price of complex derivatives. In practice, contracts are even more complex than what we have studied so far and the market models used are usually more sophisticated than the Black-Scholes-Merton model. Therefore, deriving analytical expressions for the price of a financial contract is often cumbersome or even impossible. Then, we need to resort to numerical methods.
This chapter focuses on a popular approach to price complex derivatives, namely simulation. Simulation in general refers to a set of techniques meant to artificially imitate a complex phenomenon. For example, pilots commonly use flight simulators to train in situations that would be too costly or dangerous to perform otherwise. An oft-cited example in mathematics is Monte Carlo integration in which random numbers are used to approximate the area under a curve when a closed-form expression is not available.
In statistics and actuarial science, simulation is used to generate artificial random scenarios from a specified model, e.g. a random sample from a given distribution. Once the sample is generated, it can be used to approximate quantities that could not be computed otherwise. Typical applications of simulation in actuarial finance include the pricing of advanced derivatives such as ELIAs and path-dependent exotic options, and the analysis of sensitivities (of profits and solvency) with respect to various economic scenarios, as required by regulators for capital adequacy requirements.
The main objective of this chapter is to apply simulation techniques to compute approximations of the no-arbitrage price of derivatives when the underlying market model is a BSM model. The specific objectives are to:
- understand that the price of a complex derivative does not have a closed-form expression and that simulation can be helpful;
- estimate the price of simple and path-dependent derivatives with crude Monte Carlo methods;
- apply variance reduction techniques, such as stratified sampling, antithetic and control variates, to accelerate convergence of the price estimator.
The next section lays the foundations by showing how to simulate random variables in general and from the normal distribution in particular. This is instrumental for the following sections on Monte Carlo simulations and variance reduction techniques as we will generate sample paths of geometric Brownian motions.
19.1 Primer on random numbers
Say you want to generate 1,000 outcomes from the discrete uniform distribution on {1, 2, 3, 4, 5, 6}. Naively, you could roll a die, mark the result and repeat this 999 other times. This is clearly a random experiment as it is impossible to predict the outcome on each throw, even if you try to recreate the same throw. However, this is clearly not a cost-efficient way to generate random numbers from this probability distribution. Instead of generating randomness by hand, we can use algorithms and computers.
19.1.1 Uniform random numbers
Creating randomness (or apparence thereof) with a computer is usually achieved with what is known as a pseudo-random number generator (PRNG). A PRNG is an algorithm that generates a sequence of numbers that appear to be random. It is known as pseudo-random because it will generate the same set of numbers once we know the PRNG’s parameters and the first number of the sequence, known as the seed.
Let 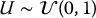 be a random variable uniformly distributed over the interval [0, 1]. PRNGs from common statistical softwares will generate independent and identically distributed realizations of U, namely u1, u2, …, un, also known as uniform random numbers. The following list shows the function names in common softwares and programming languages generating uniform random numbers:
be a random variable uniformly distributed over the interval [0, 1]. PRNGs from common statistical softwares will generate independent and identically distributed realizations of U, namely u1, u2, …, un, also known as uniform random numbers. The following list shows the function names in common softwares and programming languages generating uniform random numbers:
- ExcelTM: RAND;
- R : runif;
- SAS : RAND, specifying the distribution as ’UNIFORM’;
- Matlab : rand;
- Python : random function from the random module.
Generating uniform random numbers, also known as sampling from the uniform distribution on [0, 1], is at the core of all the simulation methods we are about to present.
19.1.2 Inverse transform method
Once we can generate uniform random numbers, we can simulate/sample from another probability distribution using its quantile function. This method is known as the inverse transform method (technique) and is described below. But first, let us recall the definition of the quantile function of a probability distribution.
Let X be a random variable with cumulative distribution function (c.d.f.) FX. The quantile function of this probability distribution (of this random variable) is denoted by F− 1X. Mathematically, the quantile function is defined, for any 0 ⩽ u ⩽ 1, by
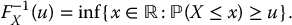
It can be shown that, for any real number x, we have F− 1X(u) ⩽ x if and only if u ⩽ FX(x).
In particular, if FX is continuous and strictly increasing, which is the case if for example its probability density function (p.d.f.) fX is strictly positive, then the quantile function F− 1X is the real inverse function of FX and
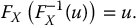
In that case, x = F− 1X(u) is the unique value such that FX(x) = u.
Example 19.1.1 Exponential distribution
It is well known that the c.d.f. of an exponential distribution with mean λ− 1 > 0 is
To identify its quantile function, we need to solve the following equation: for a fixed value of 0 ⩽ u ⩽ 1, find x such that
Consequently, we obtain
◼
For a given random variable X and a uniformly distributed random variable 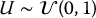 , it can be shown that the random variable F− 1X(U), which is the random variable U transformed by the function F− 1X, has the same distribution as X, i.e.
, it can be shown that the random variable F− 1X(U), which is the random variable U transformed by the function F− 1X, has the same distribution as X, i.e.

Indeed, let us assume for simplicity that FX is strictly increasing.1 Then, for any  , we have
, we have
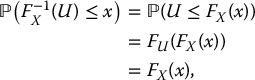
since the c.d.f. of a uniform distribution on [0, 1] is given by FU(u) = u when 0 ⩽ u ⩽ 1.
The inverse transform method builds on this relationship as follows:
- Simulate a uniform random number u from
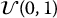 .
. - Using u, compute x = F− 1X(u).
Then, we say that x is a random number from the probability distribution given by FX.
Example 19.1.2 Sampling from an exponential distribution
We found in the previous example that if X is exponentially distributed with mean λ− 1 > 0, then
If we generate a uniform random number u, then its corresponding exponential number x is
Suppose that, with your favorite software, you have generated the following two uniform random numbers: u1 = 0.158 and u2 = 0.496. The corresponding realizations of the exponential distribution with mean 100 are given by:
◼
19.1.3 Normal random numbers
Not all random variables have explicit and invertible cumulative distribution functions. Recall from Chapter 14 that the c.d.f. of a standard normal distribution, i.e. the function
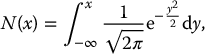
cannot be written in an explicit fashion in terms of easy-to-compute functions. We need to use a normal table or a computer to evaluate N(x). This is also true for its quantile function N− 1. Therefore, sampling from a normal distribution using the inverse transform method is conceptually easy but not always numerically efficient. For simple applications, we can still count on the inverse transform method to simulate from a standard normal distribution.
Example 19.1.3 Sampling from a normal distribution
Suppose that you have generated the following two uniform random numbers: u1 = 0.158 and u2 = 0.496.
Mapping these uniform random numbers with the standard normal quantile function N− 1, we get
◼
To generate standard normal random numbers from common statistical softwares, we can use the following functions:
- Excel: NORM.S.INV with RAND (through the inefficient inverse transform method);
- R : rnorm;
- SAS : RAND, specifying the distribution as ’NORMAL’;
- Matlab : randn;
- Python : normalvariate or gauss, both from the random module.
Instead of relying on the inverse transform method, a commonly used technique to sample from a normal distribution is known as the Box-Muller method (or transform). It is based on the following fact: if U1 and U2 are independent 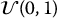 -distributed random variables and if we set R = −2ln (U1) and B = 2πU2, then
-distributed random variables and if we set R = −2ln (U1) and B = 2πU2, then 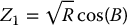 and
and 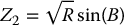 are independent and each follow a standard normal distribution
are independent and each follow a standard normal distribution 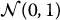 .
.
To implement the Box-Muller method and generate two normal random numbers z1 and z2, it suffices to follow these steps:
- Generate independent uniform random numbers u1 and u2.
- Set r = −2ln (u1) and b = 2πu2.
- Set
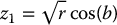 and
and 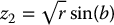 .
.
19.2 Monte Carlo simulations for option pricing
The main objective of Monte Carlo simulations is to compute approximative values of expectations such as

where X is a random variable. Whenever the distribution of X is complicated, obtaining a simple expression for θ can be difficult or even impossible. Fortunately, if we can sample from the probability distribution of X, then we can use simulation methods to approximate θ.
The crude Monte Carlo estimator of θ is defined as
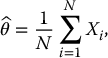
where X1, X2, …, XN are independent random variables having the same distribution as X, i.e. all with the same c.d.f. FX, and where N is the sample size. In other words, if we consider X1, X2, …, XN as a random sample from the distribution given by FX, then 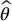 is the sample mean
is the sample mean 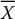 of that distribution.
of that distribution.
Example 19.2.1 Monte Carlo estimator
You have generated the following sample from the distribution of a random variable X, for example using the inverse transform method:
Then, the corresponding value of
, as given in equation (19.2.1), is
◼
The Monte Carlo estimator 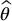 is unbiased, i.e.
is unbiased, i.e.  , and its variance goes to zero as the sample size N increases. Indeed, using the independence between the Xis, we can write
, and its variance goes to zero as the sample size N increases. Indeed, using the independence between the Xis, we can write

The precision of a Monte Carlo estimator is tied to its uncertainty which is often measured by its variance 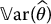 . Therefore, the preceding derivation shows that as the sample size N increases,
. Therefore, the preceding derivation shows that as the sample size N increases, 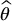 gets closer to θ and hence the estimator becomes more precise.
gets closer to θ and hence the estimator becomes more precise.
19.2.1 Notation
In this chapter we will simulate random variables and stochastic processes and therefore the reader needs to understand how notation will change and be interpreted in these contexts.
For the distribution of a random variable X, we will use the notation Xi to denote the i-th independent realization of X, i.e. from its distribution FX. For example:
- Ui, i = 1, 2, …, N denotes a sample of size N coming from the distribution of
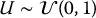 ;
; - Zi, i = 1, 2, …, N denotes a sample of size N coming from the distribution of
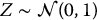 .
.
Also, as we did in Chapter 14, we will simulate stochastic processes. In particular, we will generate samples for the stock price process S = {St, t ⩾ 0} following the Black-Scholes-Merton dynamic. In this case, to avoid confusion, the index will still designate time. To identify the i-th realization, we will add the notation (i) next to the random variable. More precisely, ST(i), i = 1, 2, …, N will denote a random sample of size N coming from the distribution of ST (which is a lognormal distribution in the BSM model).
On the other hand, we will generate values of S at other times t than the final time T. Again, as we did in Chapter 14, we will simulate discretized trajectories of S. Recall that for n time points 0 < t1 < t2 < … < tn = T, the random vector
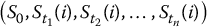
will denote the i-th discretized trajectory of S = {St, 0 ⩽ t ⩽ T}, where i = 1, 2, …, N.
Note that there are n time points and N simulated (discretized) trajectories. Those are represented in the next table where each row is a discretized path and each column is a sample for the corresponding stock price at the corresponding time point:
| Path/Time | 0 | 1 | 2 | … | n |
| 1 | S0 | 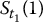 |
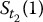 |
… | 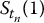 |
| 2 | S0 | 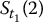 |
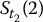 |
… | 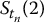 |
| ⋮ | ⋮ | ⋮ | ⋮ | 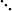 |
⋮ |
| N | S0 | 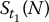 |
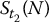 |
… | 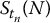 |
19.2.2 Application to option pricing
We will now see how to apply Monte Carlo estimations to approximate the initial price of a European derivative in the BSM model. We know that the initial value can be written as
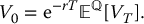
Therefore, if we can sample from the risk-neutral distribution of the random variable VT, then we will be able to approximate 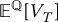 with its Monte Carlo estimator.
with its Monte Carlo estimator.
19.2.2.1 Simple derivatives
First, recall that simple derivatives have payoffs of the form VT = g(ST) where g( · ) is the payoff function. In this case, to generate a sample from the risk-neutral distribution of the random variable VT, it suffices to generate a sample from the (much simpler) risk-neutral distribution of ST which is
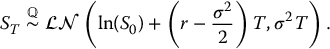
Since the lognormal distribution is an exponential function away from the normal distribution, instead of directly sampling from the risk-neutral distribution of ST, we can use the following relationship:
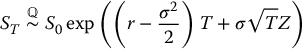
where Z is a standard normal random variable.
Therefore, the Monte Carlo pricing algorithm becomes: choose N ⩾ 1 and then
- generate a sample Zi, i = 1, 2, …, N from the standard normal distribution;
- for each i = 1, 2, …, N, set
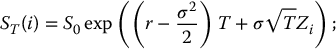
- for each i = 1, 2, …, N, set
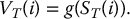
Finally, the Monte Carlo estimator of this option’s price is given by
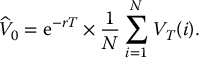
This is an approximation for the no-arbitrage price in equation (19.2.2).
Example 19.2.2 Call option price
A share of stock trades for $50 on the market. You also know that the risk-free rate is 4% and the volatility of the log-return is 30%. Compute the Monte Carlo estimator for the price of a 6-month 48-strike call option in the BSM model using the following normal random numbers:
Using the above algorithm, the second step is to compute the corresponding five realizations of the stock price S0.5 with respect to the risk-neutral probability distribution. Note that S0 = 50, T = 0.5, r = 0.04 and σ = 0.3. Then, for the first normal random number Z1 = −0.14, we set
We compute S0.5(2), S0.5(3), S0.5(4) and S0.5(5) similarly.
The next step consists in computing C0.5(i) = (S0.5(i) − 48)+, for each i = 1, …, 5.
The next table summarizes these computations:
i Zi S0.5(i) C0.5(i) 1 −0.14 48.4157 0.41571837 2 −1.19 38.7483 0 3 0.21 52.1472 4.1472 4 −1.57 35.7473 0 5 −0.50 44.8560 0 For example, if S0.5 = 52.1472, the call option pays off max (52.1472 − 48, 0) = 4.1472 at maturity.
Finally, an estimate for the initial price of this call option is given by
◼
The purpose of the last example was to illustrate the Monte Carlo algorithm for simple derivatives in the BSM model. Of course, the price C0 can be obtained with the Black-Scholes formula: in this case, we have C0 = 5.740763479. We see that the Monte Carlo estimate is far from being accurate. This was to be expected given the very small size of the sample used, i.e. N = 5. To benefit from Monte Carlo simulations, one has to generate much larger samples.
19.2.2.2 Discretely-monitored exotic derivatives
Recall that a discretely-monitored exotic derivative has a payoff of the form
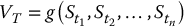
where the time points t0 < t1 < … < tn are the monitoring times. In this case, the simulation algorithm is not very different from the one we just presented for simple derivatives.
Consider for example a fixed-strike Asian put option with arithmetic average, i.e. an option with payoff
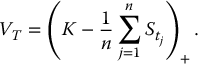
Again, as the risk-neutral distribution of VT is not known, we will:
- generate realizations of the random vector
using the algorithm given in Chapter 14 for a geometric Brownian motion;
- for each realization, compute the corresponding average (of the Asian option);
- for each realization, compute the value of the payoff.
For simplicity, let h = tj − tj − 1 = T/n, for each j = 1, 2, …, n. Equivalently, we have tj = jT/n = jh. Similarly as in equation (19.2.3), we will use the following equality of distributions: for each j = 1, 2, …, n, we have
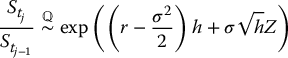
where Z is a standard normal random variable.
Here is the pricing algorithm for discretely-monitored exotic derivatives. First, choose the number of simulations N ⩾ 1. Second, perform the following steps:
- Generate a sample Zi, j, i = 1, 2, …, N, j = 1, 2, …, n, of size N × n, from the standard normal distribution.
- For each i = 1, 2, …, N, set recursively for each j = 1, 2, …, n
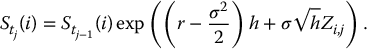
- For each i = 1, 2, …, N, set
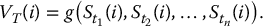
Finally, the Monte Carlo estimator of the option price is given by
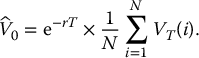
Example 19.2.3 Asian put option price
In the BSM model, a share of stock trades for $34, the volatility of its log-return is 25% and the risk-free rate is 3%. Let us calculate an estimate of the price of a 3-month fixed-strike Asian put option with a strike price of $35 whose average is computed at the end of each month.
Since the option matures in 3 months (T = 3/12), the arithmetic average is that of S1/12, S2/12 and S3/12. Therefore, we need to generate values of the random vector (S1/12, S2/12, S3/12) according to its risk-neutral distribution. If we choose N = 5, then we need to generate 5 × 3 normal random numbers. Assume we have generated the following 15 normal random numbers Zi, j:
−1 −0.79 0.85 −1.25 −1.23 0.41 1.21 −1.4 1.62 0.83 −0.29 1.06 0.26 0.21 −0.31 Let us use each row as a sample for each random vector. For example, let us set
Using the above algorithm, with S0 = 34, σ = 0.25 and r = 0.03, we get the following table:
i S0 S1/12(i) S2/12(i) S3/12(i) Average VT(i) 1 34 31.6294 29.8734 31.7601 31.0876 3.9124 2 34 31.0639 28.4223 29.2728 29.5863 5.4137 3 34 37.0987 33.5300 37.6845 36.1044 0.0000 4 34 36.0951 35.3438 38.1497 36.5295 0.0000 5 34 34.6404 35.1657 34.3841 34.7301 0.2699 For example, we have computed S1/12(4) and S2/12(4) as follows:
and
Finally, an estimate of this Asian option price is given by
◼
19.2.2.3 Continuously-monitored exotic derivatives
Recall that the payoff of a continuously-monitored exotic derivative is written as some function g of the entire path, i.e.
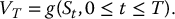
For example, the payoff of a continuously-monitored version of a fixed-strike Asian put option with arithmetic average is
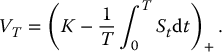
This is definitely more challenging because it is not possible to simulate a full trajectory {St, 0 ⩽ t ⩽ T} for the geometric Brownian motion S in order to compute the above integral. In this case, we need to add an extra layer of approximation, namely for the computation of the payoff itself.
For these derivatives, one will need to generate discretized trajectories of the geometric Brownian motion S = {St, 0 ⩽ t ⩽ T}. In the case of the Asian put option, we need to choose n large enough and dates 0 = t0 < t1 < … < tn = T to approximate the average:
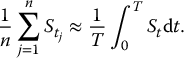
Then, we apply the algorithm for discretely-monitored exotic derivatives.
In general, the idea is that for large n, the payoff can be approximated:
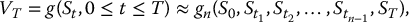
where g is a functional of the whole trajectory (St, 0 ⩽ t ⩽ T), while gn is a function of the random vector 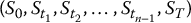 .
.
In the previous example, we had
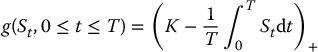
and
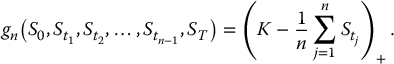
We are ready to formalize our pricing algorithm for continuously-monitored exotic derivatives. First, choose the number of simulations N ⩾ 1. Then, choose the number of discretization time-points n ⩾ 1 and an approximated version 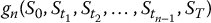 of the payoff VT = g(St, 0 ⩽ t ⩽ T) for the approximation in Equation (19.2.4) to be reasonable. Finally, perform the following steps:
of the payoff VT = g(St, 0 ⩽ t ⩽ T) for the approximation in Equation (19.2.4) to be reasonable. Finally, perform the following steps:
- Generate a sample Zi, j, i = 1, 2, …, N, j = 1, 2, …, n, of size N × n, from the standard normal distribution.
- For each i = 1, 2, …, N, set recursively for each j = 1, 2, …, n
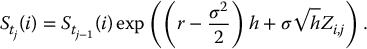
- For each i = 1, 2, …, N, set
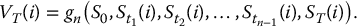
Finally, the Monte Carlo estimator of the option price is given by
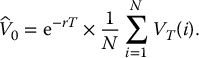
19.3 Variance reduction techniques
In practice, crude Monte Carlo simulations can be demanding, in terms of computer power, and time consuming. Variance reduction techniques aim at improving the performance of Monte Carlo estimators by reducing their variability.
Therefore, we will seek an alternate estimator 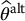 which is still unbiased for
which is still unbiased for 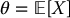 while having a lower variance (i.e. being more precise) than the crude Monte Carlo estimator
while having a lower variance (i.e. being more precise) than the crude Monte Carlo estimator 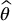 . Mathematically, we want the following two conditions to hold:
. Mathematically, we want the following two conditions to hold:
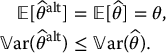
This is the goal of variance reduction techniques.
In what follows, we will present three variance reduction techniques: stratified sampling, antithetic variates and control variates.
But first, here is a motivational example for variance reduction techniques. In financial engineering and actuarial finance, many situations are such that crude Monte Carlo simulations are inefficient because a significant proportion of simulated payoffs are equal to zero. Consider, for example, the case of a fixed-strike Asian put option with payoff
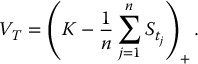
We will generate several realizations of the random vector 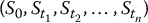 for which the corresponding mean is greater than K, resulting in a payoff equal to 0. In some sense, this is a waste of computer time. Of course, the probability of simulating such values, and thus the number of wasted simulations, depends on the parameters. More importantly, this has an impact on the variance of the Monte Carlo estimator.
for which the corresponding mean is greater than K, resulting in a payoff equal to 0. In some sense, this is a waste of computer time. Of course, the probability of simulating such values, and thus the number of wasted simulations, depends on the parameters. More importantly, this has an impact on the variance of the Monte Carlo estimator.
19.3.1 Stratified sampling
Suppose you have generated 100 uniform random numbers. You should expect to have 10 numbers/realizations on average to lie within the interval [0, 0.1]. It should also be the case for each interval of the form 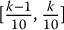 , where k = 1, 2, …, 10.
, where k = 1, 2, …, 10.
The left panel of Figure 19.1 shows a histogram counting the number of realizations in each bin, i.e. within each interval 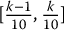 , for k = 1, 2, …, 10. It is hard to see this is actually coming from a uniform distribution. This is unfortunately a typical situation whenever we simulate a small sample from a given probability distribution.
, for k = 1, 2, …, 10. It is hard to see this is actually coming from a uniform distribution. This is unfortunately a typical situation whenever we simulate a small sample from a given probability distribution.
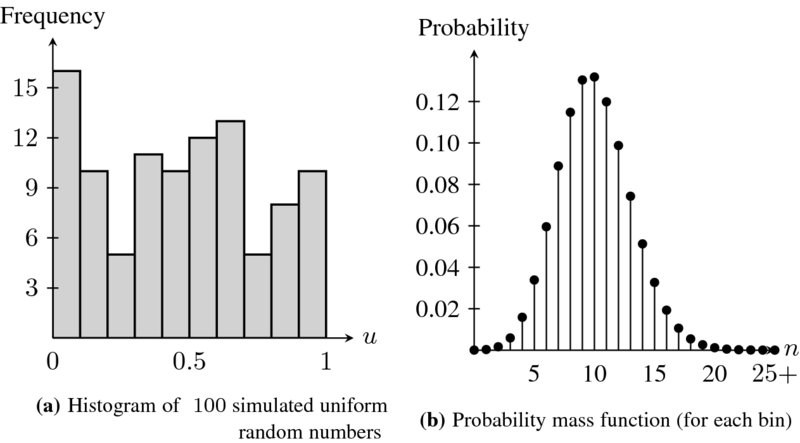
Figure 19.1 Histogram of 100 uniform random numbers (left panel) and the probability mass function of a binomial distribution Bin(n = 100; p = 0.1) (right panel)
The right panel of Figure 19.1 shows the probability distribution (a binomial distribution) for the number of realizations in each 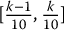 . Even if, on average, we should have 10 realizations per bin, the probability of observing from 2 to 18 realizations (out of 100) of the sample within each interval is 99.5%. In other words, with a small sample of size 100, it is likely to deviate significantly from the expected “10 elements per bin.”
. Even if, on average, we should have 10 realizations per bin, the probability of observing from 2 to 18 realizations (out of 100) of the sample within each interval is 99.5%. In other words, with a small sample of size 100, it is likely to deviate significantly from the expected “10 elements per bin.”
An easy solution to thwart this variability is simply to sample more. Figure 19.2 shows the histogram of a sample of 10,000 uniform random numbers together with the probability distribution for the number of random numbers in each interval, for a sample of 10, 000. In this case, the histogram looks much more uniform than what we had before in Figure 19.1. In this second experiment, we expect to have 1, 000 realizations per bin. The sampling variability is also much smaller. The probability of having anything between 915 to 1085 elements per bin is 99.5%. In other words, we should have 9–11% of the sample to lie within each interval with almost certainty.
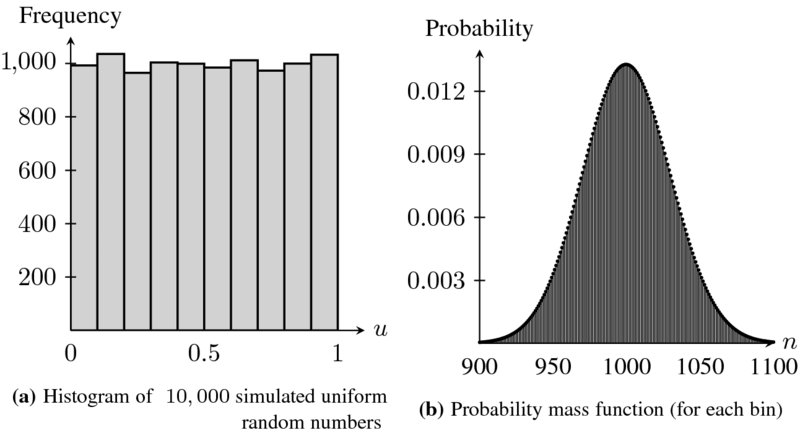
Figure 19.2 Histogram of 10, 000 uniform random numbers (left panel) and the probability mass function of a binomial distribution Bin(n = 10, 000; p = 0.1) (right panel). For the latter, only the interval [900, 1100] is displayed
Sampling more is not always a cost-effective solution. To make sure we have exactly 10% of all uniform random numbers in each of the 10 bins is the idea of stratified sampling.
19.3.1.1 Method
Fix m ⩾ 1 and partition the interval (0, 1) into m sub-intervals, called strata, i.e. let us consider each of the following sub-intervals:
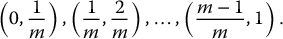
For each k = 1, 2, …, m, define
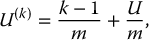
where 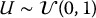 . It is easy to verify that
. It is easy to verify that 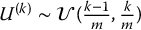 , i.e. U(k) is uniformly distributed over the k-th stratum.
, i.e. U(k) is uniformly distributed over the k-th stratum.
Instead of naively sampling N uniform random numbers from the uniform distribution 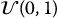 , the idea of stratified sampling consists in sampling n times from
, the idea of stratified sampling consists in sampling n times from 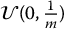 , n times from
, n times from 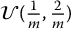 , etc., until we have sampled n realizations from each stratum, for a total of n × m = N random numbers.
, etc., until we have sampled n realizations from each stratum, for a total of n × m = N random numbers.
In other words, for each k = 1, 2, …, m, we generate n realizations of U(k), as defined in (19.3.1), to get U(k)j, j = 1, 2, …, n. The output is a set of uniform random numbers given by
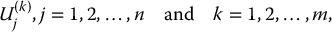
all taking values in (0, 1) but with an equal number of realizations in each stratum. In other words, stratified sampling forces each stratum to have exactly 1/m-th of the entire sample of random numbers.
Example 19.3.1 Simulation from strata
You sampled the following four uniform random numbers:
First of all, we notice there are two numbers in the first quartile (0, 1/4], none was sampled from the second quartile (1/4, 1/2], while there is one for each of the last two quartiles (1/2, 3/4] and (3/4, 1]. Using m = 4 strata, we can generate one number per stratum.
With m = 4 and n = 1, if we set
then the corresponding realizations are:
Hence, there is a realization coming from each quartile.
◼
The implementation of stratified sampling is simple and based on (19.3.1). The algorithm is as follows. First, choose m ⩾ 1, the number of strata, then choose n ⩾ 1, the number of realizations per stratum, so that N = n × m. Then:
- Simulate N uniform random numbers Ui, i = 1, 2, …, N.
- For each stratum
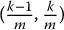 , i.e. for each k = 1, 2, …, m, and for each j = 1, 2, …, n, set:
or, alternatively, set
, i.e. for each k = 1, 2, …, m, and for each j = 1, 2, …, n, set:
or, alternatively, set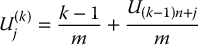
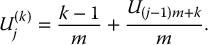
The uniform random numbers U1, U2, …, UN are allocated to each stratum to simulate realizations of U(k)j, j = 1, 2, …, n and k = 1, 2, …, m. There are two equivalent ways to allocate the Uis, as shown in the following tables.
- Here is the first way to use the uniform random numbers:
In this table, the first n realizations from
k/j 1 2 … n 1 U1 → U(1)1 U2 → U(1)2 … Un → U(1)n 2 Un + 1 → U(2)1 Un + 2 → U(2)2 … U2n → U(2)n ⋮ ⋮ ⋮ 
⋮ m U(m − 1)n + 1 → U(m)1 U(m − 1)n + 2 → U(m)2 … Umn → U(m)n  are used to generate a sample of n realizations of U(1), then the next n realizations from
are used to generate a sample of n realizations of U(1), then the next n realizations from  are used to simulate n realizations of U(2), etc.
are used to simulate n realizations of U(2), etc. - Here is the second allocation:
In this table, the first m realizations from
k/j 1 2 … n 1 U1 → U(1)1 Um + 1 → U(1)2 … U(n − 1)m + 1 → U(1)n 2 U2 → U(2)1 Um + 2 → U(2)2 … U(n − 1)m + 2 → U(2)n ⋮ ⋮ ⋮ 
⋮ m Um → U(m)1 U2m → U(m)2 … Umn → U(m)n 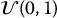 are used to generate one realization from each stratum, then the m following realizations from
are used to generate one realization from each stratum, then the m following realizations from 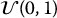 are used to generate the second realization from each stratum, etc.
are used to generate the second realization from each stratum, etc.
To simulate a random variable X using stratified sampling, we simply use the inverse transform method together with the U(k)js rather than the Uis. More precisely, for each k = 1, 2, …, m and j = 1, 2, …, n, using the inverse transform method, set
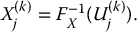
Then, the corresponding stratified sampling estimator for 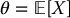 is given by
is given by
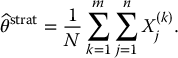
It is easy to see that this estimator is also unbiased for θ:
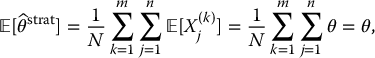
since N = n × m.
It can be verified that the variance of  is less than the variance of
is less than the variance of 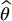 .
.
Example 19.3.2 Naive sampling and stratified sampling from the standard normal distribution
With the uniform random numbers of example 19.3.1, i.e.
we can simulate a standard normal distribution using both naive sampling and stratified sampling.
Naive simulation of a normal distribution is achieved by applying Zi = N− 1(Ui) whereas stratified sampling is obtained using Z(k)j = N− 1(U(k)j) with U(k)j computed in example 19.3.1. With n = 1, the results are shown in the next table:
i, k Ui U(k)1 N− 1(Ui) N− 1(U(k)1) 1 0.22 0.055 −0.7722 −1.5982 2 0.65 0.4125 0.3853 −0.2211 3 0.89 0.7225 1.2265 0.5903 4 0.12 0.78 −1.1750 0.7722 Then, we can compute the corresponding stratified sampling estimate of θ = 0:
Stratified sampling can also be applied together with the Box-Muller method to generate normal random numbers. This is more efficient than inverting the standard normal cumulative distribution function N( · ).
◼
19.3.1.2 Application to option pricing
Pricing simple derivatives using stratified sampling is similar to using the standard Monte Carlo estimator of  , with the only difference that uniform random numbers are generated from stratified sampling.
, with the only difference that uniform random numbers are generated from stratified sampling.
Example 19.3.3 Call option price
For a share of stock trading at $75, let us use stratified sampling to price a 1-year at-the-money call option in the BSM model with volatility parameter σ = 0.25 and risk-free rate parameter r = 0.03.
We will use the stratified sample of example 19.3.2, so N = 4 and
Then, for each i = 1, 2, 3, 4, set
and
For example, we have
The other results are shown in the table:
i/k N− 1(U(k)1) S1(i) V1(i) 1 −1.5982 50.2338865 0 2 −0.2211 70.8778828 0 3 0.5903 86.8175866 11.8175866 4 0.7722 90.8569614 15.8569614 Consequently, the Monte Carlo estimate with stratified sampling is equal to
◼
 Unfortunately, stratified sampling estimators for the pricing of path-dependent options are not easy to implement. We have to realize that a discretized path of a geometric Brownian motion is an n-dimensional vector
Unfortunately, stratified sampling estimators for the pricing of path-dependent options are not easy to implement. We have to realize that a discretized path of a geometric Brownian motion is an n-dimensional vector 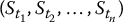 , which means that stratified sampling of N such vectors involves using n-dimensional strata. It can become cumbersome fairly quickly.
, which means that stratified sampling of N such vectors involves using n-dimensional strata. It can become cumbersome fairly quickly.
19.3.2 Antithetic variates
Recall that the variance of the Monte Carlo estimator 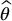 goes to 0 as the sample size N increases. If someone has time and computer power, there is a more efficient way to decrease the variance than simply simulating more values.
goes to 0 as the sample size N increases. If someone has time and computer power, there is a more efficient way to decrease the variance than simply simulating more values.
19.3.2.1 Method
Whenever  , it is easy to see that 1 − U is also uniformly distributed over (0, 1). Now, let F( · ) be the c.d.f. of some distribution with finite mean θ and finite variance s2. From the inverse transform method, we deduce that
, it is easy to see that 1 − U is also uniformly distributed over (0, 1). Now, let F( · ) be the c.d.f. of some distribution with finite mean θ and finite variance s2. From the inverse transform method, we deduce that
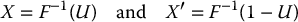
have the same distribution. In other words,
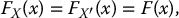
for all 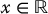 .
.
It results that
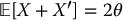
and
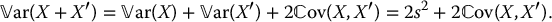
Of course, the random variables X and X′ are not independent because they are tranformations of the same random variable U.
Example 19.3.4 Standard normal distribution
Let
. Because U and 1 − U are both uniformly distributed over (0, 1), we deduce from the inverse transform method that
both have a standard normal distribution.
Since the c.d.f. of the standard normal distribution is strictly increasing, we can write N(Z) = U. Moreover, from the properties of the normal distribution, we know that 1 − N(x) = N( − x), for all
, so we can write
Finally, we deduce a very interesting property of the normal distribution for antithetic variates:
so that Z′ is the true reflection of Z.
◼
The idea of the antithetic variates technique is to generate a single uniform random number u from which two realizations of X are obtained: x = F− 1X(u) and its reflection x′ = F− 1X(1 − u). From the simulation of N uniform random numbers, we obtain 2N realizations from the distribution of X.
Algorithmically, we choose N ⩾ 1 and then we:
- generate a sample Ui, i = 1, 2, …, N of size N coming from the distribution of
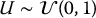 ;
; - for each i = 1, 2, …, N, set Xi = F− 1X(Ui) and X′i = F− 1X(1 − Ui).
The random couples (X1, X′1), (X2, X′2), …, (XN, X′N) are independent and have the same bivariate distribution. But for each i = 1, 2, …, N, the random variables Xi and X′i are not independent.
Example 19.3.5 Antithetic variates
Assume you have generated the following five uniform random numbers:
We want to generate standard normal random numbers.
Using the antithetic variates technique together with the inverse transform method, we can generate 10 standard normal random numbers from the above five uniform random numbers. Indeed, for i = 1, 2, …, 5, if we set zi = N− 1(ui), then we get
and
Since we are sampling from the standard normal distribution, we have seen in example 19.3.4 that the antithetic counterparts are such that z′i = −zi, for each i = 1, 2, …, 5.
Consequently,
are the other five normal random numbers.
◼
In the last example, since we were dealing with the standard normal distribution, we could have used the antithetic variates technique together with the Box-Muller approach (for the sampling of the first five normal random numbers) rather than the inverse transform method. When the sample size is large, the former approach is numerically much more efficient.
Finally, the antithetic variates estimator of θ is defined as
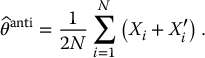
In general, the antithetic variates estimator 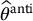 is an unbiased estimator for θ:
is an unbiased estimator for θ:
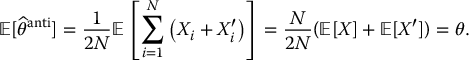
Given that the antithetic variates estimator is based on a sample twice as large as usual, we should at least make sure that 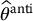 is more efficient than simply using the crude Monte Carlo estimator
is more efficient than simply using the crude Monte Carlo estimator 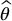 with a sample of 2N. Hence, we need to compute the variance of
with a sample of 2N. Hence, we need to compute the variance of 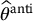 .
.
To do this, we shall note first that when i ≠ j, the random variables Xi + X′i and Xj + X′j are independent and follow the same univariate distribution. Hence, using equation (19.3.3), we obtain
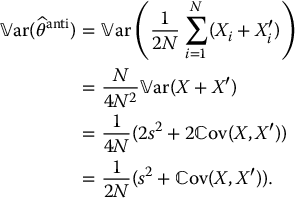
The variance of the crude Monte Carlo estimator, obtained with a sample of size 2N, is given by 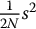 , as seen previously. Therefore, for the antithetic variates estimator to be more efficient than the crude one, we must have
, as seen previously. Therefore, for the antithetic variates estimator to be more efficient than the crude one, we must have
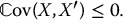
Clearly, for the standard normal distribution, since Z′ = −Z, then Z and Z′ are negatively correlated. Indeed, we have
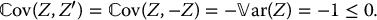
Consequently, for any increasing transformation f, the random variables f(Z) and f(Z′) will also be negatively correlated. Otherwise, the latter condition is not always met and needs to be verified.
19.3.2.2 Application to option pricing
Let us now apply the antithetic variates method to option pricing in the BSM model. The idea is to capitalize on the fact that for a standard normal random variable Z, its antithetic counterpart is its true reflection − Z.
First, we consider a simple derivative with payoff VT = g(ST) where g( · ) is the payoff function. As for crude Monte Carlo simulations, we will use the relationship of equation (19.2.3), i.e.
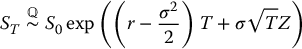
where Z is a standard normal random variable. In this case, since the antithetic counterpart of Z is − Z, we also have
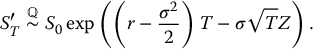
Therefore, the corresponding antithetic variates algorithm, based on (19.3.5) and (19.3.6), is: choose N ⩾ 1 and then
- generate a sample Zi, i = 1, 2, …, N from the standard normal distribution;
- for each i = 1, 2, …, N, set
and
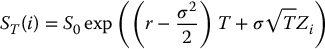
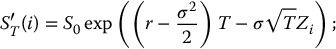
- for each i = 1, 2, …, N, set
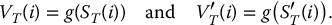
Finally, the antithetic variates estimator of this option price is given by
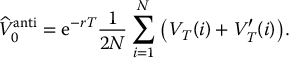
To ensure that the antithetic variates method works for option pricing, we have to make sure that VT and V′T are negatively correlated. One quick approach to verify this is to compute the sample correlation between VT and V′T. The closer to − 1, the more efficient the method.
There is one important case where the method always works efficiently and this is when VT is an increasing function of ST, as for example a call option. In this case, the relationship between VT and V′T being monotone, the covariance 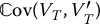 is negative.
is negative.
Example 19.3.6 Antithetic variates estimator
The current stock price is $75 and the volatility of its log-return is 20%. If the risk-free rate is 4%, calculate the antithetic variates estimator for the price of an at-the-money put option maturing in 1 year. Use the following three normal variates:
With three normal random numbers, we will get six realizations of the payoff. Since S0 = 75, σ = 0.2 and r = 0.04, we get:
i Zi Z′i S1(i) S′1(i) V1(i) V′1(i) 1 −1.45 1.45 57.2535 102.2569 17.7465 0 2 0.22 −0.22 79.9569 73.2214 0 1.7786 3 −0.07 0.07 75.4514 77.5938 0 0 For example, with z1 = −1.45, we obtain
and the corresponding payoffs are
Then, the antithetic variates estimate of this option’s initial value is
◼
Now, for path-dependent derivatives, both discretely- and continuously-monitored, the idea is similar: we apply the antithetic method for all time steps and trajectories. In the end, we get a final sample of normal random numbers which is twice the original size and hence we get twice the number of discretized trajectories of the geometric Brownian motion.
More precisely, consider dates 0 = t0 < t1 < … < tn = T and let us generate realizations of the random vector (discretized trajectory)
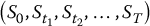
using the following risk-neutral distributions:

where Z is a standard normal random variable. In other words, at each time step, we get an increment from Z and one from its antithetic counterpart − Z.
The antithetic variates pricing algorithm for path-dependent derivatives goes as follows. First, choose the number of sample paths N ⩾ 1. Then, choose the number of time steps n ⩾ 1 and set the time-points tj = jh, j = 1, 2, …, n with h = T/n:
- discrete monitoring: according to the option payoff
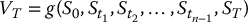 ;
; - continuous monitoring: choose a good approximation
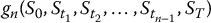
of the payoff VT = g(St, 0 ⩽ t ⩽ T), as in equation (19.2.4).
Then, perform the following steps:
- Generate a sample Zi, j, i = 1, 2, …, N, j = 1, 2, …, n, of size N × n, from the standard normal distribution.
- For each i = 1, 2, …, N, set recursively for each j = 1, 2, …, n
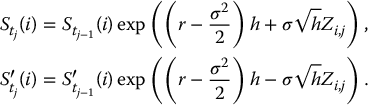
- For each i = 1, 2, …, N, set
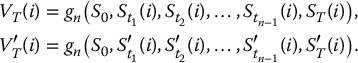
A path from a geometric Brownian motion along with its antithetic version is shown in Figure 19.3. Finally, the antithetic variates estimator of the option price with payoff VT is given by
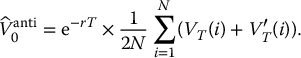
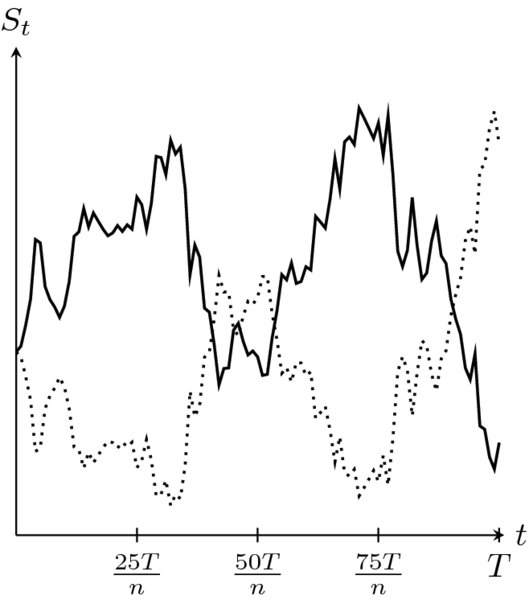
Figure 19.3 A sample path of a geometric Brownian motion (solid line) and its corresponding antithetic version (dotted line)
In the above algorithm, we use the sample of Zi, js to simulate N discretized trajectories and we compute the corresponding values of the payoff, i.e. the VT(i)s, as we did in the crude Monte Carlo approach. Again, we capitalize on the antithetic variates method and the fact that for a standard normal random variable Z its antithetic counterpart is its true reflection − Z. Therefore, without generating any new random numbers, we use the − Zi, js and obtain an extra N discretized trajectories and N payoff values.
Example 19.3.7 Floating-strike lookback call option
Let us simulate values of the payoff of a 3-month floating-strike lookback call option using the antithetic variates method. Assume the underlying asset price is monitored at the end of each month. Consider a BSM model with S0 = 100, r = 0.02, σ = 0.3. We will simulate paths of a GBM over a 3-month period with the following standard normal variates: 1.11, −1.69, 0.86.
In this example, we have N = 1. Since r − σ2/2 = 0.02 − 0.5 × 0.32 = −0.025, applying the above algorithm, we obtain:
and
The payoff of this 3-month floating-strike lookback call option being
we have V3/12(1) = 107.5079757 − min (109.86, 86.21, 107.51) = 21.30294305 and V′3/12(1) = 92.62959286 − min (90.65, 115.52, 92.63) = 1.983935288, yielding an antithetic estimate of
Of course, since N = 1, this is (probably) a very inaccurate estimate.
◼
19.3.3 Control variates
The control variates method is a technique that seeks to improve the crude Monte Carlo estimator for 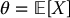 using information about another expectation
using information about another expectation 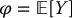 , where Y is a random variable related to X and known as the control variate. For the method to be efficient, we need to know how to (analytically) compute ϕ quickly and, ideally, we should know the relationship between X and Y.
, where Y is a random variable related to X and known as the control variate. For the method to be efficient, we need to know how to (analytically) compute ϕ quickly and, ideally, we should know the relationship between X and Y.
19.3.3.1 Method
The method is as follows. First, we choose another random variable Y. Then, we generate N independent random couples
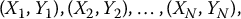
all having the same distribution as (X, Y). For a constant β, we define a new estimator for θ as
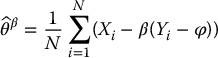
which can be rewritten as
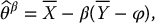
with 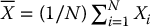 and
and 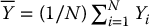 .
.
The idea of the new estimator is simple. Whenever X and Y are closely related, the approximation error of estimating ϕ by

should be tied to the approximation error we get by estimating θ with 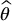 . We expect some proportionality between the difference
. We expect some proportionality between the difference 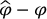 and
and 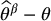 . Since we have knowledge about
. Since we have knowledge about 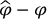 , we will use this information to improve the Monte Carlo estimator
, we will use this information to improve the Monte Carlo estimator 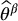 .
.
This new estimator for θ is clearly an unbiased estimator because
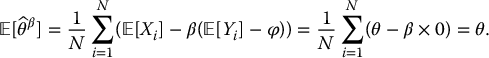
We should also analyze the variance of 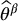 . It is obtained by making use of the independence between the (Xi, Yi)s. Recall that the couples are independent, but for each couple, i.e. for each i, the random variables Xi and Yi are dependent. We get
. It is obtained by making use of the independence between the (Xi, Yi)s. Recall that the couples are independent, but for each couple, i.e. for each i, the random variables Xi and Yi are dependent. We get
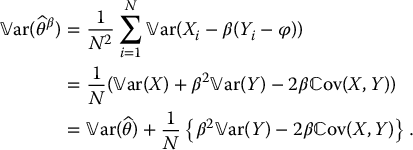
In order for this estimator to perform better than the usual Monte Carlo estimator, we want to choose β to get
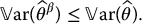
More than that, we will choose β to minimize this variance, i.e. to minimize the function
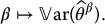
Using elementary calculus, we see that it is minimal if we choose
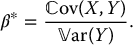
We can then verify that
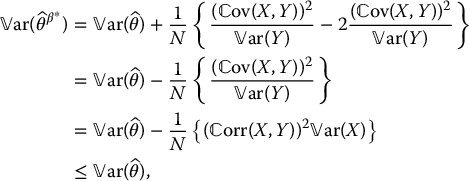
as desired. From the above computations, we see that only the magnitude of the correlation between X and Y has an impact, not its direction.
In conclusion, the exact control variates estimator is given by
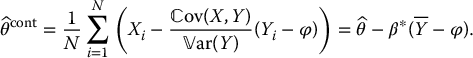
Unfortunately, in most cases, 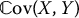 and/or
and/or 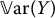 are unknown (or are too complicated to be computed), and so is β*. Then, from a computational point of view, we will need to approximate β* using an estimator that we denote by
are unknown (or are too complicated to be computed), and so is β*. Then, from a computational point of view, we will need to approximate β* using an estimator that we denote by 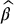 . First, recall that the sample covariance is given by
. First, recall that the sample covariance is given by
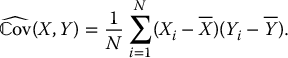
Consequently, we set
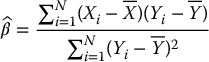
and then we replace the estimator in (19.3.8) by the following control variates estimator:
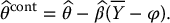
For simplicity, we used the same notation in (19.3.10) as in (19.3.8). Note that the estimator 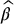 can be viewed as the slope of the regression of X on Y. This suggests that we can add more than one control variate to further reduce the variance of
can be viewed as the slope of the regression of X on Y. This suggests that we can add more than one control variate to further reduce the variance of  .
.
 It is important to realize that replacing β* by
It is important to realize that replacing β* by 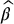 will introduce dependence and a bias. First of all, the simulated values of
will introduce dependence and a bias. First of all, the simulated values of 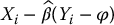 , for i = 1, 2, …, N, will be dependent (because of
, for i = 1, 2, …, N, will be dependent (because of 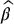 ). Moreover,
). Moreover,  as N → ∞ so there can be a bias in small samples. The combined effect is usually small and ignored in practice.
as N → ∞ so there can be a bias in small samples. The combined effect is usually small and ignored in practice.
19.3.3.2 Application to option pricing
The application of the control variates method to approximate option prices implies that X = VT and that we want to estimate 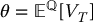 . For the method to be successful, we must choose the control variate wisely. Once this is done, the control variates method is easy to implement.
. For the method to be successful, we must choose the control variate wisely. Once this is done, the control variates method is easy to implement.
Assume we have discretely-monitored payoffs of the form
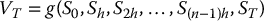
and

where g and 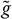 are the payoff functions, respectively, of the targeted option and the control option. Of course, if n = 1, they are simple derivatives. The case of continously-monitored exotic payoffs VT is treated as before: we approximate the continuously-monitored exotic payoff with a similar discretely-monitored payoff.
are the payoff functions, respectively, of the targeted option and the control option. Of course, if n = 1, they are simple derivatives. The case of continously-monitored exotic payoffs VT is treated as before: we approximate the continuously-monitored exotic payoff with a similar discretely-monitored payoff.
The control variates pricing algorithm is as follows:
- Choose an appropriate control variate
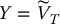 and compute analytically the value of
and compute analytically the value of 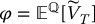 .
. - Choose the number of sample paths N ⩾ 1 and the number of discretization time-points n ⩾ 1.
- For each i = 1, 2, …, N:
- Generate a discretized path of the geometric Brownian motion using its risk-neutral distribution (i.e. with respect to
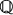 ), i.e.
), i.e.
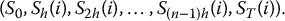
- Compute the corresponding value of the payoff:
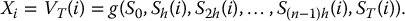
- Compute the corresponding value of the control payoff:
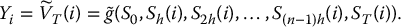
- Generate a discretized path of the geometric Brownian motion using its risk-neutral distribution (i.e. with respect to
-
Compute
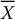 ,
,  and
and 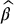 , using the above simulations.
, using the above simulations.
Finally, the control variates estimator of the option price is
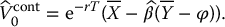
One natural choice of control variate for simple payoffs of the form X = g(ST) is the underlying asset itself, i.e. Y = ST. In principle, Y = ST should be strongly correlated with X = g(ST). The next example illustrates how to price a simple option using such a control variate.
Example 19.3.8 Application of the control variates method
Suppose we want to price a 6-month 70-strike call option, using the control variates method, in a BSM model with the following parameters: S0 = 80, σ = 0.2 and r = 0.02.
In this case, we have X = (ST − K)+. First, we want to find a suitable control variate Y: it needs to be strongly correlated to X = (ST − K)+ and ϕ should be easily computable. As mentioned above, Y = ST can be an interesting choice of control variate for a simple payoff. Indeed, when the value of Y = ST increases, the option payoff X = (ST − K)+ increases as well. Moreover, we know that
Next, we generate standard normal numbers. Assume we have obtained the following values:
This means N = 5. The next table shows the resulting values for the stock price along with their corresponding payoffs. Note that we have T = 0.5 and K = 70.
i Zi Yi = S0.5(i) Xi = (S0.5(i) − 70)+ 1 2.5464 114.6796 44.67958 2 0.8383 90.06937 20.06937 3 −1.0859 68.6113 0 4 −0.8621 70.81758 0.817581 5 1.4083 97.63054 27.63054 Then, we compute the following quantities:
where, to compute
, we used the expression in (19.3.9). Note that, in this case, we could have computed the exact value of β* as given in equation (19.3.7).
Finally, using the above quantities in (19.3.10), we obtain
and the control variate estimate of the call option price is
To better understand how the control variates method works and how it improves on the crude Monte Carlo estimator
, let us look at the approximation error made when estimating ϕ with
. In this example, we had
which means
overestimates ϕ. Since X and Y are positively correlated, we also expect
to be overestimating θ. This is why we correct the crude Monte Carlo estimator
by adding the extra term
.
◼
A typical situation where the control variates method is particularly useful is for Asian options whose payoff is based on a discrete arithmetic average. More specifically, let us consider the following fixed-strike Asian call payoff:
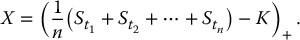
As a control variate, we can use the payoff of a similar Asian option based on a discrete geometric average instead, i.e. choose
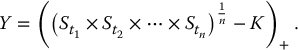
We expect the correlation between X and Y to be strong and, as we saw in Chapter 18, there exists a closed-form expression for the price of options with payoff Y in the BSM model. The control variates method can then be applied directly in this case.
Other simulation methods for option pricing
If we seek to increase the efficiency of crude Monte Carlo simulations, there are two popular approaches that we have not looked at in this chapter due to their complexity.
Importance sampling is a variance reduction technique that consists in finding an alternate distribution for X that puts more emphasis where it matters the most. For example, when pricing deep out-of-the-money options, a large proportion of the sample will have a zero payoff. Importance sampling will shift the distribution such that positive payoffs occur more often while making sure that 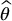 remains unbiased. The method essentially relies on a change of probability measure (see Chapter 17) and requires a deep knowledge of the problem to make sure the variance of
remains unbiased. The method essentially relies on a change of probability measure (see Chapter 17) and requires a deep knowledge of the problem to make sure the variance of 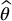 is always reduced.
is always reduced.
Quasi Monte Carlo methods consist in generating uniform numbers by using a deterministic sequence (known as low-discrepancy sequences) rather than a PRNG. As a result, any quantity computed from quasi Monte Carlo is not random anymore. Because an expectation can be written as an integral, quasi Monte Carlo is a method that is in between pure Monte Carlo (as described in this chapter) and numerical integration (trapezoid rule, Newton-Cotes, etc.). To address the lack of randomness of quasi Monte Carlo methods, one can randomize the latter by combining it with a PRNG.
19.4 Summary
Random numbers and Monte Carlo simulations
- Pseudo-random number generator (PRNG): algorithm generating numbers that appear to be random.
- Uniform random numbers: independent realizations u1, u2, …, un of
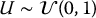 generated with a PRNG.
generated with a PRNG. - Quantile function: inverse of FX defined by
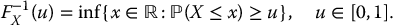
- Inverse transform method: basic simulation method to generate random numbers x1, x2, …, xn from FX, i.e. generate independent realizations of X: for each i,
- simulate a uniform random number ui from
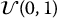 ;
; - set xi = F− 1X(ui).
- simulate a uniform random number ui from
- Normal random numbers: independent realizations z1, z2, …, zn of
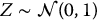 generated with the inverse transform method (or preferably with the Box-Muller technique).
generated with the inverse transform method (or preferably with the Box-Muller technique). - Monte Carlo estimator of
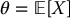 :
where X1, X2, …, XN are independent and all following the distribution FX.
:
where X1, X2, …, XN are independent and all following the distribution FX.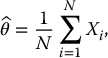
- Monte Carlo estimator
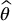 :
:
- is unbiased;
- its has a variance that goes to 0 as the sample size N increases.
- Monte Carlo pricing algorithm for the payoff VT = g(ST): choose N ⩾ 1 and then
- generate Zi, i = 1, 2, …, N from the standard normal distribution;
- for each i = 1, 2, …, N, set
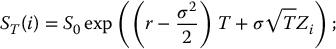
- for each i = 1, 2, …, N, set
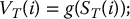
- finally, the Monte Carlo estimator of the option’s price
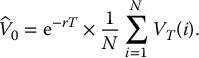
- Monte Carlo pricing algorithm for the payoff
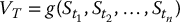 : set h = tj − tj − 1 = T/n (equally spaced), choose N ⩾ 1 and then
: set h = tj − tj − 1 = T/n (equally spaced), choose N ⩾ 1 and then
- generate Zi, j, i = 1, 2, …, N, j = 1, 2, …, n from the standard normal distribution;
- for each i = 1, 2, …, N, set recursively, for each j = 1, 2, …, n,
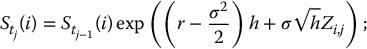
- for each i = 1, 2, …, N, set
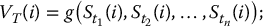
- finally, the Monte Carlo estimator of the option’s price
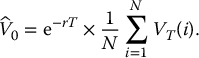
- Monte Carlo pricing algorithm for the payoff VT = g(St, 0 ⩽ t ⩽ T): choose N ⩾ 1 and then choose n ⩾ 1 and gn such that
Then apply the previous algorithm for
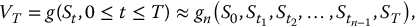
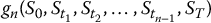 .
.
- Variance reduction technique: define an estimator
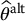 such that
such that
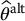 is unbiased;
is unbiased;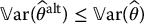 .
.
-
Stratified sampling: partitioning the interval [0, 1] into m strata and sampling n = N/m uniform random numbers from each stratum
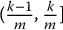 , where k = 1, 2, …, m.
, where k = 1, 2, …, m. - Pricing algorithm with stratified sampling: choose m ⩾ 1 and n ⩾ 1 so that N = n × m, and then
- simulate N uniform random numbers Ui, i = 1, 2, …, N;
- for each stratum, i.e. for each k = 1, 2, …, m, and for each j = 1, 2, …, n, set:
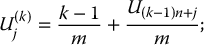
- compute the N corresponding realizations of VT using U(k)j;
- stratified sampling estimator of the option price:
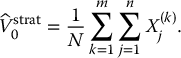
- Antithetic variates: for each uniform random number u, sample VT twice with the normal random numbers z = N− 1(u) then z′ = N− 1(1 − u).
- Pricing algorithm with antithetic variates: choose N ⩾ 1 and then
- generate a sample Zi, i = 1, 2, …, N from the standard normal distribution;
- for each i = 1, 2, …, N, set
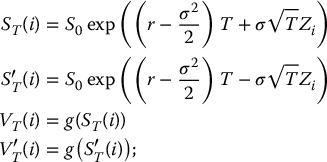
- antithetic variates estimator of the option price:
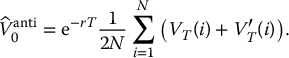
-
Control variates: approximating the error committed with
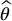 by computing the true error committed by estimating
by computing the true error committed by estimating 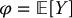 with
with 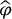 , where Y is the control variate.
, where Y is the control variate. - Pricing algorithm with control variates:
- choose
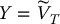 and compute
and compute 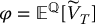 ;
; - choose the number of sample paths N ⩾ 1 and the number of discretization time-points n ⩾ 1;
- for each i = 1, 2, …, N: generate a discretized path of the GBM (using its risk-neutral distribution)
and compute
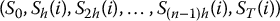
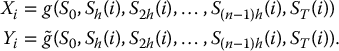
- compute
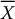 ,
, 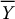 and
and 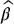 .
. - control variates estimator of the option price:
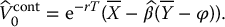
- choose
19.5 Exercises
For the following exercises, the random numbers in Table 19.1 have been generated with a computer. Note that Ui is drawn from a uniform distribution whereas Zi = N− 1(Ui). For exercises 1–3 and 5, assume the BSM model holds with the following parameters: S0 = 100, μ = 0.08, r = 0.03 and σ = 0.25.
Table 19.1 Random numbers
| i | Ui | Zi |
| 1 | 0.0371 | −1.7861 |
| 2 | 0.6421 | 0.3641 |
| 3 | 0.8604 | 1.0818 |
| 4 | 0.032 | −1.8536 |
| 5 | 0.8116 | 0.8838 |
| 6 | 0.4274 | −0.1831 |
| 7 | 0.2277 | −0.7465 |
| 8 | 0.7707 | 0.7411 |
| 9 | 0.9266 | 1.4508 |
| 10 | 0.6797 | 0.4669 |
| 11 | 0.3265 | −0.4499 |
| 12 | 0.3631 | −0.3503 |
-
Compute the crude Monte Carlo estimate of the initial price for the following derivatives:
- a 105-strike 6-month call option;
- a 100-strike 3-month gap put option with H = 97;
- a 3-month asset-or-nothing call option with strike price K = 108;
- an investment guarantee maturing in 1 year that applies on 75% of an initial investment of 1, 000.
For each contract, use the first five random numbers of Table 19.1.
-
In the preceding exercise, use simulations to compute the probability that each of these derivatives will mature in the money.
-
Compute the crude Monte Carlo estimate of the initial price of the following exotic derivatives:
- a 3-month floating-strike lookback call option monitored monthly;
- a 3-year CAR EIA with participation rate of 75% and an initial investment of 1000;
- a 3-month floating-strike Asian put option monitored monthly;
- a 3-month up-and-in barrier call option with H = 102 and K = 99.
For each contract, generate four paths using the first three random numbers of Table 19.1 for the first path, the next three random numbers for the second path, and so on.
-
Let X be an exponentially distributed random variable with mean 100.
- Using four strata with three random numbers each, compute a stratified sampling estimator of
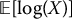 . Use the first three random numbers to fill in the first stratum (0, 0.25], the next three random numbers to fill in the second stratum (0.25, 0.50], and so on.
. Use the first three random numbers to fill in the first stratum (0, 0.25], the next three random numbers to fill in the second stratum (0.25, 0.50], and so on. - Compute the antithetic variates estimator of
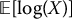 using the first five random numbers.
using the first five random numbers. - Compute the control variates estimator of
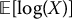 using X as a control variate and the first five random numbers.
using X as a control variate and the first five random numbers.
- Using four strata with three random numbers each, compute a stratified sampling estimator of
-
Consider a 1-year at-the-money call option.
- Compute the stratified sampling estimator of the initial price of that option. Use the first three random numbers to fill in the first stratum (0, 0.25], the next three random numbers to fill in the second stratum (0.25, 0.50], and so on.
- Compute the antithetic variates estimator of the initial price of that option using the first five random numbers.
- Compute the control variates estimator of the initial price of that option using the payoff of an asset-or-nothing call option with same strike as the control variate. Use only the first five random numbers.
-
For the antithetic variates estimator, show that:
- If
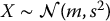 , then
, then 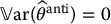 .
. - If X = bZ2 with
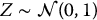 , then
, then 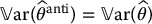 .
.
- If
-
Let Y be a random variable with mean m and variance s2 (not necessarily normal) and X be such that
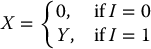
where I is a Bernoulli random variable with distribution
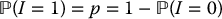 which is independent of Y.
which is independent of Y.- Show that
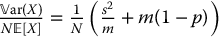 .
. - Provide an interpretation for
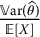 and analyze its behavior when p increases.
and analyze its behavior when p increases.
- Show that