Preface

What is actuarial finance?

The work of actuaries has been strongly impacted by the deregulation of financial markets and the financial innovation that followed. Nowadays, there are embedded options in many life insurance and annuity products. Moreover, the use of weather and catastrophe derivatives in P&C insurance, to manage losses from earthquakes, hurricanes, floods and extreme weather, is constantly increasing, while longevity derivatives have been created to manage longevity risk on pools of pensioners.

As a consequence, in recent years actuarial finance has become an emerging field at the crossing of actuarial science and mathematical finance, i.e. when both actuarial and financial risks have to be taken into account. Despite its common roots with modern financial mathematics, actuarial finance has its own challenges due to:

the very long-term nature (several years or decades) of insurance liabilities;
the presence of mortality risk and other contingencies;
the structure and regulations of the insurance and pension markets.

Therefore, it is now widely recognized that actuaries should have a basic knowledge of:

derivatives and other assets to manage actuarial and financial risks;
embedded options in actuarial liabilities.

A book written by and for actuaries

As we are writing this book for the typical actuarial science (undergraduate) student or practitioner, our main goal is to find an appropriate balance between the level of mathematics and finance in the presentation of classical financial models such as the binomial tree and the Black-Scholes-Merton model. Given the growing complexity of many actuarial liabilities and their ties to financial markets, we also felt the need for a book with actuarial applications at the forefront.

Therefore, this book has been motivated, designed and written for actuaries (and by actuaries). This means that we spend more time on and put more energy into what matters to actuaries, i.e. topics of particular relevance for actuaries are introduced at a more accessible level and analyzed in greater depth. For example, in this book, we:

compare pricing in insurance and financial markets;
present credit default swaps which are largely used by insurance companies to manage credit risk and we compare them with term life insurance;
discuss event-triggered derivatives such as weather, catastrophe and longevity derivatives and how they can be used for risk management;
introduce equity-linked insurance and annuities (EIAs, VAs), relate them to common derivatives and describe how to manage mortality for these products;
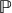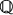put more emphasis on replication in the (two-period and n-period) binomial model and in the Black-Scholes-Merton model to better grasp the origins of the so-called actuarial/real-world and risk-neutral probabilities (or the (in)famous and measures);
implement and rebalance dynamic hedging strategies over several periods;
introduce pricing and replication in incomplete markets and analyze the impact of market incompleteness on insurance and risk management;
derive the Black-Scholes formula using simple limiting arguments rather than using stochastic calculus;
implement Monte Carlo methods with variance reduction techniques to price simple and exotic derivatives;
present immunization techniques alongside Greeks-based hedging;
cover in details how to delta-gamma/rho/vega hedge a liability and how to rebalance periodically a hedging portfolio.

Moreover, the book contains many actuarial applications and examples to illustrate the relevance of various topics to actuaries.

To meet the above-mentioned objectives, we assume the reader has basic skills in calculus (differentiation and integration of functions), probability (at the level of the Society of Actuaries’ Exam P), interest theory (time value of money) and, ideally, a basic understanding of elementary stochastic processes such as random walks.

Structure of the book

This book is targeted mainly toward undergraduate students in actuarial science and practitioners with an actuarial science background seeking a solid but yet accessible introduction to the quantitative aspects of modern finance. It covers pricing, replication and risk management of derivatives and actuarial liabilities, which are of paramount importance to actuaries in areas such as asset-and-liability management, liability-driven investments, banking, etc.

The book is divided into three parts:

Part 1: Introduction to actuarial finance
Part 2: Binomial and trinomial tree models
Part 3: Black-Scholes-Merton model

In each chapter, on top of the presented material, there is a set of specific objectives, numerical examples, a point-form summary and end-of-chapter exercises. Additional complementary information, such as historic notes or mathematical details, is presented in boxes. Finally, warning icons appear in the margin when a given topic, a concept or a detail deserves extra care or thought.

The content of the book is as follows.

Part 1: Introduction to actuarial finance

After an introductory chapter that puts into perspective the work of actuaries in the financial world, more standard chapters on financial securities, forwards and futures, swaps and options follow. Then, the next two chapters are devoted to the engineering of derivatives payoffs and liabilities, i.e. to the analysis of the structure of payoffs/liabilities, which is at the core of no-arbitrage pricing. Finally, a whole chapter describes insurance products bearing financial risk, namely equity-linked insurance and annuities (ELIAs).

In Chapter 1 – Actuaries and their environment, we put into context the role of the actuary in an insurance company or a pension plan. We explain how to differentiate between (actuarial) liabilities and (financial) assets, and between financial and insurance markets. We describe the various insurance policies and financial securities available and we compare actuarial and financial risks, short- and long-term risks, and diversifiable and systematic risks. Finally, we analyze various risk management methods for systematic risks.

In Chapter 2 – Financial markets and their securities, we provide an introduction to financial markets and financial securities, especially stocks, bonds and derivatives. We present the term structure of interest rates, we calculate the present and future value of cash flows and we explain the impact of dividends on stock prices. We also explain how actuaries can use derivatives and why pricing in the financial market is different from pricing in the insurance market. Finally, we look at price inconsistencies and how to create arbitrage opportunities.

In Chapter 3 – Forwards and futures, we provide an introduction to forwards and futures. We look at situations where forward contracts and futures contracts can be used to manage risks, and we explain the difference between a forward contract and a futures contract. We explain how to replicate the cash flows of forward contracts and calculate the forward price of stocks and of foreign currencies. Finally, we describe the margin balance on long and short positions of futures contracts.

In Chapter 4 – Swaps, we provide an introduction to swaps with an emphasis on those used in the insurance industry, namely interest rate swaps, currency swaps and credit default swaps. We present their characteristics, explain their cash flows and compute their values.

In Chapter 5 – Options, we give an introduction to standard options. We explain the differences between options to buy (call) and options to sell (put), as well as the difference between options and forward contracts. We explain when an option is used for hedging/risk management or for speculating purposes. Finally, we describe various investment strategies using options.

In Chapter 6 – Engineering basic options, we want to understand how to build and relate simple payoffs and then use no-arbitrage arguments to derive parity relationships. We see how to use simple mathematical functions to design simple payoffs and relate basic options and how to create synthetic versions of basic options, including binary options and gap options. Finally, we analyze when American options should be (early-)exercised.

In Chapter 7 – Engineering advanced derivatives, we provide an introduction to exotic/path-dependent options and event-triggered derivatives. We describe the payoff of various derivatives including barrier, Asian, lookback and exchange options, as well as weather, catastrophe and longevity derivatives. We explain why complex derivatives exist and how they can be used. Finally, we show how to use no-arbitrage arguments to identify relationships between the prices of some of these derivatives.

In Chapter 8 – Equity-linked insurance and annuities, we give an introduction to a large class of insurance products known as equity-linked insurance and annuities. First, we present relationships and differences between ELIAs and other derivatives. Then, after defining three indexing methods, we show how to compute the benefit(s) of typical guarantees included in ELIAs. We explain how equity-indexed annuities and variable annuities are funded and analyze the losses tied to these products. Finally, we explain how mortality is accounted for when risk managing ELIAs.

Part 2: Binomial and trinomial tree models

In the second part, we focus on the binomial tree model and the trinomial tree model, two discrete-time market models for the replication, hedging and pricing of financial derivatives and equity-linked products. By keeping the level of mathematics low, the binomial model allows greater emphasis on replication (as opposed to pricing), a concept of paramount importance for actuaries in asset and liability management. The intuition gained from the binomial model will be used repeatedly in the Black-Scholes-Merton model. Finally, as market incompleteness is a crucial concept in insurance markets, the trinomial tree model is treated in a chapter of its own. This model is simple and yet powerful enough to illustrate the idea of market incompleteness and its consequences for hedging and pricing.

In Chapter 9 – One-period binomial tree model, we first describe the basic assets available and we identify the assumptions on which this model is based. Then, we explain how to build a one-period binomial tree. Most of the chapter is devoted to the pricing of derivatives by replication of their payoff, from which we obtain risk-neutral pricing formulas.

In Chapter 10 – Two-period binomial tree model, we consider again the replication and the pricing of options and other derivatives, but now in a two-step tree. First, we explain how to build a two-period binomial tree using three one-period binomial trees. Then, we build dynamic replicating strategies to price options, from which we obtain risk-neutral pricing formulas. Finally, we determine how to price options in more complex situations: path-dependent options, options on assets that pay dollar dividends, variable annuities or stochastic interest rates.

In Chapter 11 – Multi-period binomial tree model, we see how to build a general binomial tree. We relate the asset price observed at a given time step to the binomial distribution and we highlight the differences between simple options and path-dependent options. We explain how to set up the dynamic replicating strategy to price an option and then obtain risk-neutral pricing formulas in a multi-period setup.

In Chapter 12 – Further topics in the binomial tree model, we extend the binomial tree to more realistic situations. We determine replicating portfolios and derive risk-neutral formulas for American-style options, options on stocks paying continuous dividends, currency options and futures options.

In Chapter 13 – Market incompleteness and one-period trinomial tree models, we define market incompleteness and we present the one-period trinomial tree model. We build sub-replicating and super-replicating portfolios for derivatives and explain that, in incomplete markets, there is a range of prices that prevent arbitrage opportunities. Then, we derive bounds on the admissible risk-neutral probabilities and relate the resulting prices to sub- and super-replicating portfolios in a one-period trinomial tree model. Second, we show how to replicate derivatives if the model has three traded assets. Also, we examine the risk management implications of ignoring possible outcomes when replicating a derivative. Finally, we analyze how actuaries cope with the incompleteness of insurance markets.

Part 3: Black-Scholes-Merton model

The third and last part of the book is devoted to the Black-Scholes-Merton model, the famous Black-Scholes formula and its applications in insurance. Both the model and its main formula are presented without the use of stochastic calculus; justifications are provided mainly by using the detailed work done previously in the binomial model and taking the appropriate limits. For the sake of completeness, a more classical treatment with stochastic calculus is also presented in two starred chapters, which can be skipped. In the last chapters, we apply generalizations of the Black-Scholes formula to price more advanced derivatives and equity-linked products, we provide an introduction to simulation methods and, finally, we present several sensitivity-based hedging strategies for equity risk, interest rate risk and volatility risk.

In Chapter 14 – Brownian motion, we provide the necessary background on Brownian motion to understand the Black-Scholes-Merton model and how to price and manage (hedge) options in that model. We also focus on simulation and estimation of this process, which are very important in practice. First, we provide an introduction to the lognormal distribution and compute truncated expectations and the stop-loss transform of a lognormally distributed random variable. Then, we define standard Brownian motion as the limit of random walks and present its basic properties. Linear and geometric Brownian motions are defined as transformations of standard Brownian motion. Finally, we show how to simulate standard, linear and geometric Brownian motions to generate scenarios, and how to estimate a geometric Brownian motion from a given data set.

In Chapter 15 – Introduction to stochastic calculus***, we provide a heuristic introduction to stochastic calculus based on Brownian motion by defining Ito’s stochastic integral and stochastic differential equations (SDEs). First, we define stochastic integrals and look at their basic properties, including the computations of the mean and variance of a given stochastic integral. Then, we show how to apply Ito’s lemma in simple situations. Next, we explain how a stochastic process can be the solution to a stochastic differential equation. Finally, we study the SDEs for linear and geometric Brownian motions, the Ornstein-Uhlenbeck process and the square-root process, and understand the role played by their coefficients.

In Chapter 16 – Introduction to the Black-Scholes-Merton model, we lay the foundations of the famous Black-Scholes-Merton (BSM) market model and we provide a heuristic approach to the Black-Scholes formula. More specifically, we present the main assumptions of the Black-Scholes-Merton model, including the dynamics of the risk-free and risky assets, and connect the Black-Scholes-Merton model to the binomial model. We explain the difference between real-world (actuarial) and risk-neutral probabilities. Then, we compute call and put options prices with the Black-Scholes formula and price simple derivatives using risk-neutral probabilities. Also, we analyze the impact of various determinants of the call or put option price. Finally, we derive replicating portfolios for simple derivatives and show how to implement a delta-hedging strategy over several periods.

In Chapter 17 – Rigorous derivations of the Black-Scholes formula***, we provide a more advanced treatment of the BSM model. More precisely, we provide two rigorous derivations of the Black-Scholes formula using either partial differential equations (PDEs) or changes of probability measures. In the first part, we define PDEs and show a link with diffusion processes as given by the Feynman-Kač formula. Then, we derive and solve the Black-Scholes PDE for simple payoffs and we show how to price and replicate simple derivatives. In the second part, we explain the effect of changing the probability measure on random variables and on Brownian motions (Girsanov theorem). Then, we compute the price of simple and exotic derivatives using the risk-neutral probability measure.

In Chapter 18 – Applications and extensions of the Black-Scholes formula, we analyze the pricing of options and other derivatives such as options on dividend-paying assets, currency options and futures options, but also insurance products such as investment guarantees, equity-indexed annuities and variable annuities, as well as exotic options (Asian, lookback and barrier options). Also, we explain how to compute the break-even participation rate or annual fee for common equity-linked insurance and annuities.

In Chapter 19 – Simulation methods, we apply simulation techniques to compute approximations of the no-arbitrage price of derivatives under the BSM model. As the price of most complex derivatives does not have a closed-form expression, we illustrate the techniques by pricing simple and path-dependent derivatives with crude Monte Carlo methods. Then, we describe three variance reduction techniques, namely stratified sampling, antithetic and control variates, to accelerate convergence of the price estimator.

In Chapter 20 – Hedging strategies in practice, we analyze various risk management practices, mostly hedging strategies used for interest rate risk and equity risk management. First, we apply cash-flow matching or replication to manage interest rate risk and equity risk. Then, we define the so-called Greeks. We explain how Taylor series expansions can be used for risk management purposes and highlight the similarities between duration-(convexity) matching and delta(-gamma) hedging. We show how to implement delta(-gamma) hedging, delta-rho hedging and delta-vega hedging to assets and liabilities sensitive to changes in both the underlying asset price and the other corresponding financial quantity. Finally, we compute the new hedging portfolio (rebalancing) as conditions in the market evolve.