2
The Passage of Time
In Chapter 1 we distinguished static from dynamic theories of time. According to dynamic theories of time temporal passage is an objective, mind-independent feature of reality. When we introduced the concept of temporal passage we noted that much of the discussion surrounding this topic is cloaked in metaphor. Our goal in this chapter is to try and get behind the metaphor even more, and provide a more sustained analysis of temporal flow. We will consider a range of philosophical arguments for the view that temporal passage is incoherent. These arguments suggest that there may be no consistent unpacking of the metaphorical language that is so often used to describe the flow of time. Along the way we will consider the prospects for addressing these arguments and thus rescuing the dynamic theory of time.
2.1. What is Temporal Passage?
One of the earliest accounts of temporal passage in the contemporary philosophy of time is the account proposed by McTaggart. As we discussed in Chapter 1, McTaggart draws a distinction between the A-series and the B-series. It is useful to briefly remind ourselves of the distinction. A B-series ordering is one that orders times in terms of the B-relations. These relations are the relations of earlier-than, later-than and simultaneous-with. Importantly, these relations are unchanging: if X is earlier than Y, then this is a fact about the universe that never changes. It is not the case, for instance, that X is earlier than Y on Tuesday, and later than Y on Wednesday. An A-series ordering of times is an ordering of times in terms of the A-properties. Whereas the B-series makes use of relations between times, the A-series makes use of intrinsic, monadic (i.e. non-relational), irreducible properties of being present, being past and being future. In an A-series ordering, there is exactly one time that possesses the property of being present. For any time that is earlier than the present, that time possess the property of being past, and for any time that is later than the present, that time possesses the property of being future.
As we noted briefly in Chapter 1, the A-series is one way to understand what it is for there to be temporal passage. But it is not the only way of understanding that notion. One of the limitations of understanding temporal passage purely in A-series terms is that temporal passage so understood presupposes the existence of properties of being present, being past and being future. Moreover, it assumes that every time that there is possesses one of these properties.
This way of thinking about temporal passage won’t work for some of the dynamic theories of time discussed in Chapter 1. Consider, for instance, presentism. According to presentism, only present entities exist. Because only present entities exist, there are no past or future entities available that can possess properties like being past or being future. Indeed, about the only dynamic theory of time that neatly fits the A-series conception is the moving spotlight theory. And, indeed, the A-series does illuminate that view. We can now see what the moving spotlight posited by the moving spotlight model is: it is the property of being present, sweeping across the universe, leaving the property of being past in its wake, and progressively eating up the property of being future. But for dynamic theories of time that are not moving spotlight views, a different conception of the passage of time is required.
We will look at the precise nature of temporal passage for these other views in the next section. First, however, it is useful to have a general statement of temporal passage that will apply to all versions of the dynamic theory of time. To this end, we may characterise the passage of time in terms of a moving present. There is some time – the present – that is metaphysically special in some respect. Exactly which moment is metaphysically special in this manner changes. So, on Tuesday at 2pm, 2pm is the metaphysically special present. When it is 3pm, 3pm will be the metaphysically special present, and 2pm will lose its special status. And on it goes.
General conception of passage: There is an objective, metaphysical fact, regarding which moment is present, and which moment that is, changes.
The A-series fits under this general conception. In the A-series, the present is metaphysically special in virtue of the existence of a monadic property of presentness. This property moves in so far as the A-series is constantly changing. But while the above basic conception of temporal flow subsumes the A-series, it is broader still. For it allows for there to be ways of conceiving of temporal passage that make no use of monadic properties of presentness, pastness and futurity, as we shall now see.
2.2. Flavours of Passage
Each version of the dynamic theory of time will understand the notion of temporal passage just articulated in a different way. In particular, each version will provide a different account of what it is for there to be a metaphysically special moment; they differ over what it is to be present. As noted, a moving spotlight theory of time will maintain that the metaphysical specialness of the present consists in the possession, by some time, of a monadic, intrinsic, irreducible property of presentness. The flow of time, on this view, consists in the shift in which moment possesses this property.
A presentist, by contrast, will equate the metaphysical specialness of the present with existence. What it is to be present is to exist, according to presentism. The flow of time, on this view, involves a constant shift in what exists. At 2pm on Tuesday all of the things that are simultaneous with one another at 2pm exist. None of the 1pm things exist and none of the 3pm things exist. As time passes, however, the 2pm things will go out of existence and the 3pm things will come into existence. For the presentist, past and future are still understood in terms of the earlier- and later-than relations. To be past is to be earlier than the present and to be future is to be later than the present. One of the chief challenges facing presentism is how to give an account of cross-temporal relations such as these, relations that link things that exist with things that do not.
A growing block theorist, by contrast, equates the metaphysical specialness of the present with the notion of being the most recent moment to come into existence. The flow of time, on this view, involves the progressive coming into existence of new times. The flow of time is therefore accretive: it is constantly enlarging the sum total of existing things. So when 2pm on Tuesday is present, 2pm is the latest moment to have come into existence. When it is 3pm, 3pm will be the latest moment to have come into existence. 2pm, by contrast, will have shifted to being past, since it is no longer the latest moment to come into existence. The growing block theorist has an easy account of the distinction between the past and the future: what it is to be past is to be an existing thing that is earlier than the present. What it is to be future is to be a non-existent thing that is later than the present. As with the presentist, the growing block theorist may need to provide an account of how there can be relations between present existing things and future non-existent things.
We have before us three concepts of temporal passage. These different approaches to passage provide unique interpretations of the flow of time. They are all united, however, in their understanding of passage in terms of a moving present, but they differ over what it is for the present to move in this way. While there is disagreement of this kind, there is also a very general agreement about what’s going on when time passes. On every one of the views just discussed, the passage of time involves a shift in ontology: what exists and which things have which properties. The moving spotlight view involves a shift in the things that possess the property of being present. Presentism involves a constant shift in what exists. The growing block view involves the gradual increase in what exists.
It is an interesting question as to whether the passage of time must be thought of in these terms. Do we have to think of it ontologically, in terms of some change in what exists and the properties that existing things possess? Or are there other ways to conceptualise this notion? We leave these questions to the reader.
2.3. Problems for Passage
Let us focus on the first concept of flow articulated above: the notion of a moving present. One of the core aspects of this account of temporal passage is that it seems to require a certain kind of change: either change in what exists, or change in which things possess which properties and so on. Because the passage of time involves a constant change in ontology, it is open to some fairly serious objections. In what follows we will outline the two most pressing such objections: the rate of flow argument and McTaggart’s paradox. Before considering these objections in detail it is worth asking what they would show, were they to succeed. As will become apparent, if either argument succeeds then it shows that there is something internally incoherent in the very notion of temporal passage. As such, if either argument succeeds we should conclude that, of necessity, there is no temporal passage. That is, we should conclude that temporal passage is impossible. That leaves us with two options. We could reject both the constitutive and extensional A-theory in favour of the B-theory or C-theory, and conclude that temporal passage is not essential for there being time. Indeed, given the impossibility of temporal passage we will conclude that there is no world with temporal passage. Alternatively, we could accept the constitutive A-theory and reject the extensional A-theory. Then we will hold that temporal passage is essential to there being time, which means that we will conclude not only that there is actually no time, since there is no temporal passage, but, more strongly, that time is impossible because time would require there to be temporal passage, and temporal passage is impossible. It is worth bearing these options in mind as we consider each of the arguments.
2.3.1. The Rate of Flow Argument
The first of these objections can be set out as follows. Change is usually understood as variation over time: X changes when X takes on different values at different times. But how, then, do we understand the idea that time itself changes? Without invoking an extra dimension of time (more on this later on) the only option is to understand the idea that time itself changes in terms of times taking different values at different times. But this is difficult to understand. One way to draw out the problem is to think of the rate of such change.
If time passes, then it must pass at some rate. That’s because all changes happen at some rate. For instance, when a light changes from red to green, that change can happen slowly (taking an hour) or quickly (taking a second). Either way, the change happens at some rate. The question about the flow of time, then, is this: if time passes at some rate, at what rate does it pass? A rate is a measure of some change over time. So how fast does time pass, thought of in this manner? The only reasonable answer, it would seem, is that time passes at one second per second: for every second that elapses, the present has moved one second into the future. But there are serious doubts about the idea that ‘one second per second’ is a coherent rate at all. Rates are usually understood in terms of the change of one quantity as a function of a change in another quantity. For instance, one might understand velocity in terms of the spatial distance travelled per unit of time. When we’re talking about the passage of time, however, it seems we are forced to measure the rate of time’s passing against itself. But that’s just not a meaningful rate. So time has no rate. So it doesn’t flow. So there is no such thing as temporal passage.
In order to address the rate of flow argument there are, broadly, three options available to the dynamic theorist. First, she might attempt to argue that the rate of flow specified above is a meaningful rate after all. There is nothing incoherent about the idea that time passes at one second per second, she might say. By way of analogy, suppose that Suzy and Billy both have ten dollars. Suppose that Suzy says to Billy: ‘for every dollar you give me, I will give you a dollar back’. The exchange rate between Suzy and Billy, then, is one dollar per dollar. Now, to be sure, Suzy and Billy are not going to become millionaires by exploiting this particular exchange rate. Indeed, they cannot bring it about that either of them has more than ten dollars. But that doesn’t make the exchange between them incoherent or otherwise meaningless. They can meaningfully exchange one dollar per dollar and can reasonably characterise their shifting financial situations in terms of this exchange rate.
One might worry about this analogy, however, for a couple of reasons. First, it is not obvious that the time and financial cases are genuinely analogous. In the time case, we are trading one second of time for one second of time. In the financial case, we are trading one of Suzy’s dollars for one of Billy’s dollars. So in the financial case, the rate of flow between Suzy and Billy involves two distinct quantities. In the time case, by contrast, we are exchanging only a single quantity. We can further grasp the difference by thinking in terms of other possible exchange rates between Suzy and Billy. Although Suzy and Billy are exchanging one dollar per dollar, they could exchange two dollars per dollar, or three dollars per dollar. Or some other rate entirely. In short, we can easily make sense of variations in the rate of exchange between them. In the temporal case, however, we cannot easily make sense of this. It just doesn’t make sense to say that time could flow faster: we cannot say that time could flow at two seconds per second or three seconds per second. That’s because all we have is a single quantity, and so any variation in the quantity that appears on one side of the rate of flow must be carried over onto the other side.
A second response to the rate of flow argument is to deny that the right characterisation of the flow of time is that it flows at one second per second. This is not the right characterisation precisely because it makes use of a single quantity only, and a single quantity cannot meaningfully vary with respect to itself. The challenge in defending this approach, however, is to find some second quantity against which the rate of flow can be meaningfully measured. One option, which we will explore below, is to invoke a second time dimension and use this as the measure of time’s flow. Barring that, however, the only other thing that we could possibly use to measure the flow of time is space. It is quite unclear, however, how we might understand the rate of temporal flow as variation over space. Such an account would involve saying that time flows at, say, one second per metre. But what could that mean? And would it correspond to the notion of temporal passage as we have been describing it, as involving a moving present?
The third and perhaps most promising response is to take issue with the initial formulation of the problem. As the problem was formulated, it relied on the idea that the passage of time is a kind of change. If the passage of time is a kind of change, where by ‘change’ we mean what we ordinarily mean by that term, then temporal passage must be understood as a variation in one quantity as a function of another. But, the dynamic theorist might argue, this is to misunderstand the claim that temporal flow is a kind of change. Change, after all, is something that happens in time as, for example, when we say that the weather has turned foul. What we mean is that, over time, the weather has shifted from being nice to being nasty. Temporal passage is not something that happens in time, it is something that happens to time. Because it is something that happens to time, we should not expect it to obey the normal rules that change in time obeys. We should not, for instance, expect that temporal passage should be understood as a variation in one quantity as a function of another. Temporal passage is something else entirely. Accordingly, we are simply making a mistake when we ask after the rate of time’s flow. It doesn’t have a rate, because it is not change in the normal sense.
The trouble with this third type of response to the rate of flow argument is that it renders the notion of temporal passage mysterious once more. At best, the claim that temporal passage involves change is another metaphor, at least in so far as ‘change’ is understood in the usual sense. But then what is temporal passage? How should it be understood? The dynamic theorist will probably reply that there just is no answer to this question. The flow of time is a primitive, unanalysable aspect of their theory. This might seem untoward. But, actually, it is perfectly acceptable to take something as primitive in the context of a theory. Indeed, every theory has to take something as primitive. It has to start from somewhere. For the dynamic theory of time, then, that starting point is temporal passage.
2.3.2. McTaggart’s Paradox
The second problem with the idea that time passes also aims to show that the passage of time is not a coherent notion. This problem, called McTaggart’s paradox (named for the philosopher who first proposed the paradox) focuses on the three notions of past, present and future. Suppose, as the dynamic theorist does, that these three notions are not merely perspectival. Rather, the distinction between the past, present and future is a metaphysically substantive one. Now, suppose further that the passage of time involves a shift in which events or objects possess the properties of being future, being present and being past. That is, time passes as the moving spotlight theorist says it does. The paradox proceeds as follows. Consider a particular event, E. Suppose that E is future. As time passes, E will become present and then it will become past. Accordingly, E will come to possess all three of these temporal attributions. But no event can possess more than one of these attributions: an event cannot both be future and past, or future and present, or present and past. So it cannot be the case that E possesses all three temporal attributions. But then it would seem that the flow of time is not possible, since it requires of a single event that it possess incompatible temporal attributions.
The obvious response to the problem as it has just been stated is this: an event E never possesses incompatible temporal attributions all at once. Rather, E possesses these three attributions successively. E is now future, but it will become present and then, after that, it will become past. But the italicised tenses in the preceding sentence give us nine further temporal attributions to deal with. To say that E is now future is to say that E is future in the present. To say that E will become present is to say that E is present in the future, and to say that E will be past is to say that E is past in the future. Call these further temporal attributions ‘second order’ temporal attributions. There are nine such attributions:
(1) Present in the present
(2) Present in the past
(3) Present in the future
(4) Past in the present
(5) Past in the past
(6) Past in the future
(7) Future in the present
(8) Future in the past
(9) Future in the future
The paradox can be reformulated using these nine temporal attributions. As time passes a single event E will come to possess all nine temporal attributions. But some of these temporal attributions are incompatible. For example, an event cannot be both future in the past and present in the past. So E cannot possess all of these temporal attributions. So E cannot be subject to the passage of time.
Again, the obvious response is: E does not possess all nine of these attributions at once. Rather, it possesses these attributions successively. It was present in the future, it will be past in the present and so on. But the italicised tenses give us twenty-seven third-order temporal attributions. The paradox can, however, be reformulated with respect to these twenty-seven attributions, and the same response is available: no event has them all at once, but has them successively. Spelling out the relevant notion of succession will give us eighty-one attributions, and so on. The passage of time thus seems to give rise to an infinite regress: an infinite series of temporal attributions at higher and higher orders.
Now, infinite regression is not always a problem. There are some infinite series that are completely well-behaved and give no reason for concern (think of the manner in which the successor function in number theory (i.e. X comes after Y) gives rise to an infinite sequence of numbers (e.g. the natural or ‘counting’ numbers 1, 2, 3, 4 …). The infinitely expanding series of temporal attributions is troubling because at each level of the series a paradox can be formulated. That is, when there are three temporal attributions, a paradox can be formulated for those three attributions. Avoiding the paradox requires rising up to the next level. But a paradox can be formulated there, and so on forever. There is a sense in which the paradox is never completely solved: it keeps revenging against us as we move up through this infinitely expanding sequence of temporal attributions.
Actually, it pays to be a bit careful here. Let us differentiate between a vicious regress and a non-vicious regress. Roughly, a regress is vicious with respect to a problem P if the problem at level n can only be solved at level n+1. A regress is non-vicious with respect to a problem P if the problem at level n can be solved at level n, but the solution forces the existence of another level, n+1, and the problem can be reformed at n+1. Intuitively, the concept of a vicious regress just articulated is tracking any problem that is only really solved in the infinite limit, if at all. The concept of a non-vicious regress is any problem that gives rise to a regress in the solution of that problem, but where the solution itself is not obtained only within the infinite limit but, rather, is obtained at any finite step in the regress.
With these sharper definitions in hand, is McTaggart’s paradox vicious or not? Maybe not. At each level, the paradox seems to get resolved. True, the paradox can then be reformulated at the next level. But the problem itself is still being solved, it is just that the solution forces an infinite series. McTaggart’s paradox, in other words, does not seem to be solved only in the limit. It seems to be solved at any finite step in the regress, it is just that the problem can be infinitely reformulated. Notice, however, that it’s a slightly different problem each time (the difference being the number of distinct temporal attributions that are used to formulate the problem).
One response to McTaggart’s paradox, then, is to deny the viciousness of the regress. Another response is to deny that the paradox hits every dynamic theory of time. As it was formulated above and, indeed, as McTaggart himself formulated it, the paradox focuses on the properties of being present, being past and being future. As we have already discussed, however, not every dynamic theory of time conceptualises temporal passage in these terms. So perhaps the paradox can be avoided by simply shifting to a different dynamic theory.
In the first instance, at least, this suggestion is no good. There is nothing essential about the use of properties in the formulation of McTaggart’s paradox. Every dynamic theory of time maintains a distinction between past, present and future. While the nature of this distinction changes, every dynamic theorist wants to be able to say things like ‘dinosaurs are past’ and ‘the big crunch is in the future’. But these statements are enough to get the paradox going. For every dynamic theorist will accept that ‘dinosaurs are both past and present’ is incoherent. And every dynamic theorist accepts that things shift from being future, to being present, to being past. So every dynamic theory faces the problem.
Still, one might disagree, at least to a certain extent. While the paradox strikes most dynamic theories of time, one might argue, it leaves presentism untouched. Why so? Well, in order for the paradox to succeed, we need to be able to say, truly, that there are some things that are both past and present (or some other incoherent temporal attribution). But there are no past things, if presentism is true. So nothing is ever both past and present. The same broad response applies to any set of incompatible temporal attributions: only present entities exist. So there is never going to be a case of a thing that resides under multiple temporal attributions, let alone incompatible ones.
A version of the paradox can, however, be reformulated against presentism as well. Here’s the basic idea. For the presentist, only present entities exist. Now, imagine the entire universe as a photograph at some present moment. The photograph would show present entities existing at a particular time, t1, and would show nothing existing at any other time. It would be a photograph in which pretty much everything is black, except for the thin sliver of the present. But, the presentist maintains, the present changes as time passes. To represent the passage of time, we can imagine a series of photographs. Each photograph represents the present moment. The first photograph represents the present moment at t1. The next represents the present moment at t2 and so on until the end of the universe.
All of these photographs represent the same universe. Accordingly, the presentist is ultimately going to have to combine all of these photographs into a single image, one that represents reality. But how do we do that? Suppose that we have just two photographs. In the first photograph t1 exists and is present, but t2 is future and is not present. In the second photograph, t2 exists and is present, but t1 is past and is not present. When we try to combine these photographs into a single consistent image, we end up with contradictions: t1 both exists and does not exist; t2 both exists and does not exist. The only way to avoid this outcome, it would seem, is to say that both t1 and t2 exist, or that both fail to exist, and reconcile the two photographs that way. But to take the first option is to admit that more than a single present moment exists, and to take the second is to admit that nothing exists. Neither option is a way of recovering presentism.
A similar argument can be used against any dynamic theory of time. Each dynamic theory will treat the world as a series of photographs; in each photograph the world looks different. Reconciling the series of photographs into a single, consistent image of the world will force the types of contradictions that seem to arise from McTaggart’s paradox. What’s nice about this way of stating the paradox is that it doesn’t rely on any regresses. The point is simply that the dynamic theory of time does not seem to admit of a single, consistent account of the universe. So the worries about whether McTaggart’s paradox involves a regress of some kind can reasonably be set aside. Of course, the dynamic theorist might, at this point, simply accept this consequence. Several philosophers have recently considered (or defended) views according to which there simply is no single, consistent, model of our universe: instead there are many inconsistent ‘fragments’ or ‘perspectives’ on the universe. Each fragment is consistent, but it is not possible to put these fragments together into a single model or picture of our world. If the dynamic theorist is willing to accept some sort of fragmentalism, or radical perspectivalism, then she has another way of resisting McTaggart’s paradox. This is not, however, an avenue we will pursue here.
2.4. Time and Hypertime
So far we have looked at some different accounts of what temporal passage is, and have considered two of the chief difficulties facing any account of temporal passage: the rate of flow argument and McTaggart’s paradox. In this section we will look at a unified solution to both problems. Consider, again, the rate of flow argument. The core problem here related to the fact that temporal passage cannot be reasonably understood as a kind of change. Change, it would seem, requires a variation of one quantity against another. But there is no second dimension of variation against which we can measure the type of change that is posited by the dynamic theory of time.
But what if there were some extra dimension of variation? Suppose that we have one time dimension, time, and a second dimension, hypertime. If we have a second temporal dimension, then it seems possible to define the rate of time’s passing in a meaningful manner. What we might say is that the present in time, t, moves at one second of time per one second of hypertime, ht. In other words, we may be able to use a second temporal dimension to provide a meaningful rate of passage for time, in much the same manner that we might give an analysis of velocity in terms of change in spatial location over time.
Positing hypertime also provides a solution to McTaggart’s paradox. The most straightforward way to see this is to focus on the generalised form of the paradox discussed at the end of the previous section. Consider, again, a presentist universe. As before, let us imagine such a universe as a sequence of snapshots. Let us suppose, for simplicity, that there are just four snapshots: S1, S2, S3 and S4. In S1, t1 is present and t2, t3 and t4 are future. So only t1 exists. In S2, t2 is present and t1 is past while t3 and t4 are future. In S3, t3 is present, t1 and t2 are past and t4 is future. In S4, t4 is present and t1, t2 and t3 are past. In each snapshot, only a single time exists. If we try to compile the snapshots into a single, flattened image, we get contradictions: t1 both exists and does not exist; t2 is both present and past, and so on. But now suppose that instead of combining the snapshots into a single, flattened image, we stack them, one atop the other. We then treat the entire stack as our ‘picture’ of the universe.
This is, effectively, what the addition of hypertime allows us to do. In order to combine photographs into a stack, we need to arrange them through a third spatial dimension. In order to arrange our snapshots of the universe into a stack, we need an extra temporal dimension in which to arrange them. With the addition of such a dimension, however, the stack can be produced. So, for example, S1 corresponds to our first hypertime, ht1. S2 corresponds to ht2. S3 corresponds to ht3 and S4 corresponds to ht4. If we look along the hypertime dimension, and scan across ht1 to ht4, we will see a universe animated. In one moment, the present is at t1. In another moment, it is at t2 and so on all the way through to t4. The universe pictured in such a way is consistent. Nothing is ever both present and past, at least not at the same hypertime. For instance, at ht1, t1 is present. At ht2, t2 is present. But at ht2 it is not the case that t1 is also present. Rather, at ht2, t1 is past. And so on for each of the snapshots. The same broad solution will work for any dynamic theory of time. For any dynamic theory of time the sequence of snapshots can be consistently arranged along a hyper-temporal dimension so as to avoid attributing incompatible temporal aspects to any one thing.
The appeal to hypertime, then, has a lot to recommend it. Unfortunately, it faces some fairly serious problems. First of all, there is very little evidence that our world has two temporal dimensions. Indeed, our best current physics is not obviously compatible with such an idea. General relativity uses a four-dimensional geometry to describe the universe. In this four-dimensional geometry, there is only a single dimension of time. Adding an extra dimension of time would force us to radically redevelop the geometry. Since gravity is, effectively, a function of the topology of a four-dimensional universe, altering the dimensionality of our universe may have profound implications for the nature of gravity. At the very least, the differential equations that correspond to general relativity would need to be rewritten, with an added dimension of freedom. Until this is done it is quite unclear how we might add a second temporal dimension into our understanding of the universe.
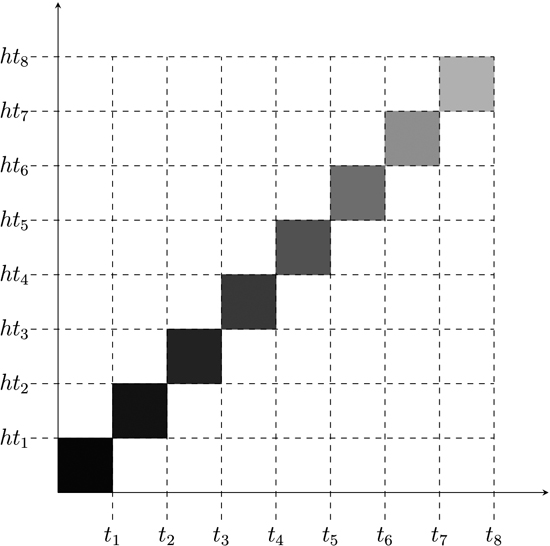
Figure 5 Time and Hypertime: Each hypertime corresponds to a different snapshot, enabling all of the snapshots to be reconciled into a single consistent picture of reality.
Second, there are substantial questions to be asked and answered surrounding the nature of hypertime itself. Is hypertime static or dynamic? Suppose that it is dynamic. If it is dynamic, then we will require a third dimension of time in order to avoid two-dimensional versions of the rate of flow argument or McTaggart’s paradox. If three-dimensional time is also dynamic, then we will require a fourth dimension of time and so on ad infinitum. This regress is vicious: the rate of flow argument and McTaggart’s paradox are only resolved in the infinite limit.
Suppose, then, that hypertime is static. If hypertime is static, then the rate of flow argument and McTaggart’s paradox are put to rest. But then one wonders what motivation one might have for adopting the dynamic theory of time. After all, the metaphysical foundations of the static theory have been ushered into the dynamic theory as well. Both theories ultimately stand on a static conception of the universe. But if both theories ultimately stand on a static conception of the universe, then why not just simply say that time is static and be done with it? Indeed, simplicity would seem to demand that we do away with the dynamic aspect of time and this extra temporal dimension and just go with what we know: a single, static dimension. A dynamic theorist will no doubt respond that the dynamic aspect of time is needed to do justice to our experiences of time. The static aspect of time alone is not enough to do justice to experience. Once again, then, we see the prospects for the dynamic theory of time come to hang on the weight of an argument that moves from the experience of time to the metaphysics of time. It is to this issue that we will turn, in Chapter 3.
2.5. Summary
In this chapter we have provided an overview of the two main problems for the idea that the passage of time is an objective, mind-independent phenomenon. Along the way, we have gained a better sense of what it might mean to say that time passes, as well as the way in which the passage of time is conceptualised differently on different versions of the dynamic theory. The core points covered in this chapter are as follows:
(1) The passage of time can be understood in terms of a moving present.
(2) The moving present can be understood in terms of a shift in the monadic properties of presentness, pastness and futurity or in terms of a changing ontology.
(3) The rate of flow argument challenges the idea that time passes by showing that there is no meaningful rate at which time passes.
(4) McTaggart’s paradox challenges the idea that time passes by maintaining that the passage of time leads to some form of inconsistency, e.g. inconsistent temporal attributions for events.
(5) The dynamic theorist may need to take the flow of time as a primitive notion in order to avoid these difficulties.
(6) The dynamic theorist might appeal to hypertime to avoid the problems, but then she must explain how hypertime works, and must reconcile it with our best current physics.
2.6. Exercises
i. Try to come up with a rate of change that we can apply to the passage of time that is meaningful.
ii. Consider a view according to which future and present entities exist and past entities do not. What notion of temporal passage would we need for such a view?
iii. Try to describe the difference between a vicious and a non-vicious regress. Provide an example unrelated to time of a regress of each kind.
iv. Consider the idea that temporal passage is a primitive notion. What do you think this means? Do you think it is plausible to think of the passage of time in this way?
v. Identify two difficulties with the idea that the passage of time can be reduced to the direction of time.
2.7. Glossary of Terms
Hypertime
A second temporal dimension.
Infinite Regress
An infinite series generated by repeatedly applying some condition, or repeatedly applying a problem.
Non-Vicious Regress
A regress is non-vicious with respect to a problem P if the problem at level n can be solved at level n, but the solution forces the existence of another level, n+1, and the problem can be reformed at n+1.
Ontological Change
A change in what exists and/or the properties that existing things possess.
Temporal Passage
The flow of time, often understood in terms of a moving present.
Vicious Regress
A regress is vicious with respect to a problem P if the problem at level n can only be solved at level n+1.
2.8. Further Readings
- H. Dyke (2011) ‘Time, Metaphysic of’, in Routledge Encylopedia of Philosophy, https://www.rep.routledge.com/articles/thematic/time-metaphysics-of/v-2. Section 6 of Dyke’s Routledge entry provides a fairly accessible introduction to McTaggart’s paradox.
- S. Prosser (2016) ‘The Passage of Time’ in Heather Dyke and Adrian Bardon, eds, A Companion to the Philosophy of Time (Wiley-Blackwell), pp. 315‒27. A useful introductory reading of the idea that time passes.
- J. J. C. Smart (1949) ‘The River of Time’ Mind 58 (232): 483‒94. This paper was the first to really articulate the rate of flow argument. Although it is not introductory it is fairly accessible.
- J. M. E. McTaggart (1908) ‘The Unreality of Time’ Mind 17 (68): 457‒74. This paper is the first to outline a paradox for the A-series. It is also the origin of the A-series/B-series distinction. The paper is not introductory and is really for more advanced students.
- D. Williams (1951) ‘The Myth of Passage’, The Journal of Philosophy 48 (15): 457‒72. Also for the advanced student, this paper presents a beautifully written and lucid argument against the objective reality of temporal passage.