… is to explain in as simple and non-technical a manner as possible the original breakthrough in quantitative finance that led to such a growth in the industry and the development of the subject. By now you will know all the mathematical tools to follow this chapter, and by the end of the chapter will be ready to apply the ideas to new situations.
the foundations of derivatives theory: delta hedging and no arbitrage the derivation of the Black–Scholes partial differential equation the assumptions that go into the Black–Scholes equation how to modify the equation for commodity and currency optionsThis is, without doubt, the most important chapter in the book. In it I describe and explain the basic building blocks of derivatives theory. These building blocks are delta hedging and no arbitrage. They form a moderately sturdy foundation to the subject and have performed well since 1973 when the ideas became public.
In this chapter I begin with the stochastic differential equation model for equities and exploit the correlation between this asset and an option on this asset to make a perfectly risk-free portfolio. I then appeal to no arbitrage to equate returns on all risk-free portfolios to the risk-free interest rate, the so-called ‘no free lunch’ argument.
These ideas are identical to those we saw in Chapter 3, it’s just that the math is different.
The arguments are trivially modified to incorporate dividends on the underlying and also to price commodity and currency options and options on futures.
This chapter is quite theoretical, yet all of the ideas contained here are regularly used in practice. Even though all of the assumptions can be shown to be wrong to a greater or lesser extent, the Black–Scholes model is profoundly important both in theory and in practice.
In Chapter 2 I described some of the characteristics of options and options markets. I introduced the idea of call and put options, amongst others. The value of a call option is clearly going to be a function of various parameters in the contract, such as the strike price E and the time to expiry T − t, T is the date of expiry, and t is the current time. The value will also depend on properties of the asset itself, such as its price, its drift and its volatility, as well as the risk-free rate of interest.1 We can write the option value as
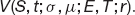
Notice that the semi-colons separate different types of variables and parameters:
I’m not going to carry all the parameters around, except when it is important. For the moment I’ll just use V(S, t) to denote the option value.
One simple observation is that a call option will rise in value if the underlying asset rises, and will fall if the asset falls. This is clear since a call has a larger payoff the greater the value of the underlying at expiry. This is an example of correlation between two financial instruments, in this case the correlation is positive. A put and the underlying have a negative correlation. We can exploit these correlations to construct a very special portfolio.
Use Π to denote the value of a portfolio of one long option position and a short position in some quantity Δ, delta, of the underlying:
The first term on the right is the option and the second term is the short asset position. Notice the minus sign in front of the second term. The quantity Δ will for the moment be some constant quantity of our choosing. We will assume that the underlying follows a lognormal random walk
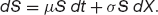
It is natural to ask how the value of the portfolio changes from time t to t + dt. The change in the portfolio value is due partly to the change in the option value and partly to the change in the underlying:
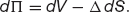
Notice that Δ has not changed during the time step; we have not anticipated the change in S. From Itô we have
Thus the portfolio changes by
Time Out…
Just like the binomial
Many people feel more at home with the binomial analysis than with the stochastic analysis of the Black–Scholes model. Well, in principle they are nearly identical, it’s just that the math is a little bit more abstract with the Black–Scholes model.
For example, all that Equation (6.2) says is that our special portfolio takes different values depending on what the asset does over the next time step. In the binomial model there were two different values that the portfolio could take, represented by the up and down movements of the asset. In the Black–Scholes model there’s a whole spectrum of possible values represented by the dS terms…so the dS terms represent the risk in the portfolio. And just as in the binomial model we’re going to make these terms disappear.
From a technical point of view, in the binomial model we did lots of modeling, hedging, etc. first before arriving at the Black–Scholes partial differential equation by performing a Taylor series expansion. In the Black–Scholes analysis the Taylor series expansion, in its stochastic form, comes first and the hedging, etc. comes later.
The right-hand side of (6.2) contains two types of terms, the deterministic and the random. The deterministic terms are those with the dt, and the random terms are those with the dS. Pretending for the moment that we know V and its derivatives then we know everything about the right-hand side of (6.2) except for the value of dS. And this quantity we can never know in advance.
These random terms are the risk in our portfolio. Is there any way to reduce or even eliminate this risk? This can be done in theory (and almost in practice) by carefully choosing Δ. The random terms in (6.2) are
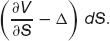
If we choose
then the randomness is reduced to zero.
Any reduction in randomness is generally termed hedging, whether that randomness is due to fluctuations in the stock market or the outcome of a horse race. The perfect elimination of risk, by exploiting correlation between two instruments (in this case an option and its underlying), is generally called delta hedging.
Delta hedging is an example of a dynamic hedging strategy. From one time step to the next the quantity 
changes, since it is, like V, a function of the ever-changing variables S and t. This means that the perfect hedge must be continually rebalanced.
Delta hedging was effectively first described by Thorp & Kassouf (1967) but they missed the crucial (Nobel prize winning) next step. (We will see more of Thorp when we look at casino blackjack as an investment in Chapter 20.)
After choosing the quantity Δ as suggested above, we hold a portfolio whose value changes by the amount
This change is completely riskless. If we have a completely risk-free change dΠ in the portfolio value Π then it must be the same as the growth we would get if we put the equivalent amount of cash in a risk-free interest-bearing account:
This is an example of the no-arbitrage principle.
To see why this should be so, consider in turn what might happen if the return on the portfolio were, first, greater and, second, less than the risk-free rate. If we were guaranteed to get a return of greater than r from the delta-hedged portfolio then what we could do is borrow from the bank, paying interest at the rate r, invest in the risk-free option/stock portfolio and make a profit. If, on the other hand, the return were less than the risk-free rate we should go short the option, delta hedge it, and invest the cash in the bank. Either way, we make a riskless profit in excess of the risk-free rate of interest. At this point we say that, all things being equal, the action of investors buying and selling to exploit the arbitrage opportunity will cause the market price of the option to move in the direction that eliminates the arbitrage.
Time Out…
The money-in-the-bank equation
Equation (6.5) is the same as ‘our first differential equation’ for money in the bank. The notation has changed from M to Π.
Substituting (6.1), (6.3) and (6.4) into (6.5) we find that
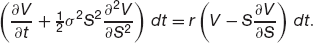
On dividing by dt and rearranging we get
A simulation of delta hedging
This is the Black–Scholes equation. The equation was first written down in 1969, but a few years passed, with Fischer Black and Myron Scholes justifying the model, before it was published. The derivation of the equation was finally published in 1973, although the call and put formulæ had been published a year earlier.2
The Black–Scholes equation equation is a linear parabolic partial differential equation. In fact, almost all partial differential equations in finance are of a similar form. They are almost always linear, meaning that if you have two solutions of the equation then the sum of these is itself also a solution. Financial equations are also usually parabolic, meaning that they are related to the heat or diffusion equation of mechanics. One of the good things about this is that such equations are relatively easy to solve numerically.
The Black–Scholes equation contains all the obvious variables and parameters such as the underlying, time, and volatility, but there is no mention of the drift rate μ. Why is this? Any dependence on the drift dropped out at the same time as we eliminated the dS component of the portfolio. The economic argument for this is that since we can perfectly hedge the option with the underlying we should not be rewarded for taking unnecessary risk; only the risk-free rate of return is in the equation. This means that if you and I agree on the volatility of an asset we will agree on the value of its derivatives even if we have differing estimates of the drift.
Another way of looking at the hedging argument is to ask what happens if we hold a portfolio consisting of just the stock, in a quantity Δ, and cash. If Δ is the partial derivative of some option value then such a portfolio will yield an amount at expiry that is simply that option’s payoff. In other words, we can use the same Black–Scholes argument to replicate an option just by buying and selling the underlying asset. This leads to the idea of a complete market. In a complete market an option can be replicated with the underlying, thus making options redundant. Why buy an option when you can get the same payoff by trading in the asset? Many things conspire to make markets incomplete such as transaction costs.
Time Out…
Slopes, gradients, etc.
The Black–Scholes partial differential equation is a relationship between the option value, the gradient in the S and t directions and the gradient of the gradient in the S direction. This sounds complicated. I can understand why. But it is really very simple when you actually come to solve the equation numerically. Here’s a foretaste of what’s in Chapter 28.
Imagine you’re at expiry of a call option. At that time do you know the option value as a function of the underlying asset S? Yes, of course, it’s just the payoff function
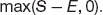
So you know one term in Equation (6.6), the last one.
Do you know the slope of the option value in the S direction at expiry? You certainly do. It’s zero for S < E and one for S > E. (Let’s not worry about what the value is at S = E, we’ll leave that to others to lose sleep over.) So you know the second-to-last term in the equation. Mathematically, this is represented by the Heaviside function, H(·), zero when its argument is negative and one when it is positive.
So
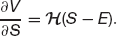
What about the slope of the slope in the S direction? Well, if the slope is zero or one, the slope of the slope is zero. So you know the second term in the equation.
To recap, we’ve got
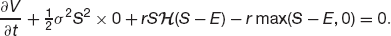
This is an equation for 
. For example, if S < E we have
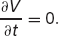
If S > E we have
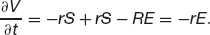
And the significance of this?
If we know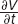 
then we know the slope of the option value in the t direction. If we know this slope then we can find the option value at the time just before expiry. If we are at time T − δt, where St is small, then the option value will be approximately
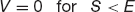
and
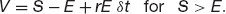
See how we have found the option value one time step before expiry? We can keep repeating this procedure over and over, working backwards in time until we get to the present. And as the time step gets smaller, so this approximation to the option value gets more accurate.
One, not-so-minor point. How does the option value ever become non-zero for S < E? I guess we should worry about what happens at S = E after all. This’ll sort itself out later on, don’t worry. What I’ve described here is the basis for the important numerical method known as the explicit finite-difference method, which we’ll be seeing lots of later on.
What are the ‘assumptions’ in the Black–Scholes model? Here is a partial list, together with some discussion.
There are many more assumptions but the above are the most important.
The Black–Scholes equation (6.6) knows nothing about what kind of option we are valuing, whether it is a call or a put, nor what is the strike and the expiry. These points are dealt with by the final condition. We must specify the option value V as a function of the underlying at the expiry date T. That is, we must prescribe V(S, T), the payoff.
For example, if we have a call option then we know that
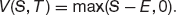
For a put we have
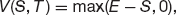
for a binary call
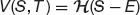
and for a binary put
where H(·) is the Heaviside function, which is zero when its argument is negative and one when it is positive.
The imposition of the final condition will be explained in Chapters 7 and 8, and implemented numerically in later chapters.
As an aside, observe that both the asset, S, and ‘money in the bank,’ ert, satisfy the Black–Scholes equation.
The first generalization we discuss is how to value options on stocks paying dividends. This is just about the simplest generalization of the Black–Scholes model. To keep things simple let’s assume that the asset receives a continuous and constant dividend yield, D. Thus in a time dt each asset receives an amount DS dt. This must be factored into the derivation of the Black–Scholes equation. I take up the Black–Scholes argument at the point where we are looking at the change in the value of the portfolio:
The last term on the right-hand side is simply the amount of the dividend per asset, DS dt, multiplied by the number of the asset held, −Δ. The Δ is still given by the rate of change of the option value with respect to the underlying, but after some simple substitutions we now get
(6.7)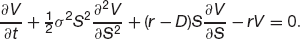 
Options on currencies are handled in exactly the same way. In holding the foreign currency we receive interest at the foreign rate of interest rf. This is just like receiving a continuous dividend. I will skip the derivation but we readily find that
(6.8)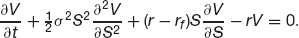 
The relevant feature of commodities requiring that we adjust the Black–Scholes equation is that they have a cost of carry. That is, the storage of commodities is not without cost. Let us introduce q as the fraction of the value of a commodity that goes towards paying the cost of carry. This means that just holding the commodity will result in a gradual loss of wealth even if the commodity price remains fixed. To be precise, for each unit of the commodity held an amount qS dt will be required during short time dt to finance the holding. This is just like having a negative dividend and so we get
(6.9) 
In the Black-Scholes equation there is no mention of the drift rate of the underlying asset μ. It seems that whether the asset is rising or falling in the long run, it doesn’t affect the value of an option. This is highly counter-intuitive. But we saw exactly the same thing happening in the binomial model of Chapter 3. At the same time as hedging away exposure to randomness, we hedge away exposure to direction.
We also saw in Chapter 3 that an option value can be thought of as being an expectation. But a very special expectation. In words:
We can write
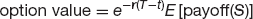
provided that the expectation is with respect to the risk-neutral random walk, not the real one.
But what do ‘real’ and ‘risk neutral’ mean exactly?
Real refers to the actual random walk as seen, as realized. It has a certain volatility σ and a certain drift rate μ. We can simulate this random walk on a spreadsheet very easily, and calculate expected future option payoffs, for example.
Risk neutral refers to an artificial random walk that has little to do with the path an asset is actually following. That is not strictly true, both the real and the risk-neutral random asset paths have the same volatility. The difference is in the drift rates. The risk-neutral random walk has a drift that is the same as the risk-free interest rate, r. So simulate risk-free random walks to calculate expectations if you want to work out theoretical option values. In Chapter 29 we will see how this is done in practice.
Time Out…
Real and risk neutral
This idea is probably more confusing than anything else in quantitative finance, but is extremely important. I will use the phrase ‘risk-neutral (random walk)’ several times in this book. Watch out for it, and remember that all it means is that you must pretend that the random walk of the underlying has a drift rate that is the same as the risk-free interest rate.
But remember also that such risk-neutral valuation is only valid when hedging can be used to eliminate all risk. If hedging is impossible, risk-neutral valuation is meaningless.
The derivation of the Black–Scholes equation above is the classical one, and similar to the original Black and Scholes derivation. There are other ways of getting to the same result. Here are a few, without any of the details. The details, and more examples, are contained in the final reference in the Further reading.
The value of an option can be shown to be an expectation, not a real expectation but a special, risk-neutral one. This is a useful result, since it forms the basis for pricing by simulation, see Chapter 29. The concepts of hedging and no arbitrage are obviously still used in this derivation. The major drawback with this approach is that it requires a probabilistic description of the financial world.
The binomial model is a discrete time, discrete asset price model for underlyings and again uses hedging and no arbitrage to derive a pricing algorithm for options. We have seen this in detail in Chapter 3. In taking the limit as the time step shrinks to zero we get the continuous-time Black–Scholes equation.
We’ll be seeing the Capital Asset Pricing Model later, for the moment you just need to know that it is a model for the behavior of risky assets and a principle and algorithm for defining and finding optimal ways to allocate wealth among the assets. Portfolios are described in terms of their risk (standard deviation of returns) and reward (expected growth). If you include options in this framework then the possible combinations of risk and reward are not increased. This is because options are, in a sense, just functions of their underlyings. This is market completeness. The risk and reward on an option and on its underlying are related and the Black–Scholes equation follows.
With the Black–Scholes continuous-time model, as with the binomial discrete-time model, we have been able to eliminate uncertainty in the value of a portfolio by a judicious choice of a hedge. In both cases we find that it does not matter how the underlying asset moves, the resulting value of the portfolio is the same. This is especially clear in the binomial model. This hedging is only possible in these two simple, popular models. For consider a trivial generalization: the trinomial random walk.
In Figure 6.1 we see a representation of a trinomial random walk. After a time step St the asset could have risen to uS, fallen to vS or not moved from S.
Figure 6.1 The trinomial tree.
What happens if we try to hedge an option under this scenario? As before, we can ‘hedge’ with −Δ of the underlying but this time we would like to choose Δ so that the value of the portfolio (of one option and −Δ of the asset) is the same at time t + δt no matter to which value the asset moves. In other words, we want the portfolio to have the same value for all three possible outcomes (see Figure 6.2). Unfortunately, we cannot choose a value for Δ that ensures this to be the case: this amounts to solving two equations (first portfolio value = second portfolio value = third portfolio value) with just one unknown (the delta). Hedging is not possible in the trinomial world. Indeed, perfect hedging, and thus the application of the ‘no-arbitrage principle’ is only possible in the two special cases: the Black–Scholes continuous time/continuous asset world, and the binomial world. And in the far more complex ‘real’ world, delta hedging is not possible.4
Figure 6.2 Is hedging possible?
Can we find values for forward and future contracts? How do they fit into the Black–Scholes framework? With ease. Let’s look at the simpler forward contract first.
Notation first. V(S, t) will be the value of the forward contract at any time during its life on the underlying asset S, and maturing at time T. I’ll assume that the delivery price is known and then find the forward contract’s value. At the end of this section I’ll turn this on its head to find the forward price. If you can’t remember the differences between all these terms, take a look at Chapter 1 again.
Set up the portfolio of one long forward contract and short Δ of the underlying asset:
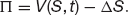
This changes by an amount
from t to t + dt. Choose
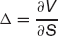
to eliminate risk. By applying the no-arbitrage argument we end up with exactly the Black–Scholes partial differential equation again.
The final condition for the equation is simply the difference between the asset price S and the fixed delivery price 
, say. So
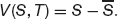
The solution of the equation with this final condition is
This is the forward contract’s value during its life.
How does this relate to the setting of the delivery price in the first place, and the newspaper-quoted forward price?
The delivery price is set initially t = t0 as the price that gives the forward contract zero value. If the underlying asset is S0 at t0 then
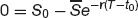
or
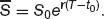
And the forward price, as quoted? This (see Chapter 1 for a reminder) is the delivery price, as varying from day to day. So the forward price for the contract maturing at T is
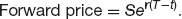
Emboldened by the above, let’s try to calculate the futures price. This is more subtle, that’s why I calculate it second. Use F(S, t) to denote the futures price.
Remember that the value of the futures contract during its life is always zero because the change in value is settled daily. This cashflow must be taken into account in our analysis.
Set up a portfolio of one long futures contract and short Δ of the underlying:
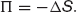
Where is the value of the futures contract? Is this a mistake? No, because it has no value it doesn’t appear in the portfolio valuation equation. How does the portfolio change in value?
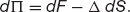
The dF represents the cashflow due to the continual settlement. Applying Itô’s lemma,
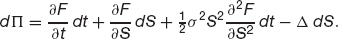
Choose
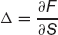
to eliminate risk. Set
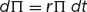
to get
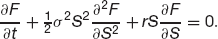
Observe that there are only three terms in this, it is not the same as the Black–Scholes equation.
The final condition is
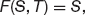
the futures price and the underlying must have the same value at maturity.
The solution is just
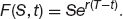
We’ve just seen that the forward price and the futures price are the same when interest rates are constant. They are still the same when rates are known functions of time. Matters are more subtle when interest rates are stochastic. But we’ll have to wait a few chapters to investigate this problem.
The final modification to the Black–Scholes model in this chapter is to value options on futures. Recalling that the future price of a non-dividend paying equity F is related to the spot price by
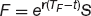
where TF is the maturity date of the futures contract. We can easily change variables, and look for a solution V(S, t) = V(F, t). We find that
(6.10)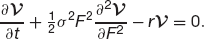 
The equation for an option on a future is actually simpler than the Black–Scholes equation.
This was an important but not too difficult chapter. In it I introduced some very powerful and beautiful concepts such as delta hedging and no arbitrage. These two fundamental principles led to the Black–Scholes option pricing equation. Everything from this point on is based on, or is inspired by, these ideas.
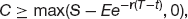
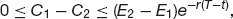
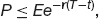
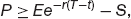
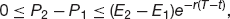
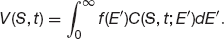
1 Actually, I’m lying. One of these parameters does not affect the option value.
2 The pricing formulæ were being used even earlier by Ed Thorp to make money.
3 Life, and everything in it, is based on arbitrage opportunities and their exploitation. Evolution is statistical arbitrage.
4 Is it good for the popular models to have such an unrealistic property? These models are at least a good starting point.
