© Springer Nature Switzerland AG 2020
E. Lindner et al. (eds.)Mathematical Modelling in Real Life ProblemsMathematics in Industry33https://doi.org/10.1007/978-3-030-50388-8_12

12. Networks of Antennas: Power Optimization

Stéphane Labbé1  
(1)
Univ. Grenoble Alpes, CNRS, Inria, Grenoble INP (Institute of Engineering Univ. Grenoble Alpes), Grenoble, France
 
 
Stéphane Labbé
Email: stephane.labbe@univ-grenoble-alpes.fr
Keywords
Applied mathematicsElectromagnetismModellingOptimization

12.1 Introduction of the Problem

In this text, we illustrate the process leading from a physical problem to an effective simulation. This process will display to three types of models. The first one, the most simple, will provide the opportunity to familiarise with the model and the existence of solutions to the problem, a second, more complex, will illustrate the necessity of numeric computations and at last we will give a complete formulation. The example we chose is the optimisation of a network of antennas. For the sake of simplification, the antennas taken into consideration will be assimilated to discrete dipolar systems. The goal of this study is to give an algorithm for antennas placement and power regulation. In a first part, we will focus on the modelling of the problem. We will start by setting the problem and choose the notations, and will, then, focus on the modelling of an antenna, explaining the link between the electromagnetic equations and a dipolar antenna. In the second, third and fourth parts, we will treat the three optimisation problems.

12.2 A Network of Antennas: Modelling

The first work to perform in order to model a situation, is to set the problem in mathematical terms. The built model will enable the study and optimisation of the situation parameters. This first milestone of the modelling and simulation process is very important and must be carefully treated. The key of the modelling process is to answer the question: “what do you want to do?”. This question is, not only about what we are modelling but also about what we want to do with this model. Is this work will be exploited in order to forecast the behaviour of a system, to understand and enhance a modelling or to compute specific parameters? In our case, the objective is clear: how to optimise the topology of an antenna network in order to provide a given signal strength on a given territory. The accuracy of the physical hypothesis is not required, then we can simplify the model with the assumption that antennas are dipoles and the signal is not harmonic in time. These antennas, in finite number, are set on a collection of points in space. The set of antennas will induce a resultant power in the whole space, the question we want to tackle here is how to optimise the number of antennas, their position and power to ensure that, in a given part of the space, the resultant power would stay between a minimum and a maximum. The questioning is quite common even if simplified here: how to optimise a network to certify that the power of the signal is sufficient to ensure its good functioning and sufficiently small to guarantee the safety of the system for users?

12.2.1 The Global Problem: Setting of a Mathematical Model

We define Σ as set of elements of $$\mathbb {R}^3$$ , the locations of the dipoles. This set indexes the dipoles; the set of dipoles is M = (μ x)x ∈ Σ, subset of $$S^2=\{u\in \mathbb {R}^3\vert \vert u\vert =1\}$$ , and the set of powers P = (p x)x ∈ Σ, subset of $$\mathbb {R}$$ . Moreover, we set Ω a subset of $$\mathbb {R}^3$$ , the location where measures have to be performed and $$( \underline {m},\overline {m})\in \mathbb {R}^2$$ , respectively the minimum and maximum required power. Given f, from $$\mathbb {R}^3\times S^2\times \mathbb {R}^3$$ into $$\mathbb {R}^3$$ , the function evaluating the power emitted by an antenna of power 1 in a given place of the space. Hence, for the whole space, except a small ball around the antenna position, we set:
$$\displaystyle \begin{aligned} \displaystyle \forall x\in\mathbb{R}^3\backslash\bigcup_{y\in\varSigma}B(y,\varepsilon),\mbox{ for every }\varepsilon\in\mathbb{R}^+_*,\\ F_\varepsilon(\varSigma,M,P)(x)=\left\vert\sum_{y\in\varSigma} p_y\ f(y,\mu_y,x)\right\vert,\end{aligned} $$
where F ε(Σ, M, P)(x) is the power developed by the network on a given point x. The problem now is to optimise the power P, the directions of dipoles M and the locations Σ, of dipolar antennas, in order to ensure on optimal power in Ω ε = Ω∖⋃y ∈ ΣB(y, ε), it is to say a power such that, locally, $$ \underline {m}\le F_\varepsilon (\varSigma ,M,P)(x)\le \overline {m}$$ .
To tackle this problem, we define the set of admissible solutions:
$$\displaystyle \begin{aligned} \mathcal{A}_\varepsilon=\left\{ (\varSigma, M, P)\subset \mathbb{R}^3\times S^2\times\mathbb{R}\vert \forall x\in\varOmega_\varepsilon,\; \underline{m}\le F_\varepsilon(\varSigma,M,P)(x)\le\overline{m} \right\}. \end{aligned} $$
Here, the question is: how to find the best triplet (Σ, M, P) and, what does means best?
First, we would be tempted to redefine, more exactly to restraint, the problem by freezing one or more parameters. For X subset of (Σ, M, P), we set $$\mathcal {A}_\varepsilon (X)$$ the function $$\mathcal {A}_\varepsilon $$ where the values X have been fixed. Hence, the problem to solve is: find (Σ, M, P) in $$\mathcal {A}_\varepsilon $$ such that
$$\displaystyle \begin{aligned} \sum_{x\in P} p_x \mbox{ is minimal}.{} \end{aligned} $$
(12.1)
This condition is motivated, in terms of modelling, by the goal to minimise the required energy needed to obtain an admissible network.
As we see, the problem is complex and several bottlenecks will be encountered

  • Does solutions exist?

  • If a solution exists, is this solution unique?

  • Can we compute explicitly this solution?

12.2.2 Power of an Antenna

In this section, we will focus on the power of a single antenna. The model we chose for the antenna is the dipolar one. In this approximation, we focus on a stationary problem but we could imagine a dynamical version based upon the complete Maxwell equations. For our purpose this level of precision in the model will be useless. For a complete and clear description of the physic of electromagnetism, see the book of J.D. Jackson [3]. The complete Maxwell equations are
$$\displaystyle \begin{aligned} \left\{\begin{array}{ll} \displaystyle \frac{\partial D}{\partial T}-\mbox{curl} \;H =0 \;\;\;& \displaystyle \frac{\partial B}{\partial T} + \mbox{curl}\; E = 0 \\ \displaystyle \mbox{div}\; D=\varepsilon_0 \rho &\displaystyle \mbox{div}\; B=0\\ \displaystyle D=\varepsilon_0 E & \displaystyle B=\mu_0(H+M) \end{array}\right.{} \end{aligned} $$
(12.2)
where D and E characterises the electric field, B and H the magnetic field, μ 0 and ε 0 physical constants, ρ the distribution of electric charges and M the distribution of magnetic moments.
In this study, as evoked above, we focus on the stationary part of the system and more exactly the magnetic part. Then, we will work on equations (12.2) (first line, first column and third line, second column):
$$\displaystyle \begin{aligned} \varepsilon_0\displaystyle \frac{\partial E}{\partial t}-\mbox{curl} \;H =0,\;\;\; \displaystyle B=\mu_0(H+M). \end{aligned} $$
Now, let perform a formal dimension study of the equation. In order to do so, we set, for $$(\overline {e},\overline {h},\overline {\mu },\overline {t},\overline {x})$$ , positive real, dimension factors:
$$\displaystyle \begin{aligned} E=\overline{e}e, H=\overline{h} h, M=\overline{\mu} m, T=\overline{t} t, X=\overline{x} x. \end{aligned} $$
Then, the equation in their dimensionless version becomes
$$\displaystyle \begin{aligned} \frac{\varepsilon_0 \overline{e}}{\overline{t}} \frac{\partial e}{\partial t}-\frac{\overline{h}}{\overline{x}}\mbox{curl}_x \;h =0,\;\;\; \displaystyle \overline{b}b=\mu_0(\overline{h} h+\overline{\mu} m), \end{aligned} $$
moreover we have
$$\displaystyle \begin{aligned} \frac{\overline{b}}{\overline{t}} \displaystyle \frac{\partial b}{\partial t} + \frac{\overline{e}}{\overline{x}}\mbox{curl}_x\; e = 0. \end{aligned} $$
The process we engage in order to obtain dimensionless equation implies, from the previous equations
$$\displaystyle \begin{aligned} \overline{\mu}=\overline{h}, \mu_0\overline{h}=\overline{b},\frac{\varepsilon_0 \overline{e}}{\overline{t}}=\frac{\overline{h}}{\overline{x}}, \frac{\overline{b}}{\overline{t}} = \frac{\overline{e}}{\overline{x}}. \end{aligned} $$
This leads to
$$\displaystyle \begin{aligned} \overline{h}=\frac{\overline{e}\overline{t}}{\mu_0\overline{x}}=\frac{\varepsilon_0 \overline{x} \overline{e}}{\overline{t}} \end{aligned} $$
then
$$\displaystyle \begin{aligned} \frac{\overline{x}^2}{\overline{t}^2}\varepsilon_0\mu_0 \frac{\partial e}{\partial t}-\mbox{curl}_x \;h =0,\;\;\; \displaystyle b= h+ m. \end{aligned} $$
We notice (see for example [3]) that $$\displaystyle \varepsilon _0\mu _0=\frac {1}{c^2}$$ , where c is the speed of light, and we have
$$\displaystyle \begin{aligned} \left(\frac{\overline{x}}{c\overline{t}}\right)^2 \frac{\partial e}{\partial t}-\mbox{curl}_x \;h =0,\;\;\; \displaystyle b= h+ m,\;\;\mbox{div}_x (h+m)=0.{} \end{aligned} $$
(12.3)
Under the hypothesis that $$\eta =\frac {\overline {x}}{c\overline {t}}$$ is small compared to 1, we obtain formally the following approximated system
$$\displaystyle \begin{aligned} \mbox{rot}_x h=0,\;\;\mbox{div}_x h = -\mbox{div}_x m.{} \end{aligned} $$
(12.4)
To understand this equation and determine its solution, we use several theoretical elements developed, for example, in [2, 4]. As we will not focus on this problem in this article, we next summarize the ideas, with no theoretical details, used in order to solve this problem. First, from the equation rotxh = 0, we deduce that, up to a constant, there exists φ, a function form $$\mathbb {R}^3$$ into $$\mathbb {R}$$ , such that ∇xφ = h. This step leads to a Laplace equation:
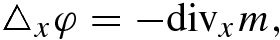
../images/475466_1_En_12_Chapter/475466_1_En_12_Equj_HTML.png
whose solution exists and is unique when m is a sum of Diracs like in our case; but, better than the uniqueness of the solution, we have a representation formula for this solution, using the Green kernel on $$\mathbb {R}^3$$ :
$$\displaystyle \begin{aligned} \forall x\in\mathbb{R}^3\backslash\{0\},\; G(x)=\frac{1}{4\pi \vert x\vert}, \end{aligned} $$
solution of the equation △xG = δ 0 [4]. Thanks to this formula, we can give the expression of the solution of equation (12.4)
$$\displaystyle \begin{aligned} h=- \nabla_x\mbox{div}_x \left(G* m\right), \end{aligned} $$
where ∗ designates the two entries operator of convolution (see for example [4]). In our case, we can explicit this solution, in particular, using the properties of the convolution, we focus on ∇xdivxG(x − y)
$$\displaystyle \begin{aligned} \nabla_x\mbox{div}_x G(x-y)=\begin{pmatrix}\partial_{x_1}^2 G(x-y) & \partial_{x_1}\partial_{x_2} G(x-y) & \partial_{x_1}\partial_{x_3} G(x-y)\\ \partial_{x_1}\partial_{x_2} G(x-y) & \partial_{x_2}^2 G(x-y) & \partial_{x_1}\partial_{x_2} G(x-y)\\ \partial_{x_1}\partial_{x_3} G(x-y) & \partial_{x_2}\partial_{x_3} G(x-y) & \partial_{x_3}^2 G(x-y)\end{pmatrix}, \end{aligned} $$
for (i, j) in {1, 2, 3}2, if i≠j
$$\displaystyle \begin{aligned} \partial_{x_i}\partial_{x_j}G(x-y)=\frac{-1}{4\pi}\left(3\frac{(x_i-y_i)(x_j-y_j)}{\vert x-y\vert^5}\right), \end{aligned} $$
if i = j
$$\displaystyle \begin{aligned} \partial_{x_i}^2 G(x-y)=\frac{-1}{4\pi}\left(3\frac{(x_i-y_i)^2}{\vert x-y\vert^5}-\frac{1}{\vert x-y\vert^3}\right), \end{aligned} $$
then
$$\displaystyle \begin{aligned} \nabla_x\mbox{div}_x G(x-y)=\frac{1}{\vert x-y\vert^3}\left(-\mbox{Id}+3\frac{(x-y)^t\; (x-y)}{\vert x-y\vert^2}\right), \end{aligned} $$
Hence, using the fact that δ 0 is a neutral element for the convolution, we obtain, for a magnetic moment mδ 0
$$\displaystyle \begin{aligned} \forall x\in\mathbb{R}^3\backslash B(0,\varepsilon),\;\; h(m)(x)=\frac{1}{4\pi \vert x\vert^3} \left(m - 3 \frac{x^t x}{\vert x\vert^2} m\right). \end{aligned} $$
In our case, we are interested on vertical antennas, then m = (0, 0, 1)t and on the measure at ground level, it is to say for x = (x 1, x 2, 0). Finally, with these hypothesis we obtain
$$\displaystyle \begin{aligned} \forall x\in\mathbb{R}^3\backslash B(0,\varepsilon),\;\; h(m)(x)=\frac{1}{4\pi \vert x\vert^3} \begin{pmatrix}0\\0\\1\end{pmatrix}. \end{aligned} $$
In what follows, we can only consider the third component of the magnetic field, h d,3, which corresponds to the local power. This result can be directly generalised to the networks of antennas defined at the beginning of the modelling description and give f $$\displaystyle \forall x\in \mathbb {R}^3\backslash \bigcup _{y\in \varSigma }B(y,\varepsilon )$$ , for every $$\varepsilon \in \mathbb {R}^+_*$$
$$\displaystyle \begin{aligned} F_\varepsilon(\varSigma,M,P)(x)=\left\vert \sum_{y\in\varSigma} p_y \frac{m_y}{4\pi \vert x-y\vert^3} \right\vert. \end{aligned} $$
In particular, using the previous results we set
$$\displaystyle \begin{aligned} \forall m\in\mathbb{N}, \alpha\in\mathbb{R}, W^m_\alpha=\left\{v\in\mathcal{D}'(\mathbb{R}^3),\forall\lambda\in\mathbb{N}^3,0\le\lambda\le m,(1+r^2)^{\frac{\alpha-m+\vert\lambda\vert}{2}}D^\lambda v\in L^2(\mathbb{R}^3)\right\}, \end{aligned} $$
where $$\displaystyle \mathcal {D}'(\mathbb {R}^3)$$ is the space of distributions (see [1]), D λ denotes the partial derivative application. The topological dual space of $$ W^m_\alpha $$ is $$ W^{-m}_{-\alpha }$$ .
Theorem 12.1

There exists φ in $$W^1_0$$ , unique up to a constant, such that ∇xϕ is solution of the equation rot xh = 0.

Then, we can use this theorem to analyse the equation rotxh = 0: there exists a unique φ in $$W^1_0$$ , up to a constant, such that ∇xφ = h, which implies
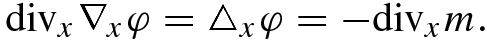
../images/475466_1_En_12_Chapter/475466_1_En_12_Equu_HTML.png
If m was in $$L^2(\mathbb {R}^3;\mathbb {R}^3)$$ , we use the following theorems
Theorem 12.2

The operator △xis an isomorphism from $$W^1_1$$ into $$W^{-1}_1\perp \mathbb {R}$$ where $$W^{-1}_1\perp \mathbb {R}=\{f\in W^{-1}_1, (f,1)=0\}$$ .

Lemma 12.1

Given f in $$L^2(\mathbb {R}^3)$$ , compactly supported, then div f is an element of $$W^{-1}_1\perp \mathbb {R}$$ .

$$\displaystyle \frac {\overline {x}^2}{\overline {t}^2}=\frac {1}{\varepsilon _0\mu _0}=c^2$$ , where c is the speed of light.

12.3 Two Fixed Antennas and Yet, Problems…

Let us begin with the case of two antennas. The power transmitted by this system, considering two antennas at distance λ with M = {e 3, e 3}1 and P = {p, p}, is the following, for ε, p and h in $$\mathbb {R}^+_*$$ with h > ε
$$\displaystyle \begin{aligned} F_\varepsilon(\{(0,0,h),(\lambda,0,h)\},M,P)(x)=p \frac{1}{4\pi \vert x-y_1\vert^3} + p \frac{1}{4\pi \vert x-y_2\vert^3}. \end{aligned} $$
Here, to simplify our problem, we focus on what happens at ground level: given R in $$\mathbb {R}^+_*$$ , R > λ, $$\varOmega =\{x\in \mathbb {R}\vert x\cdot e_3=0, \vert x-\frac {\lambda }{2}\vert \le R\}$$ , then, by construction in this particular case, Ω ε = Ω. Now, we re-write the power developed, setting x = u ⋅ e 1 + v ⋅ e 2:
$$\displaystyle \begin{aligned} \begin{array}{ll} F_\varepsilon(\{(0,0,2\varepsilon),(\lambda,0,2\varepsilon)\},M,P)(x)&=G(u,v)\\ &=\frac{p}{4\pi}\left(\frac{1}{\sqrt{u^2+v^2+h^2}^3} + \frac{1}{ \sqrt{(u-\lambda)^2+v^2+h^2}^3}\right),\\ \end{array} \end{aligned} $$
hence, we compute the gradient2 of G(u, v): $$\displaystyle \forall (u,v)\in \mathbb {R}^2$$ ,
$$\displaystyle \begin{aligned} \begin{array}{ll} \nabla G(u,v)&=\frac{3p}{4\pi} \left(\frac{ u}{\sqrt{u^2+v^2+h^2}^5} + \frac{u-\lambda}{\sqrt{(u-\lambda)^2+v^2+h^2}^5}\right)\cdot d_1 +\\ & \frac{3p}{4\pi} \left( \frac{v}{\sqrt{u^2+v^2+h^2}^5} + \frac{v}{\sqrt{(u-\lambda)^2+v^2+h^2}^5}\right)\cdot d_2. \end{array} \end{aligned} $$
Then, the critical points of G on $$\mathbb {R}^2$$ cancel this gradient and are: $$(0,0), (\lambda ,0), (\frac {\lambda }{2},0)$$ , the first and last are global maxima on $$\mathbb {R}^2$$ and the second is a local minimum. This property is obtained thanks to the fact that G is an element of $$C^\infty (\mathbb {R}^2;\mathbb {R})$$ . Now, we take into account the place of interest of the solution in Ω, then, let find the global minimum of G on Ω. We can easily prove that, if another minimum than the one exhibited in $$(\frac {\lambda }{2},0)$$ exists, it must take place on the boundary of Ω. Then, let explore this boundary:
$$\displaystyle \begin{aligned} \forall (u,v,0)\in\partial\varOmega, \exists\alpha\in [0,\pi]\;\vert\;u=R\ \cos{}(\alpha)+\frac{\lambda}{2},v=R\ \sin{}(\alpha),\mbox{ then }\\ G(u,v)=G(\alpha)=\frac{p}{4\pi}\left(\frac{1}{\sqrt{(R\ \cos{}(\alpha)+\frac{\lambda}{2})^2+R^2 \sin{}(\alpha)^2+h^2}^3} + \right.\\ \left.\frac{1}{ \sqrt{(R\ \cos{}(\alpha)-\frac{\lambda}{2})^2+R^2\sin{}(\alpha)^2+h^2}^3}\right), \end{aligned} $$
by a direct computation of the critical points of G(α), we obtain that the global minimum is attained for $$\alpha =\frac {\pi }{2}$$ and $$\frac {3\pi }{2}$$ . Now, the question is: can we ensure the admissibility of the solution? Here, admissibility means that on the domain of interest, the power developed by the antennas network is, on each point, comprised between $$ \underline {m}$$ and $$\overline {m}$$ :
$$\displaystyle \begin{aligned} \underline{m}\le G(\frac{\pi}{2}) \le F_\varepsilon(\{(0,0,2\varepsilon),(\lambda,0,2\varepsilon)\},M,P)(0,0,0)\le \overline{m}. \end{aligned} $$

12.4 More Antennas and No Analytic Solving

Now, let add more antennas in the network. Typically, we have to choose parameters to move in order to ensure the suitability of the configuration. We could have no constrains on the number of antennas, their positions, orientations and power, but it will be too complex. In order to manage this problem, we will treat two versions, in these versions, we keep the same orientation for all the antennas, it is to say (0, 0, 1). This means in our case:

  • Problem 1: Fixed number of antennas, fixed powers, the positions vary among a finite predetermined set of positions.

  • Problem 2: Fixed ground positions of the antennas, but the power and the height of the antennas vary.

  • Problem 3: Fixed power and heights of the antennas, the number of antennas is fixed and the positions vary freely.

Here, it will not be possible to treat analytically these cases in general case, we must use a powerful tool: the numerical optimisation (see for example [1]). In these three cases, the existence of at least a solution is almost every time guaranteed (classical proof), but not the uniqueness of this solution. In the first case, a systematic exploration of the set of solution may be long but possible. Here is a glimpse for each of these three problems.

12.4.1 Problem 1

Imagine that n is the number of antennas and p the number of possible position, then the number of possibilities is given by $$\displaystyle N(n,p)=A_p^n=\frac {p!}{(p-n)!}$$ . If p increases but n does not change, we see that a not so bad approximation of N(n, p) would be $$\displaystyle \tilde {N}(n,p)=p^n$$ . Then, when p becomes huge, if we want to compute F ε(Σ, M, P)(x), we must perform p computations of the function composed mainly by a sum of n real numbers. In this context, if n + is the elementary computation time, the total computation time becomes: np n+1n +. For example, if p = 100 and n = 10, on a computer whose performance is 3 GHz (109 Hz) and if we accept approximatively 100 cycles for n +, we have a total computation time of:
$$\displaystyle \begin{aligned} T=10.100^{11}.10^{-9}.100\, \mathrm{s} = 10^{16}\, \mathrm{s}, \end{aligned} $$
it means almost 317 millions of years! Even on the most powerful computer, 1017 flops, the computation time would be almost 11 days. This is not acceptable and in order to minimise the computation time, we could develop new efficient algorithms.

It is necessary to be careful as, for this problem, even if you find an algorithm sufficiently fast to performs computations, you do not know if the problem admits a solution; in fact, the constraints may not be fulfilled, in particular the maximum constraint if the power is too high but also the minimum constraint if the power is too low and the assigned position not sufficiently close.

12.4.2 Problem 2

Strangely, this problem is in fact simpler than the previous one. The positions are fixed but power and height of the antennas vary. The existence of a solution, like in the previous problem, is not guaranteed if the network of position is ill-prepared. Here, we can, starting from a well chosen configuration, apply a gradient method adapted to the constraint. Two problems appear: gradient method adapted to the constraint and good starting configuration. Here, the first step is to find a starting position. But, even if we find this kind of position, we are not sure to be able to attain the optimal solution. The projected gradient method will guarantee that the power decreases, respecting the constraints, but this decreases ensures that we arrive in a local minimum which is not necessarily the global minimum. The question is then: if we arrive in a local minimum, do we stop or do we try to find a better one in order to attain the global one. One algorithm is the so called simulated annealing, this method is inspired from the technics of heating and cooling when injecting heat in a system.

The main principle of this algorithm is then the following: a gradient descent algorithm (projected in our case), perturbed regularly in order to push out of possible non optimal minima bowl.

12.4.3 Problem 3

This case is much more difficult than the previous ones, but quite similar to Problem 2. We could see it as a simple adjunction of a third dimension (vertical position of the antenna and height). Here, we can imagine to apply the previously described algorithm.

12.5 A Complex Situation

In fact, modelling of the antennas covering is much more complex and would require the resolution of Maxwell equations in “town” represented by volume with given electric permittivity and magnetic permeability. The models used effectively are combining, in order to accelerate the computation, a ray tracing part, using the classical geometrical light propagation and, when necessary, a complete electromagnetic resolution in order to catch the diffraction phenomena.

12.6 Conclusion

This text is not extensive but gives the tracks in order to treat a simplified version of an important optimisation problem. Nevertheless, in scientific literature, there exists several occurrences treating the wave propagation in complex areas. In particular, the perfect simulation of problem is almost impossible. The propagation of electromagnetic wave using the Maxwell model is highly dependant of the exact geometry and composition obstacles, mobile or fixed, the humidity ratio and many other parameters not manageable exhaustively. In this context, the modelling process describe gives an example of simplification in order to build a manageable problem in finite time. This process is essential and must be carefully documented in order to identify the simplification and prevent errors of interpretations of the results obtained by simulation.

Acknowledgements

I thank Christophe Picard for his carefully reading this article and his pertinent remarks and propositions.