© Springer Nature Switzerland AG 2020
E. Lindner et al. (eds.)Mathematical Modelling in Real Life ProblemsMathematics in Industry33https://doi.org/10.1007/978-3-030-50388-8_2

2. 1D Models for Blood Flow in Arteries

Alexandra Bugalho de Moura1  
(1)
REM—Research in Economics and Mathematics; CEMAPRE—Center for Applied Mathematics and Economics, ISEG—Lisbon School of Economics and Management, Universidade de Lisboa, Lisbon, Portugal
 
 
Alexandra Bugalho de Moura
Email: amoura@iseg.ulisboa.pt
Keywords
Simplified mathematical modelsHyperbolic PDEWave propagationBlood flowArterial network

2.1 Introduction

Cardiovascular diseases remain one of the major causes of death in developed countries, with great social and economic impact. The simulation of the cardiovascular system helps understanding the physiology of blood circulation and enables non-invasive based clinical predictions. In the past years a large research activity has been devoted to complex 3D models of blood flow, using patient-specific cardiovascular geometries obtained through medical imaging, see [1–5] for some examples. The 3D simulations provide great detail on the blood flow patterns and allow to quantify a number o clinical indices. However, in many situations, the detailed information of the 3D model is not crucial, and the analysis of average quantities, such as flow rate and pressure, suffices to make clinical predictions and decisions [6, 7]. One of the features of blood circulation that is best captured by 1D simplified models in large arterial networks is its pulsatility. The elastic deformations in large arteries, such as the aorta or the carotid, are very important, helping to regularize blood flow during the cardiac cycle and leading to the pulse propagation that characterizes the arterial tree. This pulsation feature of blood flow in arteries has been observed and used in medical practices for hundreds of years. For example, the superposition of the waves reflected by medical devices, such as prosthesis or stents, with those produced by the heart can generate anomalous pressure peaks [8].

Several approaches can be followed to derive 1D models for blood flow in arteries, and different 1D models can be obtained depending on the level of simplification and on the characteristics of blood circulation kept during the simplification process. Here, the 1D model is derived by integrating the 3D Navier-Stokes equations for fluid flow coupled with a model for the vessel compliance, considering some simplifying assumptions [8, 9]. The resulting mathematical model consists of an hyperbolic system of partial differential equations (PDE’s). This means that it has wave-like solutions, with characteristic propagation speed and wave length. The numerical discretization of the 1D hyperbolic model is briefly discussed and numerical results are presented by considering an application to the study of blood circulation in the human brain. The purpose of the application here introduced is to answer the question “What are the effects of anatomical changes in the main arteries of the arterial system of the human brain?”. Regarding this subject and other clinical applications of 1D blood flow models, see for instance [6–8].

Following the same methodology of integrating over a generic axial section, more complex 1D models are derived, namely accounting for vessel curvature. This is achieved by relaxation of some simplifying assumptions. The inclusion of curvature means more complexity on the model, and the resulting system of PDEs reflects that extra complexity. In this context we discuss on the balance between simplicity and accuracy when doing mathematical modeling.

2.2 The 1D Model for Blood Flow in Arteries

The 1D model dates back to Euler [10], that already in 1775 introduced a 1D model of the human arterial system, yet claiming “the incredible difficulties for its solution”. Here the 1D model for blood flow in arteries is derived from the 3D model. We start by considering the Navier-Stokes equations for Newtonian incompressible fluids [11]:
$$\displaystyle \begin{aligned} \begin{array}{ll} \left\{ \begin{array}{rcl} \displaystyle \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} + \frac{1}{\rho} \nabla P-\nu \varDelta \mathbf{u} &=& \mathbf{f}, \\ \operatorname{div}{\mathbf{u}} &=& 0, \end{array} \right. & \mbox{ in } \varOmega \end{array} {} \end{aligned} $$
(2.1)
where the unknowns are the fluid velocity u = (u x, u y, u z) and pressure P, depending on space x = (x, y, z) and time t, with Ω the 3D vascular district of interest (see Fig. 2.1). Here f is a given function representing the volume forces exerted on the fluid, as e.g. the gravity, ρ is the constant blood density, and ν is the constant blood viscosity. We will neglect body forces, f = 0.
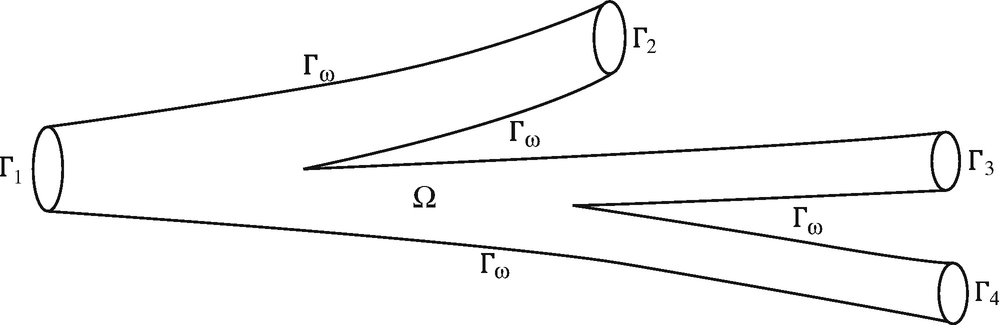
../images/475466_1_En_2_Chapter/475466_1_En_2_Fig1_HTML.png
Fig. 2.1

Generic vascular district Ω

The first equation of (2.1) describes the momentum conservation, while the second is the continuity equation and represents the conservation of mass.

The Navier-Stokes equations (2.1) are coupled with a model for the vessel wall displacement. Due to their complex structure, it is very difficult to devise appropriate and accurate models describing the mechanical behaviour of the artery walls. We will not go into detail on this subject, but we will consider that the walls of the vessel can move as the result of the fluid pressure. Equations (2.1), together with a model for the vessel wall, constitute a 3D FSI (fluid-structure interaction) model for blood flow in vascular districts.

2.2.1 Deriving the 1D Model

To derive the 1D model, we assume some simplifying hypothesis and then we integrate the 3D FSI model in each cross section S(z) of the vessel [9]. Applying this procedure, the only spatial coordinate remaining is the axial direction, denoted z. The simplifying assumptions are as follows:
  1. H1

    Axial symmetry. All quantities are independent from the angular coordinate, implying that each axial section S(z) remains circular during the wall motion. Hence, the tube radius R is a function of time t and axial direction z, R = R(t, z).

     
  2. H2

    Radial displacements. Wall displacements occur only in the radial direction. Defining R 0 as the reference radius, the wall displacement is d = de r, with e r the outward unit vector in the radial direction and d(t, z) = R(t, z) − R 0(t, z). The reference radius R 0, usually the radius of the vessel at rest, may depend on the axial direction z. Indeed, one characteristic of arteries is its tapering geometry.

     
  3. H3

    Fixed cylinder axis. The axial axis is fixed in time and the vessel expands and contracts around it.

     
  4. H4

    Constant pressure on each axial section. Pressure is assumed constant in each section, depending only on z and t, P = P(t, z). This is reasonable, since the pressure field of the fluid flow in 3D straight tubes is mainly constant in each section.

     
  5. H5

    No body forces. External forces are neglected. This is often considered already at the 3D model level.

     
  6. H6
    Axial velocity dominance. The velocity components orthogonal to the axial direction are neglected, since they are considered negligible when compared to the axial velocity: u = u z. In cylindrical coordinates we have u = (u r, u θ, u z) and
    $$\displaystyle \begin{aligned} u_z(t,r,\theta,z) = u_z(t,r,z) = \bar{u}(t,z) \times s \left(\frac{r}{R(t,z)}\right) {} \end{aligned} $$
    (2.2)

    where s(⋅) is the velocity profile, assumed constant in time, t, and space, z, which is in fact in contrast with the observations and 3D models. In this simplifying setting, s(⋅) may be though of as a profile representative of an average flow configuration. In practice, it will be considered flat or parabolic.

     
The unknown variables of the 1D model will be averaged quantities. The area is related with wall displacement and is given by A(t, z) =∫S(t,z)ds = πR 2(t, z); the flow rate, $$Q(t,z)=\int _{S(t,z)} u_z ds = A(t,z)\bar {u}(t,z)$$ , and mean velocity, $$\bar {u}(t,z) = \frac {1}{A(t,z)} \int _{S(t,z)} u_z ds =\frac {Q(t,z)}{A(t,z)}$$ , are related with fluid velocity. Due to H4, the mean pressure is $$\bar {p}(t,z)=\int _{S(t,z)} P(t,z) ds = P(t,z)A(t,z)$$ . All these quantities depend on t and z. In the notation, we will usually omit, unless needed, this dependence. From H6, H1, and (2.2) we have
$$\displaystyle \begin{aligned} \bar{u}(t,z) = \frac{1}{\pi R^2} \int_{0}^{2\pi} \int_{0}^{R} \bar{u}(t,z) s \left(\frac{r}{R}\right) r dr d\theta = \frac{\bar{u}(t,z)}{\pi R^2} 2\pi \int_{0}^R s\left(\frac{r}{R}\right) r dr \end{aligned}$$
meaning that $$\frac {R^2}{2} = \int _{0}^R s\left (\frac {r}{R}\right ) r dr$$ , and $$\int _0^1 s(y)ydy=0.5$$ by doing the change of variable r = Ry. We also define the momentum-flux coefficient or Coriolis coefficient, related with the fluid velocity profile:
$$\displaystyle \begin{aligned} \alpha=\frac{\int_{S}u_z^2 ds}{A \bar{u}^2} = \frac{\int_{S}\bar{u}^2 s^2 ds}{A\bar{u}^2} = \frac{\int_{S} s^2 ds}{A} \end{aligned}$$
It is easy to see that $$\alpha \geqslant 1$$ . In general α varies with time, t, and space, z. Here it is considered to be constant as a consequence of H6, since α is related with u r. For steady flow in circular rigid tubes the Navier-Stokes equations have the very well known Poiseuille solution, consisting of a parabolic velocity profile. For a Poiseuille profile we have s(y) = 2(1 − y 2) and α = 4∕3. For blood flow it has been found that the velocity profile is rather flat [11], corresponding to s(y) = 1 and α = 1.
From assumptions H4, H5 and H6, the Navier-Stokes equations (2.1) become:
$$\displaystyle \begin{aligned} \begin{array}{ll} \left\{ \begin{array}{rcl} \displaystyle \frac{\partial u_z}{\partial t} + \operatorname{div}(u_z \mathbf{u}) + \frac{1}{\rho} \frac{\partial P}{\partial z} - \nu \varDelta u_z &=& 0, \\ \operatorname{div}{\mathbf{u}} &=& 0, \end{array} \right. & \mbox{ in } \varOmega \end{array} {} \end{aligned} $$
(2.3)
On the wall of the vessel, Γ w, we have the kinematic condition $$\mathbf {u}=\frac {\partial \mathbf {d}}{\partial t} = \frac {\partial d}{\partial t} {\mathbf {e}}_r$$ , meaning that the wall moves at the same velocity as the fluid.
We will integrate equations (2.3) on the generic cross section S(z) term by term. Consider the portion V  of the vascular tube Ω around point z, comprising the axial region $$\left (z-\frac {dz}{2},z+ \frac {dz}{2}\right )$$ , see Fig. 2.2. We denote the boundary of V  by ∂V = S −∪ S + ∪ Γ, with Γ the part of the boundary of V  intercepting the vessel wall. The 1D model is derived by integrating equations (2.3) in V  and doing the limit as dz → 0, assuming all quantities are smooth enough.
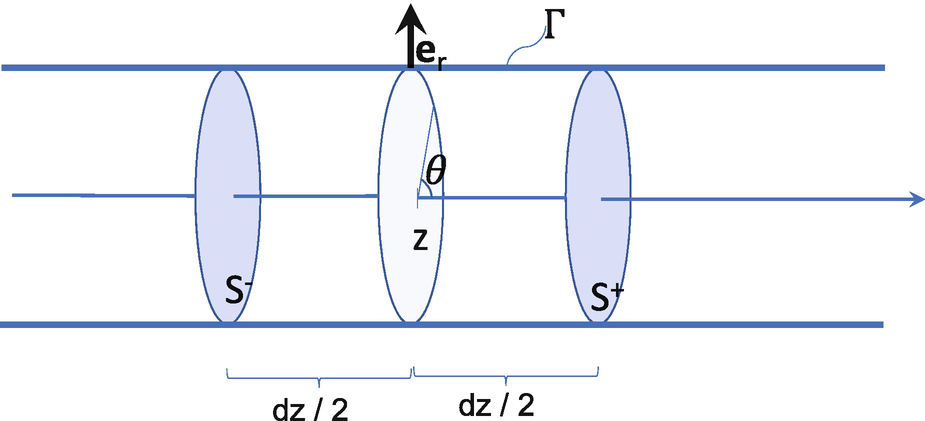
../images/475466_1_En_2_Chapter/475466_1_En_2_Fig2_HTML.png
Fig. 2.2

Portion of the tube between $$z- \frac {dz}{2}$$ and $$z+ \frac {dz}{2}$$

Using the Reynolds transport theorem [12], taking into account that the border of V  intercepting the vessel wall, Γ, moves with time t, it can be shown that $$\frac {\partial A}{\partial t}=2\pi R\frac {\partial d}{\partial t}$$ . Using this expression, the divergence theorem and the mean-value theorem for integrals, we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} 0=\int_{V} \operatorname{div}(\mathbf{u}) dv &\displaystyle = &\displaystyle \int_{\partial V} \mathbf{u} \cdot \mathbf{n} ds = -\int_{S^-} u_z ds + \int_{S^+} u_z ds + \int_{\varGamma} \frac{\partial \mathbf{d}}{\partial t} \cdot \mathbf{n} ds \\ &\displaystyle = &\displaystyle Q\left(z +\frac{dz}{2}\right)- Q\left(z - \frac{dz}{2}\right) + \frac{\partial A(z )}{\partial t} dz + o(dz) \end{array} \end{aligned} $$
where n denotes the outward unitary normal. Dividing by dz and doing the limit as dz → 0 we obtain $$\frac {\partial A}{\partial t} + \frac {\partial Q}{\partial z} = 0$$ for the continuity equation.
From Reynolds theorem we have $$ \frac {d}{dt} \int _{V} u_z dv = \int _{V} \frac {\partial u_z}{\partial t} dv + \int _{\partial V} u_z\frac {\partial \mathbf {d}}{\partial t} \cdot \mathbf {n} ds. $$ Due to H2, boundaries S − and S + do not move longitudinally, and due to H6, u z = 0 on Γ. Thus $$\int _{\partial V} u_z \frac {\partial \mathbf {d}}{\partial t} \cdot \mathbf {n} ds=0$$ and
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \frac{\partial u_z}{\partial t} dv = \frac{d}{dt} \int_{V} u_z dv = \frac{\partial}{\partial t} \left(A(z )\bar{u}(z )dz+o(dz)\right) = \frac{\partial Q(z )}{\partial t} dz +o(dz) \ {} \end{array} \end{aligned} $$
(2.4)
Using the divergence theorem and again assumptions H2 and H6, we have:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \operatorname{div}(u_z\mathbf{u}) dv = \int_{\partial V} u_z \mathbf{u}\cdot \mathbf{n} dv =-\int_{S^-} u_z^2 ds + \int_{S^+ } u_z^2 ds + \int_{\varGamma} u_z \frac{\partial \mathbf{d}}{\partial t} \cdot \mathbf{n}ds \end{array} \end{aligned} $$
Remembering that u z = 0 on Γ and that $$\alpha = \int _{S}u_z^2 ds / (A\bar {u}^2)$$ , we obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \operatorname{div}(u_z\mathbf{u}) dv &\displaystyle = &\displaystyle \alpha \left[ A\left(z + \frac{dz}{2}\right)\bar{u}^2\left(z +\frac{dz}{2}\right) -A\left(z - \frac{dz}{2}\right)\bar{u}^2\left(z -\frac{dz}{2}\right) \right]\\ &\displaystyle \approx&\displaystyle \alpha\frac{\partial (A\bar{u}^2)}{\partial z} {} \end{array} \end{aligned} $$
(2.5)
Considering now hypothesis H4 and again the divergence theorem, we obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \frac{\partial P}{\partial z} dv = -\int_{S^-} P ds + \int_{S^+} P ds +\int_{\varGamma}P{\mathbf{n}}_zds \approx \frac{\partial (AP)}{\partial z} (z ) +\int_{\varGamma}P{\mathbf{n}}_zds \end{array} \end{aligned} $$
From the mean-value theorem for integrals ∫ΓPn zds = P(z)∫Γn zds + o(dz). Also, since V  is closed, ∫∂Vn zds = 0 and $$ \int _{\varGamma } {\mathbf {n}}_z ds = -\left (\int _{S^+} ds - \int _{S^-}ds\right ), $$ thus
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{\varGamma} P {\mathbf{n}}_z ds &\displaystyle =&\displaystyle -P(z ) \left(\int_{S^+} ds - \int_{S^-}ds\right) + o(dz) \\ &\displaystyle =&\displaystyle -P(z ) \left[A\left(z +\frac{dz}{2}\right) - A\left(z -\frac{dz}{2}\right)\right] + o(dz) \approx - P(z )\frac{\partial A}{\partial z}(z) \end{array} \end{aligned} $$
Thus, we obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \frac{\partial P}{\partial z} dv &\displaystyle \approx&\displaystyle \frac{\partial (AP)}{\partial z} - P\frac{\partial A}{\partial z} = A\frac{\partial P}{\partial z} {} \end{array} \end{aligned} $$
(2.6)
Finally, we consider the viscous term Δu z. Applying the divergence theorem and noticing that $$\nabla u_z = \left (\frac {\partial u_z}{\partial r}, \frac {\partial u_z}{\partial \theta },\frac {\partial u_z}{\partial z}\right )$$ , we have:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \varDelta u_z dv &\displaystyle = &\displaystyle \int_{\partial V} \nabla u_z \cdot \mathbf{n} ds = -\int_{S^-} \frac{\partial u_z}{\partial z} ds + \int_{S^+} \frac{\partial u_z}{\partial z} ds + \int_{\varGamma} \nabla u_z \cdot \mathbf{n} ds \end{array} \end{aligned} $$
We neglect the term $$\frac {\partial u_z}{\partial z}$$ by assuming that the variation of axial velocity u z along the axial direction z is small compared to the other terms. From H1 the gradient of u z becomes $$\nabla u_z = \left (\frac {\partial u_z}{\partial r},0,0\right )$$ , and ∇u z ⋅n becomes $$\frac {\partial u_z}{\partial r}$$ . Recalling expression (2.2), we have that $$\frac {\partial u_z}{\partial r} = \frac {\bar {u}(t,z)}{R(z)} s'\left (\frac {r}{R(z)}\right )$$ . Noticing that r = R on Γ, we obtain:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{V} \varDelta u_z ds &\displaystyle =&\displaystyle \int_{\varGamma} \frac{\bar{u}}{R} s'(1) ds = 2\pi \int_{z -\frac{dz}{2}}^{z +\frac{dz}{2}} \bar{u}s'(1) dz = 2\pi \bar{u}(z )s'(1)dz+o(dz) \\ {} \end{array} \end{aligned} $$
(2.7)
Finally, putting together expressions (2.4), (2.5), (2.6) and (2.7), diving (2.4) and (2.7) by dz, and passing to the limit as dz → 0, the momentum equation becomes
$$\displaystyle \begin{aligned} \frac{\partial Q}{\partial t} + \alpha \frac{\partial}{\partial z} \left(\frac{Q^2}{A}\right) +\frac{A}{\rho}\frac{\partial P}{\partial z} -2\pi \nu s'(1) \frac{Q}{A} = 0 \end{aligned}$$
The friction parameter is defined as K r = −2πνs′(1) and depends on the velocity profile s(⋅). For a parabolic profile K r = 8πν, which corresponds to the value commonly used in practice. In the case of a flat profile, α = 1 and K r = 0, meaning that there is no friction.
The 1D model for blood flowing in a cylindrical vessel is given, for all t, by
$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcll} \frac{\partial Q}{\partial t} + \alpha \frac{\partial}{\partial z} \left(\frac{Q^2}{A}\right) +A\frac{\partial P}{\partial z} &=&-K_r \frac{Q}{A}, & \qquad z \in (a,b)\\ \frac{\partial A}{\partial t} + \frac{\partial Q}{\partial z} &=&0, & \qquad z\in (a,b) \end{array} \right. {} \end{aligned} $$
(2.8)
where L = b − a is the vessel length, and the unknowns are the cross section area A(t, z), the flow rate Q(t, z), and the constant cross sectional pressure P(t, z). The friction parameter is here a source term on the momentum equation. We have three unknowns and two equations, meaning an extra equation is required. We close system (2.8) by providing a relation linking pressure and area. This is reasonable, since the tube wall moves as a response to the pressure inside the vessel. We consider the following simple pressure-area algebraic relation:
$$\displaystyle \begin{aligned} P=\beta\frac{\sqrt{A}-\sqrt{A_0}}{A_0} {} \end{aligned} $$
(2.9)
where A 0 is the cross section area at rest and $$\beta =\frac {\sqrt {\pi }hE}{1-\xi ^2}$$ , with E and ξ the Young Modulus and the Poisson ratio of the wall material, and h is the wall thickness. Parameters A 0 and β may vary with z. We define $$c=\sqrt {\frac {A}{\rho }\frac {\partial P}{\partial A}}$$ , which becomes $$c=\sqrt {\frac {\beta }{2\rho A_0}}A^{1/4}$$ for expression (2.9) and considering A 0 and β constant along z. In this case, system (2.8) can be diagonalized, meaning it is a strictly hyperbolic system of PDEs, describing very well wave propagation phenomenon. Indeed, system (2.8) with (2.9) has two eigenvalues, given by $$\lambda _{1,2}=\alpha \bar {u}\pm \sqrt {c^2 + \bar {u}^2\alpha (\alpha -1)}$$ . If we choose α = 1, corresponding to a flat profile, we obtain $$\lambda _{1,2}=\bar {u}\pm c = \bar {u} \pm \sqrt {\frac {\beta }{2\rho A_0}} A^{1/4}$$ . Under physiological conditions, the mechanical properties of blood and of the arterial wall, reflected on c through β, are such that $$c>>\bar {u}$$ , meaning that the two eigenvalues have opposite signs. Indeed, characteristic values of c are of the order of 103m/s [13], while $$|\bar {u}|$$ is of the order of 101 [14]. This means that system (2.8) describes two waves travelling along the cylindrical vessel, one moving forward and the other backwards.

Let R = [r 1r 2] and L = [l 1l 2] be the matrices of the right and left eigenvectors, respectively, such that LR = I, with I the identity matrix. Then, if there exist quantities W 1 and W 2 such that $$\frac {\partial W_1}{\partial U}=l_1$$ and $$\frac {\partial W_2}{\partial U}=l_2$$ , for U = [A, Q]T, which is the case if α = 1 and K r = 0 (see for instance [9]), functions W 1 and W 2 are characteristic variables [15]. This means that, up to the additive source term, variables W i, i = 1, 2 are constant along the characteristic lines, that is, along the lines satisfying the differential equation $$\frac {d}{dt} y_i(t)=\lambda _i(t,y_i(t)), i=1,2.$$ Given the pressure-area relation (2.9) and α = 1, W 1 and W 2 are given by $$W_{1,2}=\bar {u}\pm \sqrt {\frac {8\beta }{\rho A_0}}\left (A^{1/4}-A_0^{1/4}\right )$$ .

Finally, to completely define problem (2.8), we must provide initial conditions A(0, z) = A 0, Q(0, z) = Q 0 and boundary conditions, which in general can be written as ϕ 1(A(t), Q(t)) = h 1(t), at z = a, and ϕ 2(A(t), Q(t)) = h 2(t), at z = b, where h 1 and h 2 are given functions. The number of boundary conditions to apply at each end is the number of incoming characteristics at that point. Thus, here we must impose exactly one boundary condition at z = a and z = b, respectively [15]. Functions ϕ i, i = 1, 2, produce admissible boundary conditions as long as they do not depend only on the exiting characteristic.

2.3 Numerical Approximation of the 1D Model

The numerical discretization of the 1D hyperbolic model is carried out using the finite element Lax-Wendroff method, [15, 16]. Being a second-order explicit scheme in time, it has excellent dispersion error properties and it is easily implemented.

Being explicit, the stability of the numerical scheme depends on the satisfaction of a CFL type condition (see [9]) relating the time step Δt with the space step h i: $$\varDelta t \leqslant (\sqrt {3}/3) \min _{0 \leqslant i \leqslant N} \left [ \frac {h_{i}}{\max _{k=1,2} \lambda _{k}(z_{i})} \right ]$$ , where z i, i = 0, …, N, are the mesh nodes, and h i = z i+1 − z i is the measure of the i-th spacial element.

2.3.1 Boundary and Compatibility Conditions for the Discrete Problem

The numerical solution is defined only on the internal nodes. The solution values at the boundary points are computed from the boundary conditions. Yet, these data are not enough to close the numerical problem. Indeed, for the problem at hand we have to impose exactly one boundary condition at each end of the domain at the continuous level [15, 16]. However, at the discrete level we need to provide two boundary data at each end, corresponding to the unknowns Q n+1 = Q(t n) and A n+1 = A(t n). That is, at the numerical level we need an extra boundary condition at each extremity. To obtain the complete boundary data we need additional equations, which must be compatible with the original problem. Usually, the compatibility conditions are obtained by projecting the equation along the characteristic lines exiting the domain [15, 16]. The values of Q n+1 and A n+1 at the boundaries are found by solving the following non linear systems:
$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcl} \phi_{1}(A^{n+1}_{h}(a),Q^{n+1}_{h}(a)) &=& h_{1}^{n+1} \\ \\ W_{2}(A^{n+1}_{h}(a),Q^{n+1}_{h}(a)) &=& W^{n+1}_{2} \end{array} \right. \,\, \left\{ \begin{array}{rcl} \phi_{2}(A^{n+1}_{h}(b),Q^{n+1}_{h}(b)) &=& h_{2}^{n+1} \\ \\ W_{1}(A^{n+1}_{h}(b),Q^{n+1}_{h}(b)) &=& W^{n+1}_{1} \end{array} \right. {} \end{aligned} $$
(2.10)
If we consider α = 1 and K r = 0 (no source term in (2.8)), $$W_i^{n+1}$$ is obtained following the characteristic line from t = t n: $$W_i^{n+1}=W_i^n(x_k)$$ , where x k is the foot of the characteristic line of W i at t n, i = 1, 2.
For instance, if the user provides the pressure, at z = a, as P(t, a) = h 1(t), from (2.9) and from the compatibility condition (2.10) at z = a we need to solve the system
$$\displaystyle \begin{aligned} \left[ \begin{array}{cc} \frac{1}{A^{n+1}(a)}\beta\frac{\sqrt{A^{n+1}(a)}-\sqrt{A_0}}{A_0} & 0 \\ -\sqrt{\frac{8\beta}{\rho A_0}}\frac{(A^{n+1}(a))^{1/4}-A_0^{1/4}}{A^{n+1}(a)} & \frac{1}{A^{n+1}(a)} \end{array} \right] \left[ \begin{array}{c} A^{n+1}(a) \\ Q^{n+1}(a) \end{array} \right] = \left[ \begin{array}{c} h_1^{n+1}\\C_{x_a}^{n} \end{array} \right] \end{aligned}$$
where $$C^n_{x_a}=\frac {Q^n(x_a)}{A^n(x_a)}-\sqrt {\frac {8\beta }{\rho A_0}} \left ((A^{n}(x_a))^{1/4}-A_0^{1/4}\right )$$ and x a = a − Δtλ 2(Q n(a), A n(a)) is the foot of the exiting characteristic W 2 at z = a. If, at z = b, a condition on the entering characteristic is imposed W 2(t, b) = h 2(t), then the non-linear system to be solved at each time step is
$$\displaystyle \begin{aligned} \left[ \begin{array}{cc} -\sqrt{\frac{8\beta}{\rho A_0}} \frac{(A^{n+1}(b))^{1/4}-A_0^{1/4}}{A^{n+1}(b)} & \frac{1}{A^{n+1}(b)} \\ \sqrt{\frac{8\beta}{\rho A_0}} \frac{(A^{n+1}(b))^{1/4}-A_0^{1/4}}{A^{n+1}(b)} & \frac{1}{A^{n+1}(b)} \end{array} \right] \left[ \begin{array}{c} A^{n+1}(b) \\ Q^{n+1}(b) \end{array} \right] = \left[ \begin{array}{c} h_2^{n+1}\\C_{x_b}^{n} \end{array} \right] \end{aligned}$$
where $$C^n_{x_b}=\frac {Q^n(x_b)}{A^n(x_b)}+\sqrt {\frac {8\beta }{\rho A_0}} \left ((A^{n}(x_b))^{1/4}-A_0^{1/4}\right )$$ and x b = b − Δtλ 1(Q n(b), A n(b)) is the foot of the exiting characteristic W 1 at z = b.

Very often the incoming characteristic is put equal to zero at the exiting point, W 2(t, z) = 0, corresponding to an absorbing boundary condition, meaning nothing enters the domain. This fact has been exploit to impose absorbing boundary conditions on 3D FSI models for blood flow [17].

2.3.2 Modular Simulation of Arterial Networks

So far we have the mathematical 1D model and corresponding numerical method to simulate blood flow in a single elastic tube. However, the interest is often the simulation of arterial networks. Hence, we need to couple two or more arteries. The most usual combination of arteries in the human arterial system are:

  • Coupling single tubes: used to model, for instance, long tubes where physical characteristics vary.

  • Bifurcation of an artery into two arteries: this is the most common, since almost all arteries enventually bifucarte to carry out blood for the whole body.

  • Merging of two arteries into one artery: this situation is more rare, occurring for instance with the vertebral arteries (left and right), that merge into the basilar artery before reaching the Circle of Willis at the bottom of the brain.

Having the numerical scheme for one tube, couplings, bifurcations and mergings are possible by defining coupling conditions. These consist in imposing the continuity of the fluxes, Q, and of the total pressures, $$P_t=P+\frac {\rho }{2}\bar {u}^2$$ , [7, 9].
Couplings lead to two (in the case of coupling) or three (in the case of bifurcating or merging) more boundary conditions. Thus, we also need more compatibility conditions, obtained again by means of the exiting characteristics. For instance, for the coupling of two tubes, the following coupling conditions are set
$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcl} Q_1(b_1)&=&Q_2(a_2) \\ P_{t,1}(b_1)&=&P_{t,2}(a_2)\\ W_1(t^{n+1},b_1)&=& W_1(t^n,x_{b_1})\\ W_2(t^{n+1},a_2)&=&W_2(t^n,x_{a_2}) \end{array} \right. \end{aligned}$$
where a i, b i, i = 1, 2, 3 are respectively the initial and final extremities of artery i and $$x_{k_i}$$ , k = a, b, i = 1, 2, 3 are the foot of the outgoing characteristic lines passing in point (k i, t n+1). For the bifurcation (b) and merging (m) we have the following systems
$$\displaystyle \begin{aligned} b= \left\{ \begin{array}{rcl} Q_1(b_1)&=&Q_2(a_2)+Q_3(a_3) \\ P_{t,1}(b_1)&=&P_{t,2}(a_2)\\ P_{t,1}(b_1)&=&P_{t,3}(a_2)\\ W_1(t^{n+1},b_1)&=&W_1(t^n,x_{b_1}) \\ W_2(t^{n+1},a_2)&=&W_2(t^n,x_{a_2}) \\ W_2(t^{n+1},a_3)&=&W_2(t^n,x_{a_3}) \end{array} \right. \quad m= \left\{ \begin{array}{rcl} Q_1(b_1)+Q_2(b_2)&=&Q_3(a_3) \\ P_{t,1}(b_1)&=&P_{t,3}(a_3)\\ P_{t,2}(b_2)&=&P_{t,3}(a_3)\\ W_1(t^{n+1},b_1)&=&W_1(t^n,x_{b_1}) \\ W_1(t^{n+1},b_2)&=&W_1(t^n,x_{b_2}) \\ W_2(t^{n+1},a_3)&=&W_2(t^n,x_{a_3}) \end{array} \right. \end{aligned}$$
All these systems are non-linear. For each internal coupling point of the 1D arterial network, a system of this type must be solved, for instance using Newton’s method, to set the discrete boundary conditions of all tubes in the network.

2.4 Simulating Anatomical Variations of the Circle of Willis

Here we illustrate the application of the 1D hyperbolic model to the study of anatomical variations of the Circle of Willis (CoW), see [1, 5, 7] for simulations at different levels of accuracy of the brain circulation. The CoW is a redundancy set of arteries guaranteeing that blood reaches the brain by distributing it from the basilar and internal carotid arteries, see Fig. 2.3. We choose the parameters of each artery, namely length, radius, wall thickness and Young modulus (related to wall elasticity) as in [7]. We consider a sinusoidal impulse at the basilar artery (artery 22 in Fig. 2.3) and at the internal carotid arteries (ICAs, arteries 11 and 12 in Fig. 2.3):
$$\displaystyle \begin{aligned} Q(t,0)=\left\{ \begin{array}{rr} 2.5 \sin\left( \frac{\pi t}{0.003} \right), &\mbox{if } t\leqslant 0.003 \\ 0,\mbox{if } t>0.003 \end{array} \right. \end{aligned}$$
As customary, we consider that the system starts at rest A(0, z) = A 0 and Q(0, z) = 0.
../images/475466_1_En_2_Chapter/475466_1_En_2_Fig3_HTML.png
Fig. 2.3

Representation of the main arteries of the Circle of Willis (CoW)

Figure 2.4 represents the flow rate through the main arteries of the healthy CoW, represented in Fig. 2.3, at a particular time t. We can observe that as long as the CoW is vertically axis-symmetric, the flow rate through symmetric arteries is the same. Several people have anatomical changes in the CoW [7], including absence of some arteries. Figure 2.5 shows the flow rate when the right posterior cerebral artery is missing (right PCA, artery 28 in Fig. 2.3). It can be seen that the flow rate of symmetric arteries is not the same anymore. Indeed, the flow rate in arteries 32 and 33 differ. In both these cases, there is still blood perfusion to the brain through arteries 32 and 33, even though one artery is absent. In Fig. 2.6 we can observe the flow rate in the arteries going to the brain when both the right posterior communicating artery (PCoA, artery 20 in Fig. 2.3) and the left posterior cerebral artery (PCA, artery 27 in Fig. 2.3) are absent. We can see that in this case there is almost no blood perfusion in artery 32, that is, almost no blood perfusion on that part of the brain. This is thus a very serious anatomical variation of the CoW.
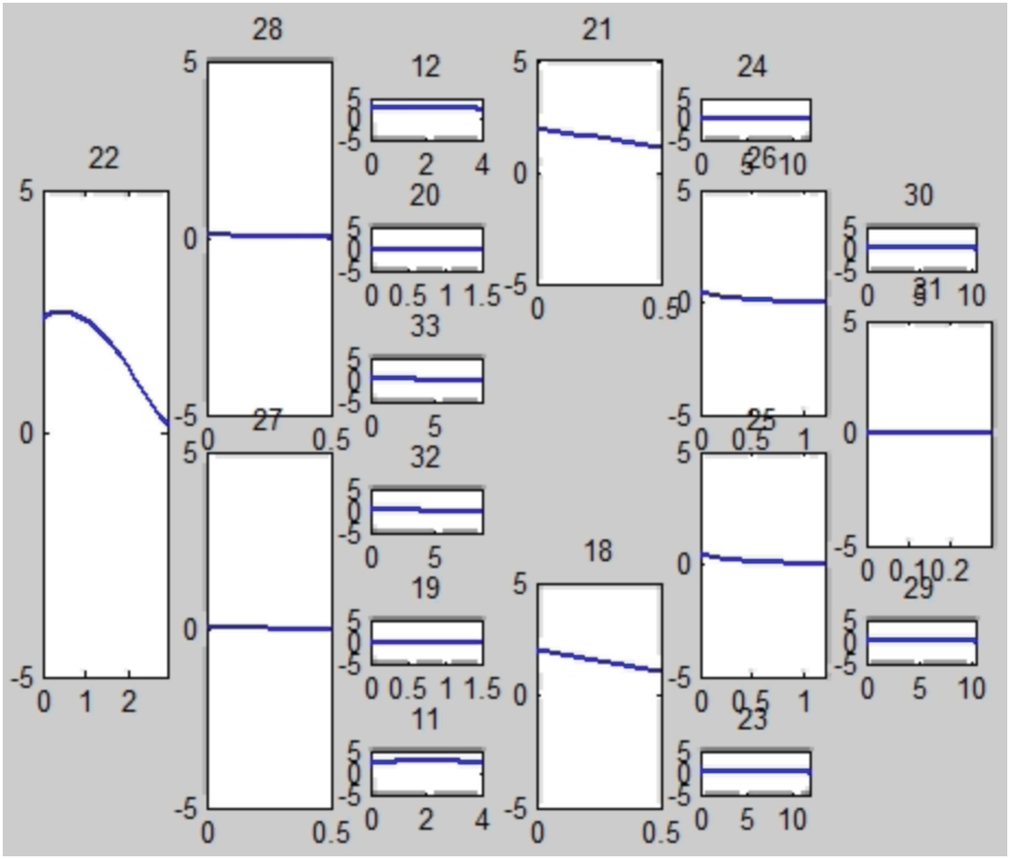
../images/475466_1_En_2_Chapter/475466_1_En_2_Fig4_HTML.png
Fig. 2.4

Flow rate [cm3∕s] through the main arteries of the complete CoW at a particular time t

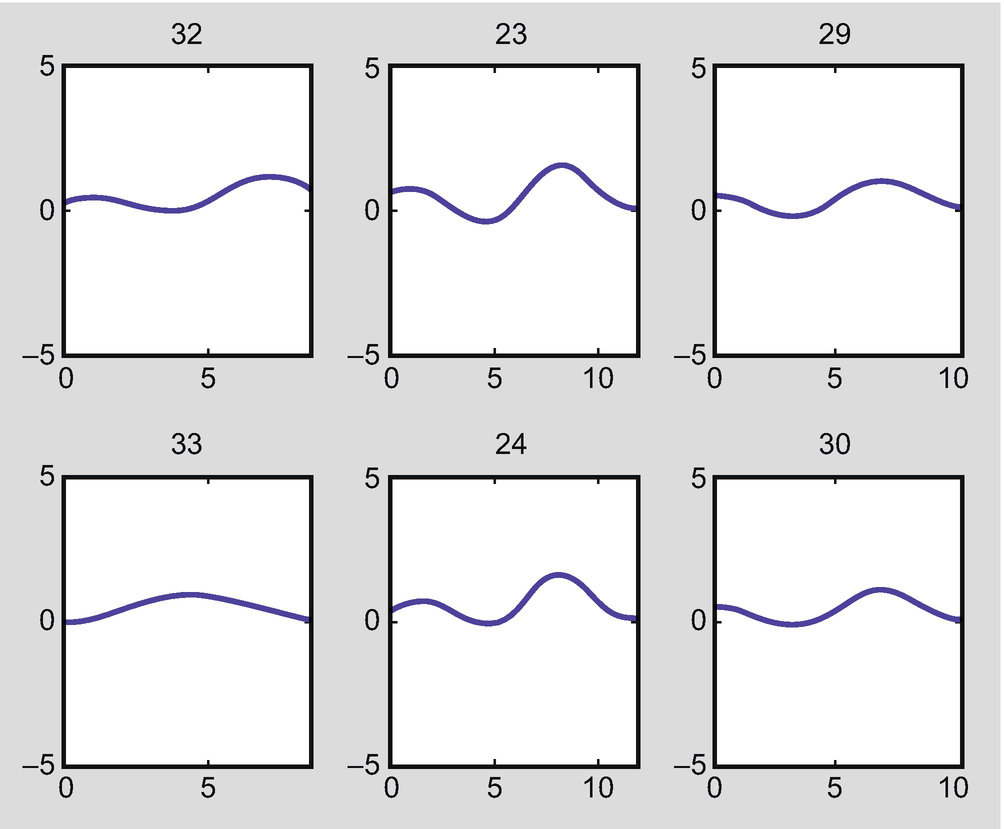
../images/475466_1_En_2_Chapter/475466_1_En_2_Fig5_HTML.png
Fig. 2.5

Flow rate when the right posterior cerebral artery is missing (right PCA, artery 28 in Fig. 2.3)

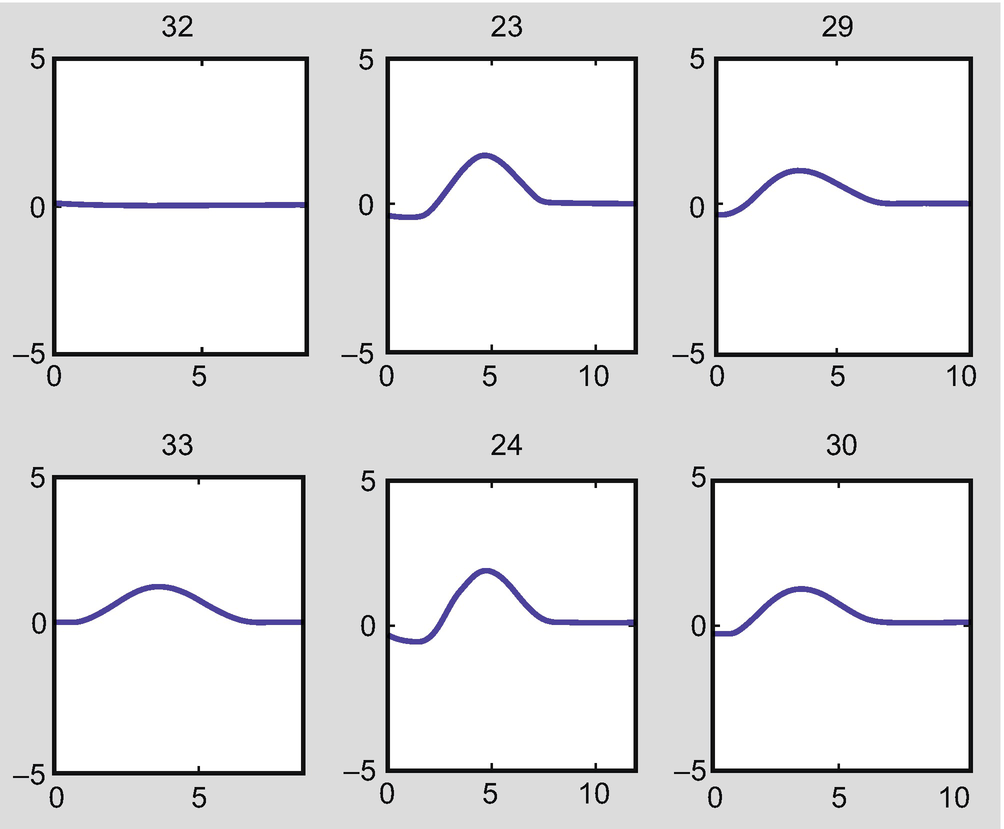
../images/475466_1_En_2_Chapter/475466_1_En_2_Fig6_HTML.png
Fig. 2.6

Flow rate in the arteries when both the right posterior communicating artery (PCoA) and the left posterior cerebral artery (PCA) are absent (arteries 20 and 27 in Fig. 2.3)

2.5 Increasing the Complexity of the 1D Model: Including Curvature

The 1D hyperbolic model for blood flow in arteries studied in the previous sections is a simplified model with desirable mathematical properties, namely it is an hyperbolic system of PDEs. It may be considered one of the simplest 1D model for blood pulse. More complex models can be considered by accounting for variations of the radius or the wall properties along z, which introduce derivatives of the parameters A 0 and β, to be included on the source term. Also, more sophisticated pressure-area relations can be used, leading to the appearance of higher order derivatives. These derivatives alter the characteristic of the differential problem, making the numerical treatment and the identification of proper boundary conditions more problematic [9]. These effects also imply the inclusion of new parameters for which it is often difficult to obtain reasonable values.

On the other hand, some simplified assumptions can be relaxed. An example is to consider curvature. In this case hypothesis H3, of fixed cylinder axis, as well as H2, of only radial movements, are dropped. Now, the wall movements are not only radial, depending also on the x and y directions. Denoting η the wall displacement, then η = (η x, η y) + de r. In this setting, the fluid velocity depends not only on the axial direction through u z, but also on the directions u x and u y:
$$\displaystyle \begin{aligned} u_x=\frac{\partial \eta_x}{\partial t} + \frac{1}{R}\frac{\partial d}{\partial t}x=\frac{\partial \eta_x}{\partial t} + \frac{1}{R}\frac{\partial d}{\partial t}r\cos\theta, u_y=\frac{\partial \eta_y}{\partial t} + \frac{1}{R}\frac{\partial d}{\partial t}y=\frac{\partial \eta_y}{\partial t} + \frac{1}{R}\frac{\partial d}{\partial t}r\sin\theta \end{aligned}$$
Considering, for simplicity, a parabolic profile on the axial direction, from (2.2) we know that $$ u_z=\left (1-\frac {r^2}{R^2}\right )a(t,z)=\bar {u}(t,z)s\left (\frac {r}{R}\right )$$ , with a∕2 = Q∕A. In this case, the 3D Navier-Stokes system (2.3) has two extra equations, related to u x and u y:
$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial u_x}{\partial t} + \operatorname{div}(u_x\mathbf{u})+\frac{1}{\rho} \frac{\partial P}{\partial x}-\nu \varDelta u_x &=&0 \\ \frac{\partial u_y}{\partial t} + \operatorname{div}(u_y\mathbf{u})+\frac{1}{\rho} \frac{\partial P}{\partial y}-\nu \varDelta u_y &=&0\\ \frac{\partial u_z}{\partial t} + \operatorname{div}(u_z\mathbf{u})+\frac{1}{\rho} \frac{\partial P}{\partial z}-\nu \varDelta u_z &=&0 \\ \frac{\partial u_x}{\partial x} + \frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}&=&0 \end{array} \right. {} \end{aligned} $$
(2.11)
We integrate each equation in (2.11) over the volume V  and then make dz → 0. Applying this procedure to the two last equations in (2.11) results in the two equations of system (2.8). Indeed, noticing that $$\int _{\varGamma } n_{r_1}\cos \theta \eta _xds=\int _{\varGamma } n_{r_2}\sin \theta \eta _yds=0$$ , we have:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{\varGamma}\frac{\partial\boldsymbol{\eta}}{\partial t}\cdot\mathbf{n} ds= \int_{\varGamma} n_{r_1}\cos\theta \eta_xds+\int_{\varGamma} n_{r_2}\sin\theta \eta_yds+\int_{\varGamma}\frac{1}{R}\frac{\partial d}{\partial t} r{\mathbf{e}}_r\cdot \mathbf{n}ds \approx\frac{\partial A}{\partial t} \end{array} \end{aligned} $$
where $$\mathbf {n}=(n_{r_1}\cos \theta ,n_{r_2}\sin \theta ,n_z)$$ is the outward unitary normal. Thus
$$\displaystyle \begin{aligned}\int_{V}\operatorname{div}{\mathbf{u}}dv=\int_{\partial V} \mathbf{u}\cdot\mathbf{n}ds =\int_{S^+}u_zds-\int_{S^-}u_zds+\int_{\varGamma} \frac{\partial\boldsymbol{\eta}}{\partial t} \cdot \mathbf{n}ds\approx \frac{\partial A}{\partial t} + \frac{\partial Q}{\partial z} \end{aligned}$$
Since $$\int _{z-\frac {dz}{2}}^{z+\frac {dz}{2}}\int _{0}^{2\pi }\int _{0}^R \frac {\partial d}{\partial t}\frac {r\cos \theta }{R}rdrd\theta dz=0$$ , then
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_V u_x dv &\displaystyle =&\displaystyle \int_{z-\frac{dz}{2}}^{z+\frac{dz}{2}}\int_{0}^{2\pi}\int_{0}^R \frac{\partial\boldsymbol{\eta}_x}{\partial t} rdrd\theta dz =\frac{\partial{\eta}_x}{\partial t} (z) A(z)dz + o(dz) \approx \frac{\partial{\eta}_x}{\partial t} A \end{array} \end{aligned} $$
Thus, defining $$\varPhi _x=\frac {\partial \boldsymbol {\eta }_x}{\partial t} A$$ , then $$\frac {d}{dt} \int _V u_xdv\approx \frac {\partial \varPhi _x}{\partial t} $$ . Since $$\frac {\partial \boldsymbol {\eta }}{\partial t}=0$$ on S, we have
$$\displaystyle \begin{aligned}\int_{\partial V} u_x \frac{\partial \boldsymbol{\eta}}{\partial t} \cdot \mathbf{n}ds = \int_{\varGamma} u_x \frac{\partial \boldsymbol{\eta}}{\partial t}\cdot \mathbf{n} ds\end{aligned}$$
Hence, we obtain:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_V \frac{\partial u_x}{\partial t} dv= \frac{d}{dt} \int_V u_x ds- \int_{\partial V} u_x \frac{\partial \boldsymbol{\eta}}{\partial t}\cdot \mathbf{n}ds \approx \frac{\partial \varPhi_x}{\partial t} - \int_{\varGamma} u_x \frac{\partial \boldsymbol{\eta}}{\partial t}\cdot \mathbf{n}ds \end{array} \end{aligned} $$
Using the divergence theorem and noticing that $$\int _S \frac {1}{R}\frac {\partial d}{\partial t} r \cos \theta \, ds =0$$ and that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{S}u_xu_zds &\displaystyle =&\displaystyle \int_S \left( \frac{\partial \eta_x}{\partial t} + \frac{1}{R}\frac{\partial d}{\partial t} r \cos\theta \right)\left(1-\frac{r^2}{R^2}\right)a(t,z)ds =\frac{\partial \eta_x}{\partial t} A \frac{Q}{A}=\varPhi_x\frac{Q}{A} \end{array} \end{aligned} $$
we obtain
$$\displaystyle \begin{aligned} \int_V \operatorname{div}(u_x\mathbf{u}) dv &= \int_{S^+} u_x u_z ds- \int_{S^-} u_x u_zds +\int_{\varGamma} u_x \frac{\partial\boldsymbol{\eta}}{\partial t} \cdot \mathbf{n}ds\\ & \approx \frac{\partial}{\partial z} \left( \varPhi_x \frac{Q}{A} \right) + \int_{\varGamma}u_x\frac{\boldsymbol{\eta}}{\partial t} \cdot \mathbf{n}ds \end{aligned} $$
Pressure is still considered to be constant over each cross section, so that $$\frac {\partial P}{\partial x}=0$$ and hence $$\int _{V} \frac {\partial P}{\partial x}=0$$ . Finally, for the diffusive term on x, we may neglect $$\frac {\partial u_x}{\partial z}$$ , obtaining
$$\displaystyle \begin{aligned} \int_V \varDelta u_xdv=\int_{\partial V} \nabla u_x \cdot \mathbf{n}ds =\int_{S^+} \frac{\partial u_x}{\partial z} ds- \int_{S^-} \frac{\partial u_x}{\partial z} ds +\int_{\varGamma}\nabla u_x\cdot \mathbf{n}ds =\int_{\varGamma}\nabla u_x\cdot \mathbf{n}ds \end{aligned}$$
Noticing that $$\nabla u_x \cdot n_z \varpropto \frac {\partial u_x}{\partial z}=0$$ we get
$$\displaystyle \begin{aligned} \int_{\varGamma}\nabla u_x\cdot \mathbf{n} ds=\int_{\varGamma} \nabla u_x \cdot n_r ds= \int_{\varGamma} \frac{\partial u_x }{\partial r} ds= \int_{\varGamma} \frac{1}{R}\frac{\partial d}{\partial t} \cos \theta ds= 0 \end{aligned}$$
Doing the limit as dz → 0, the first equation of (2.11) becomes
$$\displaystyle \begin{aligned}\frac{\partial}{\partial t}(\varPhi_x) +\frac{\partial}{\partial z} \left(\varPhi_x \frac{Q}{A}\right) =0.\end{aligned}$$
A similar equation is obtained by integrating the second equation in (2.11), defining $$\varPhi _y=\frac {\partial {\eta _y}}{{\partial t}}A$$ . The resulting 1D system of equations is
$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial A}{\partial t} + \frac{\partial Q}{\partial z} &=&0 \\ \frac{\partial Q}{\partial t} + \frac{4}{3}\frac{\partial}{\partial z} \left(\frac{Q^2}{A}\right) +\frac{A}{\rho}\frac{\partial P}{\partial z}&=& -8\pi \nu \frac{Q}{A}\\ \frac{\partial \varPhi_x}{\partial t} + \frac{\partial}{\partial z} \left( \varPhi_x \frac{Q}{A} \right) &=&0\\ \frac{\partial \varPhi_y}{\partial t} + \frac{\partial}{\partial z} \left( \varPhi_y \frac{Q}{A} \right) &=&0 \end{array} \right. {} \end{aligned} $$
(2.12)
Notice that for a parabolic profile α = 4∕3. This system of PDEs is no longer strictly hyperbolic, being more difficult to deal with than system (2.8), both from the mathematical and numerical points of view. This 1D model can be further extended to the case where the axial velocity profile depends on x and y: $$u_z=\left (1-\frac {r^2}{R^2}\right )(a+bx+cy)$$ . In this case, two extra equations are needed, for the added quantities b and c, related with the axial velocity profile. These equations are obtained by integrating over the cross section the third equation of (2.11) multiplied by x and y, respectively. Using the same approach and arguments as before, the 1D model in this case becomes:
$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial A}{\partial t} + \frac{\partial Q}{\partial z} &=&0 \\ \frac{\partial Q}{\partial t} + \frac{4}{3}\frac{\partial}{\partial z} \left(\frac{Q^2}{A}\right)+6\pi \frac{\partial}{\partial z} \left(\frac{H^2}{A^2}\right)+6\pi \frac{\partial}{\partial z} \left(\frac{G^2}{A^2}\right)+A\frac{\partial P}{\partial z}&=& -8\pi \nu \frac{Q}{A}\\ \frac{\partial H}{\partial t} + 2\frac{\partial}{\partial z}\left(\frac{QH}{A}\right) + \frac{1}{2}\frac{H}{A}\frac{\partial Q}{\partial z} + \frac{Q}{A}\varPhi_x&=& -24\pi \nu \frac{H}{A} \\ \frac{\partial G}{\partial t} + 2\frac{\partial}{\partial z}\left(\frac{QG}{A}\right) + \frac{1}{2}\frac{G}{A}\frac{\partial Q}{\partial z} + \frac{Q}{A}\varPhi_y&=& -24\pi \nu \frac{G}{A} \\ \frac{\partial \varPhi_x}{\partial t} + \frac{\partial}{\partial z} \left( \varPhi_x \frac{Q}{A} \right)-\frac{1}{2}\frac{\partial}{\partial z} \left( \frac{H}{A}\frac{\partial Q}{\partial z} \right) &=&0\\ \frac{\partial \varPhi_y}{\partial t} + \frac{\partial}{\partial z} \left( \varPhi_y \frac{Q}{A} \right) -\frac{1}{2}\frac{\partial}{\partial z} \left( \frac{G}{A}\frac{\partial Q}{\partial z} \right)&=&0 \end{array} \right. {} \end{aligned} $$
(2.13)
where $$Q=\frac {a\pi R^2}{2}=\frac {aA}{2}$$ , as before, and $$H=\frac {b\pi R^2A}{12}$$ and $$G=\frac {c\pi R^2A}{12}$$ . This system of PDE’s is significantly more complex than the usual 1D model (2.8). Its mathematical and numerical analysis becomes extremely cumbersome, since many of the nice mathematical characteristics of system (2.8) are lost. Being simplified models, the usefulness o such complex 1D models is questionable. If we need more detail and the cost is such an increase in model complexity, than possibly the best is to use full detailed 3D models.

2.6 Conclusions

One dimensional models for blood flow in arteries are simplified and computationally low cost models, obtained by making simplifying assumptions and performing averaging procedures on the 3D FSI model. The simplest 1D model is described by an hyperbolic system of PDE’s. Despite having a lower level of accuracy compared to the full 3D representation, it captures very effectively the pulsation of blood flow. More complex 1D models can be obtained by relaxation of some simplifying hypothesis, as for instance accounting for curvature. In these cases the 1D mathematical model becomes significantly more complex, losing some of the appealing mathematical properties of the simpler straight tube 1D model. Namely, it is no longer hyperbolic. Being simplified models, the extra complexity introduced in these cases is hardly justified. Except for very particular cases, in general when high accuracy on the blood flow solution is required, 3D FSI full mathematical models tend to be preferable.