E. Lindner et al. (eds.)Mathematical Modelling in Real Life ProblemsMathematics in Industry33https://doi.org/10.1007/978-3-030-50388-8_4

4. Nuclear Accidents: How Can Mathematicians Help to Save Lives?

Simone Göttlich¹

(1)

University of Mannheim, Department of Mathematics, Mannheim, Germany

Simone Göttlich

Email: goettlich@uni-mannheim.de

Keywords

EvacuationNetwork flowsDiffusion-advectionSimulation

4.1 Introduction

The description of real-life problems by using mathematical modeling techniques enables the simulation and optimization of complex systems. In the present case study, this is the investigation of an evacuation process caused by a nuclear accident. To build up a real scenario and to work with data freely available, the problem was restricted to one of Germany’s largest nuclear power plant located in Biblis (south-west of Germany) that has been closed in 2011 after the Fukushima accident.

The modeling includes a combined model to tackle the evacuation of people from a designated area and the spread of a radioactive cloud. From a mathematical point of view, this means to deal with flows on graphs and the approximation of travel times. Furthermore, knowledge on diffusion-advection equations is needed for the evolution of nuclear material over time and space. However, the main challenge is the combination of both approaches into an integrated framework, i.e., to set up an evacuation plan that is dependent on the current spread of radioactivity.

Within this contribution, a successful modelling approach is introduced which has been worked out by eight students during the 23-th ECMI Modelling Week 2010 in Milan/Italy. The major subject of all students was related to applied mathematics. Due to the ECMI Modelling Week philosophy, the students came from different European universities so that the conversations were exclusively in English.

4.1.1 Problem Description

A radiation accident is defined by the International Atomic Energy Agency¹ as “an event that has led to significant consequences to people, the environment or the facility. Examples include lethal effects to individuals, large radioactivity release to the environment, or reactor core melt.” The worst-case scenario of a major nuclear accident is one in which a reactor core is damaged and large amounts of radiation are released, such as in the Chernobyl Disaster in 1986, or more recently, the Fukushima nuclear power plant accident in March 2011. So there is definitely a strong need for a fast and most of all safe evacuation, even nowadays.

For the description of a concrete scenario, we focus on the surrounding area of the Biblis power plant, see left picture in Fig. 4.1.

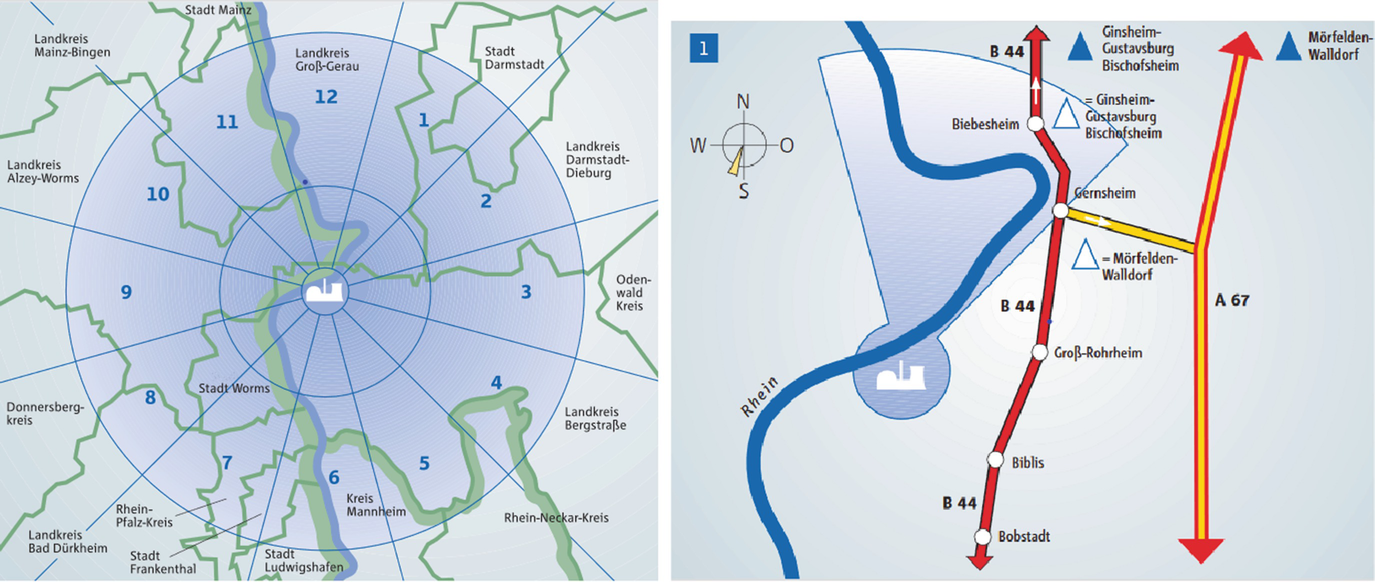
../images/475466_1_En_4_Chapter/475466_1_En_4_Fig1_HTML.png — Fig. 4.1
Evacuation zones around Biblis (Germany) on the left and zoom into sector 1 on the right

The picture is taken from the official emergency protection that is still available.² As we can see the immediate neighborhood is mainly divided into three zones: the central zone (radius of 1.5–2 km), the middle zone (radius of 10 km) and the outer zone (radius of 25 km). The zones are again arranged into 12 sectors to meet geographical restrictions, see right picture in Fig. 4.1.

A rough estimate on the number of inhabitants in the entire outer zone is given by 1.4 million people in 2010, see right picture in Fig. 4.2. Most of the people live in sectors 6–12, i.e. on the right side on the river Rhine, including cities such as Darmstadt, Mannheim or Ludwigshafen. However, this area can be only evacuated in the direction north or south since there is a mountain region in the east. The evacuation on the left side of the river is open to all directions (except east). The safety points for all sectors are seven cities outside the outer zone marked in red, see left picture³ in Fig. 4.2.

../images/475466_1_En_4_Chapter/475466_1_En_4_Fig2_HTML.png — Fig. 4.2
Road network around Biblis with safety points in red (left) and estimates on the number of inhabitants per sector (right)

A further idea of an evacuation plan is also to identify bottlenecks due to the given road network, see again Fig. 4.2. The critical area could be separated into two parts, east and west, where several highways are available. The main roads east of the river are A67, A5, B3, B44 and B47, where the prefix A denotes a German highway (average speed 130 km/h) and B a federal road (average speed 100 km/h). On the west of the river we have the roads A61, A63, A6 and B9. In the special case of Biblis, there are seven cities considered as safety points, namely Frankfurt, Mainz, Daxweiler, Kaiserslautern, Schweigen-Rechtenbach, Stettfeld and Aschaffenburg. We note that people should avoid traversing the road B9 since it is close to the Biblis power plant and might be massive congested.

Another important information is that the wind direction is usually (more than 70%) from west to east meaning that most of the radiation is spread towards the hilly region called Odenwald. Summarizing, an evacuation can be only carried out in north, south or west direction. This is an important aspect while rerouting the people to the safety points.

In the following, we present and comment on the key ideas of the group to solve the evacuation problem. We introduce mathematical models, solution methods and numerical simulations that might help to set up a reasonable evacuation plan. Several assumptions are needed to emphasize on features such as traffic congestion, people’s behavior in case of panic and weather influences.

4.2 Solution of the Problem Provided by the Group

The proposed solution approach can be mainly divided into three parts: the mathematical description of the evacuation process, the propagation of nuclear material and the combination of both.

As we have seen the evacuation model is influenced by predefined properties such as geographical restrictions, local infrastructure, road capacities and population densities. However, other modelling inputs as for instance individual human behavior or weather conditions are harder to predict.

In order to scale down the problem the following assumptions and simplifications have been suggested:

The evacuation is considered by cars on highways or dederal roads, where each car drives at the maximum speed allowed.
Accidents may occur and lead to a certain delay factor.
The radioactive cloud is assumed to be homogeneous and the spread is only driven by the wind.

For the modelling of the people’s behaviour, a kind of network model was applied to give each individual certain attributes and to include the spread of radiation later on. In contrast, the radioactive cloud was modelled using a diffusion-advection equation in two space dimensions that could be solved by standard numerical methods. After modelling these two parts separately, a combined model was introduced to find an evacuation plan which is as safe and smoothly as possible according to the radiation spread.

4.2.1 Modelling of the Evacuation Process

Biblis is connected to its surrounding towns and safety points by several highways, see Fig. 4.2. These towns, safety points and highways are modelled as a network or graph, respectively. As described by Bondy and Murty[2], a graphG is an ordered pair (V (G), E(G)) consisting of a set of vertices V (G) and a set of edges E(G). If u, v ∈ V (G), then an edge connecting both vertices is denoted as e = uv ∈ E(G). A path is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path has a start vertex, an end vertex, but no repeated vertices and edges.

This means from an application point of view:

V is the set of towns in 25 km radius Biblis area,
E is the set of type A and B roads considered in the evacuation network,
p is a set of cars, each transporting 5 people,
S(p) = v ∈ V is the safety point of p,
L(p, t) is the location of car p at time t.

Then, the aim is to find the shortest paths between cars and the nearest safety point, i.e. $\min ||L(p,t)-S(p)||.$ The dynamics between different towns or on a certain path is driven by the people’s behavior and the resulting consequences. This is explained in details in the next subsections on the initialization of the evacuation and the network dynamics.

4.2.2 Initialization of Evacuation Process

In the sense of an initialization of the problem, a delay factor is introduced to model the time that is needed to leave a town and enter the road network. In the given model, to each “individual” p (i.e. a car) there is an attributed delay factor that can be written as

$\displaystyle \begin{aligned}D_{p}=D_{global}+D_{individual},\end{aligned}$

where D _global is a global delay factor describing the information spread over the media. From the viewpoint of an individual, it is the difference of time between the nuclear accident and the first moment when the individual might get the media information. The global delay factor has been estimated as

$\displaystyle \begin{aligned}D_{global}=30\,{\mathrm{min}} = 360~TimeUnits,\end{aligned}$

where 1 TimeUnit = 5 s.

The second delay factorD _individual is an individual-based factor and describes the time needed by each individual before to reach the highway and enter the given road network. Considering the whole set of individuals for a certain town, the goal of the D _individual-modeling is to obtain a distribution describing the amount of cars arriving per TimeUnit at the local highway. Therefore the two factors size of the town, i.e. the number of inhabitants and the individual-based panic factor contribute to this modelling and are now explained in more detail:

1.
each car has an attributed panic factor. This factor is sampled from a distribution of panic factors P(cars):
$\displaystyle \begin{aligned}P(cars) \sim \begin{cases} N\left(0,0.5\right) & \text{for a calm population, } \\ 1-N\left(0,0.5\right) & \text{for a panicked population. } \end{cases}\end{aligned}$

Taking into consideration only the absolute values of the samples, the panic factors are p _ind ∈ [0, 1], where
$\displaystyle \begin{aligned}p_{ind}=\begin{cases} \text{low panic factor, direct movement} & \text{if } p_{ind} \leq 0.5, \\ \text{high panic factor, indirect movement} & \text{if }p_{ind}>0.5 . \end{cases}\end{aligned}$
2.
All towns have a circular shape and a similar population density that is 500 people per km ². Each town has a sufficient number of highway exits at the border of the town, so cars can therefore go straightforward along the radius of a town and reach a highway. The number of cars arriving in the network model per TimeUnit is the sum of cars reaching all highways per TimeUnit. The 2D-model can be therefore interpreted as a 1D-model, see Fig. 4.3.
Fig. 4.3
Modeling the individual local delay factor for a single example town. (a) Schematic 2D-representation of an idealized town: in yellow the assumed continuous distribution of highways at the border of the town (X = r). Five individuals are placed randomly in a certain distance X to the city center X ₀ and their moving direction is denoted. (b) Reduction to a 1D-model: all highways of the town count in a sum at the border of the town. For better visibility, individuals are labeled. (c) Different panic factors: percentage of new arrivals at the highway per time unit for the example town with 100,000 inhabitants. For a calm population, there are move arrivals after few time-steps. A panic real population needs more time to find the highways due to the loss of orientation
3.
People with direct movement (p _ind ≤ 0.5) move the slower the higher the panic factor. The movement of people with indirect movement (p _ind > 0.5) becomes more random with rising panic factor.

Individuals move in-between the center of the city X ₀ = 0 and the highways at the border of the town X _end = r. This r denotes the radius of the town and it can be calculated using the given inhabitants and population density in the city as

$\displaystyle \begin{aligned}r=\sqrt{\frac{\text{inhabitants}}{500 \pi}}.\end{aligned}$

The considered time grid is given by discrete time steps t ₀, …, t _k = t ₀ + k ⋅ Δt with Δt = 5 s. At time t ₀, the individuals are distributed as a $N\left (0,0.4\right )$ . Their position denotes the distance to the city center. The direct movement of an individual can be then defined as

$\displaystyle \begin{aligned}X_{t_k}=X_{t_{k-1}}+\varDelta X= \begin{cases}X_{t_{k-1}}+dir \cdot \left(1-p_{ind}\right) & \text{low panic factor,} \\ X_{t_{k-1}}+dir \cdot \left(1-p_{ind}\right)& \text{high panic factor,} \end{cases}\end{aligned}$

with

$\displaystyle \begin{aligned}dir=\begin{cases}2.5 & \text{low panic factor,} \\ ~U[-1,2.5] & \text{high panic factor.} \end{cases}\end{aligned}$

This means that individuals with a low panic factor move directly with a panic-factor scaled velocity of maximal 30 km/h while individuals with a high panic factor may obtain negative velocities, i.e. they move towards the center and away from the highways.

4.2.3 Dynamics on Road Network

There are a few assumptions necessary to describe the movement of cars through the road network such that every car tries to reach its safety point as fast as possible, i.e.

every driver knows its safety point,
if a car reaches the safety point, it will be considered safe,
every driver has basic knowledge of the roads in the area,
every driver reconsiders his/her route only at the vertices of the graph,
every driver has knowledge on the traffic situation in front.

Mathematically, the perceived distance to the safety point can be calculated as

$\displaystyle \begin{aligned} \sum_{i,j\in P}\frac{D_{ij}}{\hat{v_{ij}}},\end{aligned}$

where P is a path from the current node to the safety point, i and j are vertices on the graph G, D _ij is the distance between vertex i and vertex j along the edge ij and $\hat {v_{ij}}$ is the estimated velocity on the edge.

A path-finding algorithm is needed to compute the routes between the multiple vertices. One commonly used algorithm for finding the shortest route through a graph is the A* search algorithm, as described by Nilsson et al. [6]. A* is a best-first search algorithm, which uses a heuristic cost function to find the shortest path to destination.

Furthermore, the traveling speed $\hat {v_{ij}}$ on a given edge from vertex i to j is determined by:

$\displaystyle \begin{aligned} \begin{array}{rcl} \rho = \frac{P_{ij}}{200w_{ij}D_{ij}}\quad \text{and } \; \rho_{crit} = \frac{0.125}{\left(1 + \alpha A_{ij}\right)}, \end{array} \end{aligned}$

where P _ij is the amount of people on the road, w _ij the amount of lanes, A _ij the amount of accidents happened on this road and α an experimental constant. Then, vmax _ij is the maximum speed on the road and determined by

$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{v_{ij}} = vmax_{ij},\text{ when }\rho < \rho_{crit},\\ \hat{v_{ij}} = \left(1-\rho_{ij}^2\right)vmax_{ij},\text{ when }\rho \geq \rho_{crit}. \end{array} \end{aligned}$

This represents a typical behavior of traveling speed, where on an empty road full speed is possible until ρ exceeds a threshold value ρ _crit and the speed drops down. Note that also the road capacity is reduced when accidents occur.

4.2.3.1 Modeling Car Accidents

Given the car density on each highway and the speed of the individuals, a simplified model for the number of accidents implies that the maximum speed of cars is thereby reduced.

Doing so, the minimal safety distance is given by a certain speed v of all individuals on a highway as

$\displaystyle \begin{aligned}x_{min}=v/2.\end{aligned}$

However, the actual distance depends on the car density ρ ∈ [0, 1] on each highway. Remember that the density counts the number of 5 m-long cars on a piece of 1 km of the highway. A density of 100% means therefore that 200 cars are on the highway without any distance in-between them. So the space $sp\left (\rho \right )$ in-between two 5 m-long cars given a density ρ can be computed as:

$\displaystyle \begin{aligned} \begin{array}{rcl} cars{\rho} = 200 \cdot \rho \text{and } \; sp\left(cars\right) = \frac{1000}{cars}-5. \end{array} \end{aligned}$

If the actual space is smaller than the minimum safety distance ( $sp\left (\rho \right )<x_{min}$ ) then there are accidents occurring.

4.2.4 Modeling of the Radioactive Cloud

From a modelling point of view, a nuclear accident releases many types of different radioactive materials characterized by different weights, different particle sizes, different decay constants and different responses to weather conditions. To reduce complexity, the main assumption is to consider a homogenous cloud only and not to distinguish different material properties. As already pointed out, meteorological conditions play a major role for the spread of radiation once it has been released. The wind field is here the key ingredient to describe the drift or the direction of spread, respectively.

The unknown variable is then the concentration of the homogenous radioactive material in a unit volume, i.e. $C\left (t,\mathbf {x}\right )$ with $\mathbf {x} \in \mathbb {R}^2$ . One possible way is to derive a differential equation that describes first the diffusion of the radioactive material is the continuity equation approach. Considering an arbitrary volume V , the equation reads

$\displaystyle \begin{aligned} \left[\begin{array}{c} \text{rate of}\\ \text{change of}\\ \text{radioactive}\\ \text{material in } V\end{array}\right] =\left[\begin{array}{c} \text{rate of}\\ \text{production of}\\ \text{radioactive}\\ \text{material in } V\end{array}\right]-\left[\begin{array}{c} \text{rate of}\\ \text{decay of}\\ \text{radioactive}\\ \text{material in } V\end{array}\right]-\left[\begin{array}{c} \text{rate of}\\ \text{leakage of}\\ \text{radioactive}\\ \text{material in } V\end{array}\right]\end{aligned}$

and therefore,

$\displaystyle \begin{aligned} \intop_{V}\frac{\partial C}{\partial t}dV=\intop_{V}SdV-\intop_{V}\lambda CdV-\intop_{A}\phi^{T}\cdot\mathbf{n}dA,\end{aligned}$

where $S=S\left (t,\mathbf {x}\right )$ the source of radioactive material, λ the radioactive decay constant and $\phi ^{T}=\phi ^{T}\left (t,\mathbf {x}\right )$ the total radioactive material flux. Note that ϕ ^T is exactly the total radioactive material flux crossing the unit area of the unit volume, orthogonal to the flow direction.

Introducing the wind field in a second step, the problem becomes a diffusion-advection equation. Then, the total radioactive material flux ϕ ^T also consists of convective fluxes ϕ ^C and diffusive fluxes ϕ ^F. So, considering an isotropic scattering radioactive material, Fick’s law yields

$\displaystyle \begin{aligned} \phi^{F}=-D\nabla C\end{aligned}$

where ϕ ^F measures the amount of concentration that flows through a small area during a small time interval, while D is the constant diffusion coefficient.

Wind is modelled as a vector field describing the motion of the air. The length of each vector is the flow speed, in particular:

$\displaystyle \begin{aligned} \mathbf{u}=\mathbf{u}\left(\mathbf{x},t\right)\end{aligned}$

which gives the velocity at a position x at time t.

Supposing that the radioactive material moves as fast as wind, u is the average velocity of the radioactive material. The convective flux is then

$\displaystyle \begin{aligned} \phi^{C}=\mathbf{u}C.\end{aligned}$

Remembering that ϕ ^T = ϕ ^C + ϕ ^F, substitution and the use of the divergence theorem leads to:

$\displaystyle \begin{aligned} \intop_{V}\frac{\partial C}{\partial t}dV=\intop_{V}SdV-\intop_{V}\lambda CdV+\intop_{V}\left[D\nabla^{2}C-\nabla\cdot\left(\mathbf{u}C\right)\right]dV\end{aligned}$

Since the volume V is arbitrary, the following partial differential equation (PDE) of diffusion-advection type can be derived:

$\displaystyle \begin{aligned} \frac{\partial C}{\partial t}=D\nabla^{2}C-\nabla\cdot\left(\mathbf{u}C\right)-\lambda C+S \end{aligned}$

with initial condition $C\left (\mathbf {x},0\right )=f\left (\mathbf {x}\right )$ and boundary conditions $C\left (0,y,t\right )=C\left (1,y,t\right )=C\left (x,0,t\right )=C\left (x,1,t\right ) =0.$

In view of combining the solution of the PDE problem with the road network model, a finite domain in 2D is needed. This a is reasonable choice due to the given infrastructure. Note that the main unknown variable is then just the concentration of the homogenous radioactive material in a unit surface instead of in a unit volume.

4.2.5 Combined Model

The combined model consists of the road network model and the diffusion-advection equation. Both approaches can be computed and simulated separately. In particular, for the network model this means:

First, the delay for people leaving their current locations and entering the highways, i.e. the road network, is modelled as an influx to the network vertices. The rate of influx on each time step is determined by the distribution of people’s delay times. This can be done in some preprocessing manner.
Second, the congestion and accident models are closely connected. Both affect the traveling speeds on each road, which are used as input for the movement of people and the calculation of the escape route.
Third, the coupling of the radioactive cloud model to the network model. The parameters for radioactive cloud model are set so that both of the models operate on the same time and space domain, i.e. one time step in the radioactive cloud model equals one time step in the network model and a coordinate point in the radioactive cloud model corresponds to the same point in the network model.

More precisely, the dosage D received in place vecx on time step t is directly correlated with the concentration of radioactive material C:

$\displaystyle \begin{aligned} Dose\left(x,y,t\right) = \varphi C\left(\left(x,y\right)^T,t\right) \end{aligned}$

The constant φ is an empirically determined parameter for radiation effectiveness and depends on the weather—rainy or clear—and the type of fallout—small dust particles or large pieces of radioactive material. The total dosage and thus the effect of radiation, i.e. E _r on person i in a short time span, can be calculated as a sum of doses received (see [5]),

$\displaystyle \begin{aligned} E_r\left(i,t\right) = \sum_{s = t_0}^t\varphi C\left(\left(X\left(i,s\right),Y\left(i,s\right)\right),s\right), \end{aligned}$

where X(i, t) and Y (i, t) are the coordinates of the person i on time step t.

4.3 Simulation Results

Running now the simulations on the Biblis test case, several important aspects about the evacuation planning can be identified. An illustration can be seen in Fig. 4.4.

../images/475466_1_En_4_Chapter/475466_1_En_4_Fig4_HTML.png — Fig. 4.4
Simulation results for the evacuation of the area around Biblis

A surprising results is that the total time taken for evacuation does not significantly change when using either the calm or panicky population distributions. The calm people exit the city in a short time frame, causing massive traffic jams immediately outside of the city. The exiting of panicked people in comparison is much slower, but this lessens the effect of congestion significantly, allowing the evacuation on highways be much more faster.

Other important observation is the fact that closing a safety point due to high radiation, the people are redirected. In such a situation, a new safety point is chosen that is closest in the euclidean metric. In some cases this meant that the people had to go back and forth between multiple safety points. A good way to inform people about and a good selection criteria for the new safety point would lead to another optimization problem.

Concerning the given infrastructure, a bottleneck/dangerous road is the federal road B9, which goes in the north-south direction from Mainz to Mannheim. This road is the shortest route across the map domain in the north-south direction and thus selected by a large fraction of the population. It passes very close to the Biblis nuclear power plant as the shortest distance is approximately 3 km between the plant and the road. This means that the road might get congested rather fast and is potentially highly radioactive.

4.4 Conclusion and Comment on Solution

The presented modelling problem requires competencies in different mathematical fields. On the one hand, ideas on network flows by Ahuja et al. [1] are needed to describe the traffic flows and, on the other hand, partial differential equations and their numerical solutions (see e.g. Grossmann et al. [3], Habermann [4]) to manage the spread of radiation. Therefore, the model approaches were developed simultaneously by different small groups and finally combined in the entire simulation.

The complexity of this modeling problem has been reduced in a good way such that first results were available after 1 week only. With the simulation tool at hand, more scenarios than shown here have been analyzed. The students did a great job to carry over various mathematical concepts for the evacuation planning. So the original challenge to provide numerical simulations for different evacuation scenarios has been solved successfully.

Acknowledgements

The author wants to thank the group members Aapo Koivuniemi (Lappeenranta University of Technology, Finland), Agney Kilgi (University of Tartu, Estonia), Cathleen Heil (TU Dresden, Germany), Giuseppe Codazzi (University of Milan, Italy), Muhammad Soecipto Wibowo (TU Kaiserslautern, Germany), Vanja Tufvesson (Lund University, Sweden), Victor Bayona (Carlos III University of Madrid, Spain), Yiannis Hadjimichael (University of Oxford, UK) for the fruitful working atmosphere during the Modelling Week and providing their results.