© Springer Nature Switzerland AG 2020
E. Lindner et al. (eds.)Mathematical Modelling in Real Life ProblemsMathematics in Industry33https://doi.org/10.1007/978-3-030-50388-8_5

5. Drug Delivery from Ophthalmic Lenses

José Augusto Ferreira1  
(1)
CMUC, Department of Mathematics, University of Coimbra, Coimbra, Portugal
 
 
José Augusto Ferreira
Email: ferreira@mat.uc.pt
Keywords
GlaucomaTherapeutic contact lensMathematical modellingNumerical simulation

5.1 Introduction

Glaucoma is one of the most common diseases and is a consequence of disorders in the anterior segment of the eye. It is the result of anomalies in the aqueous humor dynamics that lead to increasing intraocular pressure (IOP). This pressure pushes the lens and consequently, the vitreous humor, inducing a pressure on the retina. It can lead to damaging of the optical nerve with subsequent vision loss. In extreme situations, it can even lead to blindness.

The mathematical modelling of drug delivery from a device and its transport until the target tissue requires the knowledge of the physiology of the eye, mainly (1) the anterior segment (2) the dynamics of the aqueous humor, responsible for such anomalous pressure. The increase in IOP is due to an increase of the resistance to the fluid outflow, an increase of the aqueous humor production or even both. It is necessary to identify the physiologic processes involved in aqueous humor production and in its drainage.

Therapeutical contact lenses is one of the drug delivery devices used to treat high IOP. Different drugs have been considered depending on the pathology that leads to IOP increasing:
  1. 1.

    beta blockers and carbonic anhydrase inhibitors reduce eye pressure by decreasing the production of intraocular fluid;

     
  2. 2.

    prostaglandin analogs induce a reduction of IOP, diminishing the resistance to aqueous humor outflow;

     
  3. 3.

    alpha agonists induce a decrease in the production of fluid and also increase the aqueous humor drainage.

     

This article aims to contribute to the mathematical modelling of drug delivery from therapeutical contact lenses to treat glaucoma. We start by presenting the anterior segment of the eye and the dynamics of aqueous humor. The set of anomalous situations that lead to increasing intraocular pressure is then described. An overview on some therapeutic strategies that can be used to treat open-angle glaucoma is presented. The main part of this work concerns a mathematical model that describes the drug release from therapeutic lenses and its evolution in the cornea and anterior chamber. To simplify, the model is built under some assumptions on the phenomena involved as well as on the geometry of the anterior chamber. We conclude remarking that this work was published in the ECMI Annual Report 2016 [9].

5.2 Anterior Segment of the Eye and Aqueous Humor Dynamics

Glaucoma is a group of diseases that lead to the damage of the optical nerve and it is usually associated with an increase of the IOP. This increase is due to pathological modifications of the physiology of the anterior segment of the eye, see Fig. 5.1. This part of the eye is composed by the cornea (the outer boundary), the anterior chamber, the iris, the lens and the ciliary body that define the anterior boundary of the anterior chamber. The cornea is composed by several layers:
  1. 1.
    the epithelium (the outer layer);
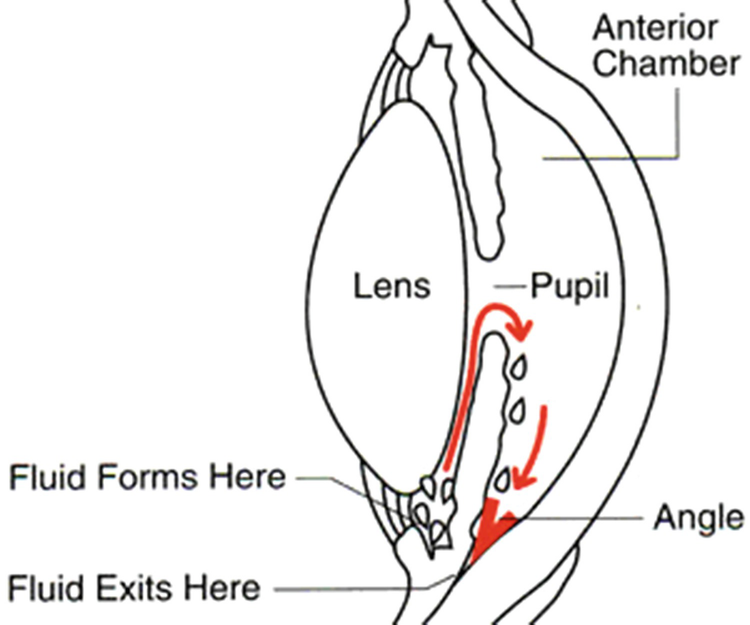    ../images/475466_1_En_5_Chapter/475466_1_En_5_Fig1_HTML.png
    Fig. 5.1

    Anatomy of the eye (http://​www.​theeyecenter.​com/​educational/​005.​htm)

     
  2. 2.

    the stroma;

     
  3. 3.

    the endothelium (the inner layer). It is coated by a tear film known as precorneal film, see Fig. 5.1.

     
The anterior segment of the eye is filled with the aqueous humor. This clear watery fluid is produced by the ciliary epithelium of the ciliary processes located in the ciliary body. It flows from the posterior chamber to the anterior chamber by the narrow space between the posterior iris and the anterior lens and enters in the anterior chamber by the pupil. The aqueous humor leaves the anterior chamber mainly through the trabecular meshwork. It reaches the episcleral venous system via Schlemm’s canal. It is also drained from the anterior chamber by the uveoscleral route. The aqueous humor has a multi-purpose nature, see [3]:
  1. 1.

    provides nutrients to the avascular tissues of the anterior segment;

     
  2. 2.

    removes metabolic excretory products;

     
  3. 3.

    stabilizes the ocular structure;

     
  4. 4.

    contributes to the homeostasis of these tissues.

     
Two main factors contribute to aqueous humor flow:
  1. 1.

    the pressure difference between the trabecular meshwork, that induces a resistance to the outflow (porous structure), and the end of Schlemm’s canal, which is similar to the blood pressure (8–10 mmHg);

     
  2. 2.

    the temperature difference near the cornea and lens.

     
Two convective flows are then induced that are driven by a pressure gradient and a temperature gradient. The balance between the aqueous humor production and its drainage maintains the IOP stable. The drainage through the uveoscleral route appears to be pressure independent, see [10].

5.3 Glaucoma

The closed-angle glaucoma can be induced by different causes that influence an iris dilation and its adheration to the lens.

The aqueous humor is produced in the ciliary body involving complex phenomena that include ultrafiltration, diffusion and active transport (active secretion). The ultrafiltration occurs in the capillaries of the ciliary processes and it is a passive movement of water and water soluble substances across cell membranes, diffusion of solute takes place in the tissue between the capillaries and the posterior chamber in response to concentration gradient. Active transport occurs in nonpigmented epithelial cells and it is the main responsible for the aqueous humor formation, see [10, 15]. An abnormal production of the aqueous humor can lead to increased IOP.

In the human eye, 75% of the resistance to the fluid outflow is due to the trabecular meshwork and 25% occurs beyond the Schlemm’s canal. Trabecular meshwork’s resistance to the drainage of aqueous humor is due to the hydration of the trabecular meshwork structure that can cause obstruction of its structure. Such obstruction is also associated with the formation of deposits within this tissue. Recently, the region of the trabecular meshwork that is responsible by the IOP regulation was identified: the juxtacanalicular tissue, which is adjacent to Schlemm’s canal. To keep the aqueous humor flow channels open in the juxtacanalicular tissue, the extracellular matrix of this tissue presents a continuous remodelling. An interference in this remodelling process compromises the aqueous humor drainage and increases the IOP, see [14].

The hypothesis that the biomechanical properties of Schlemm’s canal contribute to the aqueous humor outflow was studied, for instance, in [2, 16]. It was observed that the pore formation is a mechanosensitive process: an increase of the biomechanical strain induces an increase of the porous density. Changing this biomechanical behaviour, it was observed that the porous formation decreases, leading to increased IOP.

5.4 Therapeutics Strategies to Open-Angle Glaucoma

To decrease the IOP it is necessary to attack the anterior segment of the eye fortress and introduce drugs in the anterior chamber. This fortress is defended by the tear fluid barrier, the tear film that coats the corneal epithelium, the permanent blink, the cornea (lower impermeable structure) and the blood-aqueous barrier. Eye drops are the most used ocular route to administer drugs. However the drug bioavailability in the anterior chamber is very low. The tear film turnover is one of the main contributors to this fact. The drug residence time in the corneal epithelium is equal to 5–6 min before being completely washed way. The permanent continuous blinking removes the mixture of drug solution with tear fluid from the corneal epithelium to the nasolacrimal ducts.

The low permeability of the corneal layers also contributes to the reduced amount of drug that reaches the anterior chamber. Less than 5% of the drug present in the eye drops reaches the ocular tissue. The use of the systemic rout to delivery drug into the anterior segment of the eye is also very inefficient. In fact, the blood-aqueous barrier restricts the entry of drugs from the blood stream into the posterior segment and consequently, to the anterior chamber. The poor eye drug absorption requires repeated applications during long periods to achieve drug concentrations in the anterior chamber within the therapeutic window.

Different drugs have been used to decrease the IOP and they depend on the specific pathology. For instance, if the increased IOP is due to an anomalous production of aqueous humor, β-blockers, α-agonists and carbonic anhydrase inhibitors lead to decreasing of aqueous humor inflow. Other approaches use prostaglandin analogs to enhance the uveoscleral outflow or muscarinic agonists to enhance the trabecular outflow, see [17].

Several approaches have been followed to avoid the limitations of classical topical administration, like, for instance, the use of viscosity enhancers, mucoadhesive and lens which aim at increasing the drug corneal residence time. Other strategies, like the use of penetration enhancers, prodrugs and colloidal systems aim to increase the corneal permeability, see [19]. The purpose of such strategies is to delivery drug into the anterior chamber at a sustained and controlled rate complying the drug concentration in the target tissue to therapeutic window .

Since the nineties, several types of therapeutical contact lenses have been proposed by researchers to increase the drug residence time in the cornea. Without being exhaustive we mention
  1. 1.

    soaked contact lenses, see [1];

     
  2. 2.

    compound contact lenses with a hollow cavity, see [18];

     
  3. 3.

    entrapment of proteins, cells and drugs by polymerization of hydrogel monomers, see [20];

     
  4. 4.

    biodegradable contact lenses, see [4].

     
We remark that the corneal drug residence time for soaked lenses increases (it is around 30 min) by increasing the drug bioavailability. However, such increase is not significantly high because there are no barriers to the delivery and the loading is limited by the drug solubility. Compound lenses with hollow cavities as drug reservoirs present lower permeability to oxygen and carbone dioxide. In the polymerization process the drug can loose its therapeutic characteristics, see [21].

To delay the drug delivery process such that the corneal drug residence time and loading increases, several authors propose to encapsulate the drug in polymeric particles that are dispersed in the lens, see [5, 11–13]. In this case, the drug can also be dispersed in the polymeric structure leading to increasing drug loading. Such drug can be in three states in the polymer: free, bounded or encapsulated. The dispersed drug, when in contact with the tear fluid, is immediately released followed by the delivery of the bounded drug. The release on the encapsulated drug is delayed by the particles structure and the corneal drug residence time increases significantly. One of the main advantages of such devices is the possibility to build lenses that deliver the drug with a pre-defined profile.

5.5 Mathematical Modelling of Drug Delivery from Therapeutic Lenses

Building a mathematical model that describes the drug delivery process from a specific device and its transport to the target tissue is a complex work that requires different tasks. Let us consider the case of a therapeutic lens used to treat open-angle glaucoma, that is to deliver a specific drug in the anterior chamber to decrease IOP. Different tasks can be identified in the mathematical modelling of this drug delivery process.

The drug release and transport involves a set of complex phenomena presented before:
  1. 1.

    the drug release from the polymeric structure;

     
  2. 2.

    its clearance by the tear turnover;

     
  3. 3.

    the drug transport through the different layers of the cornea;

     
  4. 4.

    the drug transport and its drainage by the aqueous humor;

     
  5. 5.

    the dynamics of the fluid, which includes the aqueous humor production in the ciliary body, its transport in the posterior chamber and in the anterior chamber, its drainage through the trabecular meshwork and uveoscleral route, and its transport in the Schlemm’s canal.

     
It should be remarked that a mathematical model describing all phenomena taking place will be very complex and its numerical simulation will be a very difficult task. Therefore it is necessary to identify the main phenomena involved and the spatial domains were they occur.
The drug delivery from a lens and its transport in the anterior chamber is naturally a three dimensional problem. However, to simplify the geometry of the domain we reduce the domain to a two dimensional one using the symmetry of the anterior segment of the eye and lens. We remark that in [6] the mathematical model is defined in bounded intervals for the lens and cornea and the anterior chamber was considered as a sac with passive role in the process. The mathematical models introduced in [7, 8] were defined in a two dimensional domain and the influence of the aqueous humour motion was taken into account. It is assumed that the fluid enters the anterior chamber through the space between the iris and the lens that we denote by Γ ac,i, see Fig. 5.2, and it is drained through the trabecular meshwork. The tear turnover and the uveoscleral drainage were neglected, the aqueous humor production is not explicitly considered as well as its transport through the trabecular mesh until the Schlemm’s canal. The last transport is described by a condition on the flux that leaves the anterior chamber through Γ ac,tm. The aqueous humor production is described by a boundary source term specified at the fluid entrance Γ ac,i. These assumptions allow us to consider the domain plotted in Fig. 5.2.
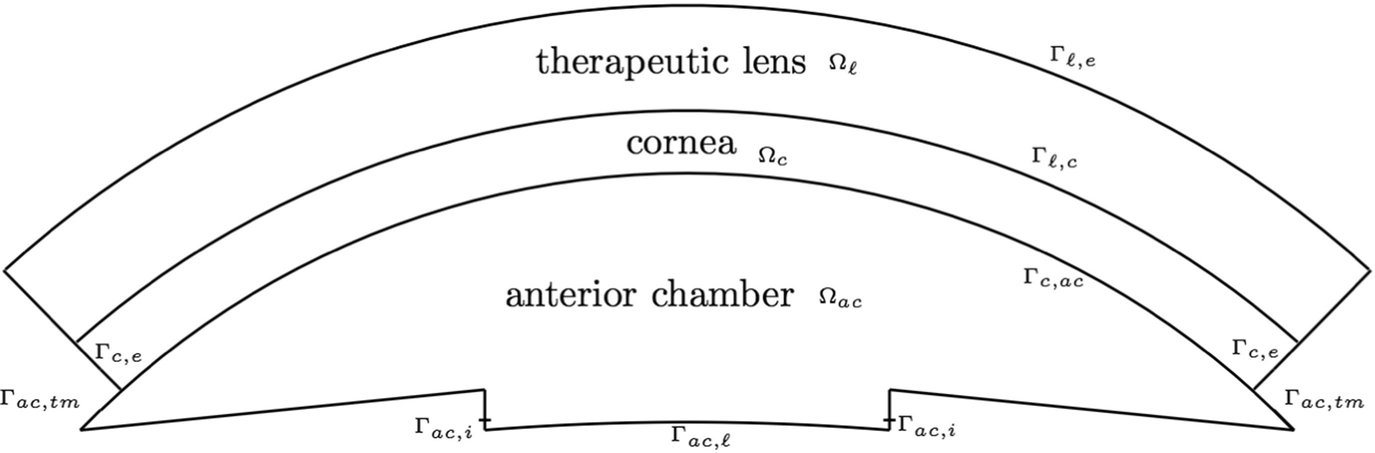
../images/475466_1_En_5_Chapter/475466_1_En_5_Fig2_HTML.png
Fig. 5.2

Spatial domain

We point out that the properties of the polymer used to construct the lens and particles entrapping the drug should be provided. We assume that the drug is dispersed in the polymeric lens presenting three different states, free, bounded and entrapped, while the cornea is composed by a single layer.

Let Ω ℓ, Ω c and Ω ac denote the lens, the cornea and the anterior chamber, respectively. By c f, c b and c e we denote the free, bound and entrapped drug concentrations (g∕m 3). In what follows we specify the phenomena and their mathematical laws in each domain:
  1. 1.
    Ω ℓ—In the lens three different phenomena occur: the links between the polymeric chains and the drug molecules break and the bounded drug is converted in free drug that diffuses. Let λ b,f, λ e,f be the transference coefficients (1∕s) between bounded and free drug and entrapped and free drug, respectively, and D f,ℓ denote the free drug diffusion tensor (m 2∕s). Then the behaviour of the free and bound drugs is described by the diffusion equations
    $$\displaystyle \begin{aligned} \left\{ \begin{aligned} \frac{\partial c_f}{\partial t}&=\nabla \cdot({\mathbf{D}}_{f, \ell}\nabla c_f)+\lambda_{b,f}(c_{b}-c_f)\\ &\quad +\lambda_{e,f}(c_{e}-c_f),\\ \frac{\partial c_b}{\partial t}&= -\lambda_{b,f}(c_{b}-c_f) ,\\ \frac{\partial c_e}{\partial t}&= -\lambda_{e,f}(c_{e}-c_f),\ \end{aligned} \right. \end{aligned} $$
    (5.1)

    in Ω ℓ × (0, T], where T > 0 denotes a fixed time.

     
  2. 2.
    Ω c—Only the free drug is released from the lens and enters in the cornea where it diffuses. If D f,c represents the free drug diffusion tensor in the cornea then
    $$\displaystyle \begin{aligned} \frac{\partial c_f}{\partial t}= \nabla.({\mathbf{D}}_{f, c}\nabla c_f)-\lambda_cc_f \end{aligned} $$
    (5.2)

    in Ω c × (0, T]. Equation (5.2) is established assuming that the clearance of the drug occurs here being λ c the clearance rate (1∕s).

     
  3. 3.
    Ω ac—In the anterior chamber the free drug diffuses and its transported by the aqueous humor to the trabecular meshwork. The evolution of c f is described by the following convection-diffusion-reaction equation
    $$\displaystyle \begin{aligned} \frac{\partial c_f}{\partial t}+\nabla (\mathbf{v}c_f)= \nabla.({\mathbf{D}}_{f, ac}\nabla c_f)-\lambda_{ac}c_f \end{aligned} $$
    (5.3)
    in Ω ac × (0, T]. In Eq. (5.3), D f,ac and λ ac (1∕s) represent the drug diffusion tensor and the drug clearance rate in the aqueous humor. As the aqueous humor is mainly composed by water, and its dynamics is mainly driven by the IOP, the velocity field v can be described by the incompressible Navier–Stokes equations
    $$\displaystyle \begin{aligned} \left\{ \begin{aligned} \rho \frac{\partial \mathbf{v}}{\partial t}+\rho (\mathbf{v} \cdot {\boldsymbol \nabla}) \mathbf{v}- \nu {\boldsymbol \varDelta} \mathbf{v} +\nabla p &=\mathbf{0},\\ \nabla \cdot \mathbf{v}&=0,\ \end{aligned} \right. \end{aligned} $$
    (5.4)

    in Ω ac × (0, T]. In system (5.4), p represents the intraocular pressure, ρ the density of the aqueous humor and ν its kinematic viscosity.

    The velocity field v is time and space dependent if the drug molecules have a therapeutic effect in the trabecular meshwork. Otherwise the velocity does not change in time and then the system of equations (5.4) should be replaced by steady Navier–Stokes equations.

     
The boundary conditions are specified now. We start by defining the boundary conditions for drug concentration:
  1. 1.
    Let Γ ℓ,e be the exterior boundary of Ω ℓ, see Fig. 5.2. We assume that this surface is isolated, meaning that the drug mass flux is zero. Then
    $$\displaystyle \begin{aligned} {\mathbf{D}}_{f,\ell}\nabla c_f \cdot \boldsymbol\eta=0 \,\mbox{ on } \varGamma_{\ell,e}\times (0,T], \end{aligned} $$
    (5.5)

    where η denotes the outward unit normal to Ω ℓ on Γ ℓ,e.

     
  2. 2.
    By Γ c,e we represent the exterior boundary of Ω c, see Fig. 5.2. As no drug mass flux occur on Γ c,e we have
    $$\displaystyle \begin{aligned} {\mathbf{D}}_{f,c}\nabla c_f\cdot \boldsymbol\eta=0 \,\mbox{ on } \varGamma_{c,e}\times (0,T], \end{aligned} $$
    (5.6)

    where η denotes the outward unit normal to Ω c on Γ c,e.

     
  3. 3.
    On the fluid outflow boundary Γac, tm (see Fig. 5.2) we assume that the drug mass flux depends on a function A c(c f) that reflects the drug effect in the increasing of the porosity of the trabecular mesh. This function should increase as c f increases reaching a maximum threshold. Therefore we assume that
    $$\displaystyle \begin{aligned} \mathbf{J} \cdot \boldsymbol\eta=A_c(c_f)c_f \,\mbox{ on } \varGamma_{ac,tm}\times (0,T], \end{aligned} $$
    (5.7)

    where J = −D f,ac∇c f + vc f, and η denotes the outward unit normal to Ω c on Γ ac,tm.

     
  4. 4.
    In the boundary Γ ac,ℓ ∪ Γ ac,i (see Fig. 5.2) we take
    $$\displaystyle \begin{aligned} \mathbf{J}\cdot \boldsymbol\eta=0 \,\mbox{ on } (\varGamma_{ac,e}\cup \varGamma_{ac,i})\times (0,T], \end{aligned} $$
    (5.8)

    where η denotes the outward unit normal to this portion of the boundary.

     
The boundary conditions for the Navier–Stokes equations are specified in what follows:
  1. 1.
    In the inflow boundary Γ ac,i we assume that the normal component of the velocity is known
    $$\displaystyle \begin{aligned} \mathbf{v}\cdot \boldsymbol\eta=v_{in} \,\mbox{ on } \varGamma_{ac,i} \times (0,T]. \end{aligned} $$
    (5.9)
     
  2. 2.
    There are several approaches to define the boundary condition when the pressure is known. One of them is to consider
    $$\displaystyle \begin{aligned} (\nu\boldsymbol\nabla \mathbf{v} - p\boldsymbol I)\boldsymbol\eta=-p_0\boldsymbol\eta \,\mbox{ on } \varGamma_{ac,tm} \times (0,T], \end{aligned} $$
    (5.10)

    where p 0 denotes the pressure in Schlemm’s canal which is taken equal to the blood pressure and I is the identity matrix.

     
  3. 3.
    On ∂Ω ac∖(Γ ac,i ∪ Γ ac,tm) the normal component of the velocity is null
    $$\displaystyle \begin{aligned} \mathbf{v}\cdot \boldsymbol\eta=0 \end{aligned} $$
    (5.11)

    on (Γ c,ac ∪ Γ ac,e) × (0, T].

     
For interface boundaries we assume the next conditions for the free drug concentration.
  1. 1.
    Interface between the lens and cornea:
    $$\displaystyle \begin{aligned} \left\{\begin{aligned} {\mathbf{D}}_{f,\ell}\nabla c_{f,\ell}\cdot \boldsymbol\eta &={\mathbf{D}}_{f,c}\nabla c_{f,c}\cdot \boldsymbol\eta \\ -{\mathbf{D}}_{f,\ell}\nabla c_{f,\ell}\cdot \boldsymbol\eta&=A_{\ell,c} (c_{f,\ell}-c_{f,c}) \end{aligned} \right. \end{aligned} $$
    (5.12)

    on Γ ℓ,c × (0, T], where η denotes the outward unit normal to Ω ℓ on Γ ℓ,c. Here c f,ℓ and c f,c represent the drug concentrations in the lens and cornea, respectively, and A ℓ,c (m∕s) denotes the partition coefficient on Γ ℓ,c.

     
  2. 2.
    Interface between the cornea and anterior chamber:
    $$\displaystyle \begin{aligned} \left\{\begin{aligned} {\mathbf{D}}_{f,c}\nabla c_{f,c}\cdot \boldsymbol\eta &={\mathbf{D}}_{f,ac}\nabla c_{f,ac}\cdot \boldsymbol\eta \\ -{\mathbf{D}}_{f,c}\nabla c_{f,c}\cdot \boldsymbol\eta &=A_{c,ac}(c_{f,c}-c_{f,ac}) \end{aligned} \right. \end{aligned} $$
    (5.13)

    on Γ c,ac × (0, T], where here c f,ac denotes the drug concentration in the anterior chamber, η the outward unit normal to Ω c on Γ ℓ,c and A c,ac (m∕s) represents the partition coefficient on Γ c,ac.

     
Finally, the initial conditions should be imposed to complete the system of partial differential equations (5.1)–(5.4) complemented with the boundary conditions (5.5)–(5.11) and interface conditions (5.12) and (5.13). We impose the following
$$\displaystyle \begin{aligned} c_f(0) &= \left\{ \begin{aligned} c_{f,0}& \mbox{ in } \varOmega_\ell\\ 0 & \mbox{ in } \varOmega_c\cup \varOmega_{ac} \end{aligned} \right.\\ c_b(0)&=c_{b,0} \mbox{ in } \varOmega_\ell,\\ c_e(0)&=c_{e,0} \mbox{ in } \varOmega_\ell,\\ \end{aligned}$$
and
$$\displaystyle \begin{aligned} \mathbf{v}(0)= {\mathbf{v}}_0 \mbox{ in } \varOmega_{ac}, \end{aligned}$$
where c f,0, c b,0, c e,0 and v 0 are known functions.
In Figs. 5.3 and 5.4 we present two typical plots for the drug distribution included before in [8]. Figure 5.3 illustrates the drug distribution in the anterior chamber when a lens is used where the drug is dispersed in the polymeric structure and entrapped in particles. The results obtained for the drop case are plotted in Fig. 5.4.
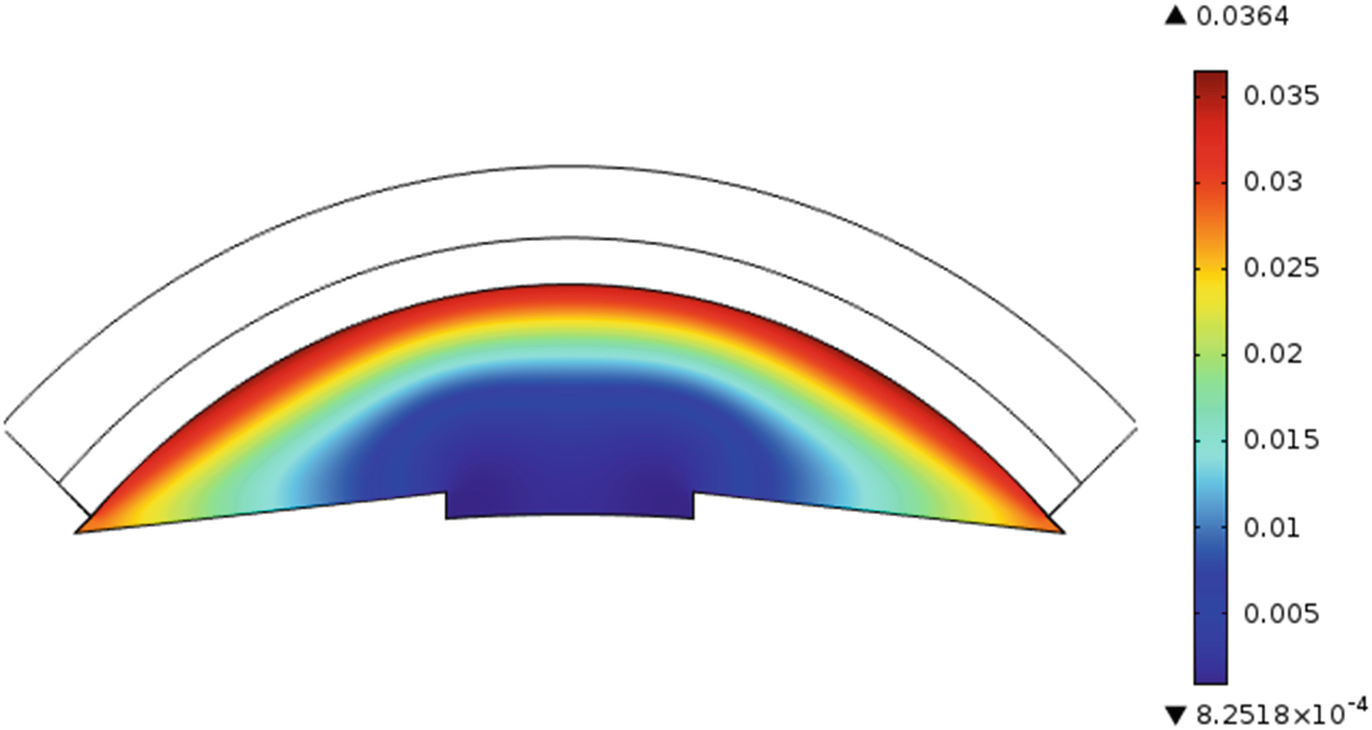
../images/475466_1_En_5_Chapter/475466_1_En_5_Fig3_HTML.png
Fig. 5.3

Drug distribution in anterior chamber after 20 min for a lens

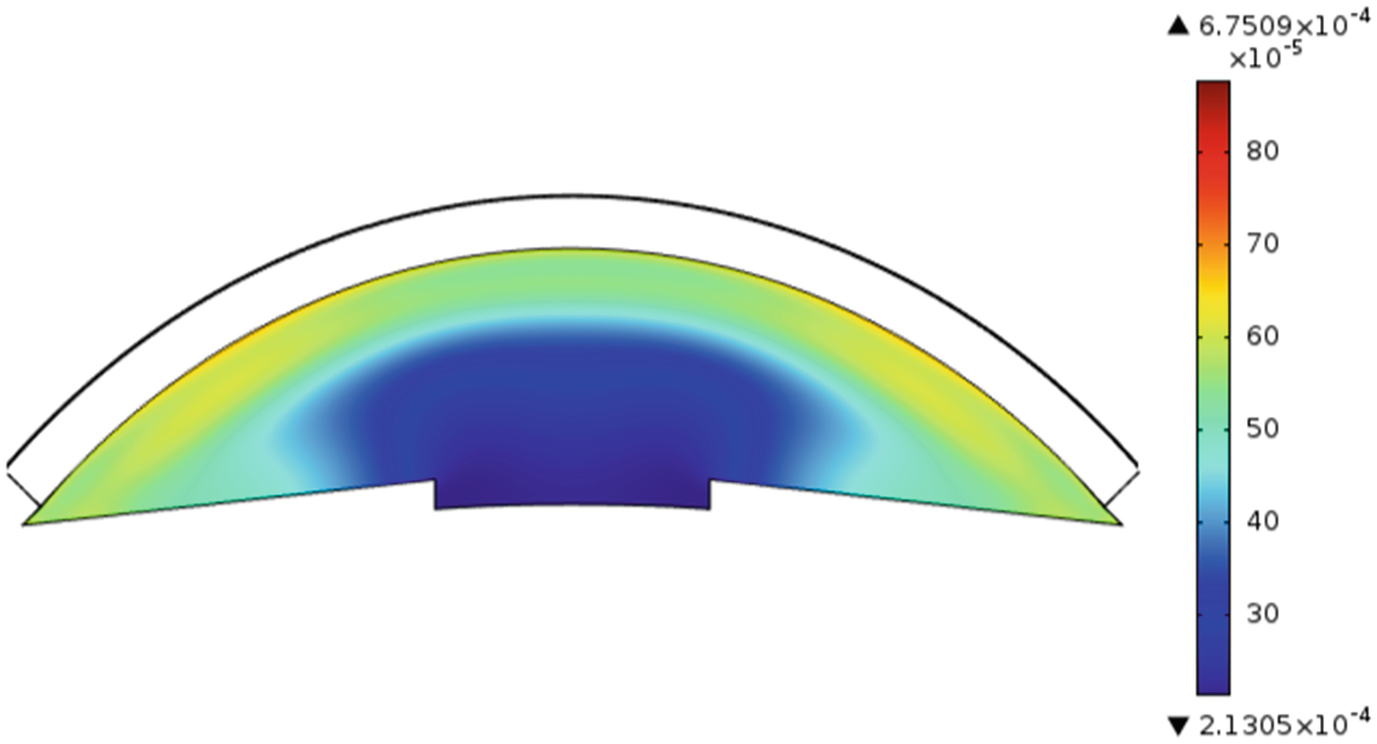
../images/475466_1_En_5_Chapter/475466_1_En_5_Fig4_HTML.png
Fig. 5.4

Drug distribution in anterior chamber after 20 min for an eye drop

From the plots we can infer that the amount of drug that reaches the anterior chamber with lens is higher than for drops due to the initial loading. Moreover the drug release from a therapeutic lens is a slower process due to the polymeric barrier for the dispersed and entrapped drugs.

5.6 Conclusions

This work aims to contribute to the mathematical modelling of the drug delivery from a drug delivery device—the therapeutic lens—used to decrease IOP in a glaucoma scenario. The model is established under several simplifying assumptions in what concerns the geometry of the spatial domain and the phenomena involved.

Some new models can now be deduced with increasing complexity adding new phenomena and changing the geometry of the spatial domain to include new tissues or organs. For instance the tear turnover can be included requiring the inclusion of a tear film layer in the spatial domain. New equations should be added to the existing set of partial differential equations that describe the drug dynamics in this fluid. Different corneal layers—epithelium, stroma and endothelium—can also be added to the model where the drug presents different diffusion properties. Consequently, the diffusion equation in the cornea should be replaced by three diffusion equations with the correspondent compatibility conditions on the contact surfaces between layers. If the trabecular meshwork is considered (Ω tm) with or without juxtacanalicular tissue, the drug transport is defined by an equation similar to (5.3) where the convective velocity v is given by Darcy equation (coupled with an incompressibility constraint)
$$\displaystyle \begin{aligned} \left\{ \begin{aligned} \mathbf{v}&=-\frac{\mathbf{K}}{\mu\phi }\nabla p\\ \nabla \cdot \mathbf{v}&=0 \end{aligned} \right. \end{aligned} $$
(5.14)
in Ω tm × (0, T]. In (5.14) K denotes the permeability tensor and the porosity coefficient is represented by ϕ. It should be stressed that in this case the coupling between the Navier–Stokes equations (5.4) and (5.14) is a challenging topic namely due to the conditions required on the boundary of the trabecular meshwork that is contact with the anterior chamber.

There is a compromise between the complexity of the mathematical model and its utility to predict the IOP evolution in different scenarios. In fact, the number of parameters needed increases with the complexity and some of them are not known.

Acknowledgements

This work was partially supported by the Centre for Mathematics of the University of Coimbra—UID/MAT/00324/2019, funded by the Portuguese Government through FCT/MEC and co-funded by the European Regional Development Fund through the Partnership Agreement PT2020.