
2.1. Difference methods for linear problems. A very general theory of difference methods is available for linear problems of the form (0.1a,b), which have unique solutions. The theory states in essence that a difference scheme is stable and consistent for the boundary value problem if and only if it is so for the initial value problem. For practical purposes it is only the sufficiency part that is important. But a simple result relating pairs of boundary value problems makes the necessity proof trivially follow from sufficiency. So we first present this useful theoretical result as :
THEOREM 2.1. Consider the pair of boundary value problems BV(v), v = 0, 1 given by
The corresponding fundamental solution matrix, Y(v)(t), defined by
exists if and only if BV(v) has a unique solution.
If BV(0) has a unique solution, then BV(1) has a unique solution if and only if 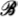 (1)Y(0)(t) is nonsingular.
(1)Y(0)(t) is nonsingular.
Proof It is clear from Theorem 1.5 that BV(v) has a unique solution if and only if
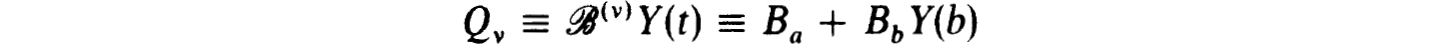 nonsingular. When this is so we can define Y(v)(f) as
nonsingular. When this is so we can define Y(v)(f) as
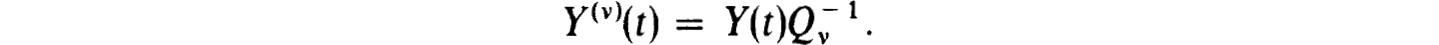
On the other hand if Y(v)t) exists, then it must have this representation.
Now suppose BV(0) has a unique solution. Then  exists and
exists and 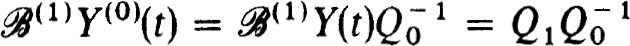 . Thus
. Thus 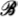 (1)Y(O)(t) is nonsingular if and only if Q1 is nonsingular.
(1)Y(O)(t) is nonsingular if and only if Q1 is nonsingular. 
The difference schemes employ a net of the form
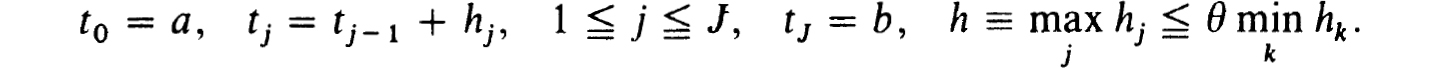
Then corresponding to each interval [tj-1, tj] of this net we consider an approximation to (0.1a) in the form:
The boundary conditions (0.1b) are simply taken over as
The net function 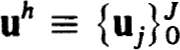 is to approximate
is to approximate 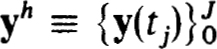 , the exact solution on the net. The n × n coefficient matrices {Cjk(h)} and inhomogeneous terms {Fj(h, f)} define a very general family of difference schemes for which we develop a complete stability theory.
, the exact solution on the net. The n × n coefficient matrices {Cjk(h)} and inhomogeneous terms {Fj(h, f)} define a very general family of difference schemes for which we develop a complete stability theory.
It will frequently be useful to formulate the difference equations (2.3a,b) in block matrix form as
where
The truncation errors in (2.3a,b) as an approximation to (0.1a,b) are
and the scheme is consistent or accurate of order m if for every (smooth) solution of (0.1 a,b) there exist constants K1 > 0, h0 > 0 such that for all nets {tj} with h  h0
h0
The scheme is said to be stable provided there exist constants K1 > 0 and h0 > 0 such that for all nets {tj}with h  h0 and for all net functions vh,
h0 and for all net functions vh,
It is more or less well known, and easy to prove, that stability is equivalent to the existence and uniform boundedness of the inverses of the family of matrices  h; that is, for some K1 > 0, h0 > 0 and all h
h; that is, for some K1 > 0, h0 > 0 and all h  h0,
h0,
(Norms on block matrices, say, B = (Bij), are always to be taken as
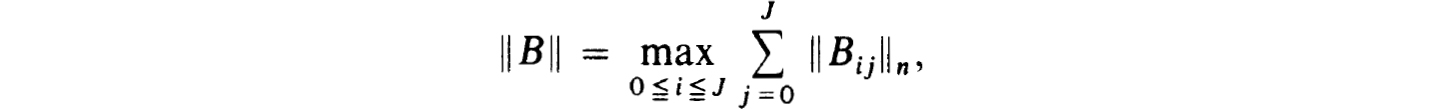
where || · ||n„ is the matrix norm induced by the vector norm used on  n.) It is also well-known that consistency and stability imply convergence as in
n.) It is also well-known that consistency and stability imply convergence as in
Proofs of these facts are simple consequences of the definitions and can be found, for example, in Keller [24].
Now consider a pair of linear problems of the form (2.1a,b). The corresponding difference schemes resulting from applying (2.3a,b) to each of these problems differ only in the boundary conditions, say :
The deep and important connection between these schemes is contained in
THEOREM 2.9. Let each problem BV(v), v = 0, 1, have a unique solution. Then the corresponding difference schemes BVh(v), v = 0, 1, consisting of (2.3a) and (2.8) are such that BVh(0) is stable and consistent for BV(0) if and only if BVh(1) is stable and consistent for BV(1).
Proof. The equivalence of consistency is trivial since the schemes differ only in the boundary conditions which, in each case, are exact.
For stability consider each matrix 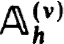 in which Ba and Bb in (2.4b) are replaced by those of (2.8). We note that
in which Ba and Bb in (2.4b) are replaced by those of (2.8). We note that
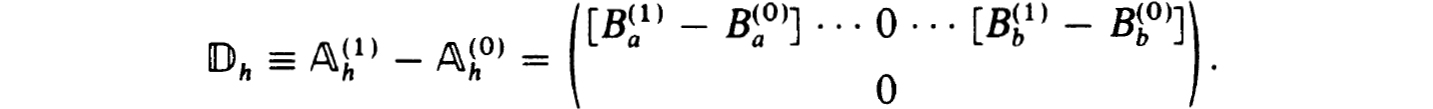
Then, assuming BVh(0) is stable, 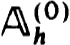 is nonsingular with
is nonsingular with
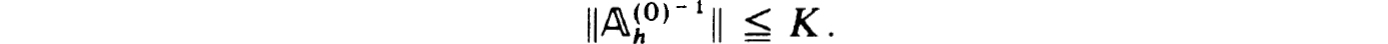
So we can write
Denote the block structure of 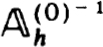 by
by
where the 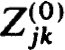 are n × n matrices, 0
are n × n matrices, 0  j, k
j, k  J. Now we have the form
J. Now we have the form
where
This follows from the fact that 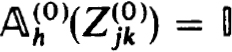 . In particular then,
. In particular then, 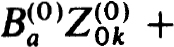
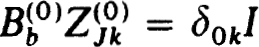 and
and 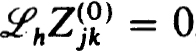 , 1
, 1  j
j  J, 0
J, 0  k
k  J. Note that the column of blocks
J. Note that the column of blocks 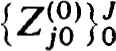 is just the difference approximation, using BVh(0), to Y(0)(t). Thus
is just the difference approximation, using BVh(0), to Y(0)(t). Thus
and hence
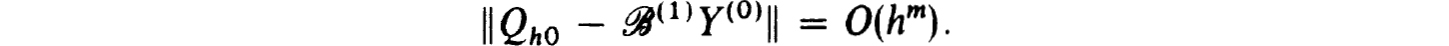
But 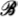 (1)y(0) is nonsingular by Theorem 2.1. Thus Qh0 is nonsingular for h0 sufficiently small and so is
(1)y(0) is nonsingular by Theorem 2.1. Thus Qh0 is nonsingular for h0 sufficiently small and so is 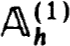 . In fact now
. In fact now
It easily follows, using
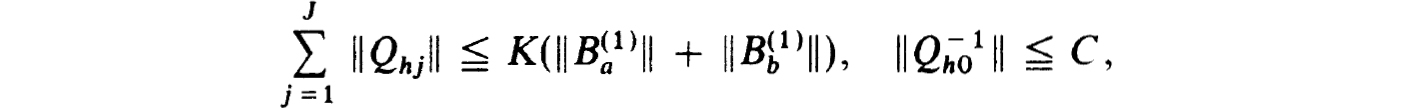
that, if C > 1,
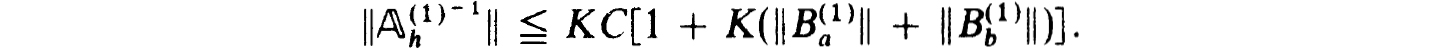
So BVh(l) is stable.
The converse follows by interchanging v = 0 and v = 1 in the above. 
As the most important application of Theorem 2.9 we have
COROLLARY 2.11. Let problem (0.1a,b) have a unique solution. Then the difference scheme (2.3a,b) is stable and consistent for (0.1a,b) if and only if the scheme
is stable and consistent for the initial value problem
Proof. We need only identify BV(1) with (0.1a,b), BVh(1) with (2.3a,b), BV(0) with (2.11b) (which has a unique solution) and BVh(0) with (2.11a). 
We can now devise many stable schemes for boundary value problems by simply using the well-developed theory for initial value problems. In addition asymptotic error expansions are easily obtained in the usual manner (see Stetter [51]). The required truncation expansions are given by Gragg [19] for a special midpoint scheme and by Henrici [22] and Engquist [12] for multistep schemes. We point out, however, that not all schemes are included in our theory—but we believe that all the useful ones are included.
The factorization in (2.10c) or inverse in (2.10e) yields specific procedures for solving the difference equations when 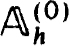 represents an explicit scheme (as would be the case in most initial value schemes). But we do not advocate using this obvious procedure. It would in effect be an initial value or shooting scheme with no special features to recommend it.
represents an explicit scheme (as would be the case in most initial value schemes). But we do not advocate using this obvious procedure. It would in effect be an initial value or shooting scheme with no special features to recommend it.
2.2. One-step schemes; solution procedures. A most important class of difference schemes of the form (2.3a,b) for problems of the form (0.1a,b) are one-step or two-point schemes. That is, schemes in which
If such schemes are consistent, then they are stable as a result of Corollary 2.11 and a result for initial value problems (see Isaacson and Keller [23, p. 396]). If in addition the boundary conditions are separated, as in (1.9a) but with Cba ≡ 0, and we write those conditions at t = a first, then the difference equations (2.3a) using (2.12a), and then the boundary conditions at t = b last, the matrix of the scheme becomes, in place of (2.4b),
We recall that Ca is p × n, Cb is q × n, and all Lj, Rj- are n × n. Thus  h can be written as a block tridiagonal matrix
h can be written as a block tridiagonal matrix
where the n × n bidiagonal matrices have the forms :
To solve linear systems
with  h of the above form we consider first block-
h of the above form we consider first block- 𝕌 decompositions or band-factorizations. A general class of such procedures can be studied by writing
𝕌 decompositions or band-factorizations. A general class of such procedures can be studied by writing
Here αj, βj, γj, δj, and 0 are n × n matrices so that  n and 𝕌h are block lower- or upper-triangular. They may indeed be strictly triangular, as in band-factorization, if öj and a, are, respectively lower- and upper-triangular. In order for this factorization to be valid we must have :
n and 𝕌h are block lower- or upper-triangular. They may indeed be strictly triangular, as in band-factorization, if öj and a, are, respectively lower- and upper-triangular. In order for this factorization to be valid we must have :
Then (2.14) can be solved by writing
and solving, in order :
The indicated factorizations are not uniquely determined and do not exist in general. However, with a simple form of pivoting that does not introduce new zero elements we can justify such schemes. They become unique if we specify, for example:
Cases (i) and (ii) yield standard block-tridiagonal factorizations while (iii) and (iv) are standard band-factorization or Gauss eliminations accounting for zero elements. When these schemes are valid it turns out that the βj have the same zero pattern as the Bj in (2.13b) while the δj have zeros as in the C, of (2.13b) only in Cases (i), (iii) and (iv). Surprisingly Case (ii) may fill in the γj and so should not be used. Operational counts (see Keller [26]) assuming the indicated zero patterns, show that (i) is preferable to (iii) when p/n < 0.38 (approximate) (see Varah [52]); (iii) is preferable to (iv) when p < q and (i) is always preferable to (ii). In production codes we have generally used (i) or (iii) with some form of pivoting. To justify these procedures we have
THEOREM 2.17. Let  h of(2.13a) be nonsingular. Then with appropriate row interchanges within each of the n rows with indices k jn: jn + p < k < (j + 1)n + p for each j = 0,1, ···, J – 1, the block-factorization
h of(2.13a) be nonsingular. Then with appropriate row interchanges within each of the n rows with indices k jn: jn + p < k < (j + 1)n + p for each j = 0,1, ···, J – 1, the block-factorization  h = [βj, I, 0] [0, α,-, Cj]is valid (Case (i) of (2.16)).
h = [βj, I, 0] [0, α,-, Cj]is valid (Case (i) of (2.16)).
The proof is given in White [57] or Keller [26], where Cases (iii) and (iv) are also justified with a mixed partial row and column pivoting, 
Alternative schemes using maximal partial row and column pivoting have been studied by Lam [35] and Varah [53] to reduce the growth of the pivot elements. These procedures are quite stable but a bit more involved to program. Their operational counts are quite similar to those above. The study and development of effective procedures for solving systems of the form (2.12a,b), (2.13a,b) is very important ; extensions to partially separated endpoints are also of great interest and so we consider them briefly.
For partially separated endpoints we get, in place of (2.12b) and (2.13a,b) a coefficient matrix of the form
Here Ĉa is p × n while Ĉba and Ĉb are q × n. These matrices have been used to replace Ca, Cba and Cb in the partially separated endconditions (1.9a). The zero patterns in (2.13a,b) are maintained and Ĉj has the same form as the other Cj’s. In place of the factorizations (2.15a) we seek a “bordered” form, say,
Thus the α;, βj and λj must satisfy
If this procedure can be carried out, then the A, have the same zero pattern as the Cj (i.e., the first p-rows null). Note that (2.19a,b,c) is the analogue of Case (i) in (2.16); we could just as easily consider the other cases. To solve  huh = F we again use
huh = F we again use

The recursions are the same as those in (2.15d) using δj ≡ I, with the single exception of vJ which is now given by
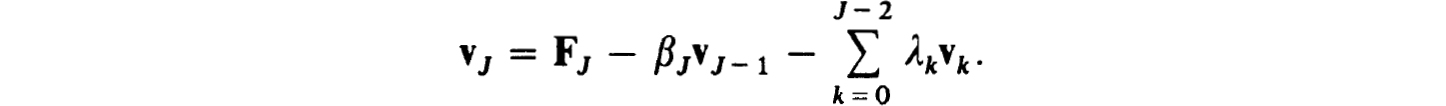
The additional operations caused by partial separation are easily obtained by simply adding all operations involving the nonzero elements of the λj matrices.
To justify this procedure we have
THEOREM 2.20. Let the partially separated endpoint problem (0.1a) subject to (1.9a) (with the C’s replaced by Ĉ’s) have a unique solution. Let the one-step scheme (2.12a) be consistent for the initial value problem for (0.1a). Then if h0 is sufficiently small, for all h  h0 the factorization (2.19a) of
h0 the factorization (2.19a) of 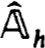 in (2.18) is valid with the same restricted partial pivoting of Theorem 2.17.
in (2.18) is valid with the same restricted partial pivoting of Theorem 2.17.
Proof. Our hypothesis and Corollary 2.11 ensure that 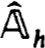 is nonsingular. Pick some q × n matrix
is nonsingular. Pick some q × n matrix 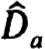 , say, such that
, say, such that
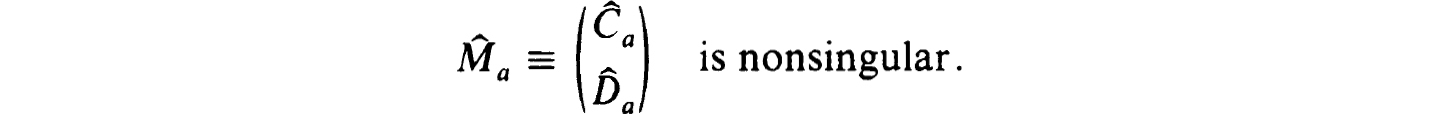
Define Ca ≡ Ĉa and 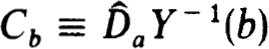 so that the separated endpoint problem (0.1a) subject to (1.9a) with Cba = 0 and Ca, Cb as defined has a unique solution. (This follows since for this problem
so that the separated endpoint problem (0.1a) subject to (1.9a) with Cba = 0 and Ca, Cb as defined has a unique solution. (This follows since for this problem 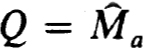 .) Now the hypothesis and Corollary 2.11 imply
.) Now the hypothesis and Corollary 2.11 imply  h of (2.12b) is nonsingular. Thus Theorem 2.17 implies that, with the indicated form of partial pivoting,
h of (2.12b) is nonsingular. Thus Theorem 2.17 implies that, with the indicated form of partial pivoting,
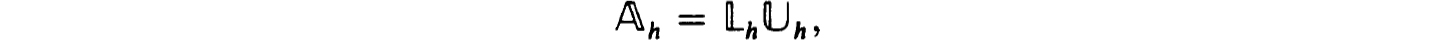
as in (2.15a) (with all δj ≡ I and all γ, = Cj).
Define
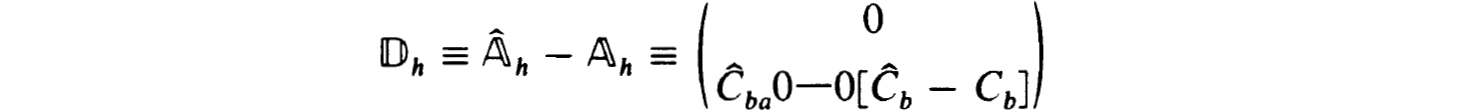
and use the indicated factorization to get
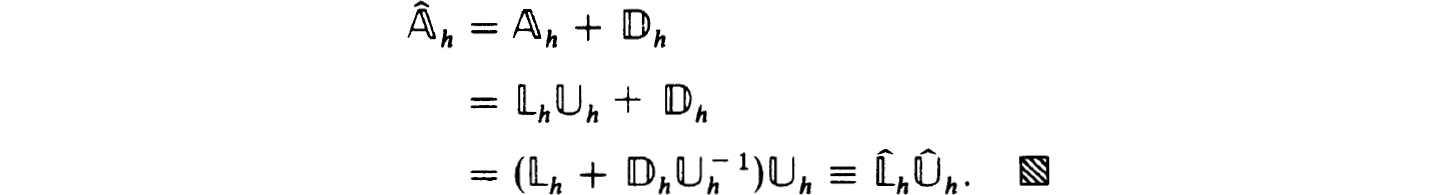
Of course the factorization in the last line of the above proof does not in general give exactly that obtained in (2.19a,b,c). The difference can occur only in the last n × n blocks of  and
and  . But since the choice of
. But since the choice of 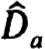 was arbitrary and we can insert the identity in the form
was arbitrary and we can insert the identity in the form  -1
-1  , where
, where

to get 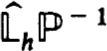 * and P
* and P 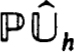 in place of
in place of 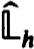 and
and 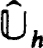 the ambiguity is resolved. It is clear, or should be on reflection, that all of the proposed schemes for factoring
the ambiguity is resolved. It is clear, or should be on reflection, that all of the proposed schemes for factoring  h including mixed partial pivoting as in Keller [26] or Varah [53], go over unaltered for the first J blocks, to that of
h including mixed partial pivoting as in Keller [26] or Varah [53], go over unaltered for the first J blocks, to that of 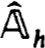 . In fact even if
. In fact even if 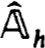 is singular but rank Ĉa = p, the factorization works but a, turns out to be singular. Our statement of Theorem 2.20 merely stressed the most important case.
is singular but rank Ĉa = p, the factorization works but a, turns out to be singular. Our statement of Theorem 2.20 merely stressed the most important case.
One-step difference schemes can be chosen or used to get high order accuracy. The two simplest and most popular forms are the Box-scheme (or centered Euler) with
and the trapezoidal rule with
The former can be used easily with piecewise smooth coefficients provided all jump discontinuities lie on points of the net {tj}. In both cases the truncation error expansions (2.5a) are of the form
Then it easily follows (see Keller [25]) that the errors have asymptotic expansions of the corresponding form
where the ev(r) are independent of h. However these results are valid only on special families of nets; for example, any arbitrary initial net {tj} with h sufficiently small which is then uniformly subdivided in any manner (i.e., all subintervals are divided in the same ratios). Then Richardson extrapolation or deferred corrections can be used (see § 2.4) to get two orders of accuracy improvement per application.
Higher order one-step schemes than those in (2.21a,b) are easily formulated. An interesting class of them, called gap- or Hermite-schemes can be devised by writing (0.1a) as
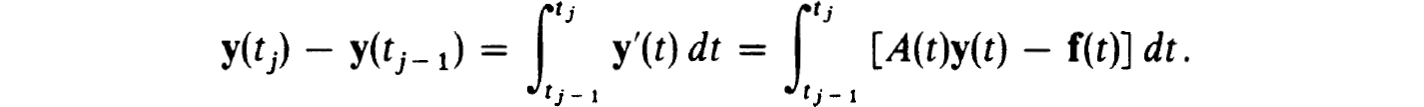
Then using Hermite interpolation of degree 2m + 1 for the integrand, evaluating the higher derivatives up to order m by differentiating in (0.1a), we obtain one-step schemes of accuracy h2m+3. Furthermore, the truncation error expansions start with the (2m + 3) rd derivative of y(r), hence the name “gap-schemes”. If the derivatives of A(t) and y(t) are easily evaluated these schemes can be quite effective. More details are contained in Keller [31] and White [57].
2.3. Difference methods for nonlinear problems. The general theory of difference schemes for linear boundary value problems, as in §2.1, can be used to develop a fairly complete theory of difference methods for isolated solutions of nonlinear problems. In particular to approximate (1.20a,b) on the net 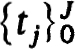 we consider
we consider
The truncation errors are now defined as
and (2.22a,b) is consistent (accurate) for (1.20a,b) of order m if for each solution z(t) :
for some constants K0 > 0, h0 > 0 and all h  h0. The scheme is stable for zh provided there exist positive constants Kρ, ρ and h0 such that for all net functions vh, wh in
h0. The scheme is stable for zh provided there exist positive constants Kρ, ρ and h0 such that for all net functions vh, wh in
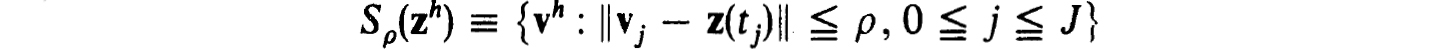
and on all nets 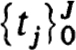 with h
with h  h0,
h0,
Again it easily follows from consistency and stability, if the appropriate solutions exist, that
To demonstrate stability of (2.22a,b) and also to give a constructive existence proof of solutions of (2.22a,b) we require some properties of the linearized difference’ equations :
Here the n × n coefficient matrices are defined by
Stability is covered by
THEOREM 2.27. Let z(t) be an isolated solution of (1.20a,b). Assume that the linear difference scheme
is stable and consistent for the initial value problem (recall (1.23a,b))
Let 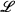 h[wh] be Lipshitz continuous In wh about zh ; that is,
h[wh] be Lipshitz continuous In wh about zh ; that is,
for all wh ∈ Sρ (zh), h  h0 and some KL > 0, ρ > 0, h0 > 0. Similarly let
h0 and some KL > 0, ρ > 0, h0 > 0. Similarly let
Then if ρ is sufficiently small, the schemes {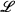 h[vh],
h[vh], 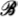 h[vh]} are stable for all vh ∈ Sρ(zh) (that is,
h[vh]} are stable for all vh ∈ Sρ(zh) (that is,  h[vh] has a uniformly bounded inverse for all vh ∈ Sρ(zh)), and the nonlinear scheme (2.22a,b) is stable for zh.
h[vh] has a uniformly bounded inverse for all vh ∈ Sρ(zh)), and the nonlinear scheme (2.22a,b) is stable for zh.
Proof. With  h[uh] defined by (2.4b) using the n × n matrices (2.26c) it follows from (2.27a,b,c,d), the isolation of z(f) and Corollary 2.11 that
h[uh] defined by (2.4b) using the n × n matrices (2.26c) it follows from (2.27a,b,c,d), the isolation of z(f) and Corollary 2.11 that 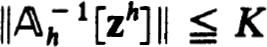 . Then (2.27c,d) and the Banach lemma imply the uniform boundedness of
. Then (2.27c,d) and the Banach lemma imply the uniform boundedness of 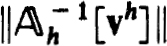 for all vh ∈ Sp(zh), provided p is sufficiently small.
for all vh ∈ Sp(zh), provided p is sufficiently small.
If we write (2.22a,b) as the system
the identity
with
follows from the assumed continuous differentiability of the Gj (·) and g(·,·). But || h[vh wh] -
h[vh wh] -  h[zh]||
h[zh]||  KLρ for all vh, wh in Sρ(zh). Then
KLρ for all vh, wh in Sρ(zh). Then
and the stability of (2.22a,b) follows from
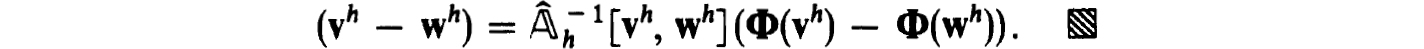
Newton’s method can be used to prove the existence of a unique solution of the nonlinear difference equations (2.22a,b) in Sρo(zh), for some ρ0  ρ. The iterates
ρ. The iterates  are defined, using (2.28), as
are defined, using (2.28), as
Equivalently the iterates can be defined by
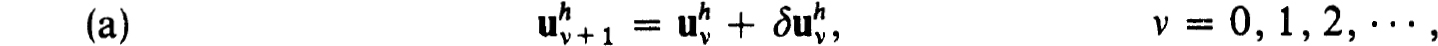
where 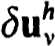 is the solution of the linearized difference equations :
is the solution of the linearized difference equations :
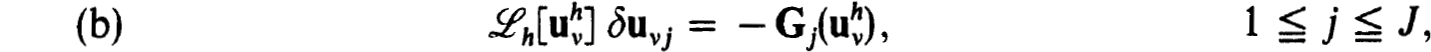
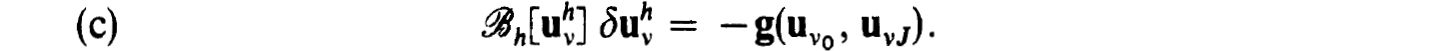
The actual computation of the 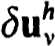 can be carried out using the stable and efficient schemes discussed in § 2.2 when one-step schemes are used with separated endpoint conditions.
can be carried out using the stable and efficient schemes discussed in § 2.2 when one-step schemes are used with separated endpoint conditions.
THEOREM 2.31. Let the hypothesis of Theorem 2.27 hold. Let (2.22a,b) be accurate of order m for (1.20a,b). Then for some ρ0  ρ and h0 sufficiently small (2.22a,b) has for all h
ρ and h0 sufficiently small (2.22a,b) has for all h  h0, a unique solution uh ∈ Sp(zh). This solution can be computed by Newton’s method (2.30a,b) which converges quadratically.
h0, a unique solution uh ∈ Sp(zh). This solution can be computed by Newton’s method (2.30a,b) which converges quadratically.
Proof. We simply verify the hypothesis of the Newton-Kantorovich Theorem 1.28 using φ = Φ(uh) of (2.28) and Q =  h(uh) with elements in (2.26c). From (2.27c,d) we can use y = KL to satisfy (1.28c). Also (2.29c) implies (1.28b) with β = Kρ0. To estimate a as in (1.28a) we write, recalling (2.29a),
h(uh) with elements in (2.26c). From (2.27c,d) we can use y = KL to satisfy (1.28c). Also (2.29c) implies (1.28b) with β = Kρ0. To estimate a as in (1.28a) we write, recalling (2.29a),
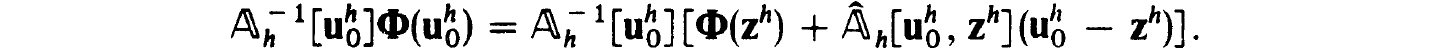
However,
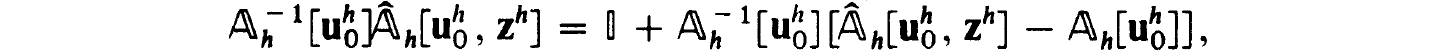
and so
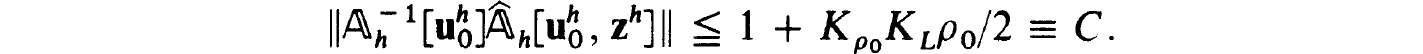
Thus we get, recalling that Φ(zh) is the vector of truncation errors,
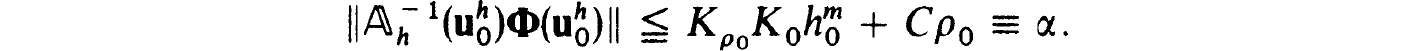
Now taking h0 and ρ0 sufficiently small we are assured that
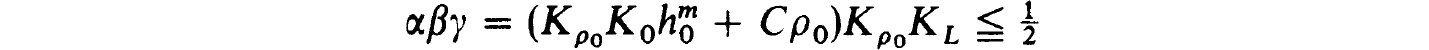
and
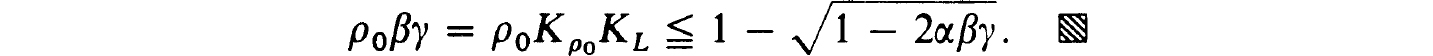
The difficulty in finding a suitable initial guess 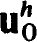 in some sphere about the exact solution zh is generally much less for finite difference methods than it is for shooting methods on the same problem. The reason is to be found in the close analogy between parallel shooting methods (see § 1.3, § 1.5) and finite difference methods. In fact, 7, the number of mesh intervals for finite differences is usually much larger than the number of shooting intervals one would normally think of employing. However, a closer inspection of our finite difference schemes and parallel shooting analysis shows that the same procedures can frequently belong to both classifications !
in some sphere about the exact solution zh is generally much less for finite difference methods than it is for shooting methods on the same problem. The reason is to be found in the close analogy between parallel shooting methods (see § 1.3, § 1.5) and finite difference methods. In fact, 7, the number of mesh intervals for finite differences is usually much larger than the number of shooting intervals one would normally think of employing. However, a closer inspection of our finite difference schemes and parallel shooting analysis shows that the same procedures can frequently belong to both classifications !
2.4. Richardson extrapolation and deferred corrections. The accuracy of a given finite difference scheme may frequently be improved in a very efficient manner. So much so in fact that the most effective difference procedures are based on one-step schemes of second order accuracy enhanced by Richardson extrapolation or deferred corrections. The basis for these techniques is the existence of an asymptotic expansion of the local truncation error, say, of the form
Of course 0 < m1 < ··· < mN + 1 and we assume that for a subset of the subscripts {vk}, say, with v1 = 1,
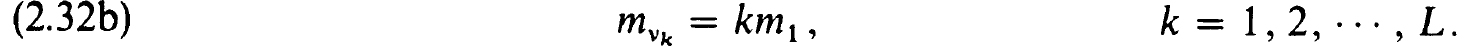
For example, the Box-scheme and trapezoidal rule applied to nonlinear problems still yield truncation expansions of the form (2.21c). Here m1 = 2 and vk = k. In other schemes, the first gap-scheme beyond trapezoidal rule for instance, m1 = 4 and vk = 2k – 1.
When (2.32a) holds for a stable scheme on a uniform net it is not difficult to show that the errors in the numerical solution also have asymptotic error expansions of the form
Here the functions ev(t) are independent of h and they are defined as the solutions of linear boundary value problems. For linear problems, for example, they satisfy
In the nonlinear case, 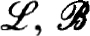 are replaced by
are replaced by 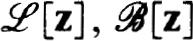 and the inhomogeneous terms are slightly more complicated (as a result of the nonlinearity). Nonuniform nets of appropriate families are easily included as shown in Keller [25].
and the inhomogeneous terms are slightly more complicated (as a result of the nonlinearity). Nonuniform nets of appropriate families are easily included as shown in Keller [25].
The knowledge that an expansion of the form (2.32c) exists enables us to apply Richardson extrapolation on a sequence of refined nets. Each successive refinement requires only the solution of the difference scheme (2.22a,b) on the latest net. At the kth refinement the error term of order hmk is removed ; the details are rather well known being based on iterative extrapolation so we do not repeat them here. It should be stressed however that successive halvings of the net spacing is an unfortunate choice of refinement, assuming that some fixed maximum number of extrapolations, say, 10 or less, are to be done. Rather an arithmetic reduction with h(k) = (k + l)-1h(0) is much more efficient. In anticipation of Richardson extrapolation we must use an appropriately severe convergence criterion for the iterative solution of the difference equations. That is, the iteration error (as well as the truncation error) must be reduced beyond what is anticipated of the final truncation error. The particular effectiveness of quadratic convergence, and hence Newton’s method, in this regard is very important (see, for example, Keller [26], [31]). Specifically if the initial guess 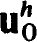 is within 0(h) of the solution at the kth stage, then at most vk = log2 mk iterations are required ; that is, h8 accuracy would require 3 Newton iterations.
is within 0(h) of the solution at the kth stage, then at most vk = log2 mk iterations are required ; that is, h8 accuracy would require 3 Newton iterations.
The deferred correction technique need only be based on (2.32a) rather than on (2.32c), as is frequently stated. In effect this method determines successively higher order difference schemes by including sufficiently accurate approximations to the leading terms in (2.32a) in the latest scheme. In more detail, suppose (2.32a,b) hold. We seek a set of net functions  such that
such that
We assume that the net {tj} and operators Tv[z(0] are such that for some “difference” operators Tv,j,k[·] and net functions uh(k), satisfying (2.34a),
Then the set of net functions can be determined recursively by solving, in order,
To show that (2.34a) holds for the net functions defined in (2.35a,b) we use the stability of the scheme (2.22a,b), (2.32a) and (2.34a,b) to get
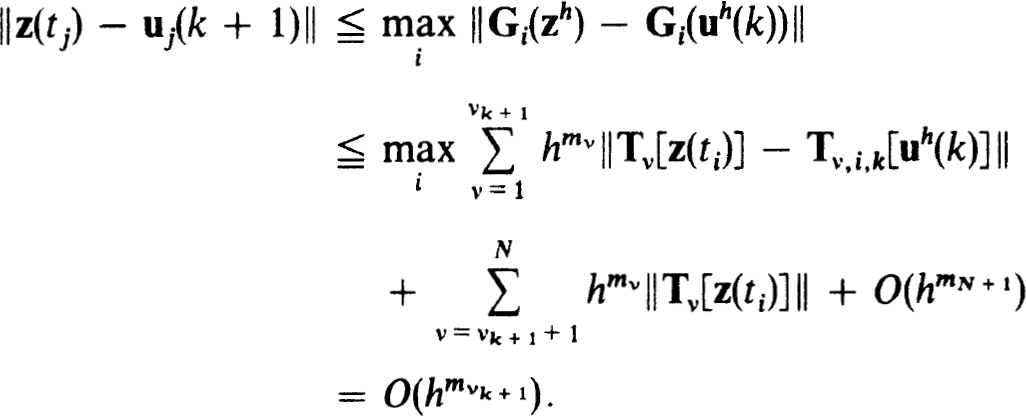
Thus the result follows by induction.
The important practical problem is thus reduced to constructing the difference approximations to the truncation terms. This is done in some generality by Pereyra [42] where “centered” formulae are used at the interior netpoints and uncentered formulae are used near the endpoints. This causes considerable complications in coding the scheme as well as in justifying it rigorously. However, all these difficulties can be circumvented by simply extending the net {tj} to include points external to [a, b] and computing the original solution on the complete extended net. Then on each successive improvement, u;(k), the approximations need to be computed over fewer external points. However, this procedure assumes that the maximum intended order of correction is known in advance and that the correspondingly extended net is used.
Another theoretically simple way to determine appropriate operators Tv,j,k[uh(k)] is to define and compute approximations to the μth derivative, z(μ)(tj), of the exact solution by differentiation of the equation (1.20a). Thus since
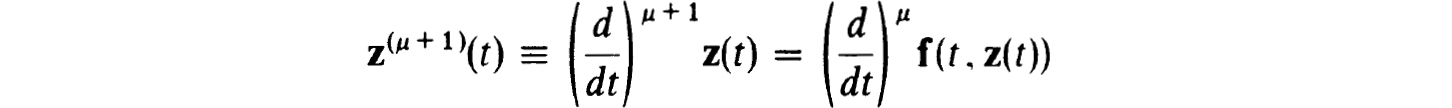
we define, starting with 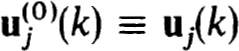
It follows by induction from (2.34a,b) and the assumed smoothness of f(t, z) that
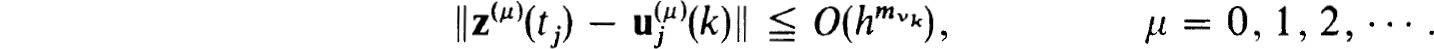
The number of function evaluations in (2.36) grows extremely fast and so it is unlikely to be practical for a general purpose code.
Finally we point out that the first correction, of order hm1 to get an O(hm2) accurate solution, can be done by solving only one linear difference system. In fact it is just equivalent to one more Newton iterate when the Tv,j,1[uh(l)] have been evaluated for v = 1, 2, · · ·, v2. This idea was first used by Fox [14] and has also been used by Pereyra [42].
2.5. Collocation and implicit Runge-Kutta. Collocation has been studied and used increasingly for two-point problems. We shall show in some generality that it is identical to difference schemes based on implicit Runge-Kutta methods when C0[a, b] piecewise polynomials are used in the standard fashion. Then our theory of § 2.3 and the work of Axelsson [3] shows the stability of the method and its super-convergence properties. This work follows closely that of Weiss [56] who first carried out such an analysis.
To define the schemes a basic net 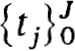 with
with
is refined in each interval to get 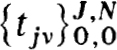 , where
, where
Using the θV as nodes on [0,1] we define N -f 1 interpolatory quadrature rules:
If θ0 > 0 and θN < 1 we can define an (N + 2) nd rule {wN + 1+k} over [0,1] which has maximum degree of precision 2N + 1, i.e., Gaussian quadrature. If θ0 = 0 and θN = 1 the Nth rule can have degree of precision 2N – 1, i.e., Lobatto quadrature. If θ0 > 0 and θn = 1 (or conversely) the Nth rule can have degree of precision 2N, i.e., Radau quadrature. In the Lobatto case all w0k ≡ 0 and we only have N nontrivial quadrature formulas in (2.37c). We shall only employ the latter case, i.e., θ0 = 0, θN = 1, in our present study. The others are easily treated in a similar manner (see Weiss [56]).
The difference scheme for (1.20a,b) based on the quadrature rules (2.37c) is formulated as :
If uj0 is known we see that (2.38a) for 1  v
v  N, j fixed, consists of a system of nN equations for the nN components of ujv, 1
N, j fixed, consists of a system of nN equations for the nN components of ujv, 1  v
v  N. This is an implicit Runge-Kutta scheme of the type studied by Axelsson [3]. If we imagine these equations solved for each ujN in terms of uj0 the scheme can be viewed as a one-step scheme. More important it is stable for the initial value problem and the accuracy at the nodes
N. This is an implicit Runge-Kutta scheme of the type studied by Axelsson [3]. If we imagine these equations solved for each ujN in terms of uj0 the scheme can be viewed as a one-step scheme. More important it is stable for the initial value problem and the accuracy at the nodes 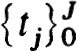 is the same as that of the quadrature scheme over [0,1]. In the Lobatto case we get O(h2N + 1) accuracy. The linearized version of (2.38a,b) clearly satisfies the conditions (2.27a,b,c,d) of Theorem 2.27. Then it follows from this result, the results of Axelsson and Theorem 2.31 that the scheme (2.38a,b) is stable and accurate to O(h2N + 1) on the net {tj} for isolated solutions of (1.20a,b). Similar results hold for the Radau and Gaussian cases. Now we turn to the relation with collocation.
is the same as that of the quadrature scheme over [0,1]. In the Lobatto case we get O(h2N + 1) accuracy. The linearized version of (2.38a,b) clearly satisfies the conditions (2.27a,b,c,d) of Theorem 2.27. Then it follows from this result, the results of Axelsson and Theorem 2.31 that the scheme (2.38a,b) is stable and accurate to O(h2N + 1) on the net {tj} for isolated solutions of (1.20a,b). Similar results hold for the Radau and Gaussian cases. Now we turn to the relation with collocation.
To approximate the solution of (1.20a,b) by collocation we introduce a piecewise polynomial function, v(r), which on each interval [tj-i, tj] of (2.37a) is a polynomial of degree N + 1, say:
We seek to determine the coefficients {ajk} by collocating (1.20a) with z(t) replaced by v(t) at each of the tjv, by imposing the boundary conditions (1.20b) on v(r) and by requiring continuity of v(t) at each internal netpoint tj. This yields the system :
In (2.39) there are (N + 2)J unknown coefficient vectors ajk and in (2.40a,b,c) there are the same number of vector equations. The basic relation between collocation and our implicit Runge-Kutta scheme is given in
THEOREM 2.41. (A) Let pj(t) satisfy (2.40a,b,c). Then the ujv ≡ pj(tjv) satisfy (2.38a,b).
(B) Let ujv satisfy (2.38a,b). Define 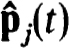 to be the unique polynomials of degree N+1 which interpolate the ujv, 0
to be the unique polynomials of degree N+1 which interpolate the ujv, 0  v
v  N (i.e., satisfy
N (i.e., satisfy 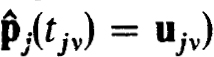 and satisfy (2.40a) for v = 0. Then the
and satisfy (2.40a) for v = 0. Then the 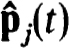 satisfy (2.40a,b,c).
satisfy (2.40a,b,c).
Proof. Since the pj(t) are of degree N + 1 and the quadrature schemes (2.37c) being interpolatory have degrees of precision at least N, we must have that
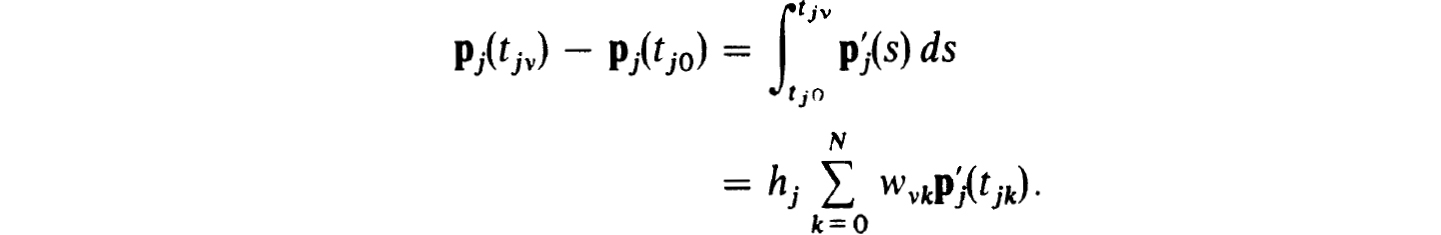
Using (2.40a) we get that (2.38a) is satisfied by pj(tjv) = ujv. Trivially (2.40b) implies (2.38b) so our collocation solution does satisfy the difference scheme and part (A) is proven.
In a similar fashion, since the 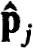 (t) interpolate the ujv and are of degree N + 1,
(t) interpolate the ujv and are of degree N + 1,
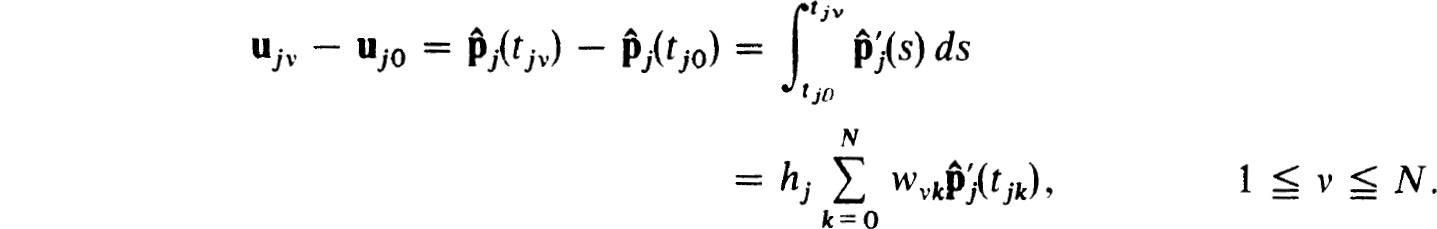
Now use (2.38a) to get that
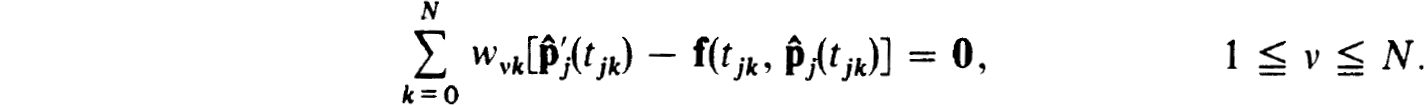
However, the n × n matrix Ω = (wvk), 1  v,k
v,k  N is nonsingular1 so we get that (2.40a) is satisfied by the
N is nonsingular1 so we get that (2.40a) is satisfied by the 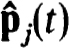 for 1
for 1  v
v  N, j
N, j  J. For v = 0 these relations were imposed in defining the
J. For v = 0 these relations were imposed in defining the 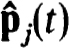 . The continuity (2.40c) follows since
. The continuity (2.40c) follows since 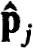 (tj0) = uj0 = uj0 ≡
(tj0) = uj0 = uj0 ≡ 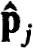 – 1 (tj1-N). The boundary conditions are similarly satisfied as a result of interpolating the difference solution.
– 1 (tj1-N). The boundary conditions are similarly satisfied as a result of interpolating the difference solution. 
We do not believe that implicit Runge-Kutta schemes are as efficient as the same order one-step schemes using the techniques of §2.4 (see Keller [31]). Thus we do not advocate C0[a, b] collocation either. However, Russell [48], [49] has shown that collocation with smoother piecewise polynomials is much more efficient, so collocation cannot be ruled out in general.
1 To see this, apply the rules (2.37c) to 𝛹(s) ≡ sm,m = 1, ···, N, recalling θ0 = 0 and degree of precision at least Ω. Then Q times a nonsingular Vandermonde matrix equals another.