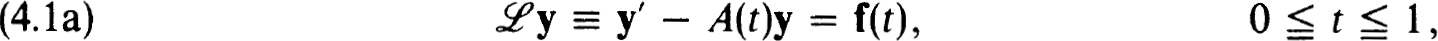
4.1. Regular singular points. We study linear boundary value problems with a regular singularity at one endpoint, say,
where A(t) has a simple pole at t = 0 :
The boundary conditions are posed as
This allows the typical incident wave conditions or those resulting from singular coordinate systems. With B0(t) = B0t-R conditions can be imposed on the regular part of the solution, as studied by Natterer [37]. In (4.1a,b,c): y(f), f(t), b(r) are n-vectors, R, A0(t), B0(t) and B1 are n × n matrices. We assume A0(t) analytic on [0,1], while B0(t), b(t) and f(t) may be singular at t = 0 but sufficiently smooth on (0,1].
We examine and justify the more or less standard procedure of expanding about the singular point, solving a regular problem over a reduced interval, [δ,1], say, and then matching to the expansion. The extension of these techniques to problems with two singular endpoints, an interior regular singular point and even unbounded intervals, if the point at ∞ is regular, are indicated in Brabston [6]. The first serious study of this device was by Gustafsson [20] who applied it to scalar problems. More detailed accounts of our present work are given in Brabston [6] and Brabston and Keller [7].
Let the fundamental solution matrix, Y(t), for (4.1a) be defined by
It is well known that we may take
where P(t) is analytic on 0 
t δ0. Then every solution of (4.1a) can be written as
where the particular solution yp(t) satisfies
Thus we can use the representation
If y(t) given by (4.3a) is to satisfy the boundary conditions (4.1c), then we must have
where
Since B0(t), b(t), A(t) and hence Y(t) have a finite number of singularities only at t = 0 we can write, without loss of generality, that for some integer s and for some scalar functions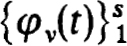 
where for some N > 0,
Here M0(t) and g0(t) are analytic on [0, δ0] while Mv and gv are constant. From these assumptions we easily obtain the following theorem.
THEOREM 4.6. Let (4.5a,b,c) hold. Then (4.1a,b,c) has a solution if and only if
The solution is unique if and only if
For practical applications it should be noted that the matrices Mk and the vectors gk can be determined explicitly if B0(t), b(t), A(t) and hence B(t) and g(f) are analytic in 0 < |t| δ0. We shall employ the representations (4.3a,b,c) and (4.5a,b,c) in devising numerical procedures.
The numerical scheme is to employ an approximation to the solution (4.3a,b,c) on some interval 0 < t δ, with δ δ0, and by means of this to define a regular boundary value problem on [δ,1]. The justification of this procedure which is also used for obtaining error estimates is based on an exact such reduction to a regular boundary value problem. This procedure has also been used by Gustafsson [20] in treating a second order scalar problem. In particular from (4.3a) it follows, assuming (4.6a) holds, that y(δ) = Y(δ)c + yp(δ). Using this in (4.4a) to eliminate c in the term B(t) c, and using Y(1)c = y(l) - yp(l) to eliminate Y(l)e, we get the boundary conditions satisfied on [δ, 1] by any solution of (4.1a,b,c) tobe:
Here B0δ and B1δ are n(s + 1) × n matrices while bδ is an n(s + 1)-vector:
With yp(t) uniquely defined by (4.3b) it is not difficult to show that : the boundary value problem (4.1a,b) has a (unique) solution if and only if the boundary value problem (4.1a), (4.7a,b) has a (unique) solution. The solution of (4.1a,b,c) on [δ, 1] satisfies (4.7a,b). This result is formally established in Brabston and Keller [7].
To determine the boundary conditions (4.7a) we need only Y(t) and yp(t) on (0, δ] and then the matrices and vectors in (4.7b) can be evaluated. By, the assumed analyticity of A0(x) on 0 x δ0 we can obtain as many terms as desired in the expansion of P(x) in (4.2c). Thus for some integer N we define the approximate or ‘“truncated” fundamental solution matrix :
We also define the truncated particular solution :
If N is sufficiently large we can use (4.8a,b) in (4.4b,c) to determine the exact values of Mv and gv, v = 1,2, ···, s. The largest value of N required for this is Nmax = maxv Re [-λV(R)] + 1, where λV(R) are the eigenvalues of R. This of course assumes that the “highest order” singularity occurs in Y(t). If singularities of B0(t) or of f(t) increase the order, then a larger N may be required.
Employing (4.8a,b) we define the truncated quantities
Then expansions analogous to (4.5a,b,c) yield the Mv and gv for v = 1, 2, ···, s and the truncated quantities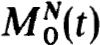 
and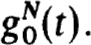 
. Using the appropriate truncated quantities in (4.7b) we define
The exact boundary conditions (4.7a) are now replaced by the truncated boundary condition
where yN(t) is a solution of
If the original boundary value problem (4.1a,b,c) has a unique solution, then it is established in [7] that for sufficiently large N the truncated regular boundary value problem (4.10a,b) also has a unique solution. The truncated solution yN(t) defined on [δ,1] is extended to (0, δ] by using
Our numerical procedure is to solve the linear boundary value problem (4.10a,b) by finite differences, say, with an accuracy O(hr) on some net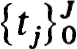 
with t0 = δ, tJ = 1. Denoting this numerical solution by 
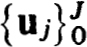we replace yN(δ) in (4.1 la) by u0 to define 
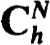and then use this in (4.11b) to define 
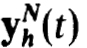on 0 < t δ.
The error in our numerical solution is estimated by using
For fixed N and δ we obviously have
assuming a stable, consistent of order m scheme has been used to solve 4.10a,b). The error in the truncated solution yN(t) can be estimated in terms of
It is clear for any fixed δ in 0 < δ δ 0 that limN → ∞ ∆N(δ) = 0. In particular cases it is easy to establish more precise estimates of the form
for some fixed K1 and ρ independent of ô and N. It is now easy to deduce that, for N sufficiently large,
Combining (4.14a,b) and (4.15) in (4.12a) we get error estimates on δ t 1.
On the interval 0 < t δ we obtain, in a similar fashion, estimates of the form
Since ||Y(t)|| may be unbounded as t ↓ 0, the absolute accuracy may degrade as t↓ 0. This is unavoidable if, as may be the case, the exact solution is singular at t = 0. It would seem that relative error estimates are desirable in such cases, but they are unknown at present. On the other hand, if any row of the matrix Y(t) is nonsingular, then a more careful analysis reveals that the corresponding component of the error is bounded as in (4.16) with ||Y(t)|| replaced by the norm of the appropriate row. For such components we can thus obtain small absolute errors on the entire closed interval 0 t 1.
Numerical examples of this method, showing also that Richardson extrapolation can be employed, are contained in [6] and [7]. Very recent work of de Hoog and Weiss [11] shows that some one-step difference schemes can be used directly on (4.1a,b,c) provided the solutions are bounded. They also examine eigenvalue problems and some nonlinear singular equations.
The techniques employed here can also be used to develop and justify numerical methods for problems with irregular singular points. The convergent power series expansions are essentially replaced by asymptotic expansions and somewhat more work must be done to determine appropriate values for the integer N, if it exists in a given case. The use of one-step difference schemes up to the singular point, as in de Hoog and Weiss [11], may also be used in many cases. Calculations on such problems are performed very often but theoretical studies along the above indicated lines are just now in progress. Another aspect of frequently occurring irregular singular point problems is considered in § 4.2.
4.2.∞-intervals; irregular singular points. There is at present no theoretical work justifying numerical methods for solving problems with irregular singular points. The main practical occurrence of such problems seems to be those formulated on infinite intervals and we examine some simple examples here.
We consider first problems of the form
It is assumed that
so that the point at ∞ is an irregular singular point. The matrix Ca is p × n of rank p < n and α ∈ Ep. If we let A(t) and Ca depend analytically on X and set α = 0 our theory includes an important class of eigenvalue problems. Most numerical work on such problems proceeds by replacing the infinite interval by a finite one, say, [a, ∞] → [a, b]. However, the boundary conditions to be imposed at t = b are not always chosen correctly. To do this correctly we examine the eigenvalues and eigenvectors of A∞.
Suppose the eigenvalues, λj, of A∞ satisfy
Further assume ξj = 1,2, ···, q, are q independent left eigenvectors of A∞ belonging to the corresponding λj. Then with the q × n matrix
we can replace (4.17c) by
To see that these are the correct conditions assume ζj, 1 j n, are the right eigenvectors of A∞. Then every solution of y’ = A∞y has the form
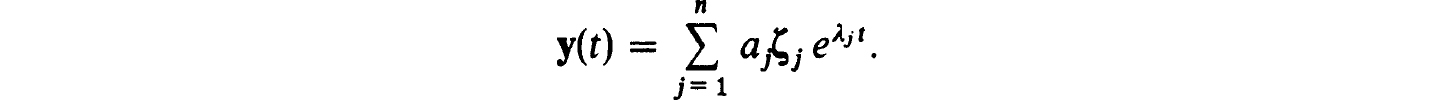
Since the ξj and ζj are bi-orthogonal, condition (4.17d) simply ensures that aj = 0 if Re λj 
0. More briefly it projects the solution into the subspace of decaying solutions at ∞. It is assumed that p + q = n so (4.17b) and (4.17d) represent n constraints. The appropriate replacement of (4.17a,b,c) by a finite problem is now :
To see how well the above procedure works compared to frequently used alternatives consider the trivial example
whose solution is
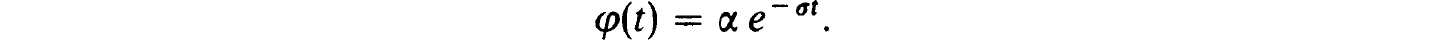
A common approach to (4.21) is to replace the condition at t = ∞ by φ(L) = 0 for some finite t = L. Calling the solution of the altered problem φ0(t) we have
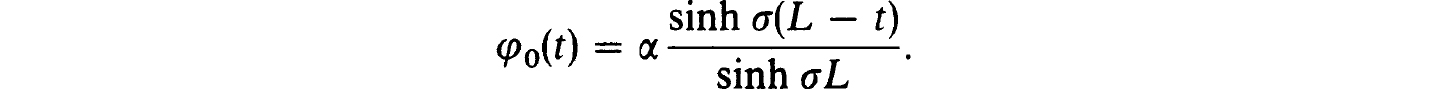
To get the equivalent of (4.20c) for (4.21) we note that as a system with yT(t) =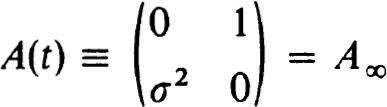 
. Hence p = q = 1 with 
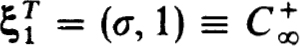Thus the finite condition should be σφ(L) + φ’(L) = 0. The altered problem now yields the exact solution. Of course this example seems extreme but it illustrates the important feature that using (4.20c) yields better approximations over any finite interval [a, b] than does frequently used alternatives. We shall see in fact that it is not such an extreme example.
The general formulation of (4.20c) does not require the assumptions inherent in (4.19a,b). Rather we need only assume that, for some nonsingular n × n matrix P,
where A+ is q × q, A- is p × p, p + q = n and
Then the first g-rows of P suffice for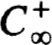 
. In fact we partition both P and P-1 as follows :
Now a rather striking generalization bf the treatment of (4.21) can be given.
Consider (4.17a,b,d) where A(t) ∈ C[a, ∞] and has a constant “tail”, that is,
We replace this problem by the finite problem (4.20a,b,c) with b t0. By our previous analysis we know that this finite problem has a unique solution if and only if
is nonsingular. We first examine the nonsingularity question in
LEMMA 4.25. Let Q(b) be nonsingular for some b 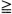t0. Then Q(t) is nonsingular for all t 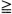t0.
Proof. The fundamental solution Y(t, a) has the property that
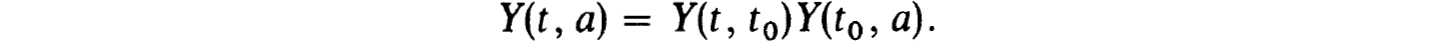
particular by (4.23) and (4.22a,b,c), for t 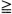t0,
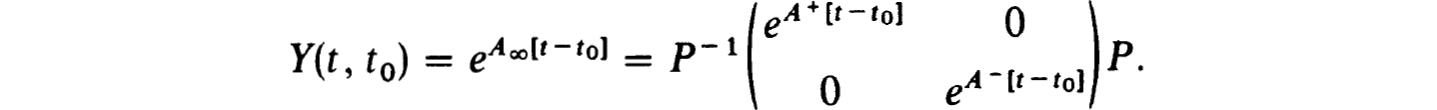
Further recall that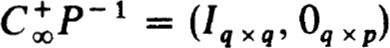 
since PP–1 = I. Thus we see that for t 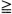t0
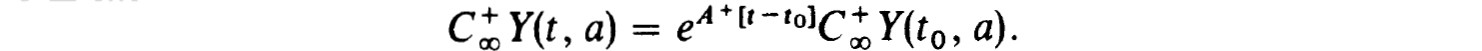
Now (4.24) with b = t 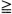t0 yields
So if Q(r) is nonsingular for any t 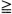t0, then the same is true for all t 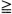t0. 
Now we have the more dramatic result in
THEOREM 4.26. Let A(t) be as in (4.23). Let (4.20a,b,c) have the unique solution u(t) ≡ u(t, b) for some b 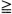t0. Then u(t,b) is independent of b for b t0, i.e., u(r, t1) = u(t, t0)for all t1 t0 and all t a.
Proof. If Q(t1) is nonsingular, then the solution of (4.20a,b,c) for b = 11 > t0 is simply
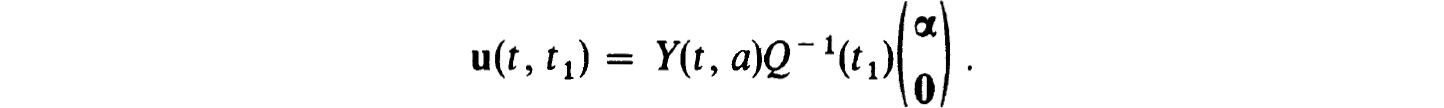
However, from (4.25a) it follows that
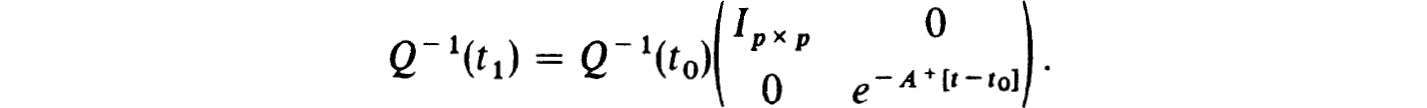
Now note that
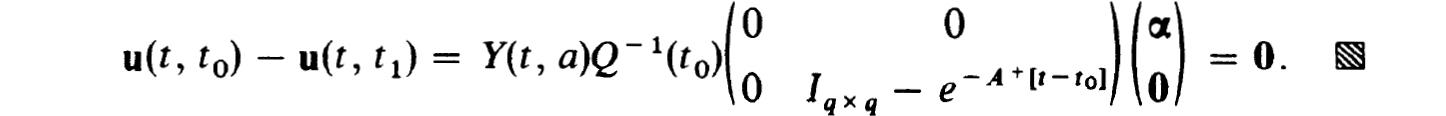
The result above shows how effective our procedure can be for problems with constant tails in the coefficients. Similar but not quite so dramatic results hold if the approach of A(t) to A∞ is sufficiently rapid. Such studies are in progress. It should also be stressed that for eigenvalue problems on infinite domains the same technique can be used. The analysis for the constant tail case is quite similar and indeed the exact eigenvalues and eigenfunctions can be found in terms of a finite interval eigenvalue problem. The key element here is again the identity (4.25a) where now A∞ (λ) and Q(t0, λ) depend analytically on the eigenvalue parameter λ.
In problems of physical significance over semi-infinite intervals the proper condition at infinity is usually the “outgoing wave” condition (i.e., Sommerfield radiation condition). That is what our above analysis yields in all such cases. Indeed from the physical point of view the results for constant tail at infinity are not surprising at all. If at any point in a homogeneous tail there are no incoming waves present, then none can be generated in the entire uniform tail. However, it is surprising that so many quantum mechanical eigenvalue problems and fluid mechanical stability problems are treated numerically without employing the outgoing wave condition.
In particular it is of interest to consider the Orr-Sommerfield equation for external flow problems (see, for example, Rosenhead [47]) :
Here U(η) is the “external” velocity profile normalized such that lim, η → ∞ U(η) = 1. Indeed it is usually more realistic to assume that U(η) = 1 for all η η∞ this results in the constant tail case treated above. The boundary conditions at η = 0 are
Conditions at η = ∞ are specified in various ways (see, for instance, Gill and Davey [17] or Rosenhead [47]). The simplest statement seems to be φ(∞) = φ(∞) = 0, which, for numerical purposes, is then imposed at a finite point.
We shall derive the proper “outgoing wave” conditions here by first reformulating (4.27a) as a first order system with
Then we get, with a = (α, γ, β),
In the tail η η∞ we have
It easily follows that the eigenvalues of A∞ (σ) are ± α and ±β. Suppose the roots are taken such that λ1 = a and λ2 = β have Re λi > 0. The corresponding left eigenvectors are found to be
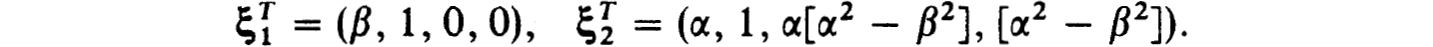
Then the boundary conditions are from (4.27b) and the above in
Note that all of the parameters σ = (α, R, c) in the Orr-Sommerfield equation also enter into the boundary conditions at η = η∞. Our methods for eigenvalue problems in Chapter 3 can now be applied to (4.28b) subject to (4.30a,b). In fact for such problems solutions are frequently desired for large ranges of some of the parameters and hence continuation procedures are also quite relevant.
It is of interest to note that the conditions (4.30b) are, in terms of ϕ(η) and with D ≡ d/dη, simply
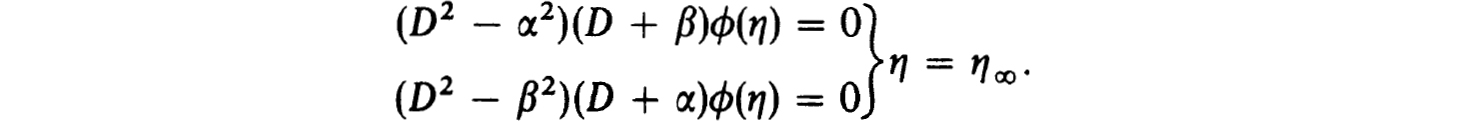
We have never seen these conditions imposed on the Orr-Sommerfield equation although related forms, such as
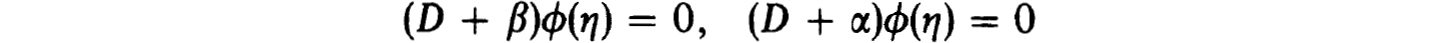
have been used. The latter are incorrect attempts to eliminate the growing components of φ(η) while the former clearly do the job.
[1]K. W. ATKINSON, Convergence rates for approximate eigenvalues of compact integral operators, SIAM J. Numer. Anal., 12 (1975), pp. 213-222.
[2]J. A VILA, The feasibility of continuation methods for nonlinear equations, Ibid., 11 (1974), pp. 102-122.
[3]O. AXELSSON, A class of Astable methods, BIT, 9 (1969), pp. 185-199.
[4]L. BAUER, E. L. REISS AND H. B. KELLER, Axisymmetric buckling of hollow spheres and hemispheres, Comm. Pure Appl. Math., 23 (1970), pp. 529-568.
[5]W. BOSARGE, Iterative continuation and the solution of nonlinear two-point boundary value problems, Numer. Math., 17 (1971), pp. 268-283.
[6]D. C. BRABSTON, JR., Numerical solution of singular endpoint boundary value problems, Doctoral thesis, Part II, California Institute of Technology, Pasadena, Calif., 1974.
[7]D. C. BRABSTON AND H. B. KELLER, Numerical solution of singular endpoint boundary value problems, submitted to SIAM J. Numer. Anal.
[8]J. H. BRAMBLE AND J. E. OSBORN, Rate of convergence estimates for nonselfadjoint eigenvalue approximations, Math. Comp., 27 (1973), pp. 525-549.
[9]E. A. CODDINGTON AND N. LEVINSON, Theory of Ordinary Differential Equations, McGraw-Hill, New York, 1955.
[10] S. D. CONTE, The numerical solution of linear boundary value problems, SIAM Rev., 8 (1966), pp. 309-321.
[11] F. R. DE HOOG AND R. WEISS, Difference methods for boundary value problems with a singularity of the first kind, Tech. Summary Rep. 1536, Mathematics Research Center, University of Wisconsin, Madison, 1975.
[12] B. ENGQUIST, Asymptotic error expansions for multistep methods, Reas. Rep., Computer Sei. Dep., Uppsala Univ., 1969.
[13] J. C. FALKENBERG, A method for integration of unstable systems of ordinary differential equations subject to two-point boundary conditions, BIT, 8 (1968), pp. 86-103.
[14] L. FOX, The Numerical Solution of Two-Point Boundary Problems in Ordinary Differential Equations, Oxford University Press, Fairlawn, N.J., 1957.
[15] C. W. GEAR, Numerical Initial Value Problems in Ordinary Differential Equations, Prentice-Hall, Englewood Cliffs, N.J., 1971.
[16] J. H. GEORGE AND R. W. GUNDERSON, Conditioning of linear boundary value problems, BIT, 12 (1972), pp. 172-181.
[17] A. E. GILL AND A. DAVEY, Instabilities of a buoyancy-driven system, J. Fluid Mech., 35 (1969), pp. 775-798.
[18] T. R. GOODMAN AND G. N. LANCE, The numerical solution of two-point boundary value problems, Math. Tables Aid. Comput., 10 (1956), pp. 82-86.
[19] W. B. GRAGG, On extrapolation algorithms for ordinary initial value problems, SIAM J. Numer. Anal., 2(1965), pp. 384-403.
[20] B. GUSTAFSSON, A numerical method for solving singular boundary value problems, Numer. Math., 21 (1973), pp. 328-344.
[21] P. HENRICI, Discrete Variable Methods in Ordinary Differential Equations, John Wiley, New York, 1962.
[22] ———, Error Propagation for Difference Methods, John Wiley, New York, 1963.
[23] E. ISAACSON AND H. B. KELLER, Analysis of Numerical Methods, John Wiley, New York, 1966.
[24] H. B. KELLER, Numerical Methods for Two-Point Boundary Value Problems, Ginn-Blaisdell, Waltham, Mass., 1968.
[25] ———, Accurate difference methods for linear ordinary differential systems subject to linear constraints, SIAM J. Numer. Anal., 6 (1969), pp. 8-30.
[26] ———, Accurate difference methods for nonlinear two-point boundary value problems, Ibid., 11 (1974), pp. 305-320.
[27] ———, Approximation methods for nonlinear problems with application to two-point boundary value problems, Math. Comp., 29 (1975), pp. 464-474.
[28] ———, Newton’s method under mild differentiability conditions, J. Comput. System Sei., 4 (1970), pp. 15-28.
[29] ———, Shooting and embedding for two-point boundary value problems, J. Math. Anal. Appl., 36 (1971), pp. 598-610.
[30] H. B. KELLER AND A. B. WHITE, JR., Difference methods for boundary value problems in ordinary differential equations, SIAM J. Numer. Anal., 12 (1975), pp. 791-802.
[31] H. B. KELLER, Numerical solution of boundary value problems for ordinary differential equations: Survey and some recent results on difference methods, Numerical Solutions of Boundary Value Problems for Ordinary Differential Equations, A. K. Aziz, ed., Academic Press, New York, 1975, pp. 27-88.
[32] H. B. KELLER AND A. W. WOLFE, On the nonunique equilibrium states and buckling mechanism of spherical shells, SIAM J. Appl. Math., 13 (1965), pp. 674-705.
[33] H.-O. KREISS, Difference approximations for boundary and eigenvalue problems for ordinary differential equations. Math. Comp., 10 (1972), pp. 605-624.
[34] F. T. KROGH, Variable order integrator s for the numerical solution of ordinary differential equations, J. P. L. Tech. Memo, California Institute of Technology, Pasadena, Calif., 1969.
[35] D. C. L. LAM, Implementation of the Box scheme and modal analysis of diffusion-convection equations, Doctoral thesis, Univ. of Waterloo, Ontario, 1974.
[36] P. LANCASTER, Error analysis for the Newton-Raphson method, Numer. Math., 9 (1966), pp. 55-68.
[37] F. NATTERER, A generalized spline method for singular boundary value problems of ordinary differential equations, Lin. Alg. & Appl., 7 (1973), pp. 189-216.
[38] J. ORTEGA AND W. RHEINBOLDT, Iterative Solution of Nonlinear Equations in Several Variables, Academic Press, New York, 1970.
[39] M R. OSBORNE, On shooting methods for boundary value problems, J. Math. Anal. Appl., 27 (1969), pp. 417-433.
[40] ———, On the numerical solution of boundary value problems for ordinary differential equations, Information Processing ‘74, North-Holland, Amsterdam, 1974, pp. 673-677.
[41] V. PEREYRA, Iterated deferred corrections for nonlinear boundary value problems, Numer. Math., 11 (1968), pp. 111-125.
[42] ———, High order finite difference solution of differential equations, Comp. Sei. Rep. STAN-CS- 73-348, Stanford University, Stanford, Calif., 1973.
[43] L. RALL, Computational Solution of Nonlinear Operator Equations, John Wiley, New York, 1969.
[44] W. C. RHEINBOLDT, Methods for Solving Systems of Nonlinear Equations, Regional Conference Series in Applied Mathematics, no. 14, SIAM, Philadelphia, Pa., 1974.
[45] S. M. ROBERTS AND J. S. SHIPMAN, Two-Point Boundary Value Problems: Shooting Methods, American Elsevier, New York, 1972.
[46] ———, Continuation in shooting methods for two-point boundary problems, J. Math. Anal. Appl., 18 (1967), pp. 45-58.
[47] L. ROSENHEAD, Laminar Boundary Layers, Oxford University Press, Fairlawn, N.J., 1963.
[48] R. D. RUSSELL, Collocation for systems of boundary value problems, Numer. Math., 23 (1974), pp. 119-133.
[49] ———, Application of B-splines for solving differential equations, preprint, 1975.
[50] L. SHAMPINE AND M. GORDON, Computer Solution of Ordinary Differential Equations, W. H. Freeman, San Francisco, Calif., 1974.
[51] H. J. STETTER, Asymptotic expansions for the error of discretization algorithms for non-linear functional equations, Numer. Math., 7 (1965), pp. 18-31.
[52] J. M. VARAH, On the solution of block-tridiagonal systems arising from certain finite-difference equations, Math. Comp., 26 (1972), pp. 859-868.
[53] ———, Alternate row and column elimination for solving certain linear systems, preprint, 1975.
[54] E. WASSERSTROM, Numerical solutions by the continuation method, SIAM Rev., 15 (1973), pp. 89-119.
[55] R. WEISS, The convergence of shooting methods, BIT, 13 (1973), pp. 470-475.
[56] ———, The application of implicit Runge-Kutta and collocation methods to boundary value problems, Math. Comp., 28 (1974), pp. 449-464.
[57] A. B. WHITE, Numerical Solution of Two-Point Boundary Value Problems, Doctoral thesis, California Institute of Technology, Pasadena, Calif., 1974.
[58] J. H. WILKINSON, The Algebraic Eigenvalue Problem, Oxford University Press, Fairlawn, N.J., 1965.
