The Parallax Method
The Scale of the Universe
EVERYONE KNOWS THE Universe is a big place but just how big is it? It is very easy to rattle off distances in the Universe, from the Earth to the Moon at around a quarter of a million kilometres, to the Sun at 150 million kilometres, all the way out to the most distant object ever seen at 124,000 million trillion kilometres! Yet we cannot use a giant tape measure to work these out so how have the immense distances in space been calculated? The answer is, simply with a dash of human ingenuity.
As we’ve seen, the Greek mathematician and astronomer Eratosthenes once used shadows cast by the Sun to calculate, with some accuracy, the circumference of the Earth. It was this discovery that laid the foundations to allow mathematicians and scientists through the ages to gain an understanding of the distances in space. Knowing the circumference of the Earth, Eratosthenes then successfully calculated the distance to the Sun, but little is known of the method he used. He estimated it to be ‘of stadia myriads 400 and 80,000’ but it is not known whether this means 4,080,000 stadia or 804,000,000 stadia. It all hinges on the application of the phrase ‘stadia myriads’, where a stadion is considered to be around 185m and myriad refers to a multiplier of 10,000. It could mean either 400 myriad plus a further 80,000 or simply 80,400 myriad and, interestingly, if we understand it to be the latter, then it translates to 149 million kilometres to the Sun. This figure is impressively close to our current average figure of just under 150 million kilometres.
One of the later methods used for calculating the distance between the Earth and Sun was demonstrated by Jeremiah Horrocks in 1639, when he observed a transit of Venus. This event occurs when the planet Venus passes directly between the Earth and Sun making it visible against the bright solar disc. Using projection techniques to observe the event safely through a telescope, Horrocks and a colleague timed the exact start and end time of the transit from their separate observation points. Thanks to Johannes Kepler’s Laws of Planetary Motion published earlier that century, they also knew the relative distances of the planets based on how long they took to go around the Sun. Using these measurements for the Earth and Venus and the apparent shift in the position of Venus from the different observation points, Horrocks was able to calculate the distance to the Sun as a multiple of the radius of the Earth. The answer he came up with was 13,750 Earth-radii which, using the modern figure of 6378.1km, gives a figure of just under 88 million kilometres.
Although the figure Horrocks suggested is significantly lower than the currently accepted figure of just under 150 million kilometres, the principle of the experiment was sound; only its execution was wrong. Later in the seventeenth century the approach was improved upon by James Gregory and a more correct figure obtained. More recently, radar measurements of the position of Venus have enabled an exact distance of Venus to be determined, which finally allowed the distance between the Earth and Sun to be accurately calculated. The actual distance between the two varies throughout the year due to the elliptical nature of the Earth’s orbit, but the average distance is used as a unit of measurement within our Solar System and, called the astronomical unit, has a value of 149,597,871km.
Other than the astronomical unit, there is another popularly used measure in astronomy, which I’ve already mentioned: a light year equates to the distance light can travel in one year in a vacuum. The value of one light year is equal to just under 10 trillion kilometres. The first time it was demonstrated that light travelled at a finite speed was in 1676, by the Danish astronomer Ole Rømer, but it was sixty years earlier, in 1616, that the foundations were laid for his historic experiment. The determination of longitude at sea was a major problem, but Galileo suggested that the moons of Jupiter could be used as a celestial clock and, by using them to determine the local time, longitude could be calculated. For this to work, accurate predictions of the movement of the four moons of Jupiter were needed. Unfortunately Galileo’s idea did not work at sea due to the movement of a ship, but it proved to be a brilliant method on land.
The Italian astronomer Giovanni Cassini worked hard to improve the predictions of the moons of Jupiter and to that end needed some accurate observations and timings. He worked with another astronomer, the Frenchman Jean Picard, and his assistant, Ole Rømer, who between them logged hundreds of observations. From these observations, Rømer noticed that the time period between successive events of Jupiter’s innermost moon, Io, seemed shorter when Earth was moving towards Jupiter and longer when it was receding. His conclusion was that it must take a finite period of time for light to travel the extra distance across the orbit of the Earth and he determined this delay to be around 22 minutes. The Dutch astronomer and mathematician Christiaan Huygens took this figure and, combining it with an estimate for the diameter of the Earth’s orbit, arrived at a figure for the speed of light of 220,000km per second, not bad compared to our current figure of about 300,000km per second.
Measurements within our Solar System tend to be expressed in the astronomical unit (Au), and radar can be used to measure distances to the nearer planets, so with mathematics it is possible to calculate the distances to other planets with astonishing accuracy. Measurements beyond the Solar System are generally described in light years, but one other measure is also used, the parsec, and this has its origins in the Earth’s orbit around the Sun.
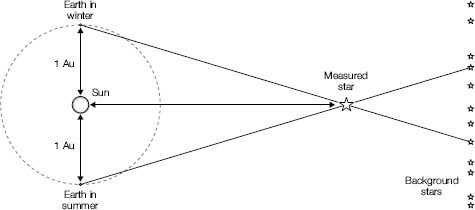
The parsec is equal to 3.26 light years or approximately 31 trillion kilometres and its name comes from its definition, in which the distance corresponds to a PARallax of one arc-SECond. This is not as complicated as it sounds. Consider the Earth in its yearly orbit around the Sun, the diameter of which orbit is about 300 million kilometres. As the Earth moves on its orbit it changes its position in space, so much so that nearby stars seem to shift due only to the movement of the Earth. This apparent shift is known as parallax and you can demonstrate it for yourself now. Extend your arm in front of you and point one finger up. Shut one eye and notice where your finger is in relation to a background object. Now open that eye and shut the other, and without moving your finger it will seem to have shifted its position against the more distant background objects. If you were to measure the angular shift of your finger (assuming you are at the centre of a 360-degree circle, your finger will have moved by just a few degrees) and also measure the distance between your eyes, you could calculate the length of your arm. In the case of one parsec, the shift in position or angular shift is one arc-second, which is equal to 1/3600th of a degree (one degree is the area of sky equivalent to the width of a finger held at arm’s length).
The same approach is used in astronomy to measure the parallax of relatively close stars, but instead of using the distance between two eyes, measurements are taken six months apart when the Earth is at the extremes of its orbit. We know the distance to the Sun and therefore the diameter of the Earth’s orbit, so by measuring the apparent shift of a star we can work out how far away it is. The parallax method of measuring distances in space is used by the Hipparchus spacecraft, which can measure stellar parallax at about 1500 light years. To put this in context, the parallax of the nearest star, Proxima Centauri, is the same angle that a large coin would display at a distance of about 5 kilometres.
A parsec then is a measure of distance just like metres, kilometres and light years, where one parsec is the distance a star will be from Earth if it displays a parallax shift of one arc-second (the full moon, for example, measures 1800 arc-seconds in diameter). Like many metric measures, there are further multiples of this, such as the kiloparsec (1000 parsecs) and the megaparsec (1 million parsecs).

The Parallax Method
As technology improves it will be possible to measure even smaller parallax shifts, but to measure the vast distances to the galaxies, another approach is needed. Before looking at how this can be done, it is useful to put into context the sheer vastness of space. The nearest major galaxy to our own, the Andromeda Galaxy, is 2.3 million light years away (approximately 770 kiloparsecs). That means that if you could travel at the speed of light, which is almost 300,000km per second, it would take you 2.3 million years to get there. Even the Helios 2 space probe, which holds the record for the fastest manmade object at an incredible 252,800km per hour, would take over 10 billion years to get there. The most distant object discovered so far is a galaxy called UDFj-39546284, which lies at a distance of 13.2 billion light years.
Measuring the huge distances in intergalactic space requires a special technique, and some of the galaxies close enough for individual stars to be detected hold the secret to this. Back in the first half of the 1900s Henrietta Leavitt was studying variable stars in our satellite galaxies, the Large and Small Magellanic Clouds. She spotted around fifty stars that seemed to share a special relationship: they were brighter and had longer periods of variability than those that were fainter. Making the assumption that they were all at roughly the same distance she realized the differences in brightness in the sky or apparent magnitude would mean an equal difference in real luminosity or absolute magnitude (see Chapter 9 for a full description of this). Studying the results in detail, she discovered there was a distinct relationship between the time it took the stars to change in brightness and their actual brightness, the so-called period–luminosity relationship. The principle is simple: if you can see two of these so-called Cepheid Variable stars in the sky with the same period of variability but one is brighter than the other, then the fainter one must be further away.
Leavitt’s discovery was of profound importance and turned out to be key in understanding the scale of the Universe. The Danish astronomer Ejnar Hertzsprung was the first to realize the significance of this. If one of these Cepheid Variable stars was identified from its light curve (a graph showing the way its brightness changes with time), a quick measure of the brightness with which it appeared in the sky would allow its distance to be calculated. The American astronomer Harlow Shapley was the first to apply this technique to measure distances in space and was able to use it along with other observations to calculate the size of our own galaxy, the Milky Way, and even to calculate our approximate position within it. The next leap in understanding came in 1924, when Edwin Hubble studied the Andromeda Galaxy and the spiral galaxy in the constellation of Triangulum and identified Cepheid Variables using the 2.5m telescope on Mount Wilson. From this, he calculated their distances as 900,000 light years and 850,000 light years respectively, and although we now know they are somewhat further away than this, it did conclusively show them to be objects well outside our own galaxy.
Cepheid Variables have been successfully used to measure distances in the Universe many times now, but this technique is limited to galaxies where individual stars can be discerned. A similar approach can be applied to the type 1a supernova, which is a white dwarf star that slowly collects matter from a neighbouring star. Over time, the increasing pressure from the matter slowly heats the core of the white dwarf star until a runaway fusion process starts, rapidly converting the star’s material into heavier elements. As this continues, the temperature increases violently until the star rips itself apart. This brings with it a dramatic increase in brightness that can be seen across the vast distances of space.
Because the fundamental process that causes the type 1a supernova is dependent on a certain critical mass, the brightness that accompanies the final explosion is always the same. Not only is the same brightness observed but so too are characteristic features in the spectrum. With these reliable properties it is possible to identify a type 1a supernova and, just as with a Cepheid Variable, comparing its apparent brightness with how bright it really is can determine its distance. This method can be used over much greater distances than the Cepheid Variables approach.
To understand the final method for determining distances in space it is necessary to understand a little about the characteristics of light. If you put white light through a prism or a device called a diffraction grating, then the white light is split into its component parts and you see all the colours of the rainbow. The reason this happens is because the different wavelengths are bent or diffracted by varying amounts, so the individual coloured light is spread out. Extending further out either side would be the other types of radiation that were discussed in Chapter 4. Using specialist devices called spectroscopes, astronomers can look at the light coming from stars and separate it into its component parts, revealing its spectrum. When the German optician Joseph von Fraunhofer studied the solar spectrum in the first half of the nineteenth century he noticed strange dark lines superimposed on the rainbow of colours, but it was not until 1859 that the German chemist Robert Bunsen discovered their origins. He realized that tiny particles inside the atom, called electrons, were absorbing very specific wavelengths of light and stopping them from coming through to the observer. In the case of the solar spectrum, the electrons present in certain gases in the Sun, but also in the Earth’s atmosphere, were responsible for absorbing some of the incoming light. This effect is of great use to astronomers as different gases produce specific patterns of lines, called absorption lines. They appear in very particular positions, and identifying these lines in the spectrum of a distant object allows its chemical make-up to be determined.
The absorption lines can be seen in the spectrum of stars and galaxies alike, and it is the latter that allows us to measure the vast distances to the edge of the observable universe. By studying the position of absorption lines in the spectrum of a star in 1848, the French physicist Hippolyte Fizeau noticed the expected pattern of lines had shifted very slightly from where they should have been and he put this down to a phenomenon known as the Doppler effect. The effect is named after the Austrian mathematician and physicist Christian Doppler, who explained that sound or light emanating from a moving object would change its frequency as the object moved. A popular example of the effect is a moving emergency vehicle: as it approaches, the pitch of its siren seems to go up, and as it moves away, the pitch goes down. The reality is that sound waves emitted by the siren are ‘squashed up’ as the vehicle approaches you, and you receive a higher-frequency noise (the pitch goes up), and the waves are stretched out as it recedes, leading to a lower frequency being received (the pitch goes down).
Just as Fizeau discovered, the effect is not restricted to sound waves but is seen in light too. It manifests itself in light as a shift in position of the absorption lines against the background spectrum. Vesto Slipher noticed in 1912 that most spiral nebulae seemed to show quite a significant jump in the position of the lines, all of which seemed to shift towards the red end of the spectrum. From measuring the apparent red shift it is possible to calculate the speed at which the object is moving away from the observer. Edwin Hubble took this one step further and realized there was a mathematical relationship between the speed the galaxies were moving away at and how far away they were. He had found the final piece of the mathematical puzzle (now called Hubble’s Law) in measuring the incredible distances in intergalactic space, and with it the vast scale of the Universe was finally revealed.
Interestingly, the relationship between speed of movement and distance is related to something that goes back nearly 14 billion years, the Big Bang. Before this explosive event, the entire Universe, everything, was compressed into a tiny point called a singularity, and after the Big Bang the whole Universe, space included, was catapulted into violent expansion. It is important to realize that it is not the galaxies themselves that are shooting out in all directions but space itself, with the galaxies being dragged along with it. The red shift phenomenon is seen because space itself has grown since the light left its origin and, with the intervening expansion of space, the spectrum has been stretched, shifting the absorption lines.
It is difficult to really visualize the enormous dimensions of the Universe so it is sometimes useful to look at scaled-down representations, but even then to consider the entire Universe on one scale is almost impossible. For example, if the Earth were represented as a grain of sand, with the Sun about one metre away, then Proxima Centauri, the nearest star, would be 354km away, and the nearest galaxy just over 2 million kilometres away (that is, roughly six times the distance to the Moon).
It is not just the distances in space that are hard to imagine; the size of objects varies enormously too. The structure, evolution and even appearance of the Universe are dictated by the very small, so in considering the size of objects we should start at the atom. In the same way that it is hard to imagine the size of the very big, it is hard to imagine the size of the very small and atoms definitely come into this category. If an atom were enlarged to the size of a football, then in comparison a small coin would become the size of the Earth! There are even smaller components making up the atom: the neutrons and protons in the nucleus and the electrons in orbit around it. While this may seem the stuff of science fiction – after all, no one has actually ‘seen’ an atom – it is their influence that determines stellar evolution, the crushing power inside black holes and even the features in spectra that enable us to probe the nature of distant objects.
A little easier to visualize are the bits we can actually see, like the particles inside the glowing clouds called nebulae where stars form, through to the dust particles making up the rings of Saturn. The most common, comprising the interstellar dust that pervades the majority of galaxies, are tiny fractions, often millionths, of a millimetre in size. Moving up a little on the scale takes us to the average pieces of interplanetary dust, which we often see ‘burning up’ when they fall through our atmosphere as the streaks of light known as meteors. They range from the size of a grain of sand up to a few millimetres. This is in contrast to the size of the particles in Saturn’s rings, which are mostly water ice, and vary from a centimetre up to several metres.
It is not just tiny pieces of dust and small chunks of ice that join the planets in the Solar System. The bodies making up the asteroids and comet nuclei are a little larger but they differ in composition, comets generally being more icy than rocky. The smallest of the asteroids and cometary nuclei are tens of metres across, while the largest asteroid, Ceres, measures 975km.
Ceres is actually considered a dwarf planet like Pluto, whose diameter is 2306km, making it the second-largest of the dwarf planets after Eris, which also goes round the Sun beyond the orbit of Neptune. Dwarf planets differ from planets because they have not ‘cleared their neighbouring region of other objects’ and it is because of its relatively large companion, Charon, that Pluto was demoted from its planetary status. The remaining ‘major’ planets vary in size considerably, from the smallest, Mercury, at 4879km across, to the mighty Jupiter at 142,984km. In fact, Jupiter is so large that you could fit all the other planets inside it and still have room to spare.
Surprisingly, even some stars are of comparable size to the planets, such as the red dwarf Proxima Centauri, which is thought to be around 200,000km in diameter (compared to Jupiter’s 142,984km). There are even some stars like Sirius B, the companion star of the much brighter star Sirius, at just 12,000km, that are smaller than the Earth. It belongs to a class of star known as white dwarfs, which are remnants of massive stars that have blown most of their layers off into space, revealing the cool and dying core. There is a giant leap in magnitude between the smallest stars and the largest ones, with VY Canis Majoris measuring a staggering 2.7 billion kilometres. It is so large that you could fit just over 218,000 planet Earths across its diameter!
VY Canis Majoris is around 2000 times the size of the Sun, and if you were to put it in the Sun’s position then it would be so large it would swallow up the orbits of Mercury, Venus, Earth, Mars and Jupiter, but stop just short of the orbit of Saturn. There is no doubt that VY Canis Majoris is a monster among stars yet even it is dwarfed by the Solar System. Defining the size of the Solar System is more about identifying its edge but this is no mean feat. The edge can only really be defined by the point at which it is difficult to differentiate between the influence of the Sun and the influence of the nearest star, or the interstellar medium. This distance is known as the heliopause and it is expected to lie somewhere between 8 billion and 14 billion kilometres from the Sun. In the next five to ten years Voyagers 1 and 2 are expected to confirm its exact location as they become the first manmade spacecraft to leave the Solar System.
The stars and their systems of planets (over 700 planets have been discovered around other stars) make up the vast proportion of objects found inside galaxies. Our own galaxy, the Milky Way, measures around 100,000 light years from side to side, which is on a completely different scale to the familiar size of the planets, but as galaxies go, even the Milky Way is dwarfed by IC1101. This supergiant elliptical galaxy lies 1.07 billion light years away in the constellation of Serpens and is a member of the Abel 2029 galaxy cluster. Measuring 5.5 million light years across, it is the largest known galaxy in the Universe and is fifty-five times the diameter of the Milky Way.
Whether it is the sizes or distances in the Universe being considered, it is incredibly difficult to demonstrate either of these on a single scale as the range from smallest to largest is so immense. From the size of the atom to the monstrous elliptical galaxies, or from the relative proximity of the Moon to the far edge of the observable Universe, the extremes are truly astronomical. It is unfortunately a limitation of the human brain that we cannot comprehend such gigantic numbers, but while they may well be beyond the reach of our imagination, the quest to understand them will continue.
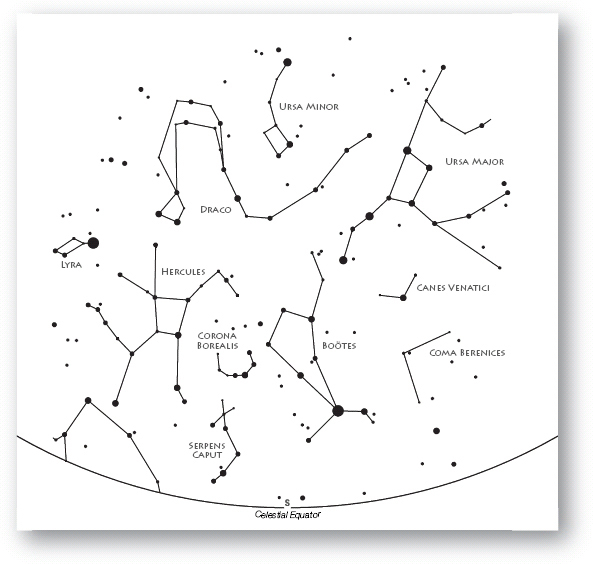
Arcturus is unmistakable in the southern part of the northern hemisphere sky during May. It is by far the brightest star in the region and with its orange glow is easy to identify. Shining at magnitude 0.15 it is a great place to start this month’s guide to the night sky. Stretching to the north and slightly to the east is the rest of the constellation of Boötes, home to Arcturus and several other moderately bright stars. Pick out the second-brightest star in the constellation, Izar, which is a beautiful binary star to the north-west of Arcturus and almost 200 light years more distant. The brighter of the two stars can be seen by the naked eye and is an orange giant star with a surface temperature of 4500 degrees. A telescope with an aperture of at least 75mm is needed to detect the fainter companion star, which is a white star shining at magnitude 5.12. Through a telescope the system looks stunning and is well worth seeking out. The rest of the stars trace out the shape of a kite to the north-west of Arcturus, which is supposed to represent a herdsman.
Just to the north-west of Arcturus is the familiar sight of Ursa Major and to the south of its tail is the rather less conspicuous constellation of Canes Venatici. The two brightest stars form a line which runs parallel to the tail, and between its easternmost star, Cor Caroli, and Arcturus is one of the real treasures of the northern night sky, the globular star cluster M3.
M3 was discovered by Charles Messier in 1764 and is just visible to the unaided eye from a dark site. Binoculars show a rather more hazy patch but a telescope with a diameter of at least 20cm is needed to reveal individual stars, although in reality there are around half a million stars in the cluster. The galactic centre which is seen in the direction of Sagittarius is closer than M3, which lies at a distance of just under 34,000 light years.
Another great example of a globular cluster can be found fractionally to the north of the celestial equator, using Arcturus as a guide to spot it. Look to the south-east of Arcturus and find Zeta Boötis, which is fainter than Arcturus and about 10 degrees away (a clenched fist at arm’s length measures around 10 degrees against the sky). Follow the line these two stars make towards the celestial equator and, at just over twice the same distance again, the faint fuzzy-looking star is the cluster M5. At 165 light years in diameter it is one of the largest of its kind.
Just a couple of degrees to the north of M5 is IC1101, the largest known galaxy in the Universe, although it is so faint that it takes a telescope about 35cm in diameter to pick it up. To the north-east of M5 is the brightest star in the constellation of Serpens, Alpha Serpentis, and it is easily recognized as a moderately bright orange star. It is nearing the end of its life and is burning helium in its core, producing carbon and oxygen, a phase that our Sun will go through in a few billion years’ time.
Directly to the north of M5 and Alpha Serpentis is a small constellation called Corona Borealis, which looks like a curve of stars, open to the north and with its brightest star, Alphecca, to its south-west corner. This star is one member of a pair of stars known as an eclipsing binary, like Spica in Virgo, which means they appear along the same line of sight from Earth and seem to keep eclipsing each other.
To the north-west of Corona Borealis is the northern end of Boötes and directly to the north of Nekar, the second-brightest star in the constellation, lies Edasich in Draco. This is one of the largest constellations and extends out to the east, taking it north of Hercules, and to the west by Ursa Major. Edasich, or Iota Draconis, is an orange supergiant star with a surface temperature of around 4500 degrees, about 1000 degrees cooler than the Sun. With a mass just a little greater than the Sun’s, Iota Draconis is thought to be a little ahead of the Sun in its evolutionary cycle and gives us a glimpse of the Sun’s future. In 2001 a planet was discovered in orbit around this giant star, and by studying its movement an estimate could be made of its mass at around nine times that of Jupiter. It has a highly elliptical orbit and the planet, now called Iota Draconis B, moves from its furthest point 2.1 times the Earth–Sun distance to its nearest point of 0.4 times. This means that it is very unlikely for any smaller rocky Earth-type planets to exist within the system.
A little further to the north is another orange giant star similar to Iota Draconis but much larger. At a distance of just under 130 light years Kochab in Ursa Minor shines with a brightness equivalent to around 500 Suns, yet it is giving off a lot less light and energy than Polaris to its north. Known as the Pole Star, Polaris lies at a point in the sky directly above the Earth’s axis of rotation, so all objects in the sky seem to rotate around it over a 24-hour period. It is the brightest star in the constellation of Ursa Minor, the Small or Lesser Bear, with Kochab just slightly fainter. The reality is that Polaris gives off about five times as much light as Kochab, but at a distance of around 430 light years it appears at a similar brightness in the sky. As well as having two fainter companion stars, Polaris is a Cepheid Variable and, as we have seen, it was stars like this that allowed us to map some of the distances in space. Between them, these two stars mark the far ends of Ursa Minor, which looks like a smaller version of the Plough, with Polaris remaining almost motionless at the end of the handle and Kochab representing the end of the pan along with Gamma Ursae Minoris.

Two prominent stars lie either side of Libra just to the south of the celestial equator in the May sky: Spica in Virgo to the east and Sabik, or Eta Ophiuchi, to the west in Ophiuchus. Spica is by far the brightest star in that region of sky, which is not surprising as it gives off as much light as 2300 of our Suns.
Between Spica and Eta Ophiuchi is the constellation of Libra, which resembles a set of scales. Beta Librae has the most incredible alternative name of Zubeneschamali, is the most northerly star in the constellation and is found about the same distance south of the celestial equator as Spica. With a surface temperature of around 12,000 degrees, which is over double the Sun’s, it should appear blue-white in colour, yet it is the only star that some people have reported as appearing green to the eye. Unusually Beta Librae is the brightest star in the constellation – given its ‘beta’ designation it should be the second-brightest. There is no known reason for this other than Beta Librae and its neighbouring star, Antares, which it was once compared to, possibly changing in brightness in the long term. Alpha Librae, to the south-east, is the second-brightest star in Libra and is a visual binary star system, with its companion in orbit at a distance of 5500 astronomical units, or 5500 times the average Earth–Sun distance. The brighter of the two is white in colour and the fainter one yellow. Both are just visible to the naked eye but are much easier to spot with binoculars.
To the south-west is the constellation of Scorpius and the unmistakable brilliance of the red supergiant star Antares. This area of sky is well known for its extensive emission and reflection nebulosity, which seems to have been formed by strong stellar winds blowing from Antares and ejecting some of its outer layers into space. The nebulosity is so extensive that it is engulfing nearby Rho Ophiuchi too.
To the south of Libra is the prominent constellation of Lupus, which is said to look like a wild animal being carried by the neighbouring constellation of Centaurus, the Centaur. Ten stars define the shape of Lupus, which is to all intents visible as a rather ragged rectangular shape to the south-east of Antares. Within the borders and just to the north of Zeta Lupi, one of the most southerly stars is a rather lovely double star system called Kappa Lupi, easily observed with binoculars as a pair of blue-white stars with the brightest visible to the naked eye. The pair are not in orbit around each other but they may well have formed out of the same cloud of gas and dust several billion years ago. Scan the sky with binoculars just to the south-east of Zeta Lupi this time and there is a beautiful open cluster of stars, NGC5822, which has around 120 members. This area of sky is rich with background stars of the Milky Way, but look carefully and another fainter cluster, NGC5823, lies just over a degree to the south.
Nearby to the south of Lupus is another unmistakably bright star, Alpha Centauri, which is a Sun-like yellow star, although it has a slightly cooler surface temperature of around 4990 degrees. The star is actually a triple star system composed of two close stars similar to the Sun and a third more distant, a faint red dwarf called Proxima Centauri. This is the nearest star to our own Solar System and is among the smallest stars, only a little larger than the planet Jupiter. Just to the east of Alpha Centauri is Hadar, a blue-coloured star, which gives a clue to its high surface temperature of around 25,000 degrees.
Like its bright companion to the west, Hadar is actually two stars which are individually undetectable to the naked eye. The two have similar properties and orbit each other over a period of around 357 days. They are both giant stars and, as with all stars of this size, have evolved rapidly, taking just 30 million years to get to a stage that will take the Sun around 10 billion years. Quite what will happen to these stars when they finally die is unknown but ultimately their decay is determined by their mass. They are thought each to have a mass around ten times that of the Sun, which could mean they will explode violently as supernovae or will fade gently away, releasing their outer layers into space. Hadar and Alpha Centauri are together known as ‘the Pointers’, because a line between them and extended through to the east points at Gacrux, or Gamma Crucis, the northernmost star of the Southern Cross. Gacrux and Acrux, the brightest star in the constellation, together point to the South Celestial Pole.
Over to the south-east of Alpha Centauri is a triangular constellation called Triangulum Australe. The angles of the triangle are marked by Atria, the brightest star in the constellation, over to the east, Beta Trianguli Australis at the most northerly angle, and Gamma Trianguli Australis, a star five times the diameter of the Sun, to its south-west. A rather nice yet faint open star cluster is found by following the direction of the triangle as it points to the north. It is given the name of NGC6025 and is easily visible with binoculars about 3 degrees to the north of Beta Trianguli Australis. Another triangle of stars can be seen to the south of Triangulum Australe but it is more elongated. The constellation is called Apus and is thought to represent a Bird of Paradise, but its stars are no brighter than 4th magnitude, making it unremarkable. Stars in the constellation of Octans even further to the south are not much brighter than those in Apus and it is within this constellation that we find the South Celestial Pole. One of its stars, Sigma Octantis, lies within 1.5 degrees of the pole and, although it is only just visible, at magnitude 5.4, it holds the title of the southern Pole Star, or Polaris Australis.