Linear equations
Linear equations take their name from the fact that their graph is a line. They are equations that contain the first power of a variable. No exponents or radicals are involved, and no variables show up in denominators. Linear equations can be simplified to the form ax +b = 0. Examples of simplified linear equations include 3x + 7 = 0 and
but before being simplified, they might look like 4x − 9 = 2x + 1 or −5(8 − y) = 2(y + 4) − 9. If an equation has more than one variable term and one constant term on either side of the equal side, take the time to simplify it before starting to solve.
Solving a linear equation is an inverse, or undoing, process. In the equation 3x + 7 = 0, the variable x was multiplied by 3 and then 7 was added. Solving the equation involves performing opposite operations—subtraction and division—in the opposite order.
Addition and subtraction equations
If y + 4 = 7, then you can find the value of y that makes the equation true by subtracting 4 from both sides of the equation to undo the addition.
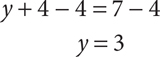
If the equation was formed by adding, you solve it by subtracting. If it was formed by subtracting, you solve it by adding. The equation p − 7 = 2 can be solved by adding 7 to both sides.
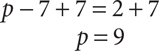
Solve each equation by adding or subtracting the appropriate number to both sides.
1. x + 8 = 12
2. y − 5 = 11
3. t + 3 = 6
4. w − 13 = 24
5. 
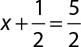
6. z − 2.8 = 10.3
7. 
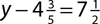
8. x + 14 = 8
9. y − 7 = −4
10. t + 3 = −4
Multiplication and division equations
The key to solving any equation is getting the variable all alone on one side of the equation. You isolate the variable by performing inverse operations. If the variable has been multiplied by a number, you solve the equation by dividing both sides by that number.
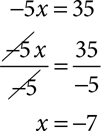
If the variable has been divided by a number, you multiply both sides by that number to find the value of the variable.
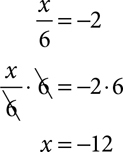
Solve each equation by multiplying or dividing both sides by the appropriate number.
1. 8x = 32
2. 
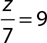
3. −5y = 42
4. 
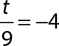
5. 1.5x = 45
6. 
7. 
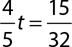
8. 
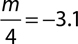
9. −1.3x = 3.9
10. 
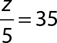
Two-step equations
Most equations require two or more operations to find a solution. The equation 4x – 5 = 19 says that if you start with a number x, multiply it by 4, and then subtract 5, the result is 19. To solve for x, you will need to perform the opposite, or inverse, operations in the opposite order. You are undoing, stripping away, what was done to x and working your way back to where things started. Undo the subtraction by adding 5.
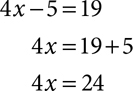
Then undo the multiplication by dividing by 4.
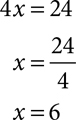
Solve each equation.
1. 3x − 7 = 32
2. −5t + 9 = 24
3. 4 − 3x = −11 (Rewrite as −3x + 4 = −11 if that’s easier.)
4. 9 + 3x = 10
5. 
6. −3x + 5 = −16
7. 
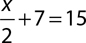
8. 11 − 3x = 9.5
9. 
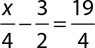
10. 2x − 7 = −23
Variables on both sides
When variable terms appear on both sides of the equation, add or subtract to eliminate one of them. This should leave a one- or two-step equation for you to solve.
Eliminate the extra variable term by adding or subtracting; then solve the equation.
1. 5x - 8 = x + 12
2. 11x + 18 = 3x - 14
3. 3x + 8 = 4x - 9
4. 9 - 4x = 16 + 3x
5. 2x - 5 = 3 - 4x
6. 8x - 17 = 12 + 3x
7. x - 3 = 2 - x
8. 1.5x - 7.1 = 8.4 + x
9. 7 - 9x = 7x - 19
10. -5x + 21 = 27 - x
Simplifying before solving
If the equation contains parentheses or has more than two terms on either side, take the time to simplify each side of the equation before you try to solve. If there is a multiplier in front of the parentheses, use the distributive property to multiply and remove the parentheses. Focus on one side at a time and combine like terms. There should be no more than one variable term and one constant term on each side of the equation when you start the process of solving by inverse operations.
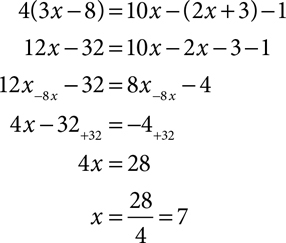
Simplify the left side and the right side of each equation. Leave no more than one variable term and one constant term on each side. Then solve each equation.
1. 5(x + 2) = 40
2. 4(x-7) + 6 = 18
3. 5(x-4) = 7(x-6)
4. 4(5x + 3) + x = 6(x + 2)
5. 8(x-4)-16 = 10(x-7)
6. 6(2x + 9)- 30 = 4(7x - 2)
7. 7(x-1) + 2x = 12 + 5(x +1)
8. 6(x-1)- 2x = 2(x +1)+4(2 -x)
9. 5(6x + 2)+7(4 - 12x) = 35 - (6+27x)
10. 8(2x - 5)- 2(x - 2) = 5(x + 7) - 4(x + 8)
Absolute value equations
An absolute value equation, with a variable expression inside the absolute value signs, isn’t actually a linear equation, but it’s closely related. The graphs of absolute value functions aren’t lines; they’re V-shaped. Absolute value equations will usually have two solutions. The expression between the absolute value signs may be equal to the expression on the other side of the equal sign, or it may be equal to the opposite of that expression.
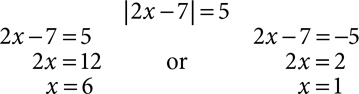
Always isolate the absolute value before considering the two cases. All terms other than the absolute value should be moved to the other side before you say that the expression in the absolute value signs could equal the other side or its opposite. If there are two or more terms on that side, be sure to form the opposite correctly by distributing the negative.
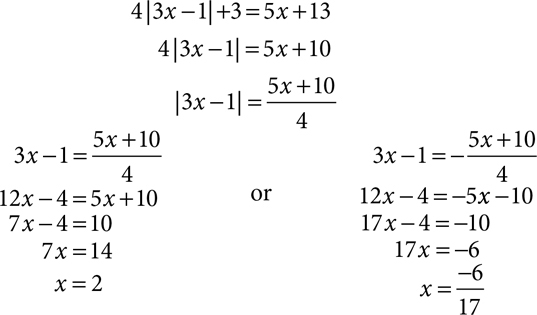
Each equation involves absolute value. Solve each equation by the method above.
1. |3x + 5| = 23
6. |30 + 3x| = 18x
2. |6x − 3| = 17
7. |40 − 2x| = 6x
3. |5x + 2| = 47
8. |3x − 11| = 8 + x
4. |3 + 6x| = 33
9. |8x − 2| = 2x + 22
5. |7 + 8x| = 51
10. |9x + 2| − 3x = 17 + x
Mixture problems: coffee, coins, and cars
Many of the problems you encounter in algebra fall into common types, and if you recognize the type and have a strategy for dealing with it, the problems are easier to solve. Often these problems are about mixing things. A merchant wants to mix different types of coffees or nuts. An amount of money is a mixture of different denominations of coins or bills. A laboratory is mixing chemicals in a solution, or a theater is offering different admission prices for adults and children. Even the famous “Two trains leave Chicago …” problems are mixing the distances traveled by the trains (or cars).
When you’re faced with a problem from this mixture family, you may find it easier to solve if you organize the information in a chart before you try to write and solve an equation. If a merchant is blending 10 lb of coffee, for example, you want a row for each of the individual coffees and the blend, and columns for pounds of coffee, price per pound, and total value. If you call the amount of one coffee x and the other 10 − x and you enter the per-pound price of each, you can multiply across to get the total value. The total value of the individual coffees should add up to the total value for the mixture, so your equation comes from adding down the last column.
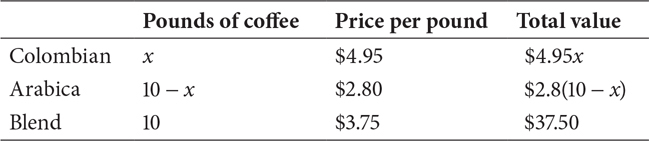
For coin problems, the column headings are number of coins and value of the coins, and the equation is formed the same way.
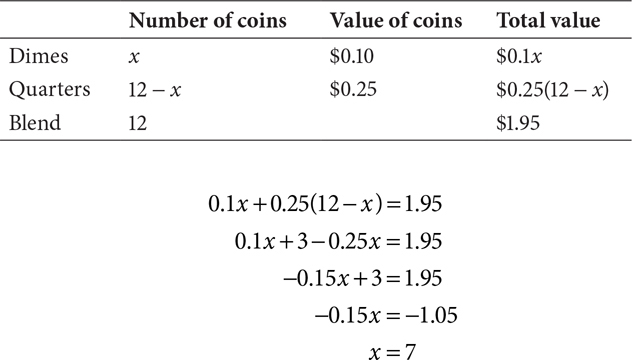
You end up with 7 dimes and 5 quarters.
The cars, trains, and planes take a little more analysis, but the setup of the problem is very much the same. You want a row in the table for each vehicle, and your column headings come from a familiar formula: rate (of speed) times time equals distance. Suppose two trains leave ÂChicago, traveling in opposite directions. One travels at 80 mph and the other at 75 mph. When will the trains be 1085 mi apart? Let x be the time it takes for this to happen.
Here’s where the little bit of extra thinking comes in. What do you do with the distances? Since the trains are going in opposite directions, you add the distances. If they were traveling in the same direction at different speeds and you wanted to know how far ahead the faster one had gotten, you’d subtract the distances they’d traveled. Draw a picture to help you imagine what’s happening in a particular problem.
Solve each problem by writing and solving an equation.
1. Jake had 12 coins in his pocket, totaling 95 cents. If the coins were all dimes and nickels, how many nickels did Jake have?
2. Two cars leave Omaha at the same time. One travels east at 55 mph and the other travels west at 65 mph. When are the cars 500 mi apart?
3. You decide to make 10 lb of a peanut-and-raisin mixture to sell at the class snack sale. You can buy peanuts for $2.50 per pound and raisins for $1.75 per pound. If you want to sell the mixture for $2 per pound, how many pounds of peanuts and how many pounds of raisins should you use?
4. The Fletcher family puts loose change into a jar every evening. Once a month, the family counts the coin and prepares to take it to the bank, but removes all the pennies first. Last month, they found there were 14 more quarters than dimes, and the number of nickels was 8 less than 4 times the number of dimes. If the total value of the nickels, dimes, and quarters was $15.75, how many dimes did they have?
5. Jessie and her friends pack a tailgate picnic and, at exactly 1 p.m., set out for the football game, driving at 35 mph. Half an hour after they leave the house, Jessie’s mom notices their picnic basket, fully packed, sitting on the driveway. She grabs the basket, jumps in her car, and drives at 40 mph, the legal limit. When will Mom catch up with Jessie?
6. Bert and Harriet collect quarters and pennies. When they wrapped coins to take to the bank, they had $42.50. If they wrapped a total of 410 coins, how many were pennies?
7. Admission to the school fair is $2.50 for students and $3.75 for others. If 2848 admissions were collected for a total of $10,078.75, how many students attended the fair?
8. Alisha designs a new tea blend by mixing Sweet Rose Tulsi tea with Orange Blossom green tea. Sweet Rose Tulsi tea sells for $4.98 an ounce and Orange Blossom green tea sells for $1.98 an ounce. If she wants to blend 16 ounces of the tea blend to sell for $4.23 per ounce, how many ounces of each tea should she use?
9. At precisely noon, one plane leaves New York, heading for Orlando, and another leaves Orlando, heading for New York. The distance from New York to Orlando is 1300 mi. The plane from New York flies at 450 mph and the Orlando plane flies at 490 mph. When will the planes be 125 mi apart?
10. I leave my family’s vacation cabin at 8 a.m. and start driving home at a nice, safe 45 mph. Two hours later, my husband, who always drives as fast as the law will allow, leaves the cabin and starts driving home at 65 mph. When can I expect him to pass me?
Calculator notes #2
To check the solution of an equation (or to approximate the solution(s) of an equation beyond your current skills), you can use the graphing functions of your calculator.
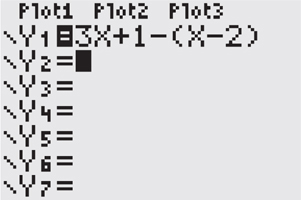
• Start by moving all the terms of the equation to one side, equal to zero. Simplify if you wish, but the calculator won’t care if you leave it messy.
• Graph the non-zero side by pressing 
, clearing any previous equations, and typing in the non-zero side of your equation.
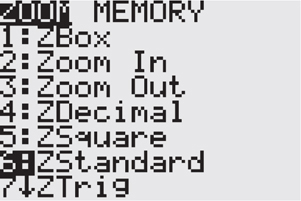
• Press 
and choose 6: ZStandard to set to the standard viewing window.
• Look to see where the graph crosses the x-axis. The x-intercept is where the expression you typed equals zero. (For certain types of equations, there may be more than one.) If the equation has no solution, there will not be an x-intercept, but before you decide that, zoom out or change window.
• Once you’ve located the x-intercept, move your cursor to the left of it. Press 
and choose 2: ZERO. Make sure your cursor is left of the x-intercept, press 
.
• Move to the right of the x-intercept, press .
• Move close to the x-intercept, press .
The coordinates of the x-intercept will display at the bottom of the screen. The x-coordinate is the solution of the equation.
