Plate Section

1. A Renaissance image of Aristotle: from The Triumph of St Thomas Aquinas (1471) by Benozzo Gozzoli. The book Aristotle is holding is his Metaphysics; the text, translated, reads: ‘A sign of those who know is that they can teach.’ Aristotle, with Galen and Ptolemy, was taken to be the basis of all knowledge of the natural world until the Scientific Revolution, and within universities he continued to be the basis of teaching until the end of the seventeenth century.

2. Richard of Wallingford (1292–1336) constructing a mathematical instrument, probably an astrolabe. Richard, an Oxford mathematician and abbot of St Albans, made sophisticated instruments and designed an important clock. He was the closest thing the medieval world had to what we would call a scientist; however, he assumed that mathematics could be employed to interpret the heavens but not the sublunary world, and he had no notion of the experimental method. His face is spotted with what his contemporaries believed to be leprosy.

3. The earth as envisaged in Oresme’s manuscript Du ciel et du monde (1377). Oresme took the idea of a rotating earth seriously, and thus prefigures Copernicus. The earth floats in space; one quarter of the sphere is habitable, but half of it is covered by water, and the remaining quarter represents terra or aqua incognita. Earth and water together make up what looks like a single globe, although they are in fact distinct spheres with different centres. Consequently, although Oresme can think of this globe as rotating, he cannot allow for the possibility of antipodes (areas of land separated by 180°) except along the equator.

4. The oldest surviving celestial globe, made in Valencia by Ibrâhim ’Ibn Saîd and his son Muhammad in year 478 of the Hegira (1085 of the Christian era). Arabic astronomy was highly sophisticated, and at least the equal of any Western astronomy until Copernicus – indeed, Copernicus may well have used technical solutions devised by Arab astronomers.

5. A late fifteenth-century equatorium and astrolabe. The equatorium (top) enables one to calculate the positions of the moon (using one of the inner circles), of Mercury and Venus (using another), and of Mars, Saturn and Jupiter (with the third). This would primarily have been used for astrology.

The astrolabe on the other side (above) calculates the position of the sun, tells the time from the height of the sun in the sky (if you know your latitude) or establishes your latitude from the height of the noon sun, shows which stars will be visible at any time and determines the direction of true north. This fine instrument must have belonged to a mathematician who, unless on a journey, would have used it primarily to tell the time. Such instruments, however well constructed, could not make sufficiently exact measurements or calculations to test the limits of Ptolemaic astronomy.

6. Waldseemüller’s world map of 1507, the first to include the name ‘America’, the first to show the New World as, in effect, a new continent, and the first to show antipodes. This map was crucial in destroying the two spheres theory, and in making Copernicanism possible. At the top are the figures of Ptolemy (with a map of the Old World) and Vespucci (with a map of the New).

7. The Ptolemaic, Copernican and Tychonic systems from Andreas Cellarius, Harmonia macrocosmica (1660), an atlas of star maps. The Ptolemaic system shows the earth at the centre, with, working outwards, the spheres of air, fire, the moon, Mercury, Venus, the Sun, Mars, Jupiter, Saturn, and the signs of the Zodiac.

The Copernican system shows the Sun at the centre, with, working outwards, Mercury, Venus, the Earth and the Moon, Mars, Jupiter with its moons, Saturn, and the fixed stars.

The Tychonic system shows the Moon and the Sun orbiting the earth, and the planets (with Jupiter’s moons shown) orbiting the Sun; but the text suggests that the outer planets orbit not the Sun but the earth – these are in fact two alternative versions of the system. At this date the Ptolemaic system was of historical interest (which is why it has not been updated to show Jupiter’s moons), but both the Copernican and Tychonic systems had their advocates.

8. Galileo’s Compasso geometrico et militare. While he was teaching at the University of Padua, Galileo made a significant income from teaching young gentlemen how to use the compasso (the proportional, or military, compass is commonly called a sector in English). Instruments of this general sort were common in the early seventeenth century, but Galileo’s were made especially for him and were perhaps the most sophisticated. A sighting device could be attached for measuring the elevation of objects at a distance; a plumb line could be attached for measuring the angle of elevation of a cannon’s barrel; and the scales on the arms could be used for mathematical calculations such as converting from one currency to another or a volume of wood into board feet. Thus Galileo’s sector was a primitive theodolite, slide rule and protractor all in one. Just as the astrolabe embodies the medieval application of mathematics to the heavens, the sector embodies the new technical skills of the mathematician applying himself to the world.

9. This seventeenth-century instrument, known as Galileo’s jovilabe, was used to predict the positions of Jupiter’s moons. Galileo certainly invented an instrument of this sort, and such instruments were common later in the seventeenth century, when they were used by the Cassinis, Rømer and Halley in their efforts to predict accurately the positions of the moons and so calculate longitude. The jovilabe allowed the modelling of a highly complicated theoretical system without endless calculations or any loss of precision.

10. Giotto, The Annunciation to St Anne, 1304, from the Scrovegni Chapel in Padua. The painting depends on the successful creation of a sense of depth, but note that the roof beams do not converge towards a vanishing point, and that there is considerable ambiguity about the spaces: where would you find yourself, for example, if you entered the room by the door? Although Giotto was perfectly capable of producing a geometrically legible space, doing so is not his primary concern. He sees the world qualitatively, not quantitively.

11. Ambrogio Lorenzetti’s Annunciation, 1344, originally in the town hall of Siena, is a very early example of the geometrical representation of space. The tiled floor establishes a spatial framework, although this is not maintained in the bodies of Mary and the angel or in the architecture. Lorenzetti portrays the moment when Mary becomes pregnant. The angel is saying, ‘Nothing is impossible for the word of God.’

12. Masaccio’s Holy Trinity, 1425, in Santa Maria Novella in Florence, is the earliest rigorous perspective painting to survive, and is evidently dependent on Brunelleschi’s studies. An altar originally stood in front of the fresco, marking the transition between the upper and lower portions. The lines Masaccio drew to plot out the composition on geometrical principles are still visible in the plaster.

13. Fra Angelico, Annunciation, 1451. Mary is told by the angel that she is about to become pregnant. The door beyond represents both the entry to Mary’s womb and the gates of Paradise. In this, 14 and 17, the vanishing point, incomprehensible in Aristotelian terms, is mysteriously obscured, showing how sensitive artists were to the clash between mathematics and philosophy.

14. Piero della Francesca, Annunciation c.1470, from the Polittico di Sant’Antonio. Piero, who was a mathematician as well as a painter, demonstrates his total command of perspectivist illusion and uses the vanishing point to convey God’s incomprehensibility.

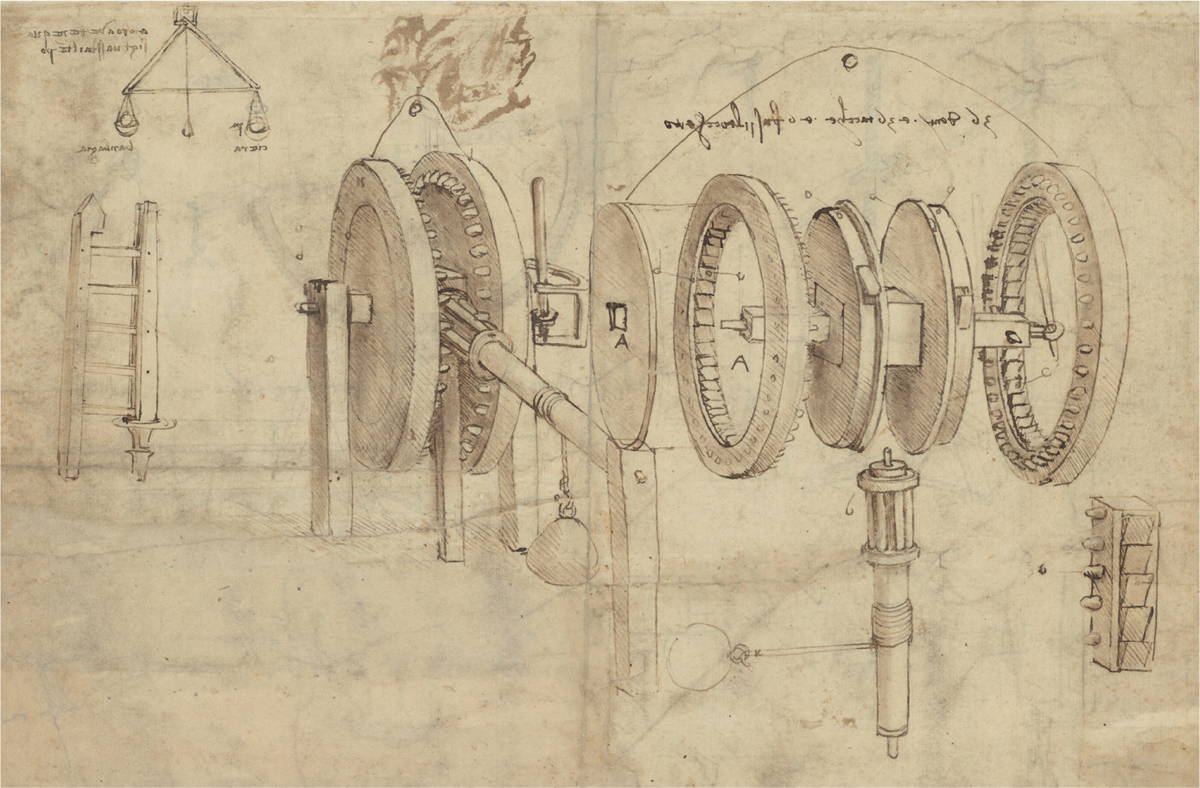
15. Leonardo da Vinci’s perspective drawing of a ratchet winch with exploded construction diagram, from the Codex Atlanticus (1478–1519), demonstrates the capacity of perspective to transform engineering.

16. Leonardo’s ‘perspectograph’, also from the Codex Atlanticus. The artist looks through a small hole at the object he wants to draw or paint. Between the hole and the object is a pane of glass on to which he can draw the outline of the object. The pane of glass thus constitutes the picture plane, and the image drawn on to it can then be copied on to another surface. This may have been Brunelleschi’s technique when he produced the first accurate perspective representation.

17. A view of an ideal city, after 1470, variously attributed (perhaps Fra Carenvale or Francesco di Giorgio Martini), and apparently commissioned for the palace of Duke Federico da Montefeltro of Urbino. The whole painting focuses the viewer’s attention on the vanishing point, and then playfully hides it behind a half-open door. The full mathematization of perspective is combined with a hint of the impossibility of a purely mathematical world.

18. This portrait of Luca Pacioli, often mistakenly attributed to Jacopo de’ Barbari, was apparently painted in 1495 (the slip of paper on the desk gives the date). Pacioli is teaching from Euclid, and a copy of one of his own books on mathematics is in the right foreground. This is how mathematics was taught in the Renaissance and indeed for centuries afterwards.

19. One of several portraits of Kenelm Digby by Anthony van Dyck. Digby, a friend of Hobbes and a founding member of the Royal Society, played a crucial role in popularizing the word ‘fact’. The sunflower is a symbol of constancy, and the portrait represents Digby in mourning for his wife, Venetia, who had died suddenly in 1633. The sunflower’s ability to follow the Sun could not be explained in Aristotelian terms, and Digby presented it (along with magnetism and the weapon salve) as a paradigmatic example of the problems addressed by the new science of experiment.